Programming molecular self-assembly of intrinsically disordered proteins containing sequences of low complexity

Abstract

Dynamic protein-rich intracellular structures that contain phase-separated intrinsically disordered proteins (IDPs) composed of sequences of low complexity (SLC) have been shown to serve a variety of important cellular functions, which include signalling, compartmentalization and stabilization. However, our understanding of these structures and our ability to synthesize models of them have been limited. We present design rules for IDPs possessing SLCs that phase separate into diverse assemblies within droplet microenvironments. Using theoretical analyses, we interpret the phase behaviour of archetypal IDP sequences and demonstrate the rational design of a vast library of multicomponent protein-rich structures that ranges from uniform nano-, meso- and microscale puncta (distinct protein droplets) to multilayered orthogonally phase-separated granular structures. The ability to predict and program IDP-rich assemblies in this fashion offers new insights into (1) genetic-to-molecular-to-macroscale relationships that encode hierarchical IDP assemblies, (2) design rules of such assemblies in cell biology and (3) molecular-level engineering of self-assembled recombinant IDP-rich materials.

Graphical abstract

A programmable model of membraneless organelles comprised of intrinsically disordered proteins (IDPs) containing sequences of low complexity has now been developed. The rules governing the assembly of archetypal IDPs into biologically inspired mixed-, layered- and size-controlled configurations provides a new means for understanding intracellular phase behaviour of IDPs.

Macromolecular interactions within multicomponent aqueous solutions enable the formation and partitioning of discrete aqueous phases, each of which harbours a distinct polymeric composition^1–3. Cells use a wide variety of protein-phase transitions to assemble and disassemble liquid-like focal bodies within membranes and the cytoplasm as a method to organize bioactivity^4–6. A variety of transient cytoplasmic aqueous protein phases that comprise diverse, unstructured polypeptides enriched with low-complexity domains^7–9 have been reported, including P bodies and granules, purinosomes, nuclear bodies and Cajal bodies^10–14. It is thus important to establish how subtle mutations in the protein sequence and chain length govern the design rules for encoding multicomponent intrinsically disordered protein (IDP)-rich bodies. Here we present a simple in vitro model for predicting and programming the intermolecular self-assembly of multicomponent protein-rich liquid phases that spans multiple length scales and architectures. Our investigation offers new means to (1) understand and predict multicomponent IDP-rich liquid phases that provide relevant insights into the principles that drive the organization of naturally occurring IDP assemblies, and (2) engineer new recombinant polypeptide assemblies that hold promise as bioinspired, functional materials for several important applications.

As they possess sequences of low complexity (SLCs) and are structurally similar to the IDPs in cellular assemblies⁹, we chose elastin-like polypeptides (ELPs) as model, archetypal IDP components to assemble a library of phase-separated structures, which includes multilayered, mixed and size-controlled protein droplets that span multiple length scales (Fig. 1a). Although ELPs and phase-separating intracellular IDPs differ substantially in their sequence composition, their sequences share three key features: (1) highly repetitive, (2) of low complexity and (3) enriched in a limited set of similar disorder-promoting amino acids), which leads to a high propensity for chain disorder in solution¹⁵. ELPs are SLCs that comprise pentameric repeats of Val-Pro-Gly-X₁-Gly, where X₁ is a guest residue that can be used to modulate protein-phase behaviour¹⁶. ELPs exhibit a lower critical solution temperature phase-transition behaviour in water; above their cloud-point transition temperature (T_t), they phase separate to form dense, protein-rich liquid assemblies termed coacervates^16–18. It is important that ELPs undergo simple coacervation—driven by a preference for homotypic self-interactions over protein–solvent interactions—as opposed to charge-mediated complex coacervation, in which oppositely charged species form coacervates in solution¹⁹. The relationship between the molecular parameters of a diverse family of ELPs—their guest residue, chain length and block architecture—and their aqueous solubility is well characterized as a function of temperature, concentration and the presence of cosolutes^18,20–24.

Figure 1. Programming of artificial liquid coacervates from ELPs.

a, Schematic of the temperature-triggered assembly of multilayered microscale coacervates (top) and coacervates with a programmable domain size generated within homogeneous microdrops that contain aqueous mixtures of ELPs encoded for coacervate self-assembly. b, Cloud-point transition temperature (T_t) as a function of volume fraction (ϕ)—the fraction of solution volume occupied by the ELP chains¹—for each ELP (E1–E4) as determined by temperature-controlled spectrophotometry. The solid line represents the best logarithmic fit for each ELP (Supplementary equations (1)–(5)).

Results

We designed and synthesized four model ELPs (denoted E1 through E4) and one diblock ELP sequence (D) for this study (Table 1 and Supplementary Table 1). These model ELPs display different phase behaviours (that is, miscibility and concentration-dependent cloud point) in water. We modulated, in a predictable fashion based on previous studies^17,18, the ELP phase behaviour by changing the guest residue (sequence composition) and molecular weight (Table 1). To increase the ELP T_t, we (1) substituted X₁ = Val with a less hydrophobic X₁ = Ala and (2) decreased the polypeptide molecular weight and/or chain length. This is illustrated by Fig. 1b, which graphically depicts the dependence of T_t on the protein volume fraction ϕ for E1–E4, as measured by temperature-controlled spectrophotometry. Here we converted the molar concentration of the solution of ELP to volume fraction ϕ by using a pentapeptide molar mass of M = 427 g mol⁻¹ (the mass of one Val-Pro-Gly-Val-Gly pentapeptide) and an ELP mass density of ρ = 1 g cm⁻³ (ref. 24). The data in Fig. 1b clearly illustrate that the solubility of ELPs depends on the following parameters: sequence, molecular weight and concentration.

Table 1.

Intrinsically disordered protein sequences herein.

Protein	Sequence	X1 or X2	N
E1	(VPGX1G)160	V	160
E1–40	(VPGX1G)40	V	40
E2	(VPGX1G)80	V50%,A50%	80
E3	[(VPGX1G)10-GKG]8	V80%,A20%	80
E4	(VPGX1G)80	A	80
D	(VPGX1G)80-(VPGX2G)80	V/S	160

X₁ and X₂ represents the tailorable guest residue within the canonical ELP motif that controls the ELP phase behaviour and N represents the number of ELP pentamer repeats. ELPs E1–E4 are numbered according to increasing T_t; E1–40 is an ELP generated by a reduction of the chain length of E1 by a factor of four; D is a diblock copolymer that comprises comparatively hydrophobic (X₁ = V) and hydrophilic (X₂ = S) blocks. The table shows only ELP sequences; Supplementary Table 1 gives full sequences of the proteins, including N-terminal leader and C-terminal trailer peptides.

We chose water-in-oil emulsion droplets as our model microenvironment to study ELP phase behaviour within simple cell-like compartments. We used a microfluidic emulsion droplet generator to create uniform, roughly cell-sized aqueous microdrops (Supplementary Fig. 2) that contained multiple ELP components. We controllably triggered ELP phase transitions within the microdrops by changing their temperature to generate a range of coacervate structures with controllable architecture, size and composition (Fig. 1a). Although temperature was used to control the phase state of the ELPs in this study (for example, soluble or phase separated), other means to control the protein-phase behaviour, such as concentration, cosolute concentration, ionization and pH can also be used to drive the phase separation of ELPs isothermally²⁵.

As the simplest case of ELP phase behaviour within microdrops, we first investigated the formation of a liquid coacervate sphere from a single-component ELP. We initiated a phase transition by heating aqueous emulsions that contain the protein designated E3. The heat stimulus triggered the phase separation of E3, and resulted in the formation of an aqueous two-phase system, the dynamics of which were readily observable within each microdroplet (Fig. 2a and Supplementary Movie M1). At 44 °C, a temperature well above the T_t of E3 (T_t = 37 °C at ϕ = 0.1), the incipient stages of a phase transition occur homogeneously throughout the droplets; this rapid and simultaneous formation of protein-rich mesoscopic domains suggests demixing through spinodal decomposition^1,26. As time proceeds, the clusters of concentrated phase coalesce with one another and grow in size until coarsening is complete, a phenomenon well described for phase-separating mixtures^1,27. After coarsening, each emulsion microdrop exhibits a monodisperse spherical core–shell arrangement in which the dark core is a dense protein-rich coacervate and the light shell is a protein-poor phase (Fig. 2a). The spherical shape of the protein-rich phase results from the surface tension between the two phases, which minimizes the interfacial area and so indicates the formation of a liquid concentrated aqueous protein coacervate²⁸. Cooling the two-phase droplets below the ELP T_t (to T = 30 °C) results in a rapid dissolution of the protein coacervates and reversion of each droplet to a homogeneous single phase (Fig. 2b and Supplementary Movie M1). Toggling between the homogeneous and two-phase core–shell aqueous structures can be repeated numerous times (Supplementary Movie M2), a process analogous to the reversible formation of protein assemblies within subcellular domains¹².

Figure 2. Reversible formation of ELP coacervates inside droplets by spinodal decomposition and resolubilzation.

a, Time-lapse dark-field microscopy images of thermally induced spinodal decomposition of E3 (ϕ = 0.1) within water microdrops; the phase-separated mesoscopic domains coarsen over time to form a single concentrated coacervate droplet (dark spherical centre) surrounded by a dilute protein solution. Insets are magnified images of the phase separation and coarsening of concentrated protein-phase domains (dark regions) in a protein-poor phase (light regions). b, Time-lapse images of coacervate dissolution on cooling. c, Lower critical solution temperature phase diagram of E3. The green points represent the phase boundary (the corresponding dashed line is from Supplementary equation (12)) and the black points represent the spinodal boundary (the corresponding dashed line is to guide the eye). Error bars represent the standard deviation of triplicate measurements.

To understand further the phase behaviour, we observed within the microdrops, we performed static light-scattering measurements on bulk aqueous solutions²⁹ to determine the phase diagram of E3 (Fig. 2c). In brief, the coexistence (binodal) point at a particular ELP concentration was determined by slow, stepwise heating until the first nucleation events were detected by the scattering autocorrelation function (ACF). In addition, the spinodal point at each concentration, thermodynamically defined as the boundary of instability above which instantaneous and rapid phase separation occurs, was determined by extrapolating to the temperature at which there is an infinite scattering intensity in a one-phase system (Supplementary Fig. 3)²⁹. The phase diagram for E3 (Fig. 2c) verifies that the phase separation observed in Fig. 2a takes place in the unstable region of the phase diagram in which spinodal decomposition occurs. Additionally, we used Fig. 2c to (1) develop a relationship between cloud point T_t data and the lower branch of the binodal boundary and (2) estimate the phase boundaries of single and multicomponent ELP solutions (Supplementary Fig. 6).

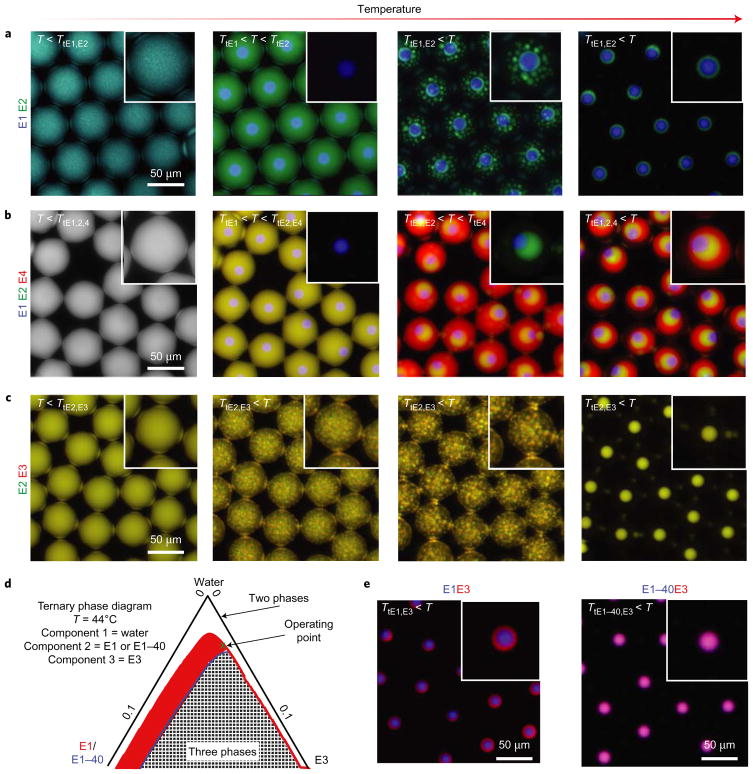
A recent report demonstrates the existence of multiphase vacuolated compartments in cells that contain orthogonally phase-separated regions, each of which strikingly comprises TDP43 IDPs with ~95% sequence similarity³⁰. To understand further and predict the phase separation of multicomponent solutions of ELPs based on their sequences, and to produce synthetic models of naturally occurring IDP-rich coacervate assemblies, we made microdrops containing combinations of ELPs–We hypothesized that it would be possible to form layered core–shell coacervates from solutions of two ELPs, depending on their sequence, molecular weight and concentration. We heated microdrops that contained E1 and E2, which have well-separated cloud-point curves (Fig. 1b) in a stepwise manner to induce successive spinodal decomposition of E1 followed by E2, which resulted in a multilayered coacervate (Fig. 3a) in which each ELP coacervate layer is immiscible with the other. Biological analogues of these structures, which include cellular coacervates such as stress granules and nucleolus bodies, have been shown to exist as multilayer arrangements^30–32. To demonstrate that E1 and E2 coacervate immiscibility is encoded by the ELP sequences and independent of the heating profile, we rapidly heated droplets of E1 + E2 + water to co-precipitate both ELPs into transient patchy coacervates with distinct immiscible E1 and E2 microcompartments (Supplementary Fig. 4 and Supplementary Movie M3). Additional ELPs introduced into the system can result in the formation of n-layered coacervates, where n is the number of immiscible ELP components. For example, we programmed the formation of a three-layer coacervate sphere within microdrops utilizing a quaternary E1 + E2 + E4 + water system (Fig. 3b). In contrast to aqueous mixtures of E1 and E2, heating an aqueous solution of E2 and E3 results in fully miscible coacervates that comprise a homogeneous mixture of E2 and E3 (Fig. 3c). Combining mixtures of E1 + E2 + E3 enables the formation of a single-component E1 coacervate engulfed by a shell that comprises a mixed E2 and E3 coacervate (Supplementary Fig. 5). Our observations indicate that after 48 hours, these layered and mixed structures remained intact, which suggests that they are thermodynamically equilibrated stable phases.

Figure 3. Multicomponent solutions of ELPs enable the formation of layered and mixed coacervates.

a,b, Fluorescence microscopy images of the formation of hierarchically structured coacervates—double-layered coacervates made of blue-labelled E1 (ϕ = 0.01) and green-labelled E2 (ϕ = 0.03) (a), and triple-layered coacervates made of blue-labelled E1 (ϕ = 0.01), green-labelled E2 (ϕ = 0.03) and red-labelled E4 (ϕ = 0.05) (b). c, Mixed coacervates made of miscible green-labelled E2 (ϕ = 0.03) and red-labelled E3 (ϕ = 0.03). d, Ternary phase diagrams of the unstable regions of mixtures of E1 + E3 (red) and E1–40 + E3 (blue line and grey-and-white grid, respectively) at T = 44 °C demonstrate that the three-phase region shrinks as the E1 chain length decreases, resulting in coacervate miscibility. (Only the region that comprises 85–100% v/v water is shown and the axes numbers represent the ELP volume fraction. Supplementary Fig. 7 shows the full diagram.) e, Equilibrium coacervate structures of phase-separated mixtures that contain combinations of blue-labelled E1 + red-labelled E3 and blue-labelled E1–40 + red-labelled E3 above their respective T_t values (T = 44 °C for each image; ϕ_E1 = ϕ_E1–40 = 0.01; ϕ_E3 = 0.03). Insets in the micrographs show magnified views; for all the insets with Tt < T only the coacervates are depicted.

To investigate further how the ELP sequence encodes coacervate (im)miscibility, we studied how the molecular weight and composition of ELPs can be tuned in an ELP ternary mixture to design rationally either immiscible layered or miscible mixed coacervates using a model system of two ELPs with dissimilar cloud points, E1 and E3. We developed a framework to understand coacervate (im)miscibility based on the classical Flory–Huggins (FH) mean-field theory, which describes the intermolecular interactions between different ELP monomers in solution and predicts the phase diagram of ternary E1 + E3 + water systems (Supplementary equations (6)–(20) and Supplementary Figs 6 and 7). The landscape of the multicomponent free energy of mixing per lattice site, which consists of entropic and energetic contributions, is dependent on the ELP chain length (N), composition (ϕ) and pairwise interaction parameters (χ_ij) with the solvent (χ_E1,water and χ_E3,water) and between ELPs (χ_E1,E3). Here, the FH interaction parameter χ_ij quantifies the free-energy differences when molecules exchange homologous interactions for heterologous ones¹.

In the E1 + E3 + water ternary system, we estimated χ_ij values using surface-tension scaling²⁴ (Supplementary equations (6)–(15)) and FH approximations to generate a ternary phase diagram (Supplementary equations (16)–(20)). We chose an operating point (that is, volume fractions of ϕ_E1 = 0.01 and ϕ_E3 = 0.03) inside the three-phase region for E1 + E3 + water (Fig. 3d and Supplementary Fig. 7), which corresponds to immiscible two-layered coacervates within microdrops (Fig. 3e and Supplementary Fig. 8). To investigate how ELP chain length modulates E1 + E3 coacervate miscibility, we reduced the chain length of E1 by a factor of four to generate an ELP that we term E1–40 (N_E1–40 = 40 and N_E1 = 160). The reduction in chain length enhances the mixing entropy and noticeably reduces the size of the three-phase region of the phase diagram (Fig. 3d and Supplementary Fig. 7). Experimentally, the reduction of the three-phase region corresponds to a striking shift in the assembly of immiscible two-layer coacervates in the case of E1 + E3 + water (Fig. 3e and Supplementary Fig. 8) to miscible mixed coacervates in the case of E1–40 + E3 + water (Fig. 3e and Supplementary Fig. 9) despite no change in the ELP surface tension. Note that in the E1 + E1–40 + water ternary system, E1 and E1–40 form mixed coacervates (Supplementary Fig. 9) because E1 and E1–40 are chemically indistinguishable at the monomeric level. Thus, in addition to adjusting the mixing energy of ELPs via their chemical composition, tailoring (1) the ELP volume fraction and (2) the mixing entropy of ELPs through the protein chain length provides simple, yet powerful, approaches to programme the coacervate (im)miscibility of a diverse set of ELPs.

To extend the range of coacervate sizes across multiple-length scales, we incorporated a diblock ELP (termed D (see Table 1 and Fig. 4a)) in which the more hydrophobic block comprises Val-Pro-Gly-Val-Gly pentameric repeats, matching those of E1, and the second block is tuned to be more hydrophilic by selecting the guest residue to be Ser (for example, pentameric repeats of Val-Pro-Gly-Ser-Gly). The amphiphilic nature of D enables its self-assembly into monodisperse nanoscale micelles (~56 nm) on heating above its critical micellization temperature (T_CMT ~304 K of D and E1 within microdrops and induced simultaneous micellization and E1 phase separation by heating above the cloud point of E1 and T_CMT (Fig. 4b and Supplementary Movie M4). In contrast to droplets containing only E1, diblock D acts as a surfactant by stabilizing the interface between the E1 coacervate and the dilute phase to resist coacervate coarsening. Izzo and Marques showed how diblock copolymers can solubilize homopolymers in a poor solvent within the cores of the micelles (to result in structures termed puncta in this study) in a concentration-dependent manner³³. The size of the phase-separated puncta can be programmed to span the nanoscale, mesoscale and microscale by controlling the amount of available D surfactant. The coacervate domain size increases with increasing the E1:D ratio (Fig. 4b,c). It is important that D (fluorescently labelled but, for clarity, false coloured as black in Fig. 4b,c) is distributed outside the E1 coacervates, as well as at the coacervate–dilute phase interface. (Supplementary Figs 12–14 show the distribution of fluorescently labelled D in multicomponent solutions.) The D-stabilized E1 puncta exhibit stability for at least 24 hours (Supplementary Fig. 11) and have a narrow size distribution (Fig. 4c).

Figure 4. Amphiphilic proteins kinetically arrest coalescence of ELPs during phase separation to produce uniform nano-, meso- and microscale puncta.

a, Schematic showing sequences of D (diblock, left) and E1 (right). b, Fluorescence microscopy images of water droplets that contain different ratios of D (shown as black, variable concentration) and blue-labelled E1 (ϕ = 0.01). c, D arrests the coarsening of E1 domains during the phase separation at 44 °C by acting as a surface-stabilizing agent. The T_CMT is that of D. The diameters of the resultant protein puncta for different E1/D ratios are shown as percentage plots. Insets in the micrographs show magnified views. d, Diameter of E1 and E2 puncta stabilized by D diblocks as a function of the E1/E2:D ratio. e, Confocal microscopy image of coexisting populations of blue-labelled E1 puncta and green-labelled E2 puncta in the presence of D. The volume fractions of E1, E2 and D are ϕ_E1 = ϕ_E2 = ϕ_D = 0.01. at ϕ_D = 0.01) (Supplementary Fig. 10)²². We encapsulated a mixture

We repeated the above experiments with E2 instead of E1 to investigate whether or not D could stabilize E2 puncta because the hydrophobic block of D and E2 has a large free energy of mixing. In this system, D also arrested the coarsening of E2, but at larger puncta diameters (Supplementary Fig. 12) when compared with those of E1:D mixtures at the same molar ratios (Fig. 4d and Supplementary Figs 12 and 13), presumably because of the increased free energy of mixing between the hydrophobic block (VPGVG)₈₀ of D and E2. We also mixed E1 and E2 (which form immiscible coacervates by themselves under the conditions studied) with D to enable multimodal populations of protein coacervates within a single suspension (Fig. 4e). Simple changes in the stoichiometric ratios of the quaternary system of E1 + E2 + D + water enabled us to create distinct orthogonally phase-separated populations of microscale puncta that contained either E1 or E2 (Fig. 4e and Supplementary Fig. 14) and a single E1 coacervate that coexists with numerous smaller E2 microscale puncta (Supplementary Fig. 14).

Discussion

Cells probably employ subtle changes in the amino acid composition and concentration (and resultant phase behaviour) of IDPs to control their coacervation and compartmentalization locally³⁴. This was demonstrated recently within Xenopus laevis cells that contain layered immiscible RNA/IDP-rich coacervates within their nucleoli³¹. We have developed a simple model system that recapitulates such phenomena in vitro and enables in-depth studies of the phase separation of minimal genetically encodable IDPs that can be completely and rationally tunable at the sequence level within droplet microenvironments to understand and build a new range of coacervate architectures (that is, multilayer, mixed coacervate and puncta (Supplementary Fig. 15). We showed that FH mean-field theory is a robust method for generating interpretive frameworks of multicomponent phase-separated IDP assemblies. Such analyses will enable the prediction and design of the reversible self-assembly of highly uniform coacervates of controllable number, size and hierarchical structure by providing multicomponent phase diagrams of the expected phases/geometries based on the bulk characterization of individual IDPs. Our observations indicate that for the archetypal class of IDPs studied here (ELPs), sequence composition, molecular weight and concentration (volume fraction) all influence the (im)miscibility of their coacervates. The rules that govern phase-separated ELP–ELP interactions are summarized as follows: (1) ELP chains with a highly similar amino acid content tend to lead to mixed coacervates, (2) ELPs with a dissimilar amino acid content tend to lead to layered coacervates; (3) ELPs with dissimilar amino acid content can be miscible when phase separated by decreasing the molecular weight of one or both species, which leads to mixed coacervates, and (4) sufficiently amphiphilic polypeptide chains can act as surfactants to stabilize liquid coacervates from coalescing. These rules and the presented sequence-encodable assemblies (single, layered, mixed and size-controlled) provide a new platform to (1) investigate further how biology compartmentalizes IDP-rich coacervates within cells by studying their phase behaviour in similar in vitro systems and (2) to design new biologically inspired IDP-based biomaterials for a wide variety of applications and engineered systems.

Methods

Gene synthesis

Genes that encode for the proteins used in this study were constructed using plasmid reconstruction by recursive directional ligation, a method described previously³⁵. To summarize, we modified a pET-24+ cloning vector to contain endonuclease recognition sites for AcuI, BseRI and BglI. We digested the modified vector with BseRI and ligated the desired ELP (or any inserted domain) sequence into the vector. The ELP sequence was created by annealing together complementary ssDNA chains that encode for the desired amino acid sequence with ‘sticky end’ overhangs. The vector that contained the ELP sequence was then digested with (1) AcuI and BglI to create an ‘A’ population and (2) BseRI and BglI to create a ‘B’ population. The two cut vectors are complementary to one another such that when ligated together the monomer sequence doubles in length. This process was continued until the desired length of protein was achieved. The same procedure was applied for the insertion of leader and trailer motifs. The genes that encode for the final sequences of E1–E4 and D were confirmed by DNA sequencing.

Protein expression and purification

The genes that encode for E1–E4 and D (Supplementary Table 1 for the full amino acid sequences) were transformed into chemically competent Escherichia coli BL21 cells. The cells were incubated overnight and one colony per sequence was used to inoculate a starter culture of sterilized Terrific Broth media supplemented with 45 μg ml⁻¹ kanamycin. The starter culture was shaken overnight at 37 °C and 220 revolutions per minute (r.p.m.). The starter culture was then used to inoculate sterilized Terrific Broth media in 4 l glass flasks, each containing 1 l of media supplemented with 45 μg ml⁻¹ of kanamycin. The media was then shaken at 37 °C and 220 r.p.m. for 6–8 h before induction with 0.1 mM isopropyl-β-D-thiogalactoside. The cultures were subsequently shaken for 12–14 h at 37 °C and 220 r.p.m. before harvesting and centrifuging at 4 °C and 3,000 r.p.m. for 10 min. The resultant cell pellets were used to remove and purify the proteins.

We purified the proteins from harvested cells by lysing the cells via sonication to release the proteins. We then removed the impurities using inverse transition cycling, a method described elsewhere¹⁶. This method takes advantage of the controlled and reversible aqueous-phase transition from soluble to insoluble inherent to ELPs. This is done by cyclic centrifugation steps at high and low temperatures in water. In most cases, three rounds of centrifugation were sufficient to remove >95% of impurities.

Light scattering

Dynamic and static light-scattering (DLS and SLS, respectively) measurements of ELP protein solutions were performed using an ALV/CGS-3 goniometer system. Samples for the ALV/CGS-3 goniometer system were prepared in PBS at varying concentrations and filtered through 0.22 μm Millex-GV filters into a 10 mm disposable borosilicate glass tube (Fischer). The temperature of the tubes was controlled to within ±0.1 °C.

Coexistence curve (binodal) measurement

To estimate the coexistence curve, ELP solutions of known concentrations were placed in the light-scattering spectrometer and the temperature was initially fixed to be well below the cloud-point temperature. To estimate the coexistence line, we raised the temperature in 0.1 K increments, which allowed time for the temperature to stabilize, and subsequently maintained the sample at a given temperature for at least 15 min. For each temperature step, we observed the DLS ACF in real time. If no new ACF peaks were observed, we increased the sample temperature by 0.1 K and repeated the above protocol. On observation of a secondary DLS ACF peak, which corresponds to the onset of nanocoacervates because of nucleation and growth, the temperature was lowered slightly until the solution clarified and both ACF and the average scattering-intensity fluctuations returned to the appropriate values observed prior to the onset of nucleation. We performed this procedure in triplicate to obtain error estimates. Nucleation and growth clouding were further substantiated by visual observation of the sample in which turbid regions interspersed with transparent regions within the solution vial.

Spinodal curve measurement in binary solutions

The spinodal of two-component solutions (that is, ELP–water) is located in the two-phase region of the phase diagram. It separates the region with a metastable homogeneous state from the region in which the homogeneous state is unstable. In both cases the two-phase state is thermodynamically more favourable. In the metastable region, a free-energy barrier delays the phase separation that proceeds by nucleation and growth of the dense phase, whereas in the unstable region with the absence of the barrier, phase separation proceeds by spinodal decomposition¹. The intensity, I, of the scattered light measured at a single scattering angle of ϕ = π/2 was recorded as a function of temperature. As the temperature of the sample is raised so that the spinodal curve is approached, this intensity increases dramatically. Reciprocal SLS intensity is plotted as a function of temperature (Supplementary Fig. 3). The spinodal temperature is determined as the point at which the extrapolated line through the data intersects the temperature axis. Conceptually, this corresponds to an infinite scattering intensity and represents the inflection points of the composition dependence of the free energy, where the second derivative of the free energy with respect to composition is zero^29,36.

Data availability

All the data presented and analysed in this study are either included in this article or in the Supplementary Information, which includes the materials used, methods used, theory development, Supplementary Figs 1–15, Supplementary Movies M1–4 and references.