INCORPORATING THE LENGTH-DEPENDENT PASSIVE-FORCE GENERATING MUSCLE PROPERTIES OF THE EXTRINSIC FINGER MUSCLES INTO A WRIST AND FINGER BIOMECHANICAL MUSCULOSKELETAL MODEL

Abstract

Dynamic movement trajectories of low mass systems have been shown to be predominantly influenced by passive viscoelastic joint forces and torques compared to momentum and inertia. The hand is comprised of 27 small mass segments. Because of the influence of the extrinsic finger muscles the passive torques about each finger joint becomes a complex function dependent on the posture of multiple joints of the distal upper limb. However, biomechanical models implemented for the dynamic simulation of hand movements generally don’t extend proximally to include the wrist and distal upper limb. Thus, they cannot accurately represent these complex passive torques. The purpose of this short communication is to both describe a method to incorporate the length-dependent passive properties of the extrinsic index finger muscles into a biomechanical model of the upper limb and to demonstrate their influence on combined movement of the wrist and fingers. Leveraging a unique set of experimental data, that describes the net passive torque contributed by the extrinsic finger muscles about the metacarpophalangeal joint of the index finger as a function of both metacarpophalangeal and wrist postures, we simulated the length-dependent passive properties of the extrinsic finger muscles. Dynamic forward simulations demonstrate that a model including these properties passively exhibits coordinated movement between the wrist and finger joints, mimicking tenodesis, a behavior that is absent when the length-dependent properties are removed. This work emphasizes the importance of incorporating the length-dependent properties of the extrinsic finger muscles into biomechanical models to study healthy and impaired hand movements.

1. Introduction

The forces produced by soft tissue structures that surround a joint (including passive muscles) play a crucial role in the control and stabilization of dynamic movements of low mass and inertia systems. Experimental work on biomechanical systems ranging from insect legs to human wrists (Charles and Hogan, 2012; Hooper et al., 2009; Souza et al., 2009; Wu et al., 2012) has demonstrated that passive viscoelastic forces, and the joint torques that result, influence dynamic movement trajectories of low mass systems more than the momentum and inertia of the segments.

Comprised of 27 bones with masses ranging between 0.002 and 0.04 kilograms (Le Minor and Rapp, 2001; McFadden and Bracht, 2003; Mirakhorlo et al., 2016; Saul et al., 2015), the hand is a small mass and inertia system. As a result, the inclusion of passive viscoelastic forces are critical for the simulation of controlled dynamic movements of the hand and fingers (Esteki and Mansour, 1997; Kamper et al., 2002). Passive viscoelastic forces in the hand are produced by soft tissue structures, either those that act within the hand (e.g., ligaments, joint capsules, skin, and intrinsic finger muscles) or the extrinsic finger muscles, which originate proximally, cross the wrist, and attach distally on the fingers (Knutson et al., 2000; Kuo and Deshpande, 2012). Because the force a muscle produces depends on length, it varies as a function of the posture of every joint the muscle crosses. Thus, forces produced by the passive extrinsic finger muscles are a complex, multi-dimensional function of joint postures of the distal upper limb (Bhardwaj et al., 2011; Knutson et al., 2000; O’Driscoll et al., 1992; Richards et al., 1996).

Biomechanical models that are implemented for dynamic simulations of finger movements include passive torques about each finger joint; however, most commonly these models exclude the wrist and distal upper limb (e.g. Babikian et al., 2016; Brook et al., 1995; Esteki and Mansour, 1997; Goislard de Monsabert et al., 2012; Kamper et al., 2002; Li and Zhang, 2009; Sancho-Bru et al., 2003; Sancho-Bru et al., 2001). While previous simulation work integrating the wrist and hand included active muscle properties that varied with proximal joint posture, the passive viscoelastic torques about each finger joint were defined as a function of a single joint, independent of other joint postures (Adamczyk and Crago, 2000). Here, we incorporate the length-dependent passive forces of the extrinsic index finger muscles into a biomechanical model of the hand and demonstrate their influence on combined passive movements of the wrist and hand.

2. Methods

2.1 Dynamic biomechanical musculoskeletal model development

A dynamic biomechanical model was developed in OpenSim v3.2 (Delp et al., 2007) by adapting an existing dynamic model of the upper extremity (Saul et al., 2015). The original model included the kinematics of the shoulder, elbow, and wrist, without additional degrees of freedom distal to the wrist. As described previously (Blana et al., 2016), the kinematics of the original model were augmented to include degrees of freedom for digits 1 (thumb) through 5 (pinky finger) (Figure 1). Mass and inertia properties of the individual hand bone segments were distributed (Le Minor and Rapp, 2001; McFadden and Bracht, 2003) such that the sum of the individual bones are equal to the total mass of the hand segment from Saul et al., 2015 (Table 1). Because critical data needed for the hand model (e.g., moment arms, passive joint torques) currently only exist for the index finger (digit 2), the simulations of wrist and hand movement described here only involve the index finger. Muscle-tendon paths of the four extrinsic index finger muscles, flexor digitorum superficialis indices (FDSI), flexor digitorum profundus indices (FDPI), extensor digitorum communis indices (EDCI), and extensor indicis proprius (EIP), defined by Saul et al. (2015) were edited so that the moment arms replicated experimental data about the metacarpophalangeal (MCP), proximal-interphalangeal (PIP), and distal-interphalangeal (DIP) joints of the index finger (Figure 2) (Buford et al., 2005; Fowler et al., 2001).

Figure 1.

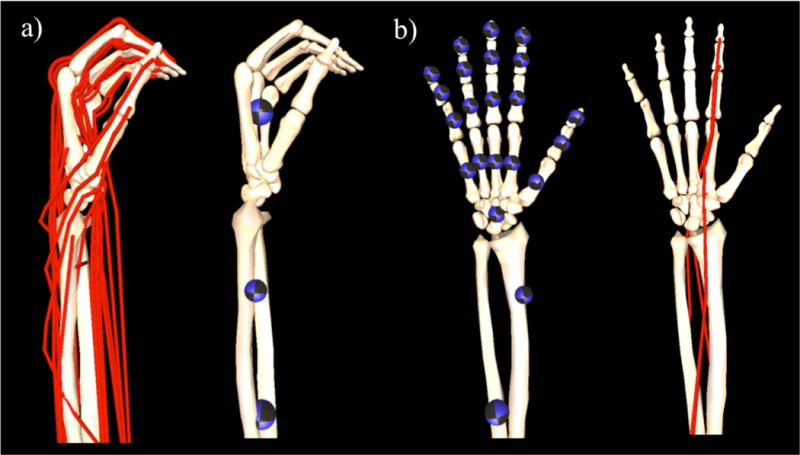
To enable simulation of combined wrist and finger motions, (a) the kinematic tree of the dynamic model described in Saul et al. (2015) was augmented to (b) include the degrees of freedom and kinematics of the fingers, thumb, and carpal-metacarpal joints. Location of the colored spheres represent the location of center of mass of each individual segment in the distal upper limb within the original model (Saul et al., 2015) and the adapted model; the diameter of each sphere indicates the mass of the modeled segment (see Table 1). Red lines represent simulated muscle-tendon paths within the model; for the purposes of this study, we only included the extrinsic muscles of the index finger.

TABLE 1.

INTERIAL PARAMETERS FOR BONE SEGMENTS

Segment	Mass (kg)	Center of Mass in Segment Reference Frame (m)			Inertia about Center of Mass (kg m)
		Rx	Ry	Rz	Ixx	Ixy	Ixz	Iyy	Iyz	Izz
Carpal Bones*	0.3274	−0.0003	0.0033	−0.0045	1.51E−05	0.00E+00	0.00E+00	3.37E−05	0.00E+00	3.96E−05
First metacarpal	0.0160	0.0078	−0.0147	−0.0060	2.38E−06	9.44E−07	5.02E−07	1.42E−06	−8.17E−07	2.52E−06
Second metacarpal	0.0364	0.0000	0.0000	0.0000	9.78E−06	1.45E−06	−2.40E−07	5.29E−07	1.56E−06	9.74E−06
Third metacarpal	0.0381	0.0000	0.0000	0.0000	8.89E−06	1.28E−07	−1.68E−08	2.95E−07	1.12E−06	8.74E−06
Fourth metacarpal	0.0333	−0.0020	−0.0214	0.0034	6.85E−06	−7.04E−07	1.00E−07	3.49E−07	9.37E−07	6.79E−06
Fifth metacarpal	0.0296	−0.0061	−0.0177	0.0054	4.77E−06	−1.06E−06	2.23E−07	5.73E−07	9.36E−07	4.82E−06
Thumb proximal phalanx	0.0079	0.0096	−0.0163	−0.0063	5.21E−07	1.89E−07	7.52E−08	3.19E−07	−1.25E−07	5.85E−07
Thumb distal phalanx	0.0031	0.0056	−0.0104	−0.0044	9.21E−08	2.84E−08	1.31E−08	6.45E−08	−2.09E−08	1.00E−07
Second proximal phalanx	0.0158	0.0044	−0.0253	0.0040	2.41E−06	3.31E−07	−6.25E−08	5.63E−07	3.59E−07	2.40E−06
Second middle phalanx	0.0049	0.0022	−0.0154	0.0002	2.83E−07	2.39E−08	−1.13E−09	7.30E−08	1.01E−08	2.85E−07
Second distal phalanx	0.0018	0.0013	−0.0100	0.0000	4.55E−08	5.53E−09	−5.75E−10	1.58E−08	3.20E−09	4.62E−08
Third proximal phalanx	0.0193	0.0010	−0.0262	0.0037	3.52E−06	8.59E−08	−6.42E−09	6.16E−07	2.17E−07	3.51E−06
Third middle phalanx	0.0064	0.0007	−0.0168	0.0013	5.25E−07	1.99E−08	−8.17E−10	1.01E−07	1.74E−08	5.25E−07
Third distal phalanx	0.0025	0.0005	−0.0102	−0.0003	8.08E−08	4.06E−09	−3.80E−10	2.65E−08	5.10E−09	8.06E−08
Fourth proximal phalanx	0.0137	−0.0022	−0.0238	0.0035	1.95E−06	−2.02E−07	2.31E−08	3.91E−07	1.81E−07	1.96E−06
Fourth middle phalanx	0.0057	−0.0020	−0.0147	0.0012	3.60E−07	−2.37E−08	2.13E−09	9.43E−08	2.41E−08	3.60E−07
Fourth distal phalanx	0.0029	−0.0004	−0.0102	0.0020	9.91E−08	−5.72E−09	1.26E−09	3.64E−08	1.39E−08	9.65E−08
Fifth proximal phalanx	0.0111	−0.0081	−0.0211	−0.0021	1.18E−06	−3.28E−07	2.81E−08	3.72E−07	7.93E−08	1.29E−06
Fifth middle phalanx	0.0037	−0.0049	−0.0121	−0.0002	1.57E−07	−4.00E−08	3.69E−09	6.14E−08	1.01E−08	1.70E−07
Fifth distal phalanx	0.0022	−0.0036	−0.0089	0.0003	5.06E−08	−1.24E−08	1.15E−09	2.89E−08	2.53E−09	5.59E−08

Figure 2.

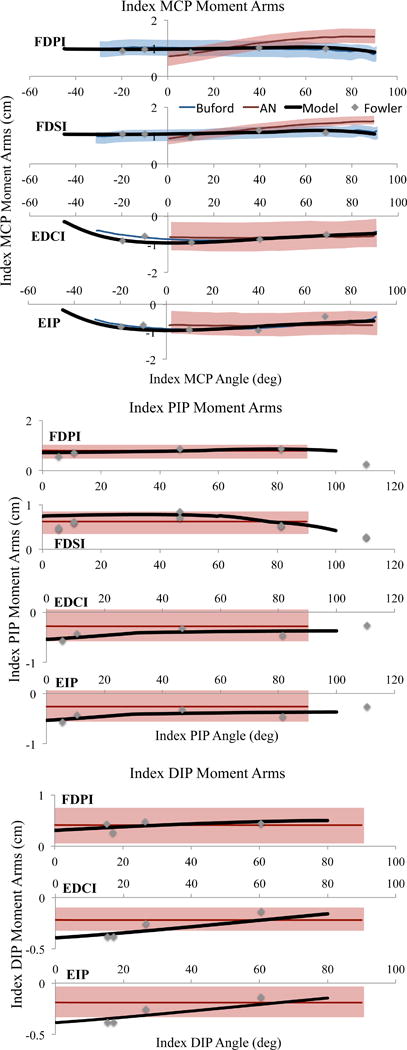
Moment arm data about the metacarpophalangeal (MCP), proximal interphalangeal (PIP), and distal interphalangeal (DIP) joints of the current model (solid black), Buford et al. (blue line), An et al. (red line), and Fowler (grey diamonds) of the flexor digitorum superficialis indices (FDSI), flexor digitorum profundus indices (FDPI), extensor digitorum communis indices (EDCI), and extensor digitorum proprius (EIP) muscles. Shaded area indicates two standard deviations when data was available.

Passive force-generating properties of the extrinsic muscles were simulated by scaling a generic, Hill-type muscle-tendon model (Millard et al., 2013). Force-generating parameters were taken from Saul et al. with the exception of tendon slack lengths (L_ts). L_ts was optimized (Table 2) to replicate length-dependent, passive force-generating properties of the extrinsic finger muscles determined experimentally (see section 2.2). L_ts was chosen as the optimization parameter because when all other parameters are held constant for a given muscle-tendon actuator, L_ts alters the relationship between joint position and fiber length, influencing the passive muscle forces produced over a given range of joint motion (Arnold et al., 2010; Holzbaur et al., 2005).

TABLE 2.

OPTIMIZED TENDON SLACK LENGTHS AND PRECENT CHANGES

	FDPI	FDSI	EIP	EDC
Initial tendon slack length	0.3015	0.275	0.21	0.365
New optimized tendon slack length	0.3044	0.2772	0.1911	0.3486
Percent change	0.95%	0.79%	−9.89%	−4.70%

Of note, to improve both computational efficiency and numerical stability, the default, normalized, active force-generating curve $\left({\stackrel{\sim }{f}}_a\left({\stackrel{\sim }{l}}_m\right)\right)$ in the “Millard2012EquilibriumMuscle” model, recommended for general use in OpenSim, yields small active forces at fiber lengths where no active force can be generated (e.g., normalized force = 0.1, 10% of maximum isometric force, at normalized fiber lengths of less than 0.5) (Millard et al., 2013). For similar computational reasons, the default minimum muscle activation is defined as 0.01 (1% of full activation). We altered these default settings, sacrificing computational robustness to enable simulations of purely passive muscle forces. Specifically, the default ${\stackrel{\sim }{f}}_a\left({\stackrel{\sim }{l}}_m\right)$ curve in the “Millard2012EquilibriumMuscle” tool in OpenSim 3.2 was modified to replicate the ${\stackrel{\sim }{f}}_a\left({\stackrel{\sim }{l}}_m\right)$ curve we have implemented previously (Holzbaur et al., 2005; Saul et al., 2015). Additionally, minimum muscle activation level was defined to be zero. To prevent numerical singularities under these conditions the fiber damping coefficient was defined to be 0.1 (Millard et al., 2013). For consistency, we also modified the default, normalized passive force-length $\left({\stackrel{\sim }{f}}_p\left({\stackrel{\sim }{l}}_m\right)\right)$ (and tendon force-strain $\left({\stackrel{\sim }{f}}_t\left({\epsilon }_t\right)\right)$ curves to replicate our previous work.

2.2 Incorporation of the extrinsic finger muscles’ length-dependent passive properties

Parameter values for L_ts for the four extrinsic finger muscles were defined by solving an optimization problem that matched simulated passive torques about the MCP joint of the index finger to experimental data (Knutson et al., 2000). An optimization algorithm was coded within MATLAB (Natick, MA) to minimize the difference between experimental torques $\left(T_E\left(\theta ,\omega \right)\right)$ and the net simulated passive torque $\left(T_M\left(\theta ,\omega \right)\right)$ produced by the extrinsic finger muscles, defined as:

$$T_M\left(\theta ,\omega \right)={\displaystyle {\sum }_{i=1}^4{\stackrel{\sim }{f}}_{t,i}}\left({\epsilon }_{t,i}\left(\theta ,\omega ,L_{ts,i}\right)\right)·m{a}_i\left(\theta \right)·F_{o,i}$$ (1)

where, for the i^th actuator: ${\stackrel{\sim }{f}}_{t,i}\left({\epsilon }_{t,i}\left(\theta ,\omega ,L_{ts,i}\right)\right)$ is the normalized tendon force at tendon strain (ε_t,i), which is a function of MCP angle (θ), wrist angle (ω), and L_ts,i; ma_i is the moment arm; F_o,i is the maximum isometric force.

The difference between T_M(θ,ω) and T_E(θ,ω) was minimized using a 3 degree-of-freedom optimization (Eq. (2) and (3)), solving L_ts for for each of the four extrinsic muscles, subject to a constraint (J), intended to limit changes from initial parameter values.

$$min\left[\left[{\displaystyle {\sum }_{\omega =-60}^{60}{\displaystyle {\sum }_{\theta =-45}^{90}{\left(T_E\left(\theta ,\omega \right)-T_M\left(\theta ,\omega \right)\right)}^2}}\right]+J\left(L_{ts}\right)\right]$$ (2)

$$J\left(L_{ts}\right)=\frac{1}{100}\left(\left|\frac{L_{ts,\mathit{FDSI}}-L_{ts,\mathit{FDSI}}^I}{L_{ts,\mathit{FDSI}}^I}-\frac{L_{ts,\mathit{FDPI}}-L_{ts,\mathit{FDPI}}^I}{L_{ts,\mathit{FDPI}}^I}\right|+\left|\frac{L_{ts,\mathit{EDCI}}-L_{ts,\mathit{EDCI}}^I}{L_{ts,\mathit{EDCI}}^I}-\frac{L_{ts,\mathit{EIP}}-L_{ts,\mathit{EIP}}^I}{L_{ts,\mathit{EIP}}^I}\right|\right)$$ (3)

$L_{ts}^I$ is the initial tendon slack length from Saul et al. (2015).

For the optimization, passive forces and torques produced by the extrinsic muscles about the MCP joint of the index finger were explicitly calculated in MATLAB (Natick, MA); ${\stackrel{\sim }{f}}_p\left({\stackrel{\sim }{l}}_m\right)$ and ${\stackrel{\sim }{f}}_t\left({\epsilon }_t\right)$ curves, all muscle force-generating parameters, muscle-tendon lengths, and moment arms needed for the calculations were exported from the OpenSim v3.2 model.

Normalized passive forces for a given iteration of L_ts parameter values were computed by solving a non-linear system of equations (Equations 4–7) using the MATLAB fsolve function. Each actuator was assumed to be passive and static, simplifying the model to two elastic elements, the tendon and the muscle fibers, arranged in series at a relative orientation specified by the muscle’s pennation angle (α). Thus, for all joint postures, muscle fiber length, L_m,i(θ,ω), and tendon length, L_t,i(θ,ω), must satisfy:

$$L_{mt,i}\left(\theta ,\omega \right)=L_{t,i}\left(\theta ,\omega \right)+\cos \left({\alpha }_i\right)L_{m,i}\left(\theta ,\omega \right)$$ (4)

where the muscle-tendon length, L_mt,i(θ,ω) is explicitly defined by the muscle-tendon lengths exported from OpenSim. The force outputs of the muscle and tendon at a given normalized fiber length, ${\stackrel{\sim }{l}}_{m,i}$, and tendon strain, ε_t,i, are specified by the generic ${\stackrel{\sim }{f}}_p\left({\stackrel{\sim }{l}}_m\right)$ and ${\stackrel{\sim }{f}}_t\left({\epsilon }_t\right)$ curves exported from OpenSim, and also must satisfy:

$${\stackrel{\sim }{f}}_{t,i}\left({\epsilon }_{t,i}\left(\theta ,\omega ,L_{ts,i}\right)\right)=\cos \left({\alpha }_i\right){\stackrel{\sim }{f}}_{p,i}\left({\stackrel{\sim }{l}}_{m,i}\left(\theta ,\omega \right)\right)$$ (5)

where ${\stackrel{\sim }{l}}_{m,i}\left(\theta ,\omega \right)$ and ε_t,i(θ,ω,L_ts,i) are functions of L_m,i(θ,ω) and L_t,i(θ,ω) from Eq. (4), respectively. Specifically,

$${\stackrel{\sim }{l}}_{m,i}\left(\theta ,\omega \right)=\frac{L_{m,i}\left(\theta ,\omega \right)}{L_{fo,i}}$$ (6)

$${\epsilon }_{t,i}\left(\theta ,\omega ,L_{ts,i}\right)=\frac{L_{t,i}\left(\theta ,\omega \right)-L_{ts,i}}{L_{ts,i}}$$ (7)

L_fo,i is the optimal fiber length.

In passive conditions the muscle-tendon actuator can only generate forces at joint angles where both the tendon is longer than its slack length and the muscle fibers are longer than optimal length. That is:

$${\stackrel{\sim }{f}}_{t,i}\left({\epsilon }_{t,i}\left(\theta ,\omega ,L_{ts,i}\right)\right)=\{\begin{array}{lll}{\stackrel{\sim }{f}}_{t,i}\left({\epsilon }_{t,i}\left(\theta ,\omega ,L_{ts,i}\right)\right)\hfill & if\hfill & L_{mt,i}\left(\theta ,\omega \right)\ge L_{ts,i}+\cos \left(\alpha \right)L_{fo,i}\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}$$ (8)

2.3 Incorporation of passive torques produced by soft tissue structures intrinsic to the hand

The optimization of L_ts allows us to simulate passive torques for the extrinsic muscles that replicate the work of Knutson et al. (2000). The net passive torques contributed by the intrinsic soft tissue structures (e.g., ligaments, joint capsules, skin, and intrinsic finger muscles) that cross the MCP, PIP, and DIP joints of the index finger are implemented into the model as three, torsional, spring-dampers, each acting independently about a single joint. In each case, the relationship between passive joint torque and joint angle was specified via the “FunctionBasedBushing” tool (DeMers, 2015) in OpenSim. A cubic spline curve parameterized additional data reported in Knutson et al. (2015) to define the constitutive relationship between the net, passive, elastic torques produced by intrinsic hand structures and MCP joint angle. Similarly, the constitutive torque-angle relationship for the PIP and DIP joints, and the viscous property of each spring-damper acting about the three joints were defined from the literature (Kamper et al., 2002).

2.4 Forward dynamic simulation of wrist and finger motion

Forward dynamic simulations of combined wrist and finger motion were performed in two forearm postures. The hand was oriented horizontally; gravity either opposed (pronated forearm) or assisted (supinated forearm) wrist extension. Wrist motion was prescribed (Figure 3a). First, 60° extension, maintained for one second, yielded the initial equilibrium position of the index finger. Second, wrist flexion was prescribed at 20°/second, until achieving 60° flexion. The remaining unconstrained degrees of freedom in the model (MCP, PIP, and DIP joint angles) were simulated with time.

Figure 3.

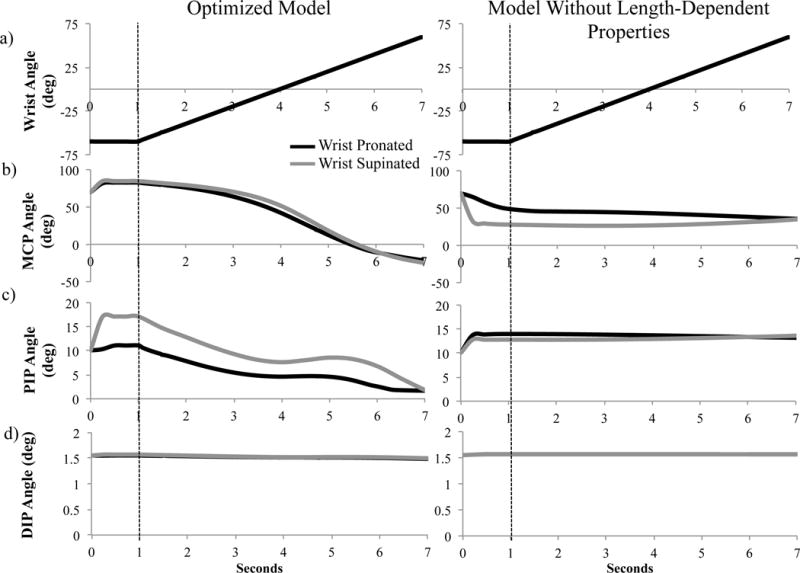
Wrist and index finger joint postures as a function of time in a pronated (black lines) and supinated (grey lines) forearm position; optimized model results on the left, model without the length-dependent passive properties on the right. (a) Wrist posture was prescribed identically in both sets of simulations, (b) metacarpophalangeal (MCP), (c) proximal interphalangeal (PIP), and (d) distal interphalangeal (DIP) joints postures were simulated. The dotted line indicates start of wrist motion.

Simulations were repeated with all length-dependent passive properties removed from the hand model. In these simulations, passive torques about each finger joint were implemented only by the torsional spring-dampers. Torque magnitudes were re-defined using the sum of the passive torques produced by the intrinsic structures and those produced by the extrinsic finger muscles at a single wrist posture (0° wrist extension).

3. Results and Discussion

Simulation of length-dependent passive force-generating properties of extrinsic finger muscles yielded coupled movements between the wrist and index finger during dynamic forward simulations (Figure 3). With the forearm pronated, prescribed wrist flexion produced coordinated MCP extension (initial position: 83° flexion, final position: 21.8° extension) and PIP extension (11.1° to 1.7° flexion; Figure 3b–d), mimicking tenodesis (Johanson and Murray, 2002; Su et al., 2005). With the forearm supinated, the finger joints followed similar trajectories but were more flexed (Figure 3b–d). Muscle-tendon lengths of the extrinsic finger flexors increase by 1–2% with supination, increasing the passive flexion torques generated. Without length-dependent passive properties, the posture of the index finger was determined by gravity; coupled motion was absent and the finger joints were more extended with the forearm supinated (Figure 3).

4. Conclusion

Passive torques are critical to achieve controlled and stabilized dynamic free movements of the wrist and fingers (Babikian et al., 2016; Blana et al., 2016; Charles and Hogan, 2012; Kamper et al., 2002). Additionally, passive coupling of the fingers and wrist is a fundamental component of hand function in the severely disabled hand, such as following tetraplegia (Johanson and Murray, 2002; Su et al., 2005). The methods implemented in this study are novel in that they enable incorporation of experimentally measured, length-dependent passive torques produced by the extrinsic muscles in biomechanical models of the hand. Given experimental data for both healthy and impaired hands, the methods described here will enable simulation-based analysis of healthy hand function and evaluation of how musculoskeletal alterations after an injury, that are often associated with increases in passive joint stiffness, affect impaired populations. The extent to which the passive coupling between the hand and distal upper limb joints affects both endpoint force production with the fingers and high-speed movements is unknown; the tools described here facilitate future work in this direction.