Predictable invasion dynamics in North American populations of the Eurasian collared dove Streptopelia decaocto

Abstract

Species invasions represent a significant dimension of global change yet the dynamics of invasions remain poorly understood and are considered rather unpredictable. We explored interannual dynamics of the invasion process in the Eurasian collared dove (Streptopelia decaocto) and tested whether the advance of the invasion front of the species in North America relates to centrality (versus peripherality) within its estimated fundamental ecological niche. We used ecological niche modelling approaches to estimate the dimensions of the fundamental ecological niche on the Old World distribution of the species, and then transferred that model to the New World as measures of centrality versus peripherality within the niche for the species. Although our hypothesis was that the invasion front would advance faster over more favourable (i.e. more central) conditions, the reverse was the case: the invasion expanded faster in areas presenting less favourable (i.e. more peripheral) conditions for the species as it advanced across North America. This result offers a first view of a predictive approach to the dynamics of species' invasions, and thereby has relevant implications for the management of invasive species, as such a predictive understanding would allow better anticipation of coming steps and advances in the progress of invasions, important to designing and guiding effective remediation and mitigation efforts.

1. Introduction

Invasive species represent a significant agent of global change [1] with potentially serious economic and environmental implications in the form of negative effects on agriculture, public health and transportation [2,3]. Indeed, as invasive species spread across novel landscapes, they can affect broad areas, such that the ability to predict and anticipate their geographical potential is much desired [2]. Given the importance of anticipating and understanding the complexities of invasion dynamics in real-world applications, new methodological frameworks are needed for predicting species’ invasions [2,4,5].

A predictive framework that has been applied to questions of species' invasions is that of ecological niche modelling (ENM; [6]). The idea is that the geographical occurrence of the species in question is related to digital maps summarizing relevant environmental parameters to estimate coarse-resolution, non-interactive dimensions of the fundamental ecological niche. Such a ‘niche model’ can be transferred to other regions to anticipate the invasive potential of the species on a given landscape [6], although this potential is clearly dependent on context and many contingencies. ENM transfers are not without significant complications and challenges [4,7–9]; however, the most significant shortcoming is that the models provide only a snapshot of the invasive potential of the species without consideration of the dynamics of how the species may or may not be able to access different sectors of its potential distribution [10,11]. Still, ENM approaches have now been applied to many invasive species, providing useful information about their invasive potential (e.g. [12,13]).

Therefore, an important goal is to progress beyond simply estimating potential geographical distributions of species towards understanding elements of the dynamics of invasions [4]. Progress in this area has been made to incorporate dispersal to enrich model projections [14,15], yet models remain rather assumption-laden, lacking detailed information on how dispersal relates to environments across complex landscapes [16]. A crucial and related challenge is understanding how a given locality's position in fundamental niche space determines population features, such as abundance or the direction and strength of movement rates [17–19].

In this contribution, we address the latter challenge, by testing how the speed of the invasion relates to environmental centrality within the ecological niche, in the spread of Eurasian collared doves (Streptopelia decaocto) across North America. Our approach centres on ideas regarding relationships between the centrality of conditions within the fundamental ecological niche of species and population density or abundance [19]. We estimate coarse-resolution aspects of the fundamental ecological niche of the species in its distributional areas across Eurasia, calculate distances in environmental space from all existing conditions to the centroid of the ecological niche of the species, and classify North American environments by niche centroid distances relative to conditions estimated in Eurasia. We aim more to increase understanding of how niche structure affects invasion dynamics, rather than to obtain a detailed and specific prediction for the future distribution of Eurasian collared doves since such predictions have already been presented [20]. Overall, then, we set out to test the idea that the species would expand its range faster across more favourable conditions, a relationship that would ideally have predictive power regarding the interannual dynamics of range expansion in an invasive species.

2. Methods

As we explore and test a number of rather novel methodologies in this analysis, we provide a flowchart summarizing our methods in the electronic supplementary material. We refer to labelled parts of this flowchart in the methods descriptions below.

(a). Study species and occurrence data

We sought a model species that: (i) is broadly invasive on continental extents (i.e. a species with distributional limits not set principally by dispersal considerations [21], and (ii) has extensive occurrence data available across both native and invaded range areas. A clear choice was the Eurasian collared dove, which is native to Asia and limited areas of Europe, but invaded across Europe in the 1930s. In the early 1970s, it arrived in the Americas on New Providence in the Bahamas [22]. The species probably arrived in Florida during the late 1970s, with the first definitive nesting record on mainland North America coming from Homestead (Florida) in 1982 [22]. It has since spread across much of North America. We obtained occurrence data from eBird [23] and the Global Biodiversity Information Facility (GBIF; www.gbif.org, 9 February 2015); institutions providing data used in these analyses via the GBIF portal are available at http://hdl.handle.net/1808/23373.

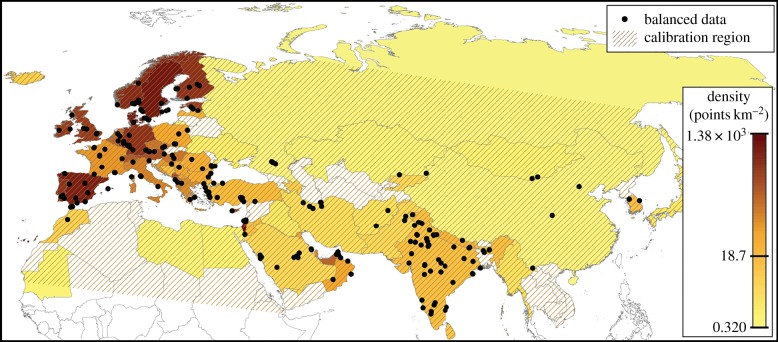
We downloaded an initial set of 639 623 occurrence records, and subjected them to a variety of quality- and bias-control steps (step ‘a’, in the methods flowchart in the electronic supplementary material). We removed records that were extralimital for the reported observation date (particularly as regards North American data), as individuals of this species have appeared in many far-flung sites that do not result in population establishment in succeeding years, particularly in view of local releases that may have occurred. Next, we filtered travelling counts (reports of birds sighted along a path or road) in eBird data to ≤20 km; we also excluded all records from prior to 1970. We reduced the data by removing records lacking geographical coordinates or with latitude and longitude of 0, 0; we also discarded nine points from Australia. For Eurasia, then, the dataset reduced to 64 078 records; owing to coarse spatial resolution and other problems, an additional 7895 records were also removed, leaving 54 125 records from 63 countries (figure 1; data available at http://hdl.handle.net/1808/23356).

Figure 1.

Balanced training data (black circles). Countries are filled on a shading ramp denoting relative density of records of Eurasian collared doves, such that lightest shading represents low density, and darkest shading denotes high density. Hatched lines show the model calibration region. Projection: Eckert III. (Online version in colour.)

We termed this dataset the ‘thinned’ occurrence dataset. Because models can be affected by biases in sampling (e.g. between western Europe and central Asia; [24]), in addition to the niche-related environmental biases shown by species' occurrences, it is necessary to remove these biases to every extent possible, which we have accomplished by several means. First, we generated a ‘bias layer’ by extracting from the same data sources a geographical summary of the number of records of any bird species (step ‘b’, in the methods flowchart in the electronic supplementary material). We derived this summary using customized code developed in R v. 3.2.5 [25], and consisted of a raster grid data layer at 5′ spatial resolution (approx. 9 km at the Equator), which had pixel values ranging 0–783 376; because of the massive differences in sampling intensity among regions (i.e. five orders of magnitude), we also explored a natural-logarithm-transformed version (‘ln bias’) that rescaled the bias layer values to a more compact range.

In light of diverse results regarding use of bias layers in ENM calibration in previous studies (e.g. [26]), we explored an alternative approach: we further refined Eurasian collared dove occurrence data by balancing the density of occurrences on a country-by-country basis (step ‘c’, in the methods flowchart in the electronic supplementary material), given that much of reporting variation worldwide depends on national boundaries [27]. We then used the thinned dataset to calculate the occurrence record density per country, dividing the number of records by the land area of the country. As a reasonable intermediate-density reference point, we arbitrarily chose the record density in India (18.7 records 10⁻⁶ km⁻²) as a reference point. Hence, for all countries with record densities of more than 25 records 10⁻⁶ km⁻², we reduced record density to 25 records 10⁻⁶ km⁻² by random sampling. In countries for which record density was less than 25 records 10⁻⁶ km⁻², we retained all points. The final ‘balanced’ occurrence dataset for Eurasia thus comprised 1170 occurrence records (figure 1). Both the thinned and balanced datasets were divided into five replicate pairs of datasets (step ‘d’, in the methods flowchart in the electronic supplementary material), using the ‘sample’ function in R [25]. Each thinned data subset consisted of 10 725 records for model calibration and 100 records for model evaluation per sub-sample; each balanced dataset consisted of 134 records for model calibration and 100 records for model evaluation per sub-sample.

We drew records from the invaded distributional area in North America only from eBird to maximize consistency and retain as much metadata as possible, and processed them as detailed in step ‘a’ in the methods flowchart in the electronic supplementary material. We reduced the eBird dataset to 147 350 points that had implicit or explicit spatial accuracies of ≤20 km and automatically removed all points with dates prior to 1970. We restricted the data to points within the United States and Canada to avoid: (i) colonizations across the Caribbean Basin, and (ii) undersampled regions in northern Mexico and Middle America. In R, we identified localities with persistent populations (i.e. localities at which the species had been recorded within 10 km in multiple years). Conclusions about persistence were not conditional on detections in sequential years, as some localities are not visited yearly nor are all established populations detected during every visit. This refined dataset resulted in yearly subsets covering 1986–2014, with three localities in 1986 and 84 444 localities in 2014; however, because expansion during 1986–1989 was minimal, we restrict our analyses to the period 1989–2014.

(b). Environmental variables

We used climate data from the WorldClim climate data archive (v. 1.4; [28]) at 5′ spatial resolution. We used 15 bioclimatic variables (annual mean temperature, mean diurnal range, isothermality, temperature seasonality, maximum temperature of warmest month, minimum temperature of coldest month, temperature annual range, mean temperature of warmest quarter, mean temperature of coldest quarter, annual precipitation, precipitation of wettest month, precipitation of driest month, precipitation seasonality, precipitation of wettest quarter, and precipitation of driest quarter), eliminating four variables in light of known spatial artefacts in those layers (i.e. artificial discontinuities in the midst of gentle climate gradients). To reduce dimensionality and variable intercorrelation, we subjected the 15 data layers to principal components analysis (PCA) based on the correlation matrix via the default princomp function in R [25]. We used the first five principal components, which summarized 97.1% of the overall variation in the environmental data, as summaries of environmental variation across landscapes for model calibration. In general, the first component contrasted annual means with seasonal variation, and the second contrasted temperature and precipitation variables; as such, these components provide a rich summary of the dimensions of climate across relevant regions (see the electronic supplementary material for a full summary of PCA results).

(c). Model calibration

A crucial step in calibrating ENMs appropriately is determining the region across which models are to be calibrated [29]. This region should correspond to areas that have been accessible to the species over relevant time periods [30]. We outlined an area corresponding to the limits of Eurasia, plus part of North Africa, removing distant parts of northern Asia from the calibration region (figure 1). We chose this area in view of the Atlantic, Indian and Pacific oceans acting as major barriers to dispersal; we interpreted the Sahara Desert as acting as a barrier in Africa. As regards barriers to the northeast of the species' Asian distribution, we detected no major barriers, and so relied instead on distance as a barrier.

Our model calibration efforts followed the general idea of the ‘no silver bullet’ approaches outlined by Qiao et al. [31]. That is, rather than trusting that certain modelling algorithms will perform best consistently [32], we recognize that an algorithm which may not be the ‘best’ on average may be the best in a given situation. As such, we submitted a variety of candidate models to detailed significance and performance testing to identify which modelling approach offered the most appropriate predictions for this particular species, landscape, and set of study goals. We developed niche models using two niche modelling methodologies: Maxent [33] and minimum volume ellipsoids (MVEs) [34], a variation on Mahalanobis distance methods for ENM [35], each under diverse settings and conditions, varying the bias layer in Maxent, and the E parameter that sets amount of omission permitted in MVEs. These two approaches are in some senses at opposite poles of the niche modelling universe: Maxent fits highly complex response surfaces that will fit well to complex environmental landscapes [32], whereas the MVEs are simple and convex shapes that may correspond better to the idea of a fundamental ecological niche [34]. Our goal was to compare predictive performance across the five subsamples described above as an analogue to expected performance in model transfer. We calibrated models using the two occurrence datasets (thinned versus balanced), and Maxent with one, the other, or neither of the two bias layers described above; MVEs are much less sensitive to density of points within the occurrence data cloud, and no background or pseudoabsence points are sampled in this method, so we did not consider bias for those models. We projected final models to North America for exploration of model implications.

In Maxent, we used 50% of calibration points for training, with 10 bootstrapped replicates chosen with a random seed. In all, we explored six sets of Maxent models: thinned versus balanced occurrence data and no bias layer, and raw and log-transformed bias layers. As the purpose of the ENMs was to characterize the niche centroid, final Maxent runs were developed with no clamping and no extrapolation, to avoid the extrapolation that can characterize Maxent models in model transfers [8]. We used the median of the raw outputs across 10 replicate modelling runs as a final model output.

MVEs can be used as niche models, particularly when one is interested in fitting a niche model that is only minimally affected by biases among the input occurrence data [36]. MVEs can be calculated in many dimensions, and are characterized by a centroid and a symmetric positive-definite matrix that describes the directions of the axes and their lengths. We used the first five principal component axes of the environmental data to calibrate MVEs under two thresholds of allowable omission error (E = 1% and E = 5%). We implemented MVEs in R v. 3.3.2 [25] using code available at http://hdl.handle.net/1808/23357.

(d). Model evaluation

We evaluated niche models using partial receiver operating characteristic (ROC) approaches via the PartialROC function available in the R package ‘ENMGadgets’ [37]. We chose partial ROC (pROC) as a significance test in light of critiques of the appropriateness of traditional ROC approaches [38,39]. We chose an acceptable omission rate of E = 5%, ran 100 iterations of pROC calculations based on random subsamples of 50% of the test data for each of the five testing subsamples, and determined probability values by direct count of iterations for which the area under the curve (AUC) ratio was ≤1. In view of the need for models to anticipate the full geographical (and environmental) distribution of the species, we tested models using random subsets of the balanced occurrence dataset. MVE outputs in the form of distances to the niche centroid in environmental space were converted to similarity values by standardizing and subtracting from unity prior to pROC analysis.

(e). Invasion process in North America

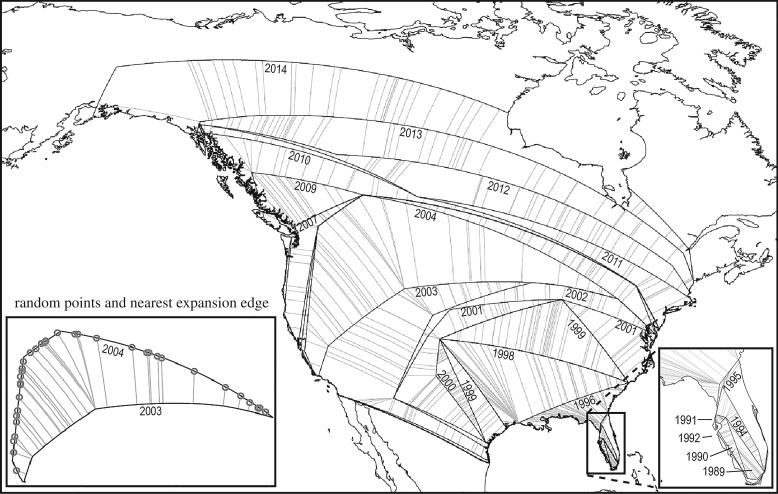
Dove occurrence data in North America (described above), were partitioned by year from 1989–2014 (initial years of the invasion process, in which the species was restricted to the Florida Keys, were removed); we also removed areas outside of the continental USA owing to the need for detailed and dense occurrence data on an interannual basis. For each year, in geographical space, we generated a convex hull around occurrences using the R package ‘rgeos’ [40]. We transformed all convex hulls to use the shortest geodetic path between vertex points using the package ‘geosphere’ [41] in R, and defined the ‘expansion edge’ as only those hull edges falling outside the hull from the previous year. We cast 50 random points along the expansion edge for each year and calculated the shortest distance to edge of the previous year's hull (figure 2) to characterize the expansion distance associated with each point; we then used the mean of those distances to characterize the amount of expansion between each consecutive pair of years. We used these distances as measures of the amount of range expansion from one year to the next.

Figure 2.

Range expansion map (convex hulls by year, 1989–2014; early years shown in detail in lower-right inset) and schematic illustrating what is being measured (lower-left inset; circles indicate the random points). Only selected years are labelled. Map is not projected for simplicity.

To summarize suitability of the landscapes across which the species was expanding its range, we used raster data layers summarizing distances in environmental space to the centroids of the ecological niches estimated across the Eurasian range of the species. This niche-centroid-distance approach is founded on previous results indicating that population abundances are a negative function of distance to the centroid in environmental space, in essence a measure of centrality versus peripherality within the niche [19,42].

To explore relationships between these niche centroid distances and population expansions, we extracted distance values for the species from: (i) the hull edge points representing the sources from which expanding populations were derived, and (ii) along the transect line connecting the hull edge and the expansion edge. For the latter, we focused on mean and maximum niche centroid distance values, as they summarize the overall suitability and the lowest suitability confronting the species; we calculated these values along the transect line using the ‘raster’ package [43] in R. In view of the triangular relationships that are common in such assessments (i.e. suitability defines the maximum possible abundance or density, but many points have values lower than this maximum; e.g. [44]), we used quantile regressions to assess tendencies in the top percentiles of the relationship of expansion distance to environmental suitability; as a consequence, we considered only the top 5% of the expansion distances (i.e. τ = 0.95).

3. Results

(a). Model calibration

We found stark imbalances in density of occurrence data across the Old World range of the species (figure 1); models based on occurrence data without a sufficient mechanism for compensation of this phenomenon showed corresponding biases towards western Europe at the expense of range areas farther to the east. Maxent models based on thinned data without a bias layer performed particularly poorly (table 1). The ln-transformed bias layer performed better than the raw bias layer, probably owing to scale differences of several orders of magnitude in terms of numbers of occurrence records between western Europe and the rest of Eurasia. MVE models were less sensitive to the differences between the two occurrence datasets, such that differences among MVE models were smaller.

Table 1.

Summary of partial receiver operating characteristic tests for Maxent and minimum volume ellipsoid (MVE) models, in terms of number of non-significant (α = 0.05) iterations, range of partial ROC AUC ratio scores, and mean AUC ratio for each sub-sample; AUC ratios above 1.0 are indicative of better-than-random model predictions. (Partial ROC (pROC) tests evaluate the statistical significance of niche model predictions in comparison with a random classifier, subject to a maximum proportional amount of omission error (E; [39]): no. NS indicates the number out of 100 random replicate analyses for which the AUC ratio was greater than 1, pROC range and mean indicate the general magnitude of the AUC ratios across the 100 replicate analyses, and ln bias indicates results from the bias surface that was natural-log transformed.)

			thinned			balanced
		subsample	no. NS	pROC range	mean pROC	no. NS	pROC range	mean pROC
MVE	E = 1%	1	100	0.963–0.998	0.979	5	0.986–1.327	1.125
		2	81	0.963–1.063	0.989	19	0.977–1.925	1.177
		3	96	0.964–1.030	0.987	3a	0.979–1.334	1.157
		4	93	0.964–1.021	0.986	2a	0.983–1.303	1.133
		5	96	0.963–1.038	0.979	21	0.962–1.344	1.129
	E = 5%	1	95	0.964–1.038	0.983	10	0.984–1.327	1.125
		2	60	0.963–1.087	0.996	5	0.981–1.300	1.197
		3	87	0.964–1.066	0.990	4a	0.974–1.342	1.177
		4	80	0.965–1.050	0.993	1a	0.980–1.326	1.210
		5	96	0.963–1.046	0.980	33	0.962–1.320	1.094
Maxent	no bias	1	0a	1.018–1.377	1.088	0a	1.196–1.467	1.353
		2	0a	1.032–1.393	1.109	0a	1.236–1.455	1.351
		3	0a	1.020–1.394	1.077	0a	1.153–1.499	1.347
		4	0a	1.013–1.171	1.056	0a	1.320–1.494	1.367
		5	0a	1.029–1.391	1.134	0a	1.140–1.532	1.334
	bias	1	15	0.994–1.092	1.028	0a	1.022–1.276	1.110
		2	2a	0.997–1.130	1.048	0a	1.010–1.207	1.054
		3	1a	0.998–1.224	1.078	0a	1.016–1.216	1.105
		4	8	0.997–1.153	1.047	0a	1.005–1.191	1.060
		5	1a	0.996–1.560	1.045	0a	1.017–1.262	1.105
	ln bias	1	13	0.996–1.099	1.029	0a	1.111–1.292	1.190
		2	4a	0.997–1.130	1.043	0a	1.076–1.245	1.153
		3	0a	1.006–1.205	1.074	0a	1.163–1.319	1.209
		4	4a	0.999–1.259	1.046	0a	1.108–1.237	1.188
		5	7a	0.996–1.141	1.036	0a	1.063–1.297	1.196

^aDenotes significant sub-sample evaluation.

We performed a simple ANOVA on the five random subsamples, first for algorithm, finding no significant effect (F = 4.968, d.f. residuals = 48, p = 0.305). Therefore, we split the dataset into Maxent and MVE analyses, and performed two ANOVAs using data type (thinned versus balanced) and type of bias as factors. For Maxent, both data type and bias type were significant (F₁ = 336.64, p = 1.21 × 10⁻¹⁵ and F₂ = 130.64, p = 1.26 × 10⁻¹³, respectively); for MVE, data type was significant (F₁ = 21194.37, p = 4.72 × 10⁻⁵) but bias type had a rather minor effect (F₈ = 155.79, p = 0.0064). Because overall best performance was from the Maxent model based on balanced data with no bias layer, we present those results here, but provide results from the MVE model based on balanced data in the electronic supplementary material.

(b). Model transfers to North America

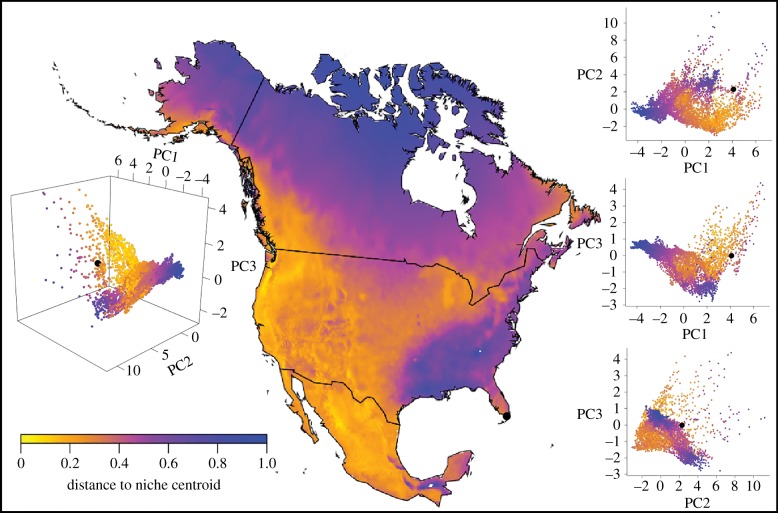
Transferring the best Maxent model (balanced occurrence data, no bias layer) indicated that the southeastern United States (except Florida) and high-latitude regions are relatively less suitable; much of the western United States was only moderately suitable (figure 3). MVE models showed high suitability across most of North America, except for a less suitable area in the southeastern United States (excluding Florida), as well as for highest-latitude regions of Alaska and Canada (electronic supplementary material, figure S1).

Figure 3.

Median projection and visualizations in North America of the Maxent model (balanced occurrence data, no bias layer) based on an adjusted least training presence threshold (E = 5%). Insets: Projected environmental suitability. Environmental distance from calculated niche centroid is displayed on a continuous gradient scale. The niche-centroid distances are shown over geography in the middle part of the figure, and in various combinations of three-dimensional and two-dimensional plots to show variation in environmental dimensions (these dimensions represent the principal components derived from analysis of the WorldClim bioclimatic dimensions). Projection: North America Lambert Conformal Conic, for purposes of visualization.

(c). Expansion distance and suitability

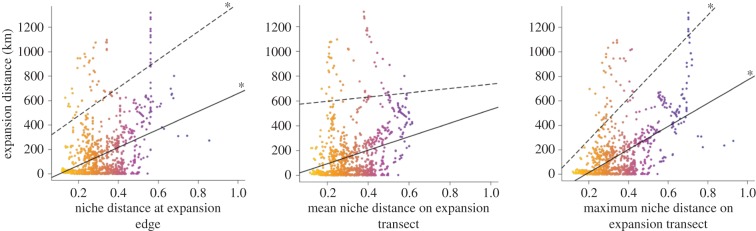
We assessed the relationship between expansion distance (figure 2) and niche centroid distance (figure 3). Although initial expectations were that the species would invade more rapidly across more suitable conditions (i.e. lower niche centroid distances), the results were the opposite: we found positive relationships between (i) expansion distance and niche centroid distance at the hull edge in the previous year (quantile regression R² = 0.0427, p = 0.0178, although, again, these values may be inflated by spatial covariances), and (ii) expansion distance and maximum niche centroid distance along the expansion lines (quantile regression R² = 0.1448, p < 0.0001, although these values may be inflated by spatial covariances; figure 4). Relationships between expansion distance and mean niche centroid distance along the expansion lines were not significant (quantile regression R² = 0.0027, p = 0.51). Results for MVE-based relationships were similar (not reported).

Figure 4.

Plots of simple linear (solid lines) and 5% quantile (dashed lines) regressions of the final Maxent model (balanced occurrence data, no bias layer) for distance from niche centroid to expansion edge, mean niche distance on expansion transect, and maximum niche distance on expansion transect. Asterisks (*) denote significance (α = 0.05).

4. Discussion

(a). Basic outcomes

Literature on species invasions emphasizes the chance nature of many aspects of invasion events [2]. Our analyses, however, point out a regularity in the process: at least in the case examined here, invasion proceeds more rapidly in areas presenting relatively unsuitable conditions. The Grinnellian ecological niche sets limits on the geographical potential of the invader as has been noted in many retrospective studies of invasive species and their spread across suitable distributional areas [6]. Clearly, the tendency for non-native species to become ‘invasive’—in the sense of expanding populations and affecting other native species—depends to some degree on the characteristics of the species [45]. The dynamics of how a species expands (once it has become invasive) across real-world landscapes to fill the potential distributional area, however, have remained rather opaque to modelling and prediction efforts.

In this study, we have appealed to recent advances in ecological niche modelling, which have connected the topology of environmental conditions within the limits of modelled ecological niches to the population biology of the species [19]. Species maintain higher abundances and densities under conditions near the centroid of the ecological niche [42], as well as higher genetic diversity [46] and more positive long-term population trends [18]. At least for Eurasian collared doves, we now note a further tie to population ecology: a species invasion proceeds more rapidly over environmental conditions less able to hold high densities of the species.

Our results offer an intriguing view of invasion dynamics. In Eurasian collared doves, the invasion front advances faster when the source areas and intervening areas are unsuitable for the species—it appears that the species has sufficient dispersal ability such that it can ‘jump’ longer distances when closer areas are not particularly attractive. When, however, no suitable areas are located beyond the unsuitable areas, of course, no long-distance colonization is possible, as can be observed in figure 2 in the northeastern United States and eastern Canada. In many ways, this suggestion runs counter to other ideas, such as the ‘Ideal Free Distribution’ of Fretwell and Calver ([47]; i.e. the best areas would fill up first, before other, less suitable areas are colonized), although this proposition depends on full information availability, which is unlikely to be fulfilled at broad extents.

(b). Caveats and limitations

We suspect that the result for Eurasian collared doves will not prove general. Rather, our guess is that further analyses of this sort will reveal dependence on species-level traits, such as reproductive rates, carrying capacities and dispersal abilities. Clearly, the geometry of suitable and unsuitable areas across landscapes will also affect results, as can be seen in this paper in the contrasting expansion patterns westwards and northwards from the southeastern United States. Certainly, though, interesting insights into invasion dynamics will derive from exploration of parallel effects and patterns in other invasive species.

This study required a number of methodological explorations and tests. Initially, we assessed diverse means of modelling niches, which took considerable time and effort in fine-tuning models and obtaining logical fits of models and data, even on the native range of the species. Our relatively large occurrence datasets, such as for the North American range of the species, required considerable cleaning and quality assessment, such as in the careful removal of single, isolated records that did not result in future, established populations, created either by isolated dispersers or by local (unsuccessful) introductions. We also had to evaluate many approaches to testing and interpreting the distance-suitability relationships that were the focus on this proposal—an outstanding challenge remains that of distinguishing true relationships from the effects of spatial autocorrelation in assessing the significance of our quantile regressions, as we have not succeeded in developing a means of taking such relationships into account in quantile regression analyses.

We adhere closely to the idea of ‘no silver bullets’ in ecological niche modelling—the idea that no single algorithm is likely to prove to be ‘best’ across diverse modelling challenges [31]. Hence, we explored two contrasting niche modelling algorithms, four ways of managing sampling bias (thinning, balancing, bias layer, log-bias layer), and different amounts of allowable omission error in thresholding niche models. Lessons learned include the observation that bias surfaces may require transformation in order not to neglect minimally sampled areas, but also more fundamentally that a lot of experimentation is necessary to create the best possible models for these situations.

(c). Implications

In one species at least, and based on what is in effect a post hoc analysis, a predictable aspect can now be perceived for the rate and direction of advance of a species invasion. Clearly, this is a first result, and will require testing and exploration in other species and other regions, so as to clarify its generality. Nonetheless, many previous studies have concluded that such predictability is lacking (see review in [2]), save for expected effects of introduction (propagule) pressure [48] and natural history traits of species [49]. This study opens a new dimension of questions: how much can one anticipate the geographical course and rate of invasion across a novel region?

If such predictability exists more generally than just in this first species analysed, then this result would have interesting and important management implications. Although the usual wisdom is that once an invasive species is established, the invasion is unstoppable and eradication is impossible, attempts at mitigation and eradication are still made, and are sometimes even at least partly successful [50,51]. The potential signalled by this study would be instrumental in guiding investment of resources in such efforts.

Ethics

No ethical concerns were involved in the development of this contribution.

Data accessibility

Datasets supporting this article can be found in KU Scholarworks: http://hdl.handle.net/1808/23356.

Authors' contributions

This study was conceived in the course of group discussions including all of the authors. K.I., C.H., A.M.S., M.S., T.A., V.B., L.P.C., L.J. and K.V.O. developed the statistical analyses. K.I. and C.H. executed the final analyses and created the figures. E.K. and L.O.-O. assisted with particular challenges in coding and analysis. H.L.O. and J.C.C. prepared the occurrence data and participated in the analysis stage. A.T.P. and J.S. provided conceptual frameworks. All authors edited and commented on the manuscript.

Competing interests

We have no competing interests.

Funding

J.S. and J.C.C. were supported partially by a grant from the National Science Foundation (DEB-1208472). A.M.S. was supported by the Graduate Fulbright Egyptian Mission Program (EFMP). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.