High-precision registration between zebrafish brain atlases using symmetric diffeomorphic normalization

Abstract

Atlases provide a framework for spatially mapping information from diverse sources into a common reference space. Specifically, brain atlases allow annotation of gene expression, cell morphology, connectivity, and activity. In larval zebrafish, advances in genetics, imaging, and computational methods now allow the collection of such information brain-wide. However, due to technical considerations, disparate datasets may use different references and may not be aligned to the same coordinate space. Two recent larval zebrafish atlases exemplify this problem: Z-Brain, containing gene expression, neural activity, and neuroanatomical segmentations, was acquired using immunohistochemical stains, while the Zebrafish Brain Browser (ZBB) was constructed from live scans of fluorescent reporters in transgenic larvae. Although different references were used, the atlases included several common transgenic patterns that provide potential “bridges” for transforming each into the other's coordinate space. We tested multiple bridging channels and registration algorithms and found that the symmetric diffeomorphic normalization algorithm improved live brain registration precision while better preserving cell morphology than B-spline-based registrations. Symmetric diffeomorphic normalization also corrected for tissue distortion introduced during fixation. Multi-reference channel optimization provided a transformation that enabled Z-Brain and ZBB to be co-aligned with precision of approximately a single cell diameter and minimal perturbation of cell and tissue morphology. Finally, we developed software to visualize brain regions in 3 dimensions, including a virtual reality neuroanatomy explorer. This study demonstrates the feasibility of integrating whole brain datasets, despite disparate reference templates and acquisition protocols, when sufficient information is present for bridging. Increased accuracy and interoperability of zebrafish digital brain atlases will facilitate neurobiological studies.

Background

Larval stage zebrafish are an increasingly popular model for neurobiological studies. With a brain that contains an estimated 10⁵ neurons, larvae are similar in complexity to adult Drosophila, another established neuroscience model. In both systems, researchers can deploy a wide range of genetic tools in efforts to decode patterns of neural structure and connectivity. In larval zebrafish, optical transparency and constrained physical dimensions (fitting within an imaging volume of 1000 × 600 × 350 μm) allow the entire brain to be rapidly scanned at cellular resolution using diffraction-limited microscopy. In principle, this enables researchers to systematically analyze effects of manipulations on a brain-wide level. However, such efforts have been hampered by the absence of a comprehensive digital atlas that would provide researchers with a unified framework in which to aggregate data from different experiments and gain deeper insights from correlations between neuronal cell identity, connectivity, gene expression, and function within the brain. Additionally, digital atlases may more clearly delineate structural boundaries that are difficult to accurately identify within individual brains, allowing for a more rigorous mapping of neuroanatomical regions onto experimental data.

These longstanding problems in zebrafish neuroscience have recently been addressed by the construction of digital atlases using 3D image registration techniques: the Virtual Brain Explorer for Zebrafish (ViBE-Z), Z-Brain, and the Zebrafish Brain Browser (ZBB) [1–3]. In these atlases, information on gene expression, structure (neuronal cell bodies, glia, vasculature, ventricles, neuropil, or axon tracts) and measures of activity (calcium or secondary messenger activity) is consolidated within a common spatial framework. By using widely available transgenic lines or immunohistochemical stains as reference templates for brain alignment, each of these atlases provides other researchers the opportunity to register their own datasets into these digital spaces and take advantage of the information contained within.

ViBE-Z was the first comprehensive 3D digital brain atlas in zebrafish that used a nuclear stain for the alignment of 85 high-resolution scans comprising 17 immunohistochemical patterns at 2–4 days post-fertilization (dpf) [3, 4]. In ViBE-Z, custom algorithms were developed to correct for variations in fluorescent intensity with scan depth, and a landmark approach was taken to perform accurate image registration and segmentation into 73 neuroanatomic regions.

In contrast, 2 other recent approaches (Z-Brain and ZBB) have generated brain atlases at 6 dpf through non-linear B-spline registration using the freely available Computational Morphometry Toolkit (CMTK) [5, 6]. Z-Brain includes 29 immunohistochemical patterns from 899 scans, which form the basis for expert manual segmentation of the brain into 294 neuroanatomic regions. These partitions facilitate the analysis of phospho-ERK expression for mapping neural activity [2]. In Z-Brain, each expression pattern was co-scanned with tERK immunoreactivity and registered to a single tERK-stained reference brain. For ZBB, we live-imaged 354 brains from 109 transgenic lines and manually annotated the expression found in each [1]. In place of tERK, a single vglut2a:dsRed transgenic brain was used as the reference in ZBB, with transgenic lines crossed and co-imaged with this channel for registration. Brain browser software enables researchers to select a transgenic line labeling a selected set of neurons for monitoring and manipulating circuit function.

While Z-Brain and ZBB are powerful datasets on their own, we saw an opportunity to merge the 2 atlases because they are both based on confocal scans of 6 dpf larvae. This would bring to Z-Brain a large number of additional transgenic lines and bring ZBB the expert manual segmentation of Z-Brain. Several similarities between Z-Brain and ZBB suggested that bridging the atlases would be possible. First, as zebrafish rearing conditions are standardized across laboratories and fish were imaged at the same time post-fertilization, Z-Brain and ZBB likely reflect the same developmental timepoint. Second, images in both atlases were acquired at similar resolution (0.8 × 0.8 × 2 μm for Z-Brain; 1 × 1 × 1 or 1 × 1 × 2 μm for ZBB) and orientation (dorsal to ventral horizontal scans). Third, despite using distinct templates (tERK for Z-Brain and vglut2a for ZBB), Z-Brain and ZBB have several transgenic markers in common that provide the possibility of bridging the datasets by using these shared patterns as references for a secondary registration step.

One of the strengths of larval zebrafish is the ability to rapidly image at cellular resolution and visualize brain-wide neuronal morphology, providing valuable information on cell type and potential connectivity. Z-Brain and ZBB both illustrate the feasibility of performing whole-brain registration with precision sufficient to ensure that the “same” neurons from different fish are aligned to within a cell diameter (∼8 μm). However, a challenge for brain registration in zebrafish is to minimize local distortions, so that cellular morphology is preserved while still allowing sufficient deformation to overcome biological variability between individual brains or malformations due to tissue processing.

Here we describe a method to co-register ZBB and Z-Brain, bridging the 2 existing 6 dpf larval zebrafish brain atlases. By using the diffeomorphic symmetric normalization algorithm (SyN) in the Advanced Normalization Tools (ANTs) software package [7, 8], we were able to overcome differences in tissue shape due to fixation, optimize the trade-off between preservation of cell morphology and global alignment, and provide precise registration in all tested brain regions. Additionally, ANTs provided superior image registration for live-scanned larvae, enabling us to improve the precision of registration and neuron morphology within our original ZBB atlas, allowing us to compile a new version with increased fidelity (ZBB_1.2).

Methods

Zebrafish lines

In order to provide additional options for bridging ZBB and Z-Brain, we scanned 2 transgenic lines that were not in the original ZBB release: Et(gata2a:EGFP)zf81 (vmat2:GFP) and Tg(isl1:GFP)rw0 (isl1:GFP) [9, 10]. Other lines referred to in this study are Tg(slc6a3:EGFP)ot80 (DAT:GFP) [11], Tg(-3.2fev:EGFP)ne0214 (pet1:GFP) [12], y264Et [13], s1181tEt [14], Tg(gad1b:GFP)nns25 (gad1b:GFP) [15], Tg(slc6a5:GFP)cf3 (glyT2:GFP) [16], Tg(-17.6isl2b:GFP)zc7 (isl2b:GFP) [17], Tg(-3.4tph2:Gal4ff)y228 (tph2:Gal4) [18], TgBAC(slc17a6b:lox-DsRed-lox-GFP)nns14 (vglut2a:DsRed) [19], Tg(slc17a6:EGFP)zf139 [20], Tg(elavl3:CaMPARI(W391F+V3987L))jf9 [21], Tg(phox2b:GFP)w37 [22], J1229aGt [23], and several Gal4 enhancer traps from ZBB: y304Et, y332Et, y341Et, y351Et, and y393Et [1]. All in vivo experimental protocols were approved by the National Institute for Child Health and Human Development Animal Care and Use Committee.

Immunohistochemistry

Immunolabeling was as described [2], with the following adaptations. Larvae were fixed overnight at 4°C in phosphate-buffered saline (PBS) with 4% paraformaldehyde and 0.25% Triton X-100. Samples were then washed in PBS containing 0.1% Triton X-100 (PBT) 3 times for 5 minutes. For antigen retrieval, samples were incubated in 150 mM Tris-HCl ph 9.0 for 5 minutes at room temperature (RT), followed by 15 minutes at 70°C and washed in PBT 2 times for 5 minutes at RT [24]. Critically, samples were then permeabilized on ice in fresh 0.05% trypsin-EDTA for no more than 5 minutes. If pigmented, samples were incubated in PBT with 1.5% H₂O₂ and 50 mM KOH for 15 minutes, rinsed 2 times in PBT, and washed again for 10 minutes, all at RT. Samples were then blocked in PBT containing 5% normal goat serum (NGS) and 0.2% bovine serum albumin (BSA) for 1 hour at RT before incubation at 4°C with tERK antibodies (Cell Signaling, 4696) diluted 1:500 in PBT with 5% NGS and 0.2% BSA for a minimum of 6 hours. Samples were then washed with PBT 4 times for 30 minutes at RT before incubation at 4°C for a minimum of 2 hours with fluorescent secondary antibodies (Alexa Fluor 488 or 548) diluted 1:1000 in PBT with 5% NGS and 0.2% BSA. Samples were finally rinsed 4 times for 30 minutes at RT prior to imaging.

Registration

Registrations were performed using the Computational Morphometry Toolkit version 3.2.3 (Computational Morphometry Toolkit, RRID:SCR_002234) and ANTs version 2.1.0 (Advanced Normalization Tools, RRID:SCR_004757) running on the National Institute of Health's Biowulf Linux computing cluster. Registrations were parallelized using Slurm-based bash scripts (available upon request). For CMTK, previously optimized registration parameters that minimize computation time while maximizing precision were used (affine parameters: registrationx –dofs 12 –min-stepsize 1; elastic parameters: warpx –fast –grid-spacing 100 –smoothness-constraint-weight 1e-1 –grid-refine 2 –min-stepsize 0.25 –adaptive-fix-thresh 0.25). For ANTs registrations, the parameters used are cited in the relevant text, and figures with optimized parameters are listed in Table 1. All deformable transformations are initiated with a rigid and affine step (parameters included in Table 1). Aside from the use of ANTs, the basic imaging and registration workflow was performed as previously described [1]. Image volumes were rendered within the Zebrafish Brain Browser, ImageJ [25], or code written in IDL (Harris Geospatial Solutions). For the conversion to/from NIfTi format required for ANTs, we used the ImageJ plugin nifti_io.jar written by Guy Williams [26].

Table 1:

ANTs command parameters for image registration

Method	Step	Function	Command
Live registration	1	Register vglut2a pattern in fish1–01.nii.gz, to the reference brain ref/vglut-ref.nii	antsRegistration -d 3 –float 1 -o [fish1_, fish1_Warped.nii.gz] –interpolation WelchWindowedSinc –use-histogram-matching 0 -r [ref/vglut-ref.nii, fish1–01.nii.gz,1] -t rigid[0.1] -m MI[ref/vglut-ref.nii, fish1–01.nii.gz,1,32, Regular,0.25] -c [200 × 200 × 200 × 0,1e-8,10] –shrink-factors 12 × 8 × 4 × 2 –smoothing-sigmas 4 × 3 × 2 × 1vox -t Affine[0.1] -m MI[ref/vglut-ref.nii, fish1–01.nii.gz,1,32, Regular,0.25] -c [200 × 200 × 200 × 0,1e-8,10] –shrink-factors 12 × 8 × 4 × 2 –smoothing-sigmas 4 × 3 × 2 × 1vox -t SyN[0.05,6,0.5] -m CC[ref/vglut-ref.nii, fish1–01.nii.gz,1,2] -c [200 × 200 × 200 × 200 × 10,1e-7,10] –shrink-factors 12 × 8 × 4 × 2 × 1 –smoothing-sigmas 4 × 3 × 2 × 1 × 0vox
	2	Apply transformation matrix from (1) to a second channel for fish 1, in file fish1–02.nii.gz	antsApplyTransforms -d 3 -v 0 –float -n WelchWindowedSinc -i fish1–02.nii.gz -r ref/vglut-ref.nii -o fish1–02_Warped.nii -t fish1_1Warp.nii.gz -t fish1_0GenericAffine.mat
Fixed registration	1	Register tERK pattern in fish1–01.nii.gz, to the reference brain ref/terk-ref.nii	antsRegistration -d 3 –float 1 -o [fish1_, fish1_Warped.nii.gz] –interpolation WelchWindowedSinc –use-histogram-matching 0 -r [ref/terk-ref.nii, fish1–01.nii.gz,1] -t rigid[0.1] -m MI[ref/terk-ref.nii, fish1–01.nii.gz,1,32, Regular,0.25] -c [200 × 200 × 200 × 0,1e-8,10] –shrink-factors 12 × 8 × 4 × 2 –smoothing-sigmas 4 × 3 × 2 × 1vox -t Affine[0.1] -m MI[ref/terk-ref.nii, fish1–01.nii.gz,1,32, Regular,0.25] -c [200 × 200 × 200 × 0,1e-8,10] –shrink-factors 12 × 8 × 4 × 2 –smoothing-sigmas 4 × 3 × 2 × 1vox -t SyN[0.1,6,0] -m CC[ref/terk-ref.nii, fish1–01.nii.gz,1,2] -c [200 × 200 × 200 × 200 × 10,1e-7,10] –shrink-factors 12 × 8 × 4 × 2 × 1 –smoothing-sigmas 4 × 3 × 2 × 1 × 0vox
	2	Apply transformation matrix from (1) to a second channel for fish 1, in file fish1–02.nii.gz	antsApplyTransforms -d 3 -v 0 –float -n WelchWindowedSinc -i fish1–02.nii.gz -r ref/terk-ref.nii -o fish1–02_Warped.nii -t fish1_1Warp.nii.gz -t fish1_0GenericAffine.mat

Volume rendering and 3D visualization

Binary masks corresponding to 25 anatomical regions from Z-Brain aligned to ZBB were converted into meshes using the Create Surfaces tool in the IntSeg_3D.jar plugin for ImageJ [27]. Edges for individual meshes were iteratively reduced below 5000, and vertices (single-precision floating points of the triangular meshes) written as OBJ files. As there is no intrinsic color or color conventions as of yet for these brain structures, we used color hue as a nominal categorical coding for each region. To maximize accessibility, we rendered meshes in Extensible 3D (X3D) format, an International Organization for Standardization standard developed by the not-for-profit Web3D Consortium [28]. This format allows portability between numerous tools and applications as well as deployment across a broad spectrum of platforms. For the rendering, OBJs were transcoded into ImageTextureAtlas PNGs using X3D’s standard IndexedFaceSet to represent mesh information and then tiled at different resolutions (4096 and 8192 pixels squared) using AtlasConversionScripts [29]. Additionally, dask and pyimg python libraries were used to generate volume norms (image and ImageTextureAtlas files) by gradient descent. All renderings were then merged into a single X3D XML scene, which was losslessly compressed (in SRC/glTF) to a final size of 4.5 MB. This makes the scene compact enough to be visualized on a cell phone, while retaining details for visualization and editing in immersive virtual reality environments. Finally, X3D files were published to HTML5 via the X3DOM library, and a simple user interface was created that allows for the visibility of different structures to be toggled on and off. Brain meshes were converted to FBX files for import into Unity using Blender 2.78a (Blender foundation, Amsterdam, the Netherlands), and mobile app development for Google Cardboard VR headsets was performed in Unity 5.4.2 (Unity Technologies SF, San Francisco, CA, USA) using the Google VR for Unity SDK (Google, Mountain View, CA, USA). Custom scripts controlling movement and mesh display were written for Unity in C#.

Measurements

Mean landmark distance

To assess registration precision using mean landmark distances (MLDs), corresponding landmarks were located and annotated on the reference brain and on unregistered brains. In each case, landmarks were chosen to be widely distributed within the brain and readily recognized in corresponding brain scans. In addition, to verify recognizability, the vglut2a landmarks in the reference brain were located by 3 blinded scorers; the mean distance from each of the 10 reference points ranged from 1.7 to 11.8 μm (mean = 4.5 ± 0.9 μm). Using ImageJ, we positioned a 3-micron cube centered on each landmark in a second channel for each brain scan; then, after registering the brain scan using the first channel, we applied the resulting transformation matrix to the second channel, using nearest neighbor interpolation for both CMTK and ANTs. Landmark distance was taken as the distance between the geometrical center of the corresponding cubes in the reference image and in the registered image.

Hausdorff distance

We manually segmented cells in a vglut:DsRed brain scan in a second channel and applied transformation matrices for registration to this second channel. Segmented cells were broadly distributed to ensure that distortion measures sampled the entire brain and cell masks conservatively drawn within the boundaries of the soma. We then compared the morphology of cells after registration (A) to their original shape (B) by calculating the partial Hausdorff distance [30]. Briefly, for every point in a segmented cell mask before registration, we found the minimum distance to a point in the same mask after registration. The Hausdorff distance is the maximum of all such distances, calculated for both A→B and B→A. Because the Hausdorff distance is highly sensitive to cell alignment and registration displaces cells from their original location, we found the optimal alignment for comparisons using a 2-step process. First, we aligned the geometric center of each cell in the original and transformed images. Second, we searched for the minimal Hausdorff distance across 4940 rigid transformations of the aligned cell within a 3 × 3 × 3 micron cube (0.25 micron steps in each dimension). Finally, as Hausdorff distances are sensitive to outliers, we used the 95th percentile distances instead of the maximum Hausdorff distance for all measures [30].

Cell volume

For each segmented cell, we calculated its change in volume as the absolute value of the fractional change in the number of pixels after application of a transformation matrix.

Elongation index

For each pixel in a segmented cell, we found the maximal distance (MD) to any other pixel in the mask. The elongation index for a given cell was the 95th percentile largest value of MD, which we take as an approximation of the diameter of the cell across its longest axis.

Cross correlation

Cross correlation between the tERK-stained reference brain and registered tERK stains was performed using the c_correlate function within IDL version 7.0. Correlations were run within 18 50-μm side cube sub-regions of the image volumes that were manually selected to encompass high-contrast boundaries, and the mean of the 18 values was taken as the mean cross correlation (MCC) for each brain in Fig. 3.

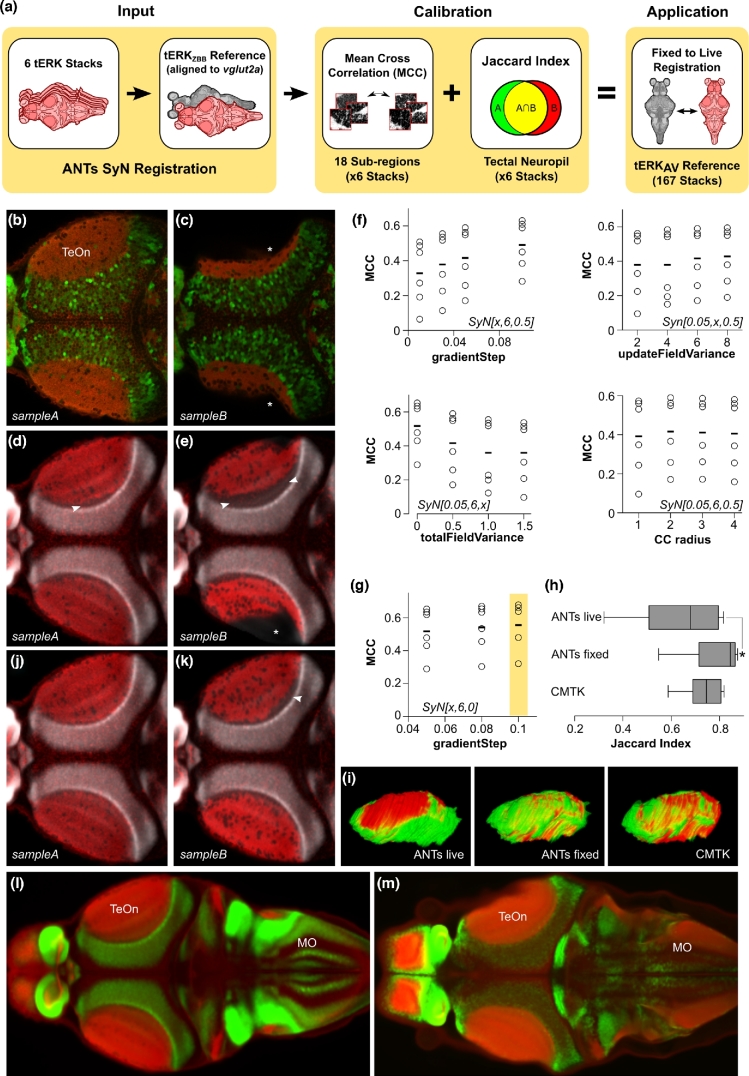
Figure 3:

Optimization of ANTs registration parameters for fixed tissue. (a) Overview of parameter optimization for fixed brain scans using ANTs. A calibration set of 6 tERK confocal stacks with segmentations of the tectal neuropil was registered to tERK_ZBB, a tERK and vglut2a:DsRed confocal scan previously aligned to the vglut2a_ZBB reference (left). MCCs were calculated between 18 50-μm side cube high-contrast sub-regions in the calibration set and in the tERK_ZBB reference to identify parameters that maximized MCC (f, g) and improved the Jaccard index of tectal neuropil segmentation (h) while compensating for fixation artifacts (c, e, k) (middle). These optimized ANTs parameters allow for the accurate registration of fixed tissue and the generation of a tERK average reference (tERK_AV) useful for bridging live and fixed tissue registrations (right). (b, c) Horizontal section through the optic tectum of tERK immunostained (red) vglut2a:DsRed (green) larvae, using diluted (b, sample A) or fresh trypsin (c, sample B). The asterisk indicates a missing area of tectal neuropil due to permeabilization artifact. (d, e) Horizontal section through the same stacks as in (b, c) registered to tERK_ZBB using the parameters previously optimized for live registration. Gray shows the ZBB_1.2vglut2a:DsRed pattern. Arrowheads highlight regions where tERK in the optic tectum neuropil fails to closely abut the adjacent glutamatergic cellular layer. (f) MCC for tERK expression after registration of 6 brains to tERK_ZBB, varying each of the parameters for the ANTs SyN transform, starting with the parameters that gave the best registration for live vglut2a:DsRed-based registration (SyN[0.05,6,0.5]). Bottom right: MCCs after varying the radius of the cross correlation metric used during registration. (g) MCCs for tERK in the same brains as in (f) after combining the 2 best parameter sets from (f) (SyN[0.1,6,0.5] and SyN[0.05,6,0]) to assess further improvement in registration precision. The yellow box highlights the final optimal parameter set. (h) The Jaccard index for the overlap of the manually segmented tectal neuropil of the reference brain, with each of the 6 brains in the calibration set. P < 0.01. (i) 3D view of the overlap between segmented tectal neuropils from tERK_ZBB (red) and the Z-Brain tERK reference brain (green), after registration with ANTs using parameters optimal for live registration, fixed registration, and CMTK. (j, k) Same brains as in (d, e), but after registration to tERK_ZBB using the parameters optimized for fixed tissue registration. (l, m) Horizontal section through the optic tectum showing tERK expression (red) and vglut2a:DsRed expression (green) in ZBB_1.2 (l) and Z-Brain (m). Matching slices within the optic tectum were selected; because the rotation around the y-axis is slightly different, sections are different within the medulla.

Jaccard index

Anti-tERK immunohistochemistry intensely stains tectal neuropil. Thus for measuring the accuracy of registration of the tectal neuropil, we manually segmented the left tectal neuropil area in 6 confocal scans of tERK-stained larvae and our reference brain. We applied transformation matrices to these masks, then calculated the Jaccard index as the volume of the intersection between each registered mask (A) and the reference brain (B), divided by the total volume of the union of A and B.

Results

Optimization of ANTs-based registration of live vglut2a:DsRed image scans

Brain registration in Z-Brain and ZBB used the B-spline elastic transformation in CMTK. Before attempting to co-align Z-Brain and ZBB, we tested an alternate algorithm for brain alignment, the SyN method in ANTs, because: (i) SyN has been shown to outperform B-spline transformations for deformable image registration in a variety of imaging modalities [31, 32]. (ii) ANTs permits registration using multiple reference channels, potentially allowing the use of multiple complementary expression patterns as references for improved registration fidelity. (iii) By calculating forward and reverse transformations simultaneously, SyN transformation matrices are intrinsically symmetric, ensuring that bridging registrations would be unbiased and that we could easily perform reciprocal transformations to register each dataset into the other's coordinate system.

To calibrate registration parameters, we assessed the alignment precision and distortion of cell morphology after the registration of 6 representative vglut2a:DsRed scans to the original vglut2a:DsRed reference brain in ZBB (vglut2a_ZBB; file vglut-dsred-ref-01.nii.gz) (procedure summarized in Fig. 1a) (available from [33]). Similar to CMTK, we employed a 3-step registration within ANTs where rigid and affine steps were used to initialize a deformable registration using the SyN diffeomorphic transformation with cross correlation (CC) as the similarity metric. We tested a range of values for each of the SyN parameters as well as the radius of the region used for cross correlation.

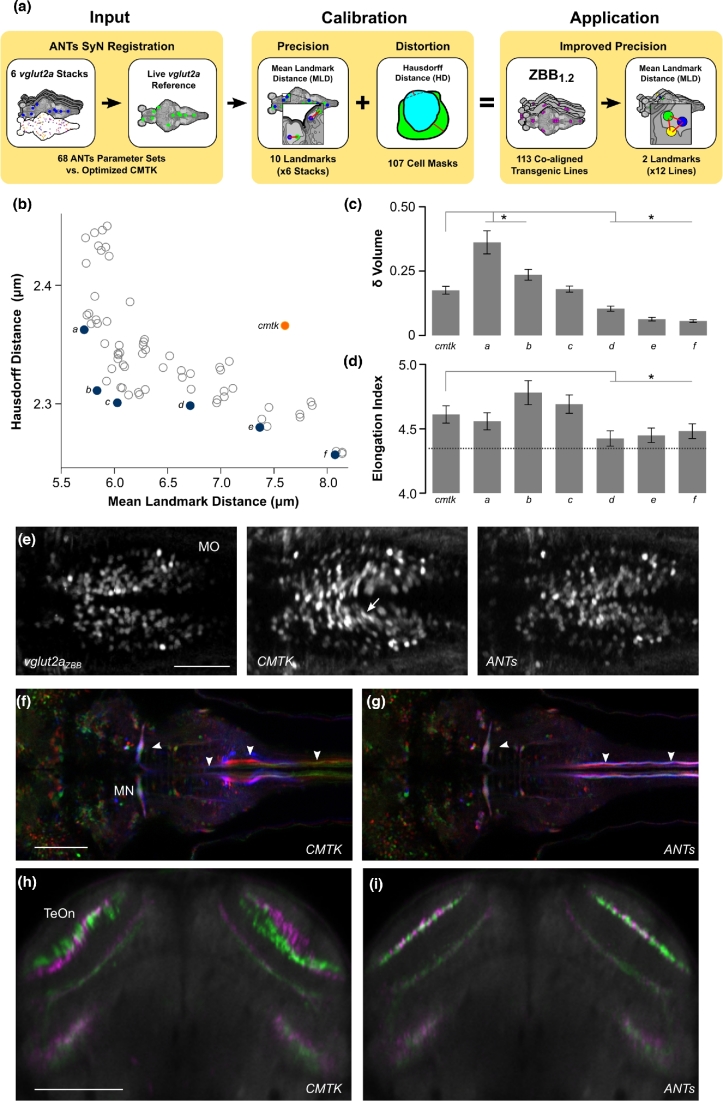
Figure 1:

Optimization of parameters for registration of live brain scans using ANTs. (a) Overview of parameter optimization for live brain scans using ANTs. A calibration set of 6 vglut2a:DsRed confocal stacks with 10 point-based landmarks and 107 cell masks was registered to the vglut2a_ZBB reference with the same 10 point-based landmarks defined (left). MLDs for landmarks and Hausdorff distance for transformed cell masks compared to their originals were measured for each parameter set (middle). Optimal parameters selected from these metrics (b–d) were used to re-register all lines generating ZBB_1.2 where MLD was measured from 2 additional landmarks in each of 12 co-aligned patterns (right). (b) Hausdorff distance for cell shape comparison plotted against MLD for 68 sets of parameters tested using ANTs (gray and blue circles) and after registration using CMTK (orange). Blue circles labeled a–f indicate the Pareto frontier. (c) Mean absolute change in cell volume (as a fraction of the original volume) produced by transformations resulting from parameter sets a–f and CMTK in (b). *P < 0.05, compared to CMTK. (d) Mean elongation index for cells after registration using parameter sets a–f and CMTK in (b). Dashed line shows index for cells before registration—all transformations produced a significant increase compared to the untransformed cells. *P < 0.05, compared to CMTK. (e) Horizontal section through the medulla oblongata in vglut2a_ZBB and of a representative vglut2a:DsRed brain after registration using CMTK or ANTs. Distortion artifacts are indicated (arrow). Scale bar = 50 μm. (f, g) Horizontal section in J1229aGt showing expression of GFP in the Mauthner cell and axon (arrowheads) for 3 individual larvae (pseudo-colored red, green, and blue). Registration was performed with CMTK (f) or ANTs (g). Scale bar = 100 μm. (h, i) Transverse section through the optic tectum in 2 separate average brain images (colored green and magenta) for y393Et. For each brain image, we independently scanned 3 individual brains and registered them using CMTK (h) or ANTs (i). Scale bar 100 μm.

To measure registration precision, we visually located 10 point-based landmarks in the vglut2a_ZBB pattern (Additional file 1a-c; file vglut-dsred-ref-01-landmarks.nii.gz) (available from [33]) and in each of the 6 vglut2a:DsRed confocal scans. We then used the vglut:DsRed channel for registration and applied the resulting transformation matrix to the landmarks in each of the 6 brains. We measured the distance of each landmark from its location in the vglut2a_ZBB reference brain (Additional file 1a and d). We designated the average of the 10 distances the MLD. To assess the amount of distortion in cell shapes produced by the parameter sets, we segmented 107 cells in an unregistered vglut2a:DsRed confocal scan (Additional file 2), and applied each transformation matrix to this set of cell masks. Changes in cell shape were measured using the partial Hausdorff distance for each cell after registration compared to its original shape (see the Methods section).

Next, we plotted the MLD against the Hausdorff distance and located points along the Pareto frontier (Fig. 1b) of these 2 measures. These points represent potentially optimal transformations, where registration accuracy can only be improved by increasing distortion, or vice versa. To distinguish between these points, we examined 2 additional measures of distortion: the change in cell volume (Fig. 1c) and maximal elongation (Fig. 1d). Three transformations showed statistically significantly reduced distortion compared to CMTK for both measures, and we selected the one (Fig. 1b, point d) with the greatest precision for further testing. With this set of parameters (see Table 1, live registration), mean registration error was within the diameter of a single neuron for both ANTs and CMTK (MLD for ANTs = 6.7 ± 0.3 μm, MLD for CMTK = 7.6 ± 0.4 μm; n = 6 brains, paired t test P = 0.056). However, cell morphology was better preserved using ANTs (Hausdorff distance for ANTs = 2.30 ± 0.14, Hausdorff distance for CMTK = 2.37 ± 0.14; n = 107 cells, paired t test P = 0.013), especially within ventral structures such as the hypothalamus and the caudal medulla oblongata (Fig. 1e).

We next examined whether these registration parameters also improved precision for the co-aligned transgenic lines. For ZBB, we co-scanned transgene and enhancer trap expression patterns with the vglut2a:dsRed transgene, allowing us to register each expression pattern to vglut2a_ZBB. We first compared the overlap and morphology of the Mauthner cells from brain scans of 3 different individuals of transgenic line J1229aGt [23]. Overlap of Mauthner cell bodies was similar for CMTK and ANTs (Fig. 1f and g). However, in CMTK registered images, the Mauthner axon was distorted in the caudal medulla, whereas axon morphology was preserved with ANTs. Second, in our previous work, we assessed the precision of CMTK registration using line y339Et by independently scanning 2 sets of 3 larvae, producing an average for each set, and visually comparing the result. With CMTK, we had noted misalignment of approximately 1 cell diameter in the neuropil of the optic tectum (Fig. 1h). This was substantially improved with ANTs, where there was much closer alignment of the 2 averages (Fig. 1i).

Improved precision of ZBB after registration using ANTs

We next recompiled ZBB using ANTs to register the entire set of 354 brain scans from 109 different transgenic lines that were part of ZBB, then, as before, averaged multiple larvae to create a representation of each transgenic line, masked the average stacks to remove expression outside the brain, and re-imported the resulting images into our Brain Browser software. We refer to this new recompilation of the atlas as ZBB_1.2. Unprocessed and registered brain images are available online [35].

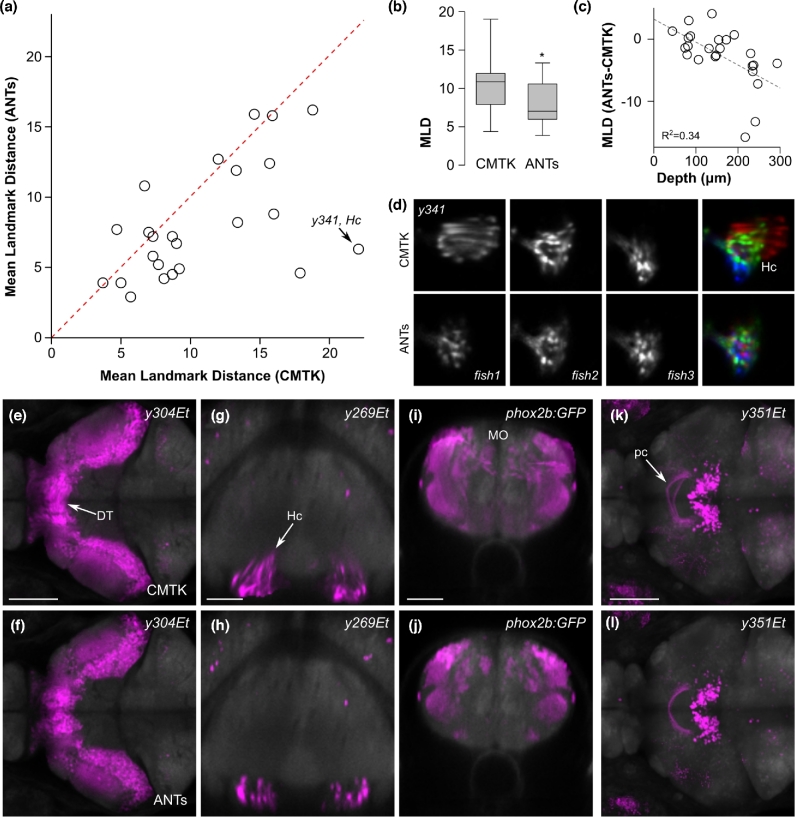
To determine whether ZBB_1.2 was a quantitative improvement over ZBB, we identified 2 conspicuously labeled cells or landmarks in each of 12 transgenic lines from the atlas (Additional file 3). We marked these positions in each of the 3 brain scans for each line, then, after registration, calculated the distance between corresponding points in each pair of brains. The mean of these distances measures how precisely landmarks are registered across the 3 brains. We performed this procedure first for brains registered using CMTK, then for the same set of brains registered using ANTs, allowing us to compare MLDs for the 2 methods (Fig. 2a and b). Overall, landmark distances decreased from ZBB to ZBB_1.2 (10.8 ± 1.02 μm to 8.1 ± 0.83 μm; n = 24 landmarks, paired t test P = 0.008), indicating that ZBB_1.2 has significantly improved precision, and confirming that the new atlas is accurate to approximately the diameter of a single neuron. The improvement was greatest deeper in the brain (linear regression, n = 24, P = 0.003) (Fig. 2c), with the largest improvement for the caudal hypothalamus in line y341, where increased alignment precision was associated with noticeably reduced distortion between the 3 brain scans (Fig. 2d).

Figure 2:

Improved precision of transgene representations in ZBB_1.2. (a) Mean landmark distances for 24 landmarks, after registration with CMTK and ANTs. Dotted line indicates 1:1 ratio. (b) Boxplot of data in (a). *Paired t test, n = 12 lines, P = 0.019. (c) Difference in MLD between ANTs and CMTK plotted against distance from the dorsal-most point in the brain. (d) Horizontal section through the caudal hypothalamus of 3 individual y341Et larvae as well as their pseudo-colored superimposition following registration with CMTK (top row) or ANTs (bottom row). (e, f) Horizontal section through the thalamus showing the averaged representation of enhancer trap line y304Et, where individual brains were registered with CMTK for ZBB (e), or with ANTs for ZBB_1.2 (f). Arrow indicates neurons that are artificially elongated across the midline. Scale bar = 100 μm. (g, h) Transverse section through the caudal hypothalamus showing the average enhancer trap line y269Et brain registered with CMTK (g) or with ANTs (h). Arrow shows distortion of cells, causing the caudal hypothalamus to appear dorsally elongated. Scale bar = 50 μm. (i, j) Transverse section through the medulla oblongata showing the average phox2b:GFP brain with CMTK (i) or ANTs (j). Scale bar = 50 μm. (k, l) Horizontal projection through the posterior commissure (arrow) for the average y351Et brain obtained with CMTK (k) or ANTs (l). Scale bar = 100 μm.

Additionally, we inspected regions of ZBB_1.2 where we had noticed poor registration precision or pronounced cell distortion in the original ZBB. One such area was the dorsal thalamus, where cell morphology was noticeably perturbed after elastic registration with CMTK, with cell somas stretching across the midline (Fig. 2e). In ZBB_1.2, cells retained a rounded morphology with distinct cell clusters on the left and right sides of the brain (Fig. 2f). Similarly, distortions in cell shape that were apparent in the caudal hypothalamus in ZBB were absent in ZBB_1.2 (Fig. 2g and h). In the caudolateral medulla, we previously obtained poor registration, with expression extending to regions outside the neural tube (Fig. 2i). In ZBB_1.2, patterns had improved bilateral symmetry and were correctly confined to the neural tube (Fig. 2j). Finally, we noticed that the posterior commissure was poorly aligned between larvae, leading to a defasciculated appearance in ZBB (Fig. 2k), whereas this tract had the expected tightly bundled appearance in ZBB_1.2 (Fig. 2l). Together, these observations confirm that ZBB_1.2 is a more faithful representation of the transgenic lines. Not only is cell morphology better preserved, but global registration precision is improved compared to the original ZBB atlas.

Optimization of ANTs registration parameters for fixed tissue

The Z-Brain atlas was derived by registering brain scans to a single brain that was fixed, permeabilized, and immunostained for tERK expression. We therefore anticipated that tERK would be a useful channel for bridging the 2 atlases if we could first successfully register a tERK-stained vglut2a:DsRed-expressing brain to ZBB_1.2. Therefore, we fixed and stained a transgenic vglut2a:DsRed larva for tERK and registered the tERK pattern to ZBB_1.2 using the vglut2a pattern. We used the resulting image as our ZBB tERK reference brain (tERK_ZBB; file terk-ref-02.nii.gz) (available from [33]).

In addition to the tERK reference brain, Z-Brain contains an average tERK representation from 197 tERK-stained larvae, which we thought might serve as a bridge between atlases. During studies on pERK-based activity mapping, we had previously generated a dataset of 167 tERK-stained brains and therefore used these to create our own average tERK representation by registering them to tERK_ZBB. However, during this process, we noticed a high degree of variability between tERK-stained brains, most salient in poor labeling of ventral brain structures and in deformation of the optic tectum neuropil. Immunohistochemistry for tERK proved highly sensitive to staining parameters, with the trypsin activity, permeabilization duration, and antigen retrieval having the strongest effects. Variability in fixed tissue was most apparent in the optic tectum, where high trypsin activity tended to disrupt morphology and reduce the volume of the tectal neuropil (Fig. 3b and c). These local distortions were not resolved by deformable image registration: alignment to tERK_ZBB with the same parameters optimized for live vglut2a-based registration failed to correct the reduced tectal neuropil volume (Fig. 3d and e, asterisk) and often created an artifact where the neuropil zone failed to abut the underlying cellular layer labeled by vglut2a expression (Fig. 3d and e, arrowheads).

We therefore varied the registration parameters that were optimal for live vglut2a registration to find settings that best rectified the variable tissue morphology following fixation and permeabilization (process summarized in Fig. 3a). For optimization of fixed tissue registration, we used a set of 6 tERK-stained brains (including the Z-Brain tERK reference), iteratively varied parameters for registration to tERK_ZBB, and assessed registration fidelity. For measuring precision, we were not able to identify unambiguous landmarks within the optic tectum, so we instead calculated the cross correlation between each of the aligned tERK stains and tERK_ZBB within small volumes, including parts of the tectum (Fig. 3f and g). To verify that the “fixed brain” parameters that yielded the greatest cross correlation did in fact improve registration within the tectum, we manually segmented the tectal neuropil in the same 6 brains, applied the transformation matrix to each mask, and calculated the Jaccard index for overlap with the segmented neuropil in tERK_ZBB. Parameters for fixed brain registration produced a significant increase in overlap compared to the live brain parameters (Fig. 3h and i), and visual inspection confirmed that the morphology of the optic tectum neuropil after registration was greatly improved (Fig. 3j and k). We therefore used ANTs with the fixed brain parameters (Table 1, fixed registration) to register our 167 tERK-stained brains to tERK_ZBB and generated an average tERK representation comparable to the 197 tERK average in Z-Brain (Fig. 3l and m).

Inter-atlas registration using multi-channel diffeomorphic transformation

Z-Brain and ZBB incorporated 8 expression patterns that we judged sufficiently similar to act either as templates for bridging the datasets and/or to provide metrics for assessing the precision of a bridging registration (Table 2; Additional file 4). For example, vglut2a_ZBB is a confocal scan of DsRed in a single larva from transgenic line TgBAC(slc17a6b:loxP-DsRed-loxP-GFP)nns14, whereas Z-Brain includes Tg(slc17a6:EGFP)zf139. In both cases, reporter expression is regulated by the same bacterial artificial chromosome [15, 20]. Crossing these 2 lines allowed us to scan DsRed and EGFP in the same larva and confirm that the patterns were largely congruous, potentially allowing us to use vglut2a expression to bridge the 2 atlases. Likewise, the expression patterns of tERK, elavl3, isl2b, and vmat2 in Z-Brain and ZBB appeared sufficiently similar to provide templates for atlas co-registration.

Table 2:

Brain images in ZBB and Z-Brain that were used as templates for registration and/or for measurement of registration precision

ZBB			Z-Brain		Used as registration channel	Used as quantification metric
Tg(vGlut2a:DsRed)nns14	Mean of 346 brains	↔	Tg(vGlut2a:EGFP)zf139	Mean of 15 brains	y	y
Tg(vGlut2a:DsRed)nns14	Single reference brain	↔	Tg(vGlut2a:EGFP)zf139	Mean of 15 brains	y	n
Tg(elavl3:CaMPARI)jf9	Mean of 3 brains	↔	Tg(elavl3:GCaMP5G)a4598	Mean of 7 brains	y	n
Tg(vmat2:GFP)pku2	Mean of 3 brains	↔	Tg(vmat2:GFP)pku2	Mean of 55 brains	y	y
Tg(isl2b:GFP)zc7	Mean of 3 brains	↔	Tg(isl2b:Gal4)zc60	Mean of 8 brains	y	y
tERK immunostain	Mean of 167 brains	↔	tERK immunostain	Mean of 197 brains	y	y
tERK immunostain	Single brain	↔	tERK immunostain	Single reference brain	y	n
Tg(isl1:GFP)rw0	Mean of 3 brains	↔	Tg(isl1:GFP)rw0	Mean of 17 brains	n	y
TgBAC(gad1b:GFP)nns25	Mean of 4 brains	↔	TgBAC(gad1b:GFP)nns25	Mean of 10 brains	n	y
Tg(glyT2:GFP)cf3	Mean of 6 brains	↔	Tg(glyT2:GFP)cf3	Mean of 13 brains	n	y

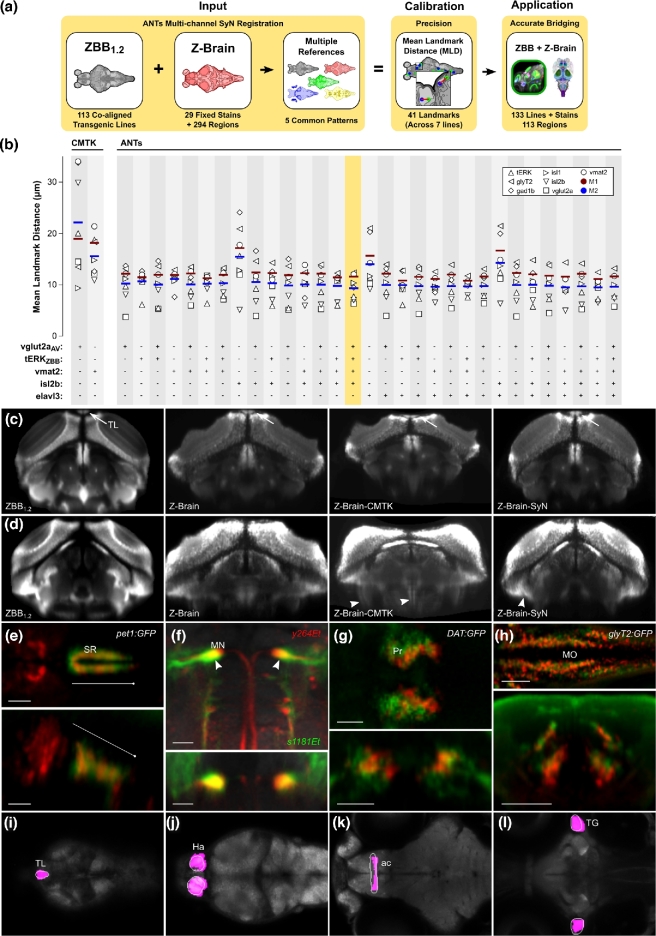
Taking advantage of the ability of ANTs to use multiple reference channels concurrently, we compared the effect of combinatorial use of complementary reference channels for inter-atlas registration (process summarized in Fig. 4a). We used 7 expression patterns to evaluate registration precision: vglut2a, isl2b, vmat2, tERK, isl1, gad1b, and glyT2. For each pattern, we identified a set of 4–10 point-based landmarks that could be identified in corresponding ZBB and Z-Brain images and that were widely distributed to represent diverse brain regions (total of 41 landmarks) (Additional file 5). We marked these points in each set of images, registered Z-Brain images to ZBB_1.2 images, measured the distance between cognate landmarks, and calculated the mean landmark distance for each of the 7 expression patterns. We used 2 summary measures of registration precision. The first metric (M₁) was the mean of MLDs for the 3 patterns that were not used to drive registration (isl1, gad1b, and glyT2). Although these channels measure precision independent of the patterns for atlas registration, they are relatively sparse and do not assess precision across the whole brain. Thus, to provide a global measure of precision, we also used a second metric (M₂) that was the mean of all 7 MLDs: those in M₁ plus 4 of the patterns used as references for registration—vglut2a, tERK, isl2b, and vmat2.

Figure 4:

Transformation between Z-Brain and ZBB coordinate systems using multi-channel registration. (a) Overview of bridging Z-Brain and ZBB using ANTs multi-channel registration. Combinations of 5 patterns common between Z-Brain and ZBB (vglut2a_AV, tERK_ZBB, vmat2, isl2b, and elavl3) were used guide multi-channel bridging registrations (left). MLDs for 41 landmarks in gad1b, glyT2, isl1, isl2b, tERK, vglut2a, and vmat2 expression were measured for all reference channel combinations (middle). The combination of vglut2a_AV, tERK_ZBB, vmat2, and isl2b enabled the most accurate bridging of ZBB and Z-Brain, allowing the combination of the large collection of live transgenic lines of ZBB with the fixed tissue techniques and expert neuroanatomic segmentations of Z-Brain (right). (b) MLDs for the expression patterns of gad1b, glyT2, isl1, isl2b, tERK_ZBB, vglut2a, and vmat2 and M₁ and M₂ metrics after registration of Z-Brain to ZBB_1.2 using either CMTK or ANTs SyN with fixed tissue registration parameters and the indicated combination of reference channels (vglut2a, tERK_ZBB, vmat2, isl2b, and elavl3). Note, similar results were obtained using tERK_AV instead of the tERK_ZBB, but they are omitted for clarity. The combination of reference channels selected for co-registration of Z-Brain and ZBB is highlighted. (c) Transverse section through the caudal optic tectum showing the vglut2a pattern in ZBB_1.2, Z-Brain, Z-Brain after registration to ZBB with CMTK (Z-Brain-CMTK), or with ANTs (Z-Brain-SyN). The torus longitudinalis (TL) is well separated from tectal neurons in live scans, but less so in fixed tissue (arrows). The TL appears flattened after CMTK registration but retains normal morphology after registration with ANTs SyN. (d) Transverse sections as in (c), but slightly more caudal, with contrast increased to highlight ventral distortion artifacts produced by registration (arrowheads). (e–h) Brain Browser views in the ZBB_1.2 coordinate (e, f) or Z-Brain coordinate (g, h) space. Scale bars = 25 μm, except 50 μm in (e). (e) Horizontal (top) and sagittal (bottom) sections, comparing the pet1:GFP expression pattern in the superior raphe in ZBB_1.2 (red) and Z-Brain after transformation to the ZBB coordinate system (green). (f) Horizontal (top) and transverse (bottom) sections through the medulla oblongata, showing the expression of y264Et from ZBB_1.2 (red) and s1181Et from Z-Brain after transformation to ZBB_1.2 (green), which both label the Mauthner cells (arrowhead). (g) Horizontal (top) and transverse (bottom) sections through the pretectum, comparing the expression of DAT:GFP from ZBB_1.2 after transformation to Z-Brain (red) and anti-tyrosine hydroxylase staining in Z-Brain (green). (h) Horizontal (top) and transverse (bottom) sections through the medulla oblongata for glyT2:GFP from ZBB_1.2 after transformation to Z-Brain (red) and the same transgenic line in Z-Brain (green). (i–l) Brain Browser horizontal sections showing manually segmented regions transformed from the Z-Brain coordinate system to ZBB_1.2 (white outlines) compared to regions previously defined in ZBB obtained by thresholding expression patterns in transgenic lines (magenta). Regions are the torus longitudinalis (i), habenula (j), anterior commissure (k), and trigeminal ganglion (l).

Using CMTK, minimal M₁ and M₂ scores were obtained using the average vmat2 pattern as the reference (mean MLD for 41 landmarks = 14.9 ± 1.3 μm) (Fig. 4b). We therefore registered all images in Z-Brain to ZBB using the vmat2 average in each dataset as the reference channel. We observed severe tissue distortions in several brain regions, with noticeable flattening of the torus longitudinalis, as well as gross tissue distortions, particularly in ventral brain regions (ZBrain-CMTK) (Fig. 4c and d). Next we used the ANTs SyN algorithm to register the atlases. Ideally, patterns for registration should include information throughout the brain. Because ANTs can use multiple concurrent reference channels to derive an optimal transformation matrix, we speculated that the best possible transformation would be achieved by a combination of channels with complementary information. We therefore produced an inter-atlas transformation matrix for every combination of the elavl3, isl2b, vglut2a_AV (vglut2a average brain), vmat2, tERK_ZBB (tERK single brain), and tERK_AV (tERK average brain) patterns as references. Because Z-Brain used fixed samples, we used the registration parameters optimized for the greater variability present in fixed tissue. Multi-channel registration significantly reduced M₁ and M₂ values compared to any single channel alone and to transformations obtained using CMTK. The registration obtained with vglut2a, tERK_ZBB, vmat2, and isl2b gave the lowest global metric (M₂) value and an M₁ score within 10% of the lowest scoring combination (Fig. 4b). With these parameters, the MLD was 9.1 ± 0.8 μm (N = 41 landmarks), and the overt tissue distortions noted after elastic registration were far less salient (ZBrain-SyN) (Fig. 4c and d). We therefore applied the transformation matrix obtained with this set of channels to the database of gene expression patterns in Z-Brain to align them to ZBB_1.2 and used the inverse of the transformation generated by SyN to register ZBB_1.2 to the Z-Brain coordinate system. We imported all Z-Brain expression patterns not previously represented in the database into ZBB_1.2, producing a total of 133 expression patterns.

The accuracy of the inter-atlas registration is evident when comparing the location of cells that are present in both datasets, such as those labeled pet1:GFP. The Z-Brain transformed pattern closely matches the transgene expression pattern in ZBB_1.2 within the superior raphe (Fig. 4e—note, however, that unexpectedly, the line in ZBB_1.2 also labels a set of more rostral cells not apparent in Z-Brain). Both atlases also include lines labeling the Mauthner cells. After registration, Mauthner cells in the atlases substantially overlapped, although they were several microns more medially positioned in ZBB_1.2 (Fig. 4f). Expression in the DAT:GFP line in ZBB_1.2 overlapped well with the tyrosine hydroxylase stain from Z-Brain in the pretectum (Fig. 4g), although, again, the ZBB_1.2 pattern was slightly more medial than in Z-Brain. Caudally, the glyT2:GFP transgenic line labels glycinergic neurons in longitudinal columns in the medulla oblongata [36]. These columns were closely aligned after ZBB_1.2 was registered to Z-Brain (Fig. 4h).

Although best practice is to align directly to either ZBB or Z-Brain, because many researchers will have already registered data sets to either ZBB or Z-Brain, or for cases where it may not be possible to directly register a dataset, we have provided transformation matrixes and detailed instructions to quickly re-align datasets to either of the coordinate systems (Additional file 6) [37].

Neuroanatomical visualization

Z-Brain includes 294 masks that represent anatomically defined brain regions or discrete clusters of cells present in transgenic lines. We selected 113 of these masks that delineate neuroanatomical regions and transformed them into the ZBB_1.2 coordinate system. We had previously defined a small number of our own anatomical masks by thresholding clusters of neuronal cell bodies located in well-defined brain regions. However, the Z-Brain masks are more comprehensive, have smoother boundaries, and include both the cell bodies and neuropil for a given region (Fig. 4i–l). We therefore imported the Z-Brain masks into ZBB_1.2, replacing most of our existing masks. We also modified the Brain Browser software to automatically report the neuroanatomical identity of a selected pixel or to display the boundaries of the region encompassing a selected point. The updated software and rebuilt database in ZBB_1.2 can be downloaded from our website [38].

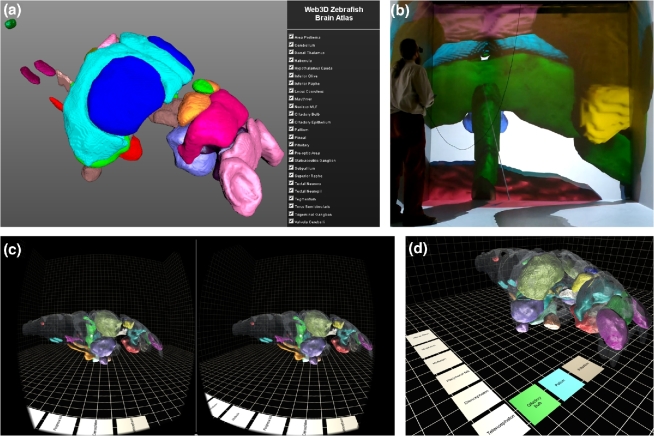
Finally, as the Zebrafish Brain Browser's strength is primarily in 2 dimensions (i.e., the visualization of horizontal, transverse, and sagittal slices through the brain), we decided to develop interactive tools to better facilitate 3D exploration. The use of 3D graphics to represent complex structure can also provide a more intuitive sensory experience that avoids cognitive bias or misinterpretation inadvertently introduced by 2-dimensional reductions [39, 40]. By taking advantage of stereoscopy and vestibular-enhanced parallax (head tracking), the more immersive and holistic experience of virtual reality (VR) can also significantly improve performance of basic tasks like searching and making comparisons [41, 42]. We therefore implemented our Zebrafish Brain Browser in both an open Web3D platform (X3D) and a custom game engine (Unity). First, we converted masks representing anatomical regions to meshes and built a Web3D interface using X3D to inspect the spatial relationship between different brain regions (Fig. 5a and b), available online [43]. Users can navigate within the brain using any web browser, rotating and zooming into brain regions to better interrogate larval neuroanatomy. Second, using the Unity platform, we wrote a VR app to view the brain and neuroanatomical regions. By running the app on a cell phone and inserting it into an inexpensive Google cardboard viewer, users can “walk into” the brain and see from the inside the inter-relationship between neuroanatomical domains (Fig. 5c and d) [44].

Figure 5:

3D visualization of brain browser data. (a) X3D zebrafish brain shown in HTML5 web browser and (b) Virginia Tech HyperCube (CAVE). (c) Virtual reality brain rendered using the Unity Game Engine for stereoscopic viewing using the Google Cardboard viewer. (d) In the VR browser, brain regions are selected using a menu on the floor of the virtual arena.

Discussion

Digitized data-derived brain atlases provide an opportunity to continuously integrate new information and iteratively improve data accuracy within a common spatial framework. Thus, as methods evolve and technology improves, new insights can be easily added to existing data to provide an increasingly rich view of brain structure and function. Because the entire larval zebrafish brain can be rapidly imaged at cellular resolution, it is possible to envisage an atlas that combines detailed information on cell type (including gene expression and morphology), connectivity, and activity under a variety of different physiological conditions. At present, biological variability presents an obstacle as brain regions contain multiple intermingled cell types that are not positioned in precisely the same manner between larvae. To compensate for this in the existing zebrafish brain atlases, multiple individuals of a given line are sampled and averaged to generate a representative expression pattern. Current atlases are thus essentially heat maps of gene expression or activity. Despite this spatial ambiguity, aggregating information from different sources into the same spatial framework still provides valuable indicators of cell type, gene co-expression, and neural activity under defined conditions.

Ideally different atlas projects might use the same reference brain; however, in practice the choice of a reference is often dictated by study-specific experimental requirements. For example, despite the deformations introduced by fixation and permeabilization, a fixed brain is essential for activity mapping using pERK immunohistochemistry. In contrast, we were able to take advantage of the optical transparency of larvae to rapidly scan and register several hundred individuals representing more than 100 different transgenic lines. For our purposes, the TgBAC(slc17a6b:loxP-DsRed-loxP-GFP)nns14 line was ideal because, through Cre injection, we generated a vglut2a:GFP line with an almost identical pattern, allowing us to co-register lines with either GFP or RFP fluorescence. However, we have also used pan-neuronal Cerulean or mCardinal as a reference channel when green and red channels both contain useful information on transgene expression. Our work now demonstrates that it is feasible to contribute to community efforts at building an integrated map of brain structure, expression, and activity, while allowing reference image selection to be guided by technical considerations.

One caveat to this conclusion is that deformable image registration can easily introduce artifacts into cell morphology if parameters are not carefully monitored and constrained. Indeed, a special challenge for brain registration in zebrafish is preserving the local morphology of neuronal cell bodies and axons while permitting sufficient deformation to correct for biological differences and changes in brain structure arising from tissue fixation and permeabilization. Thus, while B-spline registration with CMTK produced acceptable inter-atlas alignment, it also introduced noticeable distortions into local brain structure that affected neuronal cell morphology. Such artifacts were particularly severe in ventral brain regions such as the caudal hypothalamus, and may therefore be due to differences in ventral signal intensity between the datasets. In ZBB, in order to compensate for the increase in light diffraction with tissue depth, we systematically increased laser intensity with confocal scan progression (z-compensation). As a result, the Z-Brain and ZBB datasets are comparable in dorsal brain regions, but there is a noticeable discrepancy ventrally, which may account for the loss of registration fidelity. Alternatively, although z-compensation partially corrects for reduced fluorescent intensity, there is a noticeable drop-off in image resolution in ventral regions; the resulting loss of information may lead to lower-quality registration. Registration algorithms that allow parameters to vary by depth may ameliorate the effects of these physical imaging constraints.

Nevertheless, the symmetrical diffeomorphic transformation in ANTs provides a solution to these problems. For live tissue, we found parameters that allowed the ANTs SyN transform to achieve similar or better registration precision than previously achieved using CMTK, while significantly reducing distortions in tissue structure and neuronal cell morphology. In our hands, permeabilization of fixed tissue tended to produce variable changes in neuropil structure, which was most salient in the optic tectum. Specifically, neuropil volume was diminished when fresh aliquots of trypsin were used for extended durations. These artifacts can be minimized by stringent oversight of reagent viridity. However, by calibrating SyN parameters to permit larger deformations, we were able to accommodate the variability introduced in tissue processing.

Currently, limitations of the SyN registration algorithm in ANTs are the large memory demands (73 GB for a single channel registration) and long computational times (3–5 hours for a single channel using 24 cores) required for registration of images with a resolution sufficient for the brain-wide visualization of neuronal morphology (e.g., 1000 × 600 × 350 pixels). For multi-channel registrations, memory demands and computation time were even greater: 106 GB for 6 channels taking over 16 hours on 24 cores. However, our present ANTs SyN parameters likely can be further optimized to reduce these demands. For instance, our parameters currently include 10 iterations of transformation matrix optimization at full image resolution. From our experience, these full-resolution registration cycles do not significantly increase precision, but they greatly increase computation time. Thus, computation time may be reduced by adjusting registration resolution as well as other parameters without adversely affecting registration quality. Although computational resources did not present a bottleneck for registering a small number of samples, this increase in the demands of a single registration made it difficult to optimize registration parameters as extensively as we had done previously with CMTK [1]. By reducing computation time, we would be able to explore more comprehensively the parameter space available with SyN and evaluate alternative diffeomorphic transforms available with ANTs that may provide still better registration fidelity.

An obstacle to systematically calibrating registration parameters is finding a suitable metric to quantitatively evaluate precision. This is a recognized problem, and it is not clear that a general solution exists [34]. Here, we primarily assessed precision by measuring the distance between visually located landmarks in the reference brain and registered images. However, this method has 2 drawbacks: (i) it relies on the accuracy with which these landmarks are located, and (ii) at least for our sample set, a relatively limited set of landmarks could reliably be identified. We obtained similar results when we assessed precision using cross correlation within localized image neighborhoods that included high-contrast internal image boundaries (data not shown). In registering live vglut2a:DsRed image stacks, we noted the trade-off between accurate global brain alignment and biologically plausible cell morphology. Thus we also used a set of measures to assess changes in the morphology of manually segmented cells (Hausdorff distance, elongation index, and cell volume). Finally, we also inspected the output of every transformation to subjectively judge registration quality.

Potential implications

This study demonstrates that the ANTs diffeomorphic symmetric normalization algorithm (SyN) advances upon elastic registration for precise registration of whole brain images in larval zebrafish and is markedly better at preserving neuronal cell morphology. By systematically testing SyN registration parameters for registering images acquired using live scans, we improved the ZBB atlas. Then, after calibrating registration parameters for fixed tissue and using multi-channel optimization, we were able to align the Z-Brain atlas into the ZBB coordinate space, and vice-versa, achieving co-registration accuracy to approximately the diameter of a single neuron. We believe that integrating the information present in each of these atlases produces a richer framework for future studies of structural and functional relationships within the nervous system. Large digital datasets such as those present in brain atlases can be used for many types of bioinformatic analysis. Z-Brain and ZBB already include software that can be used to explore the larval zebrafish brain, and we hope that integrating these datasets into a single coordinate system, will help to stimulate the development of additional computational tools and methods for querying this information.

Availability of supporting data

All individual brain scans, both before and after registration to a ZBB reference brain, are available in the GigaScience repository, GigaDB [35]. The GigaDB repository also includes the set of reference brains used for ZBB [33, 35] and the transformation matrices used to convert between ZBB and Z-Brain coordinate systems [37, 35].

Additional Material

Additional file 1: Point-based landmarks for quantification of live-scan registration precision. (a) Landmarks used for measuring registration precision. Position specifies the coordinates on vglut2a_ZBB (transverse, sagittal, horizontal planes). View indicates whether the image plane shown in (b) is transverse (T), horizontal (H), or sagittal (S). MLDs represent the average precision for each landmark for the set of 6 calibration brains, after registration with CMTK or ANTs. (b) Images of the landmarks in vglut2a_ZBB (red) used for measuring precision superimposed on elavl3 (gray). (c) Position of the landmarks superimposed on horizontal (top) and sagittal (bottom) maximum projections of elavl3 through the brain. (d) Horizontal maximum projections showing the landmark point (red dot) and the position of the corresponding landmarks in the 6 calibration brains after registration (green dots) superimposed on vglut2a_ZBB. Scale bar = 20 μm.

Additional file 2: Cells segmented for assessing distortion introduced by registration. (a) Position of manually segmented cells for measurement of distortion introduced by registration. Views show the same cells (individually color coded) superimposed on horizontal (top) and sagittal (bottom) maximum elavl3 brain projections. (b) Two examples of cells showing (left to right): original confocal image, segmentation mask, mask after alignment with CMTK, and mask after alignment with ANTs.

Additional file 3: Point-based landmarks labeled by transgenic lines. (a) Transgenic line landmarks used for measuring registration precision of the zebrafish brain browser atlas. Coordinates give the transverse, horizontal, sagittal position. Letters in square brackets designate right side [R], left side [L], or midline [M]. The mean and standard error of the landmark distances for the 3 brains per landmark are indicated for CMTK and ANTs. (b) Position of the landmarks superimposed on horizontal (top) and sagittal (bottom) maximum elavl3 brain projections.

Additional file 4: ZBB and Z-Brain expression patterns used for atlas registration. Brain Browser 3D projections of corresponding expression patterns in Z-Brain (left) and ZBB (right) used for calibrating and verifying the precision of inter-atlas registration. The top 5 patterns were combinatorially used to drive registration, while the bottom 3 were used for assessing precision. Middle images show Z-Brain patterns after registration to ZBB.

Additional file 5: Point-based landmarks for measuring precision of Z-Brain/ZBB co-registration. (a) Transgenic line and tERK-stain landmarks used for measuring the precision of registration between Z-Brain and ZBB. Coordinates are in transverse, horizontal, sagittal sections. Letters in square brackets designate right side [R], left side [L], or midline [M]. Color blocks correspond to points in (b). (b) Position of the landmarks superimposed on horizontal (top) and sagittal (bottom) maximum brain projections.

Additional file 6: Instructions for using transformation matrices to convert between ZBB and Z-Brain coordinate systems.

Abbreviations

ac: anterior commissure; ANTs: Advanced Normalization Tools; BSA: bovine serum albumin; Ce: cerebellum; CC: cross correlation; dpf: days post-fertilization; DT: thalamus; GT: griseum tectale; Ha: habenula; Hc: hypothalamus caudal zone; Hi: hypothalamus intermediate zone; IPN: interpeduncular nucleus; MCC: mean cross correlation; MD: maximal distance; MLD: mean landmark distance; MN: Mauthner neuron; MO: medulla oblongata; MOc: anterior-most midline cell in ventral/caudal medulla; MOm: ventral-most cluster of cells in medial/caudal medulla; NGS: normal goat serum; ON: olfactory nerve; PBS: phosphate-buffered saline; PBT: phosphate-buffered saline containing 0.1% Triton X-100; pc: posterior commissure; Po: preoptic region; Pr: pretectum; R4: rhombomere 4; R5: rhombomere 5; R6: rhombomere 6; RT: room temperature; SR: superior raphe; SyN: diffeomorphic symmetric normalization algorithm; TeOn: optic tectum neuropil; tERK: total ERK; TG: trigeminal ganglion; TL: torus longitudinalis; TS: torus semicircularis; ViBE-Z: Virtual Brain Explorer for Zebrafish; VR: virtual reality; X3D: Extension 3D; ZBB: Zebrafish Brain Browser.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was supported by the Division of Intramural Research of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (1ZIAHD008884–04, H.B.) and Virginia Tech Advanced Research Computing (N.P.). The funding body played no role in the study design, collection, analysis, or interpretation of the data, or in writing the manuscript.

Author contributions

G.D.M. and H.A.B. conceived the experiments. G.D.M., K.M.T., E.J.H., and H.A.B. optimized ANTS for zebrafish brain registration. G.D.M., M.B., and A.K.G. contributed confocal brain scans and generated meshes. N.F.P. developed the X3D/HTML5-based browser. D.D.N. developed the Unity VR browser. G.D.M. and H.A.B. wrote the manuscript. All authors approved the final manuscript.