Superoptimal Perceptual Integration Suggests a Place-Based Representation of Pitch at High Frequencies

Abstract

Pitch, the perceptual correlate of sound repetition rate or frequency, plays an important role in speech perception, music perception, and listening in complex acoustic environments. Despite the perceptual importance of pitch, the neural mechanisms that underlie it remain poorly understood. Although cortical regions responsive to pitch have been identified, little is known about how pitch information is extracted from the inner ear itself. The two primary theories of peripheral pitch coding involve stimulus-driven spike timing, or phase locking, in the auditory nerve (time code), and the spatial distribution of responses along the length of the cochlear partition (place code). To rule out the use of timing information, we tested pitch discrimination of very high-frequency tones (>8 kHz), well beyond the putative limit of phase locking. We found that high-frequency pure-tone discrimination was poor, but when the tones were combined into a harmonic complex, a dramatic improvement in discrimination ability was observed that exceeded performance predicted by the optimal integration of peripheral information from each of the component frequencies. The results are consistent with the existence of pitch-sensitive neurons that rely only on place-based information from multiple harmonically related components. The results also provide evidence against the common assumption that poor high-frequency pure-tone pitch perception is the result of peripheral neural-coding constraints. The finding that place-based spectral coding is sufficient to elicit complex pitch at high frequencies has important implications for the design of future neural prostheses to restore hearing to deaf individuals.

SIGNIFICANCE STATEMENT The question of how pitch is represented in the ear has been debated for over a century. Two competing theories involve timing information from neural spikes in the auditory nerve (time code) and the spatial distribution of neural activity along the length of the cochlear partition (place code). By using very high-frequency tones unlikely to be coded via time information, we discovered that information from the individual harmonics is combined so efficiently that performance exceeds theoretical predictions based on the optimal integration of information from each harmonic. The findings have important implications for the design of auditory prostheses because they suggest that enhanced spatial resolution alone may be sufficient to restore pitch via such implants.

Introduction

Pitch is a perceptual attribute of sound that has fascinated humans for centuries. It carries the melody and harmony in music, conveys important prosodic and lexical information in speech, and helps in the perceptual segregation of competing sounds (Oxenham, 2012). Although pitch is most closely related to sound periodicity or repetition rate, the fact that it does not correspond simply to a single physical parameter of sound has complicated the decades-long search for its neural correlates. Neurons sensitive to pitch have been identified in the auditory cortex of nonhuman primates (Bendor and Wang, 2005) and, using fMRI, analogous pitch-sensitive regions have been identified in humans (Zatorre et al., 1992; Griffiths et al., 1998; Penagos et al., 2004; Norman-Haignere et al., 2013), but how the information from the auditory nerve is extracted to form a cortical code remains unknown (Micheyl et al., 2013). The information from individual harmonic components of periodic sounds is represented in the auditory nerve in at least two ways that may be used to extract the pitch. The first way is via a code based on the distribution of the overall firing rates in neurons tuned to different frequencies (Cedolin and Delgutte, 2005). This spectral “rate-place” code relies on the frequency-to-place mapping, or tonotopic organization, established along the basilar membrane in the cochlea (Wightman, 1973; Terhardt, 1974; Cohen et al., 1995). The second way is via precise stimulus-driven spike timing, or “phase locking” to the waveform (Licklider, 1951; Cariani and Delgutte, 1996; Meddis and O'Mard, 1997; Cedolin and Delgutte, 2005). Neither rate-place nor timing theories provide a comprehensive explanation of all pitch phenomena, and so it is often postulated that both codes may be used, either individually (Cedolin and Delgutte, 2005) or in combination (Loeb et al., 1983; Shamma, 1985a,b; Shamma and Klein, 2000; Loeb, 2005; Cedolin and Delgutte, 2010). An earlier study suggested that musical pitch perception was possible with harmonics that were all above the putative limits of phase locking (Oxenham et al., 2011). However, it is possible that musical pitch perception was based on the residual phase locking to individual harmonics that was not sufficient when based on a single tone, but became sufficient for accurate pitch perception when the degraded peripheral information from multiple harmonics was combined.

Here we tested humans' ability to discriminate the pitch of very high-frequency tones, beyond the putative limit of phase locking to rule out the use of timing information. Physiological studies in other mammals suggest that the temporal code for frequency degrades rapidly above 1–2 kHz (Palmer and Russell, 1986). The limit of phase locking is unknown in humans, although our ability to use timing for interaural discrimination extends only to ∼1.5 kHz, suggesting similar limitations (Hartmann and Macaulay, 2014). Nevertheless, it has been postulated, based on behavioral data and computational neural modeling, that some timing information may remain usable for pitch perception up to frequencies of 8 kHz (Heinz et al., 2001; Recio-Spinoso et al., 2005; Moore and Ernst, 2012). We presented listeners with high-frequency pure tones above 8 kHz, and found that their ability to discriminate pitch is indeed very poor, as would be expected if accurate pitch perception depended on an intact time code. However, when we combined the same high-frequency tones within a single harmonic complex tone, while still ensuring that temporal-envelope cues and distortion products from peripheral interactions between harmonics were not available, pitch discrimination improved dramatically. Pitch discrimination for the complex tones was better than predicted by optimal integration of information from each harmonic, if performance was limited by peripheral coding constraints, but was comparable to predictions based on a more central noise source. The results provide the first clear demonstration that place-based information can be sufficient to generate complex pitch perception and that the limits of peripheral phase locking alone cannot account for why pitch perception degrades at high frequencies.

Materials and Methods

Participants.

Nineteen normal-hearing subjects (13 female) between 19 and 27 years of age (mean, 22 years) participated in this study. The subject sample size was determined based on previous experiments with similar protocols. All participants were required to pass (1) an audiometric screening with pure-tone thresholds <20 dB hearing level for octave frequencies between 250 Hz and 8 kHz, (2) a high-frequency hearing screening extending to 16 kHz, and (3) a pitch-discrimination screening. Because the stimuli in this study included very high-frequency tones up to 16 kHz presented at a moderate level of 55 dB SPL, we expected that some participants with clinically normal hearing thresholds would not be able to hear the high-frequency tones. We measured detection thresholds for 14 and 16 kHz 210-ms pure tones embedded in a threshold-equalizing noise (TEN; Moore et al., 2000), extending from 20 Hz to 22 kHz, at a level of 45 dB SPL per estimated equivalent rectangular bandwidth of the auditory filter as defined at 1 kHz, the same level as was used in the main experiments. The thresholds were obtained using a three-interval forced-choice task and a three-down one-up adaptive procedure that tracks the 79.4% point on the psychometric function (Levitt, 1971). The 19 participants included in the study all had thresholds of <50 dB SPL, averaged across three runs, at both 14 and 16 kHz to ensure audibility of our stimuli. At 14 kHz, the highest component of the high-frequency complex, all participants had a masked threshold of <43 dB SPL. Sixteen additional subjects were excluded because they failed the high-frequency hearing screening.

For the pitch-discrimination screening, we measured fundamental frequency (F0) difference limens (F0DLs) and frequency difference limens (FDLs) for the same stimuli as in the main experiment but without any level randomization between tones and without the background TEN. Participants were required to have FDLs and F0DLs of <6% (one semitone) for tones in the low spectral region and <20% in the high spectral region to ensure that they would be able to perform the discrimination tasks. The mean DLs obtained in those subjects who passed the screening was 0.55% across frequencies in the low spectral region and 4.55% across frequencies in the high spectral region, which is comparable to thresholds reported in past studies (Moore et al., 1984; Moore and Ernst, 2012). Twelve additional subjects were excluded from this study because they did not meet these pitch-discrimination criteria. Our final participants' musical experience varied from 0 to 15 years of formal musical training. A linear regression was conducted to assess the relationship between musical experience and pitch discrimination in the low complex tone condition. The years of musical training received was not a significant predictor of F0DLs (β = −0.012, t = −0.051, p = 0.96, r² = 0, linear regression), suggesting no clear correlation between musical experience and pitch perception performance in these participants. Written informed consent was obtained from all participants in accordance with protocols reviewed and approved by the Institutional Review Board at the University of Minnesota. The participants were paid for their participation.

Sound presentation and calibration.

All test sessions took place in a double-walled sound-attenuating booth. The stimuli were presented binaurally (diotically) via Sennheiser HD 650 headphones, which have an approximately diffuse-field response and the sound pressure levels specified are approximate equivalent diffuse-field levels. The experimental stimuli were generated digitally and presented via a Lynx Studio Technology Lynx22 soundcard with 24-bit resolution at a sampling rate of 48 kHz.

Experiment 1.

F0DLs and FDLs were measured for harmonics 6–10 of nominal F0s 0.28 and 1.4 kHz in 16 of the participants. The tones were all presented in random phase, which in combination with the high fundamental frequency (F0) helped rule out the use of envelope repetition rate as a cue (Burns and Viemeister, 1976; Macherey and Carlyon, 2014). The inner harmonics (7–9) were presented at 55 dB SPL per component, whereas the lowest and highest harmonics (6 and 10) were presented at 49 dB SPL per component, to reduce possible spectral edge effects on the pitch of the complex tone (Kohlrausch and Houtsma, 1992). In addition to carefully controlling for audibility in the high-frequency region, we introduced two stimulus manipulations to limit the use of level cues and distortion products. The level of each pure tone was randomized (roved) by ±3 dB around the nominal level of 55 dB SPL on every presentation to reduce any loudness-related cues. The same ±3 dB rove was applied to each component of the complex tone independently. Due to the nonlinear response of the cochlea, it is also important to limit the influence of distortion products on pitch discrimination. The level of the most prominent cubic distortion product has been measured to be <20 dB SPL in stimuli comparable to the high-frequency complex used in this study (Oxenham et al., 2011). We embedded the tones in a background noise with a level of 45 dB SPL per estimated equivalent rectangular bandwidth of the auditory filters, which was >20 dB above the level necessary to ensure the masking of all distortion products.

Each subject's DLs were estimated using a standard two-alternative forced-choice procedure with a three-down one-up adaptive procedure that tracks the 79.4% correct point of the psychometric function. Each trial began with a 210 ms tone followed, after a 500 ms gap, by a second 210 ms tone. The tones were gated on and off with 10 ms raised-cosine ramps. The background noise was gated on 200 ms before the first tone and off 100 ms after the end of the second tone. Participants were asked to indicate via the computer keyboard which of the two tones had the higher pitch, and immediate feedback was provided after each trial. The starting value of ΔF or ΔF0 was 20%, with the frequencies of the two tones geometrically centered around the nominal test frequency. Initially the value of ΔF or ΔF0 increased or decreased by a factor of 2. The stepsize was decreased to a factor of 1.41 after the first two reversals, and to a factor of 1.2 after the next two reversals. An additional six reversals occurred at the smallest stepsize, and the DL was calculated as the geometric mean of the ΔF or ΔF0 value at those last six reversal points. Each participant repeated each condition four times, and the geometric mean of the four repetitions was defined as an individual's threshold. The presentation order of the conditions was randomized across subjects and across repetitions within each subject.

Experiment 2.

This experiment measured F0DLs for the complex tones in Experiment 1 with the odd harmonics presented in the left ear and the even harmonics presented in the right ear. This experiment was designed to further rule out any possibility that adjacent harmonics were interacting to generate temporal-envelope cues at the F0. By doubling the spacing between harmonics to 2800 Hz in the high-F0 condition, this possibility was eliminated. A subset of eight subjects from Experiment 1 participated in this experiment. Independent samples of background noise were presented to each ear. All other aspects of the stimuli and threshold procedure remained the same as in Experiment 1.

Experiment 3.

This experiment measured F0DLs for the complex tones in Experiment 1 with the same level rove applied to each harmonic in the complex in the eight subjects who did not participate in Experiment 2. This manipulation was done to produce similar loudness fluctuations from trial to trial as for the single pure tones. Besides the coherent level rove of the harmonics, all other aspects of the stimuli and threshold procedure remained the same as in Experiment 1.

Experiment 4.

This experiment measured DLs for the pure tones used in Experiment 1 for durations of both 30 and 210 ms. All tones were again gated on and off with 10 ms raised-cosine ramps. The same eight subjects from Experiment 3 were tested. To equate audibility between the two durations, the level of the short-duration tones was increased for each individual subject based on the difference between masked detection thresholds at the two durations. This difference was determined by first measuring masked thresholds for 1.68, 5, and 15.4 kHz pure tones embedded in a 45 dB SPL TEN (as used in Exp. 1), using a three-interval adaptive three-down one-up threshold procedure, averaged over two runs at both 30 and 210 ms durations. These frequencies were chosen because they are representative of the range of frequencies presented in the experiment. The difference in the average thresholds between the long-duration and short-duration tones was then added to 55 dB SPL when presenting the short-duration tones. This difference ranged from 5 to 7 dB across the eight subjects.

Experiment 5.

This experiment measured F0DLs and FDLs for inharmonic, “frequency-shifted” complexes, where each component was shifted upwards from the harmonic frequency by a fixed number of hertz. This results in an inharmonic stimulus that maintains the same frequency difference between each component (in hertz) as a harmonic stimulus. Frequency-shifted components are known to produce a less salient and more ambiguous pitch than harmonic components (Patterson, 1973; Patterson and Wightman, 1976). Six of the subjects from Experiment 2 in addition to three new subjects were tested. The low and high spectral regions consisted of harmonics 6–10 of nominal F0s 0.28 and 1.4 kHz, each shifted up in frequency by 50% of the F0 (i.e., by 140 and 700 Hz for the low-frequency and high-frequency conditions, respectively) and the corresponding inharmonic complex tones were composed of all five components combined, again with the lowest and highest components presented at a 6 dB lower level than the other components. All other aspects of the stimuli and threshold procedure remained the same as in Experiment 1.

Statistical analysis.

The FDLs and F0DLs were log-transformed before any statistical analysis was undertaken. This procedure is consistent with many other studies in the literature and helps maintain approximately equal variance across conditions. All tests were evaluated against a two-tailed p < 0.05 level of significance. The number of subjects tested in the main experiment was 16. Based on within-subjects (paired-samples) comparisons, this was sufficient to detect a small effect size (Cohen's d) of 0.17 with a power (β) of 0.9. The number of subjects for the control experiments was eight. This was sufficient to detect an effect size (Cohen's d) of 0.27.

Modeling.

An approach based on signal-detection theory (Green and Swets, 1966) was used to predict performance in Experiment 1. The first model was based on the assumption that the frequency information from each individual harmonic is combined optimally when judging F0 differences between the complex tones, and that performance is limited by peripheral coding variability (noise) before the integration of information (“early-noise model”). The sensitivity (d') to changes in the frequency of one harmonic can be stated as follows (Eq. 1):

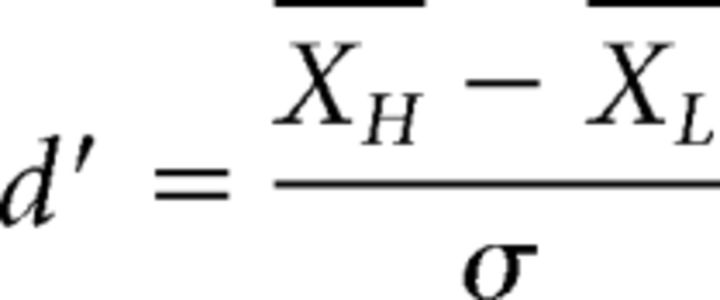where X_H and X_L are the mean internal representations of the frequencies of the higher and lower tone, respectively, and σ² is the variance of the internal noise. Assuming independent noise across peripheral channels, the optimal integration of information from each of n components results in an overall sensitivity to F0 changes in the complex tone (d′_c) that is the sum of the orthogonal individual d′ values (Green and Swets, 1966; Viemeister and Wakefield, 1991; Oxenham, 2016), expressed as follows (Eq. 2):

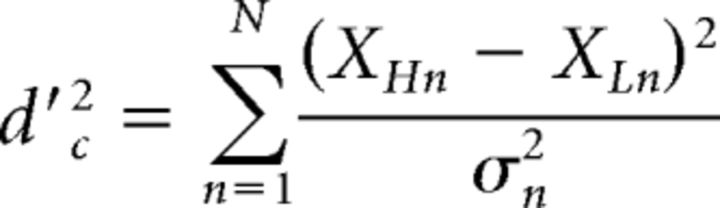or (Eq. 3):

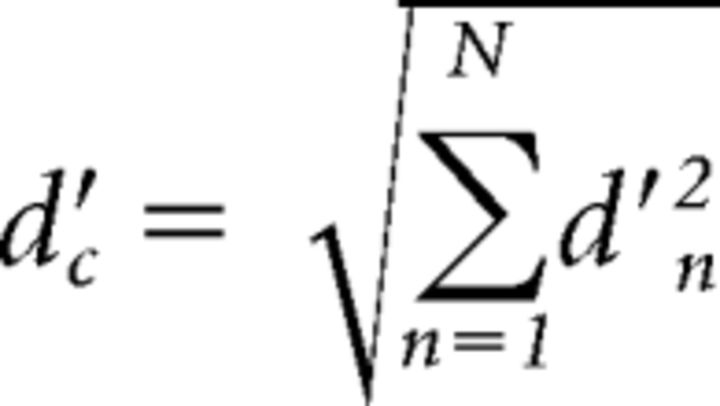Because sensitivity to frequency changes has been shown to be proportional to the difference in frequency over a wide range of conditions (Dai and Micheyl, 2011), Equation 1 implies that the threshold for the complex tone (θ̂_c) in our experiment (with harmonics 6–10) under optimal integration can be predicted as follows (Eq. 4):

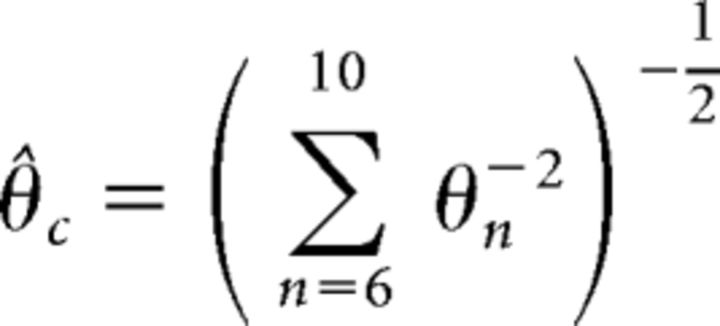where θ_n is the threshold for harmonic number n when presented in isolation. Equation 4 therefore provides the maximum improvement in thresholds that can be obtained by combining the independent information from the individual components (Goldstein, 1973). This prediction based on optimal integration of the information from each harmonic was compared with the actual thresholds obtained by each listener for the complex tones.

The second model to be tested was based on the assumption that performance is not limited by peripheral coding noise, and is instead limited by a coding (or memory) noise that occurs after the integration of information from the individual harmonics (“late-noise model”). Because the noise occurs after the addition of information from each harmonic, its variance is independent of the number of harmonics, leading to the following predicted d'_c for the complex tone (Eq. 5; Green and Swets, 1966; White and Plack, 1998):

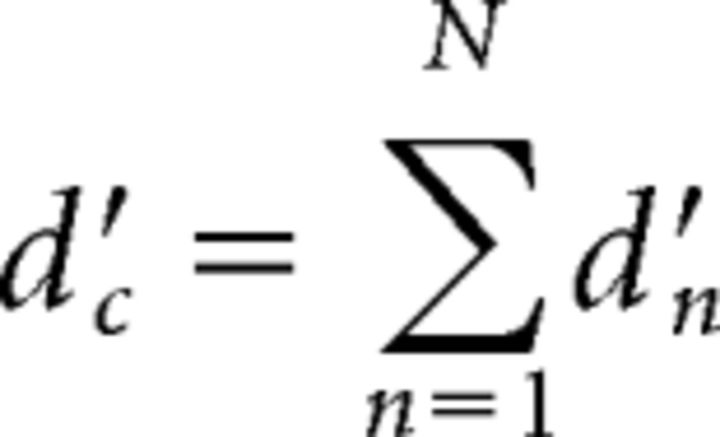In this case, the predicted threshold for the complex tone is as follows (Eq. 6):

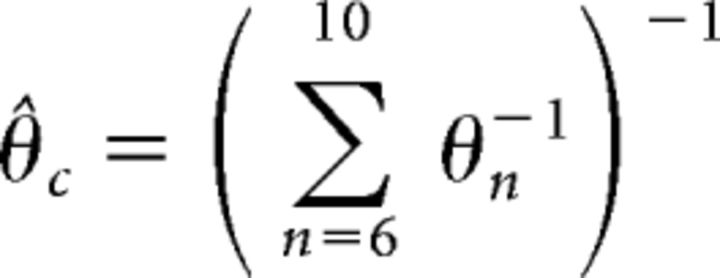The predictions from the both the early-noise and late-noise models were compared with the results from the experiments to determine whether peripheral coding noise (e.g., based on limitations of auditory-nerve phase locking) could account for the performance of the listeners.

Results

Experiment 1: integration of pitch information at high frequencies

We tested listeners' ability to discriminate frequency differences of very high-frequency tones (>8 kHz), presented either in isolation or in combination to generate harmonic tone complexes. We also tested the same listeners' frequency-discrimination abilities with much lower-frequency tones, within the normal musical range, to provide a direct comparison (Fig. 1A). Listeners' ability to discriminate the frequency of tones >8 kHz was very poor: average thresholds, or FDLs, ranged from ∼22% for an 8.4 kHz tone to 35% for a 14 kHz tone (Fig. 1B, right panel, red circles). The FDLs of the same tones in quiet, without the background noise and without level roving, were much better, averaging 4.55%, and were similar to those reported in earlier studies (Moore and Ernst, 2012). These poor DLs are consistent with listeners' general inability to recognize melodies when they are played using very high-frequency pure tones (Attneave and Olson, 1971; Oxenham et al., 2011): a semitone—the smallest interval in the musical scale—corresponds to a frequency difference of ∼6%, which is much smaller than the smallest discriminable frequency difference at these high frequencies. In contrast, the same listeners were very accurate in their discrimination of low-frequency pure tones, with average DLs of ∼1% at all frequencies tested between 1680 and 2800 Hz (Fig. 1B, right panel, blue squares).

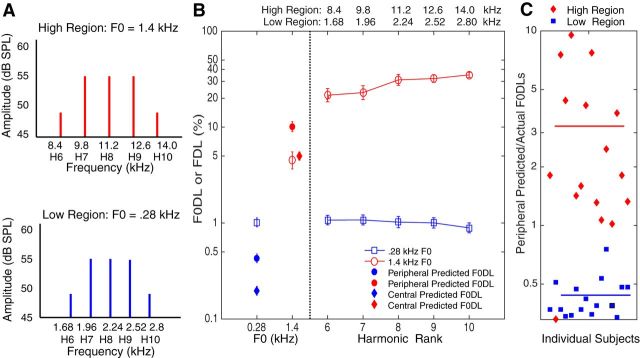
Figure 1.

Stimuli and results from the main experiment. A, Stimuli. The low and high spectral regions consisted of harmonics 6–10 (Hn) of nominal F0s 0.28 and 1.4 kHz. The tones were presented either individually or all together as a harmonic tone complex. B, Mean F0DLs (left) and FDLs (right; ±SEM, n = 16). The numbers at the top represent the pure-tone frequencies (kHz) for the high-frequency and low-frequency regions. The filled circles represent predicted F0DLs based on optimal integration of the information from the individual harmonics, assuming a peripheral source of neural noise, before the integration of information (early-noise model). A qualitatively different pattern of integration is observed at the low and high frequencies, with poorer-than-optimal integration observed for low frequencies, and significantly better-than-optimal integration observed at high frequencies. The filled diamonds represent predicted F0DLs based on a more central source of neural noise, following the integration of information from the individual harmonics (late-noise model). The observed mean threshold is poorer than predicted in the low-frequency region, but not significantly different than that predicted in the high-frequency region. C, Ratio of predicted versus actual F0DLs for each participant, based on the early-noise model, with the mean for each frequency region shown by the colored bars. Individual ratios in the low-frequency region all fall below 1 and, except for one participant, ratios in the high-frequency region fall above 1.

In the low-frequency region, when the pure tones were combined to form a complex tone with a fundamental frequency (F0) of 0.28 kHz, listeners' ability to discriminate F0 differences was very similar to their ability to discriminate each of the individual frequencies, with DLs still ∼1%, similar to earlier findings (Goldstein, 1973; Moore et al., 1984; Fig. 1B, left panel, blue square). In dramatic contrast, combining the high-frequency tones into a single complex tone led to thresholds that were better by a factor of >6 compared to the average single-tone discrimination thresholds (Fig. 1B, left panel, red circle).

Why was pitch discrimination with the high-frequency complex tone so much better than discrimination with each of the individual harmonics alone? The first possibility is that the phase-locked neural information from each individual pure tone is severely degraded at high frequencies, leading to poor performance with the single tones, but that sufficient phase-locking information exists to improve performance when the information from individual harmonics is combined. This hypothesis was tested using the early-noise model, described in Materials and Methods. We predicted F0DLs for the complex tones for each listener individually, and compared the predicted with the actual measured F0DLs. For the low-frequency tones, measured F0DLs for the complex tones were poorer than predicted by optimal information integration (t₍₁₅₎ = 15.8, p < 0.001, paired-samples t test), in line with earlier studies, suggesting some interference between the tones when presented simultaneously, and/or some loss of information during integration (Goldstein, 1973; Moore et al., 1984; Gockel et al., 2005). However, for the high-frequency tones, the F0DLs were substantially better than predicted by the optimal integration of information from the individual harmonics (t₍₁₅₎ = −3.62, p = 0.003, paired-samples t test). At an individual level, 15 of 16 subjects had complex-tone F0DLs that were better than their individual thresholds predicted by optimal integration. Furthermore, individual ratios of predicted versus actual DLs for each participant all fall below 1 in the low-frequency region and, except for one apparent outlier, all fall above 1 in the high-frequency region (Fig. 1C).

A second possibility is that discrimination is limited not by degraded coding in the auditory periphery, but by more central neural limitations, occurring at a stage of processing following the combination of the information from the individual harmonics. We tested this hypothesis by comparing our results with the predictions of the late-noise model, also described in Materials and Methods. The predictions based on the assumption of late noise are shown as filled diamonds in Figure 1B. For the low-frequency tones, F0DLs for the complex tones were again much poorer than predicted based on a more central source of noise (t₍₁₅₎ = 29.0, p < 0.001, paired-samples t test). For the high-frequency tones, however, actual F0DLs were not significantly different from those of the predictions (t₍₁₅₎ = −0.503, p = 0.662, paired-samples t test).

Comparing the actual DLs with those obtained from the models based on peripheral (early) and more central (late) noise, it seems that performance was too good in the high-frequency conditions to be explained by a combination of information limited by peripheral noise, but was consistent with predictions based on more central limitations to performance. This outcome implies that residual phase locking cannot explain the accurate pitch perception of high-frequency complex tones observed in our experiment. The remaining four experiments were designed to rule out potential confounds and to confirm the main finding of substantial integration of information in the high-frequency conditions.

Experiment 2: temporal envelope cues cannot account for superoptimal integration

When pure tones are combined into a harmonic complex tone, the resulting waveform repeats at a rate corresponding to the F0. If listeners extracted the fluctuations of the temporal envelope at the rate of the F0, then the results would not reflect the independent processing of the individual harmonics and would instead reflect the less interesting ability of listeners to follow temporal-envelope fluctuations of the composite waveform. There are several reasons to believe that temporal-envelope fluctuations were not used by our listeners: (1) low-numbered harmonics were used (harmonics 6–10) with relatively large spacing between each harmonic, meaning that any fluctuations were likely to be strongly attenuated by the effects of cochlear filtering (Houtsma and Smurzynski, 1990; Shera et al., 2002); (2) the components were added in different random phase relationships in every presentation, making temporal-envelope cues less reliable and less likely to produce a strong perception of pitch (Bernstein and Oxenham, 2003); and (3) the envelope repetition rate of 1400 Hz in the high-frequency condition was too high to be perceived as pitch (Burns and Viemeister, 1976; Macherey and Carlyon, 2014). Nevertheless, to further rule out the use of temporal-envelope cues from the composite waveform, we used dichotic presentation, with odd-numbered harmonics presented to the left ear and even-numbered harmonics presented to the right ear. If listeners were using envelope cues, performance would be worse in the dichotic condition because the spacing between the adjacent harmonics in each ear is doubled, meaning that interactions between adjacent components are even more attenuated and occur at an even higher frequency (2800 Hz). Our results show no significant difference in complex-tone F0DLs between the original diotic and new dichotic conditions in either the low-frequency region (t₍₇₎ = 1.3, p = 0.235, paired-samples t test) or the high-frequency region (t₍₇₎ = 0.682, p = 0.517, paired-samples t test). In contrast, if envelope cues had been used in the main experiment, the increase of peripheral spacing between harmonics should have led to a large degradation in performance. The results therefore confirm that envelope cues were not used in the main experiment (Table 1, left).

Table 1.

Mean thresholds in percentage for Experiments 2 and 3^a

	Mean F0DL (95% CI)
	Experiment 2: dichotic presentation (n = 8)		Experiment 3: coherent level rove (n = 8)
	Dichotic	Diotic	Coherent	Incoherent
Low region: 0.28 kHz F0	0.78 (0.59–1.02)	0.92 (0.75–1.12)	0.95 (0.68–1.32)	1.13 (0.77–1.65)
High region: 1.4 kHz F0	4.92 (2.53–9.59)	5.95 (3.87–9.15)	3.22 (1.53–6.74)	3.40 (1.78–6.5)

^aResults of dichotic presentation (temporal envelope cues results, n = 8, left) and coherent level rove (effect of loudness results, n = 8, right).

Experiment 3: effects of random loudness variations

The presentation level of our pure tones varied randomly over a 6 dB range to help rule out the use of potential loudness cues when making pitch judgments. The complex tones comprised the same pure tones, each of which was varied in level randomly and independently. It is possible that the overall loudness of the complex tones was less variable than the loudness of the individual pure tones, because the overall level of the complex tone was less variable. The larger variations in loudness of the pure tones may therefore have interfered more with listeners' pitch judgments than the smaller loudness variations of the complex tones, making the judgments less accurate. To test this possibility, we compared a condition in which all the components within the complex tone were randomly varied in a coherent manner; in other words, the same random level change was selected for all components within the complex. If loudness changes had affected performance, F0DLs should be poorer in the case where all the tones in the complex are roved coherently, producing larger fluctuations in overall loudness. In fact, thresholds for the coherently roved complex tones were slightly better than those for the incoherently roved tones, although the differences were small and failed to reach significance at the high frequencies (low-frequency complex: t₍₇₎ = −2.43, p = 0.046, paired-samples t test; high-frequency complex: t₍₇₎ = −0.727, p = 0.491, paired-samples t test; Table 1, right).

Experiment 4: temporal integration

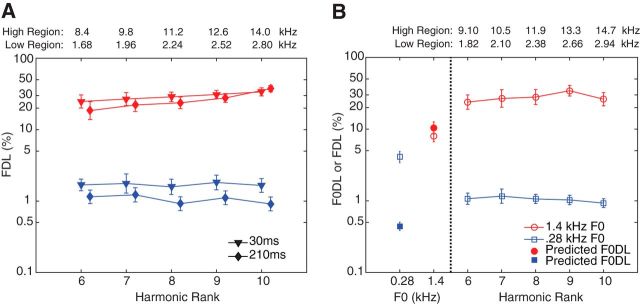
Is the high degree of information integration observed at high frequencies specific to pitch, or does it extend to other auditory dimensions? To answer this question, we considered the effects of temporal integration: increasing the duration of sounds generally leads to better detection and discrimination of both frequency and intensity (Moore, 1973; Carlyon and Moore, 1984; Gockel et al., 2007). If greater integration effects at high frequencies are not specific to pitch, then we may expect to observe greater effects of stimulus duration on frequency discrimination at high frequencies than at low frequencies. We tested this prediction by comparing frequency discrimination of pure tones with durations of 30 and 210 ms. A within-subjects (repeated-measures) ANOVA with the log-transformed thresholds as the dependent variable and factors of harmonic rank, frequency region, and duration revealed a main effect of frequency region (F_(1,28) = 296, p < 0.001, ANOVA). Although there was a trend for the longer tones to produce lower (better) thresholds than the shorter tones, this trend failed to reach significance (F_(1,28) = 3.09, p = 0.090, ANOVA). There was no interaction between frequency region and duration (F_(1,28) = 0.942, p = 0.340, ANOVA), suggesting comparable effects of temporal integration in both spectral regions (Fig. 2A). Thus, the unusual integration observed at high frequencies seems to be specific to pitch.

Figure 2.

Results from short-duration and inharmonic tones. A, Mean FDLs (±SEM) for 210 and 30 ms pure tones (temporal integration results, n = 8). The numbers at the top are the pure-tone frequencies (kHz) for the high-frequency and low-frequency regions. The results show that the increase in DLs for the pure tones with decreasing duration was not significantly different between the two frequency regions. B, F0DLs (left) and FDLs (right; ±SEM) for inharmonic tones (harmonicity results, n = 9). The numbers at the top represent the pure-tone frequencies (kHz) for the high-frequency and low-frequency regions. The low and high spectral regions consisted of harmonics 6–10 (Hn) of nominal F0s 0.28 and 1.4 kHz shifted up in frequency by 50% and the corresponding inharmonic complex tones composed of all five harmonics combined. The observed F0DLs were poorer than predictions of the early (peripheral) noise model in the low spectral region and no different than predicted in the high spectral region.

Experiment 5: harmonicity

As a final control condition, we asked whether the high degree of integration observed with the high-frequency tones depends on harmonic relations between the tones. To answer this question, we measured DLs for tones that were not harmonically related. The stimuli presented in this experiment were the tones from the main experiment, harmonics 6–10 of nominal F0s 0.28 and 1.4 kHz, shifted up in frequency by 50% of the F0 (i.e., 140 Hz for the low-frequency tones, and 700 Hz for the high-frequency tones) and the corresponding inharmonic complex tones comprised all five components combined. The frequency shift disrupts the harmonic relationship but maintains the frequency spacing and envelope repetition rate (de Boer, 1956; Patterson, 1973; Micheyl et al., 2010, 2012). With the low-frequency tones, as found in the original harmonic conditions, the observed inharmonic DLs were poorer than predicted based on optimal integration of information with peripheral limitations (t₍₈₎ = 13.5, p < 0.001, paired-samples t test), again suggesting non-optimal integration of information. With the high-frequency tones, in contrast to the findings from the original experiment, predictions of optimal integration with peripheral limitations were not significantly different from the observed DLs (t₍₈₎ = −1.06, p = 0.322, paired-samples t test; Fig. 2B). This finding suggests that the unusual integration observed in the main experiment is specific to very high-frequency harmonically related tones that combine to produce a complex pitch sensation.

Discussion

Alternative interpretations

The main finding of this study is that pitch discrimination improves dramatically when very high-frequency tones combine to form a single harmonic complex, which in turn implies that high-frequency complex pitch perception is not constrained by neural phase locking to the individual harmonics. Several alternative interpretations were also considered. The first is that listeners perceived the F0 of the complex tones based on the repetition rate of the temporal envelope. Sensitivity to temporal-envelope fluctuations decreases systematically above 150 Hz (Kohlrausch et al., 2000), and the perception of pitch based on temporal-envelope cues has not been demonstrated for F0s >800–1000 Hz (Burns and Viemeister, 1976, 1981; Macherey and Carlyon, 2014). It seemed, therefore, unlikely that listeners would be able to perceive a pitch based on temporal-envelope cues with an F0 of 1400 Hz. Nevertheless, if some residual envelope cues were available, then they should have been further degraded by presenting alternating harmonics to opposite ears, as this doubles the envelope repetition rate to 2800 Hz. No change in performance was observed (Exp. 2), indicating that envelope cues were not used. Indeed, on average, performance was slightly better in the dichotic condition than in the diotic condition, suggesting that increasing the sample size would not have resulted in a significant effect in the predicted direction. In this and in all of our control experiments, our minimum sample size of eight subjects was sufficient to detect a small-to-medium effect (Cohen's d = 0.27) with a power (β) of 0.9.

A second alternative explanation is that random level variations in the stimuli led to greater loudness variations for the pure tones than for the complex tones, so that the apparently superoptimal integration was due instead to a decrease in interference produced by loudness variations. The results from Experiment 3 ruled out that possibility by showing that increasing the loudness variations in the complex tones did not result in poorer performance. Again, the fact that average performance was slightly better in the coherently than in the incoherently roved condition suggests that the lack of an observed effect was not due to having tested an insufficient number of subjects.

A third alternative is that there is a general increase in integration of information at high frequencies that is not specific to integrating pitch information across frequency. Experiment 4 ruled out that possibility by showing that there were no differences between low and high frequencies in how frequency information was integrated across time, suggesting that the effect was specific to pitch integration across frequency.

The final experiment showed that the superoptimal integration was not observed when the individual tones were not in harmonic relation to one another, even though they maintained the same frequency spacing (and so the same temporal-envelope repetition rate). This outcome suggests that superoptimal integration requires harmonic relationships between the tones.

Comparisons with earlier data

Other studies have investigated the integration of information from multiple harmonics at low frequencies (Goldstein, 1973; Moore et al., 1984; Gockel et al., 2007). Consistent with our findings, they also reported no improvement in thresholds when the individual harmonics were combined into a complex tone. The explanation for this lack of apparent integration are either (or both) of the following: (1) information is not optimally combined from the individual harmonics, so that the best threshold from the individual harmonics predicts the threshold for the complex (Goldstein, 1973); or (2) when presented together, the harmonics interfere with each other, so that frequency discrimination of individual harmonics embedded within the complex is poorer than the discrimination of the same harmonics presented in isolation (Moore et al., 1984). Neither explanation can account for the pattern of results observed here at high frequencies, where discrimination was better than predicted even by optimal integration of the information from the individual harmonics.

One earlier study measured frequency discrimination of very high-frequency tones in isolation and in combination (Oxenham and Micheyl, 2013). That study also reported improved discrimination when the pure tones were combined within a harmonic complex; however, the improvement was worse than observed here, and did not exceed the predictions of optimal integration. At least three important factors can explain this apparent discrepancy. First, no amplitude roving was used in the earlier study, meaning that discrimination could have been based on changes in loudness of the tones as the frequency was varied. Second, the lowest frequency tested was 7 kHz, which is below the putative upper limit of phase locking proposed by Moore and Ernst (2012) and which resulted in better discrimination than found at the higher frequencies; this means that performance may have been dominated by this single harmonic. Third, the highest frequency tested was 16.8 kHz, which was close to the highest audible frequency for most subjects; in these cases, discrimination could have been based on which tone was audible, leading to artificially low discrimination thresholds. These factors would have led to better performance for the pure tones, which in turn would have led to artificially low predictions for the complex-tone thresholds. In contrast, the current experiment tested fewer harmonics within a more constrained frequency region and controlled for potential loudness artifacts by introducing level roving. We therefore believe that the current outcomes provide a more accurate reflection of frequency discrimination for high-frequency pure and complex tones.

Conclusions and implications

Two important conclusions can be drawn from our findings. First, harmonic pitch perception is possible even when all components are >8 kHz, meaning that timing cues based on neural phase locking are not necessary to induce the percept of complex pitch. This finding rules out purely timing-based theories of pitch, because no studies have found evidence for residual timing information beyond 8.4 kHz, the lowest frequency present in the high-frequency complex tones. Second, even if some residual phase locking existed at very high frequencies (Heinz et al., 2001; Recio-Spinoso et al., 2005), the very poor pitch perception found for pure tones at very high frequencies cannot be ascribed to the decrease of temporal phase locking at high frequencies because the integration of information observed was greater than would have been possible, even under optimal conditions. The qualitative difference between integration at low and high frequencies further emphasizes the special case of combining component frequencies that fall outside the region of melodic pitch perception (>4–5 kHz; Attneave and Olson, 1971; Oxenham et al., 2011) but form a fundamental frequency that falls within that region.

In contrast to traditional explanations based on auditory-nerve coding, our new results may be understood in terms of more central, possibly cortical, coding constraints beyond the point where the information from individual harmonics is first combined. Earlier studies have suggested the existence of pitch-sensitive neurons in cortical regions (Zatorre et al., 1992; Griffiths et al., 1998; Patterson et al., 2002; Penagos et al., 2004; Bendor and Wang, 2005). It can be assumed that such neurons exist only within the region of musical pitch (≤∼5 kHz; Oxenham et al., 2011) and respond most strongly to combinations of harmonically related tones (Hafter and Saberi, 2001; Bendor and Wang, 2005). Any single harmonic at a very high frequency will not activate such neurons, and will not result in the perception of the F0, but a combination of harmonics will activate pitch-sensitive neurons, leading to the perception of pitch. Thus, the dramatic difference in performance between single and multiple tones can in principle be accounted for by pitch-sensitive neurons that respond selectively to a combination of harmonics but not to any individual upper harmonic. Our results demonstrating that purely tonotopic information (without additional phase-locked temporal information) is sufficient to activate them complements a recent neurophysiological report in the auditory cortex of marmosets, demonstrating single-unit sensitivity to harmonic structure across the entire range of hearing, including for units with best frequencies above the limits of peripheral phase locking (Feng and Wang, 2017). Of course, although timing may not be necessary for pitch coding, our findings do not rule out the use of such cues at lower frequencies.

The finding that place-based (tonotopic) coding is sufficient for eliciting complex pitch perception at high frequencies has important implications for neural prostheses designed to restore hearing, such as cochlear or brainstem implants (Zeng, 2004). Pitch is currently only weakly conveyed by such devices, contributing to patients' difficulties with music perception and understanding speech in complex acoustic environments. Given that our results suggest that place information can be sufficient for complex pitch, at least at high frequencies, such pitch could potentially be restored based solely on location of stimulation, provided that sufficient resolution can be achieved, in terms of the numbers of electrodes and the specificity of the stimulation region. Such specificity, though not possible with current implants, could be achieved in future devices through neurotrophic interventions that encourage neuronal growth toward electrodes (Pinyon et al., 2014), optogenetic interventions that provide greater specificity of stimulation (Hight et al., 2015), or a different location of implantation, such as in the auditory nerve, where electrodes can achieve more direct contact with the targeted neurons (Middlebrooks and Snyder, 2007, 2008, 2010).