Plasma membrane temperature gradients and multiple cell permeabilization induced by low peak power density femtosecond lasers

Abstract

Calculations indicate that selectively heating the extracellular media induces membrane temperature gradients that combine with electric fields and a temperature-induced reduction in the electropermeabilization threshold to potentially facilitate exogenous molecular delivery. Experiments by a wide-field, pulsed femtosecond laser with peak power density far below typical single cell optical delivery systems confirmed this hypothesis. Operating this laser in continuous wave mode at the same average power permeabilized many fewer cells, suggesting that bulk heating alone is insufficient and temperature gradients are crucial for permeabilization. This work suggests promising opportunities for a high throughput, low cost, contactless method for laser mediated exogenous molecule delivery without the complex optics of typical single cell optoinjection, for potential integration into microscope imaging and microfluidic systems.

Highlights

• •Femtosecond lasers can transfect a single cell through optoporation.
• •Multiple cells are transfected with much lower power densities at 1550 nm.
• •Calculations show that temperature gradients contribute to the mechanism.
• •These mechanisms resemble those also involved in microwave biological interactions.

1. Introduction

By introducing exogenous DNA into living cells while maintaining viability, gene therapy may potentially treat numerous diseases and conditions [1], [2], [3], [4]. An ideal delivery method would be inexpensive and efficient (high delivery efficiency with high viability) with high throughput. Early gene therapy frequently used viral vectors for delivery [5]; however, side effects, such as inflammation and leukemia, prompted nonviral delivery method development [6]. Alternatives include chemical approaches, such as lipofection [7], or physical approaches, such as electric fields [8], ultrasound [9], nanoparticles [10], or lasers [11].

Electromagnetic techniques are the most common physical approach. Pulsed electric fields (PEFs) of appropriate duration and intensity electropermeabilize the membrane in a process called electroporation [12] with the membrane either resealing, as in gene therapy [13], or failing to reseal, as in cancer treatment [14] and sterilization [15]. Electroporation pulses are typically microseconds to milliseconds in duration with field strengths of approximately hundreds of volts per centimeter. PEFs of similar energy, but shorter duration (10–300 ns) and higher field strength (30–300 kV/cm) [16], may induce intracellular effects, such as apoptosis [17], changes in calcium dynamics [18], and mitochondria permeabilization [19], because the pulse duration is shorter than the charging time of the cell and on the order of the charging time of the smaller organelles. These nanosecond PEFs (nsPEFs) also create membrane pores smaller than those induced by traditional electroporation [20]. Low (~kHz–MHz) and high (~MHz) frequency AC fields similarly target external and internal membranes, respectively [21]. Lasers enable non-contact treatment and seamless integration with microscopic imaging and microfluidic systems [22]. Optical transfection has successfully delivered multiple substances, including ions, small interfering RNAs (siRNAs), and plasmids, using an automated, high-throughput process [23].

1.1. Laser mediated exogenous molecule delivery – overview

Laser-based gene delivery typically uses tightly focused beams, making it mostly a single cell permeabilization technique (optoinjection). While successful, the mechanism remains incompletely understood. Analogous to PEFs, laser pulse duration impacts the light-cell interaction. Continuous wave (CW) lasers generally favor delivery by plasma membrane heating [24]. Nanosecond lasers create shockwaves spanning multiple cell widths [24], [25], [26] while additionally inducing heat and thermoelastic stress [27]. Femtosecond lasers create free electrons at the cell surface to trigger a low density plasma that permeabilizes a single cell [23].

Laser wavelength also influences the permeabilization mechanism. The energy required for optical breakdown at femtosecond duration increases with wavelength [28]. Also, the volume of laser absorption depends upon the laser spot size (or illumination area) and absorption coefficient, which varies with wavelength [29], [30], [31], [32], [33], [34] and medium temperature [35]. Table 1 summarizes absorption coefficients for water [29] and lipids [34], [36], [37]. At 532 nm, the absorption coefficient of lipids (~0.01 cm⁻¹) is much higher than for water (~4.47×10⁻⁴ cm⁻¹), making water much more transparent to the beam than lipids. Thus, the resulting laser exposure predominantly interacts with the plasma membrane at the membrane/buffer interface, making heating and thermoelastic stress dominant mechanisms [24]. At longer wavelengths, laser radiation increasingly interacts with the surrounding medium. At 800 nm, the most successful wavelength for single cell optoporation [24], the absorption coefficient for water (0.02 cm⁻¹) is five times larger than for lipids (0.004 cm⁻¹), indicating that the laser preferentially heats the surrounding buffer to induce plasma cloud formation at the plasma membrane [23] and a membrane temperature gradient (∇T) analogous to that calculated for electric fields [38]. The ∇T may additionally induce membrane voltages due to the thermoelectric effect that could contribute to permeabilization [38]. At 1550 nm, the absorption coefficient of water (10.5 cm⁻¹) exceeds that of lipids (0.2 cm⁻¹) by approximately a factor of fifty, further increasing ∇T. Similarly, the absorption coefficient of water (32 cm⁻¹) exceeds that of lipids (1.625 cm⁻¹) at 2080 nm by approximately a factor of twenty, suggesting that ∇T may contribute to membrane permeabilization, although the mechanism remains unknown [24]. The first experimental effects of ∇T in biological samples were observed previously during microwave exposures. Greater absorption of microwave energy in the extracellular fluid [39] creates ∇T that may induce various physiological responses, without bulk heating [40], [41], such as membrane permeabilization [40], or that are irreproducible with convection heating alone [42].

Table 1.

Absorption coefficients for water and lipids at relevant laser wavelengths and the ratio (Water/Lipid) between them.

	Laser wavelength (nm)
	532	800	1550	2080
Absorption Coefficient (cm−1)
Water	0.000447	0.02	10.5	32
Lipid	0.01002	0.004	0.1996	1.625
Water/Lipid	0.045	5	52.6	19.7

Most lasers used for transfection have peak power levels of ~10 kW, pulse durations of 17–150 fs, and wavelengths of 800–1000 nm to permeabilize a single cell [43] through low density plasma formation. Reduced cell viability [44] motivated research into femtosecond pulses of longer wavelength [45]. A 170 fs, 120 mW, 1554 nm laser transiently induced propidium iodide (PI) uptake with reduced temperature rise, shock waves, and cavitation bubbles compared to 800 nm lasers [45]. However, this study used relatively narrow focus (~2 μm) with high peak power densities at the optical breakdown level to perforate a single cell at the time [45].

This paper uses a simple analytic model to quantify and assess the potential impact of ∇T on experimental results showing that a 1550 nm, 100 fs laser with wide-field illumination in both pulse and CW modes will permeabilize cells with peak power densities three orders of magnitude below the typical optoporation threshold [45]. Comparing permeabilization levels and ∇T between pulse and CW modes will further show that ∇T may drive permeabilization and that bulk temperature rise alone is insufficient. The approach outlined here promises to be inexpensive with a higher throughput than conventional optoporation.

2. Materials and methods

Fig. 1 shows the experimental setup. The laser wavelength was ~1550 nm, average power W_avg=120 mW, pulse duration τ_p~100 fs, repetition rate ν_rep=50 MHz (or 20 ns between pulses), peak power W_peak~24 kW (W_peak=W_avg/[τ_pν_rep]), and spot diameter of ~50 μm. The peak energy of the pulse (E_peak=τ_pW_peak) is 2.4×10⁻⁹ J. Despite similar W_peak (~10 kW) and τ_p (17–150 fs) to standard optoinjection [43], the power density here is three orders of magnitude lower due to the wider illumination area (~2500 μm² compared to 4 μm²). The resulting peak energy and average power densities are 9.6×10⁻⁴ J/cm³ and 4.8×10⁴ W/cm³, respectively, assuming an exposure volume equal to the product of the illumination area and the absorption coefficient. In terms of area, peak energy and average power densities are 9.6×10⁻⁵ J/cm² and 4.8×10³ W/cm², respectively. The typical laser spot measures approximately 50 μm, illuminating approximately 10–20 cells simultaneously with the exact number of cells a function of initial confluence density (approximately 80%) and the geometrical distribution of cells in the treated area.

Fig. 1.

Experimental setup for laser treatment of cells. The mechanical shutter controlling exposure time is not shown for clarity. The cells adhere to the bottom of the dish.

We followed the cell preparation method presented in more detail elsewhere [46]. We cultured adherent Chinese Hamster Ovarian cells (CHO, American Type Culture Collection (ATCC)) in F12K media supplemented with 10% FBS according to the ATCC protocol. The cells were used at early passages, typically between passage four and ten. We used a Countess^® Automated Cell Counter (Invitrogen) for cell counts. We seeded the cells at approximately 50% confluency with between 7×10⁴ and 1×10⁵ cells/well in 24 well-plate dishes. We verified cell morphology and viability twenty-four hours after seeding and observed that the cell confluency exceeded 80%. Fresh media was added to the cells to obtain a final volume of 1 ml for cells seeded in 24 well plates. The cells were incubated with propidium iodide (PI, Sigma) at 1 μg/ml for 5 min prior to laser exposure. We generated a negative control consisting of cells incubated with PI but not exposed to the laser. We also used a positive control consisting of fixed cells that were permeabilized with 4% paraformaldehyde (PFA) and 0.1% Triton X-10. Further assessments of positive (PI uptake as expected) and negative controls (no PI uptake as expected) are discussed elsewhere [46]. The electrical conductivity of the solution with PI was 5 S/m.

We assessed PI uptake ten to fifteen minutes after laser illumination by using a Nikon Eclipse DIC phase microscope with 20× and 60× Plan Fluor objective lenses and the built-in Nikon software for image acquisition. The bright-field and cy3 images were overlaid and stitched in ImageJ software by an automated macro.

3. Results and discussion

3.1. Experimental observation of propidium iodide delivery

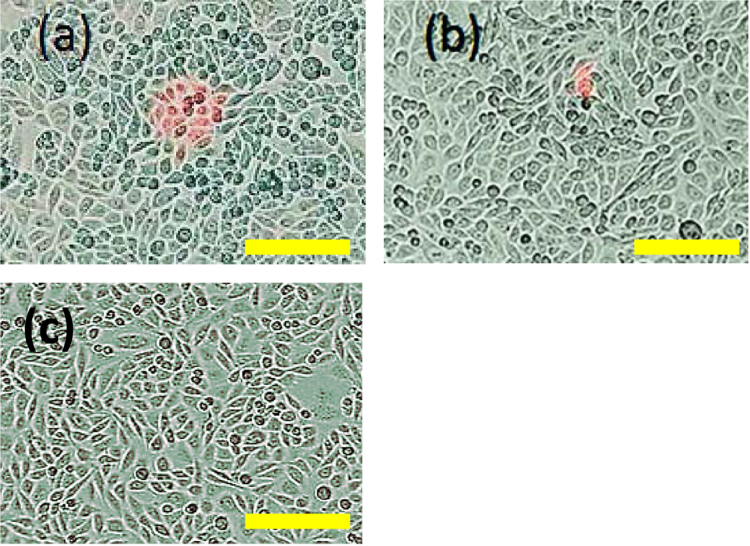
We assessed plasma membrane permeabilization following laser exposure by observing PI uptake. Fig. 2a shows that a five minute laser exposure permeabilized approximately 16 CHO cells, without changing cell viability. Fig. 2c shows the lack of PI uptake for cells in a sham experiment not treated with the laser. The delivery mechanism differs from typical optoinjection since the peak power density of 9.6×10⁸ W/cm² is well below the optical breakdown threshold of ~10¹² W/cm² [27], [45]. We successfully performed seven experiments with approximately 80% or higher efficiency of PI delivery to CHO cells using laser illumination with no changes in cell viability or morphology, as demonstrated by observation of morphology of cells post laser treatment and by calcein viability assays [46].

Fig. 2.

(a) CHO cells following a five minute treatment with a 1550 nm, 100 fs laser with 120 mW average power and 50 MHz repetition rate with the bar in (a) indicating the laser spot size. Permeabilized cells are stained red by propidium iodide (PI). (b) Illumination with the same laser in CW mode induced much less PI uptake. Calcein assays and morphological observations confirmed that cell viability was unchanged. (c) CHO cells not exposed to laser demonstrating the absence of membrane permeabilization by the lack of PI uptake. The typical laser spot size of 50 μm is shown by the bar above.

3.2. Calculation of laser induced temperature gradients

One potential mechanism involved in laser permeabilization and contributory to electroporation is ∇T generation [38]. PEFs induced ∇T depends upon pulse duration, repetition rate, and thermal diffusion time, τ_diff [38]. Electric and laser pulses differ in their typical pulse durations and repetition rates. PEFs usually have repetition rates from 1–10 Hz and durations from microseconds to milliseconds for electroporation or 10–300 ns for nsPEFs [12], [16], [20]. Lasers for transfection typically have pulse durations from femtoseconds to nanoseconds and repetition rates as high as MHz, making the time between pulses on the order of microseconds or shorter compared to the typically much longer τ_diff of 700 μs for a cell [38]. Because the absorption coefficient is proportional to the static conductivity from Drude's Law [47], we assume that the ratio between the absorption coefficients of the intracellular and extracellular fluids will be the same as between their conductivities (1.5 and 5 S/m, respectively). Since the plasma membrane has negligible impact on ∇T [38], the cell size becomes the relevant length scale for thermal diffusion, allowing us to write τ_diff=ρc_vR²/λ, where R is the cell radius (10 μm), ρ is the mass density of the suspension, c_v is the specific heat capacity of the extracellular fluid, and λ is the thermal conductivity of the cell [38]. The reduced thermal dissipation between laser pulses will promote higher ∇T across the plasma membrane than for PEFs [38]. Laser interactions with the lipids and water directly at the membrane will be secondary because they act on the smaller length scale of the membrane, which has a much shorter τ_diff. Because ∇T may impact permeabilization and molecular delivery in numerous ways, we first predict its magnitude.

We previously modeled the temperature change across a spherical cell and the resulting ∇T across the membrane for a Gaussian shaped electromagnetic pulse assuming that the temperature variation across the membrane was driven by the difference in heating between the intracellular and extracellular media [38]. For a simple first order approximation with an analytic solution, we assumed negligible cytoplasm heating, which permitted us to write the heat conduction for the extracellular fluid as [38]

$$\rho c_v\frac{\partial \mathrm{\Delta }T}{\partial t}={\sigma }_e{E}^2+\mathrm{div}\left(\lambda \mathrm{grad}\mathrm{\Delta }T\right),$$ (1)

where ΔT=T(r,t)–T₀ is the temperature increase within the cell, T₀ is the initial temperature of the cytoplasm, σ_e is the electrical conductivity of the extracellular fluid, and E is the electric field. Solving Eq. (1) analytically yields the maximum ∇T following multiple pulses, ∇T|_max, for t>τ_diff, τ_rep<τ_diff, and τ_p<τ_rep, where τ_rep is the time between pulses, as [38]

$$\nabla {T|}_{max}\approx \frac{\mathrm{\Delta }{T}_p}{R}\sqrt{\frac{{\tau }_{diff}}{{\tau }_p}}\left(1+\sqrt{\frac{{\tau }_p{\tau }_{diff}}{{\tau }_{rep}^2}}\right),$$ (2)

where ΔT_p is the temperature rise due to a single pulse.

We incorporate the laser parameters into Eq. (2) by considering two separate perspectives of laser application. A laser pulse will have a given energy density per unit volume and a given power density per unit volume. We will theoretically consider the impact of independently changing each of these on the electroporation threshold. The first condition we consider involves applying a fixed pulse energy density per unit volume, E_p=ΔT_pρc_v, where ρ and c_v are the density and specific heat of the targeted material, respectively. The second scenario uses a fixed average power density per unit volume, 〈w〉=ΔT_pρc_v/τ_rep. Table 2 shows typical parameters for commercial 1550 nm lasers and the resulting ∇T|_max. The 1 ps, 40 MHz, 1.2 W laser yields the highest ∇T (1.6×10⁵ K/m).

Table 2.

Parameters for the 1550 nm lasers used here (first row) and others at 1550 nm that are commercially available. Here, τ_p=pulse duration, ν_rep=repetition rate, W_avg=average power, W_peak=peak power, E_p=peak energy density, and ∇T|_max=maximum calculated temperature gradient.

τp (ps)	vrep (MHz)	Wavg (W)	Wpeak (kW)	Ep (J/cm3)	∇T|max (K/m)
0.1	50	0.12	24	9.6×10−4	2.7×106
10	40	1.5	3.75	1.5×10−2	1.3×107
1	40	1.2	30	1.2×10−2	1.6×107
0.5	40	0.5	25	5.0×10−3	8.0×106

Temperature gradients may generate plasma membrane electric fields that could contribute to or induce electropermeabilization [38]. The induced electric field, E_i, was estimated by E_i=kdT/dr, where r is the radial component and k ≈ 0.01 V/K is a conversion constant for water that only provides an initial estimate since it does not account for actual membrane structure [48]. While PEF induced ∇T generated insufficient electric fields for membrane permeabilization [38] assuming that the concomitant bulk temperature increase does not reduce electropermeabilization threshold [49], this estimate does permit assessing the laser parameters required to achieve a desired ∇T. Thus, we will assess ∇T|_max>∇T_ep, where ∇T_ep is the minimum ∇T that may induce electropermeabilization assuming no temperature-induced change in the electropermeabilization threshold. Assuming a voltage between 0.1 and 1 V is necessary to electroporate a 10 nm membrane and the thermoelectric conversion factor from voltage to temperature is approximately 100 K/V, 10⁹ K/m<∇T_ep<10¹⁰ K/m [38]. Rearranging Eq. (2) and substituting the expressions for E_p and 〈w〉 for fixed energy density and fixed power density, respectively, gives τ_rep to achieve ∇T_ep as

$${\tau }_{rep,E}<\left(E_p{\tau }_{diff}\right){\left(\rho c_{v}R\nabla T_{ep}-E_p{\tau }^{*}\right)}^{-1}$$ (3)

for fixed energy density or

$${\tau }_{rep,\langle w\rangle }>\left(\rho c_{v}R\nabla T_{ep}-{\tau }_{diff}\langle w\rangle \right){\left(\langle w\rangle {\tau }^{*}\right)}^{-1}$$ (4)

for fixed power density, where τ*=(τ_diff/τ_p)^1/2. Note that the inequalities differ between the two requirements. Shorter τ_rep below the threshold in Eq. (3) will exceed the electroporation threshold for fixed energy density pulses. On the other hand, longer τ_rep above the threshold in Eq. (4) will exceed the electroporation threshold.

Fig. 3 shows curves satisfying ∇T_max=∇T_ep=10⁹ K/m for constant E_p and constant 〈w〉 pulses. For a fixed energy density pulse of given τ_p, selecting τ_rep below the curve for the corresponding energy will give ∇T_max>∇T_ep. For instance, Fig. 3a shows that our laser parameters plot above the 9.6×10⁻⁴ J/cm³ curve for ∇T induced electropermeabilization by approximately three orders of magnitude, which means that the induced ∇T<∇T_ep since τ_rep,E must fall below this curve to satisfy ∇T_ep based on the inequality of Eq. (3). One can achieve ∇T_ep by changing the operating parameters of the laser, such as by raising the wavelength from 1550 nm to 3000 nm. This increases the absorption coefficient of water [29] from 50 cm⁻¹ to ~2×10⁴ cm⁻¹, which reduces the volume of laser irradiation absorption to 2×10⁻⁸ cm³, yielding E_p=0.32 J/cm³. A laser with E_p=0.32 J/cm³, τ_rep=2×10⁻⁸ s, and τ_p=100 fs gives ∇T~∇T_ep, as demonstrated in Fig. 3a by the 0.32 J/cm³ line falling inside the data point for the laser with the given τ_rep and τ_p.

Fig. 3.

(a) Peak energy density (E_p) and (b) average power density (〈w〉) to achieve ∇T_ep, the estimated temperature gradient necessary for direct electropermeabilization, as a function of pulse duration (τ_p) and time between pulses (τ_rep). Regions below (a) and above (b) the curves indicate ∇T>∇T_ep, respectively. The black square represents the experimental condition used here at 1550 nm, τ_rep=20 ns, and t_p=100 fs (E_p=9.6×10⁻⁴ J/cm³, 〈w〉=4.8x10⁴ W/cm³).

For a laser applied with a fixed power density, the laser parameter the τ_rep for a given τ_p must fall above the curve for the corresponding energy to satisfy ∇T_max>∇T_ep. Using the same basic laser parameters with a fixed power density of 〈w〉=4.8×10⁴ W/cm³, the square representing the laser parameters falls approximately three orders of magnitude below the corresponding 〈w〉 line, meaning that ∇T_max<∇T_ep since satisfying the inequality of Eq. (4) requires the experimental data point to be above the threshold. One may satisfy ∇T_max=∇T_ep for a laser with this τ_rep and τ_p by selecting a wavelength of 3000 nm, which increases the power density to 1.6x10⁷ W/cm³ by reducing the absorption coefficient. Fig. 3b shows that the laser parameters then intersect the curve represented by this power density, indicating that it satisfies ∇T_max<∇T_ep. While our experimental conditions are approximately three orders of magnitude below ∇T_ep, other factors may impact this threshold, which we will explore next.

3.3. Variation in temperature gradient electroporation threshold

The magnitude of ∇T_ep can vary by one to two orders of magnitude because the membrane voltage for electroporation can vary by approximately an order of magnitude and several of the other parameters, such as membrane thickness, density, and thermal conductivity, may also vary. As a simple example of the influence of these variations, we consider the impact of increasing and decreasing ∇T_ep by one order of magnitude from 10⁹ K/m (from 10⁸ to 10¹⁰ K/m) for E_p=9.6×10⁻⁴ J/cm³ and 〈w〉=4.8×10⁴ W/cm³. Fig. 4 shows the impact of this variation in ∇T_ep on the resulting thresholds as a function of τ_rep and τ_p. The changes in the threshold curves roughly scale with the changes in ∇T_ep. In other words, increasing ∇T_ep by an order of magnitude raises the curve by approximately an order of magnitude in τ_rep and decreasing it by an order of magnitude lowers the curve by approximately an order of magnitude. This provides some insight into the impact of variations on ∇T_ep and what laser parameters are required to satisfy the potential range of for ∇T induced electropermeabilization.

Fig. 4.

The impact of uncertainties in the plasma membrane temperature gradient electroporation threshold ranging from 10⁸ K/m to 10¹⁰ K/m for laser pulses of constant (a) Peak energy density (E_p) and (b) average power density (〈w〉). The black square represents the experimental condition used here at 1550 nm, τ_rep=20 ns, and t_p=100 fs (E_p=9.6×10⁻⁴ J/cm³, 〈w〉=4.8x10⁴ W/cm³). The experimental conditions have temperature gradients below the threshold in all cases, indicating the inability to induce electroporation through temperature gradients alone.

3.4. Bulk temperature effects on membrane permeabilization

In addition to temperature gradient effects, bulk heating may also impact membrane permeabilization and cellular behavior. Bulk heating of the cell and the laser illumination area may reduce ∇T_ep [49]. For the full illumination area, we attain a thermal steady state given by W_avg/V=λΔT/Λ², where W_avg is the average power of the laser (120 mW), V is the volume of treatment (R=50 μm, L=0.1 cm at 1550 nm), λ=0.6 W/m/K, and Λ is the heat transfer length, given by Λ⁻²=2.405²/R²+π²/L². Using R⪡L and rearranging gives ΔT=10 K. Molecular dynamics (MD) simulations show that raising the temperature a few degrees kelvin reduces the electroporation threshold [49]; therefore, laser treatment reduces ∇T_ep. While complicated because temperature impacts both membrane molecular properties and electroporation dynamics [50], [51], we can estimate the pore formation per unit area of the membrane by

$$S\left(r,T\right)~\frac{E}{KT}\exp \left(\frac{-E_a}{KT}\right),$$ (5)

where E is energy, K is Boltzmann's constant, E_a is pore formation energy, and r is pore radius [50]. Higher |S| implies closer proximity to the electroporation threshold. We assess the impact of a small temperature increase, dT, by calculating C=S(r,T+dT)/S(r,T), which gives the change of the pore formation per unit area due to dT . Assuming T̅=dT/T⪡1, we obtain T̅²–T̅+ln(C)/E^˜=0, with E^˜=E_a/(kT). For fixed C, increasing T̅ reduces E^˜, facilitating pore formation. Alternatively, achieving the experimentally observed dT=10 K for E^˜=45 [50] and T=300 K requires C=4.26.

MD simulations for assessing electroporation are often challenging because the pulses are long (~μs to ms) compared to computational capabilities (~ns). The laser pulses are subpicosecond, making them amenable to MD. MD simulations could elucidate the coupling of ∇T and electric fields on membrane permeabilization [52]. Specifically, the laser wave’s electric field will induce a membrane voltage in addition to that induced by the ∇T. Equating the laser (W_avgτ_p/τ_rep) and electromagnetic energies (ε|E_L|²/2, where ε is the buffer permittivity and E_L is the peak direct laser-induced electric field) yields E_L=0.33 kV/cm with ε=80ε₀. While much lower than the electric fields necessary to induce membrane effects for subnanosecond PEFs [53], laser exposure is more nuanced since the reduced time between laser pulses induces a greater temperature increase that may additionally reduce the electropermeabilization threshold.

3.5. Effect of CW laser heating on PI uptake and temperature gradients

One final point concerns the synergistic combination of the laser bulk temperature increase and temperature gradients. To assess the impact of bulk heating compared to temperature gradients, we also conducted experiments with the same 120 mW average power laser at 1550 nm in continuous wave (CW) mode. CW only increases ∇T up to t=τ_diff, after which the cytoplasm and buffer heat together. Using CW reduces ∇T (∇T_|CW=W_avgτ_diff/(Vρc_pR)=8x10⁵ K/m compared to 2.7×10⁶ K/m for pulsed operation) and E_L (7.5×10⁻⁴ kV/cm) by almost a factor of three compared to pulsed operation, while inducing a similar bulk temperature increase. Lower E_L reduces electropermeabilization, while lower ∇T decreased membrane voltages and thermodiffusion through membrane pores. Overall, CW laser illumination induced negligible permeabilization and PI delivery, as shown in Fig. 2b. Thus, while combining ∇T, bulk temperature increase, and electric fields likely permeabilizes membranes, the same bulk temperature increase with reduced ∇T is insufficient. The synergistic combination of these effects clearly requires further investigation.

4. Conclusion

In summary, a wide-field femtosecond laser with peak power density several orders of magnitude below the optical breakdown threshold [27], [45] permeabilizes multiple cells without impacting viability. While most experiments assessed CHO cells and PI uptake, we successfully delivered other molecules to other cells, including phalloidin to CHO and NIH3T3 cells [46], or PI to rat mesenchymal cells (unpublished work). Calculations show that ∇T, bulk temperature increase, and direct laser-induced electric fields may contribute to this phenomenon; however, the reduced PI uptake in CW mode compared to pulsed mode indicates that ∇T must play a critical role. Future experiments could focus on developing interferometry systems to measure these rapid membrane temperature gradients. The importance of ∇T for laser-induced results resembles that for microwave-induced phenomena [39], [40], [41], [42]. Potential mechanisms may include electropermeabilization due to a ∇T induced membrane voltage [38], direct electropermeabilization by the laser’s electric field, a temperature-induced reduction of the electropermeabilization threshold, or some synergistic combination of these factors. Much as electric fields induce electrophoresis in addition to electroporation, ∇T may also induce thermodiffusion, in which molecules move through pores along the ∇T across the membrane [54], [55], [56]. Thermal diffusion of electrolytes, nonelectrolytes, and macromolecules arise for temperature gradients ~100–1000 K/m [56], which are three to five orders of magnitude lower than the calculated ∇T induced by the lasers described in Table 1, suggesting a potentially important contributory mechanism for molecular transport once membrane pores are formed, which requires future study. This is similar to the combination of electroporation and either electrophoresis (during the electric pulse) or diffusion (after the electric pulse), which require pore formation for ion transport [57].

We have further demonstrated that laser wavelength determines whether the surrounding buffer or the membrane will be preferentially heated based on the absorption coefficient. The wavelength of 1550 nm permeabilized cells within the 50×50 μm² illumination area. We anticipate that the much larger absorption coefficient at 3000 nm will generate greater ∇T that could enhance biological effects. Lasers with the same peak power, frequency, and pulse widths at the 532 or 800 nm wavelengths common for optical transfection create dramatically lower ∇T due to the much smaller difference in absorption coefficient between lipids and the surrounding buffer. Much as tuning pulse durations and rise- and fall-times can control the targeting of PEF effects [16], appropriately selecting the average power, wavelength, repetition rate, illumination area, and pulse duration enables targeting laser effects to either one or multiple cells. This may yield a powerful tool for an inexpensive (the fiber laser used in these tests is relatively low cost, <$10 k), high throughput, easy to use (no complicated optics for focusing the laser beam to a narrow spot and aligning the beam to the cell of interest) laser mediated exogenous molecule delivery.