Toxicity prediction from toxicogenomic data based on class association rule mining

Abstract

While the recent advent of new technologies in biology such as DNA microarray and next-generation sequencer has given researchers a large volume of data representing genome-wide biological responses, it is not necessarily easy to derive knowledge that is accurate and understandable at the same time. In this study, we applied the Classification Based on Association (CBA) algorithm, one of the class association rule mining techniques, to the TG-GATEs database, where both toxicogenomic and toxicological data of more than 150 compounds in rat and human are stored. We compared the generated classifiers between CBA and linear discriminant analysis (LDA) and showed that CBA is superior to LDA in terms of both predictive performances (accuracy: 83% for CBA vs. 75% for LDA, sensitivity: 82% for CBA vs. 72% for LDA, specificity: 85% for CBA vs. 75% for LDA) and interpretability.

1. Introduction

New technologies such as DNA microarray and next-generation sequencer have allowed researchers to learn biological phenomena in genome or transcriptome levels. Especially in toxicology, these new technologies have led to a new subdiscipline, termed toxicogenomics. Toxicogenomics is concerned with the identification of potential human and environment toxicants, and their putative mechanisms of action, through the use of genomics resources [1]. For example, by evaluating and characterizing differential gene expressions, in humans or animals, after exposure to drugs, it is possible to use complex expression patterns to predict toxicological outcomes and to identify mechanisms involved with or related to the toxic event [2]. Traditionally, to construct a such predictive classifier, techniques in machine learning such as k-nearest neighbors, linear discriminant analysis (LDA) and support vector machine (SVM) have been mostly used [3]. However, building a classifier that is accurate and understandable at the same time is not necessarily an easy task. For example, while SVM achieves high classification accuracy, resulting classifiers are hard to interpret as variables are transformed nonlinearly into a feature space, and hence difficult to use in order to extract relevant biological knowledge from it [4]. Very often, predictive accuracy, understandability, and computational demands need to be traded off against one another, because algorithms often compromise one to gain performance in the other [5].

In this study, we applied the classification based on association (CBA) algorithm to toxicogenomic data in an aim to build a classifier that is accurate and understandable at the same time. We compared its predictive performances and interpretability of generated classifiers with those of LDA, which is considered to be one of the most standard classification methods and have a good balance between accuracy and interpretability.

CBA is one of the class association rule (CAR) mining algorithms, which integrate association rule mining (finding all the rules existing in the database that satisfy some constraints) and classification rule mining (discovering a small set of rules in the database that forms an accurate classifier) by focusing on mining a special subset of association rules, called class association rules (CARs) [6]. One of the advantages of CAR mining algorithms over conventional methods (especially SVM) is its interpretability, because classifiers are generated as a set of simple rules without much sacrifice of accuracy [7]. Another advantage is that CAR mining algorithms can be applied not only to linearly separable cases, but also to linearly inseparable cases, where LDA or other linear classification methods are not applicable [8]. SVM can handle linearly inseparable cases by mapping original data into a suitable feature space, but with loss of interpretability. Besides, especially when applied to gene expression data, CAR mining algorithms, which predict a class label based on specific sets of differentially expressed genes that are actually observed in training samples, are expected to generate more biologically reasonable classifiers, because it is generally not individual genes but sets of genes that collectively define phenotypes such as drug responses [9]. While applications of CBA and its variants in biological research have been reported in several reports [10], [11], [12], [13], [14], there is so far no reports with direct implication for toxicogenomics, which is unique in that the number of variables to be analyzed is usually far much greater in toxicogenomics (more than 30,000 genes) than in other applications and this so-called high dimensionality makes it difficult to analyze its data.

To compare the predictive performances and interpretability of CBA and LDA, utilizing the TG-GATEs database, where both microarray and toxicological data of more than 150 compounds in rats (in vivo and in vitro) and humans (in vitro) are stored, we built both CBA and LDA classifiers that predict whether a chemical compound induces increases in liver weight after 14-day repetitive treatments in rats based on transcriptomic data of 3-day repetitive treatments. Although measurable increases in mRNA (indicative of enzyme induction) are likely to precede, increase in liver weight is the most sensitive indicator of hepatocellular hypertrophy and occur prior to morphological changes. While it should be also noted that hepatocellular hypertrophy without histological or clinical pathological alterations is considered to be an adaptive non-adverse change, certain degrees of liver weight increase appeared to be correlated with the subsequent development of irreversible toxicity such as fibrosis, necrosis, vacuolization, fatty degeneration, and even neoplasia [15] and early detection of hepatocellular hypertrophy based on liver weight or gene expressions is expected to be useful, for example, in selecting compounds with less risk of hepatotoxicity in drug development.

2. Material and methods

2.1. Data source

TG-GATEs is a toxicogenomic database developed by The Toxicogenomics Project (TGP), a joint government-private sector project organized by the National Institute of Biomedical Innovation, National Institute of Health Sciences and 15 pharmaceutical companies in Japan, and The Toxicogenomics Informatics Project (TGP2), a follow-on project from TGP organized by the National Institute of Biomedical Innovation, National Institute of Health Sciences and 13 companies. Gene expression and toxicity data in vivo (rats) and in vitro (primary cultured hepatocytes of rats and humans) after treatments of more than 150 compounds are stored in the TG-GATEs database. TG-GATEs is now released for public as Open TG-GATEs (http://toxico.nibio.go.jp).

From the TG-GATEs database, we used gene expression data (n = 3 per group) one day after 3-day repetitive doses (hereinafter 4D) in the liver of rats and liver weight data (relative liver weights calculated from body weights) (n = 5 per group) one day after 14-day repetitive doses (15D) in rats for this study. For each compound, only the data of the highest dose group and its control group was used. Of 150 compounds, we omitted one compound and analyzed the remaining 149 compounds because that one compound was found to have killed animals before 15D in the study and therefore no data is available for liver weight of 15D.

2.2. CBA (classification based on association)

2.2.1. Software

In courtesy of Dr. Frans Coenen, we used a CBA program available on the LUCS-KDD website, which is implemented according to the original algorithm by [6], except that CARs are first generated using the Apriori-TFP algorithm instead of the CBA-RG algorithm.

2.2.2. Concept

The basic concept of CBA is briefly explained here based on the explanations from [6] with examples in this study. For detail, refer to [6]. Let D be the dataset, a set of records d (d ∈ D). Let I be the set of all non-class items in D, and Y be the set of class labels in D. In this study, a non-class item is a pair of gene ID and its discretized expression (Inc or Dec) (Inc: increased, Dec: decreased) and a class label is a pair of a target parameter (RLW: relative liver weight) and its discretized value (Inc or NI, or Dec or ND) (NI: not increased, ND: not decreased). The set of class labels Y in this study is either {(RLW, Inc), (RLW, NI)} or {(RLW, Dec), (RLW, ND)}. We say that a record d ∈ D contains X ⊆ I, or simply X ⊆ d, if d has all the non-class items of X. Similarly, a record d ∈ D contains y ∈ Y, or simply y ⊆ d, if d has the class label y. A rule is an association of the form X → y (e.g. (Gene_01, Inc), (Gene_02, Dec) → (RLW, Inc)). For a rule X → y, X is called an antecedent of the rule and y is called a consequence of the rule. A rule X → y holds in D with confidence c if c% of the records in D that contain X are labeled with class y. A rule X → y has support s in D if s% of the records in D contain X and are labeled with class y. The objectives of CBA are (1) to generate the complete set of rules that satisfy the user-specified minimum support (called minsup) and minimum confidence (called minconf) constraints, and (2) to build a classifier from these rules (class association rules, or CARs).

The original CBA algorithm of Liu et al. consists of two parts, a rule generator (called CBA-RG) and a classifier builder (called CBA-CB), each corresponding to (1) and (2).

The key operation of CBA-RG is to find all rules X → y that have support above minsup. Rules that satisfy minsup are called frequent, while the rest are called infrequent. For all the rulesthat have the same antecedent, the rule with the highest confidence is chosen as the possible rule (PR) representing this set of rules. If there are more than one rules with the same highest confidence, one rule is randomly selected. If the confidence is greater than minconf, the rule is accurate. The set of CARs thus consists of all the PRs that are both frequent and accurate. The CBA-RG algorithm effectively searches for all the CARs in a dataset based on the Apriori algorithm [16], assuming the downward closure property that for any X, X is frequent if and only if any subset x of X is frequent. Instead of CBA-RG, the Coenen's CBA program is implemented with the Apriori-TFP algorithm [17], [18], a variant of the Apriori algorithms that utilizes a tree-structured data representations for a higher performance.

The operation of the latter part, CBA-CB, is described as follows in [6]. “Given two rules, r_i and r_j, r_i ≻ r_j (also called r_i precedes r_j or r_i has a higher precedence than r_j) if

• 1.the confidence of r_i is greater than that of r_j, or
• 2.their confidences are the same, but the support of r_i is greater than that of r_j, or
• 3.both the confidences and supports of r_i and r_j are the same, but r_i is generated earlier than r_j.

Let R be the set of generated rules and D the training data”. CBA-CB is “to choose a set of high precedence rules in R to cover D”. A generated classifier is of the form, <r₁, r₂, …, r_n, default_class>, where r_i, ∈ R and r_a, ≻ r_b if b > a. In classifying a sample with a unknown class label, the first rule that satisfies the sample will classify it. If there is no rule that applies to the sample, it takes on the default class, default_class. Below is a simple example of classifiers.

Example:

$$\left(\text{Gene}\_01,\text{Inc}\right),\left(\text{Gene}\_02,\text{Dec}\right)\to \left(\text{RLW},\text{Inc}\right)$$

$$\left(\text{Gene}\_01,\text{Inc}\right),\left(\text{Gene}\_03,\text{Inc}\right)\to \left(\text{RLW},\text{Inc}\right)$$

$$\left(\text{NULL}\right)\to \left(\text{RLW},\text{NI}\right)$$

In this example. each line corresponds to a rule included in the classifier. The rule with the (NULL) antecedent means the default rule of this classifier. When a sample, (Gene_01, Inc), (Gene_03, Inc) with an unknown class label (it is unknown whether RLW is Inc or NI), is classified, the classifier answers (RLW, Inc), as the second rule first satisfies the sample. In another case, where a sample, (Gene_01, Inc), (Gene_02, Inc), is classified, the classifier answers (RLW, NI), as none of the rules except the default rule satisfies the sample and thus the default rule is applied.

2.3. Data analysis

Prior to the CBA analysis, we have preprocessed gene expression data in the liver (4D) and liver weight data (15D) of rats after repetitive doses for 149 compounds from the TG-GATEs database. First, gene expressions were corrected and normalized by the MAS 5.0 algorithm [19] to reduce inter-array variances [20]. Liver weights were transformed into relative liver weight, a ratio of liver weight divided by body weight to avoid large variations in body weight skewing organ weight interpretation [15]. Second, values were averaged over individual animals included in each group. Then, for each compound-treated group, a fold change was calculated as a ratio of an average value of a treatment group divided by an average value of its corresponding control group, to reduce inter-study variances [21]. Finally, we discretized gene expressions and relative liver weights based on their fold changes (fc) and p values (p) of the student's t-test conducted between a compound-treated group and its corresponding control group, according to the criteria shown below.

2.3.1. Gene expression data

If fc > 2 and p < 0.05, assign “Inc” (increased).

If fc < 0.5 and p < 0.05, assign “Dec” (decreased).

Otherwise, assign “NC” (not changed).

2.3.2. Liver weight data

• 1.When a classifier for increased liver weight was built:If fc > 1 and p < 0.05, assign “Inc” (increased).Otherwise, assign “NI” (not increased).
• 2.When a classifier for decreased liver weight was built:If fc < 1 and p < 0.05, assign “Dec” (decreased).Otherwise, assign “ND” (not decreased).

Discretization thresholds for gene expressions combined with fold changes and statistical test (e.g. student's t-test) have often been applied in microarray data analysis and is reported to be better than p value alone [22]. In general, numerical parameters obtained in toxicity studies are judged to be increased or decreased, based essentially on statistical comparison with contemporary controls and, if available, additionally on historical data [23]. In this study, we discretized liver weights based only on statistical tests, as no historical data was available.

Before proceeding to CBA, gene expressions discretized as “NC” in each group were discarded from the data, because we were interested only in genes with increased or decreased expressions. We then analyzed the data with CBA, with discretized gene expressions as non-class items and discretized liver weights as class labels.

2.4. Linear discriminant analysis (LDA)

2.4.1. Software

We used the lda function in the MASS library of R. R's lda function is implemented based on Rao's LDA [24], [25], also known as Fisher-Rao LDA, which generalized Fisher's LDA [26] to multiple classes.

2.4.2. Data analysis

Prior to the LDA analysis, the data was preprocessed as described in the CBA section, except that gene expressions were not discretized. Before proceeding to LDA, the feature selection step was conducted to reduce the number of genes, because classical LDA requires the total scatter matrix to be nonsingular, while the matrix can be singular when the sample size (149) does not exceed the number of features (genes) (more than 30,000) [27], and tends to overfit and become less interpretable in the presence of many irrelevant and/or redundant features [28]. Based on the previous reports on microarray data analysis [29], [30], we selected only the genes that were up-regulated (fc > 2 and p < 0.05) or down-regulated (fc < 0.5 and p < 0.05) in the groups with increased or decreased liver weight when compared to the not-increased or not-decreased groups, respectively.

2.5. Predictive performance comparison

To compare predictive performances of CBA and LDA, we conducted 10-fold cross validation [31] for each methods with the total of 149 records (compounds), and evaluated sensitivity, specificity, and accuracy averaged over 10 validations. These parameters are defined as follows [32].

Sensitivity	True positive/(true positive + false negative)
Specificity	True negative/(true negative + false positive)
Accuracy	(True positive + true negative)/total

10-fold cross validation, or more generally k-fold cross validation, is one of the standard methods for evaluating predictive performances of classifiers. This method divide a dataset into equally-sized k partitions (1, 2, …, k). In the first step, the first partition (1) is reserved as a test set and the other partitions (2, 3, …k) are used as a training set to build a classifier. Once a classifier is built, it is validated for its predictive performances with a test set (the first partition in this case). k-Fold cross validation repeats this steps k times changing a partition serving as a test set one by one. In the end, averaged predictive performance over k validation steps is regarded as the predictive performance of a classification algorithm.

2.6. Student's t-test

For statistical comparison of mean gene expressions or liver weights between a compound-treated group and its corresponding control group for each compound, the unpaired two tailed student's t-test without equal variance assumption was conducted. Specifically, this statistical test was conducted in the discretization step of CBA and the feature selection step of LDA. When gene expressions were compared between two groups, gene expressions were log-transformed with base of two prior to the statistical test. Log transformations of gene expression data is known to result in more consistent statistical inferences and be often considered desirable, due to its large coefficient of variation [33].

It is well known that the standard p-value method leads to the high rate of false positives when applied in repeated testing. This is the case when analyzing gene expression data collected via microarrays, as this usually involves testing from several thousands to tens of thousands of hypotheses simultaneously. While a number of adjustment procedures (e.g. controlling the false discovery rate) are available, they are often too conservative for microarray studies in that they can lead to low sensitivity [34], thus increasing the risk of missing true positives. In this study, no adjustments were applied, taking it into consideration that even if false positive genes with no or little relevance for liver weights were detected by statistical tests, the classification methods would discard many of them from a generated classifier, hence marginalize the impact of such false positives while minimizing the risk of overlooking true important changes.

2.7. Pathway analysis

Canonical pathway analysis for the genes included in the CBA-generated classifier was conducted with QIAGEN's Ingenuity Pathway Analysis (IPA) software to understand what pathway (and hence function) these genes are mainly involved. The reason why we used IPA, not a publicly available database, is its high quality of information. IPA is based on “expertly curated biological interactions and functional annotations from millions of individually modeled relationships between proteins, genes, complexes, cells, tissues, drugs, and diseases” and “reviewed for accuracy by PhD scientists” (according to QIAGEN's website: http://www.ingenuity.com/products/ipa).

Canonical pathways are a set of pre-built pathways based on the literature. Canonical pathway analysis of IPA answers how statistically significantly the pathways were affected, considering how many molecules a user-specified set and a pathway share. In this study, we conducted canonical pathway analysis with all the genes included in our CBA-generated classifier. In canonical pathway analysis, specified genes are converted to their corresponding molecules and matched up against the molecules in each pathway.

2.8. Computer

In this study, we used a personal computer with Intel Core i5-3320M 2.6 GHz CPU and 4 GB RAM for the analyses.

3. Results

3.1. Selection of minimum support and confidence

In CBA, a user must specify two parameters: minimum support (minsup) and minimum confidence (minconf). There is no universal criteria for these parameters. In this study, we assumed that lower minsup and higher confidence are basically desirable. That is to say, a rule is considered useful, if the rule X → y satisfies a large fraction of records that matches the rule antecedent X, even if the number of records that matches X is small. This is because a drug-induced response (or more generally biological response) is considered to be not caused by a single mechanism. Rather, it is expected that there are several different mechanisms, thus different gene expression patterns, finally leading to the target drug-induced response, and that each gene expression pattern occurs in a relatively low frequency among the dataset even if the dataset contains an enough records with the target drug-induced response. If set too strict, however, there is a risk of missing useful rules with few exceptions for too high minconf and of selecting accidental rules with only a few satisfying records for too low minsup. Moreover, minsup is also limited by computational resources, as the lower the minsup is set, the higher the computational demand is, in terms of both time and memory.

To explore the ideal settings of minsup and minconf, we evaluated accuracy of CBA classifiers for increased liver weight in 10-fold cross validations under various combinations of minsup and minconf (Table 1). First, we fixed the minsup at 10% and changed the minconf from 50% to 100%. While the minconf at 90% marked the highest accuracy (79%), there were no obvious differences or tendency in accuracy among the different minconfs. Next, we fixed the minconf at 90% and changed the minsup from 20% downward. Lowering the minsup remarkably improved accuracy, but prolonged computational time at the same time. The accuracy reached at 83% with minsup at 8%. We tried with minsup at 7%, but failed to finish the computation due to memory insufficiency. Similar tendencies were also confirmed when assessing accuracy of classifiers for decreased liver weight under different minsups and minconfs (data not shown).

Table 1.

Exploration of various CBA settings.

minsup (%)	minconf (%)	Average accuracy (%)	Total time (s)
(A) When minsup was fixed at 10%
10	50	77	0.61
10	80	76	0.59
10	90	79	0.58
10	100	77	0.58
(B) When minconf was fixed at 90%
20	90	0	0.42
15	90	9	0.42
10	90	79	0.58
8	90	83	22.37
7	90	Insufficient memory

Accuracy of CBA classifiers for increased relative liver weight was evaluated in 10-fold cross validations under various combinations of minsup and minconf.

Based on these results, we adopted the minsup at 8% and minconf at 90% for the following analyses.

3.2. Predictive performance

We compared predictive performance of classifiers between CBA and LDA with 10-fold cross validation (Table 2). When increased liver weight was targeted (that is, when a classifier for increased liver weight was built), CBA outperformed LDA in all of the three criteria: accuracy (83% for CBA vs. 75% for LDA), sensitivity (82% vs. 72%), and specificity (85% vs. 75%). When decreased liver weight was targeted, CBA scored better accuracy (86% vs. 73%) and sensitivity (22% vs. 6%), while LDA marked better specificity (90% vs. 95%).

Table 2.

Comparison of predictive performances.

Method	Target direction	Average over 10-fold cross validation
		Total	TP	FN	FP	TP	Hold	Accuracy (%)	Sensitivity (%)	Specificity (%)
CBA	Inc	14.9	4.4	1.1	1.4	8	–	83	82	85
LDA	Inc	14.9	2.7	1	2.8	8.4	–	75	72	75
CBA-DR	Inc	14.9	4.4	0	1.4	0.8	8.3	79	100	29
CBA	Dec	14.9	0.2	0.7	1.4	12.6	–	86	22	90
LDA	Dec	14.9	0.2	3.3	0.7	10.7	–	73	6	95
CBA-DR	Dec	14.9	0	0.7	0	12.6	1.6	95	0	100

Predictive performance of classifiers was compared among CBA, LDA, CBA-DR with 10-fold cross validation.

Target direction: a classifier was built for whether increased (Inc) or decreased (Dec) relative liver weight. Total: average number of total records in a test set of each trial in a cross validation. TP: average number of true positive records in a test set. FN: average number of false negative records in a test set. FP: average number of false positive records in a test set. TN: average number of true negative records in a test set. Hold: average number of records in a test set that did not match any rules except the default rule (only for CBA-DR).

Note that accuracy, sensitivity and specificity for the CBA-DR method were calculated excluding ‘hold’ samples. Totals are not integers here, as the number of records in the original dataset was 149 and thus cannot be divided by 10, the number of trials in the cross validation.

We also compared between CBA and CBA-DR (CBA without default rule), our modified version of the original CBA (Table 2). CBA-DR does not predict if a sample does not match any rule except the default rule in a classifier, and, in turn, return a ‘hold’. When increased liver weight was targeted, CBA-DR marked lower accuracy (83% for CBA vs. 79% for CBA-DR) and specificity (85% vs. 29%) and higher sensitivity (82% vs. 100%). When decreased liver weight was targeted, CBA-DR marked lower sensitivity (22% for CBA vs. 0% for CBA-DR) and higher accuracy (86% vs. 95%) and specificity (90% vs. 100%).

3.3. Interpretability

We compared the form of generated classifiers between CBA and LDA (Fig. 1), when all the records were used as a training set for increased liver weight. CBA tells us a set of rules, arranged in order of confidence. Each rule consists of an antecedent, which is an itemset in the form of (non-class attribute, its discretized value), and a consequence in the form of (class attribute, its class label), shown after “−>” here.

Fig. 1.

Comparison of the classifier form between CBA and LDA. The form of generated classifiers were compared between CBA and LDA, when all the records were used as a training set for increased relative liver weight. [CBA] The classifier consists of a set of rules, represented as “antecedent → consequence, support, confidence”, one rule par line, in order of confidence. An antecedent is a set of non-class items, each item represented as (gene_id, Inc or Dec). A consequence is a class label that is used as a classification result if the corresponding antecedent is satisfied, shown here as (RLW, Inc or NI). The final rule with an antecedent (NULL) is the default rule, which is satisfied for any records and applied if all the preceding rules are not met. [LDA] The classifier is shown as a discriminative function, fd. fc(gene_id) is a fold change of a gene specified with gene_id. If fd is positive, the classifier predicts RLW as Inc. Otherwise, RLW as NI. gene_id: Represented here as an Affymetrix probe ID. RLW: relative liver weight. Inc: increased. Dec: decreased. NI: not increased.

On the other hand, LDA tells us a single discriminative function (fd), which is a polynomial of non-class attribute values with their coefficients. Coefficients in a discriminative function of LDA reflect discriminative power of each non-class attribute (gene, here), with higher positive values and lower negative values meaning larger contributions to each corresponding class label of a class attribute (liver weight, here).

3.4. Biological relevance

To look into how biologically reasonable the CBA-generated classifier is, we conducted the canonical pathway analysis for the set of genes selected in the classifier when all the records were used as a training set for increased liver weight (Table 3) (for brevity, only top 10 pathways in order of −log p are shown). Because LDA itself, in contrast to CBA, does not explicitly select a set of genes in building a classifier, we did not compare CBA with LDA here.

Table 3.

Canonical pathway analysis of CBA classifier.

Pathway Name	−log p	Molecules			Corresponding Genes
		Total	Inc	Dec
Xenobiotic metabolism signaling	8.96	219	8	0	Gsta3, Aldh1a1, Ugt2b1, Nqo1,RGD1559459, Cyp2b2, Ces2c, Sult2a2
LPS/IL-1 mediated inhibition of RXR function	5.07	178	4	1	Abccg8, Gsta3
PXR/RXR activation	3.95	58	3	0	Aldh1a1, Cyp2b2, Sult2a2
Aryl hydrocarbon receptor signaling	2.94	127	3	0	Gsta3, Aldh1a1, Nqo1
Nicotine Degradation III	2.77	37	2	0	Ugt2b1, Cyp2b2
Melatonin Degradation I	2.75	38	2	0	Ugt2b1, Cyp2b2
Serotonin degradation	2.67	42	2	0	Aldh1a1, Ugt2b1
Superpathway of melatonin degradation	2.67	42	2	0	Ugt2b1, Cyp2b2
NRF2-mediated oxidative stress response	2.66	159	3	0	Gsta3, Akr7a3, Nqo1
Nicotine Degradation II	2.65	43	2	0	Ugt2b1, Cyp2b2
Histidine Degradation III	2	6	0	1	Hal

The canonical pathway analysis was conducted with the Ingenuity IPA software for the genes included in the CBA classifier when all the records were used as a training set for increased relative liver weight. Note that, for brevity, only top 10 pathways in order of -logp are shown here.

−log p: −log of p, where p is a value representing statistical significance in the analysis. A smaller p value (thus a larger −log p value) means that the pathway is more statistically significantly involved. Molecules: the total, increased (upregulated) number and decreased (downregulated) number of molecules in each pathway are shown. Corresponding genes: corresponding rat genes for the increased or decreased molecules included in the pathway are shown.

We could assume that the most significant pathways involved with the genes in our classifier were mainly drug metabolism-related ones, such as Xenobiotic Metabolism Signaling, LPS/IL-1 Mediated Inhibition of PXR Function, PXR/RXR Activation etc.

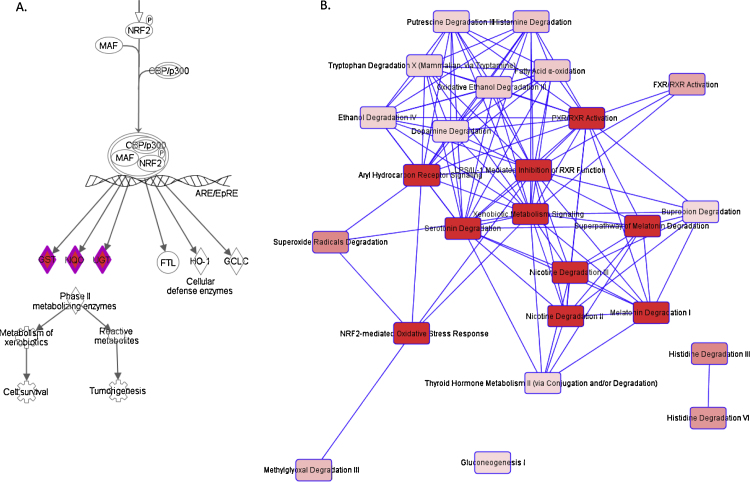
Fig. 2A is an excerpt around the NRF2 molecule from the illustration of the Xenobiotic Metabolism Signaling pathway, exported from IPA. NRF2 is a key modulator of oxidative stress responses. In response of oxidative stress, NRF2 is released into the nucleus and up-regulates downstream antioxidant enzymes, mainly drug metabolism enzymes. Actually, the genes of drug metabolism enzymes such as GST, NQO, and UGT downstream of NRF2 were included in our classifier, suggesting the induction of drug metabolism enzymes triggered by NRF-2-dependent oxidative stress responses.

Fig. 2.

Canonical pathway illustrations of CBA classifier. [A] An excerpt around the NRF2 molecule from the illustration of the Xenobiotic Metabolism Signaling pathway, exported from IPA. [B] Overlapping among the canonical pathways detected as significant, which were divided into three clusters, exported from IPA. Each node corresponds to each canonical pathway detected as significant. Each link corresponds to the number of molecules shared between two pathways. Color depth of nodes corresponds to the −log p value (the deeper depth is, the larger the −log p values is). Line width of links corresponds to the number of molecules shared between two pathways (no line means no shared molecules between two pathways). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 2B shows overlapping among the canonical pathways detected as significant, which were divided into three clusters. The largest cluster consists of drug metabolism-related pathways as described above. Interestingly, two other clusters, histidine degradation-related and gluconeogenesis-related, were also detected with no overlap between the drug metabolism-related cluster and them.

We then summarized Affymetrix probe IDs, gene symbols and gene names for each gene in our classifier and divided them into four categories, drug metabolism, gluconeogenesis, histidine degradation and the other (Table 4), based on the canonical pathway analysis. Of 22 genes, 10 genes were drug metabolism-related.

Table 4.

Details and category of the genes in our CBA classifier.

Affymetrix probe ID	Gene symbol	Changedirection	Gene name or detail
Drug metabolism
1368121_at	Akr7a3	Inc	Aldo-keto reductase family 7, member A3 (aflatoxin aldehyde reductase)
1381852_at	RGD1559459	Inc	Similar to Expressed sequence AI788959 (Ugt2b34, Mus musculus)
1387022_at	Aldh1a1	Inc	Aldehyde dehydrogenase 1 family, member A1
1368905_at	Ces2C	Inc	Carboxylesterase 2C
1371076_at	Cyp2b2	Inc	Cytochrome P450, family 2, subfamily b, polypeptide 2
1371089_at	Gsta3	Inc	Glutathione S-transferase alpha 3
1387599_a_at	Nqo1	Inc	NAD(P)H dehydrogenase, quinone 1
1370698_at	Ugt2b1	Inc	UDP glucuronosyltransferase 2 family, polypeptide B1
1387006_at	Sult2a2	Inc	Sulfotransferase family 2A, dehydroepiandrosterone (DHEA)-preferring, member 2
1371942_at	Gstt3	Inc	glutathione S-transferase, theta 3
Gluconeogenesis
1370067_at	Me1	Inc	Malic enzyme 1, NADP(+)-dependent, cytosolic
Histidine degradation
1387307_at	Hal	Dec	Histidine ammonia-lyase
Other
1387783_a_at	Acaa1b	Inc	Acetyl-Coenzyme A acyltransferase 1B
1370828_at	Zdhhc2	Inc	Zinc finger, DHHC-type containing 2
1375845_at	Aig1	Inc	Androgen-induced 1
1371143_at	Serpina7	Inc	Serpin peptidase inhibitor, clade A (alpha-1 antiproteinase, antitrypsin), member 7
1390145_at	Dmxl2	Dec	Dmx-like 2
1384225_at	(NA)	Dec	(NA)
1369440_at	Abcg8	Dec	ATP-binding cassette, subfamily G (WHITE), member 8
1377599_at	Lpin1	Inc	Lipin 1
1373814_at	R3hdm2	Dec	R3H domain containing 2
1389253_at	Vnn1	Inc	Vanin 1

Affymetrix probe IDs, gene symbols and gene names for each gene in our CBA classifier are summarized. The genes are divided into four categories, drug metabolism, gluconeogenesis, histidine degradation and the other.

Change direction: the direction of change (Inc or Dec) in the classifier. NA: not available. No further information is available for the gene with Affymetrix probe ID, 1384225_at.

Our classifier was shown again, with genes converted from Affymetrix probe IDs to gene symbols and colored according to their category (Fig. 3). The mostly drug metabolism-related nature of our classifier was confirmed, as most of the rules in the classifier included drug one or more metabolism-related genes (shown in red).

Fig. 3.

Our CBA Classifier with Categorized Gene Symbols. The CBA classifier, the same as one in Fig. 1, is shown again, with the genes converted from Affymetrix probe IDs to gene symbols and colored according to their category. Red: drug metabolism-related. Blue: gluconeogenesis-related. Green: histidine degradation-related. Black: Other. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

When increased liver weight was targeted, CBA outperformed LDA in all of the three criteria: accuracy, sensitivity, and specificity. In contrast, when decreased liver weight was targeted, both CBA and LDA scored low sensitivities and high specificities. These tendencies are attributable to the low frequency of decreased liver weight in the data set. For such a data set, a classifier returning a negative answer (i.e. no for decreased liver weight) with a high frequency, regardless of predictivity, can score a good specificity but a poor sensitivity. Except for such an imbalanced data set, CBA succeeded in building a better predictive classifier than LDA in this study. This superiority of CBA over LDA is considered to reflect the non-linear nature of the data set. Generally, a drug-induced response (or more generally biological response) is considered to be caused not by the single mechanism, but by several different mechanisms. Thus, there are several different, not necessarily linearly separable, gene expression patterns that finally lead to the same response (e.g. increased liver weight). In this light, CBA is likely to build a better classifier for a data set in toxicology, or more broadly biology, than LDA, as CBA can captures linearly inseparable patterns residing in the data set.

We also compared between CBA and CBA-DR, our modified version of the original CBA. When increased liver weight was targeted, CBA-DR marked lower accuracy than CBA. Interestingly however, CBA-DR marked 100% sensitivity. This can be said as follows: if CBA returns an “Inc” answer for liver weight and we know the default rule is not applied in the classification process, we can say that liver weight would be increased with higher confidence than if we don’t know whether the default rule is applied or not. In addition, we can also infer how reliable the classification is in CBA when non-default rule is met, based on its support and confidence. Therefore, CBA offers not only a classification result, but also additional information regarding reliability of classification. This can be another advantage of CBA over LDA, which returns only a classification result.

In terms of interpretability, while both CBA and LDA give us information regarding important genes which can discriminate increased liver weights well, LDA does not take the concept of co-expression into account. For example, in our setting, a rule (1368905_at, Inc) occurred 6 times in the CBA-generated classifier. This rule, however, always occurred with other rules, reflecting the pattern actually observed in the training data set. Therefore, even if the gene, 1368905_at, is highly increased in an unknown sample, it does not necessarily mean increased liver weight. Such co-expressed pattern was not taken into account by LDA. Besides, while coefficient values are useful to infer importance of each gene in LDA, the final prediction is determined by the total of all the terms in a polynomial, not by a single or small set of genes. The classification process of CBA is much simpler and easy to understand, because each rule is as simple as a single or small set of genes and the prediction is determined once a rule is satisfied, regardless of the other genes. This characteristic of CBA makes a generated classifier easy to understand, even for a non-expert user, because a CBA-generated classifier can be expressed also in a natural language (e.g. “If gene A is increased and gene B is decreased, then the classifier predicts liver weight to be increase”), not in a mathematical equation as is case in LDA.

Canonical pathway analysis with IPA revealed that the genes included in our CBA-generated classifier for increased liver weight were mostly drug metabolism-related ones. This is reasonable as inductions of hepatic drug metabolizing enzymes are well known to induce hepatocellular hypertrophy [35], of which increases in liver weight is the most sensitive indicator [15]. CBA succeeded in building a biologically relevant classifier without any prior knowledge such as literature. Intriguingly, the classifier included genes with other functions such as gluconeogenesis and histidine degradation, which are not directly related to increased liver weight or hepatocellular hypertrophy. While it is unclear whether these genes were actually causal or not, CBA can be used to look for genes with an unknown function but high correlation for a specified outcome as well as to build a biologically reasonable classifiers. In addition, it was also considered to be an advantage that CBA automatically selects a small set of genes to build a classifier, while LDA does not.

5. Conclusions

We applied the CBA algorithm to the TG-GATEs database, where both toxicogenomic and other toxicological data of more than 150 compounds in rat and human are stored, to build a predictive classifier of increased or decreased liver weight for an unknown compound. We compared the generated classifiers between CBA and LDA, and showed that CBA is superior to LDA in terms of both predictive performances and interpretability.

Transparency document

Transparency document

Appendix A. Supplementary data

The following are the supplementary data to this article: