A Comprehensive Comparison of Multiparty Secure Additions with Differential Privacy

Abstract

This paper considers the problem of secure data aggregation (mainly summation) in a distributed setting, while ensuring differential privacy of the result. We study secure multiparty addition protocols using well known security schemes: Shamir’s secret sharing, perturbation-based, and various encryptions. We supplement our study with our new enhanced encryption scheme EFT, which is efficient and fault tolerant. Differential privacy of the final result is achieved by either distributed Laplace or Geometric mechanism (respectively DLPA or DGPA), while approximated differential privacy is achieved by diluted mechanisms. Distributed random noise is generated collectively by all participants, which draw random variables from one of several distributions: Gamma, Gauss, Geometric, or their diluted versions. We introduce a new distributed privacy mechanism with noise drawn from the Laplace distribution, which achieves smaller redundant noise with efficiency. We compare complexity and security characteristics of the protocols with different differential privacy mechanisms and security schemes. More importantly, we implemented all protocols and present an experimental comparison on their performance and scalability in a real distributed environment. Based on the evaluations, we identify our security scheme and Laplace DLPA as the most efficient for secure distributed data aggregation with privacy.

1 Introduction

Participatory sensing and data surveillance are gradually integrated into an inseparable part of our society [8], [27]. In many applications a data aggregator may wish to collect personal data from multiple individuals to study patterns or statistics over a population. Data privacy and security issues arise frequently and increasingly in such surveillance systems [1], [35], [42], [51]. An important challenge is how to protect the privacy of the data subjects, when the data aggregator is untrusted or not present.

Example Applications

We provide a few application scenarios to motivate our problem, including smart metering, syndromic surveillance, and intelligence data collection, among others.

Smart meters measure and report electrical usage with granularity of minutes compared to traditional meters, which are read once a month. The collection of information on electricity demands for all household is useful in preventing blackouts, increasing efficiency of the electrical grid, and reducing its impact on the environment, etc. The same information reveals a lot about individual consumers and their habits. An electricity usage profile of a single household may reveal information about electric appliances used in the household as well as the number and routines of its inhabitants [14], [46]. These privacy concerns could be significantly reduced, when such usage data are aggregated and anonymized before being reported to the utility company. A group of neighboring houses that share the same infrastructure could securely sum up their electrical usage, and apply privacy mechanisms to preserve privacy of the individual consumers (Fig. 1).

Fig. 1.

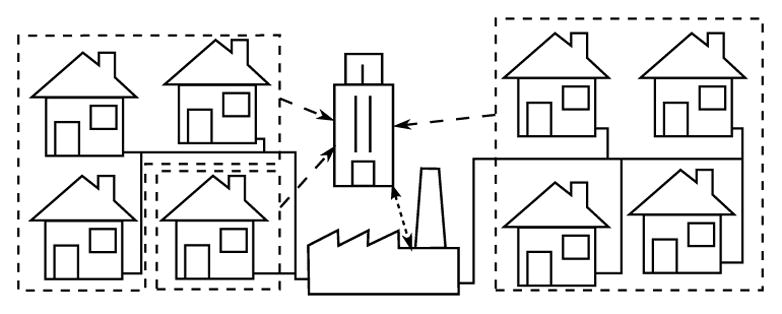
A smart metering scenario: an electric grid (solid lines) for houses that are grouped (dashed polygons) and report their aggregated and anonymized usage data (dashed arrows).

Syndromic surveillance systems monitor population in the real time for early detection of large-scale disease outbreaks and bioterrorism attacks [10], [54]. In a simple scenario, a public health agency collects data from individual visitors who report their Influenza symptoms (self surveillance). The number of detected cases can then be aggregated and anonymized based on location of individuals and their demographics. The collected data can be monitored and analyzed to detect seasonal epidemic outbreaks.

Intelligence data collection, in numerous situations, is performed in crowd settings both non-deliberately by the general public and by principals, who are anonymously embedded in the crowds. A canonical example is an uprising in a major city under hostile governmental control – the general public uses smart devices to report on various field data (third party surveillance [35]). In this case, the number of participants reporting data may change over time, and it is important to protect security of the participants (data contributors) as there is no trusted aggregator as well as privacy of data subjects.

System Settings

We consider a dynamic set of data contributors that contribute their own data (self surveillance) or other data (third party surveillance) in a monitoring or surveillance system. In our running example, contributors D_i (1 ≤ i ≤ n) collect and contribute data x_i independently, the goal is to compute an aggregate function f(x₁, . . ., x_n) of the data. In the self surveillance scenarios, the individuals represented in the collected data (data subjects) are also data contributors. We assume that collected data are used by an untrusted application or an application run by an untrusted party for analysis and modeling (e.g. disease outbreak detection or intelligence analysis). Hence our security and privacy goals are to guarantee: 1) the intermediate results are not revealed to each other during the distributed aggregation besides the final result, 2) the final result (with a random noise R) does not compromise the privacy of individuals represented in the data (Fig. 2).

Fig. 2.

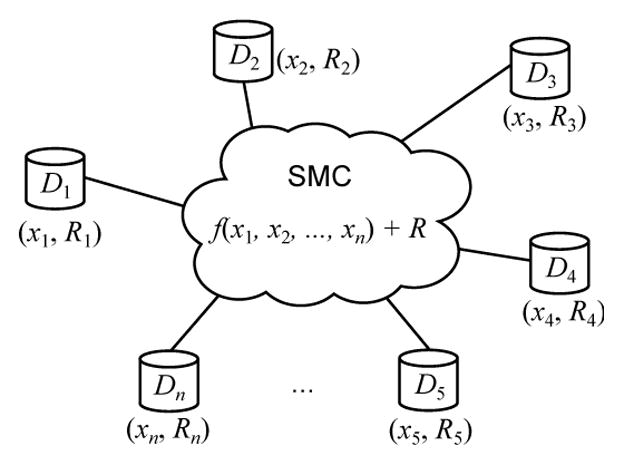
System settings with data contributors D_i, which contribute their values x_i and noise shares R_i to securely compute f and ensure differential privacy of data subjects.

Privacy of data subjects is defined by differential privacy, which is the state-of-the-art privacy notion [21], [22], [36] that assures a strong and provable privacy guarantee for aggregated data. It requires negligible change of computation results, when a single data subject had opted out of the data collection. Therefore, this assures an individual that any computation results will not unveil the presence (or absence) of its record. A common way of achieving differential privacy is perturbation of the aggregated statistics by calibrated noise R (Fig. 2).

In a centralized model, a trusted aggregator (TA) (e.g. CDC offices in the syndromic surveillance scenario) securely collects the data and outputs perturbed aggregates with privacy guarantee. In such model, each data contributor maintains a secure communication channel with the TA. Both security and privacy of computations are guaranteed by the TA, but at the cost of making it a single point of failure for the entire system.

In a decentralized model without a TA (e.g. in the smart metering or intelligence collection scenario), the data contributors perform aggregations and perturbations collaboratively through protocols implemented in secure multiparty computation (SMC) schemes (Fig. 2). Using SMC schemes only for data aggregation (without perturbation) would not guarantee privacy of data subjects. Therefore, privacy mechanisms and security schemes need to be employed together in our scenarios.

In the simplest and the most naïve approach, each data contributor perturbs its own data to guarantee their differential privacy independently. In such an approach, the noise in the aggregated result is superfluous, therefore our goal is to find distributed privacy mechanisms, which ensure privacy and minimize any redundant noise. Each participant contributes a partial noise such that the aggregated noise guarantees differential privacy for the result (Fig. 2). In addition, the protocol shall remain secure, if a few participants faulted, i.e., it should be fault tolerant.

Contributions

In this paper, we propose a new solution for the problem of secure data aggregation (focusing on addition) with differential privacy. In addition, we present a comparative study of existing solutions and compare them with our new approach. Among all secure computation schemes, we evaluate three representative groups: secret sharing [9], [49], homomorphic encryption [2], [33], [44], [50], and perturbation-based [16]. They represent different approaches to ensuring security: splitting data into shares (secret sharing), encrypting data (homomorphic encryption), and perturbing data with significant noise (perturbation-based). Our goal is not to compare all security properties of these approaches, but to present their computational characteristics in distributed computations that involve differential privacy mechanisms. Among homomorphic encryption schemes, we evaluate three of them: Paillier [44], Ács [2], and Shi [50]. We also introduce an enhanced scheme EFT that bases on Ács and Shi schemes and inherits all their advantages like minimal communication, collusion resistant, and fault tolerance with improved efficiency.

To ensure differential privacy in a distributed setting without a trusted aggregator, we evaluate existing distributed noise perturbation (how to generate partial noise at each party) mechanisms, which are named after distributions of partial noise they generate: Gamma [2], Gauss [47], Geometric [29], and Diluted Geometric [50]. We also propose a new distributed mechanism (Laplace DLPA) based on the Laplace distribution. Our mechanism is more efficient than other mechanisms and generates less redundant noise that is a side effect of achieving collusion resistance.

We compare complexities and security characteristics of various protocols. We note that while the security schemes fall into the same SMC framework, we may not be able to directly compare the security properties of some of them. We will review the security characteristics of each scheme and compare them as appropriate. Depending on users’ specific requirement, they may choose the schemes with similar security characteristics. We will then focus on comparing their computational characteristics in distributed computations that involve differential privacy mechanisms. More importantly, we implemented all distributed protocols and present a comprehensive experimental comparison of their performance and scalability.

2 Related Work

Secure Multiparty Computations

Secure two-party computations has been defined by Yao, who presented a solution to the Millionaires’ Problem, where two millionaires want to find out, who is richer without disclosing their actual wealth [55]. Yao’s protocol has been extended to secure multiparty computations (SMC) in [31] and to scenarios with active adversaries [38].

Protocols implemented in a general SMC scheme are computationally expensive. However, many specialized and efficient protocols have been developed for different operations [16], [39] such as secure sum, secure union, and secure scalar product. To compute secure sum, we applied efficient techniques based on threshold homomorphic functions [17] and random shares [52]. Paillier [44] presented an additively homomorphic cryptosystem that computes the encrypted sum using only encrypted values. Its threshold variant has been introduced by Damgård et al. [18] and used to implement an electronic voting system. Hazay et al. presented a threshold Paillier scheme for two-party setting [33].

Pedersen et al. compared encryption-based and secret sharing schemes used in privacy preserving data mining [45]. However, their comparison does not include performance evaluations, and does not cover the latest security schemes and privacy mechanisms.

Chu et al. proposed a threshold security scheme to collect data in a wireless sensor network [15]. In their scheme, encryption keys are symmetric and valid only for a requested period of time. The scheme is not homomorphic, i.e., the data recipient needs to decrypt ciphertexts before aggregating them, therefore it has to be trusted.

Brun and Medvidovic introduced a distributed secret sharing scheme using a concept of “tiles” [7]. In their scheme, data are represented by tiles, which are distributed in an untrusted network. Each tile discloses a single bit of data, but the scheme is generally secure if at least half of them are not corrupted. Note that some statistical information is always revealed with revealing each tile.

Distributed Differential Privacy

The notion of differential privacy was introduced in [24], where it was achieved by perturbing results with Laplacian noise. Several works studied distributed data aggregation with differential privacy. For example, Dwork et al. developed distributed algorithms of noise generation, in which random shares are drawn from binomial and Poisson distributions [23].

Ács et al. applied privacy-preserving and secure data aggregation to the smart metering system [2]. Their scheme was inspired by previous work on secure sensor data aggregation in a wireless network [11], [12]. The scheme uses differential privacy model and homomorphic properties of a modulo addition-based encryption scheme to ensure privacy of results and security of computations. Differential privacy is achieved by adding Laplace distributed noise to results. Noise is generated distributively, such that each meter generates one share as a difference between two Gamma distributed random variables. We named such mechanism Gamma DLPA and evaluated it.

In a similar scenario, individual users collect and aggregate time-series data. PASTE is the system that implements that and ensures differential privacy of results [47]. Differential privacy is achieved by perturbing the most significant coefficients of the discrete Fourier transform of the query answers by a Distributed Laplace Perturbation Algorithm (DLPA). Each participant generates partial noise as a tuple of four Gaussian random variables. Security of computations is ensured by the threshold Paillier cryptosystem. We named such mechanism Gauss DLPA and evaluated it.

Shi et al. also utilized a homomorphic encryption scheme, and minimized its communication complexity by generating an encryption key from the current round number and the existing key [50]. Their privacy mechanism is distributed and ensures approximate differential privacy with noise drawn from the symmetric geometric distribution [29]. We named the mechanism dGPA, generalized it to a diluted perturbation mechanism, and evaluated them.

Alhadidi et al. presented a secure two-party differentially-private data release algorithm for horizontally partitioned data [4]. Differential privacy of released data has been achieved by an exponential mechanism that samples existing records or items with an exponentially distributed probability [41]. The mechanism is used in domains where noise perturbation is not possible.

3 System Models and Requirements

In this section, we describe our adversary model, formally present security and privacy models, and discuss reliability and performance requirements.

3.1 Adversary Model

We assume that the main goal of an end user is to infer sensitive information about data subjects using final results, and any publicly known data. We further assume that data contributors are semi-honest, i.e., they follow a protocol correctly, but may passively observe and use any intermediate results to infer sensitive information of other data contributors or data subjects.

A group of contributors may also collude to increase their chances of a successful attack. Collusion is an inherent element of distributed systems, because each data contributor already knows its own data. In general, any group of collaborating contributors share all their data. In the worst-case scenario, all but one contributor are colluding.

3.2 Privacy Model

Privacy of data subjects is protected if any data recipient does not learn anything about them including their participation in the data collection. Traditional approaches such as removing identifying attributes, generalizing, or perturbing individual attribute values, are susceptible to various attacks [26]. In our study, we use differential privacy (known earlier as indistinguishability [23]), which is the state-of-the-art privacy model that gives a strong and provable privacy guarantee [21], [22], [36]. Differential privacy assures an individual that its participation in the data collection can be guessed only with negligible probability regardless prior knowledge of an attacker. Informally, the attacker that knows all but one record and the result of computations, is not able to find out, if the remaining record has been used in computations or not. Formally, differential privacy is defined as follows.

Definition 3.1 (α-Differential Privacy [20])

A randomized mechanism 𝒜 satisfies α-differential privacy, if for any neighboring databases D₁ and D₂, where D₁ can be obtained from D₂ by either adding or removing one record, and any possible output set S,

$$Pr[\mathcal{A}(D_1)\in S)\le e^{\alpha }·Pr[\mathcal{A}(D_2)\in S]$$

Later the definition of α-differential privacy has been relaxed as follows.

Definition 3.2 (δ-Approximate α-Differential Privacy [23], [36])

A randomized mechanism 𝒜 satisfies δ-approximate α-differential privacy, denoted also as (α, δ)-differential privacy, if for any neighboring databases D₁ and D₂ and any possible output set S,

$$Pr[\mathcal{A}(D_1)\in S]\le e^{\alpha }·Pr[\mathcal{A}(D_2)\in S]+\delta$$

Note that for δ ≥ 1 any mechanism is δ-approximate α-differentially private for any α. Thus, we consider only scenarios with δ ∈ [0, 1).

A few types of privacy mechanisms 𝒜 achieve differential privacy. In this paper, we analyze perturbation mechanisms, which add noise to their results. An example of non-perturbation mechanism that also achieves differential privacy is the exponential mechanism [41], in which privacy is achieved by sampling a dataset.

In distributed settings, any group of data contributors is equally likely to collude, hence no contributor is more trusted than others. Thus, a distributed mechanism 𝒜 should be designed such that participation of each contributor in perturbations is equal. Equal participation in perturbing results means that every contributor generates the same level of noise, i.e., all noise shares are independent and identically distributed (i.i.d.) random variables.

3.3 Security Model

A secure distributed system ensures that data recipients and participating data contributors learn only the final result and whatever can be derived from it.

We use the formal security notion to present the secure multiparty computation (SMC) protocols [30], [39], [55]. In an SMC protocol, parties jointly compute a function of their private data with security, which is defined as follows.

Definition 3.3 (Secure computation [30])

Let f be a function of n variables, and Π be an n-party protocol for computing f. The view of the i^th party during an execution of Π on X = (x₁, . . ., x_n) is denoted ${\text{VIEW}}_i^{\mathrm{\Pi }}(X)$, and for a group of parties with indices I ⊆ [n], we let X_I = {x_i ∈ X : i ∈ I} and ${\text{VIEW}}_I^{\mathrm{\Pi }}(X)=(I,{\text{VIEW}}_{i_1}^{\mathrm{\Pi }}(X),\dots ,{\text{VIEW}}_{i_t}^{\mathrm{\Pi }}(X))$. We say that Π securely computes f if there exists a probabilistic polynomial-time algorithm, denoted S, such that for every I, it holds that

$$\{S(I,X_I,f(X))\}\equiv \{{\text{VIEW}}_I^{\mathrm{\Pi }}(X),{\text{OUTPUT}}^{\mathrm{\Pi }}(X)\}$$

where OUTPUT^Π(X) denotes the output sequence of all parties during the execution represented in ${\text{VIEW}}_I^{\mathrm{\Pi }}(X)$.

Note that ≡ means that results of S are computationally indistinguishable from intermediate and final results of the secure protocol, i.e., VIEW and OUTPUT. Thus, S simulates the protocol and it can be differentiated from S based on their outputs only with negligible probability.

Informally, an SMC protocol is secure, if all parties learn only what can be computed from the final results, i.e., is simulated by S. Secure computations are vital in processing data with privacy and confidentiality. Note that security of f does not guarantee privacy of f(X), i.e., f(X) may still disclose sensitive information. However, applying privacy mechanisms to computations of f(X) preserves or limits disclosure of sensitive information.

3.4 Fault Tolerance

In distributed settings, data contributors can fault or can go off-line at any time. Ensuring fault tolerance, is an additional challenge for every protocol.

A security scheme achieves fault tolerance at level w, if failure of any w contributors during computations breach neither privacy of data nor security. In addition, after running a recovery procedure the final result is correct, i.e., is the same as it would be returned by active contributors running the protocol. If for n contributors a security scheme guarantees fault tolerance at level n, then such scheme is fault tolerant. We analyze fault tolerance of all protocols implementing the same computations in various schemes.

3.5 Performance Requirements

In real life scenarios, computation and communication resources are often limited. For example, contributors that collect data may have only mobile devices with minimal computation power. A very important limitation of such devices is their battery life, therefore protocols run by them shall have low energy consumption. Power consumption is frequently correlated with computation and communication complexities, which we use to evaluate both security schemes and privacy mechanisms.

In addition, communication channels among nodes may be heterogenous, and direct communication between any two nodes may not be always possible or trusted. Thus, ensuring security of these channels is an important requirement for a few presented solutions.

4 Comparison of Secure Computation Schemes

In this section, we describe and analytically compare computational characteristics of several different security schemes, which are used to implement secure aggregation protocols for n data contributors. After that, we introduce a new enhanced scheme EFT, which is fault tolerant and efficient. Experimental comparison is presented in Section 6.

4.1 Secret Sharing

Secret sharing schemes split a secret into multiple shares that are meaningless unless s of them are collected and the secret is reconstructed. Any set of fewer than s shares discloses nothing about the secret even for computationally unbounded adversary. The value of s defines also the minimal number of colluding parties necessary to breach the security of computations. After generation, shares are distributed, such that each contributor receives a few (usually one) shares. They are then used in computations and combined to reveal the final result.

As an example of secret sharing schemes, we describe the Shamir scheme [49]. In this scheme, shares of different secret numbers can be summed up to get shares of their sum, which can be then reconstructed. Other arithmetic and set operations are also possible and implemented [9].

Shamir Scheme

Each participant implements and runs the same Shamir scheme protocol outlined as follows. A participant i computes n shares of its local secret value x_i, by randomly generating a polynomial w_i of order s, such that w_i(0) = x_i. For a set of selected, and publicly known nonzero distinct points z₁, . . ., z_n, shares of x_i are computed as values of w_i in these points, i.e., x_i,j = w_i(z_j) for j = 1, . . ., n. Then, shares are distributed, such that from all participants x_i,j are sent to party j. After exchanging all shares, party j computes a share of the result at z_j, e.g., sums up received shares Σ_i x_i,j. Finally, one party collects at least s shares of the result, interpolates them to compute a polynomial w, and reconstructs the result w(0).

Note that Shamir scheme was introduced only for integer numbers. Adapting the scheme to floating point numbers requires implementing different arithmetic operation protocols [13] or encoding floating point numbers as integers, e.g., by multiplying them by the same power of 10.

Security of Shamir scheme relies on the randomness of generated shares and security of communication channels. Assuming that all communication channels are secure, Shamir scheme is information-theoretically secure, i.e., is secure against computationally unbounded attackers [5]. However, since efficient implementation of secure communication channels relies on encryption (e.g. a Secure Sockets Layer), the scheme is, in fact, computationally secure, i.e., an attacker that uses current computer technology and available resources will not be able to breach security.

Since disclosing any set of less than s shares does not reveal the secret, the scheme is immune to collusion of less than s parties. Fault of any party may require identifying its shares by other parties and dropping them, if a faulted party was able to distribute less than s of its shares. If enough shares were distributed before they faulted, the protocol is continued. If decryption requires participation of more parties than those that are active, the protocol is rerun.

Shamir scheme has low computation complexity, but since each participant sends at least (n − 1) shares to others, the amount of communication is relatively high and equal to O(n²). An example framework that implements secure operations of Shamir scheme is SEPIA [9].

4.2 Perturbation-Based Protocols

Perturbation-based protocols are an efficient alternative for other protocols, but often they require certain topology of connections, e.g., a ring. Their main idea is to perturb input data by adding some random noise, such that they become meaningless for any attacker, and then perform computations on the noisy data. This approach achieves security by obfuscating all intermediate results, but is vulnerable to collusion and is not fault tolerant. Fault of any party requires rerunning the protocol by remaining active parties.

As an example of perturbation-based protocols, we consider the secure sum protocol [16]. In this protocol, all parties are connected in a ring topology. Each party generates random noise, which is added to its private input. The starting party, which is elected randomly, sends its obfuscated value to its successor that adds its own obfuscated value and passes it further. At the end, the starting party holds the sum of obfuscated values from all parties. In the next phase, each party removes its noise from the obfuscated sum, which, at the end, reveals the correct final sum.

Unfortunately, if two neighbors of the same party collude, they can easily discover both the obfuscated value (the first phase) and the random noise (the second phase) generated by the same party. With such information they can compromise the value participated by the party. Many enhancements have been introduced to this protocol to increase its collusion resistance, e.g., shuffling party positions in the ring, and dividing computations into multiple rounds [16]. Although such enhancements may significantly increase communication complexity of protocols, they are still very efficient.

4.3 Homomorphic Encryption

An encryption scheme is homomorphic, if its computations can be carried out on ciphertext. Formally, for a given homomorphic encryption function E with respect to a function f, the encrypted result of f can be obtained by computing a function g over encrypted values of x₁, . . ., x_n, i.e.,

$$E(f(x_1,\dots ,x_n))\equiv g(E(x_1),\dots ,E(x_n))$$ (1)

Homomorphism of an encryption scheme is very useful in distributed settings. An outline of computing a value of f over distributed input x_i is defined as follows. First, each party encrypts its local data x_i and sends E(x_i) to a single party. Then, such party computes the function g on encrypted data. Due to homomorphism of the encryption scheme, the party gets the encrypted value of function f, which can be used for further computations or decryption.

Fully homomorphic schemes allow secure multiparty computation of any function f. The price for such flexibility in choosing f is high complexity of computations [28], [53]. However, a few partially homomorphic schemes are efficient enough to achieve both security and performance goals, e.g., multiplicatively homomorphic ElGamal [25] and RSA [48] schemes. Our choice of the encryption scheme is determined by the aggregation operation, which in our scenarios is addition. Examples of additively homomorphic schemes are Paillier [44], Ács [2], and Shi [50].

Paillier Scheme

The Paillier scheme is a probabilistic public-key encryption scheme [18], [33], [44], which works as follows. Initially, a single trusted third party (TTP) generates a pair of public and private keys. A party i encrypts its local value x_i using the encryption function E and the public key. Then, all encrypted values are collected by any participant or the TTP, which computes g(E(x₁), . . ., E(x_n)). The result can be decrypted or used in further computations.

The original protocol has been enhanced to a threshold scheme, in which shares of a private key are distributed, and any s out of n shares are sufficient to decrypt the ciphertext. In such scheme, the TTP is not necessary to decrypt the final result. Any s participants can do so, by partially decrypting it using their shares of the private key, and combining computed results. Details of key generation, encryption and decryption algorithms can be found in [18], [33]. For settings where the TTP is not present, generation and distribution of public and private keys can be also securely performed, by running a separate SMC protocol [19], [43], e.g., Diffie-Hellman key exchange protocol [2].

Ács Scheme

The Ács scheme is a modulo addition-based encryption scheme [2], i.e., addition is the encryption function. Encryption keys are generated in pairs by two parties, e.g., by running Diffie-Hellman key exchange protocol. Keys in each pair are inverse to each other, i.e., they sum up to 0. Each party has r encryption keys, which inverses are held by r other parties. In the final result all encryption keys are summed up, they cancel out and no decryption is necessary.

Any group of less than r colluding parties is not able to disclose local value of any other party. However, bigger groups can do so with non-zero probability. In the original scheme introduced by Ács et al., fault of any participant requires rerunning all computations from the beginning. The original scheme can be extended by a recovery subprotocol that finalizes computations and returns the correct result. We introduce and analyze such subprotocol as part of our enhanced scheme described in Section 4.4.

Establishing r keys for each party before actual computations is inefficient and requires running a key exchange protocol by $\frac{rn}{2}$ pairs of parties. Unfortunately, reusing the same keys leads to leaks in security especially when parties fault. The following scheme addresses this requirement of using different keys, by generating them from setup keys.

Shi Scheme

In the Shi scheme, a separate decryption function is reduced to computing the discrete logarithm of the output in order to get the final result [50]. If aggregated value is used in further computations, decryption can be postponed until the final result is computed. Similar to the Ács scheme, the method of generating encryption keys ensures that the final result will be already decrypted. Although all parties need to participate to compute the result, they do not need to communicate in order to establish encryption keys for the next run of the protocol. For each run, an encryption key is computed from the initially established key using a one-way function, e.g., a hashing function SHA-256. Such approach minimizes communication among parties, but requires additional computations.

Since participation of all parties is necessary to finalize computations, fault of any party during computations makes the result useless, and the protocol has to be rerun by active parties. Communication complexity is minimal, but computation complexity is high due to key generation.

4.4 An Enhanced Fault-Tolerant Scheme

Inspired by Ács and Shi schemes, we introduce an enhanced fault-tolerant scheme (EFT), which is fault tolerant, immune to collusion of parties, and adds minimal communication overhead. Our scheme is similar to the Ács scheme, but with a few crucial modifications.

In our scheme, an untrusted data aggregator, which is an independent entity or is simulated by any data contributor, initiates all protocol runs (Algorithm 1). After aggregating values from all parties N, it returns the final result (lines 1 to 8). If any data contributor faults, the aggregator will detect it (line 5). In this case, the result will be decrypted only partially and the aggregator will run the recovery subprotocol to compute the final result (lines 10 to 12).

Algorithm 1.

Data aggregation and recovery of the EFT scheme, which is run by an untrusted party.

1:	sum ← 0
2:	Faulted ← ∅
3:	for all j ∈ N do
4:	sum ← sum+ GET_ENCRYPTED_VALUE_FROM(j, timeout)
5:	if timeout happened or no connection with j then
6:	Faulted ← Faulted ∪ {j}
7:	if Faulted = ∅ then
8:	return sum
9:	// Recovery subprotocol.
10:	for all j ∈ N do
11:	sum ← sum + GET_RECOVERY_KEY_FROM(j, Faulted)
12:	return sum

Data contributors participate in the aggregation by running Algorithm 2. In the setup phase, a contributor i establishes random keys k_i,j and initiates local timestamps t_i,j with r randomly chosen parties N_i (lines 1 to 6). After fixing k_i,j no further setup is needed, and no communication is generated. During encryption, each k_i,j is hashed with the current timestamp for a pair (i, j), t_i,j, and the result is added to, or subtracted from, the contributed value x_i (lines 10 to 12). The result is sent back to the aggregator.

Note that only r collaborating neighbors N_i can breach security and reveal x_i. Therefore, when using a privacy mechanism with our scheme, the minimal number of noise shares required to ensure privacy shall be at most r.

Algorithm 2.

An encryption function run by a party i contributing x_i at local time t_i,j with encryption keys exchanged with parties N_i.

1:	if |Ni| < r then
2:	$N_i^{\prime }\leftarrow \text{CONNECT}\_\text{RANDOMLY}\_\text{WITH}\_\text{NEW}\_\text{PARTIES}(r-\mid N_i\mid )$
3:	for all $j\in N_i^{\prime }$ do
4:	ki,j ← Diffie-Hellman_key_exchange(i, j)
5:	ti,j ← 0
6:	$N_i\leftarrow N_i\cup N_i^{\prime }$
7:	ciphertext ← xi
8:	for all j ∈ Ni do
9:	if ID(i) > ID(j) then
10:	ciphertext ← ciphertext+ Hash(ki,j, ti,j)
11:	else
12:	ciphertext ← ciphertext− Hash(ki,j, ti,j)
13:	ti,j ← ti,j + 1
14:	return ciphertext

In the recovery process (Algorithm 3), each party initiates its recovery key (eg. by setting it to zero) and gets the set of all faulted parties (Faulted). For faulted neighbors each party updates its recovery key, by adding inverses of aggregated encryption keys (lines 3 to 6), dropping connection with them (line 7), and removing them from its set of neighbors N_i (line 8). If all neighbors of a party i faulted, then sending the recovery key to the aggregator would reveal the contributed value x_i. Therefore, the party subtracts x_i from the recovery key, which will remove it from the aggregated result as well.

Security

Security proofs of our scheme are the same as presented in [2] and [50]. Here we only describe a simulator S (Definition 3.3) of our protocol. Without loosing generality, we use arithmetic modulo m for sufficiently large m. The simulator gets as input the computed sum, the set of faulted parties Faulted, and the topology of connections among parties, i.e. N_i for all i. Faulted and N_i can be determined by inspecting network traffic, while the protocol is run. Assuming security of the Diffie-Hellman exchange key protocol and given the oracle for the Hash function, we define a simulator S of this protocol. Note that the Hash function outputs uniformly distributed values from [0, m), hence the ciphertext corresponding to a data value is also uniformly distributed in the same domain. The domain of secret values x_i is equal to or a subset of [0, m).

Algorithm 3.

A recovery protocol run by a party i contributing x_i at local time t_i,j with neighbors N_i and Faulted parties failing.

1:	recovery_key ← Init()
2:	for all j ∈ Faulted ∩ Ni do
3:	if ID(i) < ID(j) then
4:	recovery_key ← recovery_key + Hash(ki,j, ti,j)
5:	else
6:	recovery_key ← recovery_key − Hash(ki,j, ti,j)
7:	disconnect_from(j)
8:	Ni ← Ni \ {j}
9:	if Ni = ∅ then
10:	recovery_key ← recovery_key − xi
11:	return recovery_key

S simulates the protocol by assigning to each active party as secret $x_i=\frac{\mathit{sum}}{\mid {\cup }_i{N}_i\backslash \mathit{Faulted}\mid }$, then running Algorithm 2 with simulated GET_ENCRYPTED_VALUE_FROM (Algorithm 2) and GET_RECOVERY_KEY_FROM (Algorithm 3) and with the oracle for the Hash function. Algorithm 2 is simulated by running its last loop (lines 7 to 14). Algorithm 3 is simulated by running it entirely without line 7. A ciphertext returned by running any of the algorithm simulations will be uniformly distributed in [0, m) and indistinguishable from a ciphertext returned by the same algorithm run in the protocol. Hence, intermediate and final results of running S are also indistinguishable from results observed when running the protocol.

Encrypted keys k_i,j are computationally secure due to the hashing function used, e.g., SHA-256, and which cannot be reversed in a polynomial time. Note that the EFT scheme is immune to collusion of less than r parties. Increasing r ∈ [1, n) will increase security of the protocol, but will also reduce its scalability. The value of r should be established based on probability of faults and should be greater than the maximal number of colluding parties.

Complexity

If all parties are active and run our protocol, then they generate 2n messages in only two rounds –one to collect encrypted values by an untrusted aggregator and one to broadcast the final result. When a few parties faulted, a recovery process would generate additional 3n messages to broadcast Faulted, collect recovery keys, and broadcast the recovered result. Computational complexity of the EFT protocol is slightly higher than complexity of the Ács scheme, due to additional computations. However, since encryption keys are not reestablished before each computation, the communication overhead is significantly lower, while preserving fault-tolerance.

4.5 Comparison

Security schemes that are presented above belong to different groups of secure computations, and cannot be directly compared. However, all of them can be employed to ensure security of data aggregation and anonymization. As an example, we have implemented a secure sum protocol in each scheme. We compare their characteristics in the context of these computations, and leave the choice in hands of the reader, who knows her security requirements. Experimental performance comparisons are presented in Section 6. A summary of the comparison is presented in Table 1.

TABLE 1.

Comparison of complexity, fault tolerance level, and max. allowed collusion for SMC schemes with n parties.

Scheme	Communication complexity	Fault tolerance level	Max. collusion (max. n − 2)
Shamir (s,n)	n(n + 1)	n − s	s − 1
Perturbation-based (n)	3n	0	1
Paillier (s,n)	5n	n − s	s − 1
Ács (r,n)	2n + 2rn	n	r − 1
Shi (n)	2n	0	n − 2
EFT (r,n)	2n	n	r − 1

Setup

Communication and computation overhead caused by setting up secure communication channels, encryption key, etc. is negligible for many rounds of computations, hence they are not in Table 1. However, when there are only a few rounds of computations, costs of the setup should be considered as well. Shamir scheme starts by setting up C(n, 2) security communication channels. A perturbation based protocol establishes from n up to C(n, 2) secure communication channels. For our settings, the protocol sets n such channels. Paillier and Shi schemes require a TTP to generate C(n, 2) and n encryption keys, respectively. Ács and EFT schemes do not need a TTP, but they run Diffie-Hellman key exchange protocol $\frac{nr}{2}$ times each for r ∈ [1, n).

Communication

Shamir scheme does not require significant computational resources and its fault tolerance level depends on the number of parties required to reconstruct the secret s. However, the high communication complexity is a major drawback that limits its scalability.

Each perturbation-based protocol is suited for a specific computation and requires participation of all parties. Thus, it is not fault tolerant and faults of any party requires rerunning it. In addition, in the presence of colluding parties, the scheme does not ensure security, which is its major weakness. However, such protocols are suitable for settings where parties have limited resources, but are reliable.

Among homomorphic encryptions schemes, Paillier and Shi incur high computation overheads due to their heavy encryptions. Therefore, these schemes may be suitable for scenarios in which participants have more computational power, and high scalability is required. The minimal amount of communication is generated by Shi and our EFT scheme. Shi scheme is immune to (n − 2) colluding parties, but will not be able to recover after fault of any party. Paillier, Ács, and our schemes are fault tolerant with the level of protection against colluding parties defined as a parameter. However, after initial setup our scheme does not require any more communication, while in Ács scheme all encryption keys need to be regenerated, which causes exchanging 2rn additional messages. Reestablishing encryption keys before each computation (n messages) and decryption of results (2n messages) increase significantly the communication complexity of Paillier scheme. Among encryption schemes, our EFT scheme is the most efficient in terms of communication and computations, is also fault tolerant, and is flexible in adjusting its collusion level. None of other schemes holds all these properties.

Fault Tolerance

All schemes can be partitioned by their fault tolerance level into three groups. Perturbation-based and Shi schemes are not fault tolerant, i.e., if any party faults, the currently run protocol is stopped and run again.

Schemes from the other group deal with faults silently (e.g. Shamir and Paillier), i.e., they do not run any recovery protocol to retrieve final results, but continue computations. However, if the number of active data contributors drops below s, then protocols implemented in either of these schemes are stopped and have to be rerun with decreased value of s. Note that s cannot be less than the maximal number of colluding data contributors and the number of noise shares necessary to achieve differential privacy.

Remaining two schemes, i.e., Ács and our EFT scheme, finish computations and return results regardless of any faulted participants. However, when a data contributor faults, all remaining contributors shall run a recovery protocol, which we presented in Algorithm 3.

Collusion of Parties

Only Shi scheme remains secure after collusion of (n−2) parties, which is the maximal number of colluding parties. Collusion of any two or more parties may breach security of Perturbation-based scheme. Rearranging topology of connections among parties and dividing computations into multiple stages may improve collusion resistance of this scheme to certain extent. For remaining schemes the maximal number of allowed colluding parties is less than the number of encryption key shares required to reconstruct the result (Shamir, Paillier) or the number of keys exchanged by each party with others (Ács, EFT).

5 Comparison of Differential Privacy Mechanisms

In this section, we describe distributed privacy mechanisms that achieve differential privacy (Definition 3.1). We also introduce two efficient distributed mechanisms that ensure differential privacy. One is defined in the domain of real numbers and the other is defined in the domain of integer numbers. Let D ∈ 𝔻 be a database, and Q be an aggregated query, e.g., a count query. In addition, let ℝ be real numbers, ℤ be integer numbers, ℕ be natural numbers, and 𝒩 be a random variable (r.v.) representing noise.

All privacy mechanisms introduce perturbation to results of an aggregation query Q. Such perturbation is carefully calibrated with respect to the global sensitivity of Q, which is defined as follows.

Definition 5.1 (Global Sensitivity [24])

The sensitivity of any aggregate function Q : 𝔻 → ℝ, is equal to Δ_Q = max_D1,D2 ||𝒜_Q(D₁) − 𝒜_Q(D₂)||₁ for all D₁, D₂ differing in at most one record.

5.1 Laplace Perturbation Algorithm

A common mechanism to achieve α-differential privacy is the Laplace perturbation algorithm (LPA) [21]. LPA ensures that results of an aggregated query Q are α-differentially private, by perturbing them with a r.v. ℒ, which is drawn from the Laplace probability distribution function Lap(θ, α) with mean θ and scale α.

Definition 5.2 (Laplace Mechanism, LPA [24], [21])

For Q : 𝔻 → ℝ^k, the mechanism 𝒦_Q that adds independently generated noise ℒ with distribution Lap(0, Δ_Q/α) to each of the k output terms enjoys α-differential privacy,

$$Pr(\mathcal{L}=x)=\frac{\alpha }{2{\mathrm{\Delta }}_Q}{e}^{-\mid x\mid \alpha /{\mathrm{\Delta }}_Q}$$ (2)

Note that ℒ can be also simulated by two exponential distributed random variables as follows.

Lemma 5.1 ( [37])

Let 𝒳_λ and 𝒴_λ be random variables with the exponential distribution, i.e., Pr(𝒳_λ = x) = Pr(𝒴_λ = x) = λe^−λx for x ≥ 0. Noise ℒ in the LPA with the query sensitivity Δ_Q and parameter α (Definition 5.2) can be simulated as $\mathcal{L}=\frac{{\mathrm{\Delta }}_Q}{\alpha }({\mathcal{X}}_1-{\mathcal{Y}}_1)={\mathcal{X}}_{\lambda }-{\mathcal{Y}}_{\lambda }$ for $\lambda =\frac{\alpha }{{\mathrm{\Delta }}_Q}$.

Laplace mechanism can be directly applied by the TA in a centralized model. In a decentralized model, the TA is not present and has to be simulated by data contributors. In such model, differential privacy is achieved by distributed perturbation Laplace algorithms (DLPA). In DLPA each party generates partial noise, such that the aggregated noise follows the Laplace distribution, which is enough to guarantee differential privacy.

Due to infinite divisibility of Laplace distribution [37], a r.v. with such distribution can be computed by summing up n other random variables. We utilize this property and study a few algorithms named after distributions they use to draw partial noise, i.e., Gamma, Gauss, and Laplace. Gamma and Gauss have been already introduced in [47] and [2], respectively, while Laplace is their alternative. We describe and compare all three DLPA mechanisms below.

Gamma DLPA

This mechanism utilizes infinite divisibility of Laplace distribution and generates partial noise by drawing it from the gamma distribution [2]. Formally, a Laplace distributed random variable ℒ ~ Lap(θ, α) can be simulated by the sum of 2n random variables as follows,

$$\mathcal{L}=\frac{\theta }{n}+\sum _{i=1}^n({\mathcal{G}}_i-{\mathcal{H}}_i)$$ (3)

where 𝒢_i and ℋ_i are independent gamma distributed random variables with densities following the formula (x ≥ 0),

$$Pr({\mathcal{G}}_i=x)=Pr({\mathcal{H}}_i=x)=\frac{{(1/\alpha )}^{1/n}}{\mathrm{\Gamma }(1/n)}{x}^{1/n-1}{e}^{-x/\alpha }$$ (4)

Γ is the gamma function, such that $\mathrm{\Gamma }(a)={\int }_0^{\infty }{x}^{a-1}{e}^{-x}\mathrm{d}x$.

Note that generating a r.v. with the gamma distribution requires drawing at least 2 random variables [3]. Assuming uniform distribution of its parameter a, on average 2.54 uniformly distributed random variables need to be drawn.

Gauss DLPA

A random variable ℒ ~ Lap(0, α) can be also simulated by 4 i.i.d. random variables 𝒩₁, 𝒩₂, 𝒩₃, 𝒩₄, each is drawn from the normal distribution Gauss(0, α/2) with variance (α/2) [37] and applied as follows,

$$\mathcal{L}={\mathcal{N}}_1^2+{\mathcal{N}}_2^2-{\mathcal{N}}_3^2-{\mathcal{N}}_4^2$$ (5)

Since infinite divisibility of the normal distribution is stable, drawing a single r.v. 𝒩_i ~ Gauss(0, α/2) (i = 1, 2, 3, 4) is simulated by the sum of n i.i.d. Gaussian random variables ${\mathcal{N}}_{i,j}~\mathit{Gauss}(0,\frac{\alpha }{2n})$ as follows,

$${\mathcal{N}}_i=\sum _{j=1}^n{\mathcal{N}}_{i,j}$$ (6)

The above formulas can be implemented in distributed settings, but secure computation of squares of random variables is a challenge. An SMC protocol implementing such computations has high complexity [47].

Generating a random variable from the Gaussian distribution requires, on average, drawing a single uniformly distributed number [6]. Additional approaches that are more efficient on average but slow in the worst-case scenario have been described in [40].

Laplace DLPA

Infinite divisibility of the Laplace distribution is stable [37]. Thus, drawing a random variable ℒ ~ Lap(0, α) from the Laplace distribution can be simulated by n i.i.d. random variables ℒ_i ~ Lap(0, α) and a ℬ ~ Beta(1, n − 1), as defined in the following formula,

$$\mathcal{L}=\sqrt{\mathcal{B}}·\sum _{i=1}^n{\mathcal{L}}_i$$ (7)

Note that ℬ is a single r.v., which is drawn with probability Pr(ℬ = x) = (n − 1)(1 − x)ⁿ⁻² for x ∈ (0, 1).

Drawing ℒ_i ~ Lap(θ, α) requires generating one uniformly distributed r.v. 𝒰 taken from the range (−0.5, 0.5), which is applied to the following formula,

$${\mathcal{L}}_i=\theta -sgn(\mathcal{U})·\alpha ·ln(1-2\mid \mathcal{U}\mid )$$ (8)

Similarly, drawing a r.v. ℬ requires generating only one uniformly distributed random variable.

5.2 Geometric Perturbation Algorithm

The LPA (Definition 5.2) perturbs query results with noise drawn from the continuous Laplace distribution. When returned results are expected to be integers, such mechanism cannot be directly applied. To address this, Ghosh et al. introduced two privacy mechanisms that ensure α-differential privacy by perturbing their results with integer noise and truncating noisy values if needed [29]. Their mechanisms work only for queries with sensitivity equal to one (e.g. count queries). We leave for future study finding a discrete perturbation mechanism for different sensitivities.

Definition 5.3 (Geometric Mechanism, GPA [29])

For a function Q : 𝔻 → ℕ, a parameter ε ∈ (0, 1), the ε-geometric mechanism is an oblivious mechanism with integer range ℤ, defined as follows. When the true query result is Q(D), the mechanism outputs Q(D) + 𝒩 ∈ ℤ, where 𝒩 is a random variable drew from the following discrete GM(ε) distribution,

$$Pr(\mathcal{N}=x)=\frac{1-\epsilon }{1+\epsilon }{\epsilon }^{\mid x\mid }$$ (9)

If the result of the query Q is limited to natural numbers ℕ_m = {0, 1, . . . , m}, i.e., Q : 𝔻 → ℕ_m, the perturbed output of the GPA is outside ℕ_m with non-zero probability. The truncated geometric mechanism (tGPA) that has range ℕ_m avoids such inconsistencies by “remapping” all negative outputs to 0 and all outputs greater than m to m.

The GPA is a discretized version of the LPA, in which noise is drawn from the Lap(Δ_Q/α) distribution (ε =exp(− α/Δ_Q)) and Δ_Q = 1 for both geometric mechanisms. Ghosh et al. proved that both geometric mechanisms achieve α-differential privacy.

Decentralized GPA

Both geometric mechanisms are centralized, i.e., noise is generated by a TA that perturbs the results. We propose a distributed geometric mechanism DGPA, in which all participants contribute i.i.d. noise shares to simulate ε-geometric mechanism for ε ∈ (0, 1) and achieve α-differential privacy (α = − Δ_Q ln(ε)). Note that the distributed truncated GPA (DtGPA) is defined as DGPA with the same additional “remapping” as for the tGPA.

In order to present the distributed GPA, we prove that noise generated by the GPA can be simulated as a difference between two exponentially distributed random variables. Then, we show that such variables can be generated as sums of i.i.d. Pólya distributed random variables.

Lemma 5.2

Let 𝒳 and 𝒴 be geometrically distributed random variables with the probability of success equal to (1 − ε), i.e., Pr(𝒳 = x) = Pr(𝒴 = x) = ε^x(1 − ε). Noise 𝒩 in the ε-geometric mechanism GPA (Definition 5.3) can be simulated as 𝒩 = 𝒳 − 𝒴.

Proof

We show that 𝒩 and (𝒳 − 𝒴) have the same distribution, i.e., they have the same moment-generating functions M, M_𝒩(t) = M_{𝒳 − 𝒴}(t) for all valid t.

$$M_{\mathcal{N}}(t)=\frac{{(1-\epsilon )}^2{e}^t}{(e^t-\epsilon )(1-\epsilon e^t)},\text{for}t<-ln(\epsilon )$$ (10)

Recall also that for any two i.i.d. random variables 𝒮 and 𝒯, M_𝒮+𝒯(t) = M_𝒮(t) · M_𝒯(t). In addition, for any constant a, M_a𝒮(t) = M_𝒮(at) [34]. Note that the moment-generation function for geometric distribution with the probability of success p is equal to p(1 − (1 − p)e^t) ⁻¹ for t < −ln(p) [34].

$$\begin{array}{l}{M}_{\mathcal{X}-\mathcal{Y}}(t)=M_{\mathcal{X}}(t)·M_{\mathcal{Y}}(-t)\\ =\frac{{(1-\epsilon )}^2{e}^t}{(e^t-\epsilon )(1-\epsilon e^t)},\text{for}t<-ln(\epsilon )\end{array}$$ (11)

Thus, M_𝒩(t) = M_{𝒳 − 𝒴}(t) and 𝒩 = 𝒳 − 𝒴.

Note that truncation (“remapping”) is applied to generated noise, hence truncated (X − Y) will simulate truncated N, and Lemma 5.2 holds for tGPA as well.

In order to define DGPA, we recall the Pólya distribution. Then, we prove that such distributed random variables can be used to generate i.i.d. noise shares, such that the final noise follows the GM(ε) distribution, and therefore the DGPA achieves α-differential privacy (α = − ln(ε)).

Definition 5.4 (Polya Distribution [34])

Let 𝒳 be a random variable following the discrete Pólya (r, p) distribution with parameters r ∈ ℝ and p ∈ (0, 1). The probability distribution function is defined as follows,

$$Pr(\mathcal{X}=x)=\left(\begin{array}{c}r+x-1\\ r-1\end{array}\right)p^x{(1-p)}^r$$

If r ∈ ℕ, then the Pólya distribution is known as a negative binomial distribution NB(r, p). If r = 1, then it is known as a geometric distribution with probability of success equal to (1−p).

Theorem 5.1

Let n be a number of data contributors and 𝒳_i, 𝒴_i be i.i.d. random variables following the Pólya (1/n, ε) distribution for i = 1, 2, . . . , n. A random variable 𝒩 with the distribution GM(ε) (Definition 5.3) can be simulated by the following sum,

$$\mathcal{N}=\sum _{i=1}^n({\mathcal{X}}_i-{\mathcal{Y}}_i)$$

Proof

Both NB and Pólya distributions are infinitely divisible [34]. Therefore, the sum of i.i.d. random variables 𝒳_i ~ Pólya (r_i, ε) follows the same distribution with parameters $r={\sum }_{i=1}^n{r}_i$ and ε.

If r_i = 1/n, then both ${\sum }_{i=1}^n{\mathcal{X}}_i$ and ${\sum }_{i=1}^n{\mathcal{Y}}_i$ follow Pólya (1, ε) distribution, i.e., are geometrically distributed with probability of success equal to (1 − ε). Therefore, by Lemma 5.2 we conclude the proof.

To draw a r.v. 𝒳_i from Pólya (r, ε) distribution we utilize the Poisson-Gamma mixture [34]. First, we randomly draw λ from the Gamma(r, ε/(1−ε)) distribution. Then, we draw 𝒳_i from the Poisson distribution with parameter λ.

5.3 Distributed Noise Approximation Mechanisms

Both LPA and GPA achieve δ-approximate α-differential privacy for all δ ≥ 0 (Definition 3.2). Using these mechanisms for relaxed settings (δ > 0) is not optimal, i.e., disturbance of the result is superfluous. However, they can be modified to introduce less noise and still ensure required level of approximated ε-differential privacy. One set of modifications is to draw noise from an approximated distribution.

In [23], authors presented two methods of achieving (α, δ)-differential privacy for any values of α and δ > 0. One method utilizes a Poisson process to generate random variables that approximate exponentially distributed random variables. The other method ensures (α, δ)-differential privacy by approximating Gaussian noise with binomially distributed random variables. In both methods, random variables are drawn by tossing unbiased or biased coins, which has been implemented in distributed settings, but with significant communication and computation overheads [23]. Therefore, we skip these mechanisms in our study and consider only diluted mechanisms that also achieve (α, δ)-differential privacy and are efficient.

5.4 Diluted Distributed Mechanisms

Diluted mechanisms (Definition 5.5) have been designed as mechanisms easily applicable in distributed settings. In a diluted distributed perturbation mechanism (dDPA), each partial noise 𝒩_i is drawn by each of n parties. All 𝒩_i are securely summed up and used as noise to ensure approximated differential privacy. Note that dDPA required that the rate of non-colluding parties is at least equal to γ, which is a parameter of dDPA.

A diluted geometric mechanism (dGPA) has been introduced in [50], as a mechanism that achieves (α, δ)-differential privacy. We generalize dGPA to a privacy mechanism that uses a perturbation algorithm (PA) and ensures approximate differential privacy.

Definition 5.5 (Diluted Mechanism, dPA)

Let PA be a data perturbation algorithm used by an α-differential privacy mechanism, a parameter α ∈ (0, 1), and 𝒳_i (i = 1, . . . , n) be i.i.d. random variables drawn by PA for given α. A diluted mechanism (dPA) ensures (α, δ)-differential privacy, by adding up to n random variables 𝒩_i defined as follows,

$${\mathcal{N}}_i=\{\begin{array}{ll}{\mathcal{X}}_i,\hfill & \text{with}\text{probability}\beta \hfill \\ 0,\hfill & \text{with}\text{probability}1-\beta \hfill \end{array}$$ (12)

where $\beta (\delta ,\gamma )=min\left\{\frac{1}{\gamma n}{log}_2(\frac{1}{\delta }),1\right\}$, and γn is the minimal number of generated random variables 𝒩_i.

In dGPA results are perturbed by at most n random variables χ_i, which are drawn from the discrete two-sided geometric distribution GM(exp(−α/Δ_Q)) (Definition 5.3). Each r.v. χ_i ~GM(exp(−α/Δ_Q)) can be simulated by a difference of two geometrically distributed random variables (Lemma 5.2). Therefore, drawing 𝒩_i by this mechanism requires generation of at most three uniformly distributed random variables. The first r.v. is used to decide, if χ_i should be drawn. The second r.v., which is drawn from the uniform distribution, establishes the sign of χ_i, and the third one, which is drawn from the geometric distribution, sets the value of χ_i. On average for n tries, the χ_i will be drawn βn times, and the overall number of drawn random variables is equal to ( $n+\frac{2}{\gamma }{log}_2(\frac{1}{\delta })$).

Any differentially private mechanism may be applied to the dPA to achieve (α, δ)-differential privacy. For example, the diluted Laplace mechanism (dLPA) calls the LPA to draw χ_i with the same β(δ, γ) probability (Definition 5.5). Proving that such diluted mechanism achieves (α, δ)-differential privacy requires repeating proofs from [50], with a substitution of the noise generation function.

5.5 Comparison

All DLPA and DGPA mechanisms guarantee the same level of differential privacy, while diluted and noise approximation mechanisms guarantee approximated differential privacy. Drawing a noise share by each mechanism has different computation cost and noise shares have different statistical characteristics.

To compare complexities of noise generation, we consider the number of random variables that each party generates per method. For the Laplace DLPA mechanism, each party generates a single random variable, and one party generates 2 random variables, i.e., 1+1/n random variables per party, which makes it the most efficient mechanism. The implementation of a gamma random number generator has an indeterministic number of steps, and requires generating at least 2 (on average 2.54) uniformly distributed random variables [3]. The Gauss mechanism requires each party to generate 4 different Gaussian distributed random variables.

Each diluted mechanism requires every party to generate from one to two (LPA) or three (GPA) uniform random variables. Let γ be the minimal rate of non-colluding contributing parties and δ be a parameter of approximated differential privacy. Then, on average each party of dDLPA draws ( $1+\frac{1}{\gamma }{log}_2(\frac{1}{\delta })$) random variables and each party of dDGPA draws ( $1+\frac{1}{\gamma }{log}_2(\frac{1}{\delta })$) random variables.

Redundant Noise

Distributed settings introduce additional challenges for privacy mechanisms like collusion of participants. Since each provider knows its own data and also data from colluding parties, we need to guarantee that results computed using data provided by non-colluding parties achieve privacy. Let the rate of colluding parties in one group is less than γ, hence partial noise generated by γn parties is enough to ensure required privacy, and noise from the remaining (1 − γ)n parties is redundant. Although all parties generate i.i.d. partial noise, hence its mean and its variance are the same, experiments confirm that the amount of redundant noise indeed differs for each mechanism (Section 6.2).

If a privacy mechanism is implemented using a security scheme, then its parameters affect the value of γ and vice versa (Table 1). In order to protect privacy of data subjects, no fewer than γn parties should be able to reconstruct (Shamir) or decrypt (Paillier) the final result, therefore γ ≤ s/n. Similarly, since the maximal number of colluding parties is smaller than r for Ács and EFT schemes, noise of remaining parties should be able to guarantee privacy, therefore $\gamma \le 1-\frac{r-1}{n}$. For all schemes the value of γ limits fault tolerance levels. If there are less than γn active parties, then computations are terminated, because their results would not be differentially private. Thus, the fault tolerance levels for all protocols are always less than (1 − γ)n.

Fault Tolerance

When a few parties faulted, the partial noise generated by active parties are not sufficient to achieve the same level of differential privacy, and need to be regenerated. The EFT does so by initializing the recovery key in the recovery protocol (Algorithm 3) as follows. All noise previously added by a party is subtracted from a new partial noise that is drawn randomly. Algorithm 2 (lines 8 to 14) is run over the computed value in order to encrypt it and protect data provided by parties, whose neighbors did not fault. The ciphertext is used to initiate the recovery key (Algorithm 3, line 1).

6 Experiments

In this section, we present experimental evaluations of various privacy mechanisms and security schemes used to implement a distributed secure sum protocol. Since the security and privacy levels of schemes have been formally analyzed above, we mainly focus on their performance. The questions we attempt to answer are: 1) How do the different distributed noise generation algorithms and privacy mechanisms compare with each other in terms of efficiency and redundant noise? 2) How do the different secure computation scheme protocols perform in various settings, and how do they scale, and compare with each other in terms of computation and communication cost?

6.1 Experiment Setup

All experiments have been run using JVM 1.6. We evaluated local computations including partial noise generation, and data preparation on three different platforms: 1) a cluster of 64 HP Z210 nodes with 2 quad-core CPUs, 8 GB of RAM each, running Linux Ubuntu system, 2) a laptop with Intel Core 2 Duo T5500 and 2 GB of memory running Windows XP, and 3) a shared server Sun Microsystems SunFire V880, with 8 CPUs and 16 GB of memory running SunOS 5.10. Note that the sever assigns only limited amount of resources to our applications. All protocols are evaluated in a distributed environment using the cluster of nodes, which are connected by the 100Mbit network. All reported results are averaged from 1 000 runs for security scheme and 1 000 000 tries for privacy mechanism experiments.

Our main software framework is built on top of SEPIA [9], which uses Shamir secret sharing scheme for secure distributed computations. We extended SEPIA and implemented other SMC schemes and differential privacy mechanisms. We chose implementation of the Paillier scheme from the UTD Paillier Threshold Encryption Toolbox¹. Additionally, we used random number generators implemented in the HPC library Colt². All remaining schemes and mechanisms have been implemented by authors. Default values of experiment parameters are listed in Table 2.

TABLE 2.

Default values of experiment parameters.

Name	Description	Default Value
n	Number of running nodes.	32
k	Size of encryption keys in bits.	128
r	The number of encryption keys exchanged with neighboring parties for Ács and EFT schemes.	3
s	The minimal number of parties required to decrypt or reconstruct results in a security scheme.	3
γn	The minimal number of noise shares to achieve privacy for privacy mechanism experiments, and the minimal number of non-colluding parties.	8
δ	A parameter of approximated differential privacy	0.1
	The key size (in bits) of the AES encryption with RSA for SSL communication channels.	128

6.2 Privacy

The main goal of this experiment is to evaluate the overhead of the following mechanisms (Section 5):

• distributed LPA (DLPA): Laplace, Gamma, Gauss,

• distributed GPA (DGPA),

• diluted: Laplace (dLPA), geometric (dGPA).

DLPA and DGPA guarantee differential privacy of the final result, while diluted mechanisms ensure approximated differential privacy. For all DLPA mechanisms the final result achieves the same level of differential privacy, i.e., its final noise is drawn from the same distribution. Therefore, we compare the local computation time of the three DLPA and the DGPA geometric mechanisms, as well as their impact on the overall protocol performance.

Noise share generation

In order to ensure that enough noise is added to the final result, each node adds its share of noise. The average generation time of such shares for different mechanisms is shown in Fig. 3.

Fig. 3.

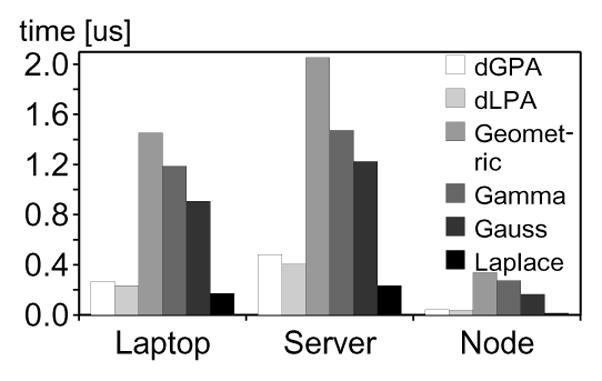
The average noise share generation times in microseconds for different mechanisms and platforms.

Generating a single noise share by the Laplace DLPA is more efficient than by other mechanisms, which confirms our expectations (Section 5.5). Drawing a uniformly distributed r.v. and a few arithmetic operations are enough to generate a noise share in Laplace DLPA mechanism with efficiency. Note that Laplace DLPA requires also a r.v. drawn from the beta distribution, which is generated and broadcasted to all parties as part of the setup message for each run, therefore it is not considered here. Geometric mechanism requires drawing two r.v., one from Poisson and one from gamma distributions, which makes it slower than most DLPA mechanisms. Gauss requires generating 4 normally distributed r.v., while gamma, on average, requires slightly over 5 uniformly distributed r.v. [3].

For default parameter values (Table 2), diluted privacy mechanisms, which achieve δ-approximate α-differential privacy, are very efficient. Performance of noise generation for diluted mechanisms depends on β(δ, γ, n), i.e., probability of generating noise (Definition 5.5), which, for default values of parameters, is approximately equal to 41.52%.

Fig. 4 shows the average runtimes of noise generations for dLPA and dGPA with different δ and γ on the server. As expected, relaxing the approximate differential privacy constraint (Definition 3.2), i.e., increasing the value of δ, decreases both the probability of noise generation β and the runtime. Similarly, increasing the fraction of non-colluding parties γ also decreases β and the runtime. Since generating Laplacian noise is more efficient than generating geometric noise, the dLPA is also more efficient than dGPA, which is confirmed in our experiments.

Fig. 4.

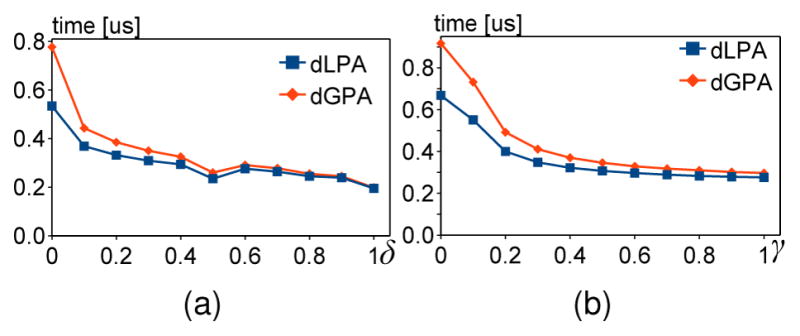
The average noise share generation times in microseconds for different δ and γ, run on the server.

Redundant Noise

To protect privacy of data subjects against colluding data providers, we run privacy mechanisms requesting that shares of γn participants (γn = 10) are enough to achieve privacy. Thus, our final results have some additional noise, which varies for different mechanisms. In this experiment, we compare redundant noise generated by all privacy mechanisms (Fig. 5).

Fig. 5.

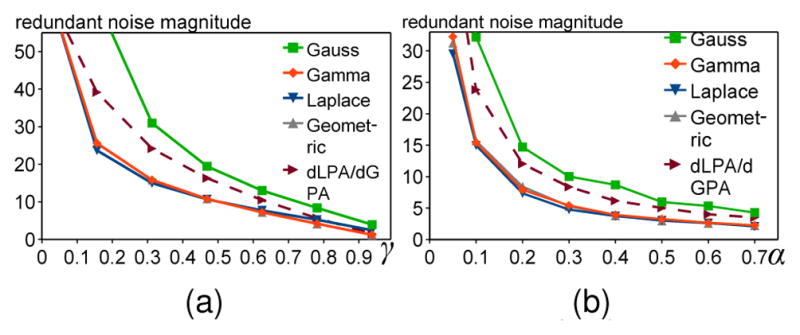
The average magnitude of redundant noise for different rate of required noise shares γ (α = 0.1), and privacy budgets α (γ = 10/32).

Laplace, Gamma, and Geometric mechanisms generate similar amount of redundant noise. Among them the Laplace mechanism generates slightly less noise than other two mechanisms for γ ≤ 0.6 and slightly more for γ > 0.6. All three mechanisms generate significantly less redundant noise than the Gauss mechanism for any γ and α.

For given settings redundant noise magnitudes of dLPA and dGPA are almost the same, therefore we represent them as a single dashed line in Fig. 5. DLPA and DGPA mechanisms cannot be compared with diluted mechanisms, in which redundant noise depends on β(γ, δ) (Definition 3.2). However, we can compare characteristics of their redundant noise. Since β is independent of α, redundant noise for diluted and other mechanisms will decrease at the same rate as α is increasing. Requiring participation of more non-colluding parties to achieve privacy (increasing γ) reduces redundant noise for diluted mechanisms slower than for DLPA (except Gauss) and DGPA.

6.3 Security

In this group of experiments, we evaluate performance of the distributed sum protocol for different security schemes. Security levels guaranteed by each scheme have been already discussed (Section 4).

Performance of Homomorphic Encryption Schemes

In this set of experiments, we evaluate homomorphic encryption schemes. In the setup phase, encryption keys of size k are generated and distributed. To ensure maximal security of the Paillier and the Ács schemes in each round new keys are used. If we lower security requirements, the same encryption key could be reused a few times. Therefore, we set up the Paillier scheme to be run in two settings named new key (maximal security) and reuse key (lower security). We note that the values of k used here are indeed not cryptographically secure nowadays, but our goal was to show the impact of varying k for different security schemes.

Fig. 6 shows the average runtime of a single round for encryption keys of different sizes and different amounts of participants. Since results of Ács, Shi, and EFT schemes are very similar, we represent them as a single line, when evaluating schemes against different encryption key sizes. Generating and distributing a set of encryption keys in the Paillier scheme is a very time consuming process. Increasing the key size k significantly increases computation time for the new key scenario, and have a negligible overhead when one key is used all the time in the reuse key scenario.

Fig. 6.

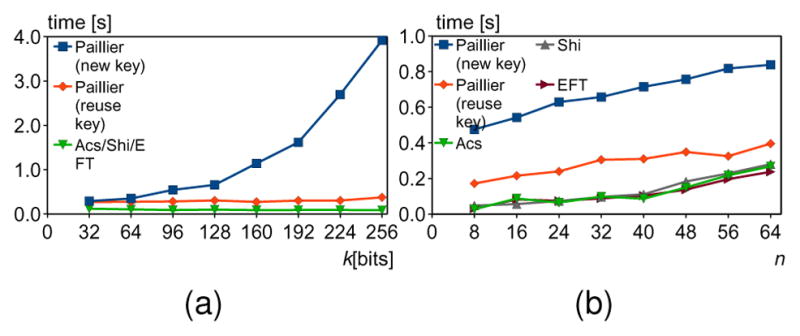
The average runtimes of a protocol for different encryption key sizes k (n = 32) and different number of participants n (k = 128).

Despite the encryption overhead, the homomorphic encryption schemes scale well. Adding new nodes, while keeping the same encryption key size, increases the average runtime of all homomorphic encryption schemes linearly.

Performance of Fault Tolerance Schemes

The goal of this experiment is to compare performance characteristics of fault tolerant schemes, i.e., Shamir, Paillier, Ács, and our EFT, with one data contributor faulting. Note that we extended the original Ács scheme with the same recovery subprotocol as used in the EFT scheme. Remaining schemes will rerun the protocol, if any participant drops. We set r = s = γn = 3.

Fig. 7 shows trends of average runtimes for fault tolerant protocols when a single data contributor faulted. In such scenario, the runtime of a protocol implemented in either Paillier or Shamir schemes is reduced due to less communication and computation that is performed. At the same time, Ács and our scheme needed more time to run a recovery protocol and retrieve the final result. Characteristics of runtimes for all schemes are preserved, i.e., they change in a similar way as for the settings without faults.

Fig. 7.

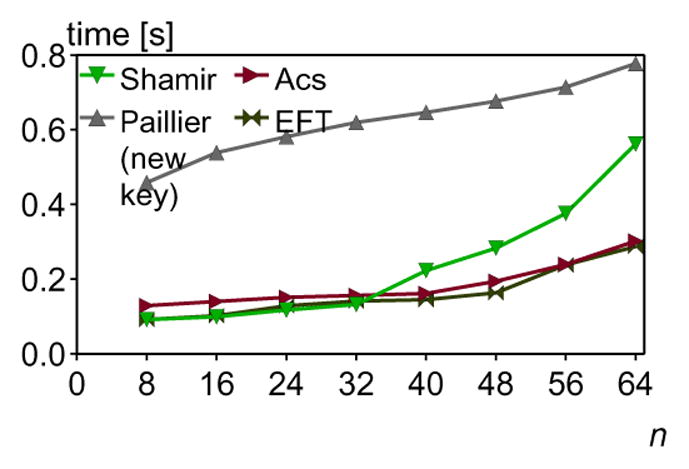
The average runtimes for different numbers of participants and fault tolerant security schemes.

Overall Protocol Performance

In this experiment, we compare the overall performance of all security schemes for different numbers of nodes. Since all privacy mechanisms have little impact on the overall performance, in all runs we used Laplace LDPA. Fig. 8 shows runtimes of the distributed sum protocol implemented in different security schemes.

Fig. 8.

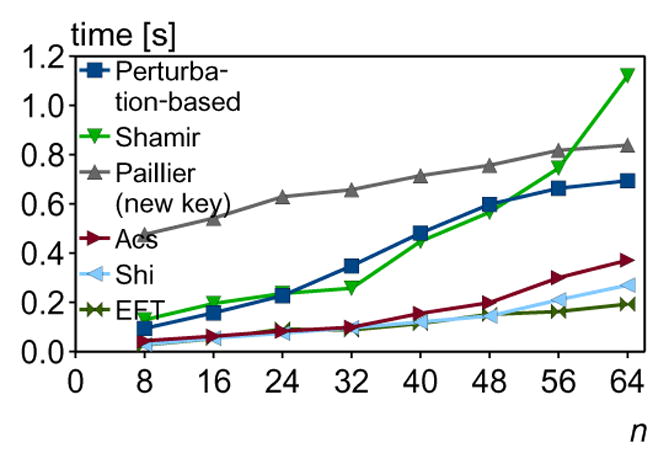
The average runtimes for different numbers of parties and security schemes.

Note that for security, all parties in both Paillier and Ács schemes reestablish their encryption keys in each round. As the number of nodes increases, both Perturbation-based and Shamir schemes do not scale well as the increasing communication cost becomes the dominant overhead. Communication in the Perturbation-based scheme grows linearly with number of participants (Table 1), but is synchronized, which impacts scalability, i.e., each party (except the one initiating computations) sends a message after receiving it from the previous party in the ring. Communication in the Shamir scheme grows quadratically with number of parties (Table 1), which is confirmed in our experiments.

On the other hand, all homomorphic encryption schemes scale well due to their low communication costs. However, the Paillier scheme has a significant computation overhead comparing to others, which limits its scalability. Among encryption schemes our scheme has the most linear characteristic of the runtime, because in each round encryption keys are not regenerated and the encryption function has low time complexity.

7 Conclusions and Future Work

In this paper, we described and compared different ways of distributed data aggregation with security and privacy. Inspired by existing schemes we introduced and evaluated a new, efficient, and fault tolerant scheme (EFT). Our scheme guarantees computational security and minimal communication together with a high reliability of the system.

All evaluated privacy mechanisms ensure differential privacy, but with different overhead. We proposed a new efficient Laplace DLPA mechanism, which introduces a small amount of redundant noise. Often the choice of a privacy mechanism does not impact performance significantly, but is crucial to preserve utility of final results. In addition, when using devices with limited power and computation resources, e.g., mobile devices, choosing the most efficient privacy mechanism extends the battery life of the device.

In future, we plan to evaluate security schemes and privacy mechanisms on devices with limited resources.

Biographies

Slawomir Goryczka holds a Ph.D. in Computer Science and Informatics from Emory University and M.S. degrees in both Computer Science and Applied Mathematics from AGH University of Science and Technology in Kraków, Poland. After M.S. graduation he worked as an Operation Research Analyst/Developer for 2 years. His research interests cover data privacy and security in distributed settings, distributed data management, and privacy preserving data mining.

Li Xiong is an Associate Professor of Mathematics and Computer Science at Emory University where she directs the Assured Information Management and Sharing (AIMS) research group. She holds a Ph.D. from Georgia Institute of Technology, an M.S. from Johns Hopkins University, and a B.S. from University of Science and Technology of China, all in Computer Science. Her areas of research are in data privacy and security, distributed and spatio-temporal data management, and biomedical informatics. She is a recent recipient of the Career Enhancement Fellowship by Woodrow Wilson Foundation. Her research is supported by NSF, AFOSR, NIH, PCORI, and research awards from Cisco and IBM.