Methods for scalar-on-function regression

Abstract

Recent years have seen an explosion of activity in the field of functional data analysis (FDA), in which curves, spectra, images, etc. are considered as basic functional data units. A central problem in FDA is how to fit regression models with scalar responses and functional data points as predictors. We review some of the main approaches to this problem, categorizing the basic model types as linear, nonlinear and nonparametric. We discuss publicly available software packages, and illustrate some of the procedures by application to a functional magnetic resonance imaging dataset.

1 Introduction

Regression with functional data is perhaps the most thoroughly researched topic within the broader literature on functional data analysis (FDA). It is common (e.g., Ramsay and Silverman, 2005; Reiss et al., 2010) to classify functional regression models into three categories according to the role played by the functional data in each model: scalar responses and functional predictors (“scalar-on-function” regression); functional responses and scalar predictors (“function-on-scalar” regression); and functional responses and functional predictors (“function-on-function” regression). This article focuses on the first case, and reviews linear, non-linear, and nonparametric approaches to scalar-on-function regression. Domains in which scalar-on-function regression (hereafter, SoFR) has been applied include chemometrics (Goutis, 1998; Marx and Eilers, 1999; Ferraty et al., 2010), cardiology (Ratcliffe et al., 2002), brain science (Reiss and Ogden, 2010; Goldsmith et al., 2011; Huang et al., 2013), climate science (Ferraty et al., 2005; Baíllo and Grané, 2009), and many others. We refer the reader to Morris (2015) for a recent review of functional regression in general, and to Wang et al. (2015) for a broad overview of FDA.

In cataloguing the many variants of SoFR, we have attempted to cast a wide net. A major contribution of this review is our attempt not merely to describe many approaches in what has become a vast literature, but to distill a coherent organization of these methods. To keep the scope somewhat manageable, we do not attempt to survey the functional classification literature. We acknowledge, however, that classification and regression are quite closely related—especially insofar as functional logistic regression, a special case of the functional generalized linear models considered below in Section 5.3, can be viewed as a classification method. Our emphasis is more methodological than theoretical, but for brevity we omit a number of important methodological issues such as confidence bands, goodness-of-fit diagnostics, outlier detection and robustness.

In the “vanilla” data setting (Sections 2 to 4), we consider an independent, identically distributed (iid) sample of random pairs $({\mathcal{X}}_i,y_i)$, i = 1, … , n, where y_i is a real-valued scalar outcome and the predictor ${\mathcal{X}}_i$ belongs to a space $\mathcal{F}$ of real-valued functions on a finite interval $\mathcal{I}\subset ℝ$. The most common choice for $\mathcal{F}$ seems to be the Hilbert space $L^2\left(\mathcal{I}\right)$ with the usual inner product $\langle {\mathcal{X}}_1,{\mathcal{X}}_2\rangle ={\int }_{\mathcal{I}}{\mathcal{X}}_1\left(t\right){\mathcal{X}}_2\left(t\right)\mathit{dt}$. Cuevas (2014) discusses more general spaces in which the functional data may “live”.

In the general practice of functional data analysis, functions ${\mathcal{X}}_1\left(t\right),\dots ,{\mathcal{X}}_n\left(t\right)$ are observed on a set of discrete grid points that can be sparse or dense, regular or irregular, and possibly subject to measurement errors. Several “preprocessing” steps are typically taken before modeling the data. Aside from smoothing the functional data, in some cases it is appropriate to apply registration or feature alignment, or if the grid points differ across observations, to interpolate to a dense common grid. Measurement error is expected to be low in some (e.g., chemometric) applications, but when it is not it can have important effects on the regression relation. Some methods (e.g., James, 2002) account explicitly for such error. Here, in order to keep the focus on the various regression models, we shall mostly assume functional data observed on a common dense grid with negligible error.

The functional linear model (FLM) is a natural extension of multiple linear regression to allow for functional predictors. Many techniques have been developed to fit this model, and we review these in Section 2. Nonlinear extensions of this basic approach are presented in Section 3. In Section 4 we discuss nonparametric approaches to SoFR, which are based on distances among the predictor functions. For simplicity of exposition, these three sections consider only the most basic and most common scenario: a single functional predictor and one real-valued scalar response. Generalizations and extensions, including the inclusion of scalar covariates, multiple functional predictors, generalized response values, and repeated observations, are reviewed in Section 5. Section 6 presents some ideas on how to choose among the many methods. Available software for SoFR is described in Section 7, and an application to brain imaging data appears in Section 8. Some concluding discussion is provided in Section 9.

2 Linear scalar-on-function regression

The scalar-response functional linear model can be expressed as

$$y_i=\alpha +{\int }_{\mathcal{I}}{\mathcal{X}}_i\left(t\right)\beta \left(t\right)\mathit{dt}+{\epsilon }_i,i=1,\dots ,n,$$ (1)

where β(·) is the coefficient function and errors ε_i are iid with mean zero and constant variance σ².

The coeffcient function β(·) has a natural interpretation: locations t with largest |β(t)| are most influential to the response. In order to enforce some regularity in the estimate, a common general approach to fitting model (1) is to expand β(·) (and possibly the functional predictors as well) in terms of a set of basis functions. Basis functions can be categorized as either (i) a priori fixed bases, most often splines or wavelets; or (ii) data-driven bases, most often derived by functional principal component analysis or functional partial least squares. The next two subsections discuss these two broad alternatives.

2.1 Regularized a priori basis functions

One general class of methods for fitting equation (1) restricts the coefficient function β(·) to the span of an a priori set of basis functions, while imposing a penalty or a prior to prevent overfitting. Assume β(t) = b(t)^Tγ where b(t) = [b₁(t), … , b_K(t)]^T is a set of basis functions and $\gamma ={({\gamma }_1,\dots ,{\gamma }_K)}^T\in {ℝ}^K$. We estimate α and γ by finding

$$(\widehat{\alpha },\widehat{\gamma })=\underset{\alpha ,\gamma }{\arg \min }\left[\sum _{i=1}^n{\left\{y_i-\alpha -{\int }_{\mathcal{I}}{\mathcal{X}}_i\left(t\right)\left(\mathit{b}{\left(t\right)}^T\gamma \right)\mathit{dt}\right\}}^2+\lambda P\left(\gamma \right)\right]$$ (2)

for some λ > 0 and some penalty function P (·). The estimate of the coefficient function is thus $\widehat{\beta }\left(t\right)=\mathit{b}{\left(t\right)}^T\widehat{\gamma }$.

In spline approaches (e.g., Hastie and Mallows, 1993; Marx and Eilers, 1999; Cardot et al., 2003), the penalty is generally a quadratic form γ^T Lγ which measures the roughness of β(t) = b(t)^T γ, and hence (2) is a generalized ridge regression problem. When $\mathit{L}={\left[{\int }_{\mathcal{I}}{b}_i^{\left(q\right)}\left(t\right)b_j^{\left(q\right)}\left(t\right)\mathit{dt}\right]}_{1\le i,j\le K}$, as in Ramsay and Silverman (2005), the quadratic form equals ${\int }_{\mathcal{I}}{\left[{\beta }^{\left(q\right)}\right(t\left)\right]}^2$ dt; cubic B-splines with a second derivative penalty (q = 2) are particularly popular. Alternatively, the P-spline formulation of Marx and Eilers (1999) takes L = D^TD where D is a differencing matrix. Higher values of λ enforce greater smoothness in the coefficient function. Standard methods for automatic selection of λ include restricted maximum likelihood and generalized cross-validation (Craven and Wahba, 1979; Ruppert et al., 2003; Reiss and Ogden, 2009; Wood, 2011). While B-splines are the basis functions most often combined with roughness penalties, other bases are possible. For example, Fourier bases may be employed when the functions are periodic. Marx and Eilers (1999) discuss smoothing of the curves ${\mathcal{X}}_i\left(t\right)$ when evaluating the integral in (2) in practice.

While splines and roughness penalties are a natural choice when the coefficient function is expected to be smooth, in some applications β(·) may be irregular, with features such as spikes or discontinuities. Wavelet bases (e.g., Ogden, 1997), which provide sparse representations for irregular functions, have received some attention in recent years. In the framework of (2), Zhao et al. (2012) propose the wavelet-domain lasso, which combines wavelet basis functions b(·) with the ℓ₁ penalty $P\left(\gamma \right)={\sum }_{k=1}^K\mid {\gamma }_k\mid$ in (2). Other sparsity penalties for wavelet-domain SoFR are considered by Zhao et al. (2015) and Reiss et al. (2015). Not all sparse approaches rely on wavelet bases; see, for example, James et al. (2009) and Lee and Park (2011).

More flexible, albeit potentially more complex, models can be built by replacing the penalty with an explicit prior structure in a fully Bayesian framework. Spline approaches of this type are developed by Crainiceanu and Goldsmith (2010) and Goldsmith et al. (2011); wavelet approaches based on Bayesian variable selection include those of Brown et al. (2001) and Malloy et al. (2010).

2.2 Regression on data-driven basis functions

Alternatively, the coefficient function in (1) can be estimated using a data-driven basis. The most common choice is the eigenbasis associated with the covariance function $\Gamma (t,s)=\mathrm{Cov}\left[{\mathcal{X}}_i\right(t),{\mathcal{X}}_i(s\left)\right]$, i.e., the orthonormal set of functions ϕ₁(t), ϕ₂(t), … such that for each j and all $t\in \mathcal{I}$, ${\int }_{\mathcal{I}}\Gamma (t,s){\varphi }_j\left(s\right)\mathit{ds}={\lambda }_j{\varphi }_j\left(t\right)$ for eigenvalues λ₁ ≥ λ₂ ≥ ⋯ ≥ 0. Expressing each of the functional predictors by its truncated Karhunen-Loève expansion

$${\mathcal{X}}_i\left(t\right)=\sum _{a=1}^A{x}_{ia}{\varphi }_a\left(t\right)$$ (3)

and the coefficient function $\beta \left(t\right)={\sum }_{a^{\prime }=1}^A{\beta }_{a^{\prime }}{\varphi }_{a^{\prime }}\left(t\right)$ using the same basis, the integral in (1) becomes

$$\sum _{a=1}^A\sum _{a^{\prime }=1}^A{x}_{\mathit{ia}}{\beta }_{a^{\prime }}{\int }_{\mathcal{I}}{\varphi }_a\left(t\right){\varphi }_{a^{\prime }}\left(t\right)\mathit{dt}=\sum _{a=1}^A{x}_{\mathit{ia}}{\beta }_a,$$

reducing (1) to the ordinary multiple regression model

$$y_i=\alpha +\sum _{a=1}^A{x}_{\mathit{ia}}{\beta }_a+{\epsilon }_i$$ (4)

(Cardot et al., 1999). In practice, the eigenfunctions are estimated by functional principal component analysis (FPCA; Rice and Silverman, 1991; Silverman, 1996; Yao et al., 2005) and treated as fixed in subsequent analysis.

The number A of retained components acts as a tuning parameter that controls the shape and smoothness of β(·). Ways to choose A as a part of the regression analysis include explained variability, bootstrapping (Hall and Vial, 2006), information criteria (Yao et al., 2005; Li et al., 2013), and cross-validation (Hosseini-Nasab, 2013).

Data-driven bases other than functional principal components can also be utilized, such as functional partial least squares (FPLS; Preda and Saporta, 2005; Escabias et al., 2007; Reiss and Ogden, 2007; Aguilera et al., 2010; Delaigle and Hall, 2012) and functional sliced inverse regression (Ferré and Yao, 2003, 2005).

2.3 Hybrid approaches

A number of papers combine the data-driven basis and a priori basis approaches of the previous two subsections. For example, Amato et al. (2006) employ so-called sufficient dimension reduction methods for component selection, but implement them in the wavelet domain. The functional principal component regression method referred to as FPCR_R in Reiss and Ogden (2007) restricts the coefficient function to the span of leading functional principal components, but fits model (1) by penalized splines (see also Horváth and Kokoszka, 2012; Araki et al., 2013). Goldsmith et al. (2011) use FPCA to pre-process predictor functions and penalized splines to model the coefficient function. The regularization strategy of Randolph et al. (2012) incorporates information from both the predictors and a linear penalty operator.

2.4 Functional polynomial regression

We conclude the discussion of FLMs with functional polynomial models. These are linear in the coefficients but not in the predictors, in contrast to the models of the next two sections, which are not linear in either sense.

The functional quadratic regression model of Yao and Müller (2010) can be expressed as

$$y_i=\alpha +{\int }_{\mathcal{I}}{\mathcal{X}}_i\left(t\right)\beta \left(t\right)\mathit{dt}+{\int }_{\mathcal{I}}{\int }_{\mathcal{I}}{\mathcal{X}}_i\left(s\right){\mathcal{X}}_i\left(t\right)\gamma (s,t)\mathit{ds}\mathit{dt}+{\epsilon }_i.$$ (5)

Here we have both linear and quadratic coefficient functions, β(t) and γ(s, t); when the latter is zero, (5) reduces to the FLM (1). By expressing elements of (5) in terms of functional principal components, responses can be regressed on the principal component scores. Adding higher-order interaction terms results in more general functional polynomial regression models.

3 Nonlinear scalar-on-function regression

In many applications, the assumption of a linear relationship between $\mathcal{X}$ and y is too restrictive to describe the data. In this section we review several models that relax the linearity assumption; Section 4 will describe models (usually termed “nonparametric”) that are even more flexible than those described here.

3.1 Single-index model

We begin by presenting the functional version of the single-index model (Stoker, 1986):

$$y_i=h\left({\int }_{\mathcal{I}}{\mathcal{X}}_i\left(t\right)\beta \left(t\right)\mathit{dt}\right)+{\epsilon }_i,i=1,\dots ,n,$$ (6)

which extends the FLM by allowing the function h(·) to be any smooth function defined on the real line. Fitting this model requires estimation of both the coefficient function β(·) and the unspecified function h(·) and is typically accomplished in an iterative way. For given β(·), h(·) can be estimated using splines, kernels or any technique for estimating a smooth function; for given h(·), β(·) can be estimated in a similar fashion; and the process is iterated until convergence. Several of the methods described in Section 2 for estimating an FLM have been combined with a spline method for estimating h(·) in (6) (e.g., Eilers et al., 2009). Alternatively, a kernel estimator can be used for h(·) (e.g., Ait-Säidi et al., 2008; Ferraty et al., 2011).

3.2 Multiple-index model

A natural extension of model (6) is to allow multiple linear functionals of the predictor via the multiple-index model

$$y_i=\sum _{j=1}^J{h}_j\left({\int }_{\mathcal{I}}{\mathcal{X}}_i\left(t\right){\beta }_j\left(t\right)\mathit{dt}\right)+{\epsilon }_i.$$ (7)

Models of this kind, which extend projection pursuit regression to the functional predictor case, are developed by James and Silverman (2005), Chen et al. (2011), and Ferraty et al. (2013).

Setting β_j(t) = ϕ_j(t), the jth FPC basis function, reduces (7) to $y_i={\sum }_{j=1}^J{h}_j\left(x_{\mathit{ij}}\right)+{\epsilon }_i$, where we use x_ij to denote FPC scores as in (3). Müller and Yao (2008) refer to this as a “functional additive model,” generalizing the FLM of Section 2.2 which reduced to the multiple regression model (4) with respect to the FPC scores. An extension of this method, incorporating a sparsity-inducing penalty on the additive components, is proposed by Zhu et al. (2014).

3.3 Continuously additive model

Müller et al. (2013) and McLean et al. (2014) propose the model

$$y_i=\alpha +{\int }_{\mathcal{I}}f\left[{\mathcal{X}}_i\right(s),s]\mathit{ds}+{\epsilon }_i,$$ (8)

where f(·, ·) is a smooth bivariate function that can be estimated by penalized tensor product B-splines. As an aid to interpretation, note that if s_ℓ = s₀ + ℓΔs, ℓ = 1, … , L, and $\mathcal{I}=[s_0,s_L]$, then for large L, (8) implies

$$E(y_i\mid {\mathcal{X}}_i)\approx \sum _{\ell =1}^{L}f\left[{\mathcal{X}}_i\right(s_{\ell }),s_{\ell }]\Delta s=\sum _{\ell =1}^L{g}_{\ell }\left[{\mathcal{X}}_i\right(s_{\ell }\left)\right],$$

where g_ℓ(x) = f(x, s_ℓ)Δs. The expression at right shows that (8) is the limit (as L → ∞) of an additive model—or in the generalized linear extension considered by McLean et al. (2014), of a generalized additive model (Hastie and Tibshirani, 1990; Wood, 2006). Hence McLean et al. (2014) employ the term “functional generalized additive model.”

4 Nonparametric scalar-on-function regression

The monograph of Ferraty and Vieu (2006) has popularized a nonparametric paradigm for SoFR, in which the model for the conditional mean of y is not only nonlinear but essentially unspecified, i.e.,

$$E(y\mid \mathcal{X})=m\left(\mathcal{X}\right)$$ (9)

for some operator $m:\mathcal{F}\to ℝ$. Note that mathematically the FLM can also be formulated as an operator, but as one that is linear—whereas Ferraty and Vieu (2006) focus primarily on nonlinear operators m. (For further discussion of the terms nonlinear and nonparametric SoFR, see Section 9.)

Approaches to estimating m extend traditional nonparametric regression methods (Ḧardle et al., 2013) from the case in which the ${\mathcal{X}}_i$ are scalars or vectors to the case of function-valued ${\mathcal{X}}_i$. For example, the most popular nonparametric approach, which we consider next, generalizes the Nadaraya-Watson (NW) smoother (Nadaraya, 1964; Watson, 1964) to functional predictors.

4.1 Functional Nadaraya-Watson estimator

The functional NW estimator of the conditional mean $m\left(X\right)=\mathrm{E}(y\mid \mathcal{X}=X)$ is

$$\widehat{m}\left(X\right)=\frac{\sum _{i=1}^{n}K\left[d\right(X,{\mathcal{X}}_i)∕h]y_i}{\sum _{i=1}^{n}K\left[d\right(X,{\mathcal{X}}_i)∕h]},$$ (10)

where K(·) is a kernel function, which we define as a function supported and decreasing on [0, ∞); h > 0 is a bandwidth; and d(·, ·) is a semi-metric. Here we define a semi-metric on $\mathcal{F}$ as a function $d:\mathcal{F}\times \mathcal{F}\to [0,\infty )$ that is symmetric and satisfies the triangle inequality, but d(f₁, f₂) = 0 does not imply f₁ = f₂. (Such a function is often called a “pseudo-metric”; our terminology has the advantage of implying that a semi-norm ∥·∥ on $\mathcal{F}$ induces a semi-metric d(f₁, f₂) = ∥f₁ − f₂∥.) Smaller values of $d(X,{\mathcal{X}}_i)$ imply larger $K\left[d\right(X,{\mathcal{X}}_i)∕h]$ and thus larger weight assigned to y_i.

Ideally, the bandwidth h should strike a good balance between the squared bias of $\widehat{m}\left(X\right)$ (which increases with h) and its variance (which decreases as h increases) (Ferraty et al., 2007). Rachdi and Vieu (2007) consider a functional cross-validation method for bandwidth selection, and prove its asymptotic optimality. Shang (2013, 2014a,b, 2015) and Zhang et al. (2014) propose a Bayesian method for simultaneously selecting the bandwidth and the unknown error density, and show that it attains greater estimation accuracy than functional cross-validation.

Observe that if the fixed bandwidth h in (10) is replaced by h_k(X), the kth-smallest of the distances $d(X,{\mathcal{X}}_i)(i=1,\dots ,n)$, then we instead have a functional version of (weighted) k-nearest neighbors regression (Burba et al., 2009).

4.2 Choice of semi-metric

The performance of the functional NW estimator can depend crucially on the chosen semimetric (Geenens, 2011). Optimal selection of the semi-metric is discussed by Ferraty and Vieu (2006, Chapters 3 and 13) and is addressed using marginal likelihood by Shang (2015).

For smooth functional data, it may be appropriate to use the derivative-based semi-metric

$$d_q^{\mathrm{deriv}}({\mathcal{X}}_1,{\mathcal{X}}_2)=\sqrt{{\int }_{\mathcal{I}}{\left[{\mathcal{X}}_1^{\left(q\right)}\left(t\right)-{\mathcal{X}}_2^{\left(q\right)}\left(t\right)\right]}^2\mathit{dt},}$$

where ${\mathcal{X}}^{\left(q\right)}$ being the q^th-order derivative of $\mathcal{X}$. In practice q = 2 is a popular choice (e.g., Goutis, 1998; Ferraty and Vieu, 2002, 2009). The use of B-spline approximation for each curve allows straightforward computation of the derivatives.

For non-smooth functional data, it may be preferable to adopt a semi-metric based on FPCA truncated at A components,

$$d_A^{\mathrm{FPCA}}({\mathcal{X}}_1,{\mathcal{X}}_2)=\sqrt{\sum _{a=1}^A{\left[{\int }_{\mathcal{I}}\left\{{\mathcal{X}}_1\right(t)-{\mathcal{X}}_2(t\left)\right\}{\varphi }_a\left(t\right)\mathit{dt}\right]}^2}=\sqrt{\sum _{a=1}^A{(x_{1a}-x_{2a})}^2,}$$

where the last expression uses truncated expansions defined as in (3). A semi-metric based on functional partial least squares components (Preda and Saporta, 2005; Reiss and Ogden, 2007) can be defined analogously. Chung et al. (2014) introduced a semi-metric based on thresholded wavelet coefficients of the functional data objects.

Given a set of possible semi-metrics with no a priori preference for any particular option, one can select the one that minimizes a prediction error criterion such as a cross-validation score; more generally one can adopt an ensemble predictor (see Section 6.2.2 and Fuchs et al., 2015).

4.3 Functional local linear estimator

The functional NW estimator (10) can also be written as

$$\widehat{m}\left(X\right)=\widehat{\alpha }\equiv \underset{\alpha \in ℝ}{\min }\sum _{i=1}^{n}K\left[d\right(X,{\mathcal{X}}_i)∕h]{(y_i-\alpha )}^2.$$

As an alternative to this “local constant” estimator, Baíllo and Grané (2009) consider a functional analogue of local polynomial smoothing (Fan and Gijbels, 1996), specifically a local (functional) linear approximation

$$m\left({\mathcal{X}}_i\right)\approx \alpha +{\int }_{\mathcal{I}}\beta \left(t\right)\left[{\mathcal{X}}_i\right(t)-X(t\left)\right]\mathit{dt}$$

for ${\mathcal{X}}_i$ near X, where $\alpha \in ℝ$ and $\beta \in L^2\left(\mathcal{I}\right)$. This motivates the minimization problem

$$(\widehat{\alpha },\widehat{\beta })=\underset{\alpha ,\beta }{\min }\sum _{i=1}^{n}K\left[d\right({\mathcal{X}}_i,X)∕h]{\left[y_i-\alpha -{\int }_{\mathcal{I}}\beta \left(t\right)\left[{\mathcal{X}}_i\right(t)-X(t\left)\right]\mathit{dt}\right]}^2,$$

whose solution yields the functional local linear estimate $\widehat{m}\left(X\right)=\widehat{\alpha }$. Barrientos-Marin et al. (2010) propose a compromise between the NW (local constant) and local linear estimators, while Boj et al. (2010) offer a formulation based on more general distances.

4.4 A reproducing kernel Hilbert space approach

A rather different nonparametric method (Preda, 2007) is based on the notion of a positive semidefinite kernel $k({\mathcal{X}}_1,{\mathcal{X}}_2)$ (Wahba, 1990; Schölkopf and Smola, 2002), which can roughly be thought of as defining a similarity between functions ${\mathcal{X}}_1,{\mathcal{X}}_2\in \mathcal{F}$; the Gaussian kernel $\exp [-{\int }_{\mathcal{I}}{\left\{{\mathcal{X}}_1\right(t)-{\mathcal{X}}_2(t\left)\right\}}^2\mathit{dt}∕(2{\sigma }^2\left)\right]$ for some σ > 0 is an example. Briefly, any such k(·, ·) (not to be confused with the univariate kernel function K(·) of (10)) defines a reproducing kernel Hilbert space (RKHS) ${\mathcal{H}}_k$ of maps $m:\mathcal{F}\to ℝ$, equipped with an inner product $\langle \cdot ,\cdot {\rangle }_{{\mathcal{H}}_k}$. Preda (2007) considers more general loss functions, but for squared error loss his proposed estimate of m in (9) is

$${\widehat{m}}_{\lambda }=\underset{m\in {\mathcal{H}}_k}{\arg \min }\left[\sum _{i=1}^n{[y_i-m({\mathcal{X}}_i\left)\right]}^2+\lambda {\parallel m\parallel }_{{\mathcal{H}}_k}^2\right],$$ (11)

where λ is a non-negative regularization parameter, as in criterion (2) for the FLM. A key RKHS result, the representer theorem (Kimeldorf and Wahba, 1971; Schölkopf et al., 2001), leads to a much-simplified minimization in terms of the Gram matrix $\mathit{K}={\left[k\right({\mathcal{X}}_i,{\mathcal{X}}_i\left)\right]}_{1\le i,j\le n}$: (11) can be written as ${\widehat{m}}_{\lambda }(\cdot )={\sum }_{i=1}^n{\gamma }_{i}k({\mathcal{X}}_i,\cdot )$, where γ = (γ₁, … , γ_n)^T minimizes

$${\parallel \mathit{y}-\mathit{K}\gamma \parallel }^2+\lambda {\gamma }^T\mathit{K}\gamma$$

with y = (y₁, … , y_n)^T.

Note that this nonparametric formulation is distinct from the RKHS approach of Cai and Yuan (2012) to the functional linear model (1)—in which the coefficient function β(·), rather than the (generally nonlinear) map $m:\mathcal{F}\to ℝ$, is viewed as an element of an RKHS—as well as from the RKHS method of Zhu et al. (2014).

Expression (11) is a functional analogue of the criterion minimized in smoothing splines (Wahba, 1990), much as (10) generalizes the NW smoother to functional predictors. We believe that, just as the RKHS-based smoothing spline paradigm has spawned a very flexible array of tools for non- and semiparametric regression (Ruppert et al., 2003; Wood, 2006; Gu, 2013), there is great potential for building upon the regularized RKHS approach to nonparametric SoFR and thereby, perhaps, connecting FDA with machine learning.

As a further link between the (reproducing) kernel approach of Preda (2007) and other nonparametric approaches (such as the NW estimator) that are based on (semi-metric) distances among functions, we note that there is a well-known duality between kernels and distances (e.g., Faraway, 2012, p. 410). Since both kernels and distances can be defined for more general data types than functional data, the nonparametric FDA paradigm is readily extensible to “object-oriented” data analysis (Marron and Alonso, 2014).

5 Generalizations and extensions

Although many of the references cited in the previous three sections have considered more general scenarios, our presentation thus far has considered only the simplest situation: a single functional predictor and a real-valued response. However, situations that arise in practice often require various extensions, including scalar covariates, multiple functional predictors, and models appropriate for responses that arise from a general exponential family distribution. In this section we describe some of these generalizations and extensions.

5.1 Including scalar covariates

Including scalar covariates in the FLM (1) is fairly straightforward. For methods based on penalization, covariates can be included by simply applying the penalty only to the spline basis coefficients. When using a data-driven basis, as noted above, the FLM reduces to the ordinary multiple regression model (4), so adding scalar covariates is even more routine. With nonlinear and nonparametric strategies, however, incorporating scalar covariates can be somewhat more challenging. For example, Aneiros-Pérez and Vieu (2006, 2008) and Aneiros-Pérez et al. (2011) considered semi-functional partial linear models of the form

$$y_i={\mathit{z}}_i^T\alpha +m\left({\mathcal{X}}_i\right)+{\epsilon }_i,$$ (12)

which include linear effects of scalar covariates z_i, estimated using weighted least squares, and effects of functional predictors ${\mathcal{X}}_i(\cdot )$, estimated nonparametrically via NW weights.

5.2 Multiple functional predictors

A number of recent papers have considered the situation in which the ith observation includes multiple functional predictors ${\mathcal{X}}_{i1},\dots ,{\mathcal{X}}_{\mathit{iR}}$, possibly with different domains ${\mathcal{I}}_1,\dots ,{\mathcal{I}}_R$. The FLM (1) extends naturally to the multiple functional regression model

$$y_i=\alpha +\sum _{r=1}^R{\int }_{{\mathcal{I}}_r}{\mathcal{X}}_{\mathit{ir}}\left(t\right){\beta }_r\left(t\right)\mathit{dt}+{\epsilon }_i.$$

Penalized or fully Bayesian approaches to selecting among candidate functional predictors have been proposed by Zhu et al. (2010), Gertheiss et al. (2013) and Lian (2013).

One can also consider two types of functional interaction terms. An interaction between a scalar and a functional predictor (e.g., McKeague and Qian, 2014) is formally similar to another functional predictor, whereas an interaction between two functional predictors (e.g., Yang et al., 2013) resembles a functional quadratic term as in (5).

The “functional additive regression” model of Fan et al. (2015) extends the functional single-index model (6) to the case of multiple predictors.

In the nonparametric FDA literature, Febrero-Bande and González-Manteiga (2013) consider the model

$$y_i=\eta \left[\sum _{r=1}^R{m}_r\left({\mathcal{X}}_{\mathit{ir}}\right)\right]+{\epsilon }_i,$$ (13)

where η can be a known function, or estimated nonparametrically; the m_r(·)’s are nonlinear partial functions of ${\mathcal{X}}_{\mathit{ir}}\left(t\right)$. Model (13), like model (8), is referred to by the authors as a “functional generalized additive model.” Lian (2011) studied the “functional partial linear regression” model

$$y_i={\int }_{\mathcal{I}}{\mathcal{X}}_{i1}\left(t\right)\beta \left(t\right)\mathit{dt}+m\left({\mathcal{X}}_{i2}\right)+{\epsilon }_i,$$ (14)

which combines linear and nonparametric functional terms. Note that both predictors in (14) are functional, whereas the linear terms in the “semi-functional” model (12) are scalars.

5.3 Responses with exponential family distributions

In all models considered to this point, the response variable has been a continuous, real-valued scalar. In many practical applications the response is discrete, such as a binary outcome indicating the presence or absence of a disease. Many of the above methods have been generalized to allow responses with exponential-family distributions, including both linear (Marx and Eilers, 1999; James, 2002; Müller and Stadtmüller, 2005; Reiss and Ogden, 2010; Goldsmith et al., 2011; Aguilera-Morillo et al., 2013) and nonlinear (James and Silverman, 2005; McLean et al., 2014) models. For a single functional predictor and no scalar covariates, the functional generalized linear model can be written as $g\left({\mu }_i\right)=\alpha +{\int }_{\mathcal{I}}{\mathcal{X}}_i\left(t\right)\beta \left(t\right)\mathit{dt}$, where ${\mu }_i=E[y_i\mid {\mathcal{X}}_i(\cdot \left)\right]$ and g is a known link function. Estimation for this model is analogous to the methods described in Section 2: using a data-driven basis recasts the functional model as a standard generalized linear model, and regularized basis expansion methods can be implemented using penalization methods for GLMs. Scalar covariates and multiple functional predictors can be incorporated as in Sections 5.1 and 5.2.

5.4 Multilevel and longitudinal SoFR

In recent years it has become more common to collect repeated functional observations from each subject in a sample. In these situations the data are $\left[{\mathcal{X}}_{\mathit{ij}}\right(\cdot ),y_{\mathit{ij}}]$ for observations j = 1, … , J_i within each of subjects i = 1, … , n. A relevant extension of the FLM is

$$y_{\mathit{ij}}=\alpha +b_i+{\int }_{\mathcal{I}}{\mathcal{X}}_{\mathit{ij}}\left(t\right)\beta \left(t\right)\mathit{dt}+{\epsilon }_{\mathit{ij}}$$

with random effects $b_i\sim N(0,{\sigma }_b^2)$ used to model subject-specific effects. Goldsmith et al. (2012) directly extended the spline-based estimation strategy described in Section 2.1 for this model, and Gertheiss et al. (2013) use longitudinal FPCA (Greven et al., 2010) to construct a data-driven basis for coefficient functions. Crainiceanu et al. (2009) considered the related setting in which the functional predictor is repeatedly observed but the response is not, and estimate the coefficient function using a data-driven basis derived using multilevel FPCA (Di et al., 2009).

5.5 Multidimensional functional predictors

While most methodological development of SoFR has focused on one-dimensional functional predictors as in (1), a growing number of authors have considered two- or three-dimensional signals or images as predictors in regression models. While this extension is relatively straight-forward conceptually (replacing the single integral in (1) with a double or triple integral), it can involve significant technical challenges, including higher “natural dimensionality”, the need for additional tuning parameter values and correspondingly greater computational requirements.

Within the linear SoFR model framework, Marx and Eilers (2005) extend their penalized spline regression to handle higher dimensional signals by expressing the signals in terms of a tensor B-spline basis and applying both a “row” and a “column” penalty. Reiss and Ogden (2010) consider two-dimensional brain images as predictors, expressing them in terms of their eigenimages and enforcing smoothness via radially symmetric penalization. Holan et al. (2010) and Holan et al. (2012) reduce the dimensionality of the problem by projecting the images on their (2D) principal components. Guillas and Lai (2010) apply penalized bivariate spline methods and consider two-dimensional functions on irregular regions. Zhou et al. (2013) and Zhou and Li (2014) propose methods that exploit the matrix or tensor structure of image predictors; Huang et al. (2013) and Goldsmith et al. (2014) develop Bayesian regression approaches for three-dimensional images; and Wang et al. (2014) and Reiss et al. (2015) describe wavelet-based methods.

5.6 Other extensions

Our stated goal in this paper has been to describe and classify major areas of research in SoFR, and we acknowledge that any attempt to list all possible variants of SoFR would be futile. In this subsection we very briefly mention a few models that do not fit neatly into the major paradigms discussed in Sections 2 through 4 or in their direct extensions in Sections 5.1 through 5.5, knowing this list is incomplete.

5.6.1 Other non-iid settings

This review has focused on iid data pairs (${\mathcal{X}}_i,y_i$), with the exception of Section 5.4. Other departures from the iid assumption have received some attention in the SoFR literature. For example, Delaigle et al. (2009) considered heteroscedastic error variance, while Ferraty et al. (2005) studied α-mixing data pairs.

5.6.2 Mixture regression

A data set may be divided into latent classes, such that each class has a different regression relationship of the form (1). This is the model considered by Yao et al. (2011), who represent the predictors in terms of their functional principal components and apply a multivariate mixture regression model fitting technique. Ciarleglio and Ogden (2016) consider sparse mixture regression in the wavelet domain.

5.6.3 Point impact models

In some situations it may be expected that only one point, or several points, along the function will be relevant to predicting the outcome. The model (1) could be adapted to reflect this by replacing the coefficient function β by a Dirac delta function at some point θ. This is the “point impact” model considered by Lindquist and McKeague (2009) and McKeague and Sen (2010), who consider various methods for selecting one or more of these points. Ferraty et al. (2010) consider the same situation but within a nonparametric setting.

5.6.4 Derivatives in SoFR

Derivatives have been incorporated in SoFR investigations in two completely different senses. The first is ordinary (first or higher-order) derivatives of functional observations with respect to the argument t. Some types of functional data may reflect vertical or linear shifts that are irrelevant to predicting y (Goutis, 1998). A key example is near-infrared (NIR) spectroscopy curves, which are used by analytical chemists to predict the contents of a sample: for example, a wheat sample’s spectrum may play the role of a functional predictor, with protein content as the response. It is sometimes helpful to remove such shifts by taking first or second differences (approximate derivatives) of the curves as a preprocessing step. For the same reason, derivative semi-metrics (see above, Section 4.2) can be more useful than the L² metric for nonparametric SoFR with spectroscopy curves (Ferraty and Vieu, 2002).

A second type of derivative, studied by Hall et al. (2009), is the functional (Gâteaux) derivative of the operator m in the nonparametric model (9). Roughly speaking, for a given $X\in \mathcal{F}$, the functional derivative is a linear operator m_X such that for a small increment $\Delta X\in \mathcal{F}$ we have m(X + ΔX) ≈ m(X) + m_X(ΔX). In the linear case, the functional derivative is given by the coefficient or slope function, i.e., $m_X\left(g\right)={\int }_{\mathcal{I}}\beta \left(t\right)g\left(t\right)\mathit{dt}$ for all X and all g. In the nonparametric case, functional derivatives allow one to estimate functional gradients, which are in effect locally varying slopes. Müller and Yao (2010) simplify the study of functional derivatives and gradients by imposing the additive model framework of Müller and Yao (2008) (see above, Section 3.2).

5.6.5 Conditional quantiles and mode

Up to now we have been concerned with modeling the mean of y (or a transformation thereof, in the GLM case), conditional on functional predictors. Cardot et al. (2005) propose instead to estimate a given quantile of y, conditional on $\mathcal{X}$, by minimizing a penalized criterion that is similar to (2), but with the squared error loss in the first term replaced by the “check function” used in ordinary quantile regression (Koenker and Bassett, 1978). Chen and Müller (2012), on the other hand, estimate the entire conditional distribution of y by fitting functional binary GLMs with I(y ≤ y₀) (where I(·) denotes an indicator) as response, for a range of values of y₀. Quantiles can then be inferred by inverting the conditional distribution function. Ferraty et al. (2005) also estimate the entire conditional distribution, but adopt a nonparametric estimator of a weighted-average form reminiscent of (10). That paper and a number of subsequent ones have studied applications in the geosciences, such as an extreme value analysis of ozone concentration (Quintela-del-Río and Francisco-Fernández, 2011). The mode of the nonparametrically estimated conditional distribution serves as an estimate of the conditional mode of y, whose convergence rate is derived by Ferraty et al. (2005).

6 Which method to choose?

Sections 2 through 5 have presented a perhaps overwhelming variety of models and methods for SoFR. How can a user decide which is the appropriate method in a given situation? We offer here a few suggestions, which may be divided into a priori and data-driven considerations.

6.1 A priori considerations

Some authors have questioned whether the flexibility of the general nonparametric model (9) is worth the price paid in terms of convergence rates. The small-ball probability ${\varphi }_X\left(u\right)=\mathrm{Pr}(\parallel \mathcal{X}-X\parallel <u)$ typically converges to 0 exponentially fast as u → 0, and consequently the functional NW estimator (10) converges at a rate that is logarithmic, as opposed to a power of 1/n (Hall et al., 2009). Geenens (2011) succinctly interprets the problem as a function-space “curse of dimensionality,” but shows that a well-chosen semi-metric d increases the concentration of the functional predictors and thus allows for more favorable convergence of the NW estimator to m.

Aside from asymptotic properties, choice of a method may be guided by the kind of interpretation desired, which may in turn depend on the application. As noted in Section 2, the FLM offers a coefficient function, which has an intuitive interpretation. Nonlinear and especially nonparametric model results are less interpretable in this sense. But for applications in which one is interested only in accurate prediction, this advantage of the FLM is immaterial.

Regarding the FLM, we noted in Section 2.1 that smoothness of the data is an important factor when choosing among a priori basis types, such as splines vs. wavelets. Among data-driven basis approaches to the FLM (Section 2.2), those that rely on a more parsimonious set of components may sometimes be preferred, again on grounds of interpretability. In this regard, FPLS has an advantage over FPCR, as emphasized by Delaigle and Hall (2012). On the other hand, if one is interested only in the coefficient function, not in contributions of the different components, then the relative simplicity of FPCR is an advantage over FPLS. A key advantage of FPCR over spline or wavelet methods is that it is more readily applied when the functional predictors are sampled not densely but sparsely and/or irregularly (longitudinal data).

We tend to view a wide variety of methods as effective in at least some settings, but one method for which we have limited enthusiasm is selecting a “best subset” among a large set of FPCs, as opposed to regressing on the leading FPCs. Whereas leading FPCs offer an optimal approximation in the sense of Eckart and Young (1936), if one is not selecting the leading FPCs then it is not clear why the FPC basis is the right one to use at all. Another basis that is by construction relevant for explaining y, such as FPLS components, may be more appropriate. This view finds support in the empirical results of Febrero-Bande et al. (2015).

Other considerations in choosing among methods include conceptual complexity, the number of tuning parameters that must be selected, sensitivity to how preprocessing is done, and computational efficiency. In practice, a primary factor for many users is the availability of software that is user-friendly and has the flexibility to handle data sets that may be more complex than the iid setup of the Introduction. Available software is reviewed in Section 7, and the real-data example presented in Section 8 highlights the need for software that is flexible.

6.2 Data-driven choice

Relying on one’s a priori preference is unlikely to be the best strategy for choosing how to perform SoFR. Next we discuss two ways to let the data help determine the best approach.

6.2.1 Hypothesis testing

Hypothesis testing is an appropriate paradigm when one wishes to compare a simpler versus a more complex SoFR model, with strong evidence required in order to reject the former in favor of the latter. By now there are enough articles on tests of SoFR-related hypotheses to justify a separate review paper; here we offer just a few remarks. Many papers have proposed tests for the FLM (1). Some methods test the null hypothesis β(t) ≡ 0 in (1) versus the alternative that β(t) ≠ 0 for some $t\in \mathcal{I}$ (e.g., Cardot et al., 2003; Lei, 2014). The (restricted) likelihood ratio test of Swihart et al. (2014) can be applied either to that zero-effect null or, alternatively, to the null hypothesis that β(t) is a constant—a hypothesis that, if true, allows one to regress on the across-the-function average rather than resorting to functional regression. McLean et al. (2015) treat the linear model (1) as the null, to be tested versus the additive model (8), while García-Portugués et al. (2014) consider testing against a more general alternative. Horváth and Kokoszka (2012) and Zhang et al. (2014) investigate hypothesis testing procedures to choose the polynomial order in functional polynomial models such as the quadratic model (5). Delsol et al. (2011) propose a test for the null hypothesis that m in the nonparametric model (9) belongs to a given family of operators.

6.2.2 Ensemble predictors

In most practical cases, there are not just two plausible models—a null and an alternative—but many reasonable options for performing SoFR, and it is impossible to know in advance which model and estimation strategy will work best for a given data set. Because of this, Goldsmith and Scheipl (2014) extended the idea of model stacking (Wolpert, 1992) (or superlearning, van der Laan et al., 2007) to SoFR. A large collection of estimators is applied to the data set of interest and are evaluated for prediction accuracy using cross-validation. These estimators are combined into an “ensemble” predictor based on their individual performance. These authors found that multiple approaches yielded dramatically different relative performance across several example data sets—underlining the value of trying a variety of approaches to SoFR when possible.

7 Software for scalar-on-function regression

Several packages for R (R Core Team, 2015) implement SoFR. The function fRegress in the fda package (Ramsay et al., 2009) fits linear models in which either the response and/or the predictor is functional. The fda.usc package (Febrero-Bande and Oviedo de la Fuente, 2012) implements an extensive range of parametric and nonparametric functional regression methods, including those studied by Ramsay and Silverman (2005), Ferraty and Vieu (2006) and Febrero-Bande and González-Manteiga (2013). The refund package (Huang et al., 2015) implements penalized functional regression, including several variants of the FLM and the additive model (8), and allows for multiple functional predictors and scalar covariates, as well as generalized linear models. Optimal smoothness selection relies on the mgcv package of Wood (2006). The mgcv package itself is one of the most flexible and user-friendly packages for SoFR, allowing for the whole GLASS structure of Eilers and Marx (2002) plus random effects; see section 5.2 of Wood (2011), which incidentally was the second paper to use the term “scalar-on-function regression”. In mgcv, functional predictor terms are treated as just one instance of “linear functional” terms (cf. the “general spline problem” of Wahba, 1990). The refund.wave package (Huo et al., 2014), a spinoff of refund, implements scalar-on-function and scalar-on-image regression in the wavelet domain.

In MATLAB (MathWorks, Natick, MA), the PACE package implements a wide variety of methods by Müller, Wang, Yao, and co-authors, including a versatile collection of functional principal component-based regression models for dense and sparsely sampled functional data. From a Bayesian viewpoint, Crainiceanu and Goldsmith (2010) have developed tools for functional generalized linear models using WinBUGS (Lunn et al., 2000).

8 A brain imaging example

Our work has made us aware of the expanding opportunities to apply SoFR in cuttingedge biomedical research, a trend that we expect will accelerate in the coming years. For such applications to be feasible, one must typically move beyond the basic model (1) and incorporate scalar covariates and/or multiple functional predictors, allow for non-iid data, and consider hypothesis tests for the coefficient function(s). The following example illustrates how FLMs can incorporate some of these features (thanks to flexible software implementation, as advocated in Section 6.1), and can shed light on an interesting scientific question. For comparisons of linear as well as nonlinear and nonparametric approaches applied to several data sets, we refer the reader to Goldsmith and Scheipl (2014).

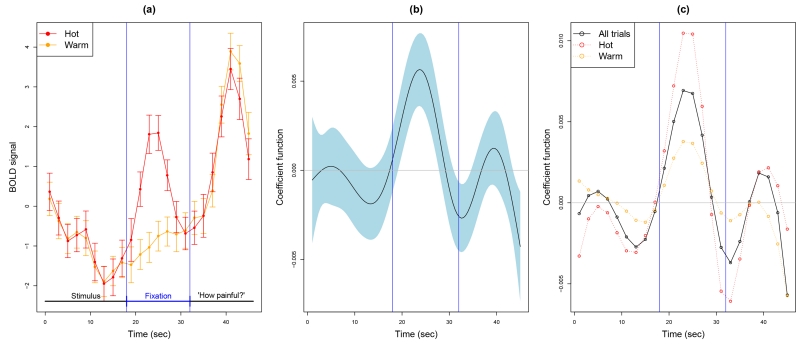
Lindquist (2012) analyzed functional magnetic resonance imaging (fMRI) measures of response to hot (painful) and warm (non-painful) stimuli applied to the left volar forearm in 20 volunteers. Here we apply SoFR to examine whether the blood oxygen level dependent (BOLD) response measured by fMRI in the lateral cerebellum predicts the pain intensity, as rated after each stimulus on a scale from 100 and 550 (with higher values indicating more pain). Each trial consisted of thermal stimulation for 18 seconds; then a 14-second interval in which a fixation cross was presented on a screen; then the words “How painful?” appeared, and after another 14-second interval the participant rated the pain intensity. The BOLD signal was recorded at 23 2-second intervals. There were J_i = 39–48 such trials per volunteer, and 940 in total. As shown in Figure 1(a), the lateral cerebellum BOLD signal tends to be higher in the hot trials, but only during the fixation cross interval.

Figure 1.

(a) Overall mean lateral cerebellum BOLD signal at each of the 23 time points, with approximate 95% confidence intervals, for warm- and hot-stimulus trials. (b) Estimated coefficient function, with approximate pointwise 95% confidence intervals, for model (15). (c) Coeffcient function estimate for the full data set (as in (b)) compared with those obtained with only the hot or only the warm trials.

We fitted the model

$$y_{\mathit{ij}}={\alpha }_i+\gamma I_{\mathit{ij}}^{\text{hot}}+{\int }_{\mathcal{I}}{\mathcal{X}}_{\mathit{ij}}\left(t\right)\beta \left(t\right)\mathit{dt}+{\epsilon }_{\mathit{ij}},i=1,\dots ,n,j=1,\dots ,J_i,$$ (15)

in which y_ij is the log pain score for the ith participant’s jth trial, $I_{\mathit{ij}}^{\text{hot}}$ is an indicator for a hot stimulus, the α_i’s are iid normally distributed random intercepts, $\mathcal{I}$ is the time interval of the trial, and the ε_ij’s are iid normally distributed errors with mean zero. Unsurprisingly, the expected difference in log pain score between hot and warm trials is found to be hugely significant ($\widehat{\gamma }=0.599$, p < 2·10⁻¹⁶). The coefficient function is also very significantly nonzero, based on the modified Wald test of Wood (2013) or the likelihood ratio test of Swihart et al. (2014).

In particular, Figure 1(b) shows that $\widehat{\beta }\left(t\right)$ is clearly positive for the same time points that evince a warm/hot discrepancy in Figure 1(a). One could venture a “functional collinearity” explanation for this, in view of the high correlation (0.28) between the indicator variable $I_{\mathit{ij}}^{\text{hot}}$ and the functional predictor term ${\int }_{\mathcal{I}}{\mathcal{X}}_{\mathit{ij}}\left(t\right)\widehat{\beta }\left(t\right)\mathit{dt}$. In other words, one might suspect that the highly positive values of $\widehat{\beta }\left(t\right)$ around the 20- to 28-second range are just an artifact of the higher BOLD signal in that range for hot versus warm trials. But that seems incorrect, since $\widehat{\beta }$ looks very similar even when we fit separate models with only the warm or only the hot trials (Figure 1(c)). A more cogent explanation is that brain activity detected by the BOLD signal partially mediates the painful effect of the hot stimulus, a causal interpretation developed in depth by Lindquist (2012).

The SoFR implementations of Wood (2011) in the R package mgcv and of Goldsmith et al. (2011) in the refund package—which were used to create Figure 1(b) and (c), respectively— make it routine to include scalar covariates and random effects, and to test the significance of the coefficient function, as we have done here. It is also straightforward to test for a “scalar-by-function” interaction between stimulus type and BOLD signal (found to be non-significant); or to include multiple BOLD signal predictors. Besides the lateral cerebellum, the data set includes such functional predictors for 20 other pain-relevant regions. Several of these have significant effects on pain, even adjusting for the lateral cerebellum signal, but the associated increments in explained variance are quite small.

9 Discussion

This paper has emphasized methodological and practical aspects of some widely used SoFR models. Just a few brief words will have to suffice regarding asymptotic issues. For functional (generalized) linear models (see Cardot and Sarda, 2011, for a survey), convergence rates have been studied both for estimation of the coefficient function (e.g., Müller and Stadtmüller, 2005; Hall and Horowitz, 2007; Dou et al., 2012) and for prediction of the response (e.g., Cai and Hall, 2006; Crambes et al., 2009); see Hsing and Eubank (2015) for a succinct treatment, and Reimherr (2015) for a recent contribution on the key role played by eigenvalues of the covariance operator. A few recent papers (e.g., Wang et al., 2014; Brunel and Roche, 2015) have derived non-asymptotic error bounds for FLMs. In nonparametric FDA, only prediction error is considered, with small-ball probability playing a central role. Ferraty and Vieu (2011) review both pointwise and uniform convergence results. A detailed analysis of the functional NW estimator’s asymptotic properties was recently provided by Geenens (2015).

Regarding the term nonparametric in the FDA context, Ferraty et al. (2005) explain: “We use the terminology functional nonparametric, where the word functional refers to the infinite dimensionality of the data and where the word nonparametric refers to the infinite dimensionality of the model.” But some would argue that, since the coefficient function in (1) lies in an infinite-dimensional space, this nomenclature makes even the functional linear model “nonparametric”. While a fully satisfying definition may be elusive, we find it most helpful to think of nonparametric SoFR as an analogue of ordinary nonparametric regression, i.e., as extending the nonparametric model (9) to the case of functional predictors.

Our use of the term nonlinear in Section 3 can likewise be questioned, since that term applies equally well to nonparametric SoFR. But we could find no better term to encompass models that are not linear but that impose more structure than the general model (9). Note that in non-functional statistics as well, nonlinear usually refers to models that have some parametric structure, as opposed to leaving the mean completely unspecified.

Other problems of nomenclature have arisen as methods for SoFR have proliferated. We have seen that “functional (generalized) additive models” may be additive with respect to FPC scores (Müller and Yao, 2008; Zhu et al., 2014); points along a functional predictor domain (Müller et al., 2013; McLean et al., 2014); or multiple functional predictors with either nonlinear (Fan et al., 2015) or nonparametric (Febrero-Bande and González-Manteiga, 2013) effects. Likewise, authors have considered every combination of scalar linear (SL), functional linear (FL) and functional nonparametric (FNP) terms, so that “partial linear” models may refer to any two of these three: SL+FL (Shin, 2009), SL+FNP (Aneiros-Pérez and Vieu, 2008), or FL+FNP (Lian, 2011). Finally, some of the nonlinear approaches of Section 3 are sometimes termed “nonparametric” since they incorporate general smooth link functions. One of our aims here has been to reduce terminological confusion.

We hope that, by distilling some key ideas and approaches from what is now a sprawling literature, we have provided readers with useful guidance for implementing scalar-on-function regression in the growing number of domains in which it can be applied.