Development of a Multivariate Predictive Model to Estimate Ionized Calcium Concentration from Serum Biochemical Profile Results in Dogs

Abstract

Background

Ionized calcium concentration is the gold standard to assess calcium status in dogs, but measurement is not always available.

Objectives

(1) To predict ionized calcium concentration from biochemical results and compare the diagnostic performance of predicted ionized calcium concentration (piCa) to those of total calcium concentration (tCa) and 2 corrected tCa formulas; and (2) to study the relationship between biochemical results and variation of measured ionized calcium concentration (miCa).

Animals

A total of 1,719 dogs with both miCa and biochemical profile results available.

Methods

Cross‐sectional study. Using 1,200 dogs, piCa was determined using a multivariate adaptive regression splines model. Its accuracy and performance were tested on the remaining 519 dogs.

Results

The final model included creatinine, albumin, tCa, phosphorus, sodium, potassium, chloride, alkaline phosphatase, triglycerides, and age, with tCa, albumin, and chloride having the highest impact on miCa variation. Measured ionized calcium concentration was better correlated with piCa than with tCa and corrected tCa and had higher overall diagnostic accuracy to diagnose hypocalcemia and hypercalcemia, but not significantly for hypercalcemia. For hypercalcemia, piCa was as sensitive (64%) but more specific (99.6%) than tCa and corrected tCa. For hypocalcemia, piCa was more sensitive (21.8%) and as specific (98.4%) as tCa. Positive and negative predictive values of piCa were high for both hypercalcemia (90% and 98%, respectively) and hypocalcemia (70.8% and 87.7%, respectively).

Conclusions and clinical importance

Predicted ionized calcium concentration can be obtained from readily available biochemical and patient results and seems more useful than tCa and corrected tCa to assess calcium disorders in dogs when miCa is unavailable. Validation on external data, however, is warranted.

Abbreviations

ALP

alkaline phosphatase

AUC

area under the curve

CI

confidence interval

GCV

generalized cross‐validation

MARS

multivariate adaptive regression splines

miCa

measured ionized calcium concentration

NDLR

negative diagnostic likelihood ratio

NPV

negative predictive value

PDLR

positive diagnostic likelihood ratio

piCa

predicted ionized calcium concentration

PI

prediction interval

PPV

positive predictive value

RMSE

root mean squared error

ROC

receiver operator characteristic

RSS

residual sum of squares

tCa

total calcium concentration

Serum total calcium concentration (tCa) is composed of 3 fractions: ionized, protein‐bound, and complexed, with each comprising approximately 56, 34, and 10% of the serum tCa, respectively.1 The ionized calcium concentration is the most biologically active fraction. It is responsible for the physiologic functions of calcium within the body and also is a sensitive indicator of pathologic states when abnormal.2 Ionized calcium concentration measurement therefore is considered the gold standard for evaluating calcium homeostasis in humans and animals.3

Ionized calcium concentration can quickly and accurately be assessed in dogs using analyzers with ion‐selective electrodes. Although these analyzers have become more and more accessible to clinicians, they remain unavailable in many veterinary hospitals.4 Thus, clinicians often rely on interpretation of tCa, which is readily available on most routine serum biochemistry profiles, to assess calcium status. However, correlations between ionized calcium concentration and tCa can be inaccurate, thereby not reflecting the true calcium status of the animal.2, 5, 6, 7, 8 In attempts to improve the accuracy of tCa at predicting ionized calcium concentration, correction equations have been derived for dogs.9 These equations adjust the tCa for either albumin or total protein concentration, based on the fact that a large fraction of tCa is protein‐bound. In utilizing these equations, serum tCa that has been adjusted into the reference range is assumed to be associated with normal ionized calcium concentration, and samples with concentrations that fall outside of the reference range after adjustment are assumed to reflect abnormal serum ionized calcium concentrations. Although initially promising, several studies have shown that adjusting tCa for albumin or total protein concentration does not improve and may even worsen the correlation between tCa and ionized calcium concentration,2, 6, 7, 10 possibly due to differences in the proportion of the complexed form of calcium, which can vary widely among patients and which is not accounted for in the correction formulas.8 A formula that takes into account complexed as well as protein‐bound calcium fractions would therefore likely be more accurate at predicting whether a patient has normal calcium homeostasis.

Routine chemistry panels can be performed in the majority of veterinary clinics and laboratories. The objectives of our study were to (1) create a model predictive of ionized calcium concentration that integrates only routinely available biochemistry results so that it could be readily usable by veterinarians, and (2) describe the relationships between routinely available biochemistry results and ionized calcium concentrations, in order to better understand the factors that influence changes in the ionized fraction of the serum calcium concentration.

Materials and Methods

Study Population and Data Collection

Medical records of all the dogs that had both an ionized calcium concentration measurement and a serum biochemistry panel (creatinine, blood urea nitrogen, total protein, albumin, globulin, tCa, phosphorus, sodium, potassium, chloride, glucose, alkaline phosphatase [ALP], alanine transferase, gamma‐glutamyltransferase, total bilirubin, cholesterol, triglycerides, and bicarbonate) performed at the University of Illinois Veterinary Teaching Hospital between 2010 and 2016 were retrospectively identified by computerized database search. Ionized calcium concentration was measured on whole blood. A volume of 0.4 mL of blood was immediately placed into a lithium heparin‐coated plastic screw‐top tube containing <15 USP units of heparin/mL of blood. The tube was immediately inverted 8–10 times to assure anticoagulation, according to the manufacturer's recommendations. The tubes remained closed in an upright position at room temperature until the time of sample analysis, which was routinely performed within 15 minutes of collection. Immediately before analysis, the tube was gently inverted several times to ensure adequate mixing of the sample. The tube was opened and the sample was drawn into a syringe for ionized calcium concentration measurement using a stat blood gas analyzer,¹ which uses ion‐selective electrode technology. The unadjusted ionized calcium concentration was reported. The biochemistry panel was obtained from 2 chemistry analyzers (1² from February to August 2010 and another³ from August 2010 to February 2016). Patient data were included in the study only if the ionized calcium concentration measurement and the biochemistry panel were performed within 24 hours of each other. Patients were excluded if any laboratory results were missing. To guarantee independence of observations, an individual could not be included more than once; if the patient was evaluated several times, only the first evaluation was included.

All biochemistry results and the measured ionized calcium concentration (miCa) were recorded for every patient. Additional data obtained from the medical records included age, breed, sex, body weight, and body condition score. When available, information regarding drug therapy that could influence calcium concentrations (eg, calcitriol, calcium supplementation, prednisone, nonsteroidal anti‐inflammatory drugs, phenobarbital, diuretics) and final diagnosis, particularly with regard to renal disease or calcium disorders, also was collected. A patient was considered to have parenchymal renal disease if the combination of a serum creatinine concentration >2.0 mg/dL and a urine specific gravity <1.030 was identified. Finally, pH and pCO₂ obtained at the same time as miCa using the same analyzer also were recorded. The reference ranges for pH and pCO₂ were 7.39–7.49 and 23.11–37.41 mmHg, respectively.

Multivariate Adaptive Regression Splines Predictive Model Creation

Data from 67% of the included dogs, rounded up to the next 100 dogs, were randomly selected using a random number generator and assigned to the training set, which was used to develop the model. The data from the remaining dogs (approximatively 33% of the included dogs) were assigned to the test set, which was used to evaluate the performance of the newly created model. Comparisons of age, weight, and body condition score, and sex and calcium status between the dogs of the training set and those of the test set were performed using the Mann–Whitney test and the chi‐square test, respectively.

The predictive algorithm was created using a multivariate adaptive regression splines (MARS) model.11 Basically, a MARS model is a nonparametric regression method that estimates complex nonlinear relationship by a series of hinge functions of the predictors expressed using the formula:

$$\widehat{y}=a_0+\sum _{k=1}^p{a}_k\ast h_k(x)$$

where $\widehat{y}$ is the predicted value (ie, predicted ionized calcium concentration), a ₀ is the intercept of the model, p is the total number of hinge functions, and a _k is the coefficient of the kth hinge function h _k(x). The hinge functions are pairs of 2‐sided truncated functions applied to all the predictors and described by the following equations:

$$h(x-t)=\left\{\begin{array}{cc}\left(x-t\right)\hfill & ifx>t\hfill \\ 0\hfill & ifx\le t\hfill \end{array}\right.$$

$$h(t-x)=\left\{\begin{array}{cc}\left(t-x\right)\hfill & ifx<t\hfill \\ 0\hfill & ifx\ge t\hfill \end{array}\right.$$

where x is a predictor variable and t is the joining point of the polynomial called knot. Therefore, the hinge functions break each predictor variable into 2 groups centered on a knot value and determine a linear relationship between the predictor and the outcome (ie, miCa) in each group. The final relationship between the predictors and the outcome is therefore nonlinear.

The MARS model selection followed a 2‐step process involving an initial forward pass and then multiple backward passes as needed until the final model was obtained. Briefly, for the forward pass, hinge functions associated with the predictor variables (biochemical and signalment variables, renal disease, drugs) were added in pairs into the model until any of the following conditions were met: (1) There were no more terms to add because all of them had been added into the model, or (2) adding a term did not increase the predictive performance of the model anymore. At the end of this process, the full model was obtained, including all of the biochemical variables that were useful a priori to predict miCa, regardless of the complexity of the model. This full model is, however, overfitted and therefore has poor predictive performance. Backward elimination then was used for final model selection and predictive performance optimization. Hinge functions were removed one by one from the model using all possible combinations. Each time a variable was removed, the accuracy and complexity of the new model were assessed by generalized cross‐validation (GCV) statistics. The smaller the GCV, the more accurate and less complex the model. The model with the lowest GCV value was selected as the final model. Finally, a prediction interval (PI) was defined as follows: predicted calcium ± 2 × regression standard error.12

Assessment of Predictive Model Performance

The test set was used to evaluate the performance of the model in predicting miCa. The correlation between predicted ionized calcium concentration (piCa) and miCa was assessed graphically using the observed‐versus‐predicted plot and mathematically using Pearson's R with its confidence interval (CI). Accuracy of the prediction was measured by calculating the root mean squared error (RMSE), which can be interpreted as the average distance between the observed values and the model prediction. The accuracy of the prediction interval (PI) was evaluated by measuring how often the miCa values were included inside the PI.

To compare the diagnostic performance of piCa with other available calcium status estimators, tCa was adjusted for albumin and total protein to obtain 2 corrected tCa variables according to the following formulas:

1. tCa (mg/dL) – albumin (g/dL) + 3.5

2. tCa (mg/dL) – (0.4 × TP [g/dL]) + 3.3

Samples were further classified as hypercalcemic if miCa was >1.37 mmol/L, and as hypocalcemic if miCa was <1.11 mmol/L. The reference range for miCa with this blood gas analyzer was determined using 30 healthy dogs. Correlations with miCa were compared among piCa, tCa, and the 2 corrected tCa using Pearson's R. Ability of piCa, tCa, and the 2 corrected tCa formulas to properly classify dogs as hypercalcemic or hypocalcemic was assessed using receiver operator characteristic (ROC) curve analysis. The areas under the ROC curves (AUC) were used as a measure of diagnostic performance for these variables and were compared by chi‐square analysis.

Sensitivity, specificity, negative (NPV) and positive predictive values (PPV), and negative (NDLR) and positive diagnostic likelihood ratios (PDLR) were calculated for piCa and its PI, tCa, and the 2 corrected tCa equations for diagnosis of hypocalcemia or hypercalcemia. Sensitivity and specificity of piCa were compared to those of tCa and both corrected tCa formulas using McNemar's test. Finally, diagnostic discordance was determined for piCa, tCa, and the 2 corrected tCa formulas by calculating the percentage of dogs with incorrect identification of calcium status, as defined by miCa inside or outside of the reference range.

Description of the Relationship between Biochemistry Predictors and Ionized Calcium Concentration

Variable importance of particular biochemical variables in miCa prediction was assessed using the GCV criterion, which corresponds to the increase in GCV when a variable is removed from the model. For ease of interpretation, the increases in GCV were scaled so the largest increase was 100. Variables that caused larger increase in GCV were considered more important.

The predicted relationship between ionized calcium concentration and the biochemical predictors finally was depicted graphically for each biochemistry variable. Statistical analyses, including MARS model creation, were performed using software in the public domain.⁴ Significance was set at a value of P < 0.05 for all comparisons.

Results

Study Population

Two thousand dogs met the criteria for inclusion in the study and 281 were excluded, leaving 1,719 included dogs. The training set was composed of the data from 1,200 (69.8%) dogs, whereas the remaining data from 519 (30.2%) dogs were used for the test set. In total, 135 breeds were represented, with the majority being mixed‐breed dogs (23.09%), and lesser numbers of Labrador Retrievers (8.14%), Dachshunds (5.22%), Yorkshire Terriers (3.72%), Golden Retrievers (3.14%), Shih Tzus (2.73%), German Shepherds (2.67%), Boxers (2.55%), Beagles (2.21%), and <2% of each remaining breed. The differences in patient characteristics among the total group, test set, and training set are outlined in Table 1. There were no significant differences regarding age, weight, and sex between the training set and test set (P = 0.52, 0.26, and 0.97, respectively). There was a significant difference between the dogs of the training set and those of the test set in terms of body condition score (P = 0.04), with the dogs of the training set having a slightly higher score than those of the test set. However, this difference was likely not clinically relevant. There was no statistical difference for the proportion of hypocalcemic, normocalcemic, and hypercalcemic dogs between the test set and training set (P = 0.56). In the test set, the 10, 50, and 90% percentiles of venous pH were 7.35, 7.42, and 7.47, respectively, with minimum and maximum values of 7.19 and 7.56. The 10, 50, and 90% percentiles of venous pCO₂ were 22.5 mmHg, 28.5 mmHg, and 36.9 mmHg, respectively, with minimum and maximum values of 13.6 mmHg and 66.8 mmHg.

Table 1.

Demographic data for the dogs of the total group, test set, and training set

Variable	Total Group (n = 1719)	Training Set (n = 1200)	Test Set (n = 519)	P‐Values
Age (years)	6.9 (0.04–19.0)	6.8 (0.04–19.0)	7.0 (0.16–16.0)	0.52
Weight (kilograms)	18.0 (0.4–96.0)	17.0 (0.4–94.0)	20.0 (0.8–96.0)	0.26
BCS (9‐point scale)	5 (1–9)	5 (1–9)	5 (1–9)	0.04*
Sex				0.97
Neutered Males	723 (42.0%)	509 (42.4%)	214 (41.2%)
Intact Males	166 (9.7%)	114 (9.5%)	52 (10.1%)
Spayed Females	718 (41.8%)	499 (41.6%)	219 (42.2%)
Intact Females	112 (6.5%)	78 (6.5%)	34 (6.5%)
Calcium Status				0.56
Hypocalcemic	280 (16.3%)	202 (16.8%)	78 (15.0%)
Hypercalcemic	99 (5.8%)	71 (5.9%)	28 (5.4%)
Normocalcemic	1340 (77.9%)	927 (77.3%)	413 (79.6%)

Table entries represent median values (minimum–maximum) for continuous variables (age, weight, and body condition score) and number of dogs (percent of dogs) for categorical variables (sex and calcium status). Calcium status categories were determined based on measured ionized calcium values. Significant differences between the dogs of the training set and those of the test set, as assessed via the Mann–Whitney (age, weight, and body condition score) and chi‐square (sex and calcium status) tests, were defined by a P‐value<0.05 and are indicated by *.

Final Model

The final model included creatinine, albumin, tCa, phosphorus, sodium, potassium, chloride, ALP, triglycerides, and age as independent predictors. Table 2 presents the 15 hinge functions included in the final model and their corresponding coefficients. An example showing how to calculate piCa from a biochemistry profile using this model is presented in Appendix 1.

Table 2.

Final multivariate adaptive regression splines model for prediction of ionized calcium from routine biochemical and patient variables determined from dogs of the training set

Hinge function of the predictors	Coefficient
(Intercept)	1.05189701
h (5 – creatinine)	0.01707569
h (3.3 – albumin)	0.01479586
h (albumin – 3.3)	−0.08887935
h (7.5 – total calcium)	−0.12828575
h (total calcium – 7.5)	0.04954995
h (total calcium – 9.9)	0.03339810
h (4.9 – phosphorus)	−0.01079317
h (154 – sodium)	0.00371181
h (potassium – 5.1)	−0.03410317
h (111 – chloride)	−0.00672129
h (chloride – 111)	0.00390011
h (848 – ALP)	−0.00003635
h (582 – triglycerides)	−0.00005582
h (triglycerides – 582)	−0.00002793
h (2.27 – age)	0.02851557

h()—hinge function; ALP, alkaline phosphatase.

Description of the Relationship between Biochemistry Predictors and Ionized Calcium Concentration

According to the results shown in Table 3, the most important variables for the prediction of miCa were as follows: tCa, chloride, and albumin had the most impact; age, creatinine, ALP, and sodium had moderate impact; and phosphorus, potassium, and triglycerides had the least impact.

Table 3.

Evaluation of the importance of the predictor variables that form the model for predicting measured ionized calcium changes

Variables in order of importance (from top to bottom)	GCV
Total Calcium	100
Chloride	68.3
Albumin	55.4
Age	40.3
Creatinine	29.9
Total ALP	23.8
Sodium	19.9
Phosphorus	16.6
Potassium	13.6
Triglycerides	9.5

ALP, alkaline phosphatase; GCV, generalized cross‐validation. For ease of interpretation, the GCV was scaled so that largest increase was 100.

The individual relationships between miCa and the biochemical predictors are presented in Figure 1. The miCa constantly increased as tCa and chloride concentration increased. On the other hand, as serum albumin concentration increased, miCa decreased. The miCa value also decreased as creatinine, sodium, and age increased up to a certain result, where creatinine (>5 mg/dL), sodium (>154 mmol/L), and age (>2.27 year) had no more influence on the ionized calcium concentration. Analogously, miCa increased as phosphorus and ALP increased up to a certain value, where phosphorus (>4.9 mg/dL) and ALP (>848 U/L) lost their impact on miCa. On the other hand, potassium had no influence on miCa until serum potassium concentration reached 5.1 mmol/L. As serum potassium concentration increased further, miCa decreased. Finally, miCa increased as triglycerides increased up to 582 mg/dL. When triglycerides increased further, miCa value consistently decreased.

Figure 1.

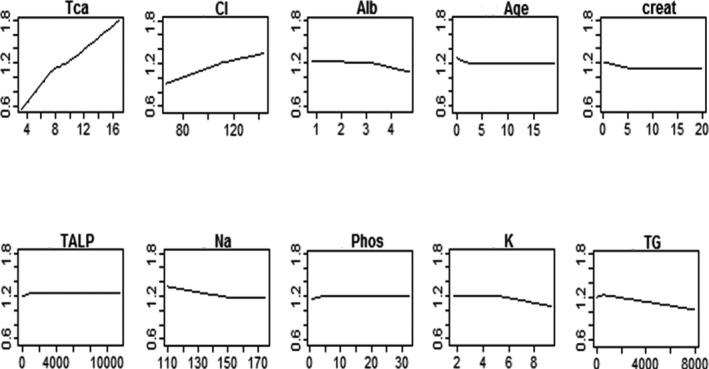
Individual relationships between measured ionized calcium and the biochemical predictors that have been retained in the final predictive model. The measured ionized calcium value is represented on the y‐axis, against the value of the predictor variables on the x‐axis. Creat, creatinine; alb, albumin; Tca, total calcium; Phos, phosphorus; Na, sodium; K, potassium; Cl, chloride; TALP, total alkaline phosphatase; TG, triglycerides.

Assessment of Predictive Model Performance

The observed‐versus‐predicted plot, displaying miCa on the y‐axis and piCa on the x‐axis, is presented in Figure 2. If miCa and piCa were exactly the same, all of the points would lay on a single line, which would be the first bisector (miCa = 0 + 1 × piCa). With our actual data, the regression line (miCa =− 0.06 + 1.05×piCa) was close to the first bisector, indicating good fit between measured and predicted ionized calcium concentration. The average difference between piCa and miCa, as estimated by RMSE, was 0.08 mmol/L. The PI included miCa 94% of the time.

Figure 2.

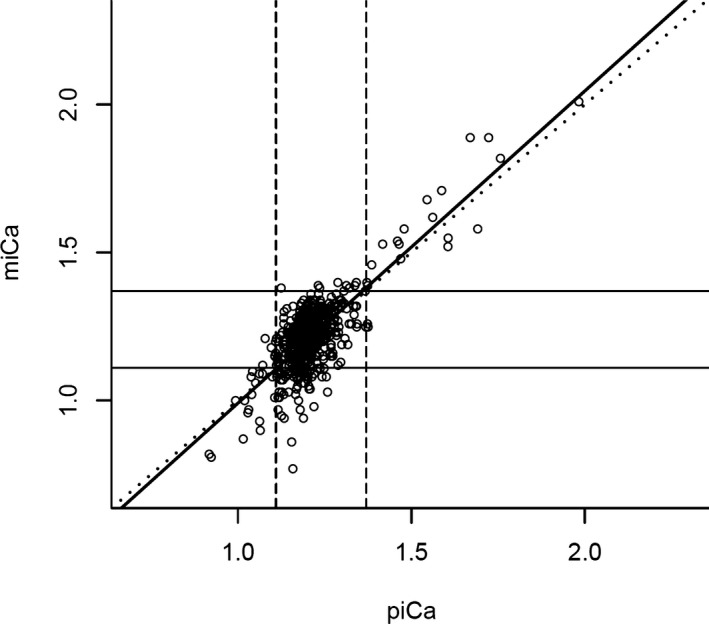
Observed‐versus‐predicted plot showing the relationship between measured and predicted ionized calcium. The upper and lower limits of normocalcemia (1.11–1.37 mmol/L) are represented by the vertical dashed lines for the predicted ionized calcium, and the horizontal solid line for the measured ionized calcium. The diagonal dotted line represents the first bisector, on which predicted ionized calcium values that perfectly match measured ionized calcium fall in. The thick solid line represents the regression line (miCa = −0.06 + 1.05*piCa). Points that fall within the 3 boxes along the first bisector were properly classified by predicted ionized calcium, and those points within the 4 boxes away from the first bisector were misclassified by predicted ionized calcium. miCa: measured ionized calcium; piCa: predicted ionized calcium.

Overall, miCa was better correlated with piCa than with tCa and corrected tCa. Pearson's R was 0.78 (CI, 0.74–0.81) for piCa versus 0.64 (CI, 0.59–0.69), 0.7 (CI, 0.65–0.74), and 0.67 (CI, 0.62–0.71) for tCa and the 2 corrected tCa formulas, respectively.

The ROC curves for both hypercalcemia and hypocalcemia are shown in Figure 3. The AUC and their CI for piCa, tCa, and the 2 corrected tCa formulas to diagnose hypocalcemia or hypercalcemia are presented in Table 4. To diagnose hypocalcemia, the AUC for piCa was significantly higher than for tCa and both corrected tCa formulas (0.80 vs 0.68–0.70, P < 0.001). For diagnosing hypercalcemia, the AUC for piCa was higher than for tCa and both corrected tCa formulas, although not significantly (0.95 vs. 0.89–0.92, P = 0.28).

Figure 3.

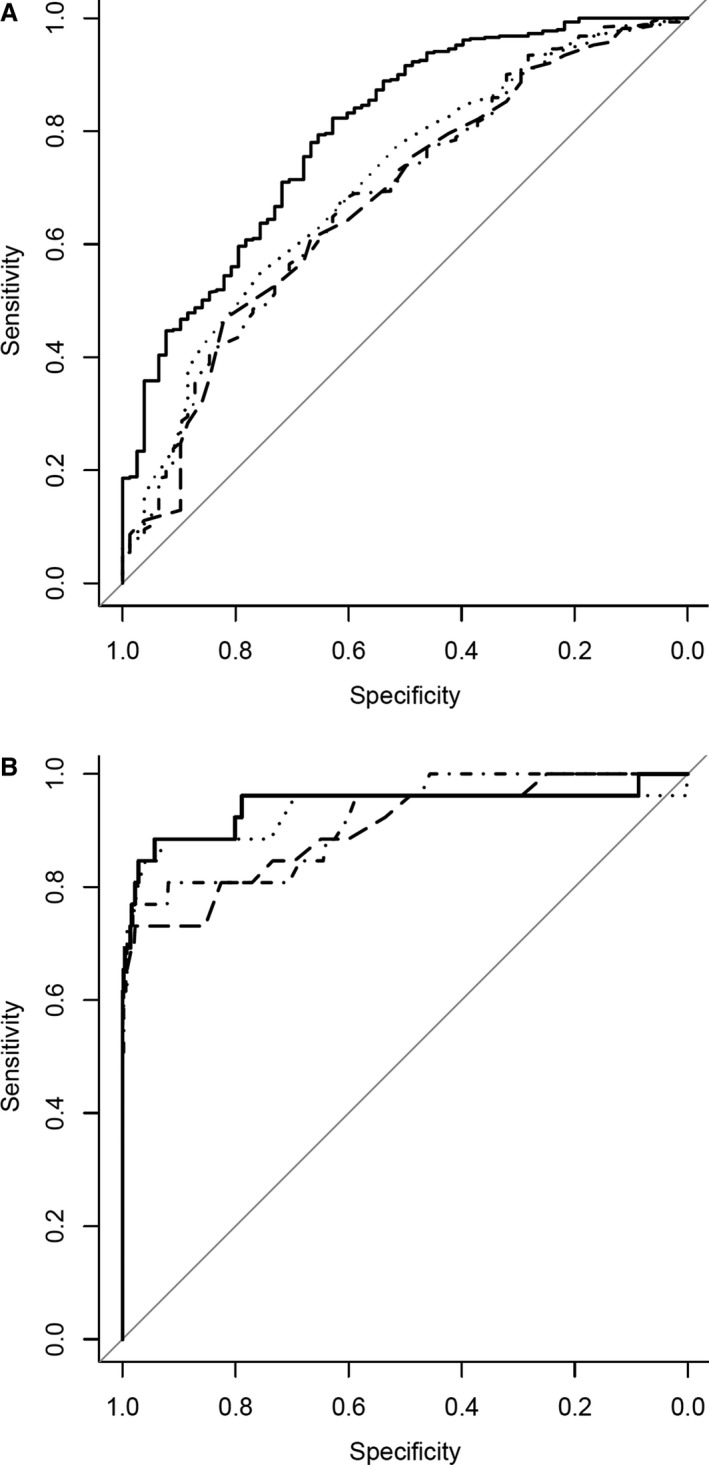
Receiver operator characteristic curves illustrating the overall diagnostic performance of predicted ionized calcium (solid line), total calcium (dashed line), total calcium corrected with albumin (dotted line), and total calcium corrected with total protein (dash‐and‐dot line), for hypocalcemia (A) and hypercalcemia (B).

Table 4.

Area under the ROC curves and their 95% confidence interval of predicted ionized calcium, total calcium, and 2 corrected total calcium formulas for diagnosis of hypocalcemia and hypercalcemia in dogs of the test set

	Hypocalcemia*		Hypercalcemia
	AUC	95% confidence interval	AUC	95% confidence interval
piCa	0.80	0.74–0.85	0.95	0.88–1.00
tCa	0.67	0.61–0.74	0.89	0.81–0.96
Corrected tCa1	0.70	0.64–0.77	0.92	0.84–0.99
Corrected tCa2	0.68	0.62–0.75	0.90	0.83–0.97

Hypocalcemia is defined as measured ionized calcium <1.11 mmol/L, and hypercalcemia is defined as measured ionized calcium >1.37 mmol/L. For hypocalcemia, there was a significant difference for the areas under the curve among the 4 techniques (*P < 0.001). piCa, predicted ionized calcium; tCa, total calcium; Corrected tCa1, total calcium corrected with albumin; Corrected tCa2, total calcium corrected with total protein; AUC, area under the curve.

Sensitivity, specificity, NPV, PPV, NDLR, and PDLR for piCa and its PI, tCa, and the 2 corrected tCa equations for diagnosis of hypocalcemia or hypercalcemia are presented in Table 5a and b, respectively. To detect hypocalcemia, sensitivity of piCa (21.8%) was significantly higher than the sensitivity of tCa (6.4%, P = 0.002) and both corrected tCa formulas (0%, P < 0.001). To diagnose hypocalcemia, specificity of piCa (98.4%) was not significantly different from the specificity of tCa (98.6%, P = 0.76), but was significantly lower than those of both corrected tCa formulas (100% for both corrected tCa formulas, P = 0.01). To detect hypercalcemia, piCa was as sensitive as tCa (64% and 71.4%, respectively, P = 0.5) and both corrected tCa formulas (82.1 and 78.6% for tCa corrected for albumin and total protein, respectively, P = 0.06 and 0.12 for both comparisons). To diagnose hypercalcemia, specificity of piCa (99.6%) was significantly higher than that of tCa (98%, P = 0.01) and both corrected tCa formulas (95.9% and 89.6%, respectively, P < 0.001 for both comparisons). At the prevalence of hypocalcemia in the test set (ie, 15%), PPV and PDLR of piCa (70.8 and 13.7%, respectively) were much higher than those of tCa (PPV, 45.5%; PDLR, 4.7) and of both corrected tCa formulas (PPV, 15% for both of them; PDLR not calculable). Similarly, at the prevalence of hypercalcemia in the test set (ie, 5.4%), PPV and PDLR of piCa (90 and 157.8%, respectively) were much higher than those of tCa (PPV, 66.7%; PDLR, 35.1) and of both corrected tCa formulas (PPV, 53.5% and 30.1%; PDLR, 20.1 and 7.5, respectively). Diagnostic discordance when piCa, tCa, albumin‐corrected tCa, and total protein‐corrected tCa were used to predict calcium status was 15.4, 18.5, 19.5, and 25%, respectively.

Table 5.

(a) Sensitivity, specificity, and negative and positive predictive values of predicted ionized calcium and its prediction interval, total calcium, and 2 corrected calcium formulas for diagnosis of hypocalcemia in dogs of the test set (prevalence of hypocalcemia = 15%). (b) Sensitivity, specificity, and negative and positive predictive values of predicted calcium and its prediction interval, total calcium, and 2 corrected calcium formulas for diagnosis of hypercalcemia in dogs of the test set (prevalence of hypercalcemia = 5.4%)

	Sensitivity	Specificity	NPV	PPV	PDLR	NDLR
(a)
piCa < 1.11 mmol/L	21.8%	98.4%	87.7%	70.8%	13.7	0.79
Lower end of PI < 1.11 mmol/L	97.4%	21.3%	97.9%	18%	1.2	0.12
Upper end of PI < 1.11 mmol/L	2.6%	100%	85.3%	100%	ND	0.97
tCa < 7.6 mg/dL	6.4%	98.6%	85.6%	45.5%	4.7	0.95
Corrected tCa1 < 7.6 mg/dL	0%	100%	ND	15%	ND	1
Corrected tCa2 < 7.6 mg/dL	0%	100%	ND	15%	ND	1
(b)
piCa > 1.37 mmol/L	64%	99.6%	98%	90%	157.8	0.36
Upper end of PI > 1.37 mmol/L	92.9%	79.2%	99.5%	20.3%	4.5	0.09
Lower end of PI > 1.37 mmol/L	35.7%	100%	96.5%	100%	ND	0.64
tCa > 11.4 mg/dL	71.4%	98%	98.4%	66.7%	35.1	0.29
Corrected tCa1 > 11.4 mg/dL	82.1%	95.9%	98.9%	53.5%	20.1	0.19
Corrected tCa2 > 11.4 mg/dL	78.6%	89.6%	98.7%	30.1%	7.5	0.24

piCa, predicted ionized calcium; PI, prediction interval; tCa, total calcium; Corrected tCa1, total calcium corrected with albumin; Corrected tCa2, total calcium corrected with total protein; NPV, negative predictive value; PPV, positive predictive value; PDLR, positive diagnostic likelihood ratio; NDLR, negative diagnostic likelihood ratio; ND, not determined because denominator is 0.

Discussion

Ionized calcium concentration is the gold standard for evaluating a patient's calcium homeostasis, but it is not always available. A novel formula that can predict ionized calcium concentration with improved accuracy compared to uncorrected and corrected tCa was created employing serum biochemical profiles and patient age, providing veterinarians with an additional option for assessing patient calcium status when miCa is not available. Additionally, tCa, albumin, and chloride were determined to have the greatest impact on miCa variation.

Several formulas have been developed in human and veterinary medicine to predict ionized calcium concentration from tCa and other biochemical variables and pH. They were all based on simple or multivariate parametric regression analysis, often linear regression models.9, 13 All of these formulas performed poorly.7, 13 In our study, we followed a different approach, by utilizing a MARS model for several reasons. First, the MARS model is nonlinear and therefore took into account the likely complexity of the relationship between ionized calcium concentration and the other biochemical variables.11 Second, it is a nonparametric technique and therefore not subject to erroneous assumptions about the variable distribution.11 It also eliminated the need to do any variable transformations.14 Third, no interaction terms were included to avoid overfitting to the observed data, which is a common problem in predictive modeling.15 Finally, it allowed us to identify and better define the relationships between ionized calcium concentration and other biochemical variables. The use of a MARS model might explain why our ionized calcium concentration prediction seems more accurate than the ones that were previously described.9, 13

Nonetheless, it is difficult to ensure accuracy of a predictive model. Ideally, it requires internal validation (ie, validity of claims for the underlying population from which the data originated, which refers to reproducibility of the model) and external validation (ie, generalizability of claims to plausibly related but different populations).16 External validation was not possible in our study because we had access only to data from our hospital. Testing our model on different populations (eg, from other institutions, in a prospective manner, with data obtained from different analyzers) remains essential to demonstrate generalizability.17 Internal validation was performed by data splitting, which allowed assessment of predictive performance on independent data that were not used to build the model.18 On the test set, the regression line of the observed‐versus‐predicted plot was very close to the first bisector. If piCa was systematically higher or lower than miCa (fixed bias), the intercept of the regression line would have been significantly different from 0. If piCa tended to overestimate or underestimate miCa as miCa increased (proportional bias), the slope of the regression line would have been significantly different from 1. According to our results, the intercept (−0.06; 95% CI, −0.15 to 0.02) and the slope (1.05; 95% CI, 0.98–1.13) of the regression line were not significantly different from 0 and 1, respectively. Furthermore, piCa was strongly to very strongly correlated with miCa.19 However, a difference was still identified between piCa and miCa (average, 0.08 mmol/L). Although this difference was small, it might affect piCa diagnostic ability. To enhance its diagnostic performance, a PI was developed, which may help distinguish hypocalcemia and hypercalcemia. For hypocalcemia, the NPV of the lower end of the PI was approximately 98%, allowing exclusion of hypocalcemia if the lower end of the PI is >1.11 mmol/L. On the other end, an upper end of the PI <1.11 mmol/L was associated with 100% PPV, allowing a certain diagnosis of hypocalcemia. Likewise, for hypercalcemia, finding an upper end of the PI <1.37 mmol/L allows exclusion of hypercalcemia, whereas a lower end of the PI >1.37 mmol/L is diagnostic for hypercalcemia with 100% certainty. These predictive values may vary with prevalence, and these results should be interpreted with caution in subpopulations of dogs where the prevalence of hypocalcemia and hypercalcemia is different.20

The PPV of tCa was mild to moderate, which means that use of tCa to diagnose a calcium disorder may be misleading. This observation is in agreement with previous studies and justifies verification when tCa is abnormal using another estimator of calcium homeostasis.7, 8 Correcting tCa with either serum albumin or total protein concentration resulted in poorer PPV and PDLR, which means that use of corrected tCa increased diagnostic discordance with regard to true calcium status and therefore cannot be recommended. This conclusion is also in accordance with another study.7 Predicted ionized calcium concentration was better correlated with miCa than with tCa and corrected tCa formulas, and its overall diagnostic performance, as assessed by the AUC of the ROC curve, was better for both hypocalcemia and hypercalcemia. In particular, piCa had much higher PPV for diagnosis of hypocalcemia, as piCa < 1.11 mmol/L was associated with a 70% chance of true hypocalcemia, as opposed to less than 50% when corrected or uncorrected tCa was used. Although a PPV of 70% remains moderate, it is 1.5 times higher than the PPV of tCa. For hypercalcemia, PPV of piCa also was much higher than those of tCa and the corrected tCa formulas, with 90% chance of true hypercalcemia when piCa > 1.37 mmol/L. This finding was corroborated by the very high PDLR of piCa. Nonetheless, diagnostic discordance was low for piCa and tCa. This low diagnostic discordance of tCa may be because almost 80% of dogs in our study had normal miCa, compared with only 50% of dogs in a previous study, where diagnostic discordance of tCa was 27%.7 Comparing the diagnostic discordances of piCa and tCa in a population of dogs with a higher proportion of abnormal miCa therefore is warranted to definitively confirm the superiority of piCa over tCa to properly classify dogs according to their calcium status. Still, these results suggest that piCa might be the most appropriate marker to verify a calcium disorder when tCa is abnormal and miCa is not available. However, miCa must still be preferred, if available, to avoid misclassification.

The MARS model also was able to provide valuable information on the relationship between biochemical variables and miCa. Total calcium and albumin concentration both had a large influence on ionized calcium concentration, which was expected due to ionized calcium being the major fraction of tCa and albumin being the main molecule that binds calcium.1, 21 Chloride was the second most influential variable on ionized calcium concentration. Overall, miCa steadily increases as chloride increases. The fact that hyperchloremia directly increases plasma ionized calcium is consistent with a previous study performed in cows in which IV administration of CaCl₂ resulted in higher plasma ionized calcium concentrations than when the same dose of calcium was administered in a calcium gluconate formulation.22 The physiologic explanation for this relationship is unclear. Increase in plasma chloride concentration is associated with a change in blood pH. The most likely sites for calcium binding on albumin are free carboxyl groups that become available for binding with increased pH.23 However, no significant correlation was observed between pH and miCa in a study of dogs with chronic kidney disease.8 Also, the lack of contribution of bicarbonate to piCa in our study and in a previous study13 suggests that the influence of chloride on miCa may not be mediated through a change in blood pH alone. A direct change of plasma ionized calcium concentration in response to an increase in plasma chloride concentration may be possible, presumably because the additional chloride displaces calcium that is bound to albumin. Another explanation could be that miCa varies along with other plasma ions to maintain blood electroneutrality. Indeed, according to our results, miCa consistently increases with an increase in anion concentration (phosphorus and chloride) and decreases when cation concentration increases (sodium and potassium).

The moderate influence of age on calcium may be related to skeletal maturation. Higher ionized calcium concentration values have been documented in puppies as compared to adults.24 The moderate influence of ALP also could be related to skeletal remodeling associated with aging or bone diseases, especially given that other liver function test results were not significantly influential on miCa. Serum creatinine concentration had a moderate effect on calcium, and miCa decreased as serum creatinine concentration increased to 5 mg/dL, where it no longer had an effect on miCa. The relationship between renal disease and calcium disorders has been studied thoroughly, and hypocalcemia occurs commonly in patients with renal disease as a consequence of decreased renal calcitriol synthesis and phosphorus retention.8, 25 It is surprising however that serum creatinine concentration was no longer influential above 5 mg/dL, although ionized calcium concentration previously was shown to become significantly lower in dogs with chronic kidney disease only when IRIS stage 4 is reached.25 These results suggest that lower plasma ionized calcium concentration in IRIS stage 4 chronic kidney disease in dogs may be preferable to other factors such as increased serum potassium concentrations rather than directly from the decrease in kidney function.26, 27, 28 Interestingly, BUN did not significantly influence ionized calcium concentration, perhaps because BUN is a less specific indicator of decreasing renal function.29 In accordance with previous findings, increasing concentration of sodium were associated with decreasing miCa.30 This association may be explained by sodium‐induced conformational change in albumin.30 Alternatively, such a relationship might be necessary to maintain serum electroneutrality.

Phosphorus had little influence on miCa. This observation is consistent with the slight negative correlation that previously has been reported between miCa and serum phosphorus concentration in dogs and the fact that serum phosphorus concentration cannot be used to predict complexed calcium status.8, 31 Lastly, fatty acids have been demonstrated to induce a conformational change in albumin, which increases its affinity for calcium.32 Alternatively, the influence of triglycerides on miCa may be due to the association between hypertriglyceridemia and pancreatitis in dogs, as hypocalcemia can occur with peripancreatic fat saponification.33 These numerous relationships illustrate how complex prediction of ionized calcium concentration is and help explain why adjustment of tCa solely on albumin or total protein concentration is inefficient and should no longer be employed.

There were several limitations to our study. First, due to its retrospective nature, some records were incomplete and there was inconsistent reporting of some of the data. It is possible that some patients were on unrecorded medications that could influence calcium or other biochemical variables or had an unrecorded condition that also could alter calcium homeostasis. Second, dogs included between February and August 2010 had a biochemistry profile that was obtained with a different analyzer than the other dogs included in the study. This subset represented 3% and 4% of the training and test sets, respectively. Although the different analyzers were unlikely to have the exact same reference intervals and measurements, the directions toward which the biochemistry results tended to change were likely similar for both analyzers. The way our MARS model was selected, based on cross‐validation statistics, allowed it to capture the underlying reproducible structure in the data in order to sense how changes in biochemistry variables influence the ionized fraction of calcium rather than trying to stringently fit a specific biochemistry result with a particular miCa value.34 Therefore, it is unlikely that the use of 2 different biochemistry analyzers negatively impacted our model accuracy. Third, proper sample collection and handling cannot be guaranteed because of the retrospective aspect of case recruitment. However, pre‐analytical methodology for ionized calcium measurement is standardized in our hospital. Ionized calcium measurement requires anaerobic sample handling, as air exposure may result in a substantial decrease in miCa.4 This analytical error is likely due to loss of CO₂ which increases sample pH.10 Our sample handling methodology required some limited air exposure, because the tubes must be opened at the time of sample analysis. However, no significant change in pCO₂ has been reported previously with the use of single sampled plastic lithium heparin screw‐top tubes.35 This finding was reflected in our study by the fact that the 10, 50, and 90% percentiles of sample pCO₂ were within the reference range, as were the 10, 50, and 90% percentiles of sample pH. Fourth, there were specific variables, such as magnesium, that were not included in the model that could also potentially influence calcium. Interestingly, both deficiencies and excesses of magnesium have been shown to directly influence calcium by a variety of mechanisms, including decreased parathyroid hormone secretion and subsequent decrease in vitamin D activation, and by causing resistance in the kidney and bone to parathyroid hormone, all contributing to hypocalcemia.36, 37, 38, 39 Treatment of hypomagnesemia has been shown to increase serum calcium concentration in people and dogs.36, 40, 41 Inclusion of other predictors such as magnesium concentrations could have increased our model performance. However, the restriction to utilize only those biochemical variables that are routinely available was maintained in order for the model to be usable by most veterinarians. Finally, the model was developed using primarily normocalcemic dogs, with a low percentage of dogs having diseases that substantially impacted calcium metabolism. This design could negatively impact the performance of our model in patients with calcium disorders. Therefore, it remains necessary to evaluate piCa accuracy specifically in dogs with hypocalcemia and hypercalcemia, and with diseases influencing calcium metabolism, such as renal failure.

In conclusion, a novel formula was developed that allows for calculation of piCa from readily available biochemical and patient variables. This piCa can be clinically useful in assessing calcium disorders in dogs when miCa is not available. The piCa is a more reliable measure of calcium homeostasis than tCa based on the improved PPV for both hypercalcemia and hypocalcemia. The most influential factors associated with miCa variation were tCa, chloride, and albumin. External validation, which implies testing the model on different populations of dogs and patients from other institutions and using different chemistry analyzers, remains warranted to assure generalizability of these results.

Appendix 1.

Biochemistry profile of a 10.2‐year‐old 40.5‐kg neutered male Greyhound dog:

Creatinine (mg/dL)	Albumin (g/dL)	Total calcium (mg/dL)	Phosphorus (mg/dL)	Sodium (mmol/L)	Potassium (mmol/L)	Chloride (mmol/L)	ALP (U/L)	Triglycerides (mg/dL)
4.2	2.7	8.9	8.8	137	5.9	100	41	130

The MARS model can be used to obtain the predicted ionized calcium. Each hinge function is calculated first. Hinge functions are under the form: h(x–t) or h(t–x). If (x–t) or (t–x) is 0 or negative, the hinge function equals 0. If (x–t) or (t–x) is positive, the hinge function equals (x–t) or (t–x), respectively. The coefficients are then applied to each hinge function. Predicted ionized calcium is finally obtained by summing all the products of the hinge functions and their coefficient and the intercept of the model:

Hinge function of the predictors	Value of the hinge function	Coefficient	Product of the hinge function and its coefficient
(Intercept)	–	1.05189701	1.05189701
h (5 – creatinine)	h(5–4.2) = 0.8	0.01707569	0.8 * 0.01707569 = 0.01
h (3.3 – albumin)	h(3.3–2.7) = 0.6	0.01479586	0.6 * 0.01479586 = 0.01
h (albumin – 3.3)	h(2.7–3.3) = 0	−0.08887935	0 * (−0.08887935) = 0
h (7.5 – total calcium)	h(7.5–8.9) = 0	−0.12828575	0 * (−0.12828575) = 0
h (total calcium – 7.5)	h(8.9–7.5) = 1.4	0.04954995	1.4 * 0.04954995 = 0.07
h (total calcium – 9.9)	h(8.9–9.9) = 0	0.03339810	0 * 0.03339810 = 0
h (4.9 – phosphorus)	h(4.9–8.8) = 0	−0.01079317	0 * (−0.01079317) = 0
h (154 – sodium)	h(154–137) = 17	0.00371181	17 * 0.00371181 = 0.06
h (potassium – 5.1)	h(5.9–5.1) = 0.8	−0.03410317	0.8 * (−0.03410317) = −0.03
h (111 – chloride)	h(111–100) = 11	−0.00672129	11 * (−0.00672129) = −0.07
h (chloride – 111)	h(100–111) = 0	0.00390011	0 * 0.00390011 = 0
h (848 – ALP)	h(848–41) = 807	−0.00003635	807 * (−0.00003635) = −0.03
h (582 – triglycerides)	h(582–130) = 452	−0.00005582	452 * (−0.00005582) = −0.02
h (triglycerides – 582)	h(130–582) = 0	−0.00002793	0 * (−0.00002793) = 0
h (2.27 – age)	h(2.27–10.2) = 0	0.02851557	0 * (0.02851557) = 0
		piCa ± 2*regression standard error	1.05 mmol/L [0.91–1.19]

Bolded values in the “Value of the hinge function” column represent patient's values. piCa, predicted ionized calcium.

Although total calcium was within the reference range (tCa = 8.9 mg/dL; RR: 7.6–11.4), predicted ionized calcium classified the patient as hypocalcemic (piCa = 1.05; RR: 1.11–1.37). However, the clinician should consider the possibility that the ionized calcium could be in the low reference range based on the prediction interval (0.91–1.19 mmol/L). Measured ionized calcium also classified this patient as hypocalcemic (miCa = 1.06 mmol/L, RR: 1.11–1.37).