Are Major Behavioral and Sociodemographic Risk Factors for Mortality Additive or Multiplicative in Their Effects?

Abstract

All individuals are subject to multiple risk factors for mortality. In this paper, we consider the nature of interactions between certain major sociodemographic and behavioral risk factors associated with all-cause mortality in the United States. We develop the formal logic pertaining to two forms of interaction between risk factors, additive and multiplicative relations. We then consider the general circumstances in which additive or multiplicative relations might be expected. We argue that expectations about interactions among socio-demographic variables, and their relation to behavioral variables, have been stated in terms of additivity. However, the statistical models typically used to estimate the relation between risk factors and mortality assume that risk factors act multiplicatively.

We examine empirically the nature of interactions among five major risk factors associated with all-cause mortality: smoking, obesity, race, sex, and educational attainment. Data were drawn from the cross-sectional NHANES III (1988–1994) and NHANES 1999–2010 surveys, linked to death records through December 31, 2011. Our analytic sample comprised 35,604 respondents and 5,369 deaths.

We find that obesity is additive with each of the remaining four variables. We speculate that its additivity is a reflection of the fact that obese status is generally achieved later in life. For all pairings of socio-demographic variables, risks are multiplicative. For survival chances, it is much more dangerous to be poorly educated if you are black or if you are male. And it is much riskier to be a male if you are black. These traits, established at birth or during childhood, literally result in deadly combinations.

We conclude that the identification of interactions among risk factors can cast valuable light on the nature of the process being studied. It also has public health implications by identifying especially vulnerable groups and by properly identifying the proportion of deaths attributable to a risk factor.

Introduction

All individuals are subject to multiple risk factors for mortality at any given time. These risk factors may interact with one another in a variety of ways that contribute to one’s risk of dying. In this paper, we consider the nature of interactions between certain major risk factors associated with all-cause mortality. We focus on two forms of interaction between risk factors, additive and multiplicative relations. We then consider the circumstances in which additive or multiplicative relations might be expected. In an exploratory analysis, we examine the nature of interactions between certain major behavioral and sociodemographic risk factors associated with all-cause mortality among middle-aged and older Americans. We explicitly ask whether the risks are additive in their effects, multiplicative, or whether they interact in some other fashion. Our principal goal is to highlight the importance of this often neglected issue in interpreting data on mortality.

Background

In studies of mortality, researchers often consider multiple risk factors jointly in statistical models. The risk factors assessed take a wide variety of forms including those that are demographic, behavioral, biological, or environmental in nature. It is not unusual to include risk factors that are drawn from two or more of these different domains. For example, studies of behavioral risk factors such as smoking often control for socio-demographic attributes such as sex and social class. Cox hazard models or logistic regression models are most often implemented to investigate these multivariate processes. Such models typically make the assumption that risk factors are multiplicative in their effects (Andersson et al., 2005). Rarely is this assumption tested or even acknowledged.

We believe that the identification of the nature of interactions among risk factors can cast valuable light on the nature of the process being studied. It may also have public health implications by identifying especially vulnerable groups and by properly identifying the proportion of deaths attributable to a risk factor.

The terminology for considering statistical interactions between variables is somewhat unsettled. Here we follow the terminology and concepts employed in an extensive review paper by VanderWelle and Knol (2014). Many forms of interaction might exist between variables, each of them expressible mathematically. We focus in this paper on the two simplest forms of interaction, those typically termed “additive” and “multiplicative”. What we mean by these terms is best illustrated algebraically. We develop an example using two major risk factors, smoking and obesity, which are treated as dichotomous variables.

Notation

• µ^ŌS̄ = Death rate of non-obese, non-smokers

• µ^OS̄ = Death rate of obese non-smokers

• µ^ŌS = Death rate of non-obese smokers

• µ^OS = Death rate of obese smokers

The relative risk of death from obesity among non-smokers is k, so that

$${\mu }^{O\overline{S}}=k{\mu }^{\overline{O}\overline{S}}$$

The relative risk of death from smoking among the non-obese is j, so that

$${\mu }^{\overline{O}S}=j{\mu }^{\overline{O}\overline{S}}$$

If the risks of death associated with obesity and smoking are additive, then

$${\mu }^{OS}={\mu }^{\overline{O}\overline{S}}+(k{\mu }^{\overline{O}\overline{S}}-{\mu }^{\overline{O}\overline{S}})+(j{\mu }^{\overline{O}\overline{S}}-{\mu }^{\overline{O}\overline{S}})={\mu }^{\overline{O}\overline{S}}(k+j-1)$$

Dividing all death rates by the death rate of non-obese non-smokers, µ^ŌS̄, produces the set of relative risks shown in Table 1a (following page). Observed values less than (j+k−1) in the upper left hand quadrant would be described as sub-additive and values larger than that value would be described as super-additive.

Table 1.

Relative Risks of Death Classified by Smoking and Obesity Status

a) Additive				b) Multiplicative
		Smoking				Smoking
		Yes	No			Yes	No
Obese	Yes	j+k−1	k	Obese	Yes	jk	k
	No	j	1		No	j	1

If, on the other hand, the risks are multiplicative, then the value in the upper left quadrant would simply be jk, as shown in Table 1b (following page). Values greater than jk would be considered super-multiplicative and values below jk would be considered sub-multiplicative.

The nature of interactions has direct implications for relative risks. If interactions are multiplicative, then the relative risk of death from one exposure is the same for different values of the other exposure (k in the case of obesity in Table lb). If interactions are additive, then the relative risks of death from one exposure will depend on the value of the other exposure [k vs. (j+k−1)/j]. k will be greater than (j+k−1)/j as long as k and j are both greater than 1.00. In other words, if additivity prevails, then the relative risk of death associated with obesity will be lower among smokers than among non-smokers. Under additivity, smokers and non-smokers would be equally “vulnerable” or “susceptible” to the effects of obesity, in the sense that being obese adds the same incremental risk of death in the two groups.

If the relative risk of death associated with obesity for smokers is between (j+k−1)/j and k, then the risks are between additive and multiplicative (i.e., they are super-additive and sub-multiplicative). In these cases it is reasonable to describe smokers as more vulnerable to the hazards of obesity than non-smokers despite the fact that their relative risks of death associated with obesity are lower. Two risks are sometimes described as “synergistic” when the presence of one exposure increases the relative risk associated with the other exposure, even when their joint effect may be sub-multiplicative.

VanderWeele and Knol (2014) refer to the relations defined above as pertaining to interactions “on an additive scale”. An alternative approach is to consider interactions “on a multiplicative scale”. In effect, interactions are considered using the logarithm of risks rather than the risks themselves. Additivity in the logarithms “on the multiplicative scale” translates into multiplicativity of risks “on the additive scale”. VanderWeele and Knol (2014) advocate using an additive scale because of its greater relevance to efforts to improve public health. We prefer it as well for its conceptual clarity. When risks are additive on the additive scale, exposures affect outcomes independently of one another; the impact of one exposure on mortality does not depend on the level of the other exposure. No such test of independence is available on the multiplicative scale.

The statistical methods for the assessment of interactions are well developed (Berrington de González and Cox, 2005; Greenland, 2009). Testing for departures from the multiplicative interactions assumed in logistic regressions or hazard models is straightforward; one needs simply to create and test the significance of a product variable. Li and Chambless (2007) have provided procedures and programming code for testing for the significance of additive interactions in hazard models. Hosmer and Lemenshow (1992) provide significance tests for additive models when logistic regression is used.

The theoretical underpinnings of the concepts are not as clear as the statistical methods for evaluating their strength. What circumstances are expected to produce additive or multiplicative relationships between two risk factors? We provide some preliminary ideas about this issue, partly based on a variety of approaches that have appeared in the literature on mortality and disease incidence.

Additivity

We expect that risk factors will be additive in their effects when they pertain to different, unrelated, disease or injury processes. For example, the excess mortality rates of men engaged in trench warfare should be additive to those of smoking; there is no reason to expect smokers to be more or less protected from the hazards of battle than non-smokers. Using this reasoning, the all-cause mortality risks associated with asbestos exposure should be approximately additive to those of obesity since the risks primarily manifest themselves in different disease processes.

Super-additive relations are more likely to pertain when two risk factors are associated with the same disease process or organ system. For example, damage done to an organ by one exposure could render the organ more vulnerable to damage by another exposure. Asbestos exposure and smoking both affect the risk of developing lung cancer and one exposure can be expected to increase the lung’s susceptibility to the other exposure. Relations between these exposures in the risk of developing lung cancer have often been shown to be super-additive (e.g., Lee, 2001).

Super-additive relations are often observed when genes and environments interact. For example, the risk of skin cancer is greater when lighter-skinned people are exposed to sunlight than when darker-skinned people are exposed. But Kendler and Gardner (2010) caution that there is rarely a straightforward translation from biological or physiological interactions to interactions in a statistical sense. Probably the clearest predictions arise when both exposures are required for a particular outcome. The development of phenylketonuria requires both a genetic variant (phenylalanine hydoxylase deficiency) and an environmental exposure (dietary phenylalanine) (Ahlbom and Alfredsson, 2005). All of the excess risk occurs in the cell in which both exposures are present.

Multiplicativity

When should strictly multiplicative relations be expected? One example occurs when the two risks apply to different stages in a Markov-like causal chain. Suppose that smoking triples the risk of developing influenza and that blacks are twice as likely to die when they develop an infectious disease as whites because they receive poorer medical attention. Then it is reasonable to expect that the risk of dying from influenza will be six times greater for black smokers than for white non-smokers. Certain multistage models of carcinoma can also produce strictly multiplicative relations between risk factors (Siemiatycki and Thomas, 1981).

Apart from such staging, it is challenging to develop plausible relations that would produce strict multiplicativity. Nevertheless, multiplicative relations are often observed when formally investigated. For example, the relation between cigarette smoking and asbestos exposure in predicting the incidence of lung cancer is multiplicative (Lee, 2001). For another example, a large cohort study of 700,000 individuals found that the incidence of diabetes, stroke, and myocardial infarction, all having a primary target of the cardiovascular system, were multiplicative in their effects on mortality (Emerging Risk Factors Collaboration, 2015).

Approaches in sociology and social epidemiology

Expectations about interactions among socio-demographic variables, and their relation to behavioral variables, have been stated in terms of additivity (yes/no) rather than multiplicativity. A perspective within sociology and social epidemiology referred to as “intersectionality” has focused attention on potential interactions among risk factors, especially those related to socioeconomic disadvantage. It is explicitly “not an additive approach” that estimates the collective impact of class, gender, and race as the sum of independent effects (Hankivsky, 2012). While this literature appears to anticipate super-additive relations, it explicitly does not make predictions about the direction or intensity of interactions (Bowleg, 2012).

Several more precise hypotheses about relations among sociodemographic variables as predictors of mortality have been offered. Hayward, Hummer, and Sasson (2015) argue that the effects of years of schooling on mortality should be greater among men than among women and among whites than non-whites. The suggested reason is that males and whites are in advantaged structural positions in society that facilitate the transformation of higher education into longevity benefits. A similar hypothesis is offered by Williams (1997, 1996). He suggests that blacks are less likely to transform socioeconomic resources, including better education, into good health because those resources are themselves degraded by racism or, in the case of schools, poor quality. These hypotheses predict that relations among sociodemographic risk factors are super-additive.

Pampel and Rogers (2004) usefully summarize hypotheses about the relations among socioeconomic and behavioral risk factors. These fall into two clusters. In one cluster, an additional behavioral exposure is expected to be less harmful among people of lower social standing because they are already beset with many hazards; new hazards are in a sense at least partially redundant, and relations between risk factors are expected to be sub-additive. In the other cluster, an additional exposure is considered more harmful because it can push a very vulnerable individual over the brink to death; each threat makes another threat more serious, so that relations among risk factors are super-additive.

We believe that theory is, in general, weak about whether interactions should be expected to be additive, multiplicative, or something else (Kendler and Gardner, 2010). More often than not, researchers do not address the issue in specific applications; the most common default option is an assumption of multiplicativity (i.e., additivity in the logarithms of the variables) because a Cox model or logistic regression is employed in the analysis. We propose to map the landscape of relations among certain major sociodemographic and behavioral variables in search of empirical regularities that might help guide these expectations in the future.

Data and Methods

We examined interactions between pairs of risk factors for mortality. We considered all pairings formed among five yes/no dichotomous variables: ever smoker; ever obese; black; male; and low educational attainment (defined by not having a high school degree or GED). The first two variables are related to behavior and the last three are socio-demographic in nature. Data were drawn from the cross-sectional NHANES III (1988–1994) and NHANES 1999–2010 surveys. Each survey was prospectively linked to death records contained in the National Death Index. We used death linkages through December 31, 2011, the latest linkages available. From the pooled samples, we constructed a person-year file and included in our analysis exposures occurring at attained ages 40–84. Respondents who were aged 25–84 at time of survey were eligible to be in the analysis. For individuals less than age 40 at time of survey, we censored exposures occurring prior to age 40. Individuals were censored from the analysis at their age on December 31, 2011 if they survived the follow-up period or at age 85 if they reached that age. Our analytic sample comprised 35,604 respondents who contributed 319,828 person-years of exposure and 5,369 deaths.

All five dichotomous risk factor variables were constructed from respondent reports. Ever smokers were those who reported current or former cigarette smoking. Ever obesity was defined as having had a body mass index (BMI) of 35.0 kg/m² or greater at some time in life up until or including the time of survey. The obesity variable was constructed by combining reported maximum lifetime body weight with clinically-measured height taken at time of survey. Women were asked to exclude times when pregnant in answering the question about maximum weight. A BMI of 35.0 or higher was defined as moderate or severe obesity by the World Health Organization. Table 2 shows the distribution of risk factors in our data (end of document).

Table 2.

Descriptive characteristics

	Percentage (unless otherwise noted)
Risk Factors, %
Behavioral
Ever Obese	19.6 (19.1, 20.0)
Ever Smoke	51.9 (51.4, 52.5)
Socio-demographic
Male	48.6 (48.0, 49.1)
Black	23.0 (22.6, 23.5)
Less HS	34.7 (34.1, 35.2)
Age at Exposure (mean, years)	59.0 (59.0, 59.1)
Sample Size (number)	36, 604
Exposure (person-years)	319,828
Deaths (number)	5,369

Note: Behavioral risk factor percentages pertain to risk factor status at time of survey (ages 25–84). Mean age pertains to age of mortality exposure over the follow-up period (1988–2011). 95% confidence intervals shown in parentheses.

Source: NHANES III (1988–1994) and NHANES 1999–2010

For all unique risk factor pairs, ten in all, we estimated death rates (deaths/person-years of exposure) in each cell of a 2×2 cross-classification of the risk factors as illustrated in Table 1. Death rates were age-standardized to the 2010 U.S. age distribution using 5-year age intervals (40–44 to 80–84). We calculated the relative risks of death pertaining to each cell using the age-standardized death rates. The reference category for the relative risks was the category that reflected the absence of both risk factors (e.g., no/no).

We were primarily interested in evaluating whether the observed relative risk in the yes/yes cell conforms to an additive or multiplicative interaction as defined above. This evaluation was conducted by testing the observed relative risk in the yes/yes category with two predicted relative risks: the first based on the assumption of an additive interaction and the second based on the assumption of a multiplicative interaction. Our sample was well powered to detect for differences on both scales: >95% power in all instances (calculated using a procedure and code provided by VanderWeele, 2012). F statistics based on the Wald test were used to assess statistical significance (Judge, 1985). All analyses were conducted using Stata 12.

Results

Table 3 presents the main results of this analysis. The left-hand column shows the pair of risk factors being considered in a particular row. The two right-hand most columns show p-values for the statistical test between the observed and predicted interactions. In all ten pairings, the observed relative risk was significantly different from one predicted relative risk at a p-value of 0.10 and statistically indistinguishable from the other. We underline the p-values where the difference was indistinguishable, i.e., the prediction to which the observed value better conforms. Note that confidence intervals for additive and multiplicative relationships in Table 3 usually overlap. However, in each instance the difference between the additive and multiplicative prediction is statistically significant (p<.05; based on F tests). If the observed interaction were to fall in the overlapping range, it would not be possible to distinguish statistically between additive and multiplicative relations. However, none of the ten sets of observed results that we present fall into a range in which the additive and multiplicative confidence intervals overlap.

Table 3.

Estimated and predicted relative risks (RRs) for pairs of risk factor combinations

Risk Factor Pairs	RR 1: (yes/no)	RR 2: (no/yes)	Additive RR Prediction (yes/yes)	Multiplicative RR Prediction (yes/yes)	Observed RR (yes/yes)	P-value: Additive	P-value: Multiplicative
Behavioral
Ever Obese - Ever Smoke	1.78	2.02	2.80	3.60	2.89	0.548	0.004
	(1.59, 1.97)	(1.88, 2.16)	(2.52, 3.08)	(3.05, 4.14)	(2.62, 3.15)
Socio-demographic
Male - Black	1.50	1.50	2.00	2.25	2.33	0.002	0.557
	(1.40, 1.60)	(1.36, 1.64)	(1.80, 2.20)	(1.94, 2.55)	(2.13, 2.53)
Male - Less HS	1.49	1.49	1.99	2.23	2.21	0.014	0.866
	(1.38, 1.61)	(1.36, 1.63)	(1.77, 2.20)	(1.91, 2.55)	(2.03, 2.38)
Black - Less HS	1.46	1.47	1.93	2.14	2.18	0.017	0.768
	(1.33, 1.59)	(1.37, 1.57)	(1.74, 2.12)	(1.87, 2.42)	(2.00, 2.37)
Socio-demographi c and Behavioral
Male - Ever Obese	1.62	1.71	2.33	2.77	2.35	0.874	0.019
	(1.52, 1.73)	(1.55, 1.87)	(2.11, 2.55)	(2.40, 3.14)	(2.12, 2.58)
Less HS - Ever Obese	1.52	1.56	2.09	2.38	2.07	0.914	0.051
	(1.42, 1.62)	(1.42, 1.71)	(1.89, 2.29)	(2.07, 2.69)	(1.88, 2.27)
Black - Ever Obese	1.57	1.57	2.15	2.47	1.92	0.068	0.001
	(1.46, 1.68)	(1.45, 1.70)	(1.96, 2.33)	(2.18, 2.77)	(1.72, 2.12)
Male - Ever Smoker	1.24	1.68	1.92	2.08	2.25	0.000	0.191
	(1.12, 1.37)	(1.54, 1.82)	(1.69, 2.15)	(1.75, 2.41)	(2.09, 2.42)
Less HS - Ever Smoker	1.66	2.03	2.69	3.37	2.81	0.250	0.010
	(1.50, 1.83)	(1.86, 2.19)	(2.39, 2.99)	(2.82, 3.92)	(2.58, 3.05)
Black - Ever Smoker	1.54	1.88	2.42	2.89	2.79	0.002	0.589
	(1.38, 1.70)	(1.75, 2.01)	(2.16, 2.67)	(2.45, 3.33)	(2.55, 3.03)

Note: The reference category for all relative risks (RRs) is the absence of both risk factors (no/no). RR 1 pertains to the presence of only the first listed risk factor (yes/no). RR 2 pertains to the presence of only the second listed risk factor (no/yes). Observed RR (yes/yes) pertains to the presence of both risk factors (yes/yes). 95% confidence intervals shown in parenthesis.

Source: NHANES III (1988–1994) and NHANES 1999–2010

We explicate the results in Table 3 using the example of obesity and smoking. The reference category for the mortality rates is someone who never smoked and was never obese. The relative risk of 1.78 refers to the relative risk of death for a never smoker who was ever-obese. The value of 2.02 refers to the relative risk of dying for an ever smoker who was never obese. If the risks of obesity and smoking were additive, the relative risk for a person who has smoked and been obese would be 2.80. If risks were multiplicative, the relative risk for such a person would be 3.60. The actual value for such a person is 2.89, close to the value of 2.80 predicted by an additive model. The significance test value for the additive model of 0.548 shows that the actual value is not significantly different from that predicted by an additive model. The significance value of 0.004 shows that the outcome is very different from that predicted by a multiplicative model.

We conclude that smoking and obesity are additive in their effects. Having been a smoker does not increase the risks associated with obesity; basically, obesity adds the same incremental risk of death for a smoker and a non-smoker. Similarly, being obese does not increase the risks associated with smoking. The morbid processes associated with obesity and smoking appear to be operating independently of one another. Such a conclusion is consistent with other research. Studies using hazard models to investigate the effects of obesity and smoking on mortality have concluded that the relative risks associated with obesity are lower among smokers than among non-smokers or never-smokers (Calle et al., 1999; Koster et al., 2008; Ma et al., 2013; van Dam et al., 2008). Such results are consistent with relations between the exposures being sub-multiplicative although these studies have not explicitly investigated additivity or multiplicativity.

Results are quite different within the set of socio-demographic variables. For all pairings of sex, race, and educational attainment, risks are multiplicative. For survival chances, it is much more dangerous to be poorly educated if you are black or if you are male. And it is much riskier to be a male if you are black. These traits literally result in deadly combinations; each additional exposure multiplies the risk associated with another exposure. Of the combinations within this category, the relative risk of death is highest for black males (2.33), where results are super-multiplicative, although not significantly different from multiplicative. The black/male relation is the only one considered here that can be compared to the equivalent relation in national vital statistics, which supply detail on race and sex. Based on age-standardized death rates for all ages combined, the relation between risks for males and blacks was also super-multiplicative in 2011 (compiled from Hoyert et al., 2012; Table 1).

We find that the relation between being black and poorly educated is multiplicative; each characteristic multiplies the survival disadvantages of the other. This finding is consistent with the super-additive hypotheses of Williams (1997, 1996) and Hayward et al. (2015). Hayward et al. (2000) claim to find evidence that is inconsistent with Williams’ hypothesis. They test for interactions between race and a variety of socioeconomic variables, including education, as predictors of the incidence of many diseases. Using a hazards model, they find no significant interactions between these variables. But that result implies that the relation between race and education is in fact multiplicative in the sense that we have defined multiplicativity at the outset of this paper; blacks, with higher mortality to begin with, suffer more than whites as a result of low educational attainment.

Table 3 shows that relations between socio-demographic variables and behavioral variables are a mixture of additive and multiplicative. All relations involving obesity are additive. In all cases, obesity adds substantially to the risk of death, but it doesn’t exaggerate the risk of death associated with being black, poorly educated, or male. Essentially, it acts independently of these other risk factors.

When risks are additive, relative risks from one exposure (e.g., obesity) will be lower among those subject to the other exposure (e.g., smoking). Two large studies of the relation between obesity and mortality among black Americans compared their results to a meta-analysis conducted among whites (Berrington de Gonzalez et al., 2010). Consistent with our results, one study of pooled data concluded that the risks associated with obesity were lower among blacks than whites (Cohen et al., 2014). The other study, (Cohen et al., 2014), using data from the Black Women’s Health Study, reported that hazard ratios were “similar in magnitude” to those among white women (Boggs et al., 2011). However, a comparison of data presented in the two articles shows that hazard ratios for obese class I, II, and III are all lower among black women than white women (Figure 1 in Berrington de Gonzalez et al., 2010 and Boggs et al., 2011). Also consistent with our results, the pooled analysis demonstrated that hazard ratios for obesity were much lower among poorly-educated individuals than better-educated individuals (Cohen et al., 2014).

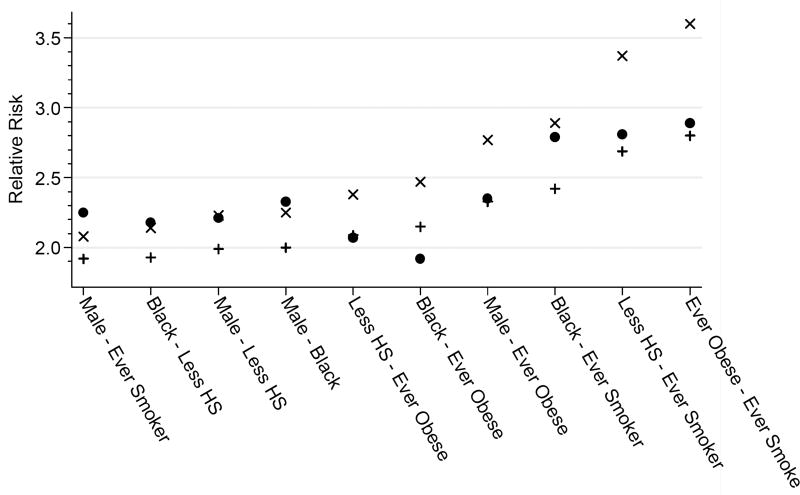
Figure 1. Observed, predicted additive, and predicted multiplicative relative risks for risk factor pairs.

Note: Circles indicate the observed relative risk for the presence of both risk factors (yes/yes). Pluses indicate the additive prediction and Xs indicate the multiplicative prediction, both pertaining the presence of both risk factors (yes/yes).

Smoking, on the other hand, is multiplicative with sex and race. One reason for this result may be that male and black smokers have smoked more intensively or for longer periods than their non-black and female smoking counterparts. Ho and Elo (2013) attribute the higher risk of death observed among black male smokers compared to white male smokers to a longer average duration of smoking among blacks. Mehta and Preston (2012) show that male current smokers have a longer duration and greater intensity of smoking than female current smokers; a comparable sex difference also exists among former smokers.

Our results indicate that smoking is multiplicative with being black or male. In apparent contrast, Pampel and Rogers (2004) conclude that mortality risks of smoking are “additive” with those of being black or male. However, their conclusion is based on the absence of interaction between smoking and the other variables in a Cox hazard model. They are using a multiplicative rather than an additive scale so that their results are additive in the logs and multiplicative on an additive scale. Their results are thus consistent with our finding of multiplicativity on an additive scale.

Figure 1 plots the data shown in Table 3 by risk factor combination, ordered from the lowest multiplicative prediction on the left to the highest on the right. Across all combinations, the three highest relative risks all include smoking as one of the risks. This outcome is primarily a result of the high relative risk of smoking itself rather than of its synergy with other risks. Across all pairs, the highest relative risk for any combined category pertains to smoking and obesity, despite the fact that individual risks in this combination are strictly additive.

Discussion

We have considered the relation between all possible pairs of five risk factors associated with mortality. For each of the 10 pairs considered, the effect on mortality is either significantly additive or significantly multiplicative. No pair demonstrates a relationship that is insignificant on both tests or significant on both; all relations are either additive or multiplicative.

We have examined the five variables as dichotomies. More complicated forms (e.g., continuous or multi-categorical) are available for three of the variables and use of these forms may produce different results. Preston et al. (2015) show that a continuous BMI variable produces predictions of mortality that are less biased by measurement error than BMI expressed categorically. Dichotomies and categories, however, dominate the epidemiologic literature, in part because of their interpretability (Turner et al., 2010). In studying the relation between two variables, we have not controlled other variables except age. Results in the literature that we cite that use more complex multivariate statistical models are consistent with our results, but we have not done an exhaustive review of all such results. And in the interests of parsimony, we have not considered the possibility of three-way or higher-order interactions.

We demonstrate that the relation between our two behavioral variables, smoking and obesity, is additive. The relations among our three sociodemographic variables are multiplicative. Between behavioral and sociodemographic variables, the relations are a mixture of additive and multiplicative.

Obesity is additive with each of the remaining four variables. We speculate that its additivity is a reflection of the fact that obese status is generally achieved later in life, so that it does not interact in important ways with other characteristics. Being male is determined prior to birth and being black is a status generally ascribed at birth; being poorly educated and an ever-smoker are generally achieved by age 20. In contrast, only 8.3% of individuals aged 25–29 were ever-obese in 1991, whereas 26.7% were ever-obese in an overlapping cohort at ages 45–49 in 2009–10 (compiled from NHANES III and NHANES Continuous). Thus, the fact that obesity is generally acquired in middle age might help to explain why obesity adds to the effects of previously fixed traits rather than magnifying them.

We showed earlier that additivity would produce relative risks that differed according to the category of other exposures. The additivity of obesity risks is a likely explanation of why relative risks of death associated with obesity are found to be lower among smokers, blacks, and poorly-educated people. Such differences in relative risks are generally labelled as examples of “effect modification”, but it is equally accurate and more informative to say that the risks of obesity are additive to, and therefore independent of, risks from smoking, being black or poorly educated. When risks are additive, it is incorrect to use the relative risks observed within one category of exposure as an estimate of the relative risks for the whole population. This error is made frequently in the literature on the mortality risks of obesity, which often takes estimates of the mortality risks of non-smokers to be appropriate for the whole population (e.g., Berrington de Gonzalez et al., 2010). Unfortunately, tests of additivity are rarely applied in epidemiology or sociology. Knol et al. (2009) reviewed 75 cohort or case-control studies in the most highly ranked epidemiological journals and found only one instance in which a measure of additive interaction was supplied.

It is intriguing that relations among being male, black, and poorly educated are multiplicative. We concluded earlier that it was difficult to develop plausible hypotheses that would predict strictly multiplicative relations. Nevertheless, multiplicativity is observed here and is often observed in other contexts. In contrast to obesity, which is typically developed in middle age, these three traits are established at birth or during childhood. They have many years to interact with one another, which may set the stage for one trait to magnify the effect of another. Evolutionary psychology offers one possible interpretation of why males are more susceptible to being black or poorly educated: the intense competition for status among males (designed to enhance their value as mates) is exaggerated among low-ranking males (Hampton, 2010). This competition is manifest in hugely disproportionate male-on-male homicide.

An accurate appraisal of the relation between risk factors can contribute to a better understanding of the process under investigation. It can also help identify appropriate targets for public health campaigns. If being obese is not synergistic with being black, male, poorly educated, or a smoker, broad population-based efforts to reduce obesity are potentially efficacious. On the other hand, if being a male or black multiplies the disadvantage of being a smoker, a public health effort targeting smoking may be advised to focus disproportionate efforts on groups that are most vulnerable to the habit.

When we refer to relations between risk factors, it should be clear that we are not referring to the joint distribution of risk factors but to their combined effects on mortality. In addition to relations among risk factors, the joint distribution of the factors would also matter for public health efforts, for example if blacks were more likely to smoke. It is also central to answering the common question of how much of sociodemographic differences in mortality are “explained by” differences in smoking, obesity, and other behavioral factors. The answer to this question is normally a function of differences in the distribution of behavioral factors across socioeconomic groups (e.g., Mehta et al., 2015; Nandi et al., 2014). However, differences in the responsiveness of various groups to behavioral factors should also be assessed in such an inquiry. This step is often omitted.

The proportion of deaths that would not have occurred in the absence of a particular exposure is commonly termed the population attributable fraction (PAF; Steenland and Armstrong, 2006). This fraction is a function of both the magnitude of relative risks and the distribution of the population across risk categories. When PAF is being calculated for two or more risk factors, it is important to recognize the nature of interaction between the factors. Given the same set of relative risks for each variable acting independently (j and k in Table 1), the overall PAF will be greater when risks are multiplicative than when they are additive (Benichou, 2007). Multiplicative or super-additive risks may even result in a situation in which the PAFs for each factor considered separately sum to more than 100% (Benichou, 2007). Although various fix-ups have been proposed to correct this apparent anomaly, it is simply a reflection of the fact that eliminating one exposure would help to disable some of the effect of the other.

Most multivariate studies of the relation between sociodemographic and behavioral risk factors and mortality do not consider the nature of interactions among risk factors. We have attempted to show that, in addition to properly specifying the relation between risk factors and mortality, identifying these interactions may cast light on the process being investigated. Furthermore, results of such inquiries may have public health implications. Whether or not an explicit inquiry is undertaken, it should be recognized that the models used to estimate associations between risk factors and mortality are making assumption about how risk factors combine. These assumptions are testable.

Research Highlights.

• 1)We map the nature of statistical interactions among pairs of behavioral and demographic risk factors for mortality.
• 2)Demographic factors operate multiplicatively. It is riskier to be poorly educated if you are black or male.
• 3)Obesity adds to but does not exaggerate risks associated with the other variables, including smoking.
• 4)Findings inform public health priorities, including procedures for calculating the proportion of deaths attributable to a risk factor.