Climbing fibers predict movement kinematics and performance errors

This article demonstrates that complex spike (CS) discharge of cerebellar Purkinje cells encodes multiple parameters of movement, including motor errors and kinematics. The CS firing is not driven by error or kinematic events; instead it provides a linear representation of each parameter. In contrast with the view that CSs carry feedback signals, the CSs are predominantly predictive of upcoming position errors and kinematics. Therefore, climbing fibers carry multiple and predictive signals for online motor control.

Abstract

Requisite for understanding cerebellar function is a complete characterization of the signals provided by complex spike (CS) discharge of Purkinje cells, the output neurons of the cerebellar cortex. Numerous studies have provided insights into CS function, with the most predominant view being that they are evoked by error events. However, several reports suggest that CSs encode other aspects of movements and do not always respond to errors or unexpected perturbations. Here, we evaluated CS firing during a pseudo-random manual tracking task in the monkey (Macaca mulatta). This task provides extensive coverage of the work space and relative independence of movement parameters, delivering a robust data set to assess the signals that activate climbing fibers. Using reverse correlation, we determined feedforward and feedback CSs firing probability maps with position, velocity, and acceleration, as well as position error, a measure of tracking performance. The direction and magnitude of the CS modulation were quantified using linear regression analysis. The major findings are that CSs significantly encode all three kinematic parameters and position error, with acceleration modulation particularly common. The modulation is not related to “events,” either for position error or kinematics. Instead, CSs are spatially tuned and provide a linear representation of each parameter evaluated. The CS modulation is largely predictive. Similar analyses show that the simple spike firing is modulated by the same parameters as the CSs. Therefore, CSs carry a broader array of signals than previously described and argue for climbing fiber input having a prominent role in online motor control.

NEW & NOTEWORTHY This article demonstrates that complex spike (CS) discharge of cerebellar Purkinje cells encodes multiple parameters of movement, including motor errors and kinematics. The CS firing is not driven by error or kinematic events; instead it provides a linear representation of each parameter. In contrast with the view that CSs carry feedback signals, the CSs are predominantly predictive of upcoming position errors and kinematics. Therefore, climbing fibers carry multiple and predictive signals for online motor control.

purkinje cells of the cerebellar cortex receive two main inputs, climbing fibers, and parallel fibers (Eccles et al. 1967; Ito 1984). The dendritic tree of a mature Purkinje cell receives extensive glutamatergic synaptic input from a single climbing fiber originating from the inferior olive. Climbing fiber activation of a Purkinje cell produces a powerful postsynaptic depolarization, which generates Ca²⁺ spikes throughout the entire dendritic tree and a complex spike (CS), which consists of a large Na⁺ somatic spike and a burst of smaller spikelets (Davie et al. 2008; Llinás and Sugimori 1980). Parallel fibers provide the second main input with over 100,000 individual glutamatergic synapses on each Purkinje cell. Parallel fibers produce small, postsynaptic excitatory responses in Purkinje cells and modulate the intrinsic simple spike (SS) discharge (Raman and Bean 1997). CS discharge occurs at a low frequency (~0.5–2.0/s) compared with the high frequency SS discharge (~50–150/s). To understand the function of CSs, we need to understand the signals carried by climbing fibers.

The primary hypothesis has been that climbing fiber input provides motor error signals. Supporting this view is the CS modulation with retinal slip during smooth pursuit adaptation and induced saccade errors (Barmack and Shojaku 1995; Graf et al. 1988; Kobayashi et al. 1998; Medina and Lisberger 2008; Soetedjo et al. 2008; Stone and Lisberger 1990b; Yang and Lisberger 2014). In addition to sensory derived errors, CSs modulate in response to inferred errors related to eye performance (Frens et al. 2001; Winkelman and Frens 2006; Winkelman et al. 2014) and prediction errors during eye blink conditioning (Ohmae and Medina 2015). During reaching movements, CSs modulate with unexpected loads (Gilbert and Thach 1977), reach redirection (Wang et al. 1987), end point errors (Kitazawa et al. 1998), and adaptation to visuomotor transformations (Ojakangas and Ebner 1994). The error signals conveyed by climbing fibers are hypothesized to play a teaching role in cerebellar motor learning, specifically in long-term depression at parallel fiber-Purkinje cell synapses (for reviews see Albus 1971; Boyden et al. 2004; Gao et al. 2012; Hansel et al. 2001; Ito 2001; Jörntell and Hansel 2006; Marr 1969).

However, climbing fiber activation cannot always be placed in an error framework. Inferior olivary neurons respond poorly to limb movement perturbations in the cat (Horn et al. 1996), as do CSs in response to error-inducing force pulses during reaching in the monkey (Hewitt et al. 2015). Complex spikes do not appear to unambiguously encode the magnitude of saccadic error (Soetedjo et al. 2008; Soetedjo and Fuchs 2006). It has even been suggested that climbing fibers are activated only by unexpected sensory input and do not respond during motor behavior (Gibson et al. 2004). One of the strongest demonstrations that climbing fiber input does not simply report errors is that, in the oculomotor vermis, changes in CS discharge during saccade and smooth pursuit adaptation are most prominent after the vast majority of adaptation has occurred, when retinal slip errors are minimal (Catz et al. 2005; Dash et al. 2010; Prsa and Thier 2011). Furthermore, CSs encode nonerror information about motor behavior, including reach and eye kinematics (Ebner et al. 2002; Fu et al. 1997b; Kitazawa et al. 1998; Kobayashi et al. 1998). These observations demonstrate that CSs do not only or always signal errors. In addition, climbing fibers are not the only source of error information in the cerebellar cortex, as SS firing provides robust performance error signals (Ke et al. 2009; Popa et al. 2012).

One common feature of CS modulation, whether with errors, unexpected sensory inputs, or kinematics, is that the responses are primarily feedback related. During limb movements and saccades, increases in CSs occur predominantly after movement onset (Catz et al. 2005; Ebner et al. 2002; Fu et al. 1997b; Mano et al. 1986; Meyer-Lohmann et al. 1977; Noda and Suzuki 1979; Soetedjo and Fuchs 2006). Recently, however, feedforward CS responses have been described during eye blink conditioning, with CS increases before and predicting the conditioned response (Ohmae and Medina 2015; ten Brinke et al. 2015). In our study of Purkinje cell firing during pseudo-random tracking, CSs occur primarily in advance of a change in hand kinematics and performance errors (Streng et al. 2017). However, that initial study focused on how CSs trigger a change in the information encoded in the SS firing and did not fully assess the spatiotemporal aspects of CS modulation during pseudo-random tracking. These observations of CSs leading behavior further the view that climbing fiber input provides signals that are not limited to error processing.

To fully understand the information signaled by the CSs, it is necessary to expand the behaviors studied. This is particularly true for previous arm movement studies that primarily used single joint movements or reaching tasks (Fu et al. 1997b; Gilbert and Thach 1977; Kitazawa et al. 1998; Mano et al. 1986; Ojakangas and Ebner 1994; Wang et al. 1987). Furthermore, most investigations of CS modulation evaluated stereotypic behaviors, including vestibular and oculomotor reflexes, reaching, or saccades, in which movement parameters are strongly correlated (Hewitt et al. 2011; Reimer and Hatsopoulos 2009). Also, there is a need to examine CS activity during tasks that require the continuous monitoring of behavior and correction for errors, as previous studies have emphasized the importance of spontaneous climbing fiber input in ongoing movements (Cerminara and Rawson 2004; Colin et al. 1980; Horn et al. 2013; Llinás et al. 1975; Montarolo et al. 1982; White and Sillitoe 2017).

Therefore, this study evaluates CS modulation during pseudo-random tracking that demands constant monitoring and adjusting for mismatches in hand movement relative to target movement and allows for the examination of the interactions between CS discharge and behavior in which the correlations between parameters are minimized (Hewitt et al. 2011; Popa et al. 2012). During this task, CS firing is strongly and linearly modulated with hand kinematics including position, velocity and acceleration, and position error, a measure of tracking performance. Intriguingly, the most frequent CS modulation occurs with acceleration. Contrary to the error feedback encoding hypothesis, the vast majority of the CS modulation leads the changes in behavior. Also, CS firing does not respond to “events,” either for position error or kinematics. These results provide novel observations about the diversity and properties of the signals carried by climbing fiber input.

MATERIALS AND METHODS

Behavioral and electrophysiological data were obtained from two rhesus monkeys (Macaca mulatta; female 6.3 kg, age 15; male 6.8 kg, age 8) during normal daytime hours. All animal experimentation was approved by the Institutional Animal Care and Use Committee of the University of Minnesota and conducted in accordance with the guidelines of the National Institutes of Health.

Random tracking.

This study utilized a previously described pseudo-random tracking task (Hewitt et al. 2011; Paninski et al. 2004; Popa et al. 2012; Streng et al. 2017) and, therefore, the paradigm is only briefly detailed here. Two monkeys were trained to use a robotic manipulandum (InMotion², Watertown, MA) that controls a cross-shaped cursor to track a circular-shaped target (2.5-cm diameter) on a computer screen (Fig. 1A). The paradigm started with an initial hold period in which the animals placed and maintained the cursor inside a stationary target for a random period of time (1,000–3,000 ms). The initial target position on the screen was also randomized. Next, during the track period, the target moved for 6–10 s along a trajectory selected randomly from 100 trajectories defined a priori. Pseudo-random target paths were generated from a sum of sine waves. Target speed was randomly varied so that the average speed was ~4 cm/s and conformed to the two-thirds power law (Lacquaniti et al. 1983; Viviani and Terzuolo 1982). The trajectories were low-pass filtered and selected to avoid sharp turns and large changes in speed, and ended with a final hold period of 1,000–3,000 ms. The paradigm required that the monkey maintain the cursor within the target and allowed only brief excursions outside the target (<500 ms). Pseudo-random tracking has several advantages, including providing more comprehensive and uniform coverage of parameter workspaces and dissociating kinematic from error parameters (Hewitt et al. 2011; Paninski et al. 2004). Random tracking also results in extensive combinations of the different kinematic parameters and position error, providing a rich data set to assess what information the CSs encode. Hand (X and Y) and target (X_tg, Y_tg) positions were sampled at 200 Hz. The velocity (VX, VY) and acceleration (AX, AY) of the hand movements were derived by numerical differentiation (Hewitt et al. 2011). Position error (XE, YE) was defined as the difference between cursor and target positions (Fig. 1B).

Fig. 1.

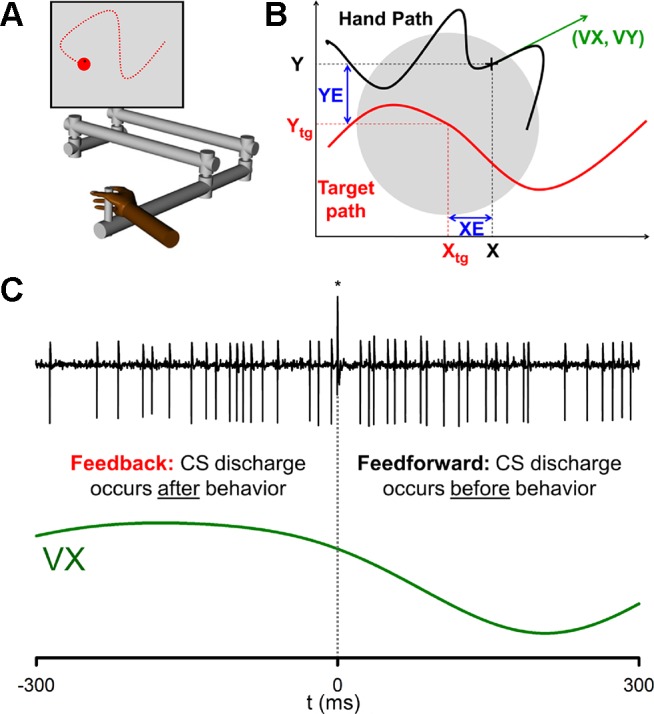
Behavioral paradigm and analysis of CS modulation. A: rhesus macaques tracked a pseudo-randomly moving target (red circle) using a cursor controlled by a manipulandum (Hewitt et al. 2011; Popa et al. 2012). B: kinematic parameters evaluated included position (X, Y), velocity (VX, VY) and acceleration (AX, AY, not shown). Position error (XE, YE) was defined as the difference between the cursor and the target center (modified from Streng et al. 2017). C: Purkinje cells were identified by the presence of complex spikes [asterisk (*)] followed by a pause in SS activity (top trace), and each parameter was aligned to CS occurrences (dashed vertical line) as shown for VX. CS modulation was quantified as the probability of behavior either 300 ms before (feedback) or 300 ms after (feedforward) CS firing.

Surgical procedures, electrophysiological recordings, and data collection.

Head restraint hardware and a recording chamber targeting lobules IV–VI of the intermediate and lateral cerebellar zones were chronically implanted over the parietal cortex ipsilateral to the arm used to track in each animal using aseptic techniques and full surgical anesthesia. The positions of the electrodes were confirmed by radiographic imaging techniques that combined a CT scan of the skull with an MRI of the cerebellum (Hewitt et al. 2011). After full recovery from chamber implantation surgery, extracellular recordings were obtained during normal daytime hours using Pt-Ir electrodes with parylene C insulation (0.8–1.5 MΩ impedance, Alpha Omega Engineering, Nazareth, Israel). Purkinje cells in lobules IV–VI of the intermediate and neighboring lateral cerebellar zones were targeted following previously established methods (Hewitt et al. 2015). Individual Purkinje cells were identified by the presence of CSs followed by a characteristic pause in SS activity (Fig. 1C) (Bloedel and Roberts 1971; Thach 1967). After conventional amplification and filtering (30 Hz-3 kHz band pass, 60 Hz notch), SSs were discriminated online using the Multiple Spike Detector System (Alpha Omega Engineering). Resulting spike trains were digitized and stored at 1 kHz. The raw electrophysiological data was also digitized and stored at 32 kHz. Using a combination of software and manual confirmation, CSs were discriminated and digitized offline (Hewitt et al. 2015). Using the fractional interval method, the SS trains were transformed to a continuous firing rate in 5 ms bins and the SS firing rates were not filtered to minimize autocorrelation artifacts. For display and analyses, the mean firing rate for each trial was subtracted from the instantaneous firing rate. The behavioral parameters were low-pass filtered (4th order Butterworth with a 5-Hz cutoff).

Analysis of complex spike modulation with behavior.

The goal of this analysis was to determine significant CS modulation associated with the three kinematic measures as well as position error. Both data and original MATLAB code written for analysis can be made available on request. The analyses, evaluating the temporal relationship and spatial tuning of the Purkinje cell firing with the behavioral variables, were restricted to the track period and used a reverse-correlation approach (Borghuis et al. 2003; Schoppmann and Hoffmann 1976). The reverse correlations were computed separately for each pair of parameters (e.g., VX and VY). First, each behavioral parameter was aligned to the times of all CSs across the recording session. Due to the low frequency of CS discharge, feedforward CS modulation was determined from behavior occurring during the 0 to 300-ms epoch after CS discharge and feedback CS modulation was determined from the behavior occurring during the 300 to 0-ms epoch before CS discharge (Fig. 1C). Each behavioral parameter was partitioned into 64 (8 × 8) equal bins ranging from −2 to 2 cm (0.5 cm × 0.5 cm bin) for XE and YE, −6 to 6 cm (1.5 cm × 1.5 cm bin) for X and Y, −12 to 12 cm/s (3 cm/s × 3 cm/s bin) for VX and VY, and −32 to 32 cm/s² (8 cm/s² × 8 cm/s² bin) for AX and AY. For each 300-ms epoch (before and after a CS), reverse correlation determines the number of data points in each bin during a given epoch normalized to the total number of data points in the same bin during entire recording session. For each parameter and epoch, we generated a two-dimensional probability map of the behavior in relation to CS discharge. Given that the reverse correlation probability is equal to the probability to observe a CS in each behavioral bin, we refer to the bin probability as CS probability.

The encoding strength and direction of either feedforward or feedback CS modulation with behavior were quantified using linear regression analysis. For each parameter, CS firing probability was modeled as a function of the x and y directions. For example, the following computations were performed for the feedforward CS firing probability ($C{S}_{\mathrm{prob}}^{\mathrm{ffwd}}$) associated with velocity (VX, VY):

$$C{S}_{\mathrm{prob}}^{\mathrm{ffwd}}={\beta }_0+{\beta }_{\mathrm{VX}}*\mathrm{VX}+{\beta }_{\mathrm{VY}}*\mathrm{VY}$$ (1)

The regression resulted in the coefficient of determination (R²) and the regression coefficients for each parameter (e.g., β_VX, β_VY). The preferred direction (θ) was then computed as the arctangent of the ratio of β_VX to β_VY:

$$\text{Preferred direction}\hspace{0.17em}\left(\theta \right)=\arctan \frac{\mathrm{\beta vy}}{\mathrm{\beta vx}}$$ (2)

The magnitude of the preferred direction vector was computed as:

$$\text{Vector magnitude}=\sqrt{{\beta }_{\mathrm{VX}}{}^2+{\beta }_{\mathrm{VY}}{}^2}$$ (3)

The significance of the CS modulation with a parameter was determined by comparing the actual R² value and the magnitude of the preferred direction vector to bootstrapped noise distributions generated by randomly shuffling the bins in each map 10,000 times (Best et al. 2016; Riehle et al. 2013). The bootstrapped noise distributions were generated by performing the linear regression analysis on each shuffled map. This analysis was performed separately for the feedforward and feedback CS epochs. CS modulation with a parameter was considered statistically significant if both the R² and vector magnitude exceeded the mean + 4SD of the shuffled distributions. This threshold ensured the identification of robust feedforward or feedback CS modulation with each behavioral parameter of interest.

Quantification of event-related complex spike modulation.

To determine whether CS modulation with the parameters is continuous or a discrete, event-related representation (e.g., increasing CS probability with increasing position error vs. evoked CS firing when the cursor leaves the target), we aligned CS firing to the timing of specific behavioral events. For positon error, we aligned the CS firing to the times during tracking when the cursor exited the target area. To account for the directional preference of CS firing and to capture the region in which CS firing increases, we restricted the analysis to the quadrant of the target within ± 45° of the preferred direction of the position error vector. For position error, the position at which the cursor exited the target edge corresponded to approximately the magnitude of the position error vector exceeding the mean + 1SD of the distribution of position error values. The experimental paradigm provides a definition of an error event, crossing out of the target, as this triggers the need for a timely corrective action. However, there are no similarly defined events for the kinematic parameters. Therefore, we used the equivalent statistical threshold found for position error events (i.e., exiting out of the target) to define events related to the kinematic parameters (mean + 1 SD of the parameter). For these error and kinematic events, we calculated the cumulative probability of CS firing within a ± 500-ms window.

Analysis of simple spike modulation with behavior.

We also assessed the SS modulation to determine the relationship between SS and CS encoding of behavior. SS modulation with behavior was analyzed using the same feedforward and feedback epochs and the same partitioning used for the analysis of CS firing. For feedforward SS modulation, we computed the average SS firing (mean-subtracted) in the 300-ms period before being in a given bin of the parameter workspace. For the feedback SS modulation, we computed the average SS firing (mean-subtracted) in the 300-ms period after being in a given bin of the parameter workspace. For each parameter, linear regression analysis was performed on the SS firing maps as for the CS probability maps, obtaining both the R² and regression coefficients (βs). The latter were used to compute the preferred direction of SS modulation and the vector magnitude (see Eqs. 2 and 3). The significance of the SS modulation was determined using the same bootstrapping method used for the CS firing maps. The interaction between SS and CS modulation was determined by comparing the preferred directions for each significant pair of CS and SS modulation for a given parameter and epoch (e.g., feedforward velocity CS vs. feedforward velocity SS modulation).

RESULTS

Random tracking and measurements of kinematics and performance error.

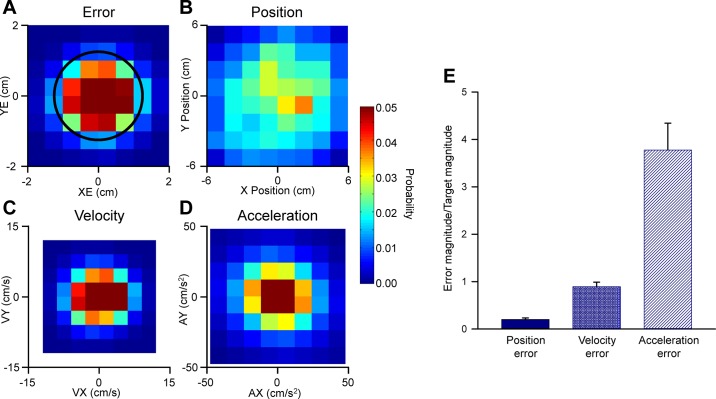
Two rhesus macaques performed a visually guided, manual pseudo-random tracking task (Fig. 1A) (Hewitt et al. 2011; Popa et al. 2012). Using a robotic manipulandum, monkeys controlled a cursor to track a pseudo-randomly moving target on a screen. Three kinematic parameters, derived from the instantaneous hand position, describe the movements of the hand including position (X, Y), velocity (VX, VY) and acceleration (AX, AY). Position errors (XE and YE) are defined as the difference between the cursor and the target center (Fig. 1B). To assess the statistics of the kinematic and error parameters relative to the workspaces, we determined the probability densities. Position, velocity, acceleration, and position error are concentrated in the center of the workspaces and are highly symmetrical. The position error plot shows that the animals strive to keep the cursor in the center of the target space (Fig. 2, A–D), as observed previously during this task (Hewitt et al. 2011; Popa et al. 2012). While it is possible to compute other error measures, such as the discrepancy between cursor and target velocity (velocity error) and acceleration (acceleration error), we focus on position error for several reasons. Performance on pseudo-random tracking is dictated entirely by position error, as excursions outside the target edge lasting more than 500 ms result in trial failure. To show this, the magnitude of position error to position magnitude was compared with similar ratios for velocity and acceleration (Fig. 2E). There are no explicit constraints placed on either velocity or acceleration error. The animals tightly control the position error ratio during tracking, but not the corresponding velocity or acceleration error ratios (Fig. 2E). This result is not unexpected as minimizing position error requires that velocity and acceleration deviate from target velocity and acceleration.

Fig. 2.

Behavioral parameters during pseudo-random tracking. Probability density plots of position error (A), position (B), velocity (C), and acceleration (D) during pseudo-random tracking. The density plots were determined from all trials for all Purkinje cells recorded. Black circle in A indicates the target edge. E: ratio of error to target kinematics for position, velocity, and acceleration error.

Complex spike modulation with kinematics and performance error.

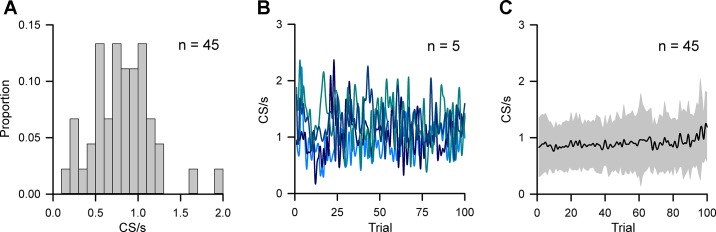
Forty-five Purkinje cells were recorded during pseudo-random tracking. This data set includes a reanalysis of 40 neurons used to describe the CS-coupled changes in SS sensitivity to kinematics and performance errors during random tracking (Streng et al. 2017) and an additional 5 Purkinje cells in which the CS firing was fully analyzed. The basic CS firing statistics are similar to previous reports, with an average of 0.87 ± 0.36 spikes/s during the track periods (Fig. 3A), which overall involved 881 ± 752 CSs per session. On average, the animals completed 110 ± 71 trials in a recording session. We also analyzed the variability in CS firing rates across trials. There was no trend in firing rate across trials either for individual Purkinje cells (Fig. 3B) or across the population (Fig. 3C, ρ = 0.16, P > 0.05, Pearson correlation). As reported in the previous paper, there was little evidence for CS rhythmicity (see Fig. 9 in Streng et al. 2017).

Fig. 3.

CS firing properties during pseudo-random tracking. A: distribution of CS firing rates for all 45 Purkinje cells. B: average CS firing rate over trials for 5 example Purkinje cells. C: population averages of CS firing rates over 100 trials.

The goal of the analyses was to determine the spatial and temporal modulation of CSs during this pseudo-random tracking task. Using a reverse correlation approach, the modulation was characterized by the probability of being in a given bin of the parameter workspace either 300 ms before (feedback) or 300 ms after (feedforward) CS discharge. The binning of the behavior in these 300 ms intervals allows for determining changes in the CS firing probability that predict or respond as feedback to position, velocity, acceleration, and position error.

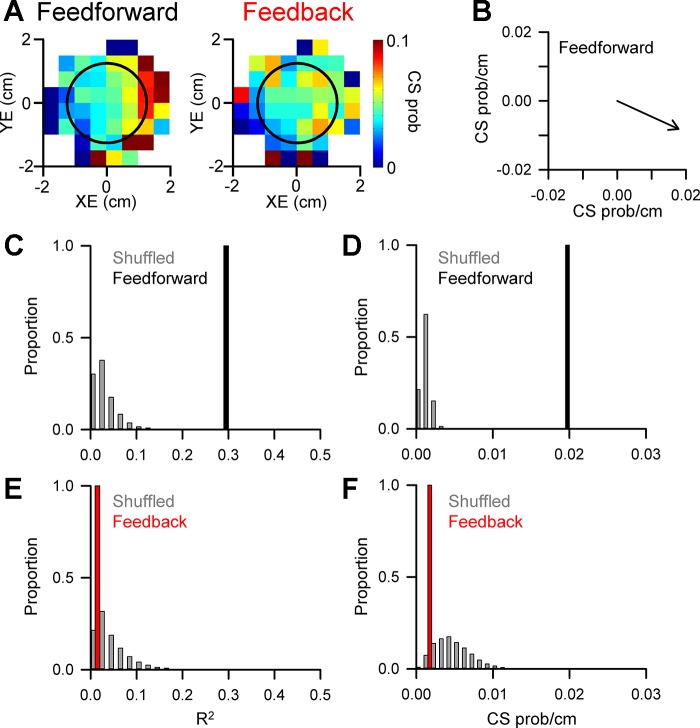
Figure 4 illustrates an example of a Purkinje cell in which CS firing modulates predictively with position error. The probability maps reveal spatial tuning in the 300-ms period before position error, as CS probability increases in the positive XE direction and decreases in the negative XE direction (Fig. 4A, feedforward). The probability maps were generated from the 371 CSs recorded during 59 successful trials for this example Purkinje cell. The spatial relationship between CS firing probability and position error was quantified by both the strength (R²) and preferred direction (Fig. 4B) using linear regression analysis (see materials and methods). The significance of the CS modulation with behavior was assessed by comparing both the R² and vector magnitude to distributions obtained from 10,000 random shuffles of the CS probability maps. A significant relationship between CS modulation and behavior required that both the R² and vector magnitude exceeded the mean + 4SD of the shuffled probability maps. For the example shown in Fig. 4A, the R² and vector magnitude (CS prob/cm) fall far to the right of the distributions obtained from the shuffled probability maps (Fig. 4, C and D, respectively), confirming the significance of the feedforward CS modulation. However, the CS firing probability is not significant for the 300-ms period following position error (Fig. 4A, feedback and E and F). For this Purkinje cell, only 4 additional CSs occur in both the feedforward and feedback epochs, demonstrating that the probability maps are not heavily influenced by the occurrence of these small number of intervening CSs. Finally, the spatial tuning is fundamentally different than the position error probability density maps (Fig. 2A), demonstrating that the increases in CS firing probability cannot be explained by the number of occurrences of the behavior within the map.

Fig. 4.

CS modulation with position error. A: probability (prob) maps of feedforward and feedback CS modulation with position error determined using 371 CSs recorded during tracking in 59 trials. Black circle indicates target edge. B: preferred direction of CS feedforward tuning with position error computed using the regression coefficients from the linear regression analysis (see materials and methods). C: magnitude of the feedforward CS modulation with position error as quantified by the R² (black bar) compared with the distribution of R² values from shuffled probability maps (gray bars). D: magnitude of the predictive CS preferred direction (black bar) compared with the distribution of vector magnitudes from shuffled probability maps (gray bars). E and F: magnitude of feedback modulation as in C and D showing that neither the R² value nor magnitude of the preferred direction vector differs from the shuffled distributions.

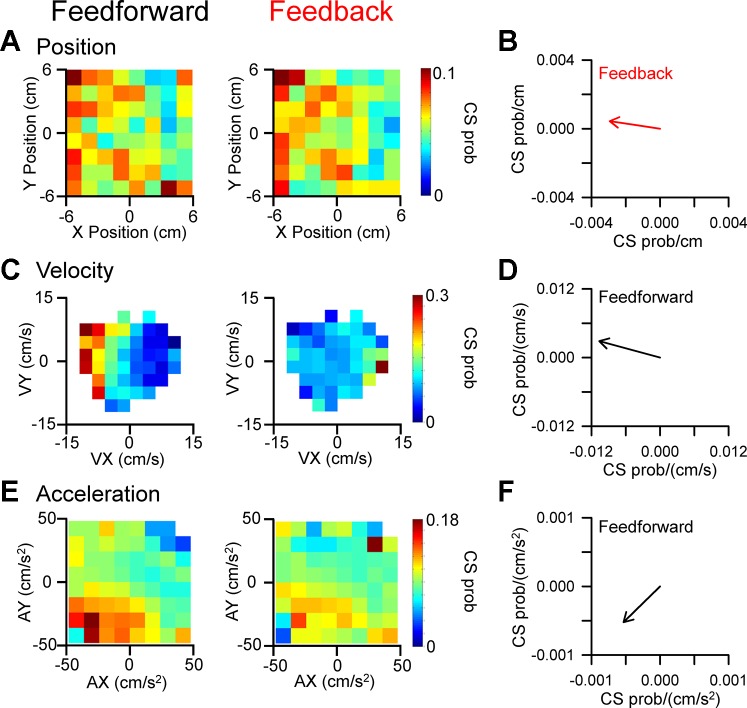
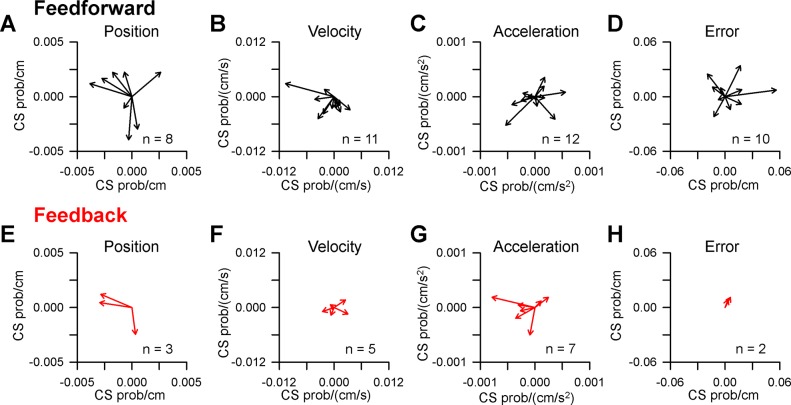
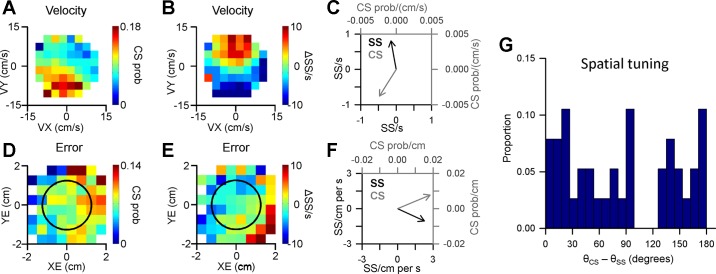
Significant CS modulation with kinematics and position error occurs in 75% of Purkinje cells (n = 30/45), with robust spatial tuning for each of the four parameters evaluated. Examples of Purkinje cells with significant CS modulation with position, velocity, and acceleration are shown in Fig. 5. For the first example (Fig. 5, A and B), increased CS firing probability occurs in the left side of the position space during the feedback epoch (quantified by the red vector in Fig. 5B), however, the modulation during the feedforward epoch is not significant. For another Purkinje cell, strong feedforward CS modulation occurs for velocity with increased probability for negative VX and decreased probability for positive VX (Fig. 5, C and D). No significant CS modulation with velocity is observed during the feedback period. The final example shows CS firing probability spatially tuned to and predicting acceleration, with increased CS firing in the lower left of the acceleration space (Fig. 5, E and F). As for velocity, there is no significant feedback modulation with acceleration.

Fig. 5.

CS modulation with kinematics. A: CS probability maps illustrating an example Purkinje cell with significant feedback tuning with position. Feedforward modulation is not significant. The maps were computed using 1,114 CSs during tracking from 110 trials. B: preferred direction of CS feedback tuning with position. C and D: CS probability maps and preferred direction plot for another example Purkinje cell with significant feedforward tuning with velocity computed using 807 CSs recorded during tracking in 182 trials. Feedback tuning was not significant. E and F: CS probability maps and preferred direction plot for a third example Purkinje cell with significant feedforward tuning with acceleration computed using 3248 CSs recorded during tracking in 337 trials. Feedback modulation was not significant.

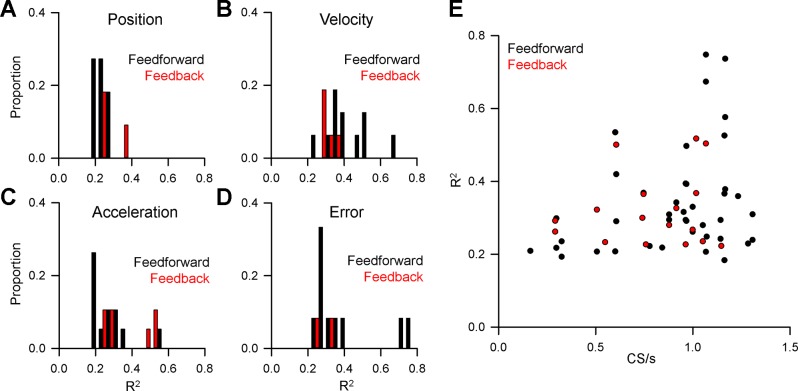
Across the population, CS modulation with behavior is strongly predictive for each parameter analyzed and considerably more frequent than feedback modulation (Fig. 6, top vs. bottom row). The CSs are most commonly modulated in relation to velocity and acceleration. Purkinje cells have a significantly greater number of feedforward (n = 41) than feedback (n = 17) relationships between CS firing and behavior [χ² (3, n = 58) = 11.17, P = 0.011]. Of particular interest given the climbing fiber error hypothesis, only 2 Purkinje cells have significant feedback CS modulation with position error and the magnitude of the modulation is small. In contrast, feedforward CS modulation with position error is found for 11 Purkinje cells. However, the strength of the relationship between CS firing probability and behavior based on the R² values is similar for both predictive (Fig. 7, black bars) and feedback (Fig. 7, red bars) across all parameters (t(56) = 0.5034, P = 0.6167). Importantly, there was no relationship between the strength (R²) of the relationship between CS firing probability and the overall CS firing rates (Fig. 7E, ρ = 0.24 P > 0.05, Pearson’s correlation). Together, these results demonstrate that CS firing is highly modulated with both kinematics and position error during tracking, though feedforward CS encoding was considerably more prevalent than feedback encoding. The strength of the CS encoding is not related to the rate of CS discharge.

Fig. 6.

Population summary of CS spatial tuning with behavior. A–D: preferred direction vectors for all Purkinje cells with significant feedforward CS modulation with position (A), velocity (B), acceleration (C), and position error (D). E–H: preferred direction vectors for all Purkinje cells with significant feedback CS modulation with the same kinematic and error parameters. N indicates the number of cells with significant modulation.

Fig. 7.

Population summary of the magnitude of CS encoding of behavior. Distribution of R² values for feedforward (black bars) and feedback (red bars) relationships between CS firing and position (A), velocity (B), acceleration (C), and position error (D). E: R² values for feedforward and feedback CS modulation as a function of mean CS firing rate.

Correlation among behavioral parameters is not reflected in complex spike modulation.

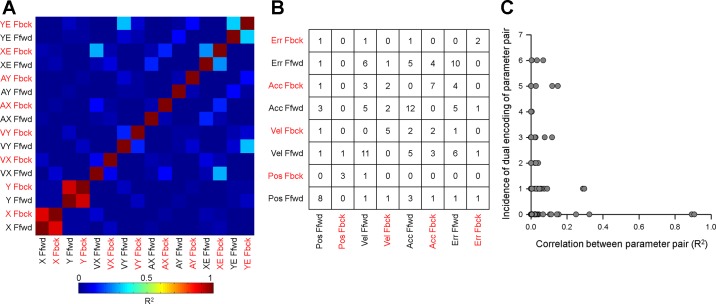
CS modulation with multiple behavioral parameters was common, with an average of 1.93 ± 0.87 parameters per neuron. To ensure that CS modulation with multiple parameters was not due to the interactions between parameters, we determined the degree to which the behavioral parameters were correlated over the 300-ms feedforward and feedback CS-aligned epochs (Fig. 8A). For most parameters, the correlations are minimal with a few exceptions. The highest correlations are for the individual position components (e.g., X_Ffwd and X_Fbck). However, correlations between the feedforward and feedback epochs for X and for Y position are expected due to the slowly changing nature of position over a 600-ms period. More modest levels of correlation include XE_Fbck with VX_Ffwd (R² = 0.29) and YE_Fbck with VY_Ffwd (R² = 0.30) (i.e., the brighter blue squares in Fig. 8A). To address this, we compared the correlation structure between a given pair of behavioral parameters (Fig. 8A) to the number Purkinje cells in which the CSs are significantly correlated with that pair of parameters (Fig. 8B). If the correlation structure in the behavior influences the CS responses, one would expect a similar correlation structure in the CS responses. This would be particularly true for any of the larger correlations observed among parameters (described above), for example for the correlations between X_Ffwd and X_Fbck, XE_Fbck with VX_Ffwd or X_Ffwd and X_Fbck. Consider position, which has the highest correlation between the feedforward and feedback epochs. Eight Purkinje cells exhibited CS feedforward modulation with position, however, none of these cells were also modulated with position feedback. The 3 Purkinje cells that had CS feedback modulation with position are different neurons and, conversely, did not have CS predictive modulation. Another key comparison is for both pairs of Err_Fbck and Vel_Ffwd parameters (i.e., XE_Fbck and VX_Ffwd, YE_Fbck and VY_Ffwd) that also exhibit higher behavioral correlations (Fig. 8A). In contrast, only one Purkinje cell had CS modulation with both Err_Fbck and Vel_Ffwd. The more common pairs of parameters with CS modulation, for example, Vel_Fwd and Err_Fwd that are dually encoded by six cells, have a negligible behavioral correlation (R² < 0.005). To relate the correlations between behavioral parameters to CS modulation, we plotted the correlation between each parameter pair (R² from Fig. 8A) against the total number of cells that had dual CS modulation with that parameter pair (from Fig. 8B). Across the population, the higher correlations between behavioral parameters are not reflected in the incidence of dual CS modulation with those parameters (Fig. 8C, ρ = −0.08, P > 0.05). Together, these results indicate that the interactions between behavioral parameters cannot explain the observed CS modulation and that the analysis of behavior in the 300-ms feedforward and feedback epochs allows for a relatively independent characterization of the CS modulation, both predictive and feedback, with each of these parameters.

Fig. 8.

Correlations between parameters and CS modulation. A: correlation matrix of the regression coefficient (R²) between each pair of behavioral parameters for both feedforward (Ffwd) and feedback (Fbck) epochs. The correlations between parameters were computed based on all trials for all Purkinje cells recorded. B: frequency of CS modulation with multiple parameters. The numbers in each cell indicate the number of Purkinje cells that had significant modulation with parameters indicated in the row and column. C: relationship between the frequency of CS modulation with behavior and the correlations between parameters.

Event-related complex spike modulation.

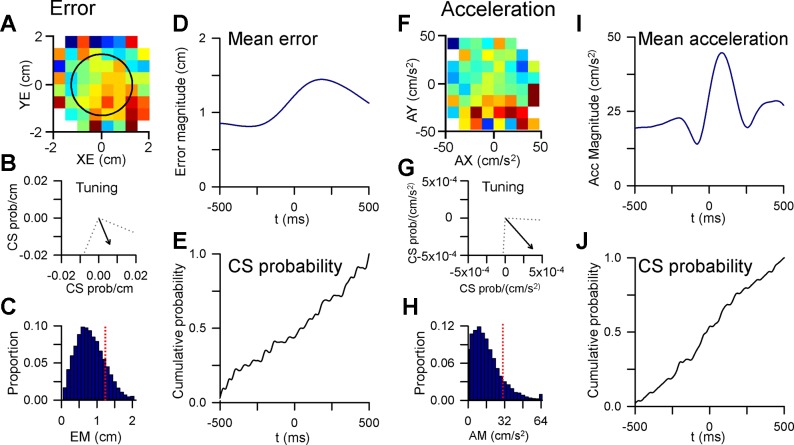
To address whether climbing fibers are evoked in response to specific error events, we determined the CS modulation to the time at which the cursor crosses from inside to outside the target. Leaving the target is clearly an error event as only brief excursions outside the target center (<500 ms) are allowed. An error event requires rapid detection and correction to continue tracking and successfully complete a trial. To account for the spatial tuning of the climbing fiber input with position error (for example, see Fig. 9A), we evaluated only excursions occurring within ± 45° of the CS preferred direction determined using the linear regression analyses (Fig. 9B). The average error magnitude aligned to these excursions provides a measure of a position error event, in which the cursor exits the target at t = 0 ms and is followed by a corrective movement to bring the cursor back into the target (Fig. 9D). If CSs are responsive to position error events, the expectation is that CS firing would show a distinct increase (or decrease) after the cursor left the target (t = 0 ms in Fig. 9D). This increase should be evident in a plot of the cumulative probability of CS firing. For the example Purkinje cell, the CS firing is not modulated by these position error events, illustrated by the lack of a distinct change in the cumulative probability of occurrence at t = 0 ms. Instead, the cumulative CS firing probability linearly increases from the inside to the outside of the target (Fig. 9E).

Fig. 9.

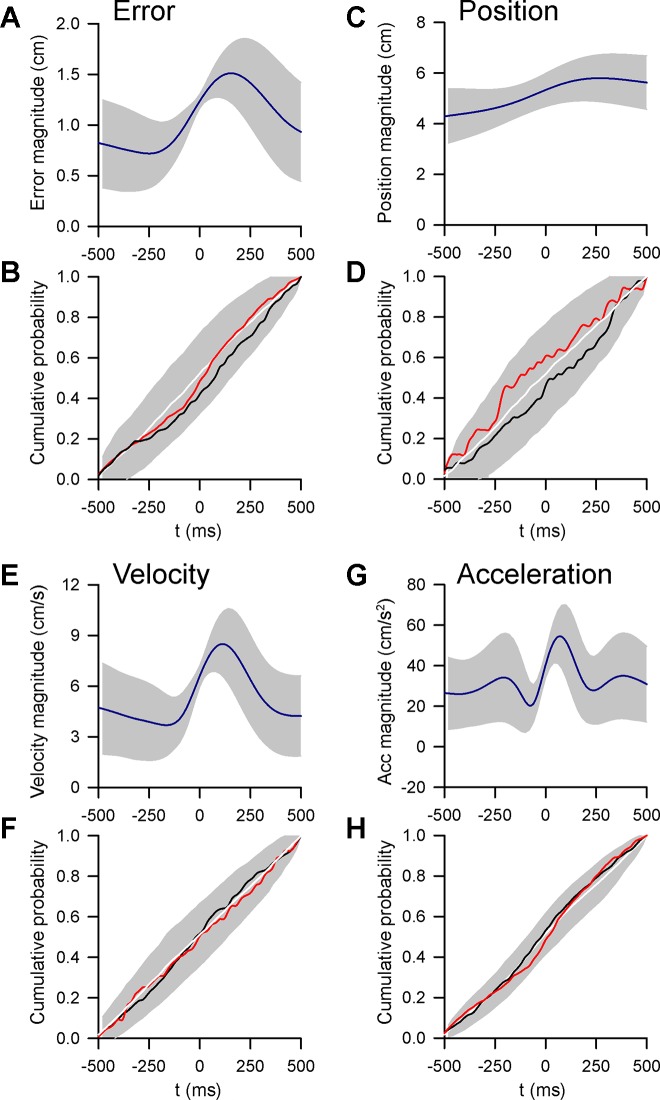
Event-related analysis of CS modulation. A: example Purkinje cell with significant feedforward CS tuning with position error. B: preferred direction of CS tuning with ± 45° window used for the analysis. C: probability distribution of error magnitude (EM) during tracking. Red dashed line indicates the target edge. D: average error magnitude aligned to the times, t = 0 ms, at which the cursor exited the target (error events) within ± 45° of the preferred direction vector shown in B. E: cumulative probability of CS firing over a ±500-ms window around the timing of error events. F: example Purkinje cell with significant feedforward CS tuning with acceleration. G: preferred direction of CS tuning. H: probability distribution of acceleration magnitude (AM) during tracking. Red dashed line indicates the mean + 1 SD of the distribution, the threshold used for identifying acceleration events. I: average acceleration magnitude aligned to the timing of acceleration events (t = 0 ms). J: cumulative probability of CS firing over a ±500-ms window around the timing of acceleration events.

A similar question is whether CSs are evoked by events related to hand position, velocity, or acceleration. While a position error event can be clearly defined as the moment the cursor exits the target, there are no such events for the kinematic parameters in our pseudo-random tracking paradigm. Therefore, we defined a kinematic event as when a specific kinematic parameter exceeded a threshold relative to the normal distribution of that parameter. The threshold for a kinematic event was based on the magnitude of a position error event in which the target edge corresponds to approximately the mean + 1SD of the total error magnitude workspace (Fig. 9C, red dashed line). Therefore, for each kinematic parameter an event was defined as the time at which the behavior exceeds the mean + 1SD of the parameter’s workspace. An example of acceleration events is illustrated in Fig. 9, F–J. For this Purkinje cell, the CS discharge is predictive and directionally tuned with acceleration, with a preferred direction toward the lower right area of the workspace (Fig. 9, F and G). As for position error events, acceleration exceeding the mean + 1SD (Fig. 9H, red dashed line) and occurring within ± 45° of the preferred direction were selected as events. The average acceleration illustrates that the analysis identifies events as the acceleration rapidly increases after t = 0 ms, peaks and then returns to within mean + 1SD (Fig. 9I). As is the case for position error, the cumulative CS firing is not strongly related to acceleration events, as there is little change after an event at t = 0 ms (Fig. 9J).

Across the population, similar results were obtained for each parameter. For Purkinje cells in which the climbing fiber input are significantly modulated with position errors (Fig. 10, A and B), cumulative CS firing probability does not exhibit an inflection around the timing of position error events (Fig. 10B), regardless of whether the relationship between CS firing and position error was predictive (black trace) or feedback (red trace). Similar results are observed for position (Fig. 10, C and D), velocity (Fig. 10, E and F), and acceleration events (Fig. 10, G and H). Together, these results show that during tracking CSs are not related to behavioral events, either for position error or kinematics. Instead, CS firing is linearly modulated across the workspace of each parameter.

Fig. 10.

CSs are not evoked by behavioral events. A: average error magnitude relative to the timing of error events for all Purkinje cells with significant CS tuning with position error (shaded region indicates ±1SD). B: cumulative CS probability for all Purkinje cells with significant feedforward (black line) and feedback (red line) CS modulation with errors relative to trial shuffled error events (white line and shaded region = mean + 1 SD). C: average position magnitude relative to timing of position events for all Purkinje cells with significant CS tuning with position. Conventions are as in A. D: cumulative CS probability for Purkinje cells with significant CS tuning to position. Conventions are as in B. Average velocity (E) and acceleration (G) magnitudes and the corresponding cumulative CS probabilities for Purkinje cells with significant CS tuning with velocity (F) and acceleration (H) are also shown.

Simple spike modulation with kinematics and position error.

We recorded Purkinje cells in lobules IV–VI of the cerebellum, areas that have been shown to be strongly involved with arm movements based on electrophysiological recordings, functional imaging, and the results of lesions (Coltz et al. 1999; Diedrichsen et al. 2005; Fortier et al. 1989; Fu et al. 1997a; Harvey et al. 1977; Hewitt et al. 2011; Kitazawa et al. 1998; Mano and Yamamoto 1980; Marple-Horvat and Stein 1987; Pasalar et al. 2006; Roitman et al. 2005; Schoch et al. 2006; Thach 1970). We thus next assessed the spatial tuning of SS discharge in the same feedforward and feedback epochs utilized for the CS firing. For each parameter, maps of the mean SS firing were determined for 300 ms before (feedforward) and 300 ms after (feedback) the behavior. The significance and preferred direction of SS firing maps were computed as for the CS firing probability maps. The Purkinje cells recorded were very engaged in pseudo-random tracking, as 44 of the 45 (98%) are significantly modulated by either kinematics or position error.

Figure 11A illustrates an example of a Purkinje cell with feedback SS modulation with position error. Feedforward SS modulation is not significant (not shown). The SS firing increases in the upper left quadrant of the position error workspace and has a preferred direction of 155° (Fig. 11B). Both the encoding and the magnitude of the SS modulation with position error are significant as assessed by noise distributions obtained from 10,000 shuffled maps (Fig. 11, C and D, respectively). For each of the 44 Purkinje cells with significant modulation, we determined the absolute difference between the largest increase and decrease in SS firing for the best encoded parameter calculated using the SS modulation maps. This analysis provides a measure of the depth of modulation in the SS firing across the workspace for a given behavioral parameter. Across the population, the SS firing is highly modulated by kinematics and position errors during tracking, with an average range of 29 ± 13 spikes/s. Therefore, these Purkinje cells are highly involved in this task.

Fig. 11.

Linear SS modulation with behavior. A: probability map of example Purkinje cell with feedback SS modulation with position error. Black circle indicates target edge. B: preferred direction of SS feedback tuning with position error. Feedforward modulation was not significant. C: magnitude of the feedback SS modulation with position error as quantified by the R² (red bar) compared with the distribution of R² values from shuffled probability maps (gray bars). D: magnitude of the feedback SS preferred direction (red bar) compared with the distribution of vector magnitudes from shuffled probability maps (gray bars). E–H: the preferred direction and magnitude of significant feedforward SS firing modulation with position (E), velocity (F), acceleration and (G), and position error (H) for the population. I–L: the preferred direction and magnitude of significant feedback SS firing modulation with the same kinematic and error parameters. N indicates the number of cells with significant modulation.

Across the population, both feedforward and feedback SS modulation with kinematics and position errors is common, as observed previously (Hewitt et al. 2011; Popa et al. 2012). Purkinje cell SS discharge is strongly modulated by position (Fig. 11, E and I), velocity (Fig. 11, F and J), acceleration (Fig. 11, G and K), and position error (Fig. 11, H and L). In contrast to the CS modulation, there is no bias toward either feedforward or feedback SS modulation with behavior [χ² (3, n = 167) = 1.61, P = 0.658]. Together, these results demonstrate that SS firing contains rich representations of all kinematic and error parameters studied, with broad coverage of the individual workspaces.

Directional tuning of complex spike and simple spike firing.

A final question was the relationship between the directional tuning of the CSs and SSs, specifically the degree to which SS and CS modulation are reciprocal. All pairs of significant CS and SS modulation with a given behavioral parameter (e.g., velocity) for the same epoch (e.g., feedforward) were selected and the differences computed between the preferred directions (n = 38). Two examples of the spatial tuning of the SSs and CSs are illustrated in Fig. 12. The first example Purkinje cell has both predictive CS and SS modulation with velocity, with approximately reciprocal spatial tuning, as evident both by the firing maps (Fig. 12, A and B) and the 138° difference in their preferred directions (Fig. 12C).

Fig. 12.

Interaction between CS and SS encoding. A and B: example Purkinje cell with significant feedforward CS (A) and SS modulation with velocity (B). C: preferred direction of CS tuning (gray vector) and SS tuning (black vector) (note the difference in scales on x- and y-axes for SS and CS). D and E: a second example Purkinje cell with significant feedforward CS modulation with position error (D) and significant feedforward SS modulation with position error (E). F: preferred direction of CS tuning (gray vector) and SS tuning (black vector). G: population distribution of the angular differences between the preferred directions for all pairs of significant CS and SS modulation with a given behavioral parameter and the same epoch.

Many Purkinje cells had CS and SS spatial tuning that was approximately reciprocal (Fig. 12G). However, many Purkinje cells did not follow this pattern as shown in the second example cell with significant feedforward CS and SS modulation with position error (Fig. 12, D and E). While the feedforward CS modulation occurs predominantly in the upper right region of the error space, the SS modulation occurs in the lower right region of the space. The difference in the preferred directions is 48° (Fig. 12F). Across the population, the difference in the preferred directions between CS and SS modulation appears to be uniformly distributed, without a significant bias for a certain difference in preferred direction [χ² (19, n = 38) = 16.74, P = 0.6077)]. Therefore, during pseudo-random tracking, there is not a fixed spatial relationship between the CS and SS modulation.

DISCUSSION

This study describes several major observations about the information carried by climbing fiber input to the cerebellar cortex. First, CS discharge modulates not only with motor performance measures but also with movement kinematics. Intriguingly, acceleration was the parameter most commonly correlated with CSs. Second, CS discharge is predominantly predictive of upcoming kinematics and position error. Third, CS discharge is not related to discrete events, either for errors or for kinematics. Instead CSs provide a linear representation of each parameter. Finally, CS and SS firing are modulated by the same parameters, though the relationship between their spatial tuning is not always reciprocal. These results show that during online motor control CS firing conveys considerable predictive information about multiple aspects of behavior rather than serving primarily as an error feedback signal.

The pseudo-random tracking task provides for a more thorough exploration of the kinematic and position error workspaces than many paradigms (Hewitt et al. 2011; Paninski et al. 2004; Popa et al. 2012). This task results in extensive combinations of kinematic parameters and performance errors and produces a robust data set to assess the signals that activate climbing fibers. The lack of correlation between many of the parameters (e.g., position and velocity) over the brief epochs reflects their orthogonality. Also, pseudo-random tracking minimizes the correlations between the feedforward and feedback epochs for most of the parameters, with the exception of position. However, the feedforward-feedback correlations for X and Y are expected and reflect the slow changing nature of hand position. Overall, this task represents a considerable departure from those involving discrete movements, such as reaching or saccade tasks, which produce more stereotypic movement patterns. For example, during reaching there is a stereotypic bell-shaped velocity profile and strong coupling between position and velocity (Abend et al. 1982; Hewitt et al. 2011) or that, during smooth pursuit, retinal slip error evokes a corrective eye movement and thus a change in acceleration (Collewijn and Tamminga 1984). The greater coverage of the workspaces and low correlations aid in uncovering the multiple signals in the CS discharge and a fuller characterization of the properties of those signals.

The finding that CSs commonly encode acceleration is intriguing. To our knowledge, this is one of a few studies describing acceleration-dependent CS firing. During ocular following, while eye velocity was the strongest driver of CSs, the acceleration contribution to the CS modulation is greater for CSs than for the SSs (Kobayashi et al. 1998). During three-dimensional vestibular stimulation, CS discharge correlates with inertial acceleration (Yakusheva et al. 2010). The prevalence of acceleration encoding may clarify the commonly observed increase in climbing fiber activity at movement onset during reaching or single joint movements (Fu et al. 1997b; Hewitt et al. 2015; Mano et al. 1986; Ojakangas and Ebner 1994), as movement onset involves large changes in acceleration. Furthermore, the observation of acceleration modulation, in combination with the other aspects of the movement encoded, emphasizes that CSs signal a wide spectrum of movement information.

For each parameter investigated, CS discharge provides a planar representation of the workspace, with a clear directional component characterized by a preferred direction vector. This planar encoding strengthens previous observations that the climbing fiber input provides graded information about behavior (Ebner et al. 2002; Fu et al. 1997b; Kitazawa et al. 1998; Kobayashi et al. 1998). In contrast, the analyses failed to detect any evidence for eventlike signals or a threshold at which CS firing was preferentially evoked. Instead, a linear model provides a better fit of the data. Linear representations may optimize separation of patterns, are less susceptible to saturation, and increase the dynamic range (Chen et al. 2016; Fujita 1982; Park et al. 2012). Similar linear encoding characterizes SS firing in a variety of tasks (Chen et al. 2016; Dash et al. 2012; Hewitt et al. 2011, 2015; Medina and Lisberger 2009; Popa et al. 2012; Shidara et al. 1993) and Purkinje cells are thought to linearly integrate parallel fiber and inhibitory interneuron inputs (Park et al. 2012; Walter and Khodakhah 2006, 2009). Therefore, the cerebellar cortex utilizes linear encoding of movement information in both the climbing fiber-Purkinje cell and the mossy fiber-granule cell-Purkinje cell circuits.

During pseudo-random tracking, angular differences in modulation between SS and CS firing was distributed uniformly among Purkinje cells (see Fig. 12). Reciprocal modulation of SSs and CSs is commonly observed during several behaviors, including the vestibulo-ocular and optokinetic reflexes (Graf et al. 1988; Kitama et al. 1999; Kobayashi et al. 1998; Stone and Lisberger 1990a). Importantly, out-of-phase modulation is not due to the pause in SS activity that follows a CS (Kobayashi et al. 1998; Yakusheva et al. 2010). The climbing fiber projection itself plays a dominant role in the reciprocity as shown in the Ptf1a::cre,Robo3^lox/lox mouse (Badura et al. 2013). In this mutant, climbing fiber input is rerouted and projects almost exclusively to the ipsilateral flocculus, yet the SS and CS discharge exhibit normal reciprocity. However, a spectrum of relationships between the directional tuning of SS and CS discharge have been observed in reaching tasks (Ebner et al. 2002; Ojakangas and Ebner 1994), and in-phase modulation has been reported for rotation in the dark and during three-dimensional vestibular stimulation (Winkelman et al. 2014; Yakusheva et al. 2010). Therefore, while a reciprocal pattern of SS and CS firing occurs in many behaviors, this is not a completely “hard-wired” relationship but instead appears to be task specific.

One of the more remarkable findings in this study is that for the majority of Purkinje cells CS occurrence led the behavior. Furthermore, predictive CS signaling was observed across all parameters, extending our initial report of feedforward CS discharge during pseudo-random tracking (Streng et al. 2017). Many previous studies emphasized that CSs respond to sensory inputs or after the onset of movement. It was even argued that CSs only respond to unexpected sensory feedback (Gibson et al. 2004). As noted in the Introduction, recent eye blink conditioning studies report CS increases before and predicting the conditioned response (Ohmae and Medina 2015; ten Brinke et al. 2015). In both of these studies, the predictive modulation was also accompanied by the CS response to the unconditioned stimulus. In contrast, during our demanding tracking task predictive CS modulation was greater than two times as common as the feedback responses (see Fig. 5).

The mechanism underlying the predictive encoding remains to be investigated and we can only speculate on the circuitry involved. The inferior olive receives a variety of excitatory and inhibitory inputs including from the spinal cord, nuclei at the mesodiencephalic junction, cerebellar nuclei, and cerebral cortex (for reviews see Apps and Garwicz 2005; De Zeeuw et al. 1998; Oscarsson 1980), integrating both feedforward and feedback information. For the development of predictive CS signals during classical conditioning it was suggested that recurrent activity within the olivocerebellar network plays a major role (ten Brinke et al. 2015). Another possibility is cerebral cortical involvement, specifically the motor cortices, in generating feedforward signals. Importantly, the responses of inferior olivary neurons to glutamatergic inputs from the motor cortex are biphasic in a manner that appears to penalize late inputs (Garden et al. 2017). This could create a bias toward early motor signals and thus a mechanism for the predictive CS modulation. Taken together, these observations suggest that, at least during pseudo-random tracking, CS discharge contains predictive motor signals about multiple aspects of the upcoming behavior instead of predominately providing sensory feedback.

Another intriguing observation is that the same behavioral parameters linearly modulate both CSs and SSs in the same reference frames. This suggests that these two activity modalities of Purkinje cells function in concert during movements as opposed to acting independently. Consistent with this hypothesis, it was demonstrated that when Purkinje cells are organized according to their CS directional tuning, the SS population response provides a better prediction of the speed and direction of saccades (Herzfeld et al. 2015). Moreover, we recently reported a mechanism that integrates online CS and SS activity, showing that CSs control the information encoded in the SS firing (Streng et al. 2017). Both increases and decreases in the SS sensitivity to these same motor parameters are tightly timed to CS occurrence. For the Purkinje cells common to both studies, a number of encoding changes are also associated with significant CS modulation with behavior (9 cells, 12 parameters). Nearly all of those CS-coupled changes in SS encoding changes are associated with predictive CS modulation with behavior (10/12 parameters), consistent with the hypothesis that climbing fiber discharge alters the SS sensitivity in anticipation of a change in behavior. Furthermore, at the population level, these changes in encoding are consistent with optimizing behavior, with increases in SS encoding of the kinematic parameters followed by kinematic changes and increases in SS encoding of position error followed by decreases in position error. Therefore, we interpret the prevalence of feedforward CS modulation as a mechanism to inform the output of the cerebellar cortex of the need to update the information represented in the SS firing in anticipation of upcoming behavioral demands.

GRANTS

This research was supported in part by NIH grants R01 NS18338, T32 GM008471, and F31 NS095408 and by NSF grant IGERT DGE-1069104.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.L.S., L.S.P., and T.J.E. conceived and designed research; M.L.S. performed experiments; M.L.S. analyzed data; M.L.S., L.S.P., and T.J.E. interpreted results of experiments; M.L.S. prepared figures; M.L.S., L.S.P., and T.J.E. drafted manuscript; M.L.S., L.S.P., and T.J.E. edited and revised manuscript; T.J.E. approved final version of manuscript.