Spatially tuned normalization explains attention modulation variance within neurons

Tuned normalization studies have demonstrated that the variance in attention modulation size seen across neurons from the same cortical area can be largely explained by between-neuron differences in normalization strength. Here we demonstrate that attention modulation size varies within neurons as well and that this variance is largely explained by within-neuron differences in normalization strength. We provide a new spatially tuned normalization model that explains this broad range of observed normalization and attention effects.

Abstract

Spatial attention improves perception of attended parts of a scene, a behavioral enhancement accompanied by modulations of neuronal firing rates. These modulations vary in size across neurons in the same brain area. Models of normalization explain much of this variance in attention modulation with differences in tuned normalization across neurons (Lee J, Maunsell JHR. PLoS One 4: e4651, 2009; Ni AM, Ray S, Maunsell JHR. Neuron 73: 803–813, 2012). However, recent studies suggest that normalization tuning varies with spatial location both across and within neurons (Ruff DA, Alberts JJ, Cohen MR. J Neurophysiol 116: 1375–1386, 2016; Verhoef BE, Maunsell JHR. eLife 5: e17256, 2016). Here we show directly that attention modulation and normalization tuning do in fact covary within individual neurons, in addition to across neurons as previously demonstrated. We recorded the activity of isolated neurons in the middle temporal area of two rhesus monkeys as they performed a change-detection task that controlled the focus of spatial attention. Using the same two drifting Gabor stimuli and the same two receptive field locations for each neuron, we found that switching which stimulus was presented at which location affected both attention modulation and normalization in a correlated way within neurons. We present an equal-maximum-suppression spatially tuned normalization model that explains this covariance both across and within neurons: each stimulus generates equally strong suppression of its own excitatory drive, but its suppression of distant stimuli is typically less. This new model specifies how the tuned normalization associated with each stimulus location varies across space both within and across neurons, changing our understanding of the normalization mechanism and how attention modulations depend on this mechanism.

NEW & NOTEWORTHY Tuned normalization studies have demonstrated that the variance in attention modulation size seen across neurons from the same cortical area can be largely explained by between-neuron differences in normalization strength. Here we demonstrate that attention modulation size varies within neurons as well and that this variance is largely explained by within-neuron differences in normalization strength. We provide a new spatially tuned normalization model that explains this broad range of observed normalization and attention effects.

directing attention to a specific location in the visual field improves perception of stimuli at that location (Posner 1980). This behavioral improvement is accompanied by modulation of visual neuron responses (for review see Bisley and Goldberg 2010; Harris and Thiele 2011; Krauzlis et al. 2013; Maunsell 2015). When neurons are recorded simultaneously during attention tasks, different neurons from the same brain area exhibit different amounts of attention modulation (Cohen and Maunsell 2010). This variance in attention modulation size across neurons in visual cortex has been linked to normalization (Lee and Maunsell 2009; Ni et al. 2012; Verhoef and Maunsell 2016).

Normalization is a neuronal computation implicated in various cortical operations (Carandini and Heeger 2011). Normalization models explain the nonlinear way that neurons sum their responses to individual stimuli when those stimuli appear together (Bonds 1989; Carandini et al. 1997; Carandini and Heeger 1994; Heeger et al. 1996; Morrone et al. 1982). Incorporating attention into these models can explain a wide assortment of observed attention effects on the responses of visual neurons (Boynton 2009; Lee and Maunsell 2009; Reynolds and Heeger 2009).

Studies that have measured both attention modulation and response normalization for individual visual neurons have found that the variance in attention modulation size across neurons is largely explained by differences in the strength of normalization between neurons (Lee and Maunsell 2009; Ni et al. 2012; Verhoef and Maunsell 2016). These studies proposed normalization models that explained differences in normalization strength between neurons by introducing terms that weighted the contributions of individual stimuli to overall normalization. The result is called “tuned normalization” because the differential weighting effectively applies a tuning function to the normalization. Tuned normalization has been described in several studies of cortical visual neurons (Carandini et al. 1997; Lee et al. 1999; Rust et al. 2006; Schwartz and Simoncelli 2001). Notably, variance in the degree of tuned normalization between cells explains much of the observed variance in attention modulation size across neurons (Ni et al. 2012).

Recent studies suggest that the strength of normalization tuning varies with space both across and within neurons in systematic ways (Ruff et al. 2016; Verhoef and Maunsell 2016). Additionally, the extent of tuned normalization for an individual neuron is reflected in the extent of the trial-to-trial variability it shares with other neurons, both within the same cortical area and across different cortical areas (Ruff et al. 2016). These findings suggest that the exact topography of tuned normalization and the specifics of this mechanism are critical to understanding variance in attention modulations.

Here we report that in addition to varying across neurons, attention modulation size varies within individual neurons as well. Furthermore, this within-neuron variance in attention modulation size is explained by within-neuron variance in normalization strength. By recording the activity of individual neurons in the middle temporal area (MT) of trained, behaving rhesus monkeys, we measured neuronal responses to both individual and multiple stimuli presented in different locations within the neuronal receptive field (RF) as well as the modulations of those neuronal responses when attention was cued to one stimulus location or another within the RF. Using the same two RF locations and the same two stimuli for each neuron, we found that switching which stimulus was presented at which location changed both attention modulation and normalization strength in a coupled way. These new findings demonstrate that the effects of tuned normalization are more spatially nuanced than previously thought. We provide an equal-maximum-suppression (EMS) spatially tuned normalization model that extends our understanding of the complex mechanism underlying stimulus interactions and thus attention modulations.

MATERIALS AND METHODS

All protocols involving animals were submitted to and approved by the Harvard Medical School Institutional Animal Care and Use Committee.

Animal training and task design.

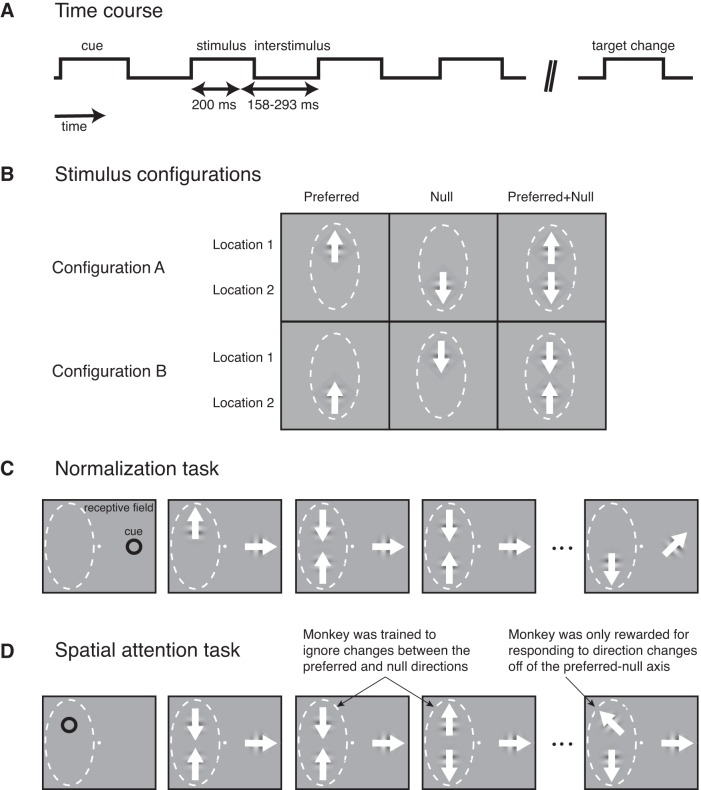
Two male rhesus monkeys (Macaca mulatta) that weighed 8 and 12 kg received a head post and a scleral search coil implant under general anesthesia. After recovery, we trained each animal to do a change-detection task (Fig. 1). In each trial the animal fixated a small white dot presented at the center of a video monitor (44° × 34°, 1,024 × 768 pixels, 75 Hz refresh rate, gamma corrected) on a gray background (42 cd/m²). The animal maintained fixation within 1° of the fixation dot while stimuli were presented peripherally at up to three stimulus locations. After the animal initially fixated for 250 ms, a cue in the shape of an annulus appeared for 250 ms, instructing the animal to attend to one of the three locations based on the location of the cue. Two of these locations were within the RF of the neuron being recorded. The third was a location symmetrical to the center of the RF of the neuron, on the opposite side of the fixation dot. All three locations were the same eccentricity from fixation. After the cue was extinguished, sets of up to three small drifting Gabors flashed on and off simultaneously. Each set of Gabors remained on the monitor for 200 ms, and each successive set was separated by an interstimulus period that varied randomly between 158 and 293 ms. We used random stimulus sequence and short stimulus flashes (200 ms each) to prevent the animal from adjusting its effort or feature attention in response to the content of each set of stimuli (Lee and Maunsell 2009, 2010; Williford and Maunsell 2006). Stimulus presentations continued until the Gabor at the cued location appeared in one presentation with a different direction axis (the target).

Fig. 1.

Experimental paradigm used to measure normalization and attention modulations of neuronal driven response rates in 2 stimulus configurations. A: time course of a single trial in the change-detection task. A trial began with a spatial cue to 1 of 3 locations on a monitor, followed by brief stimulus presentations separated by blank interstimulus periods of random duration, until the target change appeared. B: stimulus configurations. The RF stimuli were pseudorandomly presented in 1 of 6 possible stimulus conditions per stimulus presentation. Three stimulus conditions were in configuration A (the preferred stimulus in location 1, the null stimulus in location 2), and 3 stimulus conditions were in configuration B (the null stimulus in location 1, the preferred stimulus in location 2). C: task used to measure normalization effects. Attention was cued to the location outside of the RF. D: task used to measure spatial attention effects. Attention was cued to one RF location in some blocks of trials and to the second RF location in other blocks of trials.

The two Gabors presented at the locations inside the RF fell at locations separated by at least 5 times the SD of the Gabors (Gabor mean SD 0.45°, range 0.42–0.50°, mean separation of Gabor centers 4.2°, range 2.2–6.9°). Because RFs in MT are large (Desimone and Ungerleider 1986), the two stimuli fit easily within the borders of a single MT RF, and comparably large responses were generated at each location.

We trained the animal to detect when a Gabor appeared at the cued location with a drift direction axis different from the previous Gabors at that location (the target) and to make a saccade directly to the Gabor location within 100–600 ms of its onset. Correct responses were rewarded with juice. The appearance of the target stimulus was timed to follow a decaying exponential function of time within the trial (a flat hazard function for direction axis change), encouraging the animal to maintain a constant level of attention across time. Direction axis changes occurred at the two uncued locations as well (distractors), following the same probability as changes at the cued location. If the animal responded to a distractor the trial was terminated without reward. In ~20% of the trials, the trial lasted 6 s without a direction axis change occurring at the cued location, in which case the animal received a reward for maintaining fixation.

We initially measured each recorded neuron for motion direction tuning (see Single-unit electrophysiology for RF mapping methods) and assigned a preferred, a null (opposite), and an intermediate (orthogonal) direction of motion to each neuron. The purpose of the directional stimuli was to evoke differential neuronal responses from the preferred vs. the null stimuli, which allowed measurements of normalization and spatial attention effects. During the recording of each neuron, the animal performed many trials in which it was cued to pay attention to one of the three locations. Responses recorded when attention was directed to the location outside the RF (Fig. 1C) allowed us to measure the effects of normalization. Differences in the responses recorded when attention was directed to each of the two RF locations (Fig. 1D) allowed us to measure the effects of spatial attention. Trials with cuing to each of the three locations were run in consecutive blocks. We collected at least two complete blocks with attention to each location per recorded neuron. The degree of direction axis change for the target stimulus was adjusted independently for each task variant with an adaptive staircase procedure (Watson and Pelli 1983) that maintained behavioral performance at ~82% correct.

For measuring both normalization and spatial attention, the stimuli presented at the location outside of the RF always drifted in the intermediate direction of the neuron, except for target/distractor changes. This ensured that when the animal attended to this outside location for measurements of normalization its attention to direction of motion would always be intermediate between the neuron’s preferred and null directions. For the stimuli presented in the RF, one of six possible stimulus combinations was pseudorandomly assigned on each stimulus presentation flash of a trial (Fig. 1B). Three of the stimulus combinations presented the stimuli in configuration A (preferred stimulus in location 1, null stimulus in location 2), and three of the combinations presented the stimuli in configuration B (null stimulus in location 1, preferred stimulus in location 2). As described above, the purpose of the directional stimuli was to measure neuronal stimulus selectivity. The directional stimuli were not intended to evoke feature attention; in fact, our goal was to minimize the effects of feature attention for the purposes of this study. The random stimulus sequences prevented the animal from being able to adjust its feature attention in response to the random content of each quickly flashed set of stimuli. Thus for measurements of spatial attention (Fig. 1D), when attention was directed to the flashing preferred and null stimuli in the RF the animal did not have time to adjust its feature attention based on which stimuli were presented on each flash. For measurements of normalization, when attention was directed to the location outside of the RF (Fig. 1C), spatial and feature attention could not differentially modulate different stimulus conditions and affect normalization measurements. Finally, while the stimuli presented at the location outside of the RF were always presented at 100% contrast, the stimuli presented in the RF were pseudorandomly assigned a contrast of 0% (i.e., absent), 50%, or 100%.

Stimuli presented in successive presentations at one RF location could be assigned either the preferred or the null drift direction on each individual presentation within a trial. Therefore, when cued to a location in the RF for measurements of spatial attention, the animal had to ignore direction changes from preferred to null or vice versa (180° changes) at the cued location (Fig. 1D). The animal only received a reward for responding to small changes in direction (<90°, i.e., a drift direction off the preferred-null axis) at the cued location.

Single-unit electrophysiology.

After the animal completed training on the behavioral task, a recording chamber was implanted to allow electrodes to reach MT from a posterior approach (axis ~22–40° from horizontal in a parasagittal plane). We used a guide tube and grid system (Crist et al. 1988) to penetrate the dura and glass-insulated platinum-iridium microelectrodes (~1 MΩ at 1 kHz) to record single units. Extracellular signals were filtered between 250 Hz and 8 kHz, amplified, and digitized at 40 kHz, and action potentials from individual neurons were isolated with a window discriminator, with spike times recorded with 1-ms resolution.

For each isolated unit, the RF location was estimated with a hand-controlled visual stimulus. Responses to eight directions and five temporal frequencies were measured with computer-controlled presentations of Gabor stimuli while the animal performed a fixation task. The direction that produced the strongest response was taken as the preferred direction, the direction 180° from the preferred direction was taken as the null direction, and one direction 90° from the preferred direction was used as the intermediate direction. All of the Gabors were presented at the same temporal frequency, the one that produced the strongest average response. The temporal frequency was rounded to a value that produced an integral number of cycles of drift during each stimulus presentation. In this way the Gabors could start and end with odd spatial symmetry, so that the spatiotemporal integral of the luminance of each stimulus was the same as the background. The spatial frequency of all of the Gabors was set to 1 cycle/°. A Gabor moving in the preferred direction and at the preferred temporal frequency was used to quantitatively map the RF (3 eccentricities and 5 polar angles) while the animal performed a fixation task. The RF center eccentricities ranged from 5° to 14° for monkey 1 and from 7° to 14° for monkey 2. The two stimulus locations within the RF were chosen to give approximately equal responses.

Statistical analysis.

We included recorded neurons in the analyses if they exhibited positive, significant driven response ratios (response firing rate/baseline) and we collected data with at least two blocks at each of the three cuing locations. Approximately 13 repetitions of each stimulus condition (Fig. 1B) were presented per block. Additionally, we excluded two neurons from all analyses based on the application of the Tukey method to the normalization modulation indexes (NMIs; see Eq. 2) and attention modulation indexes (AMIs; see Eq. 1): we excluded one neuron with an AMI of 26.0 and one neuron with an NMI of −2.06. We excluded stimuli from the analyses if they were presented at the same time as a target or distractor stimulus, if they appeared after the target presentation, or if they were presented within 400 ms of the start of the stimulus series. Excluding the first one or two stimulus presentations of each trial reduced variance that could arise from stronger responses to the initiation of the stimulus series. We calculated neuronal firing rates using a 200-ms window that began 50 ms after stimulus presentation onset and ended 50 ms after stimulus presentation offset. Other than the peristimulus time histograms plotted in Fig. 2, which plot neuronal firing rates, analyses used neuronal driven rate (response firing rate minus baseline rate). We calculated the average response rate per stimulus condition as the mean driven rate across all included stimulus repetitions. We computed a P value for each Pearson’s linear correlation coefficient using a Student’s t-distribution (“corr”; MATLAB R2015a, The MathWorks).

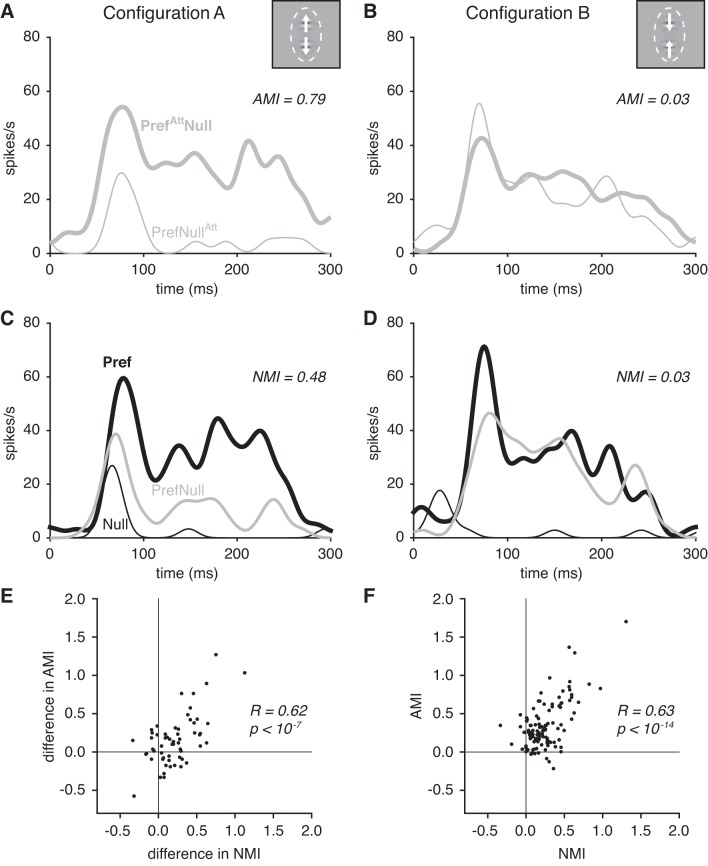
Fig. 2.

Normalization and attention modulation sizes varied with stimulus configuration. A: attention effects for an example neuron with stimuli presented in configuration A. Peristimulus time histograms show that the neuron’s average firing rate with the preferred and null stimuli presented together in the RF was strongly modulated when attention was directed to the location of the preferred stimulus (thick gray line) vs. the location of the null stimulus (thin gray line). B: attention effects for the same example neuron with stimuli presented in configuration B. Directing attention between the 2 stimulus locations did not strongly modulate the average firing rate of the same neuron. C: normalization effects for the same example neuron with stimuli presented in configuration A. Compared with the average firing rate with the preferred stimulus alone (thick black line), adding a second, null stimulus to the RF strongly modulated the average firing rate of the neuron (gray line). The average firing rate due to the null stimulus alone is illustrated as well (thin black line). D: normalization effects for the same example neuron with stimuli presented in configuration B. In this configuration, adding a second, null stimulus to the RF did not strongly modulate the average firing rate of the neuron. E: population scatterplot of within-neuron differences in AMI vs. within-neuron differences in NMI (1 data point plotted per neuron; n = 58). F: population scatterplot comparing AMI to NMI (2 data points plotted per neuron: configuration A AMI vs. NMI and configuration B AMI vs. NMI). In E and F we computed a P value for each Pearson’s linear correlation coefficient with a Student’s t-distribution.

The NMI as calculated with Eq. 2 subtracts baseline firing rates once from the numerator and three times from the denominator. While this should not affect our primary goal of comparing NMI between stimulus configurations, this calculation of NMI will result in magnitude differences between normalization strength quantifications in this report compared with others (Lee and Maunsell 2009; Ni et al. 2012; Verhoef and Maunsell 2016).

We fit the model parameters for each of the proposed models via constrained nonlinear optimizing that minimized the sum-of-squares error. The model parameters α and β were constrained in the fit for the absolute values to be <10 based on the α and β values reported by Ni and colleagues (Ni et al. 2012). The other model parameters were not constrained. Per neuron, we calculated the goodness of fit of each model as the total explained variance, which was determined by taking the square of the correlation coefficient between the estimated response rates from the model and the response rates of the neuron across the stimulus conditions fit by the model. To quantify differences in explained variance between two tested models, we calculated an F statistic based on the residual sum of squares (RSS) and degrees of freedom (df) of models 1 and 2. We used the following equation to compare two models with the same number of parameters:

$$F=\mathrm{R}\mathrm{S}{\mathrm{S}}_{\mathrm{1}}\mathrm{/}\mathrm{R}\mathrm{S}{\mathrm{S}}_{\mathrm{2}}$$

We used the following equation to compare two models with differing numbers of parameters:

$$F=\frac{\mathrm{\left(}\mathrm{R}\mathrm{S}{\mathrm{S}}_{\mathrm{1}}\mathrm{-}\mathrm{R}\mathrm{S}{\mathrm{S}}_{\mathrm{2}}\mathrm{\right)}\mathrm{/}\mathrm{(}\mathrm{d}{\mathrm{f}}_{\mathrm{1}}\mathrm{-}\mathrm{d}{\mathrm{f}}_{\mathrm{2}}\mathrm{)}}{\mathrm{R}\mathrm{S}{\mathrm{S}}_{\mathrm{2}}\mathrm{/}\mathrm{d}{\mathrm{f}}_{\mathrm{2}}}$$

P values were computed per F statistic with the built-in function “fcdf” (MATLAB R2015a, The MathWorks).

RESULTS

We analyzed the visual responses of 58 individual MT neurons from two rhesus monkeys (Macaca mulatta; 37 from monkey 1, 21 from monkey 2). Other findings based on a portion of the present data have been described previously (Ni et al. 2012). We measured the driven rate (response firing rate minus baseline rate) of individual MT neurons in each monkey while it performed a change-detection task (Fig. 1).

Within-neuron differences in attention modulation and normalization strengths covary.

Previous studies of area MT have shown that the strengths of attention modulation and normalization covary across neurons (Lee and Maunsell 2009; Ni et al. 2012). Here we extend those results by showing that the strengths of attention modulation and normalization for individual neurons can differ between stimulus configurations as well and that those within-neuron differences covary in the same way as between-neuron differences.

To examine differences in attention modulations within neurons, we compared how those modulations depended on the stimulus configuration. For each configuration, we measured attention modulations when both the preferred and null stimuli were present in the RF (PN) and attention was directed either toward the location of the preferred stimulus (P^AttN) or toward the location of the null stimulus (PN^Att). We quantified attention effects per configuration with an AMI:

$$\mathrm{A}\mathrm{M}\mathrm{I}=\frac{P^{\mathrm{A}\mathrm{t}\mathrm{t}}N-P{N}^{\mathrm{A}\mathrm{t}\mathrm{t}}}{P^{\mathrm{A}\mathrm{t}\mathrm{t}}N+P{N}^{\mathrm{A}\mathrm{t}\mathrm{t}}}$$ (1)

For many neurons, the AMI differed between the stimulus configurations. For the example neuron shown in Fig. 2, A–D, the AMI with configuration A was 0.79 (strong modulation; Fig. 2A) while the AMI with configuration B was 0.03 (almost no modulation; Fig. 2B), although the same two stimuli were presented in both configurations, randomly interleaved within the same trials.

Prior studies have shown that differences in attention modulation across neurons depend on differences in the strength of their normalization (Lee and Maunsell 2009; Ni et al. 2012), and we found that within-neuron differences in AMI are similarly related to within-neuron differences in the strength of normalization. We measured normalization while attention was held constant and was directed outside of the RF (Fig. 1C). To quantify normalization strength within neurons, we calculated an NMI for each configuration. The NMI compared the linear sum of the recorded neuronal responses to the preferred and null stimuli when each was presented individually in the RF (P+N) to the recorded neuronal response when the preferred and null stimuli were presented together in the RF (PN):

$$\mathrm{N}\mathrm{M}\mathrm{I}=\frac{\left(P+N\right)-\mathrm{PN}}{\left(P+N\right)+\mathrm{PN}}$$ (2)

Compared with the linear sum of the individually recorded responses to the preferred and null stimuli (P+N), normalization models predict a smaller neuronal response to both stimuli together (PN), based on suppressive normalization factors associated with each stimulus (Carandini et al. 1997; DeAngelis et al. 1992; Heeger et al. 1996; Morrone et al. 1982). In a prior study, Ni and colleagues (Ni et al. 2012) used neuronal firing rates to compute NMI; by calculating the linear sum of the individually recorded driven rates (firing rate minus baseline rate) instead, Eq. 2 accounts for any potential suppression on the baseline rate from the null stimulus presented alone.

For the same example neuron illustrated in Fig. 2, A and B, the strength of normalization differed depending on the stimulus configuration. The NMI was 0.48 in configuration A (robust normalization; Fig. 2C) and 0.03 in configuration B (weak normalization; Fig. 2D). For this example neuron, the within-neuron difference in AMI (AMI in configuration A − AMI in configuration B) was 0.76 and the within-neuron difference in NMI (NMI in configuration A − NMI in configuration B) was 0.45. Across the population, the within-neuron difference in AMI was correlated with the within-neuron difference in NMI (Fig. 2E; Pearson’s correlation coefficient: R = 0.62, P < 10⁻⁷; Spearman’s rank correlation coefficient: ρ = 0.43, P < 10⁻⁶; after excluding outliers based on the application of the Tukey method, Pearson’s correlation coefficient: R = 0.53, P < 10⁻⁹).

Within-neuron variation in AMI could arise trivially from within-neuron variation in selectivity for the two directions presented. Differences in stimulus selectivity are expected to produce differences in attention modulation size (Reynolds and Desimone 2003). For example, if in one configuration a neuron responded equally well to the stimuli we assigned as preferred and null, then we would expect no modulation from shifting attention between the two equally effective stimuli. If the two stimuli produced very different responses in one configuration and similar responses in the other, attention modulation size would be expected to differ between those configurations. Most MT neurons, like the example in Fig. 2, are highly direction selective and preserve their selectivity across their entire RF (Albright 1984; Maunsell and Van Essen 1983; Tanaka et al. 1986; although see Cui et al. 2013; Richert et al. 2013). Nevertheless, to test whether within-neuron differences in stimulus selectivity are related to within-neuron differences in AMI and NMI, we calculated a direction selectivity index (DSI) for each configuration:

$$\mathrm{D}\mathrm{S}\mathrm{I}=\frac{P-N}{P+N}$$ (3)

In Eq. 3, P and N refer to the average responses to the preferred and null stimuli when they appeared individually in the configuration under consideration.

There was no detectable correlation between within-neuron differences in DSI and within-neuron differences in AMI (R = 0.14, P = 0.28) or between within-neuron differences in DSI and within-neuron differences in NMI (R = 0.10, P = 0.44). Furthermore, the partial correlation between within-neuron differences in AMI and within-neuron differences in NMI correcting for within-neuron differences in DSI (R = 0.62, P < 10⁻⁷) was little changed from the uncorrected correlation.

A prior tuned normalization study specifically quantified the effect of spatial differences in stimulus excitation across the neuronal RF center and surround (Verhoef and Maunsell 2016). Here, unlike in that prior study, we instead seek to isolate the effect of differences in normalization tuning within neurons. As such, we placed the two stimuli roughly equidistant from the RF center. There was no detectable correlation between within-neuron differences in the response to the preferred stimulus (preferred response in configuration A − preferred response in configuration B) and within-neuron differences in AMI (R = 0.08, P = 0.57) or between within-neuron differences in preferred response and within-neuron differences in NMI (R = −0.04, P = 0.78). Furthermore, the partial correlation between within-neuron differences in AMI and within-neuron differences in NMI correcting for within-neuron differences in preferred response (R = 0.63, P < 10⁻⁷) was little changed from the uncorrected correlation. Correcting for within-neuron differences in null response also had little effect (R = 0.62, P < 10⁻⁷), as did correcting for all three variables described above simultaneously (within-neuron differences in DSI, within-neuron differences in preferred response, and within-neuron differences in null response; R = 0.61, P < 10⁻⁷).

Another potential confound is that the baseline firing rate of many MT neurons is suppressed by a null stimulus presented alone in the RF. Equation 2 addresses this suppression by incorporating the null driven rate (null stimulus response firing rate − baseline rate) into the calculation of NMI. However, when firing rates are driven to 0 spikes/s when a null stimulus is presented alone in the RF, it becomes impossible to measure this suppression based on spike rate because the full suppressive effect of the null stimulus alone is likely to be underestimated. For this reason, we excluded six neurons for which the firing rate with the null stimulus alone was not reliably greater than 0 Hz. For the remaining population of 52 neurons, the within-neuron differences in AMI and NMI were correlated (R = 0.60, P < 10⁻⁶), a correlation that remained significant when accounting for within-neuron differences in DSI (R = 0.59, P < 10⁻⁶), preferred response (R = 0.61, P < 10⁻⁶), and null response (R = 0.60, P < 10⁻⁶).

Finally, as in earlier studies (Lee and Maunsell 2009; Ni et al. 2012), we found a correlation between AMI and NMI across neurons. AMI and NMI were correlated across neurons when the AMI in configuration A was compared to the NMI in configuration A and the AMI in configuration B to the NMI in configuration B (Fig. 2F; R = 0.63, P < 10⁻¹⁴; 2 points plotted per neuron: configuration A AMI vs. NMI and configuration B AMI vs. NMI). However, because attention modulation and normalization strength varied considerably within neurons, this correlation was not seen when the AMI in configuration A was compared to the NMI in configuration B and the AMI in configuration B to the NMI in configuration A (R < 10⁻⁴, P = 0.99).

Consistent with this, across the population the NMI in configuration A was not correlated with the NMI in configuration B (R = 0.15, P = 0.25). The AMI between configurations was correlated (R = 0.42, P < 10⁻⁴), perhaps because of varying levels of attention across recording sessions, which each involved a different stimulus placement that might have been more or less challenging for the animal. This correlation did not appear to be due to a relationship with DSI across the population, as the partial correlation between the AMI in configuration A and the AMI in configuration B was little changed when correcting for the DSI in configuration A (R = 0.41, P < 10⁻³) or the DSI in configuration B (R = 0.42, P < 10⁻³).

A new spatially tuned normalization model explains MT responses.

The normalization of the responses of visual neurons is typically described with a divisive normalization model of the form introduced by Heeger (1992):

$$R_{P,N}=\frac{c_P{L}_P+c_N{L}_N}{c_P+c_N+\sigma }$$ (4)

In Eq. 4 (see Table 1 for a summary of all models), c_P and c_N are the contrasts of the preferred and null stimuli and L_P and L_N set the excitatory drive associated with each of those stimuli. The numerator therefore provides a linear summation of the stimulus excitation. In the denominator, c_P and c_N represent the contrast-dependent suppressive drive associated with each stimulus and σ is the semisaturation constant for the contrast-response function of the neuron. When c_P and c_N are large relative to σ, the neuronal response approximates a contrast-weighted average of the responses to the individual stimuli (Carandini et al. 1997; Heeger et al. 1996).

Table 1.

Summary of normalization models

Model	Equations	Configuration	EV	Free Parameters
Divisive normalization (Eq. 4)	$R_{P,N}\hspace{0.17em}=\hspace{0.17em}\frac{c_P{L}_P\hspace{0.17em}+\hspace{0.17em}{c}_N{L}_N}{c_P\hspace{0.17em}+\hspace{0.17em}{c}_N\hspace{0.17em}+\hspace{0.17em}\sigma }$	A	74%	LP, LN, σ
	$R_{N,P}\hspace{0.17em}=\hspace{0.17em}\frac{c_N{L}_N\hspace{0.17em}+\hspace{0.17em}{c}_P{L}_P}{c_N\hspace{0.17em}+\hspace{0.17em}{c}_P\hspace{0.17em}+\hspace{0.17em}\sigma }$	B
Spatially tuned normalization (Eq. 5)	$R_{P,N}=\frac{c_P{L}_P\hspace{0.17em}+\hspace{0.17em}{c}_N{L}_N}{c_P{\text{α}}_1\hspace{0.17em}+\hspace{0.17em}{c}_N{\alpha }_2\hspace{0.17em}+\hspace{0.17em}\sigma }$	A	78%	LP, LN, σ, α1, α2
	$R_{N,P}=\frac{c_N{L}_N\hspace{0.17em}+\hspace{0.17em}{c}_P{L}_P}{c_N{\alpha }_1\hspace{0.17em}+\hspace{0.17em}{c}_P{\alpha }_2\hspace{0.17em}+\hspace{0.17em}\sigma }$	B
Stimulus-tuned normalization (Eq. 6)	$R_{P,N}=\frac{c_P{L}_P\hspace{0.17em}+\hspace{0.17em}{c}_N{L}_N}{c_P{\alpha }_P\hspace{0.17em}+\hspace{0.17em}{c}_N{\alpha }_N\hspace{0.17em}+\hspace{0.17em}\sigma }$	A	78%	LP, LN, σ, αP, αN
	$R_{N,P}=\frac{c_N{L}_N\hspace{0.17em}+\hspace{0.17em}{c}_P{L}_P}{c_N{\alpha }_N\hspace{0.17em}+\hspace{0.17em}{c}_P{\alpha }_P\hspace{0.17em}+\hspace{0.17em}\sigma }$	B
EMS-spatially tuned normalization (Eq. 7)	$R_{P,N}=\frac{c_P{L}_P}{c_P\hspace{0.17em}+\hspace{0.17em}{c}_N{\alpha }_2\hspace{0.17em}+\hspace{0.17em}\sigma }+\frac{c_N{L}_N}{c_P{\alpha }_1\hspace{0.17em}+\hspace{0.17em}{c}_N\hspace{0.17em}+\hspace{0.17em}\sigma }$	A	92%	LP, LN, σ, α1, α2
	$R_{N,P}=\frac{c_N{L}_N}{c_N\hspace{0.17em}+\hspace{0.17em}{c}_P{\alpha }_2\hspace{0.17em}+\hspace{0.17em}\sigma }+\frac{c_P{L}_P}{c_N{\alpha }_1\hspace{0.17em}+\hspace{0.17em}{c}_P\hspace{0.17em}+\hspace{0.17em}\sigma }$	B
EMS-stimulus-tuned normalization (Eq. 8)	$R_{P,N}=\frac{c_P{L}_P}{c_P\hspace{0.17em}+\hspace{0.17em}{c}_N{\alpha }_N\hspace{0.17em}+\hspace{0.17em}\sigma }+\frac{c_N{L}_N}{c_P{\alpha }_P\hspace{0.17em}+\hspace{0.17em}{c}_N\hspace{0.17em}+\hspace{0.17em}\sigma }$	A	78%	LP, LN, σ, αP, αN
	$R_{N,P}=\frac{c_N{L}_N}{c_N\hspace{0.17em}+\hspace{0.17em}{c}_P{\alpha }_P\hspace{0.17em}+\hspace{0.17em}\sigma }+\frac{c_P{L}_P}{c_N{\alpha }_N\hspace{0.17em}+\hspace{0.17em}{c}_P\hspace{0.17em}+\hspace{0.17em}\sigma }$	B

Name and equation number, equation per stimulus configuration, average explained variance (EV), and free parameters are listed for each model.

Unlike prior studies that fit normalization models to a neuron’s responses to stimuli presented in a single configuration only (e.g., the top row of stimulus conditions of Fig. 1B only) or to the combined responses averaged across configurations (Lee and Maunsell 2009; Ni et al. 2012), here we fit the model to a neuron’s responses to stimuli presented in two stimulus location configurations (configuration A and configuration B; Fig. 1B). We fit a neuron’s responses to 16 stimulus conditions total: 8 stimulus conditions presented in configuration A (the 3 stimulus conditions illustrated in the top row of Fig. 1B with all possible combinations of each stimulus appearing at either 50% or 100% contrast) and 8 stimulus conditions presented in configuration B (the 3 stimulus conditions illustrated in the bottom row of Fig. 1B with all possible combinations of each stimulus appearing at either 50% or 100% contrast). Three free parameters from Eq. 4 (L_P, L_N, σ) were fit per neuron across the 16 stimulus conditions.

This basic divisive normalization model did a limited job of capturing MT responses, explaining an average of only 74% of the variance of the responses. In theory this could be due to the presentation of stimuli in two configurations per neuron; however, other studies have similarly found that most neurons in areas MT and V4 do not respond to multiple stimuli with a simple contrast-weighted average of the responses to the individual stimuli. They instead require a tuned normalization model to closely describe neuronal responses to multiple stimuli (Lee and Maunsell 2009; Ni et al. 2012; Ruff et al. 2016; Verhoef and Maunsell 2016) or when attention shifts between preferred and null stimuli within the RF (Ni et al. 2012). Next, we tested how well tuned normalization models capture the variance of each neuron’s responses to stimuli presented in two configurations.

Verhoef and Maunsell (2016) recently demonstrated that neurons in area V4 have spatially tuned normalization, which they modeled as

$$R_{P,N}=\frac{c_P{L}_P+c_N{L}_N}{c_P{\alpha }_1+c_N{\alpha }_2+\sigma }$$ (5a)

This model adds two free parameters to Eq. 4 to capture spatially tuned normalization: α₁ and α₂ act to modulate the suppression arising from location 1 and location 2, respectively, creating a tuning for suppression across the spatial RF. The tuning is indexed in a strictly spatial way: It does not depend on features of the stimulus like its orientation or direction of motion. As such, Eq. 5a corresponds to neuronal responses to stimuli presented in configuration A: α₁ modulates suppression from the preferred stimulus (c_P) because the preferred stimulus is presented in location 1, and α₂ modulates c_N because the null stimulus is presented in location 2. In configuration B, α₁ modulates c_N because the null stimulus is presented in location 1 and α₂ modulates c_P, as in Eq. 5b:

$$R_{N,P}=\frac{c_N{L}_N+c_P{L}_P}{c_N{\alpha }_1+c_P{\alpha }_2+\sigma }$$ (5b)

Together, Eqs. 5a and 5b can be used to describe a single neuron’s responses to stimuli presented in two different configurations, using five free parameters per neuron.

Alternatively, the α values of a tuned normalization model could modulate suppression based on stimulus feature rather than RF location, as in the stimulus-tuned normalization model proposed by a study in MT (Ni et al. 2012):

$$R_{P,N}=\frac{c_P{L}_P+c_N{L}_N}{c_P{\alpha }_P+c_N{\alpha }_N+\sigma }$$ (6)

In this model, each α term is associated with suppression from a specific stimulus value (e.g., preferred or null direction of motion), regardless of the location in which that stimulus appears: α_P always modulates c_P whether the preferred stimulus is presented in location 1 or 2, and α_N always modulates c_N. Ni and colleagues did not differentiate whether MT responses might be better fit by a spatially tuned model, as much of the data was recorded with a single configuration only (i.e., the preferred stimulus was always presented in the same location, the null stimulus always in the other location). We tested whether fitting each neuron’s responses to tuned normalization models adequately captured the variance of the responses across the two stimulus configurations and whether the spatially tuned normalization model provided a better fit to the data in MT as in V4 (Verhoef and Maunsell 2016).

The responses of MT neurons across the two stimulus configurations were equally explained by the spatially tuned (Eq. 5) and stimulus-tuned (Eq. 6) models, with both models accounting for an average of 78% of the data variance. These tuned normalization models did not explain significantly more of the data variance than the untuned normalization model (compared with Eq. 4; spatially tuned model: F statistic = 0.62, P = 0.56; stimulus-tuned model: F statistic = 1.80, P = 0.21). While Eqs. 5 and 6 adequately capture the variance in neuronal responses with the presentation of stimuli in a single configuration only (Ni et al. 2012; Verhoef and Maunsell 2016), they appear unable to adequately capture neuronal response differences within neurons, when two stimulus configurations are presented (e.g., Fig. 2, A–D).

The tuned normalization models described by Eqs. 5 and 6 allow one location or one stimulus to create less suppression than the other location or stimulus, but this aspect of these equations confers some unusual behavior. In particular, differing degrees of suppression associated with each location or stimulus means that the semisaturation contrast of the response function when one stimulus is presented alone (i.e., the contrast where cα equals σ) will differ depending on where a stimulus is presented in the RF (Eq. 5) or on which stimulus is presented (Eq. 6). This is unexpected because there is generally little interaction between a neuron’s tuning for different stimulus dimensions. For example, V1 neurons have contrast-invariant orientation tuning and, correspondingly, orientation-invariant contrast tuning (Sclar and Freeman 1982).

For this reason, we considered whether MT responses would be better fit by a model of tuned normalization that allowed for each stimulus to generate equally strong suppression of its own excitatory drive but tuned suppression of other locations’ stimuli. For spatially tuned normalization, we used a variant of the model in which each stimulus creates equally strong suppression at its own location but varies in the degree to which it suppresses responses to other stimuli. This model describes responses to configurations A and B, respectively, with the following equations:

$$R_{P,N}=\frac{c_P{L}_P}{c_P+c_N{\alpha }_2+\sigma }+\frac{c_N{L}_N}{c_P{\alpha }_1+c_N+\sigma }$$ (7a)

$$R_{N,P}=\frac{c_N{L}_N}{c_N+c_P{\alpha }_2+\sigma }+\frac{c_P{L}_P}{c_N{\alpha }_1+c_P+\sigma }$$ (7b)

For configuration A, Eq. 7a describes the suppression associated with location 1 (α₁) as fixed at 1.0 for the stimulus presented at location 1 but free to vary (tuned) for the stimulus presented at location 2. Conversely, the suppression associated with location 2 (α₂) is fixed at 1.0 for the stimulus presented at location 2 but free to vary (tuned) for the stimulus presented at location 1. Because each stimulus generates full suppression at its location in proportion to its own contrast, the semisaturation contrast measured with a single stimulus will not vary with stimulus location. Because the maximum suppression from each stimulus is the same in Eq. 7, we refer to this model as equal-maximum-suppression (EMS) spatially tuned normalization.

The EMS-stimulus-tuned normalization model takes a form similar to the EMS-spatially tuned normalization model:

$$R_{P,N}=\frac{c_P{L}_P}{c_P+c_N{\alpha }_N+\sigma }+\frac{c_N{L}_N}{c_P{\alpha }_P+c_N+\sigma }$$ (8)

This model differs from EMS-spatially tuned normalization in that each α term is associated with the suppression from a particular stimulus (preferred or null direction of motion) regardless of the location in which it appears. Eqs. 7 and 8 have exactly the same set of five free parameters as Eqs. 5 and 6.

We tested whether these same five free parameters, when modeled as EMS-spatially tuned or EMS-stimulus tuned normalization, are sufficient to adequately explain the variance in MT neurons when stimuli are presented in two configurations. The EMS-spatially tuned normalization model of Eq. 7 explained 92% of the variance of the data collected during the normalization task on average. This compared favorably with the 78% of the variance explained by Eq. 5 (F statistic = 5.01, P < 10⁻³). In contrast, the EMS-stimulus-tuned normalization model of Eq. 8 explained 78% of the total variance, which was no improvement over Eq. 6 (F statistic = 0.99, P = 0.51). The superior performance of the EMS-spatially tuned normalization model described by Eq. 7 supports the finding in V4 that normalization is weighted by stimulus location (Verhoef and Maunsell 2016) and suggests that spatially tuned normalization might be common in cerebral cortex.

Hypothetically, the within-neuron differences in NMI (and thus AMI) could be related to within-neuron differences in stimulus excitation: either within-neuron differences in L_P (the excitatory drive associated with the preferred stimulus) or within-neuron differences in L_N (the excitatory drive associated with the null stimulus). In fact, an earlier study in V4 specifically presented stimuli at different locations across the neuronal RF center and surround to measure differences in stimulus excitation across space (Verhoef and Maunsell 2016). In this study, we specifically chose two stimulus locations based on minimizing the difference in their distance from the RF center, to isolate within-neuron differences in normalization tuning. And, as described above (see Within-neuron differences in attention modulation and normalization strengths covary), there was no detectable relationship between within-neuron differences in preferred response or null response and within-neuron differences in NMI or AMI. However, to extend those observations, here we use the EMS-spatially tuned normalization model (Eq. 7) to test whether within-neuron differences in L_P or L_N affect the amount of variance explained by the model.

Above, Eq. 7 assigned a single L_P term to each neuron, such that neuronal responses to both configurations were fit with the same L_P term, and the same for L_N. We tested the model with two L_P terms per neuron (L_PA for the preferred response in configuration A, L_PB for the preferred response in configuration B) and two L_N terms per neuron (L_NA and L_NB). Compared with the five-free parameter model with a single L_P term and a single L_N term, this seven-free parameter model did not explain significantly more of the data variance (average explained variance of 96%; F statistic = 2.38, P = 0.15). And, while the within-neuron difference in α terms was correlated with the within-neuron difference in NMI (R = 0.57, P < 10⁻⁶) and with the within-neuron difference in AMI (R = 0.54, P < 10⁻⁵), neither the within-neuron difference in L_P nor the within-neuron difference in L_N was correlated with the within-neuron difference in NMI (L_P: R = 0.04, P = 0.79; L_N: R = 0.17, P = 0.20) or with the within-neuron difference in AMI (L_P: R = −0.11, P = 0.42; L_N: R = 0.08, P = 0.57).

Attention and normalization in MT.

Attention has previously been incorporated into normalization models as a multiplicative effect on both the excitatory and suppressive drive of the attended stimulus (Lee and Maunsell 2009; Ni et al. 2012; Verhoef and Maunsell 2016). Following this approach, we examined whether the EMS-spatially tuned normalization described by Eq. 7 can explain the effects of attention.

We modeled the effect of attention in the EMS-spatially tuned normalization described by Eq. 7 with the following modifications to the model descriptions for configurations A and B, respectively:

$$R_{P^{\mathrm{Att}},N}=\frac{\text{β}{c}_P{L}_P}{\text{β}{c}_P+c_N{\alpha }_2+\sigma }+\frac{c_N{L}_N}{\text{β}{c}_P{\alpha }_1+c_N+\sigma }$$ (9a)

$$R_{N^{\mathrm{Att}},P}=\frac{\text{β}{c}_N{L}_N}{\text{β}{c}_N+c_P{\alpha }_2+\sigma }+\frac{c_P{L}_P}{\text{β}{c}_N{\alpha }_1+c_P+\sigma }$$ (9b)

Equations 9a and 9b describe the effects of attention to location 1. The β parameter multiplies both the excitatory and suppressive drives of the attended stimulus, regardless of whether it is the preferred or null stimulus. We fit this model with 24 stimulus conditions: the 16 stimulus conditions from the normalization task described above (β set to 1) plus 8 stimulus conditions from the attention task (Fig. 1D), four in configuration A (P^Att, N^Att, P^AttN, PN^Att) and four in configuration B.

The EMS-spatially tuned model explained 91% of the total variance of these 24 stimulus conditions. As expected, there was no detectable correlation between the β parameter and either α₁ (R = −0.05, P = 0.73) or α₂ (R = 0.04, P = 0.77). To test for potential attention-related differences based on spatial location, we also tested the same model with two β parameters, one per attended spatial location. However, this model did not explain any more of the data variance than the same model with a single β parameter (average explained variance of 91%, F statistic = −1.25, P < 1). Additionally, each β parameter was not correlated with the corresponding α parameter associated with the same location (Pearson’s correlation coefficient: β associated with location 1 vs. α associated with location 1: R = −0.12, P = 0.38; same for location 2: R = 0.06, P = 0.67).

Prior analyses of the tuned normalization model found that variance in the tuned normalization mechanism alone could account well for variance in attention modulation magnitude across neurons (Ni et al. 2012). To test whether variance in the EMS-spatially tuned normalization mechanism alone could account for attention modulation variance within as well as across neurons, without variance in the attention parameter β, we set β for all neurons equal to 3.68 (the average fit to β as a free parameter). With the five remaining free parameters, the model explained 90% of the total variance for the 24 stimulus conditions of the normalization and attention tasks. The additional free parameter β did not significantly improve the model fit to the 24 normalization and attention conditions (F statistic = 0.29, P = 0.60). In summary, we found that EMS-spatially tuned normalization is sufficient to explain the size of the attention modulations recorded across neurons in MT and within neurons with different stimulus configurations.

DISCUSSION

Normalization explains the sublinear summation of responses that most sensory neurons show when multiple stimuli appear in their RFs simultaneously. Normalization is widespread in sensory systems and has been proposed as a canonical neural computation (Carandini and Heeger 2011). Because its nonlinear behavior can greatly amplify small changes in the strength of the input from one stimulus, responses to multiple stimuli generally cannot be understood without taking normalization into account. For this reason, normalization is a critical factor in examining how attention affects the responses of a neuron that has more than one stimulus in its RF. Many authors have noted that normalization can explain the dramatic changes in response that occur when attention is shifted between two stimuli within a neuron’s RF (Boynton 2009; Ghose and Harrison 2009; Lee and Maunsell 2009; Reynolds and Heeger 2009). Because normalization can effectively tip the balance when inputs change by small amounts, it is a lens through which the effects of attention must be viewed (see Maunsell 2015).

Normalization in visual neurons is typically described with divisive normalization (Eq. 4; Heeger 1992), which does an excellent job of describing the average behavior of neurons. However, studies of MT have shown that individual neurons can express normalization to dramatically differing degrees (Lee and Maunsell 2010; Ni et al. 2012). Some neurons show robust normalization, while others show little or no normalization. For those neurons, adding a nonpreferred stimulus can have no effect on the response to a preferred stimulus, whereas divisive normalization (Eq. 4) predicts response suppression. Because this variance in normalization cannot be accommodated by standard divisive normalization, Ni and colleagues (Ni et al. 2012) introduced a stimulus-tuned normalization model to account for the range of effects seen in MT. In this model, normalization was tuned to limit the suppressive effect of the nonpreferred stimulus rather than giving equal weight to the suppression from each stimulus.

A recent study extended previous findings by exploring variance in normalization within the RFs of individual V4 neurons (Verhoef and Maunsell 2016). By presenting preferred and nonpreferred stimuli in different spatial configurations, it was found that the apparent interactions between preferred and nonpreferred stimuli varied depending on the configuration of the stimuli used. This behavior was well explained by a spatially tuned normalization model. Because MT responses had not been examined with a spatially tuned normalization model, in the present study we compared the performance of stimulus-tuned and spatially tuned normalization models. We found that spatially tuned normalization does a better job of explaining MT responses.

The form of spatially tuned normalization that gave the best account of MT responses was EMS-spatially tuned normalization. Basic spatially tuned normalization (Eq. 5) adjusts the normalization by making the suppression associated with one RF location weaker but still applying that suppression uniformly to all inputs to the RF. In contrast, in EMS-spatially tuned normalization each stimulus generates an equally strong suppressive effect on the excitatory drive from that stimulus, but the suppression of each stimulus on other stimuli is attenuated.

It is not clear why suppression should be nonuniform across an RF. One could imagine that suppression was increasingly localized (spatially tuned) for sites near the edge of the RF. However, both stimulus locations in our study were well within the RF, so we have limited basis for considering this possibility, and location-dependent differences in the response to the preferred stimulus presented alone did not account for the nonuniformity of suppression. Differences in direction selectivity similarly did not account for the nonuniformity of suppression. Further experimental data might help address this question. In particular, more detailed mapping of the suppressive effect may clarify the extent and potential organization of variations in suppression across an RF. The present work used only two locations within the RF and could represent the tuning of normalization with a single scalar. In reality, suppression from an RF location will take the form of a two-dimensional weighting function. The detailed spatial form of suppression associated with different RF locations might be measured by mapping suppressive effects between pairs of locations in a matrix that tiles an MT RF.

As with previous studies (Lee and Maunsell 2009; Ni et al. 2012; Verhoef and Maunsell 2016), we found that variance in normalization explained much of the variance in attention-related modulations of neuronal responses. It should be noted that normalization is fixed across attention conditions in the model used (Eq. 9). Attention acts through a single term to adjust the strength of the input associated with each stimulus. This suggests that normalization operates on a neuron’s inputs in a fixed way whether attention is present or not and that the only effect of attention is to adjust the strength of the input associated with an attended stimulus.

Many questions remain about normalization and attention. One of note is the relationship between normalization and visual feature attention. Even with spatial attention directed to a stimulus outside of a neuron’s RF, the neuron’s responses can still be modulated by the features of the attended stimulus (Maunsell and Treue 2006). Our data and earlier findings on the subject have examined visual spatial attention. It is not known how feature attention will interact with normalization. Attention to a visual feature such as a direction or color typically causes neurons that prefer that stimulus to respond more strongly to any stimulus (Martinez-Trujillo and Treue 2004; Maunsell and Treue 2006). Such a gain change (on either the output or all the inputs of a neuron) would not be expected to engage normalization in a way that would amplify attention-related modulations. Similarly, because the suppression associated with normalization is not thought to be sensitive to stimulus values, shifting attention between different stimulus values should not amplify attention-related modulations. Nevertheless, although we have seen no evidence for attention acting directly on the normalization mechanism, it is at least conceivable that feature attention alters the rules of normalization to impose a stimulus-tuned normalization. Examining the relationship between feature attention and normalization might validate the spatially tuned normalization model, or it might reveal that normalization is more elaborate than currently appreciated.

GRANTS

This work was supported by National Eye Institute Grant R01 EY-005911 (J. H. R. Maunsell) and the Simons Foundation (A. M. Ni).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.M.N. and J.H.R.M. conceived and designed research; A.M.N. performed experiments; A.M.N. analyzed data; A.M.N. and J.H.R.M. interpreted results of experiments; A.M.N. prepared figures; A.M.N. and J.H.R.M. drafted manuscript; A.M.N. and J.H.R.M. edited and revised manuscript; A.M.N. and J.H.R.M. approved final version of manuscript.