Nanoscale Back Contact Perovskite Solar Cell Design for Improved Tandem Efficiency

Abstract

Tandem photovoltaics, combining absorber layers with two distinct band gap energies into a single device, provide a practical solution to reduce thermalization losses in solar energy conversion. Traditionally, tandem devices have been assembled using two-terminal (2-T) or four-terminal (4-T) configurations; the 2-T limits the tandem performance due to the series connection requiring current matching, while the standard 4-T configuration requires at least three transparent electrical contacts, which reduce the total collected power due to unavoidable parasitic absorption. Here, we introduce a novel architecture based on a nanoscale back-contact for a thin-film top cell in a three terminal (3-T) configuration. Using coupled optical–electrical modeling, we optimize this architecture for a planar perovskite-silicon tandem, highlighting the roles of nanoscale contacts to reduce the required perovskite electronic quality. For example, with an 18% planar silicon base cell, the 3-T back contact design can reach a 32.9% tandem efficiency with a 10 μm diffusion length perovskite material. Using the same perovskite quality, the 4-T and 2-T configurations only reach 30.2% and 24.8%, respectively. We also confirm that the same 3-T efficiency advantage applies when using 25% efficient textured silicon base cells, where the tandems reach 35.2% and 32.8% efficiency for the 3-T, and 4-T configurations, respectively. Furthermore, because our design is based on the individual subcells being back-contacted, further improvements can be readily made by optimizing the front surface, which is left free for additional antireflective coating, light trapping, surface passivation, and photoluminescence outcoupling enhancements.

Thermalization of hot electrons to the band edge is the largest source of power loss (∼40%) in photovoltaic solar-energy-conversion;¹ reducing this loss provides the largest opportunity to reach ultrahigh efficiency solar cells. Although many strategies have been proposed, only multijunction concepts have currently led to efficiency values above the single junction Shockley–Queisser (S-Q) limit.²⁻⁶ Unfortunately, tandem solar cells are currently too expensive to use without light concentration, which requires expensive optics, solar tracking, and often active cooling. The rise of high-efficiency, inexpensive thin-film solar cells with band gaps suitable for tandem solar cells (e.g., halide perovskites) have renewed interest in making tandem solar cells for 1-sun applications.⁷⁻¹³

Traditionally, tandem solar cells have been fabricated in either 2- or 4-terminal configurations,¹⁴ representing different extrema in the space of optical and electronic coupling. The 2-terminal (2-T) design is monolithic and requires series interconnected cells, while the 4-terminal (4-T) design is mechanically stacked and enables independently connected cells. While 2-T configurations can benefit from optically coupling the top and bottom cells to prevent loss and reflections between the devices, they remain electronically coupled as well, forcing the two cells to be current matched. Even with an optimal design, this current matching condition can only be reached for a single optical spectrum; under diffuse light conditions, the large shifts in illumination spectrum can cause large efficiency losses (e.g., up to ∼11% relative in energy-yield disadvantage^15,16). Conversely, 4-T devices benefit from electronically decoupling the two cells, alleviating the need for current matching, but thick spacer layers generally cause the tandem to lose the optical benefits of the monolithically stacked 2-T tandems, and the additional contact again introduces a ∼10% relative efficiency loss.¹⁷ The 3-terminal (3-T) configurations present a possibility for allowing the tandem cells to be optically coupled but electrically decoupled, gaining the advantages of both standard configurations, while avoiding their main drawbacks.¹⁸⁻²³

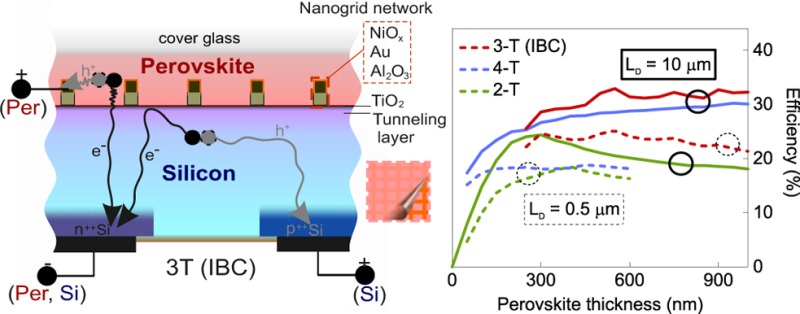
Here, we introduce a new design for a perovskite solar cell using embedded nanoscale back contacts in tandem with interdigitated back contact (IBC) silicon cells, coupled in a 3-T configuration (Figure 1). Because of the double back contact design, only one (infrared) transparent contact is required (located between the perovskite and silicon cells), reducing reflection and parasitic absorption losses. Because the top of our tandem cell does not require a contact, this design can leave the front surface free for texturing, antireflection coating, and surface passivation. These effects are not optimized in our current analysis but could lead to higher absorption due to reduced reflection, and large gains in open circuit voltage due to enhanced light outcoupling or directional emission.²⁴⁻²⁶ We use coupled optical–electrical simulations to compare the performance of planar and textured tandem cells in 2-, 3-, and 4-T configurations. The 3-T and 4-T planar tandem cells have the potential to exceed the single junction S–Q efficiency limit of ∼33% using a perovskite with minority carrier diffusion lengths, L_D, of at least 12 and 24 μm for 3-T and 4-T tandems, respectively. The 2-T configuration cannot reach such high efficiency values even for perfect perovskite quality (optical limit). More significantly, using a lower quality perovskite material with L_D = 0.8 μm, only our 3-T configuration is able to surpass the 26.3% world record²⁷ for a single junction (textured/nonplanar) crystalline silicon solar cell. The improved performance of our design relies on the embedded nanowire grid back contact that benefits from three main effects. First, enhanced charge generation near the nanogrid contact due to nanophotonics effects relaxes the diffusion length constraint for high efficiency tandems. Second, decoupling the carrier collection of the two devices removes the need for current matching (as in 2-T). And third, eliminating the front transparent electrode increases the current, particularly in the top cell. This design can be used as a future building block to create multijunction back contact photovoltaics.

Figure 1.

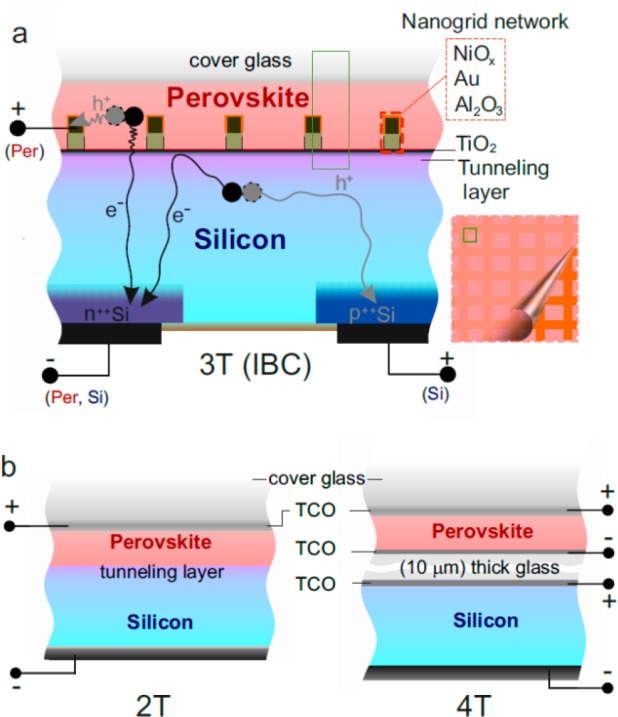
Schematic designs of perovskite-silicon tandem solar cells. (a) Double back contact with three-terminal configuration (3-T (IBC)). The top open space (cover glass) is free providing opportunities for light trapping, antireflective coating, surface passivation, directional emission or enhanced photoluminescence outcoupling. The nanoscale embedded grid is composed of NiO_x hole-transporting layer (orange), Au metal contact (dark-brown), and Al₂O₃ dielectric-insulating layer (light-brown). The negative polarity is shared between the perovskite (Per) and silicon (Si) cells in the n⁺⁺Si (emitter) back contact silicon cell. Minority carriers from the silicon cell (e^–) are collected then reinjected by the tunnel layer containing n⁺⁺Si (front-floating emitter). The inset shows a schematic top view with 3D simulated unit cell indicated as a light-green box (half-pitch square size). (b) Traditional tandem configurations with two-terminal (2-T) and four-terminal (4-T) configurations; details in the Supporting Information. These cross-sectional views are not drawn to scale (perovskite thickness ranges between 0.05 to 1 μm, and the silicon is 180 μm).

Structural Description and Theory

The 3-T design considered here is composed of a perovskite cell with embedded nanoscale back contacts as the top cell, and an interdigitated back contact (IBC) silicon cell as the bottom cell, as depicted in Figure 1. Our top cell design differs from previous works reported on back contact perovskite²⁸ and thin film^18,29,30 solar cells because it incorporates only a single patterned contact (an embedded nanogrid network) and uses a carrier-selective layer on the front surface of the bottom silicon cell as the second contact. For all simulations, we use a top surface of fused-SiO₂ representative of the front glass layer on a finished module. The nanogrid network is composed of an insulating layer (100 nm thick Al₂O₃) and a metal contact (100 nm thick Au) coated with metal oxide hole transporting layer (10 nm thick NiO_x). The grid width is 60 nm with pitch sizes from 0.25 to 6 μm. This can be fabricated lithographically^31,32 or using random nanowire mesh^33,34 structures as a self-aligned etch mask.³⁵ We use a CH₃NH₃PbI₃ perovskite (E_g ∼ 1.55 eV) absorber, where the thickness is optimized between 0.05 and 1 μm for all configurations. Although the bandgap of this perovskite is not ideal (∼1.55 eV vs the ∼1.78 eV ideal E_g) for a tandem with silicon (E_g ∼ 1.12 eV), all high-efficiency single junction perovskite devices to date have consisted of the CH₃NH₃PbI₃ material or a variation with a nearly identical band gap.³⁶

The electrons generated from the perovskite cell are collected by a metal oxide electron transporting layer (10 nm thick TiO₂) and transferred to the IBC silicon cell via a tunnelling layer. In this case, the electron contact of the IBC silicon cell will receive electrons both from the perovskite and silicon cells. Holes from the perovskite will be collected directly by the metal nanowire contact grid, via the hole transporting layer. The efficiency of electron transmission from the top to the bottom cell depends on the quality of the tunnelling layer composed of n⁺⁺Si layers (called front floating emitter/FFE); this design is just one possibility mirroring the original design of FFE.^37,38 The FFE can be thought of as the negative electrode representing a common ground between the devices, with the potential of the two cells being determined by their positive electrodes. As a result, the working principle of the 3-T IBC is equivalent to a 4-T, in which the two cells are electrically decoupled. This thereby removes the current matching condition (present in 2-T design), while still allowing for a monolithic fabrication. The presence of a nanogrid network optically couples the top and bottom cells, while also modifying the generation profile in the perovskite material, which when optimized can reduce the diffusion length requirements, and increase the optical path length in the silicon cell.

To assess the potential device performance, and hence the benefits of our architecture, we construct an optoelectronic model that couples the device optical and electrical response, as schematically described in Figure 2. We first simulate the optical response of the subcells and then use the output of the optical generation rate response as an input for our electronic modeling. The optical input is the standard solar spectrum (AM 1.5) from 300 to 1300 nm with 1 nm spectral resolution. For the perovskite cell, the light propagation is computed with a wave optics approach with all optical interference in the interlayer structures simulated using three-dimensional (3D) finite-difference time-domain calculations (FDTD, Lumerical Solutions software³⁹). The optical transmission from the top cell is used as the optical input to the bottom cell, which due to the large thickness is simulated based on a ray-optics approach, using a rigorous polarization ray tracing (PV lighthouse, OPAL⁴⁰). The values of the optical constants for all materials were obtained either from spectroscopic ellipsometry measurements or taken from the literature (Supporting Information). From the optical constants and computed electric field, we can calculate the charge generation rate as a function of position and use that as an input to solve electrostatic and drift-diffusion transport equations for each material. Realistic values of electrical bandgaps, dielectric permittivity, electron/hole effective mass, electron affinity, mobility, lifetime, density of states, and equivalent resistivity of all materials are provided as inputs to the simulation (Supporting Information). For computational efficiency, we solved the transport equation using a 3D finite element method (Lumerical Solutions, Device Multiphysics⁴¹) for the perovskite cell and using a conductive boundary approach (PV lighthouse, Quokka⁴²) for the IBC silicon cell. Unless specified, the coupled optical–electrical simulations were fully conducted in 3D (see Supporting Information for further details).

Figure 2.

Coupled optical–electrical simulation setup. The output of the optical responses, via spatial information on charge generation rate, is used as the input for the electronics modeling. A is absorption, R is reflection, T is transmission, |E|² is electric field intensity, E_g is electronic bandgap, μ is charge mobility, ε_DC is DC permittivity, DOS is density of states, m* is charge effective mass, χ is work function, J is current, V is voltage, e^– number of electrons, h⁺ is number of holes, and (x, y, z) is three-dimensional spatial information. Unless specified, all optoelectronic modeling is based on 3D simulation.

To benchmark the 3-T double-IBC perovskite-silicon tandem solar cell performance, we compare it with standard 2-T and 4-T configurations using commensurate material selections (details in schematic designs, proven compatibility of all materials involved are described in Supporting Information). The 2-T is composed of a transparent conductive oxide (TCO) as a top contact, a tunnel junction (between the perovskite and silicon), and a high quality planar silicon cell (front and back contacted) with an 18.8% power conversion efficiency (the equivalent of 25% efficiency with an optimized textured front surface and an SiN_x antireflective coating). The 4-T is composed of three TCO layers (two for the perovskite cell, and one for Si top contact), a 10 μm thick glass insulating layer between the perovskite and silicon, and an identical silicon cell as used in the 2-T. All configurations use metal oxide layers both for electron and hole transporters (as opposed to organic layers, e.g. Spiro-OMeTAD, PCBM, PEDOT:PSS) in order to minimize the parasitic absorption.

Optically Limited Performance

We begin by investigating the purely optical performance of the three configurations, equivalent to setting the diffusion length for all materials to infinity (internal quantum efficiency of 100%, Figure 3a–c). As the perovskite thickness increases, the absorption shifts from the silicon to perovskite. For electrically decoupled devices, this is uniformly beneficial as the wider band gap of perovskite allows an increased power generation, but for current-matched devices a clear optimal thickness is visible. For the 2-T tandem (Figure 3a), we see that the tandem device exceeds the Si limit (∼29.4% Auger-limited efficiency⁴³) for perovskite layers from ∼200 to 400 nm thick with the maximum efficiency of 31.7% with a 250 nm thick perovskite layer. The falloff in efficiency above 400 nm is due to the current matching condition required for the 2-T series connection (total current is limited by the cell having lower current).

Figure 3.

Limiting and realistic performance. Limiting tandem power conversion efficiency as a function of perovskite thickness on (a) 2-terminal, (b) 4-terminal, and (c) 3-terminal (IBC). The limiting efficiency is modeled by assuming infinite minority carrier diffusion length in perovskite and silicon cells; benchmarked with their respectively calculated S-Q limit (39.2%; 1.55 eV perovskite with 1.12 eV Si bandgaps), and single junction Si limit (29.4%; corrected for Auger recombination). The contribution of the Si and perovskite materials to the tandem efficiency are indicated. Similarly, in the realistic case on (d) 2-terminal, (e) 4-terminal, and (f) 3-terminal (IBC), by assuming finite minority carrier diffusion length in perovskite (L_D) and Si, benchmarked with simulated planar single junction standard front-rear contacted and interdigitated back-contact (IBC) Si cells efficiency. At L_D = 0.5 μm, the data points are missing in panels d,e because the perovskite cells are too resistive to simulate (as the thickness increases) in contrast to panel f. Some data, however, are limited (below 250 nm perovskite thickness) in panel f, because of a thickness restriction by the embedded nanogrid contacts. In panel f, the realistic tandem efficiency is plotted at global optimum pitch sizes: 5.125 μm (for L_D = 10 μm), and 1.6 μm (for L_D = 0.5 μm). All PV parameters (J_sc, V_oc, FF) are tabulated in Figure S4 (Supporting Information).

The limiting efficiency is higher for the 4-T configuration because the top and bottom cells are electrically decoupled. For the 4-T tandem (Figure 3b), the Si limit can be exceeded if the perovskite thickness is greater than ∼100 nm (with a TCO thickness of 100 nm). The TCO in the 4-T tandem also acts as an antireflection coating, as the TCO thickness was optimized to minimize reflection (Supporting Information). The maximum 4-T tandem efficiency is 36.5% within the 1 μm perovskite thickness limit chosen for practical feasibility (and comparison with diffusion-limited devices later on). The asymptotic efficiency for the 4-T tandem is 36.6%.

The 3-T IBC tandem (Figure 3c) improves further the maximum tandem efficiency, reaching 37.9% at 5.125 μm pitch and 1 μm perovskite thickness (also the asymptotic limit). The efficiency oscillates with thickness for both the 2- and 3-T, showing that in these cases, unlike the 4-T configuration, the perovskite and silicon are optically coupled, which improves the tandem performance. However, unlike the 2-T, the two cells are electrically decoupled in the 3-T IBC with additional optical coupling benefits, which enables the higher efficiency.

Coupled Optoelectronic Simulations

To evaluate the realistic performance of the three configurations, we examine two different scenarios for perovskite material quality by varying the minority carrier diffusion length (Figure 3d–f); we use diffusion lengths for the CH₃NH₃PbI₃ of 0.5 μm and 10 μm representing a realistic and optimiztic perovskite quality, respectively. The corresponding efficiency values of the perovskite materials optimized as single junction devices are 11.6% and 24.5% with 0.5 and 10 μm diffusion lengths and perovskite film thicknesses of 0.45 and 1 μm, respectively. The tandem performance is computed with high quality planar single-junction Si cells of 18.8% single-junction efficiency; these correspond to simulated efficiency values of textured devices (with optimized antireflective coatings) of 23.3% for front and rear contacted Si and 25% for IBC Si.

For the 2-T configuration (Figure 3d), the tandem efficiency does not exceed the planar Si (18.8%) unless the high quality perovskite is used. Additionally, as the diffusion length is reduced, the maximum efficiency is shifted to configurations with thicker perovskite films due to the current matching constraint, a trend that optical simulation alone cannot predict, demonstrating the importance of coupled optoelectronic simulations in tandem devices. The maximum 2-T tandem efficiency using 0.5 μm and 10 μm perovskite diffusion lengths are 18.5% (at 400 nm thick), and 24.8% (at 300 nm thick), respectively.

Similarly, for the 4-T configuration (Figure 3e), the tandem efficiency does not exceed the single junction planar Si limit (18.8%), unless a high quality perovskite is used. The maximum 4-T tandem efficiency using 0.5 μm, and 10 μm perovskite carrier diffusion lengths are 18.8% (at 450 nm thick), and 30.2% (at 950 nm thick), respectively.

In the 3-T tandem configuration (Figure 3f), the lower quality perovskite (0.5 μm diffusion length) can be used to exceed the efficiency of planar IBC Si of 18.9%, which is in contrast to the 2-T and 4-T tandems. In this case, the simulated tandem efficiencies are well above the planar IBC Si limit for perovskite thickness up to 850 nm. Thicknesses below 250 nm are not considered here, as the nanogrid contact would be outside of the perovskite material. Note that the hole collection efficiency for the perovskite in the 3-T tandem depends on the depth of the nanogrid contacts inside the perovskite, controlled by the insulator (Al₂O₃) thickness. The efficiency values presented here are based on an optimal insulator thickness of 100 nm; as a general rule, the nanogrid contact should be embedded around <40% of the perovskite thickness (Supporting Information). The global maximum 3-T (IBC) tandem efficiencies for the 0.5 and 10 μm diffusion lengths are 25.1% (at 550 nm thick with 1.6 μm pitch), and 32.9% (at 550 nm thick with 5.125 μm pitch), respectively.

To date, the world record efficiency of single junction Si photovoltaics is 26.3%. These cells use nonplanar front-side texturing with antireflection coatings. Unless a very high quality perovskite is used (greater than ∼2 μm minority carrier diffusion length), a planar perovskite-silicon tandem using a standard 2-T or 4-T configuration will not exceed the ∼26.3% textured single junction Si efficiency. We demonstrate that the 3-T (IBC) can overcome the limitation even using lower quality perovskites (e.g., with ∼0.8 μm minority carrier diffusion length). In terms of the efficiencies of the individual layers, this difference means that a > 21.7% equivalent single junction perovskite cell is needed to bring a 18.8% planar Si cell above 26.3% in a 2-T or 4-T configuration, whereas only a > 18.8% equivalent single perovskite cell is needed using our 3-T (IBC) configuration.

The Roles and Limitations of the Nanowire Grid Contacts

To elucidate the performance improvements of the 3-T (IBC) tandem design relative to the standard 2-T and 4-T tandem configurations, we investigate the influence of parasitic absorption and reflection, absorption path length enhancements, and nanophotonic effects from the nanowire grid.

We begin by first identifying losses from the device spectral response curves, shown in Figure 4a. The external quantum efficiency (EQE) spectra of the tandems are simulated in their highest steady-state performance configurations (24.8%, 30.2%, and 31.2%, for 2-T, 4-T, and 3-T, respectively), corresponding to the 10 μm diffusion length. Note that the 31.2% efficiency corresponds to 1 μm pitch size to demonstrate more clearly the nanophotonic cavity effects in the 3-T (IBC) configuration but an optimized 3-T configuration gives 32.9% efficiency.

Figure 4.

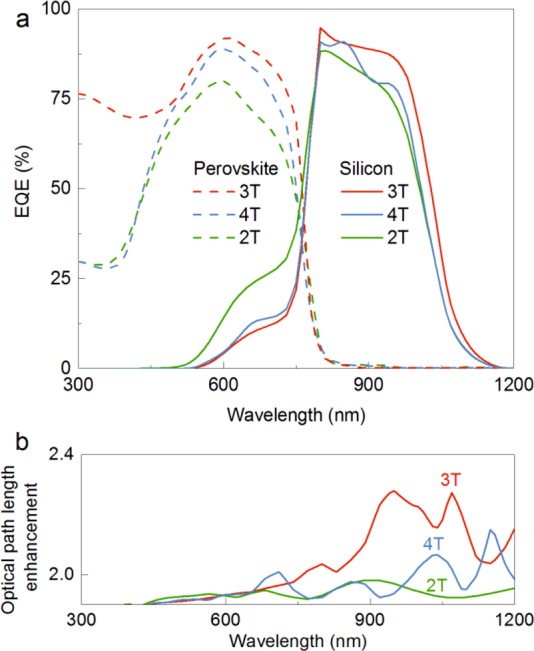
Coupled optical–electrical spectra response. (a) Simulated EQE of perovskite (dashed lines) and silicon (solid lines) cells for 2-T, 4-T, and 3-T (IBC) configuration at their optimum performances according to the Figure 3 (at perovskite thickness of 300, 950, and 550 nm for 2-T, 4-T, and 3-T (IBC), respectively with perovskite minority carrier diffusion length of 10 μm). (b) Optical path length enhancement showing significant enhancement in the 3-T (IBC) at long wavelength range that is beneficial for the bottom Si cell.

The 3-T configuration shows improved EQE most significantly in the wavelength range below 500 nm and to a lesser degree above 500 nm. We attribute the short wavelength improvements to the use of nanowire grid contacts embedded inside the perovskite. The free front surface allows blue photons, typically parasitically absorbed by the TCOs present at the front of the 2-T and 4-T geometries, to be absorbed instead in the perovskite and collected in the 3-T (IBC) tandem. Although the 4-T has three TCO layers, its performance surpasses that of the 2-T design near the perovskite band edge, due to differences in the optimized perovskite layer thicknesses (950 and 300 nm for 4-T and 2-T, respectively). The near band-edge EQE (∼780 nm; 1.58 eV) for 3-T (IBC) is higher than that of the 4-T, even with a thinner perovskite layer (550 and 950 nm, respectively). This can be explained by a higher charge generation rate from ∼700 to 800 nm due to a cavity effect provided by the nanowire grid (Supporting Information).

The EQEs for the Si bottom cells in 2-T and 3-T designs show similar behavior, suggesting that the top and bottom cells in the 2-T and 3-T tandems share a similar optical-coupling mechanism. However, the EQE for the Si cell in the 2-T is lower than that in 3-T tandem, partly due to near-IR parasitic absorption of the top TCO in the 2-T (Supporting Information) in addition to a shorter optical path length enhancement (the optical interaction length normalized to the absorber thickness) in the 2-T Si cells (Figure 4b). The presence of the nanowire grid increases the optical path length enhancement inside the Si cell at longer wavelengths (∼900 to 1100 nm) due to two features: first, scattering from the nanowire grid changes the angular distribution of light (a maximum at 1100 nm wavelength with 15° effective angle; see details in Supporting Information) thereby increasing the interaction length. Second, this scattering additionally improves the light trapping inside the device, further improving the effective optical path length in the silicon.

Having examined the influences responsible for modification of the total optical generation in the three configurations, to further understand the efficiency improvements we examine the electrical contributions by comparing the drift-diffusion transport in our 3-T (IBC) with the 4-T tandem, as both configurations similarly share electrically decoupled schemes. In the 4-T, the tandem efficiency increases with the perovskite thickness and diffusion length (Figure 5a). The tandem efficiency starts to decrease as the perovskite thickness approaches its minority carrier diffusion length due to the trade-off between the distance charges have to travel (before nonradiative recombination) and the amount of absorbed photons in the perovskite, which in the 4-T configuration is simply governed by Beer–Lambert exponential decay (see the charge generation rate decaying profile in the inset Figure 5a).

Figure 5.

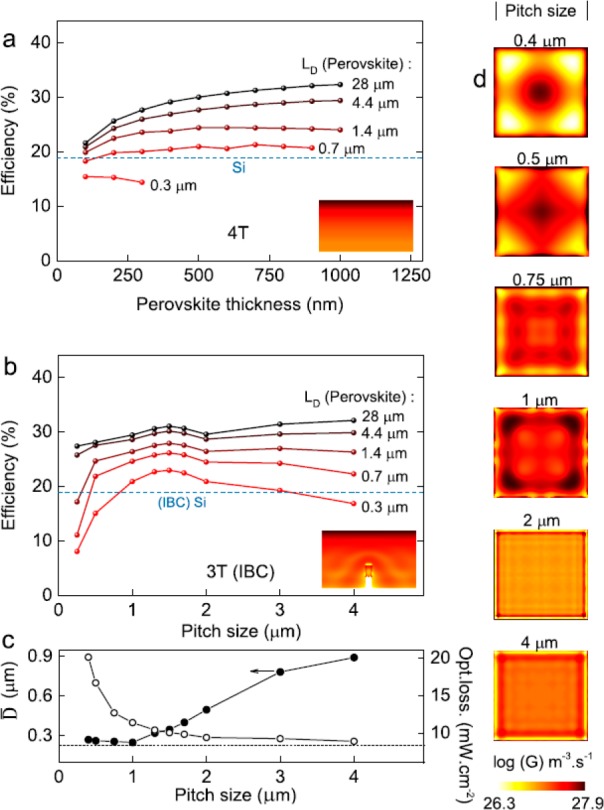
Transport and charge collection using the embedded nanoscale back contacts. (a) Tandem power conversion efficiency of the 4-T as a function of perovskite thickness; the omitted data points are due to a high (transport) resistance as the perovskite thickness increases. (b) Tandem power conversion efficiency of the 3-T (IBC) as a function of pitch size of the nanogrid; carried out at 500 nm perovskite thickness. The insets in (a,b) show cross-sectional charge generation rates that are distinct between 4-T and 3-T (IBC). The tandem performance is examined using different quality perovskites based on their minority carrier diffusion length values (L_D). (c) Calculated effective collection distance (D̅) and total optical losses (reflection and parasitic absorption) as a function of pitch size. (d) Top view of charge generation rate in 3-T (IBC) showing most charges are concentrated toward the contact (edges of the squares) as the pitch size increases (the values indicate different pitch sizes); the generation rate values are averaged over the perovskite thickness inside the cavity.

The drift–diffusion transport in the 3-T (IBC) is more complex, as the charges have to travel simultaneously in vertical and lateral directions. Similar to the influence of perovskite thickness, there is a trade-off between increased reflection at small pitches and increased transit distances at large pitches. The incorporation of the nanowire grid network, however, provides optical resonances near the metal nanowire contact that enhance the charge generation rate at the depth of the nanowire grid (inset in Figure 5b), while also modifying the lateral generation rate. Using a 500 nm thick perovskite layer, we study the tandem efficiency as a function of the nanowire grid pitch (Figure 5b). We observe a drop in tandem efficiency of the 3-T when the pitch is below 1 μm due to increased reflection and thus lower transmission of light into the Si bottom cell. A reduced reflection and higher transmission into the Si bottom cells results in an increase in the tandem efficiency when the pitch size is above 2 μm. This simple trend does not hold for a pitch size from 1 to 2 μm, where the tandem efficiency is slightly reduced. We correlate this with cavity resonance effects of the pitch on lateral generation profiles of the 3-T (IBC).

To further understand the cavity effect of the pitch on the lateral generation, we calculate the mean distance to collection (D̅) by integrating the shortest distance to the further of the two contacts at all points in the absorber volume, weighted by the total generation rate at that location (Supporting Information). The length D̅ thus represents the average distance generated charges have to travel before being collected (Figure 5c); configurations with a shorter D̅ will show higher total collection, particularly for materials with lower diffusion lengths. Remarkably, D̅ actually becomes smaller as the pitch increases from 400 nm up to 1000 nm. This indicates that by utilizing photonic cavity effects, we can double the distance between the contacts while reducing the average distance a charge carrier must traverse to be collected. To visualize this photonic cavity effect, we plot the charge-generation rate integrated over the perovskite thickness as a function of lateral position (Figure 5d). For smaller nanowire grid pitches (400–500 nm), the charge generation rate is highest far from the nanowire contact grid, whereas for larger grid pitches (>750 nm), charge generation is increasingly localized near the metal contact. This not only allows us to break from the trade-off between increasing collection probability and increasing absorber material but also partially explains the observed improvement in the 3-T perovskite EQE in the moderate wavelength region for perovskites (500 nm > λ > 780 nm, where TCO absorption is small), relative to the 4-T design. While we examine gold here, this effect holds for other common contact metals (Ag, Al) as well (Figure S10).

Conclusion and Outlook

Herein we have demonstrated the potential of a nanoscale back contact embedded in a thin film solar cell to improve tandem efficiency and relax requirements on the thin film diffusion length. We investigate a perovskite-silicon tandem to build a double back contact tandem design in a three-terminal configuration. On the basis of coupled optical and electronic simulations, we show that our design has the potential to overcome the limits of the traditional two-and four-terminal tandem configurations, in particular reducing the constraints on perovskite quality. Using even moderate-quality perovskite materials with minority carrier diffusion lengths of 0.8 μm, the 3-T IBC shows tandem power conversion efficiency surpassing the single junction silicon efficiency record of 26.3%, when used with an 18% efficiency planar silicon cell. Comparatively, achieving this performance in a 4-T tandem design requires at least a 2 μm diffusion length in the perovskite. Perhaps more dramatically with the same 18% silicon base cell, the 3-T IBC design can reach 32.9% tandem efficiency with an optimiztic 10 μm diffusion length perovskite material. Using the same perovskite quality the 4-T and 2-T configurations only reach 30.2% and 24.8%, respectively. Furthermore, in order to surpass the single junction Shockley–Queisser efficiency limit (∼33%), our design halves the requirement on the perovskite carrier diffusion length from 24 μm for a 4-T tandem to 12 μm for our nanostructured 3-T design. The improved performance of our 3-T configuration is attributable to the significant reduction of parasitic absorption/reflection and enhanced charge generation near the embedded nanowire grid contacts, reducing the necessary carrier diffusion distances.

We also confirm the same efficiency benefits of the 3-T configuration apply when using a 25% efficient textured IBC silicon bottom cell, where the 3-T tandem efficiency can reach 35.2% efficiency compared to only 32.8% for the 4-T configuration (Figure S9). Additionally, the higher absolute efficiency (32.9%) of the planar 3-T design relative to the 4-T textured configuration indicates the potential to reach high tandem efficiencies while using planar thin film devices. This is suggests further benefits are attainable with the recent “electrically flat, optically textured” Si device configurations that improve light trapping using dielectric scattering patterns but still allow for the low surface recombination losses of planar cells.^44,45

Finally, because our current design is fully based on planar tandem structures, further improvements can be readily made by optimizing the front surface of the 3-T IBC, which is left free for light-trapping, surface passivation, antireflective coating, directional emission or enhanced photoluminescence outcoupling. The presence of nanowire grid contacts in the 3-T IBC design should allow one to fabricate devices monolithically without the need for current matching present in the 2-T tandem and is also compatible with the 26.3% record efficiency interdigitated back contact (IBC) silicon cells.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b01092.

• Details in simulation setup, device structures, and discussion (PDF)

The authors declare no competing financial interest.