Salmon: fast and bias-aware quantification of transcript expression using dual-phase inference

Abstract

We introduce Salmon, a method for quantifying transcript abundance from RNA-seq reads that is accurate and fast. Salmon is the first transcriptome-wide quantifier to correct for fragment GC content bias, which we demonstrate substantially improves the accuracy of abundance estimates and the reliability of subsequent differential expression analysis. Salmon combines a new dual-phase parallel inference algorithm and feature-rich bias models with an ultra-fast read mapping procedure.

Estimating transcript abundance is a fundamental task in genomics. These estimates are used for the classification of diseases and their subtypes [1], for understanding expression changes during development [2], and tracking the progression of cancer [3]. Accurate and efficient quantification of transcript abundance from RNA-seq data is an especially pressing problem due to both the wide range of technical biases that affect the RNA-seq fragmentation, amplification and sequencing process [4] [5], the exponentially increasing number of experiments, and the adoption of expression data for medical diagnosis [6]. Traditional quantification algorithms, that use alignments of the sequencing reads to the genome or transcriptome, require significant computational resources [7] and do not scale well with the rate at which data is produced [8]. Sailfish [9] achieved an order of magnitude speed improvement by replacing traditional read alignment with the allocation of exact k-mers to transcripts. kallisto [10] achieves similar speed improvements and further reduces the gap in accuracy with traditional alignment-based methods by replacing the k-mer counting approach with a procedure called pseudoalignment, that is capable of rapidly determining the set of transcripts compatible with a given sequenced fragment.

However, existing methods for transcriptome-wide abundance estimation, both alignment-based and alignment-free, lack sample-specific bias models rich enough to capture important effects, like fragment GC content bias. When uncorrected, these biases can lead to, e.g., high false positive rates in differential expression studies [5].

Our novel quantification procedure, called Salmon, achieves greater accuracy than tools such as kallisto and eXpress, employs sample-specific bias models that account for sequence-specific, fragment-GC and positional biases, and simultaneously achieves the same order-of-magnitude speed benefits as kallisto and Sailfish. Salmon consists of three components: a lightweight-mapping model, an online phase that estimates initial expression levels and model parameters, and an offline phase that refines expression estimates (Supplementary Fig. 1). This two-phase inference procedure allows Salmon to build a probabilistic model of the sequencing experiment that incorporates information — like terms contributing to the conditional probability of drawing a fragment given a transcript — not considered by Sailfish [9] and kallisto [10]. Salmon also provides the ability to estimate abundance uncertainty due to random sampling and the ambiguity introduced by multimapping reads (Online methods).

Unlike pseudoalignment, Salmon’s lightweight mapping procedure tracks, by default, the position and orientation of all mapped fragments. This information is used in conjunction with the abundances from online inference to compute per-fragment conditional probabilities. These probabilities are used to estimate auxiliary models and bias terms, and to update abundance estimates, and are subsequently aggregated into weights for the rich equivalence classes used during offline inference.

Using experimental data from the GEUVADIS [11] and SEQC [12] studies, and synthetic data from the Polyester [13] and RSEM-sim [14] simulators, we benchmark Salmon against kallisto [10] and eXpress [15] + Bowtie2 [16]; both of these methods also implement their own bias models. We also test Salmon using traditional alignments (from Bowtie2) as input (denoted as “Salmon(a)”). We show that Salmon typically outperforms both kallisto and eXpress in terms of accuracy (Fig. 1a–d, Supplementary Fig. 2, Supplementary Fig. 3). We note that all these tools address transcript quantification, and do not identify or assemble novel transcripts (Supplementary Note 1).

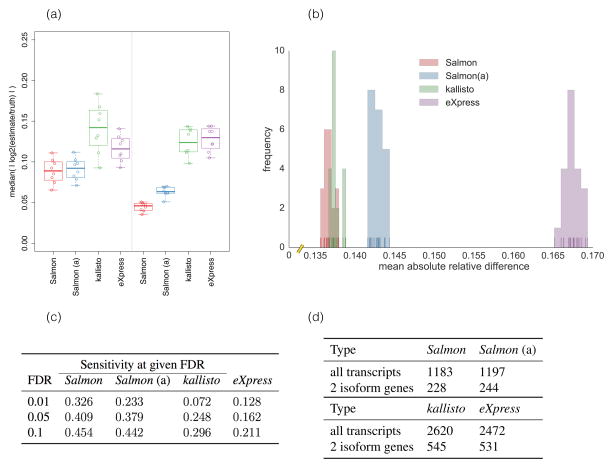
Figure 1.

(a) The median of absolute log fold changes (lfc) between the estimated and true abundances under all 16 replicates of the Polyester simulated data. The closer the lfc to 0, the more similar the true and estimated abundances. The left and right panels show the distribution of the log fold changes under samples simulated with different GC-bias curves learned from experimental data (details in Online methods, Ground truth simulated data). (b) The distribution of mean absolute relative differences (MARDs), as described in Online methods, Metrics for accuracy, of Salmon, Salmon using traditional alignments (“Salmon (a)”), kallisto and eXpress under 20 simulated replicates generated by RSEM-sim. Salmon and kallisto yield similar MARDs, though Salmon’s distribution of MARDs is significantly smaller (Mann-Whitney U test, p = 0.00017) than those of kallisto. Both methods outperform eXpress (Mann-Whitney U test, p = 3.39781 × 10⁻⁸). (c) At typical FDR values, the sensitivity of finding truly DE transcripts using Salmon’s estimates is 53%–450% greater than that using kallisto’s estimates and 210%–250% greater than that using eXpress’ estimates for the Polyester simulated data. (d) For 30 GEUVADIS samples, the number of transcripts called as DE at an expected FDR of 1% when the contrast between groups is simply a technical confound (i.e. the center at which they were sequenced). Salmon produces fewer than half as many DE calls as the other methods. Permuting samples, or testing for DE within sequencing center resulted in ≪ 1 transcript called as DE on average for all methods.

Salmon’s dual-phase inference algorithm and sample-specific bias models yield improved inter-replicate concordance (Supplementary Fig. 4) compared to both kallisto and eXpress. For example, when used for differential expression (DE) testing, the quantification estimates produced by Salmon exhibit markedly higher sensitivity at the same false discovery rate (Table 1c) — achieving a sensitivity 53% to 250% higher, at the same FDRs. Likewise, Salmon produces fewer false-positive differential expression calls in comparisons that are expected to contain few or no true differences in transcript expression (Table 1d). Salmon’s benefits persist at the gene level as well, where the use of Salmon’s estimates for gene-level DE analysis leads to a decrease by a factor of ~2.6 in the number of genes that are called as DE (Supplementary Table 1). Supplementary Fig. 5 shows specific examples from the GEUVADIS experiments where dominant isoform switching is observed (p < 1 × 10⁻⁶) between samples under the quantification estimates produced by kallisto or eXpress, but this isoform switching is eliminated under the Salmon’s GC bias aware abundance estimates. Supplementary Table 2 provides the rate of isoform switching for the different methods, underscoring that Salmon reduces this rate across various thresholds and for various categories of genes. In idealized simulations, like those generated by RSEM-sim, where realistic biases are not simulated, the accuracy estimates of different methods tend to be more similar (Fig. 1b, Supplementary Fig. 6). These idealized simulations, where the fragments are generated without bias and in perfect accordance with the generative model adopted by the quantifiers, serve as a useful measure of the internal consistency of the algorithms [14] [10]. However, we expect results on the SEQC [12], GEUVADIS [11], and Polyester [13] (simulated with bias) data sets to be more representative of typical real-world performance. On the RSEM-sim data we evaluated all methods without bias correction. On all other data, we enabled bias correction for all methods. Additionally, on the Polyester simulated data, we enabled --noBiasLengthThreshold (to allow correction of even very short transcripts) for Salmon, since we are interested in assessing the maximum sensitivity of the model, and the simulator produces fragments that are well-behaved with respect to very short transcripts (see Online methods for details).

Salmon’s rich model accounts for the effects of sample-specific parameters and biases that are typical of RNA-seq data, including positional biases in coverage, sequence-specific biases at the 5′ and 3′ end of sequenced fragments, fragment-level GC bias, strand-specific protocols, and the fragment length distribution. These parameters are automatically learned in the online phase of the algorithm, which also estimates the conditional probability of a fragment being generated from each transcript to which it multimaps, as assessed by a general fragment-transcript agreement model (Online methods, Fragment-transcript agreement model). This provides considerable information beyond simple fragment-transcript compatibility. Salmon incorporates these parameters by learning auxiliary models that describe the relevant distributions and by maintaining “rich equivalence classes” of fragments (Online methods, Equivalence classes).

Salmon encompasses both “alignment” and “quantification” in a single tool. When run in quasi-mapping mode, Salmon takes as input an index of the transcriptome and a set of raw sequencing reads (i.e., unaligned reads in FASTA/Q format) and performs quantification directly without generating any intermediate alignment files. This saves considerable time and space, since quasi-mapping is faster than traditional alignment.

Salmon is designed take advantage of multiple CPU cores, and the mapping and inference procedures scale well with the number of reads in an experiment. Salmon can quantify abundance either via a built-in, ultra-fast read-mapping procedure (quasi-mapping) [17], or using pre-computed alignments provided in SAM or BAM format. Salmon can quantify an experiment of approximately 600 million reads (75bp, paired-end) in ≈ 23 minutes (1384 seconds) using 30 threads— this roughly matches the speed of the recently-introduced kallisto, which takes ≈ 20 minutes (1198 seconds) to complete the same task using the same number of threads on the same machine (a 24 core machine with hyper-threading and 256Gb of RAM; each core is Intel® Xeon® CPU E5-4607 v2 2.60GHz).

Salmon’s approach is unique in how it combines models of experimental data and bias with an efficient dual-phase inference procedure. Salmon’s ability to compute high-quality estimates of transcript abundances at the scale of thousands of samples, while also accounting for the prevalent technical biases affecting transcript quantification [18], will enable individual expression experiments to be interpreted in the context of many rapidly growing sequence expression databases. This will allow for a more comprehensive comparison of the similarity of experiments across large populations of individuals and across different environmental conditions and cell types. Salmon is open-source and freely-licensed (GPLv3). It is written in C++11 and is available at https://github.com/COMBINE-lab/Salmon.

Online methods

Objectives and models for abundance estimation

Our main goal is to quantify, given a known transcriptome 𝒯 and a set of sequenced fragments ℱ, the relative abundance of each transcript in our input sample. This problem is challenging both statistically and computationally. The main statistical challenges derive from need to resolve a complex and often very high-dimensional mixture model (i.e., estimating the relative abundances of the transcripts given the collection of ambiguously mapping sequenced fragments). The main computational challenges derive from the need to process datasets that commonly consist of tens of millions of fragments, in conditions where each fragment might reasonably map to many different transcripts. We lay out below how we tackle these challenges, beginning with a description of our assumed generative model of the sequencing experiment, upon which we will perform inference to estimate transcript abundances.

Our approach in Salmon consists of three components: a lightweight-mapping model, an online phase that estimates initial expression levels, auxiliary parameters, foreground bias models and constructs equivalence classes over the input fragments, and an offline phase that refines these expression estimates. The online and offline phases together optimize the estimates of the transcript abundances.

The online phase uses a variant of stochastic, collapsed variational Bayesian inference [19]. The offline phase applies either a standard EM algorithm or a variational Bayesian EM algorithm [20] over a reduced representation of the data represented by the equivalence classes until a data-dependent convergence criterion is satisfied. An overview of our method is given in Supplementary Fig. 1, and we describe each component in more detail below.

Here, we use the vertical bar | to indicate that the fixed quantities following are parameters used to calculate the probability. For the Bayesian objective, the notation implies conditioning on these random variables.

Generative process

Assume that, for a particular sequencing experiment, the underlying true transcriptome is given as 𝒥 = {(t₁, … , t_M), (c₁, … , c_M)}, where each t_i is the nucleotide sequence of some transcript (an isoform of some gene) and each c_i is the corresponding number of copies of t in the sample. Further, we denote by ℓ_i the length of transcript t and by ℓ̃_ι the effective length of transcript t_i, as defined in Equation (1).

We adopt a generative model of the sequencing experiment that dictates that, in the absence of experimental bias, library fragments are sampled proportional to c_i · ℓ̃_ι. That is, the probability of drawing a sequencing fragment from some position on a particular transcript t_i is proportional the total fraction of all nucleotides in the sample that originate from a copy of t_i. This quantity is called the nucleotide fraction [14]:

$${\eta }_i=\frac{c_i·{\stackrel{\sim }{\ell }}_{\iota }}{{\sum }_{j=1}^M{c}_j·{\stackrel{\sim }{\ell }}_j}.$$

The true nucleotide fractions, η, though not directly observable, would provide us with a way to measure the true relative abundance of each transcript in our sample. Specifically, if we normalize the η_i by the effective transcript length ℓ̃_ι, we obtain a quantity

$${\tau }_i=\frac{\frac{{\eta }_i}{{\stackrel{\sim }{\ell }}_{\iota }}}{{\sum }_{j=1}^M\frac{{\eta }_j}{{\stackrel{\sim }{\ell }}_j}},$$

called the transcript fraction [14]. These τ can be used to immediately compute common measures of relative transcript abundance like transcripts per million (TPM). The TPM measure for a particular transcript is the number of copies of this transcript that we would expect to exist in a collection of one million transcripts, assuming this collection had exactly same distribution of abundances as our sample. The TPM for transcript t_i t_i, is given by TPM_i = τ_i · 10⁶. Of course, in a real sequencing experiment, there are numerous biases and sampling effects that may alter the above assumptions, and accounting for them is essential for accurate inference. Below we describe how Salmon accounts for 5’ and 3’ sequence-specific biases (which are not considered separately by kallisto) and fragment GC bias which is modeled by neither kallisto nor eXpress.

Effective length

A transcript’s effective length depends on the empirical fragment length distribution of the underlying sample and the length of the transcript. It accounts for the fact that the range of fragment sizes that can be sampled is limited near the ends of a transcript. Here, fragments refer to the (potentially size-selected) cDNA fragments of the underlying library, from the ends of which sequencing reads are generated. In paired-end data, the mapping positions of the reads can be used to infer the empirical distribution of fragment lengths in the underlying library, while the expected mean and standard deviation of this distribution must be provided for single-end libraries. We compute the effective transcript lengths using the approach of kallisto [10], which defines the effective length of a transcript t_i as

$${\stackrel{\sim }{\ell }}_{\iota }={\ell }_i-{\mu }_d^{{\ell }_i},$$ Equation 1

where ${{\mu }_i^{\ell }}_d$ is the mean of the truncated empirical fragment length distribution. Specifically, let d be the empirical fragment length distribution, and Pr{X = x} be the probability of drawing a fragment of length x under d, then ${{\mu }_i^{\ell }}_d={\sum }_{j=1}^{{\ell }_i}j·Pr\{X=j\}/{\sum }_{k=1}^{{\ell }_i}Pr\{X=k\}$.

Given a collection of observations (raw sequenced fragments or alignments thereof), and a model similar to the one described above, there are numerous approaches to inferring the relative abundance of the transcripts in the target transcriptome, 𝒥. Here we describe two basic inference schemes, both available in Salmon, which are commonly used to perform inference in such a model. All of the results reported in the manuscript were computed using the maximum likelihood objective (i.e., the EM algorithm) in the offline phase, which is the default in Salmon.

Maximum likelihood objective

The first scheme takes a maximum likelihood approach to solve for the quantities of interest. Specifically, if we assume that all fragments are generated independently, and we are given a vector of known nucleotide fractions η a binary matrix of transcript-fragment assignment Z where z_ij = 1 if fragment j is derived from transcript i, and the set of transcripts 𝒥, we can write the probability of observing a set of sequenced fragments ℱ as follows:

$$Pr\{\mathcal{F}\mid \mathit{\eta },\mathit{Z},\mathcal{J}\}=\prod _{j=1}^{N}Pr\{f_j\mid \mathit{\eta },\mathit{Z},\mathcal{J}\}=\prod _{\mathit{j}=\mathbf{1}}^{\mathit{N}}\sum _{\mathit{i}=\mathbf{1}}^{\mathit{M}}Pr\{t_i\mid \mathit{\eta }\}·Pr\{f_j\mid t_i,z_{ij}=1\}$$ Equation 2

where |ℱ| = N is the number of sequenced fragments, Pr{t_i | η} is the probability of selecting transcript t_i to generate some fragment given the nucleotide fraction η, and Pr{t_i | η} = η_i

We have that Pr{f_j | t_i, z_ij = 1} is the probability of generating fragment j given that it came from transcript i. We will use Pr{f_j | t_i} as shorthand for Pr{f_j | t_i, z_ij = 1} since Pr{f_j | t_i, z_ij = 1} is defined to be uniformly 0. The determination of Pr{f_j | t_i} is defined in further detail in Fragment-transcript agreement model. The likelihood associated with this objective can be optimized using the EM algorithm as in [14].

Bayesian objective

One can also take a Bayesian approach to transcript abundance inference as done in [21, 22]. In this approach, rather than directly seeking maximum likelihood estimates of the parameters of interest, we want to infer the posterior distribution of η. In the notation of [21], we wish to infer Pr{η| ℱ, 𝒥} — the posterior distribution of nucleotide fractions given the transcriptome 𝒥 and the observed fragments ℱ. This distribution can be written as:

$$Pr\{\mathit{\eta }\mid \mathcal{F},\mathcal{J}\}\propto \sum _{Z\in \mathcal{Z}}Pr\{\mathcal{F}\mid \mathcal{J},\mathit{Z}\}·Pr\{\mathit{Z}\mid \mathit{\eta }\}·Pr\{\mathit{\eta }\},$$ Equation 3

where

$$Pr\{\mathit{Z}\mid \mathit{\eta }\}={\prod }_{i=1}^M{\prod }_{j=1}^N{\eta }_i^{z_{ji}},$$ Equation 4

and

$$Pr\{\mathcal{F}\mid \mathcal{J},\mathit{Z}\}={\prod }_{i=1}^M{\prod }_{j=1}^{N}Pr{\{f_j\mid t_i\}}^{z_{ji}}.$$ Equation 5

Unfortunately, direct inference on the distribution Pr{η| ℱ, 𝒥} is intractable because its evaluation requires the summation over the exponentially large latent variable configuration space (i.e., all Z ∈ 𝒵). Since the posterior distribution cannot be directly estimated, we must rely on some form of approximate inference. One particularly attractive approach is to apply variational Bayesian (VB) inference in which some tractable approximation to the posterior distribution is assumed.

Subsequently, one seeks the parameters for the approximate posterior under which it best matches the true posterior. Essentially, this turns the inference problem into an optimization problem — finding the optimal set of parameters — which can be efficiently solved by several different algorithms. Variational inference seeks to find the parameters for the approximate posterior that minimizes the Kullback-Leibler (KL) divergence between the approximate and true posterior distribution. Though the true posterior may be intractable, this minimization can be achieved by maximizing a lower-bound on the marginal likelihood of the posterior distribution [21], written in terms of the approximate posterior. When run with the VB objective, Salmon optimizes the collapsed variational Bayesian objective [21] in its online phase and the full variational Bayesian objective [22] in the variational Bayesian mode of its offline phase (see Offline phase).

Fragment-transcript agreement model

Fragment-transcript assignment scores are defined as proportional to (1) the chance of observing a fragment length given a particular transcript/isoform, (2) the chance that a fragment starts at a particular position on the transcript, (3) the concordance of the fragment aligning with a user-defined (or automatically inferred) sequencing library format (e.g., a paired ended, stranded protocol), and (4) the chance that the fragment came from the transcript based on a score obtained from the alignment procedure (if alignments are being used). We model this agreement as a conditional probability Pr{f_j | t_i} for generating f_j given t_i. This probability, in turn, depends on auxiliary models whose parameters do not explicitly depend upon the current estimates of transcript abundances. Thus, once the parameters of these models have been learned and are fixed, these terms do not change even when the estimate for Pr{t_i | η} = η_i needs to be updated. Salmon uses the following auxiliary terms:

$$Pr\{f_j\mid t_i\}=Pr\{\ell \mid t_i\}·Pr\{p\mid t_i,\ell \}·Pr\{o\mid t_i\}·Pr\{a\mid f_j,t_i,p,o,\ell \}$$ Equation 6

where Pr{ℓ | t_i} is the probability of drawing a fragment of the inferred length, ℓ, given t_i, and is evaluated based on an observed empirical fragment length distribution. Pr{p | t_i, ℓ} is the probability of the fragment starting at position p on t_i and is a function of the transcript’s length. Pr{o | t_i} is the probability of obtaining a fragment aligning (or mapping) with the given orientation to t_i. This is determined by the concordance of the fragment with the user-specified library format. It is 1 if the alignment agrees with the library format and a user-defined prior value otherwise. Finally, Pr{a | f_j, t_i, p, o, ℓ} is the probability of generating alignment a of fragment f_j, given that it is drawn from t_i, with orientation o, and starting at position p and is of length ℓ; this term is set to 1 when using quasi-mapping, and is given by equation (7) for traditional alignments. The parameters for all auxiliary models are learned during the streaming phase of the inference algorithm from the first N′ observations (5,000,000 by default). These auxiliary terms can then be applied to all subsequent observations.

Sequence-specific bias

It has been previously observed that the sequence surrounding the 5′ and 3′ ends of RNA-seq fragments influences the likelihood that these fragments are selected for sequencing [4]. If not accounted for, these biases can have a substantial effect on abundance estimates and can confound downstream analyses. To learn and correct for such biases, Salmon adopts a modification of the model introduced by Roberts et al. [4]. A (foreground) variable-length Markov model (VLMM) is trained on sequence windows surrounding the 5′ ( $b_{s^{+}}^{5^{\prime }}$) and 3′ ( $b_{s^{+}}^{3^{\prime }}$) read start positions. Then, a different (background) VLMM is trained on sequence windows drawn uniformly across known transcripts, each weighted by that transcript’s abundance; the 5′ and 3′ background models are denoted as $b_{s^{-}}^{5^{\prime }}$ and $b_{s^{+}}^{3^{\prime }}$ respectively.

Fragment GC-bias

In addition to the sequence surrounding the 5’ and 3’ ends of a fragment, it has also been observed that the GC-content of the entire fragment can play a substantial role in the likelihood that it will be selected for sequencing [5]. These biases are largely different than sequence-specific biases, and thus, accounting for both the context surrounding the fragments and the GC-content of the fragments themselves is important when one wishes to learn and correct for some of the most prevalent types of bias in silico. To account for fragment GC-bias, Salmon learns a foreground and background model of this fragment GC-bias (and defines the bias as the ratio of the score of a fragment under each). Our fragment GC-bias model consists of the observed distribution of sequenced fragments for every possible GC-content value (in practice, we discretize GC-content and maintain a distribution over 25 bins, for fragments with GC content ranging from 0 to 1 in increments of 0.04). The background model is trained on all possible fragments (drawn uniformly and according to the empirical fragment length distribution) across known transcripts, with each fragment weighted by that transcript’s abundance. The foreground and background fragment GC-bias models are denoted as b_gc⁺ and b_gc⁻ respectively. Additionally, we note that sequence-specific and fragment GC biases do seem to display a conditional dependence. To account for this, Salmon learns (by default) 3 different bias models, each conditioned on the average GC content of the 5′ and 3′ sequence context of the fragment. A separate model is trained and applied for fragments with average GC content between [0, 0.33), [0.33, 0.66), and [0.66, 1]. The performance of the model appears robust to the number of conditional GC models used (Supplementary Fig. 7).

Incorporating the bias models

These bias models are used to re-estimate the effective length of each transcript, such that a transcript’s effective length now also takes into account the likelihood of sampling each possible fragment that transcript can produce — an approach to account for bias first introduced by Roberts et al. [4]. Before learning the bias-corrected effective lengths, the offline optimization algorithm is run for a small number of rounds (10 by default) to produce estimated abundances that are used when learning the background distributions for the various bias models. For a transcript t_i, the effective length becomes:

$${\stackrel{\sim }{\ell }}_{\iota }^{\prime }=\sum \sum \frac{b_{g{c}^{+}}(t_i,j,j+k)}{b_{g{c}^{-}}(t_i,j,j+k)}·\frac{b_{s^{+}}^{5^{\prime }}(t_i,j)}{b_{s^{-}}^{5^{\prime }}(t_i,j)}·\frac{b_{s^{+}}^{3^{\prime }}(t_i,j+k)}{b_{s^{-}}^{3^{\prime }}(t_i,j+k)}·Pr\{X=j\}$$

where Pr{X = j} is the probability, under the empirical fragment length distribution, of observing a fragment of length j, L is the maximum observed fragment length, f_i(j, L) = _min(ℓ_i − j + 1, L), $b_{s^{+}}^{5^{\prime }}(t_i,j)$ is the score given to transcript t_i’s j^th position under the foreground, 5’ sequence-specific bias model ( $b_{s^{-}}^{5^{\prime }}(t_i,j),b_{s^{+}}^{3^{\prime }}(t_i,j),b_{s^{-}}^{3^{\prime }}(t_i,j))$ are defined similarly) and b_gc⁺ (t_i, j, j + k) is the score given by the foreground fragment GC-content model for the sequence of transcript t_i from position j to j + k (and similarly for b_gc⁻ (t_i, j, j + k)).

Once these bias-corrected lengths have been computed, they are used in all subsequent rounds of the offline inference phase (i.e. until the estimates of α — as defined in Algorithms — converge). Typically, the extra computational cost required to apply bias correction is rather small, and the learning and application of these bias weights is parallelized in Salmon (for example, when processing sample ERR188021 of the GEUVADIS dataset using 16 threads, the full fidelity bias modeling added 2 minutes (119 seconds) to the non-bias-corrected quantification time. Moreover, since the bias model works by evaluating the bias along bases of the reference transcriptome, it scales in the number of active (i.e., expressed) transcripts rather than in the number of reads, so the extra cost of bias modeling is almost entirely independent of the number of fragments in an experiment. However, both the memory and time requirements of bias correction can be adjusted by the user to trade-off time and space with model fidelity. To make the computation of GC-fractions efficient for arbitrary fragments from the transcriptome, Salmon computes and stores the cumulative GC count for each transcript. To reduce memory consumption, this cumulative count can be sampled using the --gcSizeSamp. This will increase the time required to compute the GC-fraction for each fragment by a constant factor. Similarly, when attempting to determine the effective length of a transcript, Salmon will evaluate the contribution of all fragments longer than the shortest 0.5% and shorter than the longest 0.5% of the full empirical fragment length distribution, that could derive from this transcript. The program option --biasSpeedSamp will instead sample fragment lengths at a user-defined factor, speeding up the computation of bias-corrected effective lengths by this factor, but coarsening the model in the process. However, sampling the fragment length distribution tends to produce substantial speed improvements with only a very moderate effect on the model fidelity. For example, setting --biasSpeedSamp to 5 reduces the additional bias correction time on sample ERR188021 mentioned above from 119 to 20 seconds, yet it leads to only a marginal increase in the number of false positive calls on the GEUVADIS data (from 1183 to 1190 total transcripts, 228 to 231 transcripts from two isoform genes, and it actually decreased the number of false positive calls at the gene level slightly from 455 to 451). All results reported in this manuscript where bias correction was included were run without either of these sampling options (i.e. using the full-fidelity model).

Alignment model

When Salmon is given read alignments as input, it can learn and apply a model of read alignments to help assess the probability that a fragment originated from a particular locus. Specifically, Salmon’s alignment model is a spatially varying first-order Markov model over the set of CIGAR symbols and nucleotides. To account for the fact that substitution and indel rates can vary spatially over the length of a read, we partition each read into a fixed number of bins and learn a separate model for each of these bins. This allows us to learn spatially varying effects without making the model itself too large (as if, for example, we had attempted to learn a separate model for each position in the read). We choose 4 bins by default since this allows different models for the beginning, middle, and trailing segments of a read, which tend to display distinct error profiles. However, we note that even a single, spatially homogeneous error profile appears to work reasonably well [22], and that given sufficient training data, it is even possible to learn a separate bin for each position of a read [15]. Given the CIGAR string s = s₀, … , s_|s| for an alignment a, we compute the probability of a as:

$$Pr\{a\mid f_j,t_i,p,o,\ell \}=Pr\{s_o\}\prod _{k=1}^{\mid s\mid }{Pr}_{({\mathcal{M}}_k\}}\{s_{k-1}\to s_k\mid f_j,t_i,p,o,\ell \}$$ Equation 7

where Pr{s₀} is the start probability and Pr_(ℳk}{·} is the transition probability under the model at the k^th position of the read (i.e., in the bin corresponding to position k). To compute these probabilities, Salmon parses the CIGAR string s and moves appropriately along both the fragment f_i and the reference transcript t_i, and computes the probability of transitioning to the next observed state in the alignment (a tuple consisting of the CIGAR operation, and the nucleotides in the fragment and reference) given the current state of the model. The parameters of this Markov model are learned from sampled alignments in the online phase of the algorithm (see Supplementary Algorithm 1). When quasi-mapping is used instead of user-provided alignments, the probability of the “alignment” is not taken into account (i.e. Pr{a | f_j, t_i, p, o, ℓ} is set to 1 for each mapping).

Algorithms

We describe the online and offline inference algorithms of Salmon, which together optimize the estimates of α — a vector of the estimated number of reads originating from each transcript. Given α the η can be directly computed. An overview of the Salmon execution “timeline”, which describes when, during the execution of the algorithm different estimates are made and quantities of interest are computed, is given in Supplementary Fig. 1.

Online phase

The online phase of Salmon attempts to solve the variational Bayesian inference problem described in Objectives and models for abundance estimation, and optimizes a collapsed variational objective function [21] using a variant of stochastic collapsed variational Bayesian inference [19]. The inference procedure is a streaming algorithm, similar to [15], but it updates estimated read counts α after every small group B^τ (called a mini-batch) of observations, and processing of mini-batches is done asynchronously and in parallel. The pseudo-code for the algorithm is given in Supplementary Algorithm 1.

The observation weight v^τ for mini-batch B^τ, in line 15 of Supplementary Algorithm 1, is an increasing sequence in τ, and is set, as in [15], to adhere to the Robbins-Monroe conditions. Here, the α represent the (weighted) estimated counts of fragments originating from each transcript. Using this method, the expected value of η can be computed directly from α using equation (16). We employ a weak Dirichlet conjugate-prior with α₀ = 0.001 · ℓ̃_ι for all t_i ∈ 𝒥. As outlined in [19], the SCVB0 inference algorithm is essentially equivalent to variants of the online-EM [23] algorithm with a modified prior. The procedure in Supplementary Algorithm 1 is run independently by as many worker threads as the user has specified. The threads share a single work-queue upon which a parsing thread places mini-batches of alignment groups. An alignment group is simply the collection of all alignments (i.e. all multi-mapping locations) for a read. The mini-batch itself consists of a collection of some small, fixed number of alignment groups (1,000 by default). Each worker thread processes one alignment group at a time, using the current weights of each transcript and the current auxiliary parameters to estimate the probability that a read came from each potential transcript of origin. The processing of mini-batches occurs in parallel, so that very little synchronization is required, only an atomic compare-and-swap loop to update the global transcript weights at the end of processing of each mini-batch — hence the moniker laissez-faire in the label of Supplementary Algorithm 1. This lack of synchronization means that when estimating x_y, we cannot be certain that the most up-to-date values of α are being used. However, due to the stochastic and additive nature of the updates, this has little-to-no detrimental effect [24]. The inference procedure itself is generic over the type of alignments being processed; they may be either regular alignments (e.g. coming from a bam file), or quasi-mappings computed from the raw reads (e.g. coming from FASTA/Q files). After the entire mini-batch has been processed, the global weights for each transcript are updated. These updates are sparse; i.e., only transcripts that appeared in some alignment in mini-batch B^τ will have their global weight updated after B^τ has been processed. This ensures, as in [15], that updates to the parameters α can be performed efficiently.

Equivalence classes

During its online phase, in addition to performing streaming inference of transcript abundances, Salmon also constructs a highly-reduced representation of the sequencing experiment. Specifically, Salmon constructs “rich” equivalence classes over all the sequenced fragments. Collapsing fragments into equivalence classes is a well-established idea in the transcript quantification literature, and numerous different notions of equivalence classes have been previously introduced, and shown to greatly reduce the time required to perform iterative optimization such as that described in Offline phase. For example, Salzman et al. [25] suggested factorizing the likelihood function to speed up inference by collapsing fragments that align to the same exons or exon junctions (as determined by a provided annotation) into equivalence classes. Similarly, Nicolae et al.[26] used equivalence classes over fragments to reduce memory usage and speed up inference — they define as equivalent any pair of fragments that align to the same set of transcripts and whose compatibility weights (i.e. conditional probabilities) with respect to those transcripts are proportional. Turro et al. [27], introduced a notion of equivalence classes that considers as equivalent any pair of fragments (sequenced reads and read pairs) that multimap to the same set of target transcripts. The model of Turro et al. does not have the same restriction as that of Nicolae et al. on the proportional conditional probabilities of the equivalent fragments. Patro et al. [9] define equivalence classes over k-mers, treating as equivalent any k-mers that appear in the same set of transcripts at the same frequency, and use this factorization of the likelihood function to speed up optimization. Bray et al. [10] define equivalence classes over fragments, and define as equivalent any fragments that pseudoalign to the same set of transcripts, a definition which, like that of Turro et al., does not consider the conditional probabilities of the equivalent fragments with respect to the transcripts to which they map.

To compute equivalence classes, we define an equivalence relation ~ over fragments. Let A(𝒥, f_x) denote the set of quasi-mappings (or alignments) of f_x to the transcriptome 𝒥, and let M(f_x) = {t_i | (t_i, p_i, o_i) ∈ A(𝒥, f_x)} be the set of transcripts to which f_x maps according to A(𝒥, f_x). We say f_x ~ f_y if and only if M(f_x) = M(f_y). Fragments which are equivalent are grouped together for inference. Salmon builds up a set of fragment-level equivalence classes by maintaining an efficient concurrent cuckoo hash map [28]. To construct this map, we associate each fragment f_x with t^x = M(f_x), which we will call the label of the fragment. Then, we query the hash map for t^x. If this key is not in the map, we create a new equivalence class with this label, and set its count to 1. Otherwise, we increment the count of the equivalence class that we find in the map with this label. The efficient, concurrent nature of the data structure means that many threads can simultaneously query and write to the map while encountering very little contention. Each key in the hash map is associated with a value that we call a “rich” equivalence class. For each equivalence class 𝒞^j, we retain a count d^j = |𝒞^j|, which is the total number of fragments contained within this class. We also maintain, for each class, a weight vector w^j. The entries of this vector are in one-to-one correspondence with transcripts i in the label of this equivalence class such that

$$w_i^j=\frac{{\sum }_{f\in {\mathcal{C}}^j}Pr\{f\mid t_i\}}{{\sum }_{t_k\in {\mathit{t}}^{\mathit{j}}}{\sum }_{f\in {\mathcal{C}}^j}Pr\{f\mid t_i\}}.$$ Equation 8

That is, $w_i^j$ is the average conditional probability of observing a fragment from 𝒞^j given t_i over all fragments in this equivalence class. Though the likelihood function over equivalence classes that considers these weights (Equation (10)) is no longer exactly equivalent to the likelihood defined over all fragments (Equation (9)), these weights nonetheless allow us to take into consideration the conditional probabilities specified in the full model, without having to continuously reconsider each of the fragments in ℱ. There is a spectrum of possible representations of “rich” equivalence classes. This spectrum spans from the notion adopted here, which collapses all conditional probabilities into a single aggregate scalar, to an approach that clusters together fragments based not only on the transcripts to which they match, but on the vector of normalized conditional probabilities for each of these transcripts. The former approach represents a more coarse-grained approximate factorization of the likelihood function while the latter represents a more fine-grained approximation. We believe that studying how these different notions of equivalence classes affect the factorization of the likelihood function, and hence its optimization, is an interesting direction for future work.

Offline Phase

In its offline phase, which follows the online phase, Salmon uses the “rich” equivalence classes learned during the online phase to refine the inference. Given the set 𝒞 of rich equivalence classes of fragments, we can use an expectation maximization (EM) algorithm to optimize the likelihood of the parameters given the data. The abundances η can be computed directly from α, and we compute maximum likelihood estimates of these parameters which represent the estimated counts (i.e., number of fragments) deriving from each transcript, where:

$$\mathcal{L}\{\mathit{\alpha }\mid \mathcal{F},\mathit{Z},\mathcal{J}\}=\prod _{j=1}^N\sum _{i=1}^M\widehat{{\eta }_{\iota }}Pr\{f_j\mid t_i\}$$ Equation 9

and $\widehat{{\eta }_{\iota }}=\frac{{\alpha }_i}{{\sum }_j{\alpha }_j}$. If we write this same likelihood in terms of the equivalence classes 𝒞, we have:

$$\mathcal{L}\{\mathit{\alpha }\mid \mathcal{F},\mathit{Z},\mathcal{J}\}\approx \prod _{{\mathcal{C}}^j\in \mathcal{C}}{\left(\sum _{t_i\in {\mathit{t}}^j}\widehat{{\eta }_{\iota }}{w}_i^j\right)}^{d^j}.$$ Equation 10

This likelihood, and hence that represented in equation (9), can then be optimized by applying the following update equation iteratively

$${\alpha }_i^{u+1}={\sum }_{{\mathcal{C}}^j\in \mathcal{C}}{d}^j\left(\frac{{\alpha }_i^u{w}_i^j}{{\sum }_{t_k\in {\mathit{t}}^j}{a}_k^u{w}_k^j}\right).$$ Equation 11

We apply this update equation until the maximum relative difference in the α parameters satisfies:

$$\mathit{\Delta }({\alpha }^u,{\alpha }^{u+1})=max\frac{\mid {\alpha }_i^u-{\alpha }_i^{u+1}\mid }{{\alpha }_i^{u+1}}<1\times {10}^{-2}$$ Equation 12

for all ${\alpha }_i^{u+1}>1\times {10}^{-8}$. Let α′ be the estimates after having achieved convergence. We can then estimate η_i by $\widehat{{\eta }_{\iota }}$, where:

$$\widehat{{\eta }_{\iota }}=\frac{{\alpha }_i^{\prime }}{{\sum }_j{\alpha }_j^{\prime }}.$$ Equation 13

Variational Bayes optimization

Instead of the standard EM updates of equation (11), we can, optionally, perform Variational Bayesian optimization by applying VBEM updates as in [22], but adapted to be with respect to the equivalence classes:

$${\alpha }_i^{u+1}=\sum _{{\mathcal{C}}^j\in \mathcal{C}}{d}^j\left(\frac{e^{{\gamma }_i^u}{w}_i^j}{{\sum }_{t_k\in {\mathit{t}}^j}{e}^{{\gamma }_k^u}{w}_k^j}\right),$$ Equation 14

where:

$${\gamma }_i^u=\mathrm{\Psi }({\alpha }_i^0+{\alpha }_i^u)-\mathrm{\Psi }\left(\sum a_k^0+a_k^u\right).$$ Equation 15

Here, Ψ(·) is the digamma function, and, upon convergence of the parameters, we can obtain an estimate of the expected value of the posterior nucleotide fractions as:

$$\mathbb{E}\{{\eta }_i\}=\frac{{\alpha }_i^0+{\alpha }_i^{\prime }}{{\sum }_j{\alpha }_j^0+{\alpha }_j^{\prime }}=\frac{{\alpha }_i^0+{\alpha }_i^{\prime }}{{\widehat{\alpha }}^0+N},$$ Equation 16

where ${\widehat{\alpha }}^0={\sum }_{i=1}^M{\alpha }_i^0$. Variational Bayesian optimization in the offline-phase of Salmon is selected by passing the --useVBOpt flag to the Salmon quant command.

Sampling from the posterior

After the convergence of the parameter estimates has been achieved in the offline phase, it is possible to draw samples from the posterior distribution using Gibbs sampling to sample, in turn, from the transcript abundances given the fragment assignments, and then to re-assign the fragments within each equivalence class given these abundances. To perform this Gibbs sampling, we adopt the model of Turro et al. [27] (details in Supplementary Note 2).

Additionally, inspired by kallisto [10], Salmon also provides the ability to draw bootstrap samples, which is an alternative way to assign confidence to the estimates returned by the main inference algorithm. Bootstrap samples can be drawn by passing the --numBootstraps option to Salmon with the argument determining the number of bootstraps to perform. The bootstrap sampling process works by sampling (with replacement) counts for each equivalence class, and then re-running the offline inference procedure (either the EM or VBEM algorithm) for each bootstrap sample.

Validation

Metrics for Accuracy

Throughout this paper, we use several different metrics to summarize the agreement of the estimated TPM for each transcript with the TPM computed from simulated counts. While most of these metrics are commonly used and self-explanatory, we here describe the computation of the mean absolute relative difference (MARD), which is less common than some of the other metrics.

The MARD is computed using the absolute relative difference ARD_i for each transcript i:

$${\text{ARD}}_{\mathrm{i}}=\{\begin{array}{ll}0\hfill & \hfill \text{if}{x}_i=y_i=0\hfill \\ \frac{\mid x_i-y_i\mid }{x_i+y_i}\hfill & \hfill \text{otherwise}\hfill \end{array},$$ Equation 17

where x_i is the true value of the TPM, and y_i is the estimated TPM. The relative difference is bounded above by 1, and takes on a value of 0 whenever the prediction perfectly matches the truth. To compute the mean absolute relative difference, we simply take $\text{MARD}=\frac{1}{M}{\sum }_{i=1}^M{\text{ARD}}_{\mathrm{i}}$. We note that Salmon and kallisto, by default, truncate very tiny expression values to 0. For example, any transcript estimated to produce < 1 × 10⁻⁸ reads is assigned an estimated read count of 0 (which, likewise, affects the TPM estimates). However, eXpress does not perform such a truncation, and very small, non-zero values may have a negative effect on the MARD metric. To mitigate such effects, we first truncate to 0 all TPMs less than 0.01 before computing the MARDs.

Ground truth simulated data

To assess accuracy in a situation where the true expression levels are known, we generate synthetic data sets using both Polyester [13] and RSEM-sim [14].

RSEM-sim simulations

To generate data with RSEM-sim, we follow the procedure used in [10]. RSEM was run on sample NA12716_7 from the GEUVADIS RNA-seq data to learn model parameters and estimate true expression, and the learned model was then used to generate 20 different simulated datasets, each consisting of 30 million 75 bp paired-end reads.

Polyester simulations

In addition to the ability to generate reads, Polyester allows simulating experiments with differential transcript expression and biological variability. Thus, we can assess not only the accuracy of the resulting estimates, but also how these estimates would perform in a typical downstream analysis task like differential expression testing.

The Polyester simulation of an RNA-seq experiment with empirically-derived fragment GC bias was created as follows: The transcript abundance quantifications from RSEM run on NA12716_7 of the GEUVADIS RNA-seq data [11] were summed to the gene-level using version 75 of the Ensembl gene annotation for GRCh37. Subsequently, whole-transcriptome simulation was carried out using Polyester. Abundance (TPMs) was allocated to isoforms within a gene randomly using the following rule: for genes with two isoforms, TPMs were either (i) split according to a flat Dirichlet distribution (α = (1,1)) or (ii) attributed to a single isoform. The choice of (i) vs (ii) was decided by a Bernoulli trial with probability 0.5. For genes with three or more isoforms, TPMs were either (i) split among three randomly chosen isoforms according to a flat Dirichlet distribution (α = (1,1,1)) or (ii) attributed to a single isoform. Again, (i) vs (ii) was decided by a Bernoulli trial with probability 0.5. The choice of distributing expression among three isoforms was motivated by exploratory data analysis of estimated transcript abundance revealing that for most genes nearly all of expression was concentrated in the first three isoforms for genes with four or more isoforms.

Expected counts for each transcript were then generated according to the transcript-level TPMs, multiplied by the transcript lengths. 40 million 100bp paired-end reads were simulated using the Polyester software for each of 16 samples, and 10% of transcripts were chosen to be differentially expressed across an 8 vs 8 sample split. The fold change was chosen to be either $\frac{1}{2}$ or 2 with probability of 0.5. Fragments were down-sampled with Bernoulli trials according to an empirically-derived fragment GC content dependence estimated with alpine [5] on RNA-seq samples from the GEUVADIS project. The first 8 GEUVADIS samples exhibited weak GC content dependence while the last 8 samples exhibited more severe fragment-level GC bias. Paired-end fragments were then shuffled before being supplied to transcript abundance quantifiers. Estimated expression was compared to true expression calculated on transcript counts (before these counts were down-sampled according to the empirically-derived fragment GC bias curve), divided by effective transcript length and scaled to TPM. Global differences across condition for all methods were removed using a scaling factor per condition. Differences across condition for the different methods’ quantifications were tested using a t-test of log₂ (TPM + 1).

Software versions and options

All tests were performed with eXpress v1.5.1, kallisto v0.43.0, Salmon v0.8.0 and Bowtie2 v2.2.4. Reads were aligned with Bowtie2 using the parameters --no-discordant -k 200, and -p to set the number of threads. On the RSEM-sim data, all methods were run without bias correction. On all other datasests, methods were run with bias correction unless otherwise noted. Additionally, on the Polyester simulated data, Salmon was run with the option --noBiasLengthThreshold, which allows bias correction, even for very short transcripts, since we were most interested in assessing the maximum sensitivity of the model.

GEUVADIS data

The analyses presented in Fig. 1d, Supplementary Table 1 and Supplementary Fig. 5 were carried out on a subset of 30 samples from the publicly-available GEUVADIS [11] data. The accessions used and the information about the center at which the libraries were prepared and sequenced is recorded in Supplementary Table 3. All methods were run with bias correction enabled, using a transcriptome built with the RefSeq gene annotation file and the genome FASTA contained within the hg19 Illumina iGenome, to allow for comparison with the results in [5].

For each transcript, a t-test was performed, comparing log₂ (TPM + 1) from 15 samples from one sequencing center against 15 samples from another sequencing center. P values were then adjusted using the method of Benjamini-Hochberg, over the transcripts with mean TPM > 0.1. The number of positives for given false discovery rates was then reported for each method, by taking the number of transcripts with adjusted p value less than a given threshold.

Because the samples are from the same human population, it is expected that there would be few to no true differences in transcript abundance produced by this comparison. This assumption was confirmed by permuting the samples and performing t-tests as well as making t-test comparisons of random subsets within sequencing center, which consistently produced ≪ 1 DE transcript on average for all methods. Such an analysis comparing samples across sequencing center was specifically chosen to highlight transcripts with false quantification differences arising from technical artifacts.

SEQC data

The consistency analysis presented in Supplementary Fig. 4 was carried out on a subset of the publicly-available SEQC [12] data. Specifically, the accessions used, along with the corresponding information about the center at which they were sequences is recorded in Supplementary Table 4. For each sample, “same center” comparisons were made between all unique pairs of replicates labeled as coming from the same sequencing center, while “different center” comparisons were made between all unique pairs of replicates labeled as coming from different centers (“Center” column of Supplementary Table 4).

Statistics

Comparisons of RSEM-sim simulated data mean absolute relative differences (MARD) and Spearman correlations had sample sizes n₁ = 20, n₂ = 20. A Mann-Whitney U test (two-sided) was performed. Dominant isoform switching on GEUVADIS data had sample sizes n₁ = 15, n₂ = 15. A t-test (two-sided) was performed. Polyester simulated data differential expression analysis had sample sizes n₁ = 8, n₂ = 8. A t-test (two-sided) was performed. FDR sets were defined using Benjamini-Hochberg multiple test correction.

Salmon development, support and validation

Salmon is developed openly on GitHub (https://github.com/COMBINE-lab/Salmon), which is the primary venue for users to make feature requests and to file bug reports. However, support is also provided via a Google Users Group (https://groups.google.com/forum/#!forum/Sailfish-users) and a gitter channel (https://gitter.im/COMBINE-lab/Salmon). This provides multiple venues for users to have questions answered quickly and efficiently. Further, Salmon is available through both homebrew-science [29] and bioconda to ease installation and upgrading of the package.

Testing during the Salmon development and release process is highly-automated. In addition to any major feature branches, the Salmon repository retains both a master and develop branch. The master branch corresponds to the most recent tagged release of the software, while the develop branch is where new feature development takes place before they have been sufficiently well-tested to be included in a tagged release. A publicly-facing continuous integration service (Travis-CI) automatically builds each commit, and runs a small set of functionality tests to ensure that no breaking changes have been committed. However, these tests do not assess or track quantification accuracy. For this task, a parallel, self-hosted continuous integration system has been created. On each commit to the Salmon repository, a Drone (Drone-CI) server pulls the latest commit, and builds it in a clean CentOS5 environment using Docker [30]. In addition to the functionality tests, Salmon is run on simulated samples (generated using Polyester [13]). These test (automated using Next Flow [31]), build the Salmon index, quantify all of the simulated samples, and store the resulting accuracy metrics in a JSON formatted file. These results are copied back from the Docker container to the host, and are placed in a uniquely-named directory that corresponds with the SHA1 hash of the commit that produced them. This allows us to track accuracy over various Salmon commits, and to identify the commit corresponding to any performance regressions. We note that this setup overlaps considerably with the setup suggested for “continuous analysis” by Beaulieu-Jones and Greene [32]. Going forward, we anticipate expanding the test suite to include even more data and performance metrics.

Data availability

Accession information for experimental data used in this manuscript have been provided in the text and in Supplementary Tables 3 and 4. Simulated data has been carried out in accordance with the procedures detailed in Ground truth simulated data.

Code availability

The source code for Salmon is freely available, and licensed under the GNU General Public License (GPLv3). The latest version of Salmon can be obtained from https://github.com/COMBINE-lab/salmon.