Abstract
The role of the phase response curve (PRC) shape on the synchrony of synaptically coupled oscillating neurons is examined. If the PRC is independent of the phase, because of the synaptic form of the coupling, synchrony is found to be stable for both excitatory and inhibitory coupling at all rates whereas the antisynchrony becomes stable at low rates. A faster synaptic rise helps extend the stability of antisynchrony to higher rates. If the PRC is not constant, but has a profile like that of a leaky integrates-and-fire model, then, in contrast to the earlier reports that did not include the voltage effects, mutual excitation could lead to stable synchrony provided the synaptic reversal potential is below the voltage level the neuron would have reached in the absence of the interaction and threshold reset. This level is controlled by the applied current and the leakage parameters. Such synchrony is contingent on significant phase response (that would result, for example, by a sharp PRC jump) occurring during the synaptic rising phase. The rising phase however does not contribute significantly if it occurs before the voltage spike reaches its peak. Then a stable near-synchronous state can still exist between type-1 PRC neurons if the PRC shows a left-skewness in its shape. These results are examined comprehensively using perfect integrate-and-fire, leaky integrate-and-fire and skewed PRC shapes under the assumption of the weakly coupled oscillator theory applied to synaptically coupled neuron models.
1 Introduction
Oscillating neurons interacting with synaptic connections abound in a number of brain nuclei (Jahnsen & Llinás, 1984; Bevan & Wilson, 1999; Bolam, Hanley, Booth, & Bevan, 2000; Hutcheon & Yarom, 2000). Many of these connections are excitatory (Bevan, Magill, Terman, Bolam, & Wilson, 2002) and some are inhibitory (Filion & Tremblay, 1991). Some amount of coherent spiking (which can be termed synchrony or transient synchrony) (Wang & Rinzel, 1992; Bergman et al., 1998) (Salinas & Sejnowski, 2000; Engel, Fries, & Singer, 2001; Buzsáki, 2006) is a common phenomenon among such oscillating neurons. Tracing such coherent behavior to the mechanism of connectivity between the neurons and to the external synaptic driving influenced by the network (Stroeve & Gielen, 2001; Terman, Rubin J, Yew A, & Wilson C, 2002; Lewis & Rinzel, 2003; Galán, Fourcaud-Trocmé, Ermentrout, & Urban, 2006; Tsodyks, Mitkov, & Sompolinsky, 1993) is crucial in order to systematically understand such behavior and control it for the purpose of therapeutic intervention. For example, networks in the basal ganglia in animal models of Parkinson’s disease were observed to display spike time coherence (Raz, Vaadia, & Bergman, 2000; Wichmann, Bergman, & DeLong, 1994). Desynchronzing neuronal activity by deep brain stimulation (Wichmann & Delong, 2006; Wilson, 2013) is an effective therapeutic mechanism. These networks are complex and often emulation of the behavior by equally complex network simulations (Guo, Rubin, McIntyre, Vitek, & Terman, 2008), while being helpful in engineering the required responses, still leave unanswered several basic questions such as, the relation between the intrinsic response properties of the neurons and the network behavior. For this, one must develop sufficient understanding of such relationship in pairs of coupled neurons, and then extend it to include the network structure.
The intrinsic response behavior of an oscillating neuron is best captured by its phase response curve (PRC) which is easily measured experimentally (Winfree, 2001; Tateno & Robinson, 2007; Gouwens et al., 2010; Netoff, Schwemmer, & Lewis, 2012). (However, briefer and weaker stimuli will have be to employed in measuring such responses, or iPRCs, for the reults of weakly coupled theory that are presented here to be applicable.) Thus relating the PRC to the network behavior is insightful and rewarding in understanding neuronal synchrony particularly when the neurons are self-oscillatory (G. B. Ermentrout, Galán, & Urban, 2007; Achuthan & Canavier, 2009; Smeal, Er-mentrout, & White, 2010; Smeal et al., 2010; Krogh-Madsen, Butera, Ermentrout, & Glass, 2012; Miranda-Domínguez & Netoff, 2013). However, real PRCs occur in a variety of shapes (Tateno & Robinson, 2007; Schultheiss, Edgerton, & Jaeger, 2010), although for ease of analytical studies they may be broadly categorized into just two kinds, type-1 and type-2 (Hansel, Mato, & Meunier, 1995; B. Ermentrout, 1996), depending on whether the phase response involves for most of the neuron oscillation an advancement of the phase or not. However some type-1 PRC neuronal models do show a negative, albeit small in amplitude, phase response immediately following the spike peak. In this work we selected for analysis models that show purely positive PRC response, and a conductance based neuronal model that has a type-1 PRC but with a brief negative phase response for simulating large coupled neurons. Considerable progress was made in relating the type-1 and type-2 PRCs to the network behavior (Van Vreeswijk, Abbott, & Ermentrout, 1994; Hansel et al., 1995; B. Ermentrout, 1996). The leaky integrate-and-fire (LIF) model (Gerstner & Kistler, 2002) and the perfect integrate-and-fire (PIF) are the simplest examples of type-1 PRC neuron model, and Hodgkin-Huxley model (Hodgkin & Huxley, 1952; Hansel, Mato, & Meunier, 1993) is an example of the type-2 PRC neuron model. These models have been widely used as representative examples of these two classes of PRCs. However, The LIF and PIF models have sudden rises in the PRC level near zero phase, the LIF model also has an exponential PRC profile, the PIF model results in a constant response throughout the oscillation. The HH model shows extremely little response near zero phase - a behavior quite common in a number of other models where certain current can make the phase response shallow for considerable portion of the oscillation following a spike. These features warrant a careful examination of the role of the PRC shape on the network behavior with a goal of discovering the effect of such features on the network synchrony.
Relating the PRC types (type-1 and type-2) to their network responses (whether synchrony ensues or fails) is not a simple task due to the recognition that the shape of each of these types can not only be modulated easily by the presence of certain currents, but can result in markedly different dynamical properties than their type would suggest when allowed to interact with other neurons in a network. It was shown earlier (Arthur, Burton, & Ermentrout, 2013) that a theta model with a symmetric type-1 PRC, while retaining its oscillation period can modulate its PRC shape when a small adaptation current is added to it. In particular a skewness is effected in its shape. Such shape changes can significantly affect the neuron’s interaction with other networked neurons; Delayed rectifier and the fast sodium currents can sensitively modulate the PRC shape and can cause the PRC shape skewness (G. B. Ermentrout, Beverlin II, & Netoff, 2012). In model computations, it was also shown that the position of the PRC peak can be sensitively affected by the presence of a persistent sodium current (Pfeuty, Mato, Golomb, & Hansel, 2005).
Here we selected three models, viz., leaky integrate-and-fire (LIF), perfect integrate-and-fire (PIF), and a PRC model whose shape is altered using a parameter, to systematically study the relation between the PRC shape and the ensuing synchrony between a pair of coupled oscillating neurons using the approach of weakly coupled oscillator theory. The goal of the present work is to not only exhaustively study these models such that prior results could be understood in the larger context of parameter spaces, but also to address how PRC shape skewness can alter the coherent behavior of coupled model neurons. Thus our results complement those reported earlier on LIF and related models, in particular those in (Van Vreeswijk et al., 1994; Hansel et al., 1995; B. Ermentrout, 1996), and advance the role of PRC skewness on the synchrony mechanism in a variety of networks such as those reported in (Pfeuty et al., 2005; G. B. Ermentrout et al., 2012).
The LIF and the PIF neuron networks are some of the most popular networks being studied in neuroscience owing to their simplicity in formulation, and their predictive capacity to other networks comprising of more complex neuronal models (Lapicque, 1907; Van Vreeswijk et al., 1994; Hansel et al., 1995; Lewis & Rinzel, 2003; Jolivet, Lewis, & Gerstner, 2004; Burkitt, 2006; Ladenbauer, Augustin, Shiau, & Obermayer, 2012). Although they were not viewed from the point of view of the PRCs at the time of their original introduction, they now serve as the simplest models that show drastic differences in their PRC shapes. The LIF model is more than a century old (Lapicque, 1907), and was first proposed by an experimenter to formulate accumulation of charge on the cell membrane in response to an applied current. Despite the dynamics of only the leakage current in the model, it nevertheless became a test bed for studies on synchrony and activity of neurons (Brunel & Sergi, 1998; Kuhlmann, Burkitt, Paolini, & Clark, 2002; Feng, 2003; Brette & Gerstner, 2005). With the realization of the importance of the PRC or phase response function in determining the synchrony of a network of oscillating neurons (Winfree, 1977; Tsubo, Teramae, & Fukai, 2007; Perez Velazquez et al., 2007; Tateno & Robinson, 2007; Achuthan & Canavier, 2009; Cui, Canavier Carmen, & Butera Robert, 2009; Smeal et al., 2010) the LIF model became more useful in constructing theories that may be extended or generalized to other more complex models (Chow & Kopell, 2000; Pfeuty, Mato, Golomb, & Hansel, 2003).
The present work attempts a systematic study of the role of the PRC shape in ensuing stable synchrony or antisynchrony of mutually coupled neuron models. The present work is mainly analytical with numerical results augmenting the analytical results. We presented the results for simple systems first illustrating them with numerical simulations, and then introduced more complex phase response curves along with simulation of large number of coupled neuron models. In Section 2 the general phase reduction method of weakly coupled oscillator theory is briefly reviewed along with the method of finding stability of synchrony and antisynchrony. As a first simple example, the phase independent PRC shape is studied in detail in Section 3 by invoking the PRC of the PIF model. The jump near zero together with a rising PRC profile is studied in Section 4 by examining the LIF model network of a pair of coupled neurons. This is again illustrated extensively with numerical simulations, and the analytical results delineating the synchrony and antisynchrony regimes are illustrated in several parameter spaces. In both these models, the voltage time course is included in the analysis and it plays a major role in the stability of synchrony, particularly when the coupling is excitatory. Also, the synaptic conductance used is always initiated at zero phase, thus having their rising phases when the PRC is significantly non-zero. Then in Section 5 we introduced more complex PRC shapes by first simulating a set of 100 mutually excitatory Wang-Buzsáki model neurons, and then using PRC shapes constructed to deviate from the canonical PRC.
2 Ermentrout’s phase reduction method
Our goal is determining the steady states of the coupled neurons, and their linear stability. In addition to numerical simulations, we employ the weakly coupled oscillator theory that involves phase reduction to study the stability of synchrony and antisynchrony. The phase reduction method has been extensively used in neuroscience and applied mathematical studies where in oscillators attracted to their limit cycles receiving perturbation either by external stimulus or coupling can be reduced to a set of phase coupled oscillators (Winfree, 1967; Kuramoto, 1984; G. B. Ermentrout & Kopell, 1986; Brown, Moehlis, & Holmes, 2004). However this is not the phase computed in Cartesian coordinates, but a nonlinear function representing the time shift the original oscillator would have to undergo to accommodate the perturbation. If the oscillator’s variable is V (t), then, the perturbed variable is written as V (t+θ(τ)), where τ = εt is the slow time scale, ε is the strength of perturbation and θ is the phase of our interest. This was originally introduced by Neu (Neu, 1979b, 1979a) and then generalized and formalized by Ermentrout (G. B. Ermentrout, 1981; G. B. Ermentrout & Kopell, 1991) using Fredholm’s alternative, and then later restated as Malkin’s theorem by Hoppensteadt and Izhikevich (Hoppensteadt & Izhikevich, 1997). An excellent review of this method is found in (Lewis & Skinner, 2012).
The phase evolution can be expressed in the slow time scale after averaging over the fast time scale of the oscillator. When applied to neural oscillators, a neuron regularly spiking with a period T and whose voltage variable is V1(t) interacting with a second neuron via synaptic coupling receives a coupling perturbation proportional to where Esyn is the synaptic reversal potential, s2(t) is the synaptic conductance delivered by the coupled neuron, and is the coupling strength. Similarly the second neuron with a voltage variable V2(t) receiving an identical coupling receives a current proportional to where s1(t) is the synaptic conductance received from the first neuron. In the reduced phase coupled equations the phase derivatives are proportional to the convolutions of these currents with the phase response curve - termed the interaction function. Thus the reduced phase evolution equations for two identical and mutually coupled neurons are written in terms of their phases θ1 and θ2 as
| (1) |
| (2) |
The time t in the above equations is the slow time scale that we alluded to, but the symbol t in the definition of the interaction function H(ϕ) defined below is the oscillator’s time used here as an integration variable:
| (3) |
Note that the changes in frequency must be small for the theory to be valid, and in the normalized units, small changes in frequency are equivalent to small changes in the period. The “periodized” conductance sp(t) is defined below. Z(t) is the phase response curve (PRC). The phase is zero when the voltage time course reaches the peak of the action potential. It reaches the peak again at the end of the oscillation period, t = T. The PRC obtained in this method that uses weakly coupled oscillator theory is some times termed infinitesimal PRC or ‘iPRC’ to indicate the fact that it is obtained by using infinitesimally small stimulus strength such that the oscillation period is not significantly altered, and the integration limits in the above integral are still meaningful in the coupled state of the neurons. The term
| (4) |
which we call the ‘shunted PRC’ assumes importance in the study of the stability of synchrony (Hansel et al., 1995). This represents the modifications to the phase response introduced by the effect of the voltage and the synaptic reversal potential. The shunted PRC can become monotonically increasing or decreasing in some simple cases leading to its direct relationship with stability.
If the synaptic conductance s1,2(t) does not completely decay to zero before the start of another spike event, then the remnant conductance is added to the newly triggered conductance level. Thus in the steady state a profile of the synaptic conductance is obtained that is termed “periodized” synaptic conductance, and is computed as in (Van Vreeswijk et al., 1994; G. B. Ermentrout & Terman, 2010), and for an alpha function synaptic conductance s1,2(t) = α2te−αt where α is the inverse of the synaptic time constant, it is given by
| (5) |
sp(t) has units of frequency. It represents the contribution of all the previous synaptic events to the interaction occurring at time t, and is used in the analysis in place of s1,2(t). The conductance due to the contribution of the previous spikes causes sp(t) have its peak (tp) earlier than the peak time of the pure alpha function particularly at high frequencies. For example, for a cell firing below 50 Hz with α = 1/3 ms−1, the peak continues to be very close to 3 ms, but for 100 Hz, it occurs at 2.63 ms, and for 500 Hz it occurs at 0.89 ms. Taking the difference of the two Eqs. 1, 2, the evolution equation for the phase difference ϕ = θ2 − θ1 can be written as
| (6) |
where G(ϕ) is the growth function. Since H(ϕ) can be expressed as a sum of its odd part Hodd(ϕ) and its even part Heven(ϕ), the right hand side of the above equation can also be written as −2Hodd(ϕ). This notation is used by some authors to study the stability (Van Vreeswijk et al., 1994; B. Ermentrout, 1996).
Synchrony (ϕ = 0) and antisynchrony (ϕ = T/2) are both the steady states of this equation as it can be easily verified from Eq. 6 that becomes zero at these two steady states. Other phase-locked states could also exist but they must be computed numerically. For becoming useful, the steady states must be stable. To test the stability of the synchrony, we must examine the eigenvalue λ = G′(ϕ)|ϕ=0. This is the slope of the growth function G(ϕ) at ϕ = 0. The parameter region with the property λ < 0 is the region of stable synchrony, and that with λ > 0 is the region of unstable synchrony. The curve in the parameter spaces obtained by setting λ = 0 is the critical curve across which stability changes occur. From the relation between G and H in Eq. 6 and the expression in Eq. 3, we can directly write λ as
| (7) |
The antisynchrony is represented by the solution , and its stability is given the slope of the growth function at ϕ = T/2, i.e. the eigenvalue is given by
| (8) |
In the steady state, both neurons maintain a constant phase difference, ϕ*, and spike with an identical rate, i.e. . This common rate might be slightly different from their intrinsic oscillation frequency (1/T). By adding the Eqs. 1, 2 in the steady state (i.e. at ϕ = ϕ*), we obtain the frequency in the steady state (Hansel et al., 1993) as
| (9) |
The weakly coupled oscillator theory is strictly valid in the limit of the frequency being close to the uncoupled frequency. Having a non-zero Heven(ϕ*) is not a violation of the weakly coupled theory. The magnitude of Heven(ϕ*) which, in our definition, can be controlled by must be much smaller than 1/T.
3 Effect of phase independence of the PRC on synchrony
The perfect integrate-and-fire (PIF) neuron model displays a phase independent PRC. It has a voltage variable [V (t)] that linearly grows from a reset value (Vr) to a threshold level (Vth). If the voltage in its ongoing evolution crosses the threshold level, it is assumed to have emitted a spike, and thus is assigned the reset level. The spike itself is not represented in the model. The model is defined by a single equation for the voltage whose time derivative is a constant: such that V (t) is reset to Vr when V crosses Vth. I0 is the external constant applied current that is used to trigger oscillations in the model. The dynamics of two such coupled identical neurons are shown in Figure 1 by solving the equations for the two coupled neurons whose voltage are represented by V1(t) and V2(t):
| (10) |
| (11) |
where the synaptic conductances triggered by the spike events in the first and the second neuron are, respectively, s1(t) and s2(t), Esyn is the synaptic reversal potential, and is the constant maximum synaptic coupling strength. We let the synaptic conductances assume normalized alpha-function profile such that the synaptic conductance followed by a spike event at ts is given by , where α is the synaptic rate constant. Since the applied current is identical to both the oscillators, the neurons are identical oscillators differing only by their initial states. The simulations are shown for mutual excitation. The two neurons started with a voltage difference of 0.3 evolved into a synchronous state at I0 = 0.1 [Fig. 1(a)]. But when the current is reduced by half, the same initial conditions led to an antisynchronous state [Fig. 1(b, top)] that coexists with the synchronous state [Fig. 1(b, bottom)] which is obtained by choosing a different set of initial states.
Figure 1.
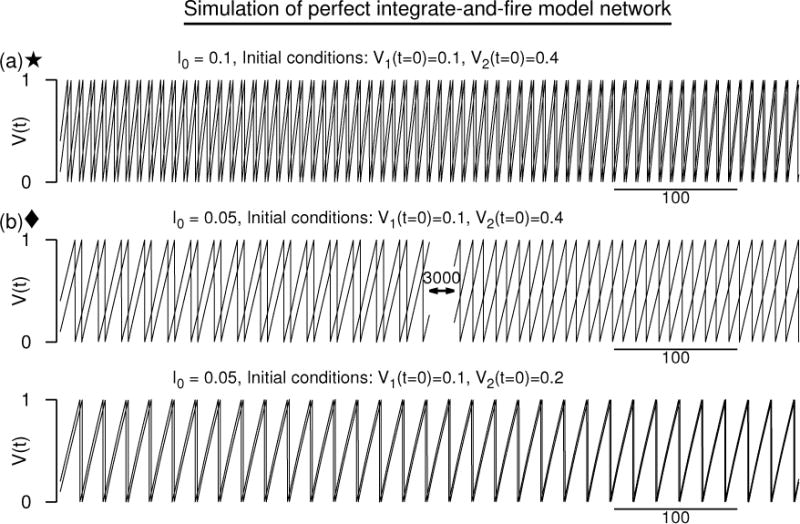
Numerical simulation of a network of two “perfect” integrate-and-fire neuron models. Coupling is excitatory, but results are qualitatively similar when the coupling is inhibitory. (a) The two voltage time courses at I0 = 0.1 approaching a synchronous state. (b) The same initial conditions as in (a) leading to antisynchronous state, but a more closely spaced initial conditions leading to a synchronous state when I0 is lowered. Synaptic conductance is an alpha function with α = 1/3. Vreset = 0, Vth = 1. Esyn = 2.
These results may appear to be counterintuitive at first because it is generally assumed that neurons of this kind (that show type-1 PRCs (Hansel et al., 1995)) should fail to synchronize for mutual excitation. The PIF model does display a type-1 phase response curve. Indeed, the voltage evolution of the uncoupled PIF model is simply a linearly growing function of time,
| (12) |
and the phase response curve is simply the inverse of the time derivative of the voltage which becomes
| (13) |
Thus the PRC is not only positive throughout, but is a constant and independent of the phase. Consequently, the shunted PRC (Eq. 4) is a linear function of time. For Esyn > Vth, the shunted PRC is a linearly decreasing function of time, but is still positive throughout. Hence we expect that the interaction function itself (Eq. 3) to be positive. This indeed is the case, and can be seen more precisely by computing H(ϕ). For the alpha-function synaptic conductance, we obtain the interaction function as
| (14) |
where , A = [1 + T(B − α)] B/α, . The time period itself is the time elapsed between spike reset and spike threshold, and is obtained from Eq. 12 as T = (Vth − Vr)/I0. The interaction function is plotted in Fig. 2(a) for which Ω = 0.4, A = 1.165, and , and the positive shift in the frequency at zero phase is . Thus in the steady state of zero phase difference (synchrony), the oscillators are uniformly sped up from 1/T (= 10) to . And at the synchronous state, the interaction function grows linearly as can also be seen by Taylor expanding H(ϕ) near ϕ = 0: indicating that if the second oscillator leads the first by a small phase, then the first oscillator increases its frequency slightly proportional to the slope of the H(ϕ) at ϕ = 0. The second oscillator slows down because the slope of H(−ϕ) ≡ H(T − ϕ) is negative at ϕ = 0. This implies that the synchrony becomes stable as is also indicated by the negative slope of the growth function [Fig. 2(b), curve for I0 = 0.1] at ϕ = 0.
Figure 2.
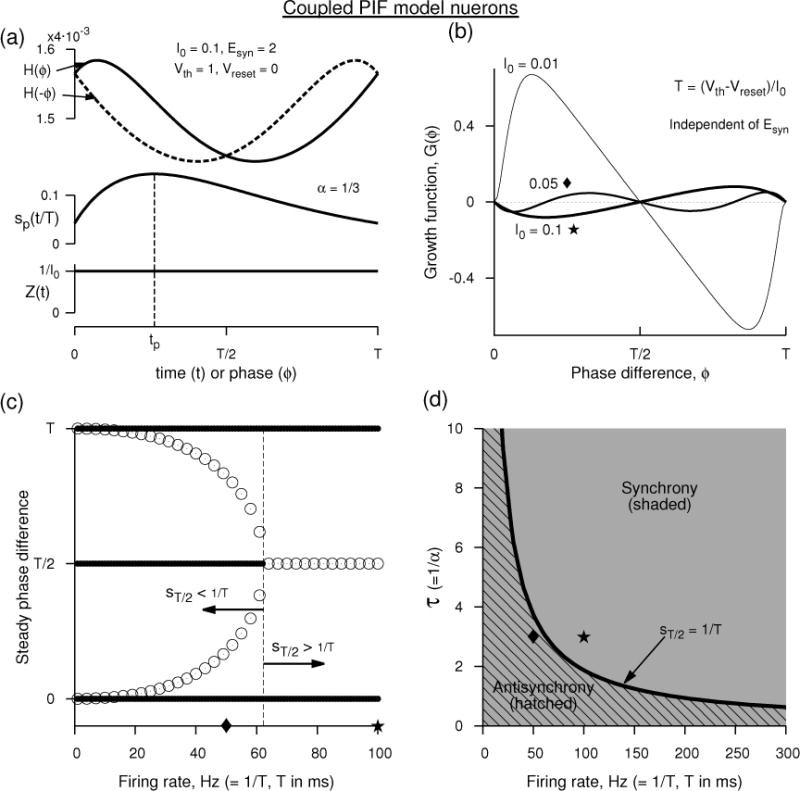
Analytical prediction of synchrony and anti-synchrony between two perfect integrate-and-fire neuron models. (a) The interaction function H(ϕ) and the alpha-function synaptic conductance at an Esyn that makes the coupling excitatory. The PRC of the model is simply 1/Iapp. (b) The growth function G(ϕ) at three different Iapp. G(ϕ), the phase-locked states and their stability are independent of Esyn, and thus the panels (b–d) remain unaltered between excitatory and inhibitory couplings. (c) The steady phase differences as a function of the frequency displaying stable synchrony (filled circles resembling thick lines at ordinate values of 0 and T) at all frequencies, stable antisynchrony (filled circles at T/2) at low frequencies. The unfilled circles represent unstable steady state phase differences. (d) Parameter display of synchrony (shaded, filling all the space) and antisynchrony (hatched) in the space of synaptic time constant τ (= 1/α) and firing rate (= 1/T). Unit of ms is assigned to time for convenience.
The expression for H(ϕ), Eq. 14, reveals that its dependence on ϕ is independent of Esyn which merely alters the frequency of neurons uniformly. So for excitatory coupling the frequency is elevated and for inhibitory coupling it is lowered, but the steady states and their stability are unaltered. This consequence is entirely due to the PRC being constant throughout the phase. The phase dependence of H(ϕ) is entirely due to the voltage and sp(t). At low rates such that sp(t) decays completely to zero before the onset of the next spike, then sp(t) becomes equivalent to the alpha-function itself, and H(ϕ) computed for slightly non-zero ϕ will have the contribution from the sp(t+ϕ) that is now mostly acting prior to the next spike time where Esyn−V (t) is lowest. This leads to a rapidly decaying H(ϕ) with ϕ, but as ϕ is advanced such that the influence of sp(t + ϕ) near the zero phase is minimized, the H(ϕ) begins to increase linearly with Esyn−V (t). This leads to skewed H(ϕ) that will result in a non-zero phase-locked state. But at very high frequencies such that sp(t) has no noticeable decaying tail, then H(ϕ) becomes more sinusoidal with dominating first Fourier mode and is similar to the well known Kuramoto phase model. At intermediate firing rates, a stability switch can occur for the antisynchronous state when the synaptic conductance at half period is equal inverse of the period. This can be easily seen when the stability of the antisynchrony is computed. The growth function G(ϕ) defined in Eq. 6 is identical to
| (15) |
and can be computed using Eq. 14 as
| (16) |
which is independent of the reversal potential. And thus, as is already noted from H(ϕ), the type of synaptic coupling (whether excitatory or inhibitory) does not dictate the stability of the steady states. The growth function is plotted in Fig. 2(b) as the rate is altered. At very low rates, the negative slope of G(ϕ) at zero-phase is not easily discernible, but its stability can be seen in the bifurcation diagram as a function of rate displayed in Fig. 2(c). In the next section we will show more systematically that synchrony is a stable solution at all rates by computing its eigenvalue, and also show that the antisynchrony becomes a stable solution when sp(T/2) < 1/T. These results are summarized in Fig. 2(d).
3.1 Stability of synchrony and antisynchrony
Synchrony
Using the expressions in Eq. 12, 13, and 5 in Eq. 7, we get the eigenvalue for synchrony as
| (17) |
This can be easily shown to be negative for αT ≠ 01. By noting that cosh(αT) is a hyperbolic function that is purely positive and its Taylor series can be re-expressed as where λ0 > 0 for αT ≠ 0, we find that
implying that the synchrony is stable. Using the method by Hansel et al. (Hansel et al., 1995), we can see how this negative sign arises due to the dominant negative contribution of the conductance downstroke overpowering the positive contribution due to the rising phase. For this, we first note that λ can be computed directly from the integral expression for H(ϕ) in Eq. 3 via the relationship between the growth function and H(ϕ) given in Eq. 6. By substituting only the expressions for Z(t) and V (t) and not sp(t), we obtain
| (18) |
In obtaining this we utilized the fact that the integral of the derivative of the periodic function (i.e. dt) is zero as a consequence of the fundamental theorem of calculus - this is also used below in computing the integrals. Since the slope of sp(t) is positive before it reaches its peak at, t = tp, and is negative afterwards, we can conveniently breakup the above integral into two parts, each having a segment of sp(t) that does not change the sign of its slope between the integration limits:
| (19) |
Just as the mean of a function computed using a probability density function lies within the integration limits, the integral becomes equal to the product of t1 and x where , and t1 is a fixed value between (and including) 0 and tp. This is guaranteed by the mean value theorem (see page 128 in (Courant, 2011)). Similarly, the integral becomes equal to or simply −t2x, where t2 is a fixed value between (and including) tp and T. Thus we can write Eq. 19 as
| (20) |
The sign is asserted because t is a monotonically increasing function, and thus t2 ≥ t1. The value of x can only become zero if α itself were zero. And t2 and t1 become identical (and zero at the same time) only when T itself were zero. We can also easily see from Eq. 17 by expanding cosh term in Taylor series that in the limit of either α or T going to zero, λ becomes 0. Thus unless T or α become zero, the eigenvalue is negative, i.e. λ < 0. Thus the synchrony is always stable for oscillating neurons (T ≠ 0) interacting with non-zero (α ≠ 0) synaptic rate constant. It is also clear that the reason for the stability is the dominant contribution of the conductance decay phase (t2) over the rising phase (t1).
Antisynchrony
The stability of antisynchrony is determined by the eigenvalue computed at ϕ = T/2, i.e. the sign of γ = G′(ϕ)|ϕ=T/2. The region where the condition γ < 0 is satisfied indicates stable antisynchrony, γ > 0 marks unstable antisynchrony, and the curve in the parameter spaces where γ = 0 is a critical curve. γ can be computed directly from the expression in Eq. 16 as
This can also be written in terms of the synaptic conductance at half period, sT/2 ≡ sp(T/2) as
| (21) |
where sp(T/2) can be computed from Eq. 5 by inserting T/2 for t. Thus antisynchrony is stable in the region given by
| (22) |
As T increases, i.e. as the rate decreases, the left hand side (sp at half period) and the right hand side (1/T) of the relation in Eq. 22 both decrease, but the conductance decreases faster than the rate due to its exponential nature. Thus the above stability relation is easier to satisfy at low rates leading to stable antisynchrony: the stable antisynchrony region falls on the left of the critical curve in Fig. 2(d).
Synchrony and antisynchrony for double exponential synaptic function
Changing the alpha-function to a double exponential synaptic function, where A = αdαr/(αr − αd), makes the periodized synaptic function
| (23) |
where and . The analysis for the stability of the synchronous state remains identical to that carried out above for the case of alpha-function synaptic conductance. And hence the synchrony remains stable at all rates and time constants. Even the condition for antisynchrony remains identical to that in Eq. 22. In particular, the eigenvalue for antisynchrony can be computed as before, and is expressed as
| (24) |
where τr = 1/αr and τd = 1/αd are the rising and decay rates of the synaptic conductance. This again can be simplified to the relation identical to that in Eq. 21, and thus the condition for stability of antisynchrony is again given by
| (25) |
where sp(T/2) is obtained from Eq. 23 by inserting T/2 for t. This condition leads to a dependence of the stability boundary on the time constants. This dependence is illustrated in Fig. 3. As before the stable antisynchrony region falls on the left of the critical curves in Fig. 3. If the rise time of the synaptic conductance is fast, then peak of the conductance occurs early leading to a reduced synaptic conductance at half period. Consequently sp(T/2) can be made equal to 1/T only for sufficiently small T (i.e. high rate). Thus the critical boundary of antisynchrony moves to smaller T or higher rates as seen Fig. 3.
Figure 3.
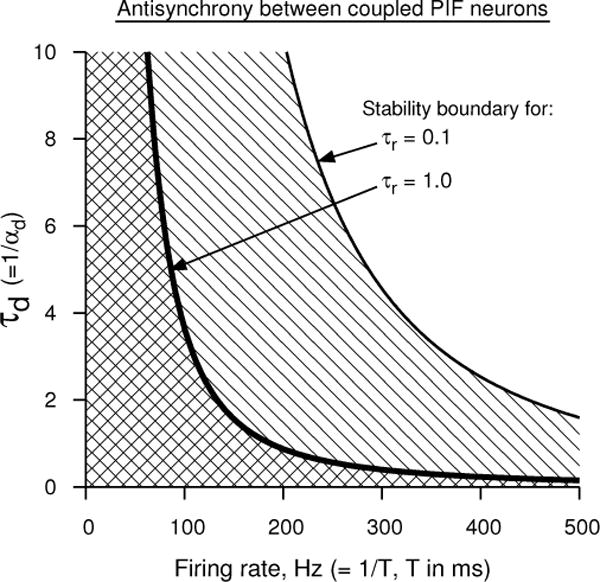
Analytical prediction of antisynchrony between two perfect integrate-and-fire neuron models using double exponential synaptic function in the plane of firing rate and synaptic decay time. The region to the left of each curve (the hatched region) marks the stability of antisynchrony for the corresponding synaptic rise time. Synchrony is stable in the entire parameter space.
4 Effect of PRC jump near zero phase
We invoke the leaky integrate-and-fire (LIF) model (Lapicque, 1907; Gerstner & Kistler, 2002) to examine the effect of the PRC jump at the zero phase. The model’s PRC, unlike that of the PIF, does depend on the phase and in fact increases monotonically. Conventionally, the LIF model is studied by setting the reset to 0 and the threshold level to 1 for convenience. However setting them to more realistic values would enable realistic synaptic reversal potential and synaptic time constants. So, although the analytical results are identical for both these choices, we present numerical results under both of them - there are some noticeable differences in the parameter regimes where stability transitions occur. For choosing realistic voltage shape, we use Wang-Buzsáki model. Under either interpretation, the LIF model displays the same type of PRC which is of type-1, and has sharp jumps at either extreme of the curve.
Model
The total current flowing through an LIF model membrane whose capacitance is Cm and voltage is V1(t), is equal to the leakage current −GL(V1 − EL) in the absence of any other input. By applying a steady external current I0 (or even by adjusting EL), the model can be made to oscillate. This is achieved by introducing a threshold level Vth crossing which V1 is reset to Vreset. The spike itself is not represented by the model, and is ignored in the analysis. Such a neuron in the presence of the applied current evolves with the time course
| (26) |
where Iapp = I0/GL + EL, and τm = Cm/GL. The model oscillates with a period
| (27) |
and its PRC is simply proportional to which can be computed as
| (28) |
where b = τm/(Iapp − Vreset). When two such neurons [whose membrane voltages are V1(t), V2(t)] are coupled synaptically with a reversal potential Esyn, they interact with their conductances [s1(t), s2(t)] which we model here with alpha-functions as in the previous section. In particular the periodized synaptic conductance has the same form as in Eq. 5. Thus when a neuron reaches its spike threshold, the corresponding synaptic conductance is generated and the interaction between two such identical neurons takes place according to the following two coupled equations:
| (29) |
| (30) |
The parameter Esyn determines whether the coupling is excitatory or inhibitory. Under the weak coupling assumption, the coupling conductance is the smallness parameter that would not significantly alter the period of oscillation of each neuron.
Simulations
In order to simulate these equations s1,2(t) are generated self-consistently using two first order differential equations (G. B. Ermentrout, 2002), and in the analysis we use the form of sp(t). Simulation of the above equations are shown in Figures 4 and 5 for two sets of parameters. The first set of parameters emulate a Wang-Buzsáki model’s voltage time course, and Esyn and α are set to realistic values. The results are shown in Fig. 4. Here we consider mutually excitatory coupling, and thus set Esyn = 10 mV, and α = 1/3 ms−1. At 100 Hz, the two coupled neurons gradually tend toward synchrony of spike times. At 50 Hz, two different sets of initial conditions exhibit two different phase differences suggesting a bistability between synchrony and antisynchrony. At very low frequency, a state that is very close to synchrony or a near-synchronous state is realized.
Figure 4.
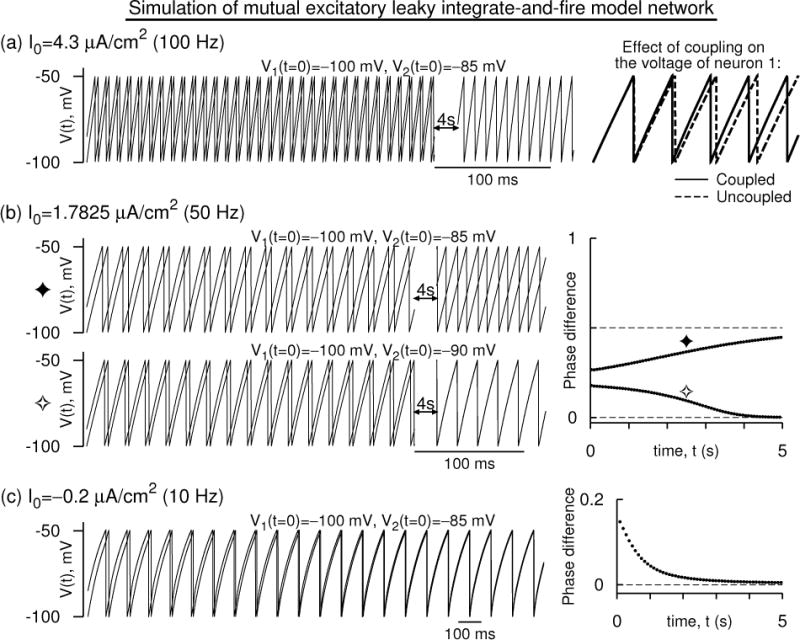
Simulation of a mutually excitatory network of two leaky integrate and fire neurons whose voltages are modeled according to those of the Wang-Buzsáki model. (a) The voltage time courses [V1(t), V2(t)] evolving in time and approaching a synchronous oscillatory state at a firing frequency of 100 Hz. Spikes are not part of the model, and hence are not drawn. On the right, the effect of the coupling on V1(t) is shown - it is excitatory. (b) Time courses as in (a) but at 50 Hz. Two sets of initial conditions lead to two different states: antisynchrony for widely separated initial conditions, and synchrony for closely separated initial conditions. Right: The difference of successive spike times of the neurons normalized to the instantaneous period of one of the neurons (i.e the phase difference) is shown for the two sets of initial conditions. (c) As in (b) but at 10 Hz. Synchrony and anti synchrony are both unstable, but a near synchronous state that is very close to the synchronous state is stable. For all the simulations The parameters are GL = 0.01 mS/cm2, EL = 0 mV, Cm = 1 μF/cm2, Vreset = −100 mV, Vth = −49.5635 mV. Esyn = 10 mV, α = 1/3 ms−1, and .
Figure 5.
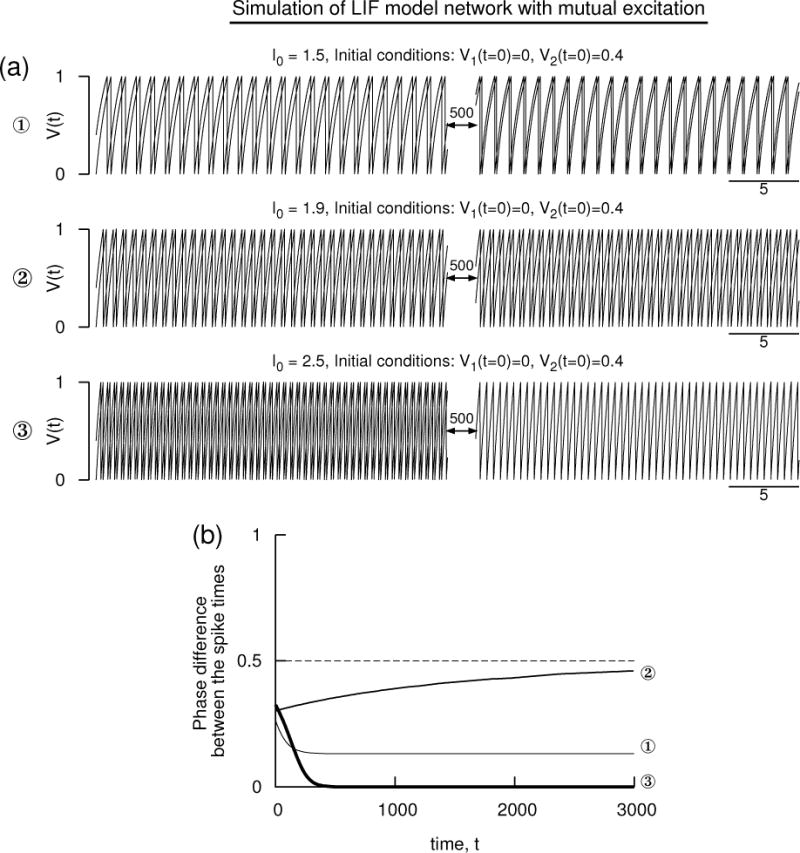
Simulation of a pair of mutually excitatory LIF model neurons with the conventional parameters without units: Cm = 1, GL = 1, EL = 0, Vreset = 0, and Vth = 1. (a) Voltage time courses of the two neuron models exhibiting antisynchrony, non-zero phase-locked state, and synchrony at three different levels of the applied current. (b) The phase difference of the consecutive spike times of the illustrations in (a) displaying the evolution toward steady states. The other parameters are Esyn = 2 that is above the threshold, and α = 6 that determines the shape of the alpha-function synaptic conductance. The membrane effect is included in the computation.
In the second set of simulations, we use the conventional set of parameters of the LIF whose voltage oscillates between 0 and 1. Units are not assigned to the time or the voltage variables. Simulation results at three different levels of I0 for the same set of initial conditions are shown in Fig. 5 for excitatory coupling with Esyn = 2 and α = 6. At high frequency, the phase difference clearly becomes zero indicating synchrony, at low frequencies the antisynchrony is stable, and at intermediate frequency a non-zero phase-locked state is stable.
Similar results can also be obtained by using a double exponential synaptic function as long as the synaptic rise time is not instantaneous. As we will see in the analysis below, the rising phase of the synaptic conductance sp(t) contributes to the stability of synchrony for excitatory coupling (i.e. for Esyn > Vth), and the decaying phase contributes to the instability. (This is counter to their contributions in the PIF network of the previous section.) Depending on how an exponential synaptic function is implemented (whether the rising branch of sp(t) appears as a curve with infinite slope or not) it may be possible to realize stable synchrony even with exponential synaptic function. If the rising phase occurs within a refractory period during which the PRC is zero, then instability of synchrony can result. Also note that there are two factors that help in stability of synchrony: For the double exponential, the peak of the periodized synaptic conductance (sp(t)) (Eq. 23) occurs later than that of the s(t), and thus the negative slope persisting beyond the synaptic rise time is in favor of the stable synchrony. And at higher rates, the fraction of the rise time in comparison to that of the decay time also increases, helping in decreasing the destabilizing factor.
Interaction and growth functions
The reduction of the coupled system (Eqs. 29 and 30) to phase coupled oscillators is carried out as outlined in Section 2, and the interaction function and the growth functions are computed using the relations in Eqs. 3 and 6. Using the expressions for the voltage and the PRC (Eq. 26 and 28), the shunted PRC can be written as
| (31) |
where the factor M is given by
| (32) |
Hansel et al. (Hansel et al., 1995) assumed that the shunted PRC is monotonically increasing. Under this assumption, the eigenvalue for stability of synchrony (Eq. 7) becomes positive making synchrony unstable. Here our goal is to fully explore the limitations of this assumption. M depends on the period of oscillation. Since the period is a logarithmic function of the parameters (Eq. 27), it is not immediately clear how M varies as a function of the rate, and consequently how depends on the parameters. However, it is clear that if M > 0, then the term becomes monotonically increasing supporting the assumption of Hansel et al. But if M < 0, then it is monotonically decreasing leading to a stable synchrony as we will show below. We also see that the eigenvalue for synchrony itself is proportional to M, and thus near the transition to synchrony the neurons possess long transients because the eigenvalue goes through zero.
Substituting for (from Eq. 31) and V (t) (from Eq. 26) in Eq. 3, we obtain the interaction function as
| (33) |
where , B = Aτmα2/(x2y2), K1 = z (τmx + Ty), K2 = zxy, K3= x2τm, and x = eαT − 1, y = ατm − 1, and z = 1 − eT/τm. The growth function G(Φ) is written from the relation in Eq. 6 as
| (34) |
For the parameters of the LIF model whose voltage is based on the Wang-Buzsáki model [Fig. 6(a–c)], two sets of growth functions are illustrated. For mutual excitation, the growth function [Fig. 6(d)] shows a negative slope at zero phase (stable synchrony) and positive slope at half period (unstable antisynchrony) at 100 Hz (I0 = 4.3 μA/cm2). Here M < 0. The antisynchrony branch retains its state until the frequency is lowered below about 60 Hz where it becomes stable [Fig. 6(e)]. The stability of antisynchrony is also controlled by other conditions that do not directly depend on M. The synchrony branch remains stable until the frequency is lowered such that the monotonicity of is affected. When I0 < (Esyn − EL)/GL, M becomes positive and the synchrony becomes unstable. The antisynchrony branch also changes its stability because its stability as we will see also depends on M.
Figure 6.
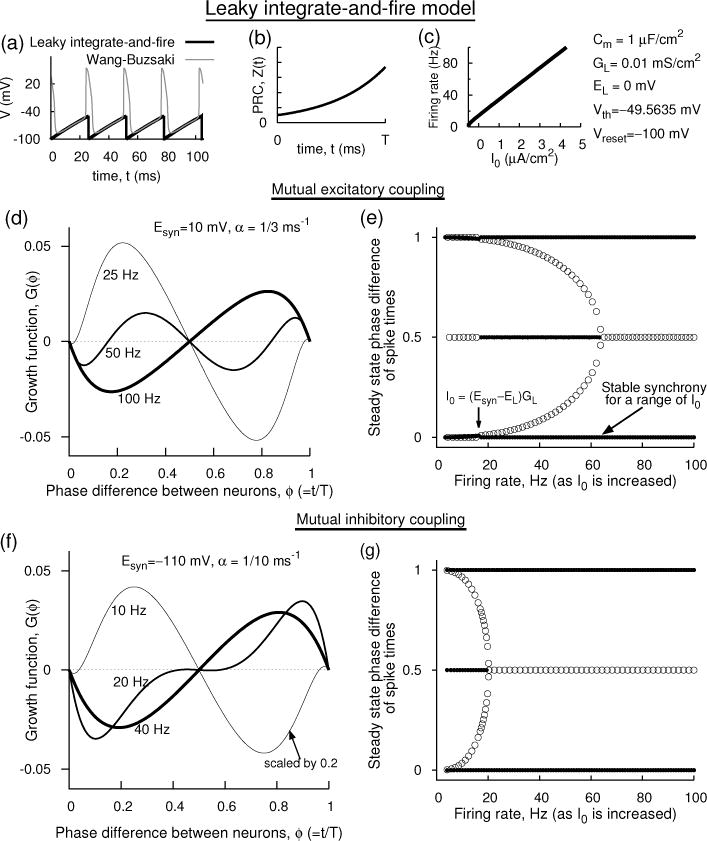
Analytical prediction of the dynamics of a network of two coupled leaky integrate-and-fire neuron models whose voltages are shaped according to those of the Wang-Buzsáki model. (a) The voltage time course of the each uncoupled LIF model (thick lines) compared to that of Wang-Buzsáki model (thin lines). (b) The PRC of the LIF model. (c) The firing rate as a function of the applied current I0. (d,e)Mutual excitation. (d) Growth functions at three levels of I0. I0 = 4.3 μA/cm2 for 100 Hz, 1.7825 μA/cm2 for 50 Hz, and 0.53 μA/cm2 for 25 Hz. (e) Stable (filled circles) and unstable (unfilled circles) steady state phase differences with frequency. A range of firing rates (or I0) can result in stable synchrony. (f,g) Mutual inhibition. (f) Growth functions are illustrated at three frequencies. (g) Steady state stability of synchrony and other states with I0.
For mutual inhibition [Fig. 6(f,g)], the growth function retains its negative slope (and hence its stability) at all frequencies because by decreasing Esyn and thus causing it to assume negative values, and in particular below Vreset, M remains negative and thus the shunted PRC is monotonically decreasing. The antisynchrony displays synchrony only at low frequencies as is also the case when the effect of the voltage time course on stability was not included (Lewis & Rinzel, 2003).
For the conventional parameters of the LIF model whose voltage ranges between 0 and 1 [Fig. 7(a–c)], growth functions and bifurcation of stable and unstable branches for mutually excitatory network are shown in Fig. 7(d–g). As it happened for the parameters of Fig. 6, the growth function has a negative slope at large I0 (giving large firing rate). This is counter to what has been believed thus far for the LIF model networks based on the assumption that the voltage plays little role in the coupling mechanism. At large I0, the PRC becomes less steep, and thus the time dependence of the factor Esyn − V dominates the monotonically increasing PRC to cause the shunted PRC decrease monotonically (M < 0). This effect would not exist if we ignored the voltage effect. As the I0 is decreased, however, the steepness of the PRC begins to dominate and when M > 0, synchrony becomes unstable. The stability of antisynchrony is determined by M as well as other independent factor. A non-zero stable phase-locked state merges with unstable synchrony at I0 that is barely sufficient to evoke spiking. We recover the stability diagram as a function of the synaptic rate [Fig. 7(f)] as reported by Van Vreeswijk et al. (Van Vreeswijk et al., 1994) at I0 small enough such that M > 0, and diagram resembles like that of a mutual inhibitory network when I0 is sufficiently high such that the shunted PRC is monotonically decreasing [Fig. 7(g)].
Figure 7.
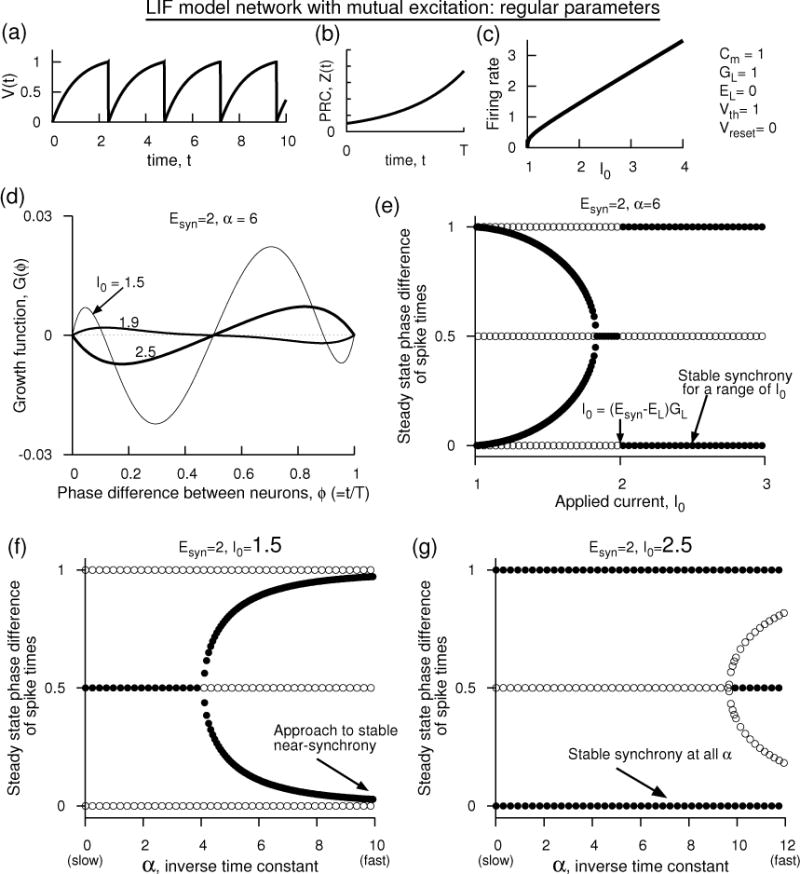
Analytical prediction of the dynamics of a pair of mutually excitatory LIF model neurons that use the conventional parameters as those set in Fig. 5. (a) Voltage time course of each uncoupled model neuron, (b) phase response curve of each neuron, (c) firing rate of each uncoupled neuron with steady input current. If time were measured in ms, then the firing rate would be measured in kHz, and achieving firing rates of the order of 10’s of Hz would become an extremely sensitive function of I0. (d) Growth functions at Esyn = 2, α = 1/3 displaying stable synchrony as I0 is increased across (Esyn − EL)GL. (e) Steady state phase differences with I0. Filled circles indicate stability, and unfilled instability. (f) Steady state phase differences with α at I0 = 1.5, and (g) same as in (f) but with I0 = 2.5. The results in (f) are similar to those of Fig. 1 of Van Vreeswijk et al. (Van Vreeswijk et al., 1994).
4.1 Stability of synchrony and antisynchrony
Using the same method as in the previous section that was first used by Hansel et al. (Hansel et al., 1995) we show below that the LIF pairs display stable synchrony if M < 0 where M is given by the relation in Eq. 32. Since the denominator of M must be positive to elicit oscillations, synchrony then can occur without any further conditions as long as Esyn < I0/GL + EL. This condition encompasses regimes of mutual excitation and mutual inhibition.
Synchrony
The eigenvalue for the stability of synchrony is computed as
We split this integral into two parts such that each part contains the portion of that does not change its sign:
where tp is the peak time of the periodized synaptic conductance sp(t). As in the previous section, by using the mean value theorem, the first integral can be written as a product of and x where t1 is between (and including) 0 and tp, and . The second integral can be written as the product of and −x where t2 is between (and including) tp and T. Thus we write the eigenvalue as
Since t2 > t1 (for non-zero T), the bracketed term is always positive. Thus the sign of λ is determined by the sign of M:
The critical curve of synchrony is thus given by M = 0, or
and the region of stable synchrony is given by M < 0. Since the denominator of M must be positive in order to elicit spiking, this condition results in the following condition for synchrony:
| (35) |
The right hand side of the above inequality is nothing but the level the voltage time course of the LIF model would have reached if not reset to Vreset after crossing Vth (see Eq. 26). This does not mean, however, that the excitation is acting like inhibition to cause stable synchrony, because in the coupled state the firing rate of the neuron increases [Fig. 4(a, right)]. The synaptic coupling would indeed begin to act like inhibitory synapse if Esyn is less than Vth when synchrony becomes stable without any further conditions. We can see this more clearly if rewrite M (from Eq. 32) as follows in terms of the oscillation period:
Since Vth − Vreset is always positive, from this form, it is easy to see that M becomes negative (i.e. synchrony becomes stable) if Esyn < Vth [see Fig. 8(a, right)] without further restrictions on the parameters. This is also when the coupling acts like an inhibitory connection. However, if Esyn > Vth, stability condition implies that the term in the square brackets must be negative, or in simplified form,
| (36) |
Figure 8.
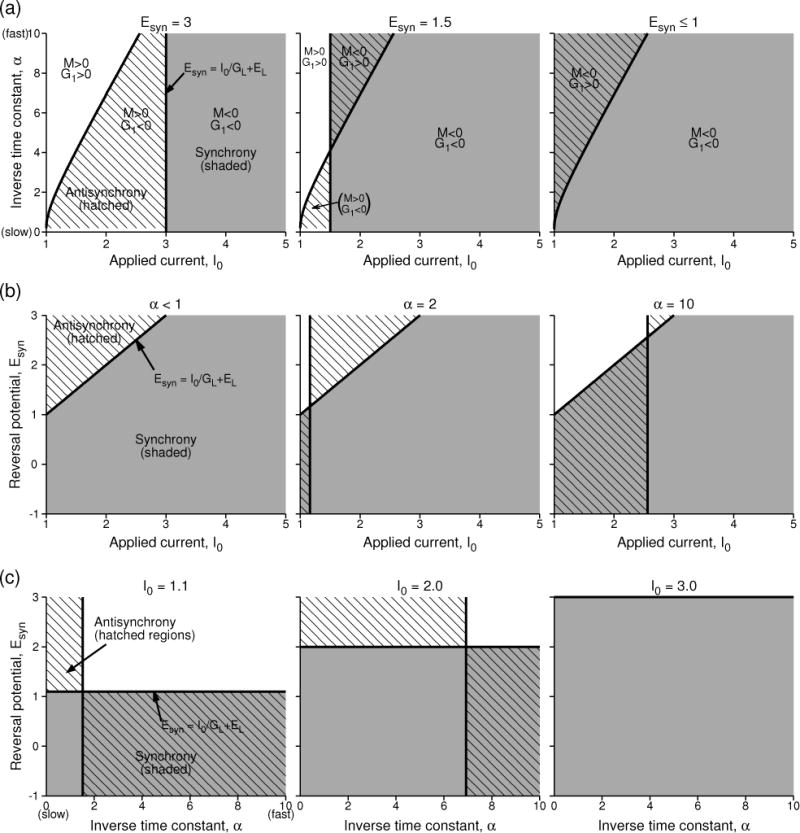
Regions of stability of synchrony and antisynchrony for the LIF model with the conventional parameters. (a) Stability region in I0 vs. α plane as the reversal potential is decreased from begin mutual excitatory to being mutual inhibitory. The shaded region is the region of stable synchrony, hatched region is the region of stable antisynchrony. Multiple regions of bistability, as well as non-zero phase-locked states (white space) also exist. (b) Stability regions in I0 and Esyn space at different levels of α. (c) Stability regions in α and Esyn space at different levels of the applied current. The model parameters are as those in Fig. 7.
Antisynchrony
Simplifications as above are not feasible for the antisynchronous state. But the eigenvalue γ can be found directly by taking the derivative of G(ϕ) at ϕ = T/2, and after simplification we obtain
where
| (37) |
and G2(α, τm, T) = αT(1 − ατm) cosh(αT/2) − 2 sinh(αT/2). Since B and the exponential term are positive, the sign of γ is determined by M and G1, and thus the critical regions of stability are bounded by the two curves M = 0 and G1 = 0. A portion of the stable synchronous region (that was defined by M < 0) also becomes a region of stable antisynchrony if in that portion the condition G1 > 0 is satisfied. In summary, the stable antisynchrony regions are defined by either or both of (i) M < 0, G1 > 0, and (ii) M > 0, G1 < 0. G1 is independent of Esyn but because M does depend on Esyn, changing Esyn alters the boundary of antisynchrony corresponding to the curve M = 0. G1 itself could be plotted as a function of its parameters to verify its sign. (Large numerical values due to G1 could be alleviated by using the positive multiplication factor B.)
These analytical results are summarized in the parameter space of (I0, α) at varying levels of reversal potential in Fig. 8(a). As we have already seen in Fig. 7(e), there can be three distinct regions displaying a non-zero phase-locked state (whose phase difference increases with rate toward half period), antisynchrony, and synchrony as I0 (or the rate) is increased. This pattern appears at large enough reversal potentials as in Fig. 8(a, left). However as Esyn is decreased, the boundary marking the stability switch of the antisynchrony remains unaltered (G1 is independent of Esyn), but the point of transition indicated by the arrow in Fig. 7(e) moves to smaller I0. If the new transition point occurs before the boundary of anti-synchrony then that regime is marked by M < 0 and G1 > 0 and exhibits bistability [Fig. 8(a, middle)]. At low enough Esyn [as directed by Eq. 35], the entire range of I0 exhibits stable synchrony, and the regime of I0 below the antisynchrony boundary exhibits bistability. This bifurcation diagram is similar to that for mutually inhibitory LIF model neurons even in the absence of the voltage effect (Lewis & Rinzel, 2003).
In Figure 8(b), the results are presented in the parameter space of (I0, Esyn) where the distinction between slow synapse (small α) and fast synapse (large α) becomes more clear. For very slow synaptic time constants [8(b, left)], synchrony and antisynchrony exist in complementary regions, and the transition from synchrony to antisynchrony occurs when Esyn is increased above I0/GL +EL. For faster synaptic time constants, this boundary can be either between a bistable region and a non-zero phase-locked state (low firing rates), or between synchrony ad antisynchrony as before (high firing rates) [Fig. 8(b, middle, right)]. Finally in Fig. 8(c), the transitions are shown at different rates in the parameter space of (α, Esyn) which makes it clear that at high enough rates most levels of Esyn, whether excitatory or inhibitory, lead to stable synchrony, a result that emerges entirely due to the effect of the voltage on the synaptic coupling. And a stable antisynchrony exists for excitatory coupling at slow synaptic rates.
5 Effect of PRC shape skewness, and the emergence of near-synchrony
Thus far we analyzed simpler models that have completely positive PRC shapes. In this section we first illustrate simulation results using a more realistic conductance based model that has a skewed PRC (along with a negative phase response immediately after spike peak), and then introduce a special class of phase response curve with a shape parameter. This allows for selectively tuning the skewness of the PRC. When the PRC was phase independent, or had a sudden rise at zero phase, synchrony depended on the synaptic rising phase taking advantage of the finite and large positive PRC level during that phase. Alternatively, if the PRC has a jump at zero phase and the rising phase of the synaptic conductance falls after the zero phase, synchrony may still become stable at appropriate firing rates. Generating the synaptic conductance (Wang & Rinzel, 1992) by solving a voltage dependent differential equation such as
| (38) |
may not allow a significant length of the synaptic rising phase occur after the spike peak. This may prevent stabilizing the synchronous state. Panels in Figure 9(a–c) illustrate this using Wang-Buzsáki model (see the Appendix for the model). The model with a small applied current (I0 = 0.211 μA/cm2), and a scale factor that scales the rates of sodium inactivation and the potassium activation uniformly (ε = 5) shows oscillations at 10 Hz and displays a type-1 PRC that looks like a bell-shaped curve except for a small insignificant negative regime near zero phase. But more importantly it displays a sudden rise in the PRC level within the first two milliseconds after the spike peak. But the synaptic conductance modeled with Eq. 38 (θsyn = 0 mV, ksyn = 2 mV, α = 12, β = 1/3) has most of its rise time before the spike peak during which the PRC is zero, and hence the opportunity to enhance the stabilizing component to the eigenvalue for synchrony of the coupled neurons is lost; The growth function [Fig. 9(b)] has a positive slope at zero spike time difference. Failure of synchrony is also seen in a network of 100 coupled neurons whose spike times are displayed in Fig. 9(c). Introducing an appropriate synaptic delay [dashed curve in Fig. 9(a)] brings the rising phase of the conductance to the regime of finite PRC level, but the growth function computed at these parameter levels still has a positive slope at synchronous state [Fig. 9(b)]. Two factors would help stabilize synchrony in this situation: one, increase the frequency of oscillation [as in the LIF model, Fig. 7(e)] by increasing the applied current while maintaining the sudden PRC rise near early phases and two, adjust the parameters of the model such a way that the sudden PRC rise occurs even earlier than two milliseconds. However in the Wang-Buzsáki model, simply raising I0 makes the jump in the PRC shallower.
Figure 9.
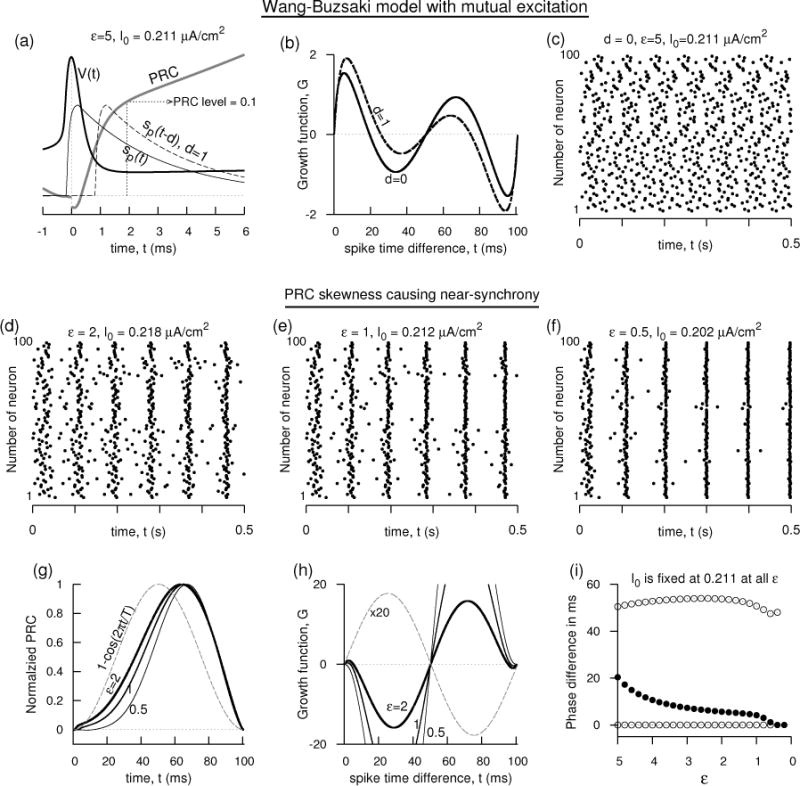
Near-synchrony in Wang-Buzsáki excitatory network. (a–c) Failure of synchrony despite sharp rise of the PRC near small phases, or delay in conductance. ε = 5, I0 = 0.211 μA/cm2. (a) V (t), the synaptic conductance of the Wang-Buzsáki model illustrated with and without delay, and PRC profile at small phases. (b) The growth function of two mutually excitatory neurons without and with (d = 1 ms) delay. (c) Spike times of a network of 100 coupled neurons without synaptic delay failing to exhibit synchrony. , Esyn = 0 mV. The initial conditions of are chosen randomly on the limit cycle orbit of the uncoupled model. (d–f) Spike times of the Wang-Buzsáki network as the skewness of the PRC is altered while keeping the firing rate at 10 Hz (by adjusting Iapp) and d = 0. Corresponding to these three simulations, the PRCs are shown in (g), and the growth functions for two coupled oscillators are shown in (h). (i) The stable (filled circle) and unstable (unfilled circle) phase-locked solutions as a function of ε. d = 0.
A near-synchrony among the coupled neurons may be realized by causing the PRC have skewness such that its response near early phases is subdued with or without having the PRC peak level move toward longer phases. We study this aspect in the rest of the section and in Figs. 9(d–i), 10, and 11. As ε is decreased, the sodium inactivation and the potassium activation both become slower, and a network of 100 coupled neurons displays increased amount of coherence with decreasing as can ε be seen in the increased level of spike time alignment in Fig. 9(d–f) (the rate is kept constant at 10 Hz by adjusting the I0). As ε is decreased, the negative feedback currents become slower making the spike broader and causing the hyperpolarization last longer. Consequently a subdued response near early phases results [Fig. 9(g)] and the sudden initial rise in the PRC diminishes. A second feature of the model is its PRC becoming asymmetric. It is shifted toward longer phases, although the PRC peak position is not affected substantially by ε. The effect of these two causes is the emergence of a stable non-zero phase-locked state in the vicinity of the synchronous state - this appears as the intersection of the growth function with the horizontal axis near zero with a negative slope. This is a dramatic change in the character of the shape of the growth function considering that it resembles mostly a sinusoidal curve for a canonical PRC shape (B. Ermentrout, 1996) [the dashed curves in Fig. 9(g,h); V (t) and sp(t) are the same as for the case of ε = 5.] The non-zero phase-locked state moves toward the synchronous state with decreasing as can be seen in Fig. 9(i).
Figure 10.
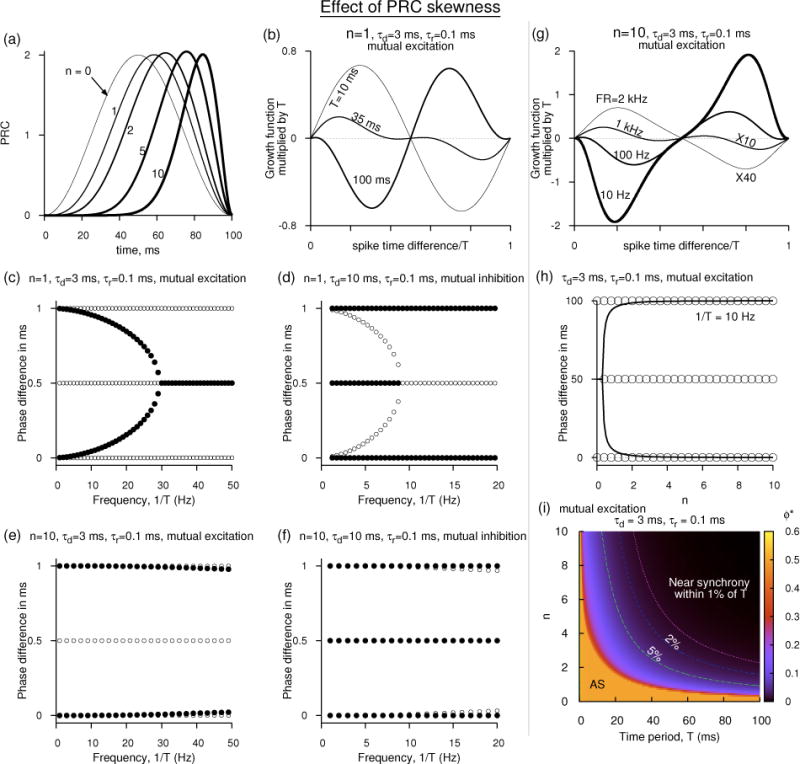
Effect of PRC skewness on synchrony. (a) PRC shapes given by Eq. 39 as n is increased. (b) The growth function for two mutually excitatory neurons getting affected by the period and in particular the antisynchrony becoming unstable as T is increased even when the PRC has a small skewness. (c) Change of stability of synchrony, antisynchrony, and the non-zero phase-locked states with the rate for excitatory network when n = 1. (d) Same as in (c) for inhibitory network. (e,f) Similar to (c) and (d) but for large skewness (n = 10), depicting only the movement at low rates. In (e) the non-zero phase-locked state is in close proximity to the unstable synchronous state (which is weakly repelling) at low rates making it a near-synchronous state. (g) The growth functions for excitatory network revealing the non-zero phase locked state surging toward the synchronous state as the rate is lowered at large skewness (n = 10). (h) Movement of steady states of the excitatory network as the skewness is increased at 10 Hz. (i) Steady states displayed in n vs. T space for the excitatory network.
Figure 11.
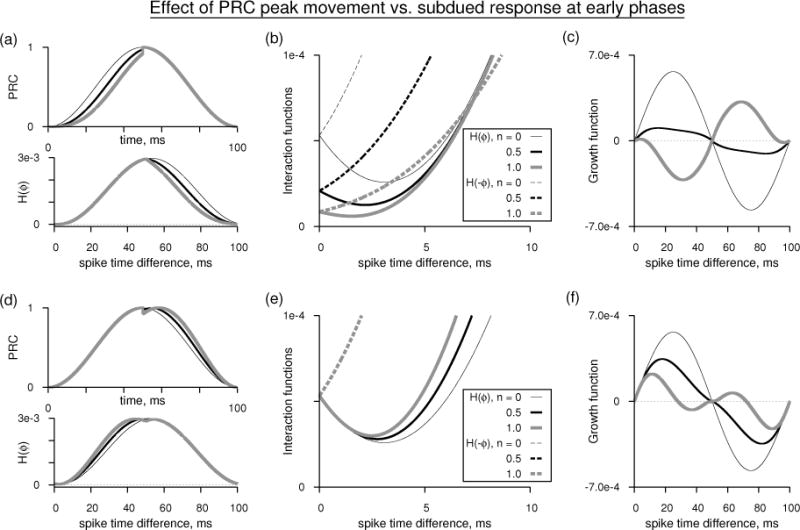
Subdued PRC response near early phases causes near-synchrony. (a, top) PRCs as in Eq. 39 for n = 0, 0.5, 1 but are reset to the case of n = 0 for phases above T/2. Period of oscillation is 100 ms. The peak levels of the PRCs are normalized to unity. (a, bottom) Corresponding interaction functions for mutual excitation using double exponential synaptic function with τd = 3 ms and τr = 0.1 ms. The interaction functions are computed without including the voltage effect. (c) The detail of the H(ϕ) and H(−ϕ) near the early phases. (d) Growth functions corresponding to the PRCs in (a). (d–f) As in (a–c) but resetting the PRCs to the case of n = 0 for phases below T/2.
Formulation of skewed PRC
The emergence of the non-zero phase-locked state can be sensitively dependent on the fine PRC features such as the overall symmetry of the PRC, the subdued response at the early phases, and the shift of the PRC peak. To study the nuances of this PRC structure, we construct a PRC as below that allows its control by a parameter:
| (39) |
where T is the oscillation period, and n is a non-negative real number that causes the left skewness (i.e. a long tail toward left of the peak). And C is a positive coefficient dependent on n introduced to control the PRC amplitude. If we set C to 1, the PRCs decrease in their amplitude considerably as n increases because of the algebraic power. Although C would appear as a coefficient multiplying the interaction function, and hence its choice does not alter the steady states or their stability, it may be set to a numerically approximate level of 1 + 0.67n + 0.17n2 so that the peak amplitude of the PRCs would be commensurate with that when n = 0. The PRCs are illustrated in Fig. 10(a). The above formulation provides modulation of the PRC between the phases 0 and T. Since the PRC is either zero or subdued near small phases, the rising phase of the synaptic function does not contribute significantly toward stability of synchrony. Thus the interaction function for mutually excitatory network can be computed without using the voltage effect using the following formula:
where sp(t) is the periodized synaptic function. We have set the coupling coefficient to unity. For mutual inhibition, the coefficient becomes negative, and the corresponding interaction is the same as the above but with a negative sign.
PRC with no skewness
When n = 0, Z(t) becomes symmetrical and is identical to the canonical type-1 PRC, and it was studied by Ermentrout (B. Ermentrout, 1996; G. B. Ermentrout & Terman, 2010). We set C = 1. When the PRC is symmetric, the frequency does not alter the stability of the steady states. However the rate can alter the eigenvalue of stability of the synchrony. For example, if the synaptic conductance is a simple exponential , the periodized function still retains the same shape . Then the symmetric PRC [1 − cos(2πt/T)] results in the following growth function for mutual excitation,
where . This cannot show any fixed points other than synchrony and anti-synchrony. But the slope of G(ϕ) at ϕ = 0 is 8π2αd/(Tc1) which shows that not only the state of synchrony is unstable (because the slope is positive) but its repulsion becomes weaker at low rates. (The slope is proportional to 1/T2 at large T.) At the same time the antisynchrony is also less tightly held at longer T: The slope of G(ϕ) at ϕ = T/2 is exactly the negative of that at ϕ = 0. These changes help the emergence of stable near-synchronous state when there is skewness present in the PRC.
PRC with small skewness
When n = 1, Z(t) acquires a small skewness [Fig. 10(a)]. PRC skewness of the kind that we have introduced can induce a number of higher order Fourier components owing to the subdued response near zero phase. Even after including many Fourier modes, one may not be able to account for the fine feature of the PRC near the zero phase. However, such a close fit is not necessary to predict the steady states and their stability accurately. 99% of the Fourier power (see (Dodla & Wilson, 2013b) for a discussion on the power) is contained in the following three modes:
where ω = 2π/T. The shape of the periodized synaptic function depends on the frequency of oscillation, and thus the resultant interaction function also changes its functional form with the rate, and the resultant Fourier approximation will have at least four harmonics of both cosine and sinusoidal terms in order to accurately predict the steady states, resulting in little insight into the relation between the Fourier modes in the PRC and the shape of the interaction function. Thus the interaction function may be computed either analytically or numerically from the original shape of the PRC. It is easily computable for n = 1, and results in the following growth function for the exponential (and excitatory) synaptic function:
where a1, a2, and a3 are constants dependent on αd and T : a1 = 4π2C/(Tc1 c2), a2 = Cα2d/c21, , and . In addition to the synchronous and antisynchronous states, this expression for the G(ϕ) can show, at appropriate rates, two other stable non-zero phase-locked states, ϕ* and T − ϕ*. The stability of the synchronous state is given by the slope of G(ϕ) at ϕ = 0, and is given by the following simplified expression
Since the factor αdT is positive, c2 is positive. Since 1/(1+αdT) decays slower than , the term inside the last pair of parentheses is also positive. And hence, resulting in an unstable synchronous state at all rates. However, at large T the slope can be seen to be proportional to 1/T4 whereas for the symmetric PRC it was proportional to 1/T2. Thus the small skewness introduced in the PRC has made the unstable synchronous state dramatically less repelling at low rates.
The stability of the antisynchronous state can also be easily computed from the expression for G(ϕ) by computing the slope of G(ϕ) at ϕ = T/2 and is given by
Since a csch term goes from infinity to zero as its argument increases from 0, this expression clearly shows that as the rate decreases (i.e. when αdT increases), the last term in the expression (including the negative sign) could go from large negative to zero indicating that the slope can transition from a negative to a positive value. That is, the antisynchrony is stable at high rates, but could lose its stability at low rates. This transition can be numerically examined by solving for the zeros of the above expression. We can also arrive at a simpler approximation for such transition. Let us assume that the transition to instability occurs at sufficiently low rates. Then the positive terms inside the square brackets can be approximated simply by α4T4, and the negative term by π2α3T3. Thus the transition occurs approximately when αdT = π2, or antisynchrony becomes unstable if T > π2/αd. For a synaptic time constant of 3 ms, this approximation states that antisynchrony becomes unstable if T > 29.6 ms (i.e. when the rate is lower than 33.8 Hz). However numerical simulations reveal that the transition occurs at high rates for higher values of n and thus such an approximation will not be accurate at higher n. Solving the above expression reveals that the transition to the instability occurs at 32.6 ms (i.e. at 30.7 Hz). Using a double exponential synaptic function with a rising time constant of 0.1 ms, and the decaying time constant of 3 ms, we obtain the transition to instability at 34.1 ms. The numerically computed growth functions for the double exponential synaptic function are shown in Fig. 10(b). We use the double exponential function with fast rise time in all our illustrations below, and are very similar to the results obtained using the pure exponential.
Thus with increasing T, the synchronous state become less repelling, and in particular the antisynchrony becomes unstable. Simulations suggest that the non-zero phase-locked state has its attracting eigenvalue that is about twice as big as the magnitude of the eigenvalue of the synchronous state. This state also moves toward the synchronous state. The movement of these steady states is illustrated in Fig. 10(c). At very low rates, the stable non-zero phase-locked state merges with the unstable synchronous state. In this limit, in the absence of any other stable steady state, network simulations would result in coherent spike output among the neurons. For mutual inhibition [Fig. 10(d)], G(ϕ) is multiplied by −1 and the decay time constant is adjusted for inhibitory synapse. The stability of the steady states is exactly converse to that of the mutual excitation, but the critical firing rate at which the antisynchrony changes its stability is now smaller than that in the excitatory network. This is easily foreseen by our earlier approximation T > π2/αd for the antisynchrony to become unstable in the excitatory network. For the inhibitory network, this approximation represents when the antisynchrony becomes stable. At smaller αd (inhibition), the criticality moves to longer T (i.e. to low rates).
Effect of large skewness
As n is increased in order to achieve large skewness, the ensuing analysis becomes unwieldy, and methods using piecewise linear models such as those in (Dodla & Wilson, 2011, 2013a) could become quite useful. However, the bifurcation structure can easily be computed numerically, and it as a function of firing rate remains qualitatively unchanged at large T, but the critical points occur at drastically different levels. For example at n = 10, the change of stability of antisynchrony occurs at 1285 Hz when the coupling is excitatory, and at 915 Hz when the coupling is inhibitory. Because these critical points are far from low rates, the branch of the non-zero phase-locked state that emanates from the antisynchronous state tends toward the synchronous branch at low rates with indistinguishable separation for extended ranges of firing rates leading to this branch act like a near-synchronous state. The structure for the excitatory and inhibitory networks at low rates is shown in Figs. 10(e,f).
At large skewness, the number of Fourier modes required to accurately represent the PRC increases. When n = 1, we were able to represent the PRC with three modes that have 99% of the Fourier power, but at n = 10, it requires more than 10 modes to achieve the same accuracy. The number of Fourier modes required to represent the resultant interaction function are not necessarily dictated by those in the PRC, but the period of oscillation and the shape of the synaptic conductance. At 2 kHz (i.e. T = 0.5 ms), the numerically computed interaction function can be represented by three Fourier modes,
where h0 = 0.765, s1 = −0.01625, c1 = 0.015, c2 = 0.00338, s2 = −0.00284, c3 = 0.001, and s3 = 0.00039. This predicts the two steady states and their stability emerging from the growth function (G(ϕ) = H(0.5 − ϕ) − H(ϕ)) correctly. The growth functions computed from the original PRC shape are illustrated in Fig. 10(g) for a few firing rates. When the network displays non-zero phase-locked states, the interaction function needs to be represented more accurately in order for those states to be captured. For example, at 10 Hz, the stable non-zero phase-locked state is so close to the unstable synchronous state, it may be missed or the synchronous state may be mischaracterized as stable. Computing steady states and examining their movement as a function of the skewness parameter n [Fig. 10(h)] or the oscillation period would reveal the nature of the near-synchronous state in proximity to the unstable synchronous state. The parameter spaces of T and n are scanned and the stability of the steady states are studied. The amplitude of the stable states between (and including) 0 and half period are shown in color in Fig. 10(i). There is only one stable state at any parameter point. The antisynchrony is stable at all rates if the PRC has no or little skewness; the synchrony is unstable. The same scenario exists at extremely high rates even if the PRC has large skewness. However the combination of low rate and large skewness (north-east corner of the plot) is favorable for near-synchrony. For mutual inhibition, the region marked AS would have stable synchronous state, and the rest of the region supports a bistable state between synchrony and antisynchrony.
To address whether the emergence of the near-synchronous state is more due to the shift of the PRC peak to longer phases or the subdued PRC response at early phases, we performed a numerical experiment (Fig. 11) by resetting the PRC shape to that of the canonical shape (n = 0) either to the right of the half period point [Fig. 11(a)], or to the left of the half period point [Fig. 11(d)], and computed their interaction functions [Fig. 11(b,e)], and the growth functions [Fig. 11(c,f)]. The PRC shape is only very slightly altered when n is changed from 0 to 1, but the subdued response near early phases altered the non-zero phase-locked state dramatically, and moved it near the synchronous state. The movement of the PRC peak alone altered the stability of the antisynchrony and caused the emergence of the non-zero phase-locked state, but it is not driven toward the synchronous state as fast. The interaction functions examined closely [Figs. 11(b,e)] reveal that, if the second neuron leads (small spike time difference), then the first neuron does in fact slowdown (H(ϕ) decreases), and the leading neuron speeds up (H(−ϕ) increases) resulting in an unstable synchrony. However if the PRC is subdued, then the neurons slowdown together, and the lagging neuron’s response is diminished making way for the synchrony to become less repelling. This can be said to be the result of the movement of the non-zero phase-locked state toward synchrony. On the other hand, if only the PRC peak moves to longer phases, then the neurons do not slowdown together, but they retain more or less their behavior near an unstable synchronous point. This is the result of the fact that the non-zero phase-locked state is not in the vicinity.
6 Discussion
We briefly discuss the dynamics of the leaky integrate-and-fire (LIF) model, and examine why such model neurons were found not-synchronizable in the past. The LIF model has a discontinuous jump in its phase response curve at zero phase. Central to the studies of networks of oscillating LIF neurons is the question of whether pairs of identical LIF neurons synchronize if coupled weakly with mutual excitation. Van Vreeswijk et al. (Van Vreeswijk et al., 1994) studied the coupled LIF network without the effect of the synaptic reversal potential or the voltage, and showed that such a coupling fails to exhibit stable synchrony. Hansel et al. (Hansel et al., 1995) included the effect of the voltage in the synaptic coupling and showed that if the PRC profile is not altered by the synaptic reversal potential, then the LIF network still fails to exhibit stable synchrony.
To understand the above result in the context of the weakly coupled oscillator theory, let us assume that Z(t) is the PRC, V (t) the voltage and Esyn the reversal potential of synapse. Then the term which we call the shunted PRC plays a critical role in determining the stability of synchrony (Hansel et al., 1995). The PRC of the LIF model is purely exponential and is proportional to et/τm (where τm is the membrane time constant), i.e. the PRC is monotonically increasing in its dependence on time. Hansel et al. showed that if the shunted PRC also has the same monotonically increasing dependence on time, then the LIF network fails to synchronize. This in fact is the case at low firing rates when the PRC has a quicker growth and can counter the decreasing trend of the term Esyn − V (t) during the depolarizing phase such that the shunted PRC would still be monotonically increasing. However at high rates when the PRC is shallow in its growth, the shunted PRC and the PRC exhibit opposing slopes leading to synchrony of the coupled LIF model neurons.
In the present work explicit conditions under which the LIF model neurons exhibit stable synchrony are derived. We find that if the term (where T is the oscillation period) is less than the ratio (Esyn − Vreset)/(Esyn − Vth), then stable synchrony is found. (Vreset is the reset voltage and Vth the spike threshold in the LIF model.) This condition is independent of the synaptic conductance profile as long as it has a rising and falling phases such that the peak of the conductance occurs within the oscillation period. We show how the regions of synchrony and antisynchrony move with varying levels of Esyn and oscillation rate.
Even simpler than the LIF model is the perfect integrate-and-fire model (Phoka, Cuntz, Roth, & Häusser, 2010; Pressley & Troyer, 2009) whose PRC becomes completely flat, i.e. independent of the phase, and whose voltage is a linearly increasing function of time. Consequently the acquires a negative slope facilitating synchrony. This also illustrates the effect of a constant PRC vs. exponentially rising PRC. We study the dynamics of a pair of such coupled identical PIF models and show that the reversal potential does not influence the steady states or their stability. Synchrony becomes a stable steady state solution at all firing rates and synaptic time constants, and a further antisynchronous state also becomes stable if the synaptic conductance level at half period becomes less than the frequency.
We now briefly discuss the effect of PRC skewness on synchrony. The PRC of the LIF model has a jump discontinuity, and the PRC of the PIF may also be considered as having a finite jump at zero phase. But many neuronal models do not show such jumps, rather the rise of the PRC immediately after the spike peak, and the decay of it before the spike peak are subdued. Some experimentally recorded PRCs also show skewness in their shape. A typical PRC that is the subject of theoretical studies is the so-called canonical PRC, 1−cos(2πt/T) (B. Ermentrout, 1996) (where T is the period of oscillation). The canonical PRC is obtained from a model that captures the subthreshold bifurcation that is the hallmark of inducing oscillations with near zero firing rates. Real PRCs also deviate from the canonical PRC shape, some times significantly when, for example, AHP current is present in the model. The AHP current can induce significant skewness in the PRC shape and thus affect synchrony of the coupled neurons (B. Ermentrout, Pascal, & Gutkin, 2001).
On the other hand, it is also not necessary to have the AHP currents to cause skewness in the PRC. A number of parameters can cause PRC skewness. For example the well-known Wang-Buzsáki model shows PRCs that are similar in shape to canonical PRC shape, but with some deviations. Slowing down the sodium inactivation and/or potassium activation can cause a shift of the PRC peak toward longer phases and a subdued response of the PRC near zero phase. Unlike in the PIF and LIF models, this subdued response can make the rising phase of the PRC ineffective in causing synchrony. Instead the shape skewness, even when small, of the PRC affects the position of the non-zero phase-locked state significantly. The antisynchrony becomes unstable and the stable non-zero phase-locked branch moves closer to the unstable synchronous state and eventually merges with it as the skewness parameter is altered. This movement is exemplified by parameterizing the shape of the canonical PRC. The parameterized PRC is studied at both low and high skewness levels. At low skewness the antisynchrony is found to become unstable if approximately T > π2/αd where αd is the inverse of the synaptic decay time constant. At large skewness the stable non-zero phase-locked branch could come indistinguishably close to the unstable synchrony branch and act like a near-synchronous state; Its eigenvalue is bigger in magnitude than the repelling synchronous state. Near synchronous states as reported in this study were earlier reported by (Dodla & Wilson, 2011), and were also the subject of a detailed study by (Canavier, Wang, & Chandrasekaran, 2013) in relation to pulse coupled neuronal oscillators. Canavier et al. also reported simulation results of Wang-Buzsaki type-1 excitatory model neurons relating the PRC skewness to the bistability of synchrony and anti-synchrony branches similar to those reported in our Figure 10(c–d).
7 Conclusions
We investigated how the PRC shape affects the synchronization dynamics between a pair of synaptically coupled neurons using simple neuronal models. The PRC studied in relation to the weakly coupled oscillator theory, and thus it is also called an infinitesimal PRC, or ‘iPRC’. We used analytical methods based on weakly coupled oscillator theory, and numerical simulations to determine the conditions under which synchrony or near-synchrony and antisynchrony are stable states for various PRC shapes. The main difference between the models we considered is in their PRC shape, and the commonality among all of them is that all of them belong to the category of type-1 (i.e. the oscillating neuron responds with phase advancement for stimuli occurring at any input phase (Hansel et al., 1995) - ignoring a small possible negative phase response immediately after the spike peak). The PIF network is characterized by a constant PRC at all phases, the LIF model has an exponential PRC with jumps at both ends of the curve, and the Wang-Buzsáki model’s PRCs are similar to the canonical PRCs but with their peak shifted toward longer phases while at the same time showing subdued or sudden responses at the early phases. Finally, our contrived PRC formula systematically creates a skewness in the PRC shape allowing us to study its effect on the steady states. Our work is mainly analytical with supporting numerical results.
Although LIF like type-1 neuron models do show synchrony if made to interact with pulse-coupling (Mirollo & Strogatz, 1990), researchers in the past used the LIF model to substantiate their main argument that type-1 PRC neurons do not generally exhibit synchronization of their spike times when synaptically coupled with mutual excitation (Van Vreeswijk et al., 1994; Hansel et al., 1995). However simulations using the LIF models often do exhibit synchronization leaving room for an exhaustive study of the synchronization properties of the LIF model neurons, the effect of the synaptic time constant, and the conditions under which they may indeed fail to synchronize. We have filled this gap in our understanding of the LIF networks. The LIF and the PIF models have peculiar PRCs with sudden jumps at zero phase. This may appear to be less important, but considering that the synaptic rising phase has greater contribution in causing synchrony, a jump at zero phase or near the zero phase during the synaptic rise (in contrast with the jump occurring during the synaptic decay) could cause stable synchrony. In the LIF model the synchronous state becomes stable when the monotonicity of the PRC is dominated by the effect of the term Esyn − V (t). This leads to a simple condition for synchrony Esyn < I0/GL + EL, i.e. when the synaptic reversal potential is less than the voltage level that the neuron would have settled if not reset. This also implies that at very large Esyn synchrony becomes unstable.
Another perspective is obtained by the study of the PIF model network. Because of its PRC being constant and thus independent of the phase, the voltage time course plays a bigger role in synchrony. In fact the term Esyn−V (t) is monotonically decreasing resulting in synchrony whether Esyn is above or below the spike threshold (i.e. whether it is excitatory or inhibitory). In the LIF network, at sufficiently high rates, the PRC would not have sufficient upward rising curvature to counter the monotonically decreasing term Esyn − V (t). That is, the LIF may essentially be behaving like a PIF model leading to a stable synchronous state. For Esyn < Vth, the coupling acts like inhibition and leads to synchrony. This case was earlier studied by Lewis and Rinzel (Lewis & Rinzel, 2003) and our results [Fig. 8(a, right)] confirm theirs, and further depict the movement of the synchrony and antisynchrony boundaries as Esyn is altered.
The PIF model network qualitatively acts like a mutually inhibitory LIF model network [see Figs. 6(g), 8(a, right)] in that at low rates a bistability between synchrony and antisynchrony is found, and at high rates only synchrony is stable. The PIF model also offers a simple formula for stability of antisynchrony: Stability is ensured if the periodized synaptic conductance at half period is less than the inverse of the period, sT/2 < 1/T. This condition is true for both purely exponential and double exponential synaptic functions. This also implies that slower synaptic rise times confine the regime of antisynchrony to lower rates. When Esyn > Vth, the antisynchrony in the LIF model network sensitively depends on both the rate and the synaptic time constant. At low rates and at very large Esyn, neither the synchrony nor antisynchrony may become stable [Figs. 6(e), 8(a)].
It is important to note that the rising phase of the synaptic function plays a major role in the stability of synchrony of the mutually excitatory LIF and the PIF networks. If the PRC of interest is stipulated to become zero or subdued at initial phases, then these models must be employed judiciously to represent the corresponding excitatory networks. Conventionally a synaptic conductance is generated from the presynaptic voltage, and hence the rising phase may be initiated some times before the spike peak. Thus the rising phase may become less relevant in the study of synchrony unless there is a synaptic delay involved in the coupling. When indeed there is a synaptic delay, the rising phase may potentially induce a synchronous state provided of course the PRC level becomes significant and the rate is high enough. A case in point is the Wang-Buzsáki model [Fig. 9(a)] where the rising phase contributes little to the stability. Introducing synaptic delay would have caused synchrony but the rate is not sufficiently high enough.
The Wang-Buzsáki model network also illustrates an excellent point that even if the PRCs are slightly left-skewed (i.e. long tails to the left of the peak), then the stability structure of the steady states changes dramatically from that of a symmetrical canonical PRC, 1 − cos(2πt/T) [Fig. 9(g)]. The canonical PRC results in an unstable synchrony and a stable antisynchrony (B. Ermentrout, 1996). But a little skewness introduced with the PRC, (1 − cos(2πt/T))(t/T) [Fig. 10(a)] caused the antisynchrony become unstable when approximately T > π2/αd, where αd is the inverse of the exponential synaptic conductance. The stable non-zero phase-locked branch that emanates from the antisynchrony branch merges with the unstable synchronous state as the neural oscillator’s firing rate goes toward zero.
Although such a complete merger may happen only at near zero firing rates, the stable nonzero branch can come indistinguishably close to the unstable synchronous branch if the skewness is increased by increasing the parameter n in the PRC formulation (1 − cos(2πt/T))(t/T)n. We term this the near-synchronous state. The near-synchronous state where the phase difference is less than 1% of the time period spans a large parameter space in (T, n) space [Fig. 10(i)]. Further simulations using these PRC models [Fig. 11] reveal that the subdued nature of the PRC near the early phases rather than the peak shift to longer phases affects sensitively the formation of the near-synchrony.
Finally, we briefly state the computational relevance of our study. The two important assumptions of a PRC based study in general are that the underlying neurons are regular oscillators and the coupling is weak (see (Smeal et al., 2010) for an excellent overview). Spiking patterns found in some brain areas including basal ganglia (Wilson, 2013, 2015; Bevan et al., 2002; Deister, Dodla, Barraza, Kita, & Wilson, 2013) and hippocampus (Klausberger et al., 2003) suggest that the assumption of the regular oscillations is relevant for computational study of these networks except in an operating regime when the dynamics is dominated by external noise which could destabilize or overpower the oscillation mechanism. Also in basal ganglia, for example, when coherence was observed in animal models of Parkinson’s disease model (Bergman et al., 1998), it could be interpreted as a state that arises from a near synchronous state between the neurons rather than a perfect synchronous state as would be described by a mathematical definition of synchrony often used as in the current study. The near synchronous state that we studied here offers a mechanism where such coherent response could be achieved. However our results must be extended for more complex networks that would involve sparse coupling and external noise to fully capture such phenomena. An implication of the bistability between synchrony and antisynchrony that is easily achieved in models involving PIF and under certain parameter regimes with the LIF models is that when the network is posited near the bifurcation point where such bistability emerges, a transient synchronous state (Golomb, 1998) could be achieved where the ratio of the eigenvalues of the synchronous and antisynchronous states determine the duration of the transient coherence. However a certain amount of noise or heterogeneity is required to cause the models dislodge from a perfect synchronous state.
Acknowledgments
The work was supported by NIH grant NS047085. We thank the Texas Advanced Computing Center at University of Texas, Austin, and the Computational Systems Biology Core at University of Texas at San Antonio for computational facilities.
Appendix. Wang-Buzsáki model (Wang & Buzsáki, 1996)
The equations for the Wang-Buzsáki model network of N coupled neurons are given by:
where i = 1, …, N. The voltage dependent functions are given by
The synaptic conductance si depends on the presynaptic neuron and evolves according to Eq. 38. The sodium inactivation h and the potassium activation n (i.e. the feedback current) variables are together slowed by decreasing the parameter ε. A network of (N =) 100 neurons is constructed from these equations. I0 (in μA/cm2) is the steady applied current that triggers regular spiking within each neuron model. is the coupling conductance. The parameters are Cm = 1 μF/cm2, GNa = 35 mS/cm2, GK = 9 mS/cm2, GL = 0.1 mS/cm2, ENa = 55 mV, EK = −90 mV, EL = −65 mV, and Esyn = 0 mV.
Footnotes
We thank the first reviewer for this insight.
References
- Achuthan S, Canavier CC. Phase-resetting curves determine synchronization, phase locking, and clustering in networks of neural oscillators. The Journal of Neuroscience. 2009;29:5218–5233. doi: 10.1523/JNEUROSCI.0426-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arthur JG, Burton SD, Ermentrout GB. Stimulus features, resetting curves, and the dependence on adaptation. Journal of computational neuroscience. 2013;34:505–520. doi: 10.1007/s10827-012-0433-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman H, Feingold A, Nini A, Raz A, Slovin H, Abeles M, Vaadia E. Physiological aspects of information processing in the basal ganglia of normal and parkinsonian primates. Trends in Neurosciences. 1998;21:32–38. doi: 10.1016/s0166-2236(97)01151-x. [DOI] [PubMed] [Google Scholar]
- Bevan MD, Magill PJ, Terman D, Bolam JP, Wilson CJ. Move to the rhythm: oscillations in the subthalamic nucleus–external globus pallidus network. Trends in neurosciences. 2002;25:525–531. doi: 10.1016/s0166-2236(02)02235-x. [DOI] [PubMed] [Google Scholar]
- Bevan MD, Wilson CJ. Mechanisms underlying spontaneous oscillation and rhythmic firing in rat subthalamic neurons. The Journal of neuroscience. 1999;19:7617–7628. doi: 10.1523/JNEUROSCI.19-17-07617.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolam JP, Hanley JJ, Booth PAC, Bevan MD. Synaptic organisation of the basal ganglia. Journal of Anatomy. 2000;196:527–542. doi: 10.1046/j.1469-7580.2000.19640527.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brette R, Gerstner W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. Journal of Neurophysiology. 2005;94:3637–3642. doi: 10.1152/jn.00686.2005. [DOI] [PubMed] [Google Scholar]
- Brown E, Moehlis J, Holmes P. On the phase reduction and response dynamics of neural oscillator populations. Neural Computation. 2004;16:673–715. doi: 10.1162/089976604322860668. [DOI] [PubMed] [Google Scholar]
- Brunel N, Sergi S. Firing frequency of leaky integrate-and-fire neurons with synaptic current dynamics. Journal of Theoretical Biology. 1998;195:87–95. doi: 10.1006/jtbi.1998.0782. [DOI] [PubMed] [Google Scholar]
- Burkitt AN. A review of the integrate-and-fire neuron model: I. homogeneous synaptic input. Biological cybernetics. 2006;95:1–19. doi: 10.1007/s00422-006-0068-6. [DOI] [PubMed] [Google Scholar]
- Buzsáki G. Rhytms of the brain. Oxford, UK: Oxford University Press; 2006. [Google Scholar]
- Canavier CC, Wang S, Chandrasekaran L. Effect of phase response curve skew on synchronization with and without conduction delays. Frontiers in Neural Circuits. 2013;7:194. doi: 10.3389/fncir.2013.00194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chow CC, Kopell N. Dynamics of spiking neurons with electrical coupling. Neural Computation. 2000;12:1643–1678. doi: 10.1162/089976600300015295. [DOI] [PubMed] [Google Scholar]
- Courant R. Differential and integral calculus, volume 1. Wiley; 2011. [Google Scholar]
- Cui J, Canavier Carmen C, Butera Robert J. Functional phase response curves: A method for understanding synchronization of adapting neurons. Journal of Neurophysiology. 2009;102:387–398. doi: 10.1152/jn.00037.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deister C, Dodla R, Barraza D, Kita H, Wilson C. Firing rate and pattern heterogeneity in the globus pallidus arise from a single neuronal population. Journal of Neurophysiology. 2013;109:497–506. doi: 10.1152/jn.00677.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodla R, Wilson CJ. 2011 neuroscience meeting planner, program no. 78.11. Society for Neuroscience; Washington, DC: 2011. Role of phase response curve skewness on network synchrony of weakly coupled oscillators. [Google Scholar]
- Dodla R, Wilson CJ. Effect of phase response curve skewness on synchronization of electrically coupled neuronal oscillators. Neural Computation. 2013a;25:2545–2610. doi: 10.1162/NECO_a_00488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodla R, Wilson CJ. Interaction function of oscillating coupled neurons. Physical Review E. 2013b;88:042704. doi: 10.1103/PhysRevE.88.042704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel AK, Fries P, Singer W. Dynamic predictions: oscillations and synchrony in topdown processing. Nature Reviews Neuroscience. 2001;2:704–716. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Computation. 1996;8:979. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- Ermentrout B, Pascal M, Gutkin B. The effects of spike frequency adaptation and negative feedback on the synchronization of neural oscillators. Neural Computation. 2001;13:1285–1310. doi: 10.1162/08997660152002861. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB. n:m phase-locking of weakly coupled oscillators. Journal of Mathematical Biology. 1981;12:327–342. [Google Scholar]
- Ermentrout GB. Simulating, analyzing, and animating dynamical systems: A guide to XPPAUT for researchers and students. Philadelphia, PA: Society for Industrial and Applied Mathematics; 2002. [Google Scholar]
- Ermentrout GB, Beverlin B, II, Netoff T. Phase response curves in neuroscience: Theory, experiment, and analysis. In: N. W. S.et al., editors. chap Phase response curves to measure ion channel effects on neurons. MIT Press; Massachusetts: 2012. [Google Scholar]
- Ermentrout GB, Galán RF, Urban NN. Relating neural dynamics to neural coding. Physical review letters. 2007;99:248103. doi: 10.1103/PhysRevLett.99.248103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB, Kopell B. Multiple pulse interactions and averaging in systems of coupled neural oscillators. Journal of Mathematical Biology. 1991;29:195–217. [Google Scholar]
- Ermentrout GB, Kopell N. Parabolic bursting in an excitable system coupled with a slow oscillation. SIAM Journal on Applied Mathematics. 1986;46:233–253. [Google Scholar]
- Ermentrout GB, Terman DH. Mathematical foundations of neuroscience. New York, NY: Springer; 2010. [Google Scholar]
- Feng J. Effects of correlated and synchronized stochastic inputs to leaky integrator neuronal model. Journal of Theoretical Biology. 2003;222:151–162. doi: 10.1016/s0022-5193(03)00022-5. [DOI] [PubMed] [Google Scholar]
- Filion M, Tremblay L. Abnormal spontaneous activity of globus pallidus neurons in monkeys with mptp-induced parkinsonism. Brain Research. 1991;547:140–144. [PubMed] [Google Scholar]
- Galán RF, Fourcaud-Trocmé N, Ermentrout GB, Urban NN. Correlation-induced synchronization of oscillations in olfactory bulb neurons. J Neurosci. 2006;26:3646–3655. doi: 10.1523/JNEUROSCI.4605-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W, Kistler WM. Spiking neuron models single neurons, populations, plasticity. Cambridge University Press; 2002. [Google Scholar]
- Golomb D. Models of neuronal transient synchrony during propagation of activity through neocortical circuitry. Journal of Neurophysiology. 1998;79:1–12. doi: 10.1152/jn.1998.79.1.1. [DOI] [PubMed] [Google Scholar]
- Gouwens NW, Zeberg H, Tsumoto K, Tateno T, Aihara K, Robinson HP. Synchronization of firing in cortical fast-spiking interneurons at gamma frequencies: a phase-resetting analysis. PLoS Comput Biol. 2010;6 doi: 10.1371/journal.pcbi.1000951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Y, Rubin JE, McIntyre CC, Vitek JL, Terman D. Thalamocortical relay fidelity varies across subthalamic nucleus deep brain stimulation protocols in a data-driven computational model. Journal of Neurophysiology. 2008;99:1477–1492. doi: 10.1152/jn.01080.2007. [DOI] [PubMed] [Google Scholar]
- Hansel D, Mato G, Meunier C. Phase dynamics for weakly coupled hodgkin-huxley neurons. EPL (Europhysics Letters) 1993;23:367–372. [Google Scholar]
- Hansel D, Mato G, Meunier C. Synchrony in excitatory neural networks. Neural Computation. 1995;7:307–337. doi: 10.1162/neco.1995.7.2.307. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. Jounal of Physiology. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoppensteadt FC, Izhikevich EM. Weakly connected neural networks. New York, NY: Springer; 1997. [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends in Neurosciences. 2000;23:216–222. doi: 10.1016/s0166-2236(00)01547-2. [DOI] [PubMed] [Google Scholar]
- Jahnsen H, Llinás R. Ionic basis for the electro-responsiveness and oscillatory properties of guinea-pig thalamic neurones in vitro. The Journal of Physiology. 1984;349:227–247. doi: 10.1113/jphysiol.1984.sp015154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolivet R, Lewis TJ, Gerstner W. Generalized integrate-and-fire models of neuronal activity approximate spike trains of a detailed model to a high degree of accuracy. Journal of Neurophysiology. 2004;92:959–976. doi: 10.1152/jn.00190.2004. [DOI] [PubMed] [Google Scholar]
- Klausberger T, Magill P, Roberts LFMJD, Cobden PM, Buzsáki G, Somogyi P. Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo. Nature. 2003;421:844–848. doi: 10.1038/nature01374. [DOI] [PubMed] [Google Scholar]
- Krogh-Madsen T, Butera R, Ermentrout GB, Glass L. Phase resetting neural oscillators: Topological theory versus the realworld. In: Schultheiss NW, Prinz AA, Butera RJ, editors. Phase response curves in neuroscience. New York, NY 10013, USA: Springer; 2012. pp. 33–52. [Google Scholar]
- Kuhlmann L, Burkitt AN, Paolini A, Clark GM. Summation of spatiotemporal input patterns in leaky integrate-and-fire neurons: Application to neurons in the cochlear nucleus receiving converging auditory nerve fiber input. Journal of Computational Neuroscience. 2002;12:55–73. doi: 10.1023/a:1014994113776. [DOI] [PubMed] [Google Scholar]
- Kuramoto Y. Chemical oscillations, waves, and turbulence. Springer; 1984. [Google Scholar]
- Ladenbauer J, Augustin M, Shiau L, Obermayer K. Impact of adaptation currents on synchronization of coupled exponential integrate-and-fire neurons. PLoS Computational Biology. 2012;8:e1002478. doi: 10.1371/journal.pcbi.1002478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapicque L. Recherches quantitatives sur l’excitation électrique des nerfs traitée comme une polarisation. Journal de Physiologie et de Pathologie Générale. 1907;9:620–635. (Translated by N. Brunel and M. C. W. van Rossum as “Quantitative investigations of electrical nerve excitation treated as polarization,” Biological Cybernetics 97:341–349, 2007) [Google Scholar]
- Lewis TJ, Rinzel J. Dynamics of spiking neurons connected by both inhibitory and electrical coupling. Journal of Computational Neuroscience. 2003;14:283–309. doi: 10.1023/a:1023265027714. [DOI] [PubMed] [Google Scholar]
- Lewis TJ, Skinner FK. Understanding activity in electrical coupled networks using PRCs and the theory of weakly coupled oscillators. In: Schultheiss NW, Prinz AA, Butera RJ, editors. Phase response curves in neuroscience. New York, NY 10013, USA: Springer; 2012. pp. 329–359. [Google Scholar]
- Miranda-Domínguez Ó, Netoff TI. Parameterized phase response curves for characterizing neuronal behaviors under transient conditions. Journal of Neurophysiology. 2013;109:2306–2316. doi: 10.1152/jn.00942.2012. [DOI] [PubMed] [Google Scholar]
- Mirollo RE, Strogatz SH. Synchronization of pulse-coupled biological oscillators. SIAM Journal on Applied Mathematics. 1990;50:1645–1662. [Google Scholar]
- Netoff T, Schwemmer MA, Lewis TJ. Experimentally estimating phase response curves of neurons: Theoretical and practical issues. In: Schultheiss NW, Prinz AA, Butera RJ, editors. Phase response curves in neuroscience. New York, NY 10013, USA: Springer; 2012. pp. 95–130. [Google Scholar]
- Neu JC. Chemical waves and the diffusive coupling of limit cycle oscilltors. SIAM Journal on Applied Mathematics. 1979a;36:509–515. [Google Scholar]
- Neu JC. Coupled chemical oscillators. SIAM Journal on Applied Mathematics. 1979b;37:307–315. [Google Scholar]
- Perez Velazquez JL, Galan RF, Garcia Dominguez L, Leshchenko Y, Lo S, Belkas J, Erra RG. Phase response curves in the characterization of epileptiform activity. Physical Review E. 2007;76:061912. doi: 10.1103/PhysRevE.76.061912. [DOI] [PubMed] [Google Scholar]
- Pfeuty B, Mato G, Golomb D, Hansel D. Electrical synapses and synchrony: the role of intrinsic currents. Journal of Neuroscience. 2003;23:6280–6294. doi: 10.1523/JNEUROSCI.23-15-06280.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeuty B, Mato G, Golomb D, Hansel D. The combined effects of inhibitory and electrical synapses in synchrony. Neural Computation. 2005;17:633–670. doi: 10.1162/0899766053019917. [DOI] [PubMed] [Google Scholar]
- Phoka E, Cuntz H, Roth A, H¨ausser M. A new approach for determining phase response curves reveals that purkinje cells can act as perfect integrators. PLoS Computational Biology. 2010;6:e1000768. doi: 10.1371/journal.pcbi.1000768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pressley J, Troyer TW. Complementary responses to mean and variance modulations in the perfect integrate-and-fire model. Biological Cybernetics. 2009;101:63–70. doi: 10.1007/s00422-009-0317-6. [DOI] [PubMed] [Google Scholar]
- Raz A, Vaadia E, Bergman H. Firing patterns and correlations of spontaneous discharge of pallidal neurons in the normal and the tremulous1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine vervet model of parkinsonism. J Neurosci. 2000;20:8559–8571. doi: 10.1523/JNEUROSCI.20-22-08559.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E, Sejnowski TJ. Impact of correlated synaptic input on output firing rate and variability in simple neuronal models. J Neurosci. 2000;20:6193–6209. doi: 10.1523/JNEUROSCI.20-16-06193.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultheiss NW, Edgerton JR, Jaeger D. Phase response curve analysis of a full morphological globus pallidus neuron model reveals distinct perisomatic and dendritic modes of synaptic integration. The Journal of Neuroscience. 2010;30:2767–2782. doi: 10.1523/JNEUROSCI.3959-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smeal RM, Ermentrout GB, White JA. Phase-response curves and synchronized neural networks. Philosophical Transactions of the Royal Society B: Biological Science. 2010;365:2407–2422. doi: 10.1098/rstb.2009.0292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stroeve S, Gielen S. Correlation between uncoupled conductance-based integrate-and-fire neurons due to common and synchronous presynaptic firing. Neural Computation. 2001;13:2005–2029. doi: 10.1162/089976601750399281. [DOI] [PubMed] [Google Scholar]
- Tateno T, Robinson HP. Phase resetting curves and oscillatory stability in interneurons of rat somatosensory cortex. Biophysical Journal. 2007;92:683–695. doi: 10.1529/biophysj.106.088021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terman D, Rubin JE, Yew AC, Wilson CJ. Activity patterns in a model for the subthalamopallidal network of the basal ganglia. Journal of Neuroscience. 2002;22:2963–2976. doi: 10.1523/JNEUROSCI.22-07-02963.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks M, Mitkov I, Sompolinsky H. Pattern of synchrony in inhomogeneous networks of oscillators. Phys Rev Lett. 1993;71:1280–1283. doi: 10.1103/PhysRevLett.71.1280. [DOI] [PubMed] [Google Scholar]
- Tsubo Y, Teramae JN, Fukai T. Synchronization of excitatory neurons with strongly heterogeneous phase responses. Physical Review Letters. 2007;99:228101. doi: 10.1103/PhysRevLett.99.228101. [DOI] [PubMed] [Google Scholar]
- Van Vreeswijk C, Abbott LF, Ermentrout GB. When inhibition not excitation synchronizes neural firing. Journal of Computational Neuroscience. 1994;1:313–321. doi: 10.1007/BF00961879. [DOI] [PubMed] [Google Scholar]
- Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. Journal of Neuroscience. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Rinzel J. Alternating and synchronous rhythms in reciprocally inhibitory model neurons. Neural Computation. 1992;4:84–97. [Google Scholar]
- Wichmann T, Bergman H, DeLong MR. The primate subthalamic nucleus. III. changes in motor behavior and neuronal activity in the internal pallidum induced by sub-thalamic inactivation in the mptp model of parkinsonism. J Neurophysiol. 1994;72:521–530. doi: 10.1152/jn.1994.72.2.521. [DOI] [PubMed] [Google Scholar]
- Wichmann T, Delong MR. Deep brain stimulation for neurologic and neuropsychiatric disorders. Neuron. 2006;52:197–204. doi: 10.1016/j.neuron.2006.09.022. [DOI] [PubMed] [Google Scholar]
- Wilson CJ. Active decorrelation in the basal ganglia. Neuroscience. 2013;250:467–482. doi: 10.1016/j.neuroscience.2013.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ. Oscillators and oscillations in the basal ganglia. The Neuroscientist. 2015;21:530–539. doi: 10.1177/1073858414560826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winfree AT. Biological rhythms and the behavior of populations of coupled oscillators. Journal of Theoretical Biology. 1967;16:15–42. doi: 10.1016/0022-5193(67)90051-3. [DOI] [PubMed] [Google Scholar]
- Winfree AT. Phase control of neural pacemakers. Science. 1977;197:761–763. doi: 10.1126/science.887919. [DOI] [PubMed] [Google Scholar]
- Winfree AT. The geometry of biological time. Second. Springer; 2001. [Google Scholar]


