Abstract
We review quantitative accounts of behavioral momentum theory (BMT), its application to clinical treatment, and its extension to post-intervention relapse of target behavior. We suggest that its extension can account for relapse using reinstatement and renewal models, but that its application to resurgence is flawed both conceptually and in its failure to account for recent data. We propose that the enhanced persistence of target behavior engendered by alternative reinforcers is limited to their concurrent availability within a distinctive stimulus context. However, a failure to find effects of stimulus-correlated reinforcer rates in a Pavlovian-to-Instrumental Transfer (PIT) paradigm challenges even a straightforward Pavlovian account of alternative reinforcer effects. BMT has been valuable in understanding basic research findings and in guiding clinical applications and accounting for their data, but alternatives are needed that can account more effectively for resurgence while encompassing basic data on resistance to change as well as other forms of relapse.
1. Behavioral momentum theory
The persistence of reinforced operant behavior in the face of disruptive challenges and its relapse following extinction may be understood within the framework of a single general expression from Behavioral Momentum Theory (BMT):
| Eq. 1 |
In this expression, x represents disruptors of various sorts, m is the behavioral equivalent of inertial mass in classical physics, and ΔB is the change in response rate during disruption. Behavioral mass depends directly on the rate or amount of reinforcement obtained within a stimulus context (see Nevin & Grace, 2000; Nevin, 2002, 2015).
In many applications, it is helpful to compare changes in behavior between conditions when results are expressed as proportions of baseline, Bx/Bo, where Bo is baseline response rate and Bx is response rate during disruption. Proportion-of-baseline response rates can be a helpful measures of response persistence because these rates represent the speed that behavior decreases during disruption while parsing out any differences in pre-disruption response rates (see Craig, Nevin, & Odum, 2014, for further discussion). In BMT, proportion-of-baseline response rates often are log (base 10) transformed. Thus,
| Eq. 2 |
Log transformation tends to convert non-linear changes in behavior across time (think of a classic extinction function) into straight lines, rendering them easier both to distinguish by inspection and to model mathematically. Further, log transformation highlights proportional differences in Bx/Bo, regardless of the absolute scale of those differences. In this article we exponentiate Eq. 2 to model Bx/Bo instead of log10(Bx/Bo) as follows:
| Eq. 3 |
This transform allows for the inclusion of zero values often observed in extinction. Moreover, proportions of baseline are often used in applied analyses.
The majority of research on resistance to change has employed multiple schedules with different reinforcer rates in two distinctively signaled components. Unlike single schedules where data must be compared between subjects or across successive conditions, multiple schedules permit within-subject, within-session comparisons of resistance to change between components. For example, with pigeon subjects, a variable-interval (VI) 30s with red key light would alternate with VI 120s with green key light within a session. Throughout this article, we will refer to VI schedules by the number of programmed reinforcers per hr; thus these schedules would be designated VI 120/hr and VI 30/hr, respectively. After stable baseline response rates are established in both components, differences in resistance to change between components are evaluated by applying some form of disruption equally to both components. Perennial favorites with nonhuman animals include presenting free food during intervals between components (ICI food), providing a large fraction of a subject’s daily food ration in the home cage before an experimental session (prefeeding), and termination of all food reinforcers (extinction – more on this below). With humans, some form of concurrent distraction is often used. Although these disruptors differ in the experimenter’s operations, their effects are ordinally the same and appear to be additive (Nevin, 2002). Further, it is important that the disruptors applied to behavior in the various components of a multiple schedule be of equal magnitude. This allows for precise comparison of the impact of variables within an organism’s reinforcement history on resistance to change. The well-nigh universal finding is that the proportion-of-baseline response rate during disruption is greater in the richer component (VI 120/hr in the example above).
Similar results have been obtained when two components of a multiple schedule have identical schedules of response-dependent (VI) reinforcement, but the reinforcer rate in one component is increased by presenting response-independent reinforcers at variable times (VT) within that component. Response rate in the component with added VT reinforcers is typically lower in baseline but more persistent during disruption, suggesting that resistance to change depends on total reinforcers in a component (e.g., Nevin et al. 1990, Experiment 1; Mace et al 1990, Experiment 1). Several studies have found that providing alternative reinforcers within a component for an explicitly defined alternative response also reduces the rate of a target response and enhances its persistence (e.g., Nevin et al. 1990, Experiment 2; Mace et al. 2010, Experiment 1). This line of research has led to the proposition that in a distinctively signaled schedule component, response rate depends on the response-reinforcer contingency, defined as the proportion of reinforcers obtained for a target response. On the other hand, resistance to change depends on the stimulus-reinforcer contingency, defined as the proportion of all reinforcers in an experimental session obtained in a target component, regardless of their source (i.e., response dependent, independent, or dependent on another response). We therefore add alternative reinforcers to the denominator of the exponent in the general expression for resistance to change above:
| Eq. 4 |
where b is a sensitivity parameter; its value is often found to be about 0.5 (Nevin, 2002), and we will use that value throughout the following development. Nevin et al. (1990) attributed the summation of reinforcer rates from different sources within a schedule component to Pavlovian stimulus-reinforcer relations. That is, all reinforcers from all sources delivered in the presence of a given discriminative stimulus (e.g., component) define the Pavlovian stimulus-reinforcer relation. After considering some applications of BMT to relapse, we will report a direct test of the role of Pavlovian processes in resistance to change.
2. Resistance to extinction
We noted above that unbiased comparisons of resistance to change between components require that the disruptor x be the same for both components of a multiple schedule (e.g., prefeeding for food-deprived animals or distraction for humans). This is not the case when extinction serves as a disruptor because the termination of very frequent reinforcement (FR1 in the limit) is more readily discriminable, and hence more disruptive, than termination of infrequent reinforcement – accounting for the partial reinforcement extinction effect (PREE). Moreover, response rate decreases if the response-reinforcer contingency is eliminated without discontinuing reinforcers (e.g., Rescorla & Skucy, 1969). Accordingly, x must include the disruptive effects of terminating the response-reinforcer contingency (c) and generalization decrement due to absence of target reinforcers as stimuli (dΔrt), where d represents the discrimininability of omitting reinforcers presented at rate rt.
The full expression is sometimes called the “augmented” model of resistance to extinction (Nevin & Grace, 2000):
| Eq. 5 |
where Bt represents response rate at time t during extinction (usually measured in sessions). Both terms in the numerator of the exponent are multiplied by t, to represent the increasing effects of suspending the contingency (c) and removing reinforcers (dΔrt) with time in extinction. Nevin, McLean, and Grace (2001) found that estimates of c and d were additive and independent.
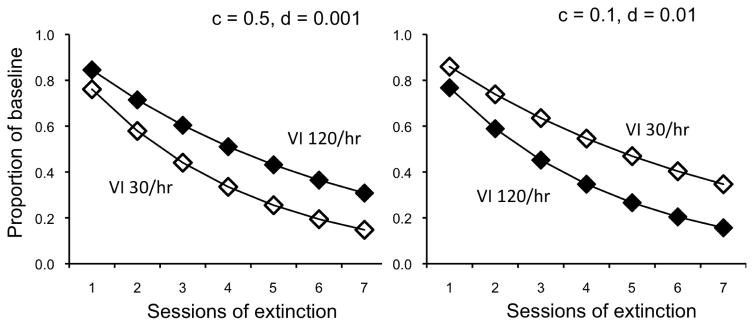
When all reinforcers are delivered intermittently, Equation 3 can account for data showing that responding in a richer multiple-schedule component is more resistant to extinction than in a leaner component, consistent with the findings described above for disruptors other than extinction (e.g., VI 120/hr vs VI 30/hr, as in the left panel of Figure 1; for overview see Nevin, 2012). However, with different parameter values – smaller c and larger d – Equation 3 can account for data showing the reverse ordering found in single schedules where more frequent reinforcement reduces resistance to extinction, as expected from the PREE (right panel of Figure 1; see Cohen, Riley, & Weigle, 1993). Thus, it appears that Equation 3 can account for either of two opposed outcomes, given sufficient freedom to adjust the values of parameters c and d. This does not, however, render Equation 3 useless by being able to account for any and all findings. For example, if we can identify experimental variables that affect generalization decrement, the fitted value of d can serve as a higher-order dependent variable characterizing the assumed process (Nevin, 1984; see Craig & Shahan, 2016, for application of this approach). Moreover, we can evaluate its independence from contingency suspension estimated by the fitted value of c (e.g., Nevin et al., 2001).
Fig. 1.
Predicted extinction functions after training on multiple VI 120 reinforcers/hr, VI 30 reinforcers/hr, showing that the parameters of Equation 5 can reverse the order of the functions.
3. Relapse
In this article, we consider extensions of Equation 5 to post-extinction relapse in the frequently employed 3-phase procedure where a target response is reinforced in Phase 1 (baseline), followed by extinction in Phase 2 (“treatment” in applied analyses), and concluding with a test for relapse in Phase 3. If Phase 3 arranges presentation of response-independent reinforcers, relapse is termed “reinstatement.” If Phase 2 involves presentation of a physical stimulus situation or context different from that in Phase 1, followed by return to the Phase-1 stimulus situation or context (or some novel situation/context) in Phase 3, relapse is termed “renewal.” And if Phase 2 arranges reinforcement for an alternative response (“differential reinforcement of alternative behavior” or DRA in applied analyses) concurrently with extinction of the target, and alternative behavior is then placed on extinction in Phase 3, relapse is termed “resurgence.” These procedural variations can be identified with different disruptors and inserted into the numerator of the exponent in Equation 5.
According to an extension of BMT by Podlesnik and Shahan (2010), post-extinction relapse arises from attenuation of the disruptor term, so that the numerator of the exponent in Equation 3 becomes −t(mc+ndΔrt), where m and n modulate the disruptive effects of suspending the target-response contingency and the omission of reinforcers, respectively. Shahan and Sweeney (2011) proposed a related model of resurgence that included Phase-2 alternative reinforcers as disruptors in the numerator; their removal during Phase 3 accounts for increases in target responding comparable in effect to attenuating the disruptive effects of c and dΔrt in Equation 3. The present article explores a framework for modeling reinstatement and renewal that is consistent with previous modeling efforts, and then describes problems with their application to resurgence. We do not attempt to bring our BMT-based interpretation to bear on the rich literature of relapse, but simply to examine whether it is capable of accounting for representative data.
3.1 Reinstatement
One way to model reinstatement in the standard three-phase procedure is to reintroduce reinforcers in the numerator of the exponent in Equation 3 during Phase 3, thus counteracting generalization decrement from reinforcer omission in Phase 2. The number of added reinforcers in reinstatement procedures is the same in both components, so degrading both rich and lean components by proportions m and n, as in Podlesnik and Shahan (2010), is not quite right. Here’s the model, with negative dxrx representing the decrease in generalization decrement:
| Eq. 6 |
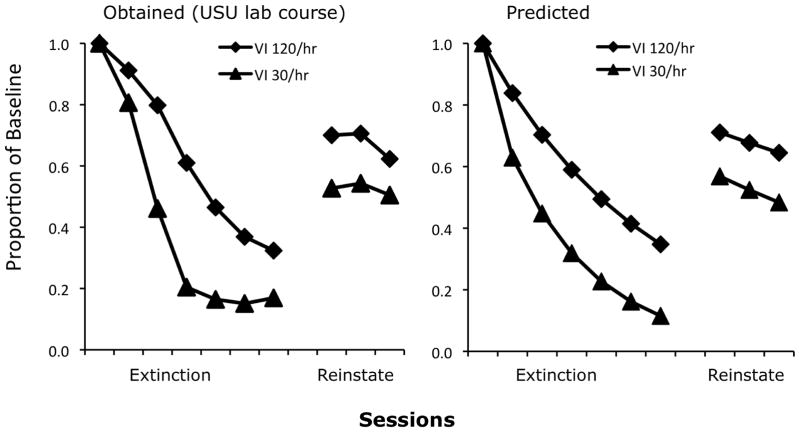
Equation 6 was fitted to multiple-schedule data obtained by an undergraduate lab class at Utah State University with VI 30-s (120 rft/hr) in one component and VI 120-s (30 rft/hr) in the other; data were averaged over seven pigeons and are presented as proportions of Phase-1 baseline in Figure 2, along with model predictions. The model performs quite well with c = 0.8, d = 0.0003, dx = 0.01, and rx = 60, the number of response-independent reinforcers per hr presented within both components during Phase-3 reinstatement sessions. With these parameter values, Eq. 6 accounted for 95% of the variance with no obvious systematic deviations. In effect, Equation 6 accounts for reinstatement by assuming that food presentations reduce generalization decrement by making the stimulus conditions less like extinction in Phase 2 and more like training in Phase 1.
Fig. 2.
The left panel presents data, expressed as mean proportions of baseline, from a reinstatement study conducted by a laboratory class at Utah State University; we thank Amy Odum for making these data available. The right panel presents predictions of Equation 6; see text for explanation and parameter values.
3.2 Renewal
Renewal has been studied in several paradigms; we consider two of the most frequently employed. In ABA renewal, the contextual stimuli present during Phase-1 training (A) differ from the contextual stimuli during Phase-2 extinction (B). Renewal tests occur upon returning to the training stimulus context (A) while extinction continues in Phase 3. In ABC renewal, contextual stimuli (B) in Phase-2 extinction differ from training as in the ABA paradigm, but Phase 3 tests for renewal by arranging a novel stimulus context (C) while extinction continues. In both ABA and ABC paradigms, the rate of an extinguished response increases during Phase 3; increases are usually greater in ABA than ABC renewal (Bouton, Todd, Vurbic, & Winterbauer, 2011). Overall, the results suggest that renewal depends on the similarity of the stimulus contexts in Phase 1 and Phase 3 (Podlesnik & Miranda-Dukoski, 2015; Todd et al., 2012). As in the case of reinstatement, BMT predicts greater renewal after training with higher reinforcer rates in Phase 1.
To account for ABA and ABC renewal, we add dSB to the numerator of the exponent during Phase 2; dSB can be construed as the effective difference between the A context and the B context in Phases 1 and 2. Similarly, dSC can be construed as the effective difference between the A context and the C context (cf. Davison & Nevin, 1999). The basic idea was introduced by Nevin et al. (2001, Exp. 3) to account for the effects of novel stimuli presented during extinction. The full model for ABA and ABC renewal is:
| Eq. 7 |
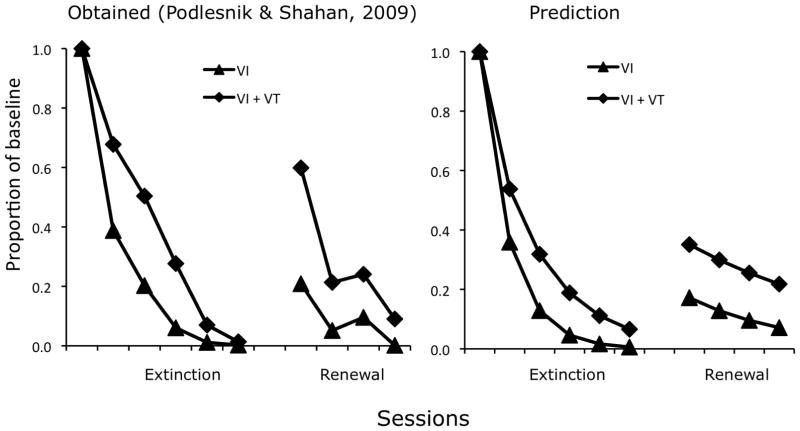
To examine the effects of training reinforcement rate on ABA renewal, Podlesnik & Shahan (2009; 2010) trained pigeons on a multiple VI 20/hr, VI 20/hr+VT 120/hr schedule so that the rate of response-dependent reinforcers was the same in both components but with added response-independent reinforcers in one component during Phase 1. During Phase 1, a steady house light comprised Context A and response rates were lower in the added-VT component. In Phase 2, a flashing house light comprised Context B and resistance to extinction was greater in the component with added reinforcers, consistent with many previous findings as noted above (e.g., Nevin et al., 1990). In Phase 3, returning to the steady house light as in baseline (Context A), responding recovered substantially more in the added-VT component. The data are shown as proportions of baseline in Figure 3, together with model predictions.
Fig. 3.
The left panel presents the data, expressed as mean proportions of baseline, from an ABA renewal study reported by Podlesnik and Shahan (2010). The right panel presents predictions of Equation 7; see text for explanation and parameter values.
During baseline (Phase 1) with a steady house light, response rates were lower in the added-VT component, but resistance to extinction (Phase 2) with a flashing house light was greater in that component relative to baseline, consistent with many previous findings as noted above. In renewal (Phase 3) with a steady house light as in baseline, responding recovered substantially more in the added-VT component.
Equation 7 was fitted to the mean data shown in Figure 3 with c = 0.56, d = 0.002, dSB = 1.3, and dSC = 0 (because there is no physical difference from the training context A). With these parameter values, Eq. 7 accounted for 93% of the variance; the major deviation is the predicted Phase-3 slope, which is shallower than the data. Podlesnik and Shahan (2010) noted the same difference between the obtained slope and that predicted by their attenuation-of-disruption model (see Reinstatement above), and suggested that renewal might be like resetting time in extinction, an ad hoc solution to the problem that is inconsistent with the disruptor-removal approach adopted here.
To account for ABC renewal, we subtract a non-zero value of dSC from dSB, in Equation 7, thus reducing the effective difference between contexts A and C. In terms of the model set forth in Equation 7, ABC renewal results from making stimulus context C more similar to the training context A than is the extinction context B. This assumption is consistent with interpretations of renewal in terms of similarity to the training context (e.g., Bouton et al. (2011). It is also consistent with the form of our reinstatement model, Equation 6.
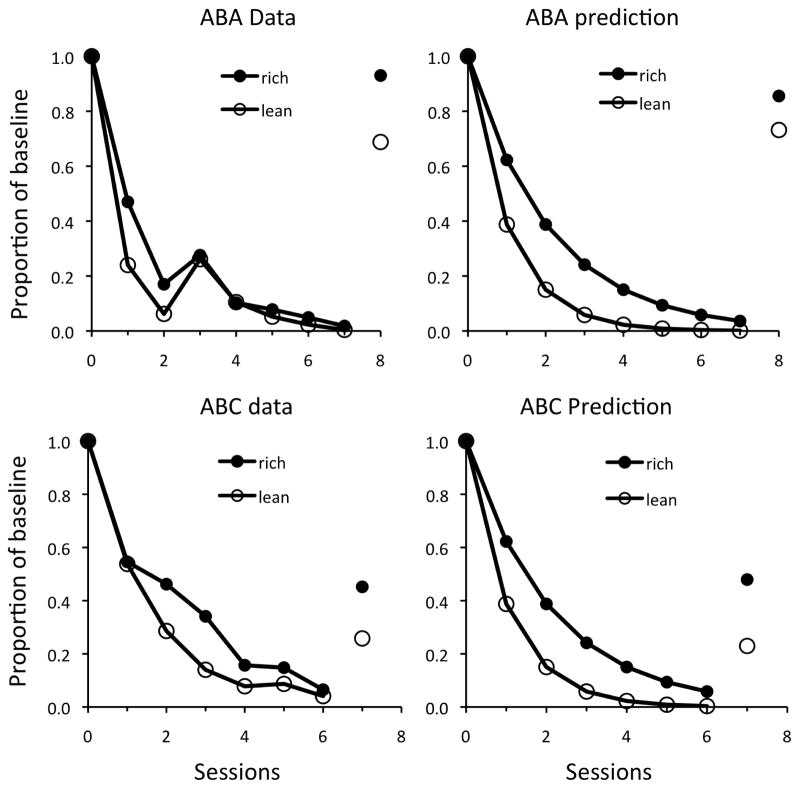
A study by Berry, Sweeney, and Odum (2014) demonstrated ABA and ABC renewal in two experiments with pigeons in a multiple schedule with rich (VI 120/hr) and lean (VI 30/hr) schedules in the components. Experiment 1 arranged an ABA paradigm in which baseline stimuli were steady key lights (A), extinction stimuli were flashing key lights (B), after which steady key lights (A) were restored for one session in a renewal test arranging extinction. Key pecking was more resistant to extinction and recovered to a greater degree in the rich relative to the lean component. In Experiment 2, baseline stimuli were white houselight in Chamber X (Context A), extinction was accompanied by orange houselight also in Chamber X (Context B), after which renewal was evaluated for one session with purple houselight in Chamber Y, also in extinction (Context C). Again, key pecking in the rich component was more resistant to extinction in Phase 2 and recovered to a greater degree in Phase 3. The average data and predictions for both experiments are shown in Figure 4. Predictions of Equation 7 are at least ordinally correct. For ABA renewal, parameters are c = 0.09, d = 0, dSB = 2.97, dSC = 0 (as for Podlesnik & Shahan, 2009; see above), accounting for 95% of the variance. For ABC renewal, parameters are c = 0.26, d = 0.002, dSB = 1.34, and dSC = 0.10, accounting for 98% of the variance. Note that ABA renewal is greater than ABC renewal in both components. Although comparison between Experiments 1 and 2 is weakened by between-experiment variations in contextual stimuli and possible order effects, and some of the fitted parameter values are unusually low, the observed and predicted differences between ABA and ABC renewal are consistent with results for rats in between-experiment comparisons by Bouton et al. (2011).
Fig 4.
The left panels present mean data from Berry et al. (2014) for post-extinction renewal in ABA (upper panel) and ABC (lower panel) paradigms. The corresponding right panels present predictions of Equation 7; see text for explanation and parameter values.
3.3 Resurgence
Podlesnik and Shahan (2010) also applied their attenuation-of-disruption model (see above) to resurgence, defined as the return of a previously reinforced and extinguished response when eliminating or reducing reinforcement for a more recently reinforced response (e.g., Shahan & Craig, in press). In the standard three-phase paradigm, target responding is reinforced in Phase 1 and then extinguished while alternative reinforcers are presented during Phase 2. In Phase 3, extinction of alternative behavior in Phase 3 typically produces an increase in target responding despite continued extinction.
For reasons summarized by Shahan and Sweeney (2011), Podlesnik and Shahan’s (2010) approach cannot predict the finding that resurgence is greater after higher rates of alternative reinforcement in Phase 2. Accordingly, they proposed that alternative reinforcers be construed as disruptors, and resurgence arises from their removal in Phase 3. The Shahan-Sweeney model for resurgence, in exponentiated form, is:
| Eq. 8 |
where p scales the disruptive effect of alternative reinforcers (ralt in the numerator of the exponent). Note that this model explicitly predicts greater resurgence when a higher rate of ralt is arranged in Phase 2. In addition, note that ralt also appears in the denominator of the exponent, as in Equation 2 above. Thus, alternative reinforcers function both to disrupt target responding as disruptors in the numerator and to strengthen target respsonses in the denominator, an awkward state of affairs with conceptual difficulties noted by Craig and Shahan (2016). Consider a condition in which a target response obtains 30 reinforcers/hr during Phase 1, and in Phase 2, target behavior is extinguished while an alternative response obtains 30 reinforcers/hr. By summing Phase-1 target reinforcers and Phase-2 alternative reinforcers, the model set forth in Equation 8 creates a total of 60 reinforcers/hr in the denominator simply by switching 30 of them from one key to another.
Despite these difficulties, Shahan and Sweeney (2011) showed that their model accorded well with some archival data in studies with nonhuman animals. Moreover, it gave a good account of the data of Wacker et al. (2011), who arranged Functional Communications Training (FCT, a form of DRA) in an applied setting to modify problem behavior in children with developmental disabilities. Wacker et al. found that resurgence diminished during repeated tests in which FCT was briefly discontinued; the Shahan-Sweeney model predicts just such effects.
We now apply Equation 9 to the data of Experiment 1 by Nevin et al. (2016), which was designed to evaluate the effects of high vs. low alternative reinforcement rates (DRA) in Phase 2 in combination with high or low rates of target-response reinforcement in Phase 1. In Phase 1 (baseline), target responding produced food reinforcement at either a high rate (120/hr, termed High-BL) or low rate (30/hr, termed Low-BL) in all three components of a multiple schedule, in two successive and counterbalanced conditions. Next, during Phase 2, a DRA plus extinction intervention for target responding was introduced in two components; to make the study relevant to application, target responding in the third component remained untreated as a control. In the DRA components, food for target responding was placed on extinction, an alternative-response key was illuminated, and pecks to this key produced food reinforcement at a high rate (120/hr, termed DRA-Rich) in one component or at a low rate (30/hr, termed DRA-Lean) in the other. All reinforcement in all three components was suspended in Phase 3.
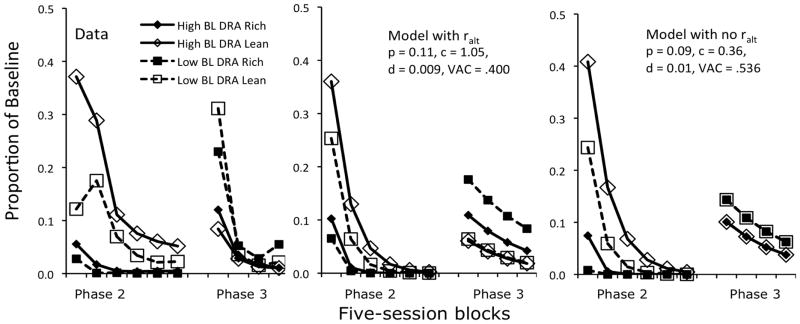
Mean data, expressed as proportions of baseline, are presented for the DRA-Rich and DRA-Lean components in the left panel of Figure 5. Equation 9 was fitted to these data with the constraints that p, c, and d be > 0. With p = 0.11, c = 1.05, and d = 0.009, the Phase-2 extinction data (left side of left panel) are at least ordinally consistent with model predictions (left side of the center panel): Target responding is most resistant to extinction in the High-BL, DRA-Lean combination and least in the Low-BL, DRA-Rich combination, with the other conditions intermediate. This ordinal prediction for Phase 2 is well described using the best-fitting parameter values.
Fig. 5.
The left panel presents the data, expressed as mean proportions of baseline, from a resurgence study reported by Nevin et al. (2016, Experiment 1). The center panel presents predictions of Equation 8 with alternative reinforcers included in the denominator of the exponent, and the right panel presents predictions of Equation 8 with alternative reinforcers excluded. Parameter values are included in the figure; see text for explanation.
With those best-fitting values, however, Phase 3 data for resurgence of target responding deviate strikingly from prediction in level and order. For instance, the data in the right half of the leftmost panel show that resurgence was greatest in the Low-BL condition with DRA-Lean (unfilled squares), whereas the model (right half of center panel) predicts a tie for least resurgence with High-BL, DRA-Lean (unfilled diamonds and squares). Not surprisingly, overall VAC is a measly .400.
In light of the conceptual problems with reinforcer summation across successive phases discussed above, we modified Equation 9 by eliminating ralt from the denominator and then repeated the fit to target-response proportions of baseline in Phases 2 and 3. As a result, the predicted ordering of Phase-2 data is unchanged, and the predicted ordering of Phase-3 resurgence across conditions is at least roughly in accord with the data, with Low-BL above High-BL responding (see far-right panel of Figure 3). VAC improved to .536 with p = 0.09, c = 0.36, and d = 0.01. The fit is still poor, but better than with summation of rt and ralt in the denominator of the exponent in Eq. 9.
Yet another difficulty pertaining to reinforcer summation of rt and ralt arises with respect to resistance to extinction of alternative behavior. Alternative behavior was established and maintained in Phase 2 with DRA-Rich or DRA-Lean in different components but were paired with High-BL or Low-BL for target behavior across separate conditions.
Extinction of alternative behavior in Phase 3 should be governed by a modification of Equation 3, with Balt in place of Bt and ralt replacing rt in the numerator of the exponent:
| Eq. 9 |
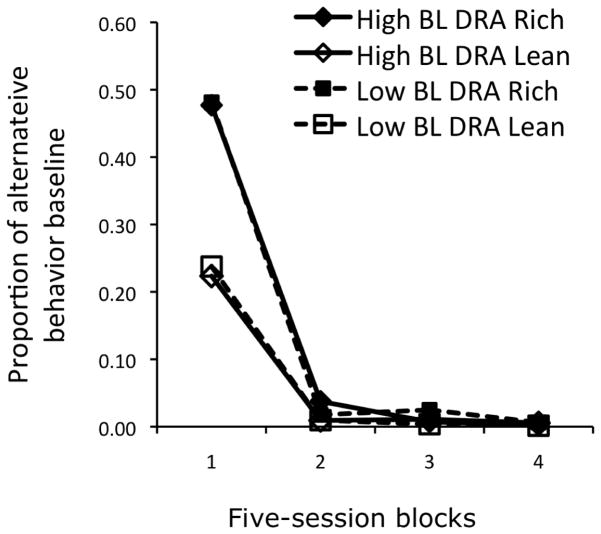
As shown in Figure 6, resistance to extinction of alternative behavior during Phase 3 was essentially identical in High-BL and Low-BL conditions, implying that Phase-1 target-behavior reinforcers rt did not summate with Phase 2 alternative-behavior reinforcers ralt in the denominator of the exponent despite the fact that reinforcers for target behavior were provided within the same general setting (chamber, key lights, etc., except for the absence of the alternative key light).
Fig. 6.
Alternative behavior during extinction as a proportion of response rates during the final five sessions of DRA treatment reported by Nevin et al. (2016, Experiment 1). Note that the functions for High-BL and Low-BL conditions are essentially identical. See text for explanation.
Overall, the data suggest that reinforcer summation operates to increase resistance to change only if all reinforcers are provided concurrently within the same stimulus context (i.e., not in successive distinguishable phases), as in the studies noted above with added response-independent or response-contingent alternative reinforcers in a multiple-schedule component (e.g., Nevin et al., 1990).
Overall, the conceptual difficulties with Equation 8, its poor predictive performance with the resurgence data of Nevin et al. (2016), and its other empirical failings (see Craig & Shahan, 2016) force us to conclude that accounts of resurgence based on behavioral momentum theory are fundamentally flawed. Therefore, an alternative approach to resurgence is sorely needed (e.g., Shahan & Craig, in press, this issue).
4. Transfer tests for Pavlovian processes in resistance to change
Is resistance to change governed by Pavlovian processes, as argued by Nevin et al. (1990)? Much of the supporting evidence is indirect, coming from serial schedules (Nevin, 1984; Nevin, Smith, & Roberts, 1987) and from inferences based on behavioral contrast in resistance to change (Nevin, 1992). The litmus test for Pavlovian determination of operant behavior is the Pavlovian-to-Instrumental Transfer (PIT) paradigm, which was introduced by Estes (1948) and employed by Morse and Skinner (1958) to evaluate the influence of previous stimulus-reinforcer pairings on an independently established operant during subsequent extinction (see Rescorla & Solomon, 1967, for a theoretical overview).
The PIT paradigm involves three successive phases: 1) pair a stimulus with reinforcers in the absence of the operant; 2) establish stable operant responding in the absence of the stimulus; and 3) present the stimulus during extinction of the operant. In the final phase, enhanced responding in the presence of the stimulus previously paired with reinforcers demonstrates the influence of the Pavlovian stimulus on operant responding. Importantly, because the Pavlovian stimulus and the operant response are independently trained, any influence of the Pavlovian stimulus on operant responding cannot be interpreted as a discriminative stimulus effect and has therefore been interpreted in relation to other processes, such as conditioned incentive value (Rescorla & Solomon, 1967).
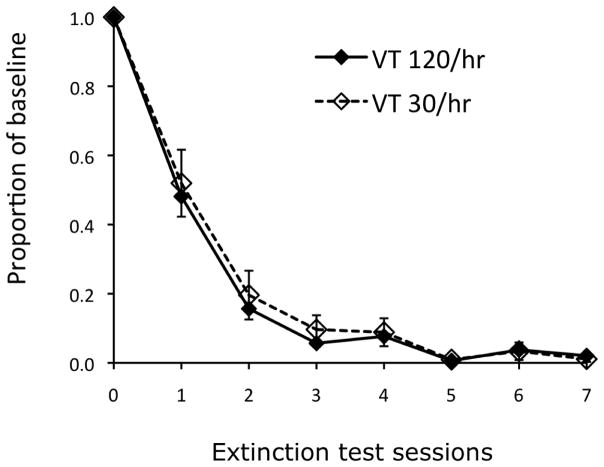
An experiment conducted by the third author at Utah State University used the PIT paradigm to directly assess the role of the stimulus-reinforcer relation on resistance to extinction. He arranged reinforcer rates comparable to those employed in research on resistance to change in multiple schedules. During Phase 1, five pigeons received 30 sessions of response-independent food delivered at variable times (VT) at a high rate in one component (VT 120/hr) and a low rate (VT 30/hr) in the other component of a multiple schedule. Components were signaled by either a red or white houselight, with the schedule-color arrangement counterbalanced across pigeons. Each 60-s component was presented 15 times per session. The first component was randomly determined and components strictly alternated thereafter, with a 30-s blackout separating component presentations. During Phase 2, pigeons pecked a white key for food on a VI 60/hr schedule for seven sessions. The houselights used in the multiple schedule of Phase 1 were absent in Phase 2. Following Phase 2, the multiple VT 120/hr, VT 30/hr schedule was reintroduced for 5 sessions as a reminder of the houselight stimulus-reinforcer relations. Finally, during Phase 3 the houselights were reintroduced with the white key light and key-peck response available in both components, but no food was delivered at any time (i.e., extinction).
If the persistence of operant behavior is determined by Pavlovian processes, then key pecking should be more resistant to extinction in the presence of the stimulus signaling the higher rate of reinforcement given the parameters arranged here. However, Figure 7 shows that key pecking extinguished at the same rate in the presence of both the high- and low-reinforcement rate stimuli. Thus, the independently established stimulus-reinforcer relations did not affect resistance to extinction in the manner predicted by BMT. Although a single failure to find an expected outcome is not decisive, because it may be specific to the particular stimuli and procedural features employed, it raises concerns about the notion that resistance to change is governed by the Pavlovian relation between a stimulus and reinforcers obtained in the presence of that stimulus (see also Podlesnik and Fleet, 2014, for similar conclusions from a different procedure).
Fig. 7.
Proportions of baseline responding during 7 consecutive test sessions in which stimuli correlated with VT 120/hr and 30/hr, presented during Pavlovian training, were superimposed on key pecking during extinction.
In view of the widely-replicated increase in persistence resulting from added reinforcers within a schedule component, whether response-independent or contingent on a separate response, we need a more precise formulation of the underlying process; invocation of something vaguely “Pavlovian” really will not do. It appears that stimulus-reinforcer effects on persistence are most clearly evident if added reinforcers are administered in a context with a reinforced target response, so a pure Pavlovian account is ruled out. An additive combination of operant stimulus control and Pavlovian incentive motivation of the sort suggested by Weiss (2014) may be required, and a quantitative expression for such a combination might perform as well or better than BMT.
5. Behavioral momentum theory reconsidered
Nevin (1974) argued that response strength – the result of reinforcement – is better construed as the resistance to change of responding than its rate or probability. Nevin et al. (1983) invoked a metaphorical equivalence between resistance to change and Newton’s laws for the motion of a physical body to quantify the behavioral equivalent of inertial mass. Further, Nevin and Grace (2000) extended the metaphor to encompass preference as the behavioral equivalent of gravitational mass. The momentum metaphor and its emphasis on resistance to change have inspired applications in domains where behavioral persistence is obviously important. For example, in behavioral pharmacology, drugs have served as disruptors (e.g., Harper, 1999) or reinforcers (e.g., Quick & Shahan, 2009), with results consistent with non-drug disruptors and reinforcers. In clinical work with children exhibiting persistent problem behavior, the metaphor has guided efforts to establish durable alternative behavior without counter-therapeutic effects such as relapse of problem behavior (e.g., Mace et al, 2010; for review see Podlesnik & DeLeon, 2015),
Over the course of this development, various mismatches between theory and data have arisen. For example, Pavlovian determination of resistance to change by stimulus-reinforcer relations requires that if obtained reinforcer rates are equated between components of a multiple schedule, operant contingencies such as differential reinforcement of low rates (DRL) or delays to reinforcement should have no impact on resistance to change. However, low rates established by DRL are generally more resistant to change than high rates (e.g., Lattal, 1989), whereas low rates established by delayed reinforcers are less resistant to change than with immediate reinforcement (e.g., Grace et al., 1998). Although the effects on resistance to change of operant contingencies and the response rates they engender vary in seemingly nonsystematic ways across studies (see McLean, Grace, and Nevin, 2012, for discussion), the very existence of such effects is problematic for BMT.
A different sort of problem arises with single as opposed to multiple schedules. For example, in single schedules, resistance to extinction is inversely related to reinforcer rate in a condition. In multiple schedules, by contrast, resistance to extinction is directly related to reinforcer rate in a component (Cohen et al., 1993; Cohen, 1998). In relation to the effects of alternative reinforcers discussed here, Lionello-DeNolf and Dube (2011) have replicated the usual additive effects on resistance to disruption in a multiple schedule component with children with intellectual deficiencies but failed to find any such effect in single schedules. These and other difficulties have been reviewed by Craig, Nevin, and Odum, 2013; see also Shahan & Craig, in press, this issue).
Two further mismatches are described in this article. First, an extension of BMT to resurgence is clearly wrong, both conceptually and in terms of its failure to account for some parametric data (see also Craig & Shahan, 2016). Second, a direct evaluation of Pavlovian determination of operant performance failed decisively to show the expected effects of reinforcer rate. Overall, the problems with BMT should prompt a search for alternatives that can address the sorts of difficulties described here and give a coherent account encompassing the broad domain of resistance to change and relapse.
6. Final musings
Despite its shortcomings, the extension of BMT to resurgence proposed by Shahan and Sweeney (2011) gave an excellent account of the data of Wacker et al. (2011). We now raise the question: Can a flawed model serve to guide application? The geocentric model of Ptolemy (ca. 150 AD) provides a relevant example. With its cumbersome epicycles revolving on deferents, offset by equants that differed for each planet, Ptolemy’s model exemplifies ad-hoc parameter invocation and adjustment similar to BMT’s treatment of extinction. Despite the complexity of the Ptolemaic model and its utter failure to capture what is now accepted as the true (i.e., heliocentric) solar system, Ptolemy’s tables for estimating the positions of the sun, moon and planets, and the times of the rising and setting of the stars, fell within the range of error inherent in early measuring instruments. As such, his tables were useful for navigation for well over 1000 years. Perhaps BMT is like Ptolemy’s geocentric model in that a) it’s intuitively reasonable; b) it’s useful in many applications; and c) it’s wrong. Nevertheless, applications addressing the persistence of behavior, desired or undesired, may find BMT useful as a heuristic until an equivalent of the heliocentric alternative is developed in the domain of behavior.
Highlights.
Resistance to extinction depends on the strengthening effects of reinforcement as well as the disruptive effects of nonreinforcement.
Behavioral momentum theory can explain extinction in multiple schedules, including the PREE in discrete trials.
The relation between resistance to extinction and rate of intermittent reinforcement differs for multiple and single schedules.
The number of reinforcers omitted to a 50% extinction criterion is an increasing function of reinforcer rate in all data reviewed here.
Acknowledgments
Preparation of this article and some of the research on which it is based were supported by NICHD Grant 064576 to the University of New Hampshire.
Footnotes
Note: This article is based on a talk presented by Nevin at the meetings of the Society for Quantitative Analyses of Behavior, Chicago IL, May 2016.
Order of authorship is alphabetical except for Nevin.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Berry MS, Sweeney MM, Odum AL. Effects of baseline reinforcement rate on operant ABA and ABC renewal. Behavioural Processes. 2014;108:87–93. doi: 10.1016/j.beproc.2014.09.009. [DOI] [PubMed] [Google Scholar]
- Bouton ME, Todd PT, Vurbic D, Winterbauer NE. Renewal after extinction of free operant behavior. Learning and Behavior. 2011;39:57–67. doi: 10.3758/s13420-011-0018-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen SL. Behavioral momentum: The effects of temporal separation of rates of reinforcement. Journal of the Experimental Analysis of Behavior. 1998;69:29–47. doi: 10.1901/jeab.1998.69-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen SL, Riley DS, Weigle PA. Tests of behavior momentum in simple and multiple schedules with rats and pigeons. Journal of the Experimental Analysis of Behavior. 1993;60:255–291. doi: 10.1901/jeab.1993.60-255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig AR, Nevin JA, Odum AL. Behavioral momentum and resistance to change. In: McSweeney FK, Murphy ES, editors. The Wiley-Blackwell Handbook of Operant and Classical Conditioning. Oxford, UK: Wiley-Blackwell; 2013. pp. 249–274. [Google Scholar]
- Craig AR, Shahan TA. Behavioral momentum theory fails to account for the effects of reinforcement rate on resurgence. Journal of the Experimental Analysis of Behavior. 2016;105:375–392. doi: 10.1002/jeab.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estes WK. Discriminative conditioning. II. Effects of a Pavlovian conditioned stimulus upon a subsequently established operant response. Journal of Experimental Psychology. 1948;38:173–177. doi: 10.1037/h0057525. [DOI] [PubMed] [Google Scholar]
- Grace RC, Schwendiman JW, Nevin JA. Effects of unsignaled delay of reinforcement on preference and resistance to change. Journal of the Experimental Analysis of Behavior. 1998;69:247–261. doi: 10.1901/jeab.1998.69-247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper DN. Drug-induced changes in responding are dependent upon baseline stimulus-reinforcer contingencies. Psychobiology. 1999;27:95–104. [Google Scholar]
- Lattal KA. Contingencies on response rate and resistance to change. Learning and Motivation. 1989;20:191–203. [Google Scholar]
- Lionello-DeNolf KM, Dube WV. Contextual influences on resistance to disruption in children with intellectual disabilities. Journal of the Experimental Analysis of Behavior. 2011;96:317–327. doi: 10.1901/jeab.2011.96-317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace FC, Lalli JS, Shea MC, Lalli EP, West BJ, Nevin JA. The momentum of human behavior in a natural setting. Journal of the Experimental Analysis of Behavior. 1990;54:163–172. doi: 10.1901/jeab.1990.54-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace FC, McComas JJ, Mauro BC, Progar PR, Taylor B, Ervin R, Zangrillo AN. Differential reinforcement of alternative behavior increases resistance to extinction: clinical demonstration, animal modeling, and clinical test of one solution. Journal of the Experimental Analysis of Behavior. 2010;93:349–367. doi: 10.1901/jeab.2010.93-349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean AP, Grace RC, Nevin JA. Response strength in extreme multiple schedules. Journal of the Experimental Analysis of Behavior. 2012;97:51–70. doi: 10.1901/jeab.2012.97-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morse WH, Skinner BF. Some factors involved in the stimulus control of operant behavior. Journal of the Experimental Analysis of Behavior. 1958;1:103–107. doi: 10.1901/jeab.1958.1-103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA. Response strength in multiple schedules. Journal of the Experimental Analysis of Behavior. 1974;21:389–408. doi: 10.1901/jeab.1974.21-389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA. Behavioral contrast and behavioral momentum. Journal of Experimental Psychology: Animal Behavior Processes. 1992;18:126–133. [Google Scholar]
- Nevin JA. Measuring behavioral momentum. Behavioural Processes. 2002;57:187–198. doi: 10.1016/s0376-6357(02)00013-x. [DOI] [PubMed] [Google Scholar]
- Nevin JA. Resistance to extinction and behavioral momentum. Behavioural Processes. 2012;90:89–97. doi: 10.1016/j.beproc.2012.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA. Behavioral momentum: A scientific metaphor. Self-published; 2015. [Google Scholar]
- Nevin JA, Mace FC, DeLeon IG, Shahan TA, Shamlian KD, Lit K, Sheehan T, Frank-Crawford MA, Trauschke SL, Sweeney MM, Tarver DR, Craig AR. Effects of signaled and unsignaled reinforcement on persistence and relapse in children and pigeons. Journal of the Experimental Analysis of Behavior. 2016;106:34–57. doi: 10.1002/jeab.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Mandell C, Atak JR. The analysis of behavioral momentum. Journal of the Experimental Analysis of Behavior. 1983;39:49–59. doi: 10.1901/jeab.1983.39-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Smith LD, Roberts JE. Does contingent reinforcement strengthen operant behavior? Journal of the Experimental Analysis of Behavior. 1987;48:17–33. doi: 10.1901/jeab.1987.48-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Tota M, Torquato R, Shull RL. Alternative reinforcement increases resistance to change: Operant or Pavlovian processses? Journal of the Experimental Analysis of Behavior. 1990;53:359–379. doi: 10.1901/jeab.1990.53-359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Grace RC. Behavioral momentum and the Law of Effect. Behavioral and Brain Sciences. 2000;23:73–130. doi: 10.1017/s0140525x00002405. [DOI] [PubMed] [Google Scholar]
- Nevin JA, McLean AP, Grace RC. Resistance to extinction: Contingency termination and generalization decrement. Animal Learning & Behavior. 2001;29:176–191. [Google Scholar]
- Podlesnik CA, DeLeon IG. Autism service delivery. Springer; New York: 2015. Behavioral momentum theory: Understanding persistence and improving treatment; pp. 327–351. [Google Scholar]
- Podlesnik CA, Fleet JD. Signaling added response-independent reinforcement to assess Pavlovian processes in resistance to change and relapse. Journal of the Experimental Analysis of Behavior. 2014;102:179–197. doi: 10.1002/jeab.96. [DOI] [PubMed] [Google Scholar]
- Podlesnik CA, Miranda-Dukoski L. Stimulus generalization and operant context renewal. Behavioural Processes. 2015;119:93–98. doi: 10.1016/j.beproc.2015.07.015. [DOI] [PubMed] [Google Scholar]
- Podlesnik CA, Shahan TA. Behavioral momentum and relapse of extinguished operant responding. Learning & Behavior. 2009;37:357–364. doi: 10.3758/LB.37.4.357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podlesnik CA, Shahan TA. Extinction, relapse, and behavioral momentum. Behavioural Processes. 2010;84:400–411. doi: 10.1016/j.beproc.2010.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quick SL, Shahan TA. Behavioral momentum of cocaine self-administration: effects of frequency of reinforcement on resistance to extinction. Behavioural Pharmacology. 2009;20:337–345. doi: 10.1097/FBP.0b013e32832f01a8. [DOI] [PubMed] [Google Scholar]
- Rescorla RA, Skucy JA. Effect of response-independent reinforcers during extinction. Journal of Comparative and Physiological Psychology. 1969;67:381–389. [Google Scholar]
- Rescorla RA, Solomon RL. Two-process learning theory: relationships between Pavlovian conditioning and instrumental learning. Psychological Review. 1967;74:151–182. doi: 10.1037/h0024475. [DOI] [PubMed] [Google Scholar]
- Shahan TA, Craig AR. Behavioural Processes. Resurgence as choice. (in press) In this issue. Editor, please replace with final details. [Google Scholar]
- Shahan TA, Sweeney MM. A model of resurgence based on behavioral momentum. Journal of the Experimental Analysis of Behavior. 2011;95:91–108. doi: 10.1901/jeab.2011.95-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd TP, Winterbauer NE, Bouton ME. Effects of the amount of acquisition and contextual generalization on the renewal of instrumental behavior after-extinction. Learning & Behavior. 2012;40:145–157. doi: 10.3758/s13420-011-0051-5. [DOI] [PubMed] [Google Scholar]
- Troisi JRI. Do Pavlovian processes really mediate behavioral momentum? Some conflicting issues. Psychological Record. 2017 (under review) [Google Scholar]
- Wacker DP, Harding JW, Berg WK, Lee JF, Schieltz KM, Padilla YC, Nevin JA, Shahan TA. An evaluation of persistence of treatment effects during long-term treatment of destructive behavior. Journal of the Experimental Analysis of Behavior. 2011;96:261–282. doi: 10.1901/jeab.2011.96-261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss SJ. The instrumentally derived incentive-motivation function. International Journal of Comparative Psychiology. 2014;27:598–613. [Google Scholar]