Refrigerant Performance Evaluation Including Effects of Transport Properties and Optimized Heat Exchangers

Abstract

Preliminary refrigerant screenings typically rely on using cycle simulation models involving thermodynamic properties alone. This approach has two shortcomings. First, it neglects transport properties, whose influence on system performance is particularly strong through their impact on the performance of the heat exchangers. Second, the refrigerant temperatures in the evaporator and condenser are specified as input, while real-life equipment operates at imposed heat sink and heat source temperatures; the temperatures in the evaporator and condensers are established based on overall heat transfer resistances of these heat exchangers and the balance of the system.

The paper discusses a simulation methodology and model that addresses the above shortcomings. This model simulates the thermodynamic cycle operating at specified heat sink and heat source temperature profiles, and includes the ability to account for the effects of thermophysical properties and refrigerant mass flux on refrigerant heat transfer and pressure drop in the air-to-refrigerant evaporator and condenser. Additionally, the model can optimize the refrigerant mass flux in the heat exchangers to maximize the Coefficient of Performance. The new model is validated with experimental data and its predictions are contrasted to those of a model based on thermodynamic properties alone.

1. Introduction

Since the mid-1980s, the refrigeration and air-conditioning sector has devoted a significant effort to identify and implement refrigerants that address environmental problems of stratospheric ozone depletion and global warming. The process of selecting the best refrigerants involves consideration of several criteria (McLinden and Didion, 1987) with the Coefficient of Performance (COP) being of dominant importance once other ‘gate’ attributes (e.g., chemical stability or lack of toxicity) have been accepted.

Domanski and McLinden (1992) discussed the merits and shortcomings of various methods for predicting the performance of refrigerants operating in vapor compression cycles. They placed these methods in five categories from theoretical analysis to laboratory equipment testing: (1) Carnot cycle analysis, (2) simple methods based on fundamental observations and principles, (3) theoretical and semi-theoretical cycle analysis, (4) detailed equipment simulation models, and (5) laboratory tests of the vapor compression equipment. In the refrigerant selection process, great reliance is placed on methods of category (3) for selecting best candidate fluids for further examination either by more sophisticated models or tests in actual equipment.

The evaluation methods of category (3) range from idealized thermodynamic cycle analysis to simulations including some forms of representation of a practical cycle, e.g., non-isentropic compression, refrigerant pressure drops in the heat exchangers and connecting tubing, or the temperature difference between fluids exchanging heat. Most often, category (3) methods employ the refrigerant’s thermodynamic properties alone and perform simulations based on specified evaporator saturation temperature and superheat, condenser saturation temperature and subcooling, and compressor isentropic efficiency [e.g., CYCLE_D model (Brown et al., 2012)]. These models are very popular among refrigeration practitioners because they are simple and easy to use.

The CYCLE11 model (Domanski and McLinden, 1992) is more advanced conceptually than CYCLE_D-type models; instead of using evaporator and condenser saturation temperatures specified as input, CYCLE11 establishes the thermodynamic cycle–including the saturation temperatures–using temperature profiles of heat-transfer fluids (HTFs) in the evaporator and condenser and respective mean effective temperature differences between these fluids and the refrigerant, ΔT_hx. This approach allows for accounting for the effect of non-linear temperature glides of zeotropic mixtures during the evaporation and condensation processes. A simulation example with a high-glide R22/123 mixture showed a COP difference as high as 8.7 % when the nonlinearity is neglected during simulation.

The cycle simulation can be further advanced by accounting for effects of refrigerant mass flux on the heat transfer and pressure drop. These effects take place in conventional equipment (air conditioners, refrigeration systems) employing air-to-refrigerant, fined-tube evaporators and condensers, which rely on refrigerant forced-convection heat transfer. In these heat exchangers the refrigerant flows through circuits formed by tubes connected in a serpentine pattern. The designer must choose the number of parallel circuits, which determines the refrigerant mass flux in these circuits. A higher mass flux improves the refrigerant heat-transfer coefficient but also increases the refrigerant pressure drop. These two phenomena have opposite effects on the system COP; the highest COP is achieved with the mass flux that provides the best balance between the benefit of improved heat transfer and the penalty related to pressure drop.

The effect of refrigerant mass flux on two-phase heat transfer and pressure drop has been noted in the literature. Domanski and Yashar (2006) compared the performance of five different refrigerants in a vapor compression system with evaporator and condenser circuitries optimized by a learnable evolution model. They found that the COP difference between low-pressure and high-pressure fluids changes in favor of high-pressure fluids when the performance comparison is done using optimized heat exchangers as opposed to the theoretical cycle evaluation at fixed saturation temperatures in the evaporator and condenser. A related study showed high-pressure refrigerants to be the best performing fluids in condensers with optimized refrigerant circuitries (Domanski and Yashar, 2007).

Cavallini et al. (2010) introduced the ‘penalty factor’ and the ‘total temperature penalization’ (TTP) parameters that combine exergy losses due to heat transfer and pressure drop. They showed that these parameters can be used either to select the optimum number of circuits in a finned-tube condenser of fixed overall geometry and number of tubes, or to compare the refrigerants’ heat transfer performance in condensation. Brown et al. (2012) applied this approach to finned-tube evaporators. Further, Brown et al. (2014) used the ‘penalty factor’ and TTP to compare the evaporation and condensation performance of several low-GWP refrigerants. Recently, Zilio et al. (2015) compared the seasonal performance of an air-to-water heat pump working with R410A and R32. They found that a system with an optimized refrigerant circuitry in the air-to-refrigerant heat exchanger had a 5 % improved seasonal efficiency over a system with a ‘non-optimal’ circuitry design.

The present paper discusses in detail the effects of refrigerant thermophysical properties and refrigerant mass flux on refrigerant two-phase heat transfer and pressure drop. Also, the paper discusses a new cycle model, referred to as CYCLE_D-HX, which accounts for these effects and can select the optimal refrigerant heat exchanger circuity for maximizing system COP. Examples of CYCLE_D and CYCLE_D-HX simulations results are presented and contrasted.

2. Effect of Refrigerant Mass Flux on Two-Phase Heat Transfer and Pressure Drop

A pressure drop in the evaporator or condenser causes a saturation temperature drop and results in an increased mean effective temperature difference, ΔT_hx, between the refrigerant and the external heat transfer fluid (HTF). The refrigerant heat-transfer coefficient h also affects ΔT_hx; a higher h yields lower ΔT_hx. A decrease in condenser and evaporator ΔT_hx lowers the temperature lift seen by the compressor and subsequently lowers the compressor work, which improves the COP.

The functional dependencies of the refrigerant heat-transfer coefficient h and pressure drop Δp are given in Eqs. 1 and 2.

$$h=f(D,\text{RSF},\text{TPP},G,T_{\text{sat}},x,q)$$ (1)

$$\mathrm{\Delta }p=f(D,L,\text{RSF},\text{TPP},G,T_{\text{sat}},q)$$ (2)

RSF stands for ‘refrigerant-side feature’ such as an in-tube insert or microfin surface, and TPP stands for ‘thermophysical property’. The heat-transfer coefficient h and pressure drop Δp are both a function of the refrigerant mass flux G, where h approximately increases proportionally to G^0.8, while Δp increases approximately to G². There is an optimum value of G that best compromises between the two opposite effects that h and Δp have on the system COP. This optimum G depends on thermodynamic and transport properties of the refrigerant, tube diameter, and refrigerant-surface features (RSF in Eqs. 2 and 3).

Figure 1 shows the dependency of h and Δp on the mass flux in evaporation for R32, a high-pressure fluid, and R1234yf, a medium-pressure fluid, at T_sat = 0 °C. We used correlations by Wojtan et al. (2005a and 2005b) and Muller-Steinhagen and Heck (1986) for generating data for h and Δp, respectively. The showed results are normalized by nominal h and Δp values for R32 at G=100 kg·m⁻²·s⁻¹, h_nom=3.16 kW·m⁻²·K⁻¹ and Δp_nom =1.26 kPa, respectively. All values are average values calculated by Eq. 3:

$$F=\frac{1}{x_{\text{End}}-x_{\text{Start}}}{\int }_{x_{\text{Start}}}^{x_{\text{End}}}f(x)$$ (3)

where f(x) is h or Δp, x_Start is the quality corresponding to the isenthalpic expansion from a condenser saturation temperature of 45 °C and 3 K subcooling to evaporator conditions of T_sat=0 °C and x_End=1.

Figure 1.

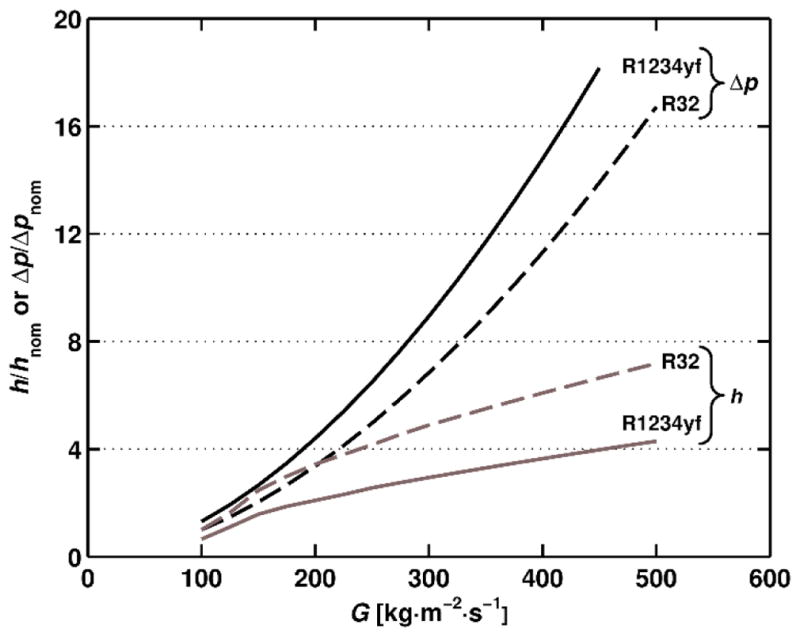
Normalized forced-convection evaporation heat-transfer coefficient and pressure drop for R32 and R1234yf as a function of mass flux (D=7 mm, smooth tube, T_sat = 0 °C, q=10 kW·m⁻²)

Figure 1 shows an important trend of exponentially increasing pressure drop and asymptotically increasing heat-transfer coefficient with increasing mass flux. R1234yf has a lower heat-transfer coefficient and a higher pressure drop than R32 at the same mass flux, and the rate of increase of heat-transfer coefficient in relation to pressure drop is less favorable for R1234yf than for R32. Also, the drop of saturation temperature of R1234yf is greater than that of R32 for the same pressure drop. For example, at T_sat=0 °C, dT/dp=0.0934 K·kPa⁻¹ for R1234yf and dT/dp=0.0384 K·kPa⁻¹ for R32, which leads to a 2.4 times greater decrease in saturation temperature for R1234yf than for R32 at the same pressure drop. Similar trends take place in condensing flows.

The optimum refrigerant mass flux G is different for each refrigerant and depends on refrigerant thermodynamic and transport properties. Ammonia, for example, which has a very high thermal conductivity and moderate saturation temperature drop due to its low vapor density, realizes the best compromise between heat-transfer coefficient and pressure drop at a low mass flux, i.e., at a high number of tube circuits. On the other hand, R32 being a higher-pressure fluid (higher vapor density) and having lower liquid conductivity than ammonia, realizes the best compromise between heat transfer and temperature drop penalization at a higher mass flux, i.e., at a lower number of circuits.

3. Effect of Thermophysical Properties on Two-Phase Heat Transfer and Pressure Drop

The thermodynamic and transport properties that affect the heat-transfer coefficient, h, and pressure drop, Δp, in two-phase flow are:

• liquid thermal conductivity, λ_l

• liquid and vapor density, ρ_l and ρ_v

• liquid and vapor viscosity, ν_l and ν_v

• liquid specific heat at constant pressure, c_p,l

• surface tension, σ (only for evaporation).

The liquid conductivity is the most influential parameter affecting the heat-transfer coefficient, while the pressure drop is independent of both the liquid and the vapor thermal conductivity. Literature correlations for h include a term proportional to λ_l^a, where a is an exponent in the neighborhood of 0.6; a higher liquid conductivity results in better two-phase heat transfer. The effect of vapor thermal conductivity is negligible because of the high flow turbulence; it only slightly modifies the heat-transfer coefficient component for a dry surface when the evaporation flow is stratified.

The liquid and vapor density also affect the two-phase heat-transfer coefficient: higher ρ_l yields a larger h, while higher ρ_v yields a lower h (for correlations including ρ_v). The effect of vapor density is greater on the pressure drop than on the heat-transfer coefficient. The vapor quality strongly affects the two-phase flow density, and subsequently the pressure drop. Furthermore, a high vapor density corresponds to a small saturation temperature drop associated with the pressure drop, as shown by the Clapeyron relation (Borgnakke and Sonntag, 2012):

$$\frac{\mathrm{d}T}{\mathrm{d}p}=\frac{T_{\mathit{sat}}}{h_{fg}}\left(\frac{1}{{\rho }_{\mathrm{v}}}-\frac{1}{{\rho }_1}\right)$$ (4)

The effect of liquid viscosity on two-phase heat transfer varies depending on the refrigerant and operating conditions, whereas the effect of vapor viscosity is small. The pressure drop increases as liquid and vapor viscosities increase. The liquid specific heat affects the heat-transfer coefficient, since it affects the liquid heat transport capacity. In most correlations h is proportional to c_p,l^a, where ‘a’ is an exponent in the neighborhood of 0.8. Pressure drop is not a function of c_p. The surface tension affects the nucleate boiling component of the evaporation heat-transfer coefficient; a low surface tension enhances h, but its effect is small compared with other transport properties.

In summary, the most important refrigerant properties for the forced-convection heat transfer are the liquid conductivity and the vapor density: the higher their values, the higher the two-phase heat-transfer coefficient is. The dominant property affecting pressure drop is the vapor density, where a high value results in low pressure drop, Δp, and low saturation temperature drop, dT/dp. Properties of refrigerants differ significantly (Table 1) so there is a spectrum of refrigerant performance relative to heat transfer and pressure drop. For example, R32 has both favorable liquid conductivity and vapor density in comparison to most fluids, whereas ammonia has a low vapor density, which is compensated for by an outstanding liquid conductivity.

Table 1.

Thermophysical properties of common refrigerants at 0 °C dew-point temperature (Lemmon et al., 2013)

Fluid	Tc	Pc	λl	ρl	νl	cp,l	ρv	νv	dT/dp
	°C	MPa	W·m−1·K−1	kg·m−3	mPa·s	kJ·kg−1·K−1	kg·m−3	mPa·s	K·kPa−1
R410A	71.4	4.90	0.103	1170.0	0.161	1.52	30.6	0.012	0.039
R32	78.1	5.78	0.145	1055.3	0.150	1.75	22.1	0.012	0.038
R1234yf	94.7	3.38	0.071	1176.3	0.208	1.29	17.7	0.010	0.093
R134a	101.1	4.06	0.092	1294.8	0.267	1.34	14.4	0.011	0.094
R717 (1)	132.3	11.3	0.559	638.6	0.170	4.62	3.5	0.009	0.062
R600a (2)	134.7	3.63	0.099	580.6	0.199	2.28	4.3	0.007	0.180

⁽¹⁾ammonia;

⁽²⁾isobutane

4. Description of CYCLE_D-HX Model

4.1 Overall modeling approach

The CYCLE_D-HX¹ model builds on the concept of using of temperature profiles of the heat sink and heat source, and ΔT_hx for the evaporator and condenser (Domanski and McLinden, 1992), which facilitates the accounting for refrigerant thermophysical properties, pressure drop, and heat-transfer coefficient on the cycle performance on a relative basis (Brown at al., 2002a and 2002b). This section provides a brief presentation of the CYCLE_D_HX modeling approach with a reference to the source publications. For simplicity of presentation, we will only discuss the basic vapor compression cycle although the simulation capabilities of CYCLE_D-HX include enhanced cycle options such as a liquid-line/suction-line heat exchanger, economizer, and intercooler.

In its simplest form, the simulated system consists of a compressor, condenser, adiabatic expansion device, and evaporator. The cycle and key thermodynamic states for this system are shown on a temperature-entropy (T-s) diagram (Figure 2). The compressor is represented by the isentropic efficiency, volumetric efficiency, and the electric motor efficiency. The evaporator and condenser can be either counter-flow, cross-flow or parallel-flow, and are represented by their ΔT_hx. The solution sequence starts with estimated values of saturation temperatures in the evaporator and condenser. Based on the established thermodynamic cycle with refrigerant temperature profiles and HTF temperature profiles, the model calculates ΔT_hx and compares them to the values specified as input. The model iterates evaporator and condenser saturation temperatures until it achieves the specified ΔT_hx values within a convergence parameter.

Figure 2.

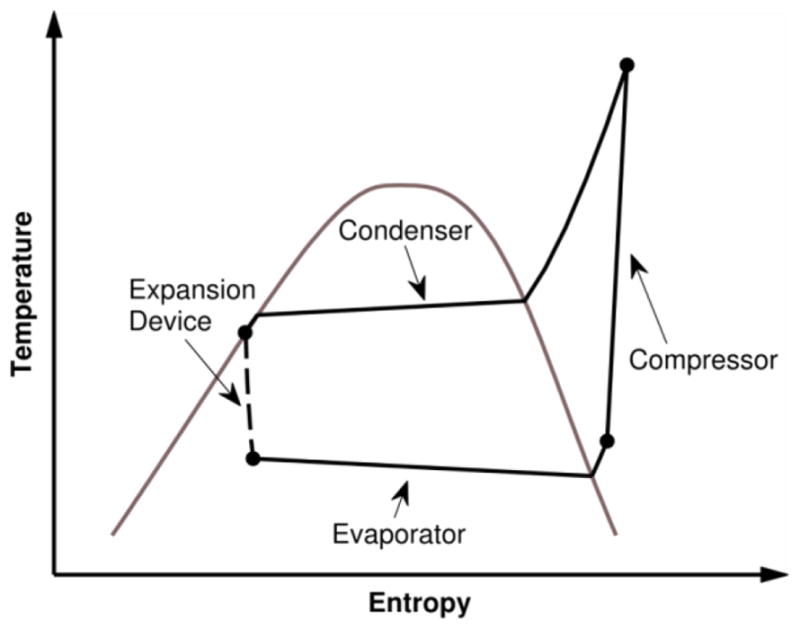
Basic vapor compression cycle

For each iteration step of saturation temperatures, CYCLE_D-HX calculates heat exchangers’ ΔT_hx using Eq. 5 (Domanski and McLinden, 1992).

$$\frac{1}{\mathrm{\Delta }{T}_{\text{hx}}}=\frac{Q_1}{Q_{\text{hx}}\mathrm{\Delta }{T}_1}+\frac{Q_2}{Q_{\text{hx}}\mathrm{\Delta }{T}_2}\dots =\frac{1}{Q_{\text{hx}}}\mathrm{\sum }\frac{Q_{\mathrm{i}}}{\mathrm{\Delta }{T}_{\mathrm{i}}}$$ (5)

In this equation, ΔT_hx is a harmonic mean weighted with the fraction of heat transferred in individual sections of the heat exchanger, based on the assumption of a constant overall heat-transfer coefficient throughout the heat exchanger. Each term represents the contribution of a heat exchanger section. At the outset of each saturation temperature iteration, the model calculates ΔT_hx based on sections corresponding to the subcooled liquid, two-phase, and superheated regions. Then, the model bisects each section and uses Eq. 5 to calculate a new value of ΔT_hx. The model repeatedly bisects each subsection until the ΔT_hx obtained from two consecutive evaluations agree within a convergence parameter.

As an alternative to specifying ΔT_hx, the heat exchangers can be characterized by the overall heat conductance UA_hx. If this input option is used, the model calculates the specified ΔT_hx from the basic heat-transfer relation, ΔT_hx = Q_hx/UA_hx, where Q_hx is the product of refrigerant mass flow rate and enthalpy change in the evaporator or condenser, as appropriate.

Representation of heat exchangers by their UA_hx allows for inclusion of heat transfer and pressure drop characteristics in comparable evaluations of different refrigerants. For this purpose, CYCLE_D-HX considers that the total resistance to heat transfer in a heat exchanger, R_hx, consists of the resistance on the refrigerant side R_r, and combined resistances of the heat exchanger material and HTF [R_tube + R_HTF]:

$$R_{\text{hx}}=1/U{A}_{\text{hx}}=R_{\mathrm{r}}+[R_{\text{tube}}+R_{\text{HTF}}]$$ (6)

$$\text{where}{R}_{\mathrm{r}}=1/(h_{\mathrm{r}}·A_{\text{hx}})$$ (7)

The resistances [R_tube + R_HTF] are independent of the refrigerant, and are assumed to be independent of operating conditions. Their combined value can be calculated from UA_hx and h_r values using performance measurements obtained in a laboratory on a system of interest. CYCLE_D-HX calculates [R_tube + R_HTF] within its ‘reference run’ and stores its value for use in subsequent simulation runs for calculation of UA_hx characterizing the heat exchanger with a new refrigerant or operating conditions.

CYCLE_D-HX requires the following operational input data for the ‘reference run’: HTF inlet and outlet temperatures for the evaporator and condenser; ΔT_hx for the evaporator and condenser (to achieve the measured evaporator and condenser saturation temperatures); evaporator superheat and pressure drop; and condenser subcooling and pressure drop. Additional ‘reference run’ inputs include compressor isentropic and volumetric efficiencies, and electric motor efficiency. Heat exchanger geometry inputs include the tube inner diameter and length, the number of refrigerant circuits, and the number of tubes per circuit. By user’s choice, CYCLE_D-HX can optimize evaporator and condenser circuitries (number of parallel circuits) to maximize the system’s COP. (This represents a design environment where the HTF and number of refrigerant tubes remains constant, but the refrigerant flow and tube circuitry can be adjusted.) Using this option, the model provides information on the relative performance potentials of refrigerants operating in systems with serpentine air-to-refrigerant heat exchangers.

For smooth tubes, CYCLE_D-HX uses correlations by Wojtan et al., (2005a and 2005b) and Shah (2009) for calculating the forced-convection heat-transfer coefficient for evaporation and condensation, respectively. For enhanced tubes, the model applies h_r correction presented by Shlager et al. (1989). The modeling of evaporator and condenser refrigerant pressure drop relies on a similar concept to that for the heat-transfer process. For smooth tubes, the model determines a pressure multiplication factor by dividing the ‘reference run’ pressure drop by the predicted value (Eq. 8).

$${\mathit{factor}}_{\mathrm{\Delta }p}=\frac{\mathrm{\Delta }{p}_{\text{ref}}}{\mathrm{\Delta }{p}_{\text{pred}}}$$ (8)

where Δp_pred is calculated by the Muller-Steinhangen and Heck (MSH) (1986) correlation for smooth tubes. For enhanced tubes the MSH value is corrected according to Choi et al. (2001).

Regarding the compressor isentropic efficiency, CYCLE_D-HX offers the option of accounting for its dependence on the compression ratio, as it was postulated by several researchers (Brown et al., 2002b). When screening different refrigerants, the model uses Eq. 9 to take into account the change in isentropic efficiency with the pressure ratio in a consistent way.

$${\eta }_{\mathrm{s}}=C-0.05\theta$$ (9)

Equation (9) has the same slope as the relation derived from experimental data by Brown et al. (2002b); C is a constant calculated within the ‘reference run’ using the isentropic efficiency and the pressure ratio obtained from the test data.

4.2 Optimization of refrigerant circuitry

The refrigerant circuitry optimization algorithm identifies the number of condenser and evaporator circuits that maximize COP. The evaporator is optimized before the condenser because the system is much more sensitive to the number of evaporator circuits (Zilio et al., 2015); the heat-transfer coefficient and pressure drop are more sensitive to G in the evaporator because the refrigerant density is lower and the viscosity is higher. Optimizing the evaporator before the condenser enables more rapid identification of the multivariate optimum.

The COP optimization algorithm is a modified Golden Section Search, which takes into account the values and trend. The Golden Section algorithm has been modified because it normally requires a non-flat and continuous function, but the computed COP function often does not satisfy these criteria. The function may be flat, for example, when varying the number of tube circuits in the condenser. Discontinuities can occur from numerical approximations or from the semi-empirical correlations used to evaluate the heat-transfer coefficient and the pressure drop. For example, Figure 1 shows a discontinuity in the correlation for heat transfer coefficient in the neighborhood of G=150 kg·m⁻²·s⁻¹, where the transition from a stratified-wavy to an annular flow takes place according to the flow-pattern map of Wojtan et al. (2005a). The algorithm starts searching in the direction of ascent until an inflection point is found and the maximum resides between the last two iterations. Then the algorithm makes at least two more iterations and stops when the absolute difference between the maximum and its two adjacent values is less than the convergence parameter.

The processing times for a simulation with optimization on personal computer (3.5 GHz processor) are on the order of 10 s, 150 s, and 350 s respectively for one-, two-, and three-component working fluids.

5. CYCLE_D-HX Validation

5.1 Experimental apparatus and test conditions

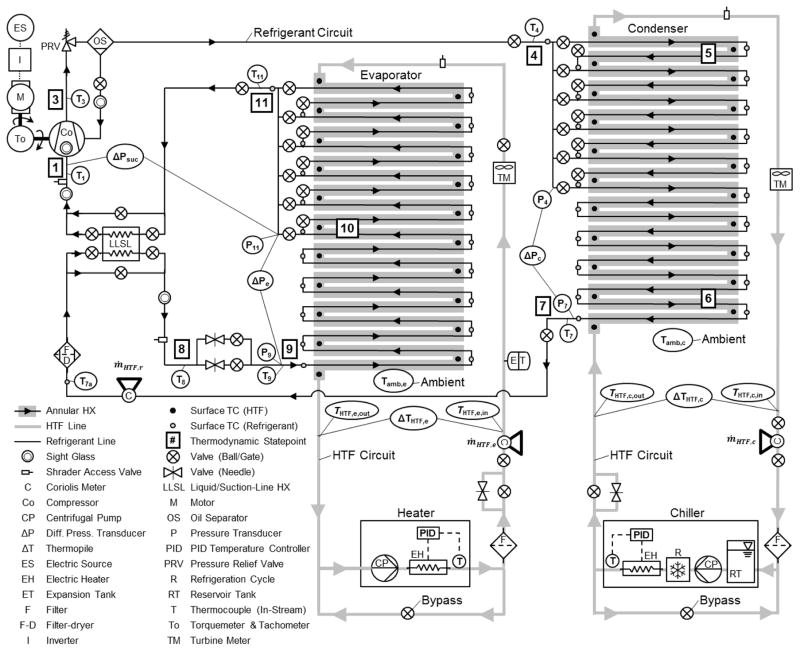
A laboratory liquid-to-liquid heat pump apparatus was used to generate data to verify the model. The apparatus (Figure A.1, in Appendix) is described briefly here; a more comprehensive description is provided in Skye (2015). The system was equipped with a variable-speed reciprocating compressor, variably-sized evaporator and condenser, manually adjusted throttling valve, and a liquid-line/suction-line heat exchanger, which could be included or bypassed. The evaporator and condenser were of the annular design arranged in the counter-current configuration; the refrigerant flowed in the enhanced inner tube (copper), while the HTF flowed in the smooth annular space. The heat exchangers’ size could be adjusted by changing the number of active refrigerant tubes; this feature enabled control of the heat flux.

The apparatus was set to achieve evaporation and condensation saturation temperatures nominal to air-source heat pumps operating at the Cooling A, Cooling B, and Heating H1 rating tests (AHRI, 2008). Table 2 shows the HTF inlet and outlet temperatures used to obtain these evaporation and condensation temperatures using R134a and a mid-range compressor speed, 1800 rev·min⁻¹. Four additional data sets at each rating test (total of 12) were generated by holding the HTF inlet temperature constant as the system capacity was varied via compressor speed, (1400 to 2200) rev·min⁻¹; these additional data sets are listed in the Appendix (Table A1(a), (b), and (c)). Note that the heat exchanger sizes were fixed for the data presented here.

Table 2.

Test operating conditions for R134a tests with 1800 rev·min⁻¹ compressor speed

Rating test	Capacity	Condenser			Evaporator
	kW	Tsat,ave °C	THTF,in °C	THTF,out °C	Tsat,ave °C	THTF,in °C	THTF,out °C
Cooling A*	1.69	43.6	33.9	39.0	8.1	20.2	15.4
Cooling B	1.95	35.8	24.9	30.9	5.5	19.8	14.2
Heating H1	1.88	39.6	32.0	36.3	0.3	10.2	6.5

^*‘reference run’ for CYCLE_D-HX model

Care was taken to configure other evaporator and condenser operating conditions (beyond refrigerant saturation temperature) to closely resemble those of a typical air-to-air heat pump. Specifically, the heat fluxes were within (5 to 9) kW·m⁻² and (5 to 10) kW·m⁻² for the evaporator and the condenser, respectively. Additionally, the ratios of HTF thermal resistance to total heat exchanger thermal resistance were nominally 0.8 and 0.6 for the evaporator and condenser, respectively; these values are representative of air-to-air heat pumps where the air-side (i.e. HTF side) thermal resistance dominates. The thermal resistance ratios were enforced by the selection of HTF mass flow rates; the HTF mass flow rates were held constant for all tests at 0.098 kg·s⁻¹ for the condenser and 0.131 kg·s⁻¹ for the evaporator. The subcooling and superheat were controlled to (2 to 3) K and (3 to 6) K, respectively. More details about these tests, including the uncertainty calculation (95 % confidence level) for the COP (0.35 %), capacity (0.2 %), and the Qvol (1.5 %) are presented in Skye (2015).

5.2 Experimental data vs. simulation results

We used the data from the Cooling A R134a test (Table 2) to carry out the CYCLE_D-HX ‘reference run’. The ‘reference run’ inputs included the 1.69 kW capacity, the evaporator ΔT_hx=8.8 K, the condenser ΔT_hx = 9.02 K, and pressure drops of 33 kPa and 45 kPa for the condenser and evaporator, respectively. We then executed simulations of the remaining Cooling A, Cooling B and Heating H1 ratings tests. The capacities, compressor isentropic and volumetric efficiencies, superheat and subcooling, discharge and suction line pressure drops, and HTF inlet and outlet temperatures were input based on measurements from each test.

We evaluated the percentage deviation between the simulation and the experimental results using Eq. 10.

$$E=\frac{{\mathit{\Pi }}_{\text{Experimental}}-{\mathit{\Pi }}_{\text{Simulation}}}{{\mathit{\Pi }}_{\text{Experimental}}}·100\%$$ (10)

where Π is any parameter of interest.

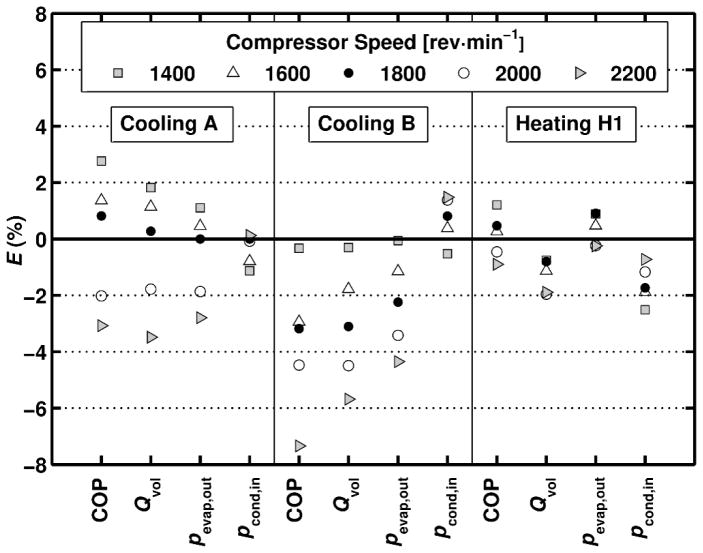
Figure 3 reports the deviations for COP, Q_vol, p_evap, and p_cond. Most of the deviations are within 4 %. The largest deviation (7.4 %) is for the Cooling B test at the highest (2200 rev·min⁻¹) compressor speed; this operating condition yielded about 20 % increase in refrigerant mass flow rate and capacity over the ‘reference run’. The model inputs (Table A2(a), (b)) and results (Table A3(a) and (b)) are tabulated in the Appendix.

Figure 3.

Deviations between experimental and CYCLE_D-HX simulations results

6. Comparison of Refrigerant Performance Evaluation Using CYCLE_D and CYCLE_D-HX

For performance evaluation we selected R134a, R600a, and R32 because they have significantly different thermophysical properties (Table 1). R600a is the lowest-pressure refrigerant of the three, and has a low vapor density and liquid conductivity. R32 is the highest-pressure refrigerant and has a high liquid conductivity and vapor density. The operating pressure, vapor density and liquid conductivity of R134a are between those of R600a and R32. We simulated the cycle performance of the three fluids at the Cooling A test operating condition (Section 5.1). The CYCLE_D-HX simulations (without and with the optimization option) were based on the CYCLE_D-HX ‘reference run’, which applied no optimization and used the R134a Cooling A test data. We conducted these simulations at the same evaporator capacity that was specified for the ‘reference run’ (1.69 kW). For all CYCLE_D simulations we used the evaporator and condenser saturation temperatures and saturation temperature drops from the ‘reference run’.

Figure 4 presents COP results normalized by the ‘reference run’ COP. CYCLE_D predictions correlate inversely with refrigerants’ P_c: the low-pressure R600a has the highest COP, followed by the medium-pressure R134a, and the high-pressure R32, which has the lowest COP. The CYCLE_D-HX simulation results display the opposite trend: the low-pressure R600a shows the lowest COP, and the high-pressure R32 has the highest COP. The R134a COPs for CYCLE_D-HX without optimization (‘reference run’) and for CYCLE_D are identical because CYCLE_D simulations used the saturation temperatures and pressure drop from the ‘reference run’. All three refrigerants benefitted from the refrigerant circuitry optimization. The COP increased for R600a and R32 by about 5 % and 9 %, respectively. R134a benefitted least, which suggests that the original refrigerant circuitry was reasonably well designed for R134a.

Figure 4.

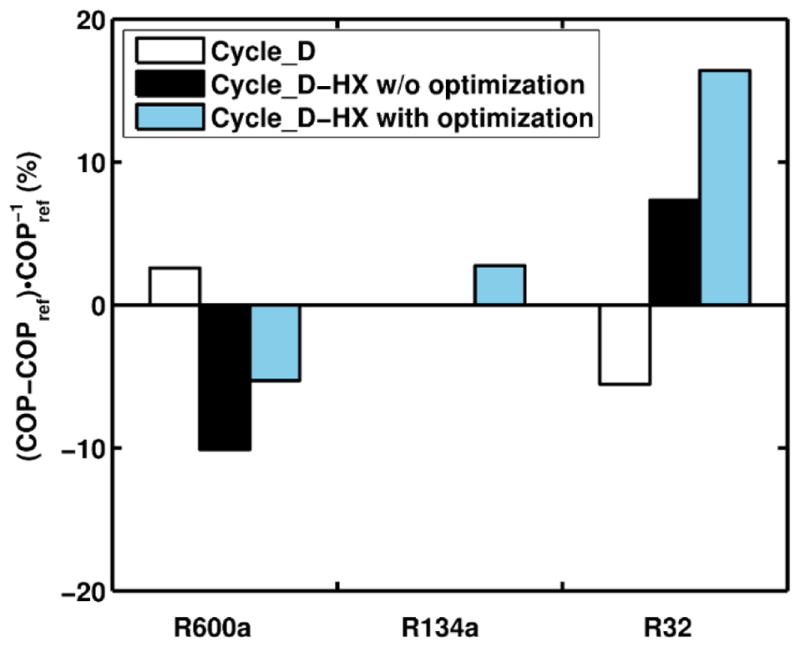
COP from CYCLE_D and CYCLE_D-HX simulations normalized by COP_ref = 2.85 (R134a Cooling A test condition, no optimization)

It is important to recognize the disparity in the COP trends between CYCLE_D and CYCLE_D_HX simulations, which affects the suitability of these simulation tools for rating competing refrigerants. With the same (imposed) saturation temperatures in the evaporator and condenser, CYCLE_D simulations tend to yield higher COPs for low-pressure refrigerants compared to high-pressure refrigerants because low-pressure fluids operate far below their critical point and tend to exhibit less irreversibilities due to the superheated vapor horn and throttling process (Domanski and Didion, 1993). However, as shown in the CYCLE_D-HX simulations, this thermodynamic advantage of low-pressure fluids may be erased in systems using heat exchangers that implement refrigerant forced-convection evaporation and condensation (e.g., air-to-refrigerant coils). Low-pressure fluids have low vapor density and therefore exhibit relatively large pressure and saturation temperature drops in forced-convection coils. These irreversibilities may render high-pressure refrigerants more efficient, particularly when refrigerant circuitries (and therefore mass fluxes) in these heat exchangers are optimized.

The COP trends discussed here are consistent with a prior study, which used a detailed air-to-air heat pump model with R600a, R134a, R290, R22, R410A, and R32 (Domanski and Yashar, 2006). These performance trends are also reflected in the engineering practice of selecting low-pressure refrigerants for water chillers with shell-and tube heat exchangers, which have low pressure drop, and applying higher-pressure refrigerants in systems with forced-convection heat exchangers. Consequently, we can conclude that the simulation methodology used by CYCLE_D-HX is preferable for screening refrigerants for systems with forced-convection heat exchangers over CYCLE_D-type simulation models using imposed saturation temperatures in the evaporator and condenser, which may provide incorrect ranking of the evaluated fluids. For systems with insignificant pressure drop, CYCLE_D-type models are likely to produce correct ranking unless liquid conductivity of the considered fluids differ substantially.

7. Conclusions

Preliminary refrigerant evaluations using theoretical models should consider the type of vapor compression equipment for which the refrigerant screening is performed. The key aspect differentiating system types is the type of evaporators and condensers used. For systems with heat exchangers relying on refrigerant pool boiling, falling film evaporation, or space condensation, cycle models based on thermodynamic properties alone may provide adequate ‘first estimate’ of relative performance merits of refrigerants of interest. However, for systems with heat exchangers relying on refrigerant forced-convection evaporation and condensation heat transfer, more appropriate simulation models are those which also involve refrigerant transport properties and can account for the effect of refrigerant mass flux on heat transfer and pressure drop.

NOMENCLATURE

A

area (m²)

c_p

specific heat at constant pressure (kJ·kg⁻¹·K⁻¹)

COP

coefficient of performance

D

diameter (mm)

E

deviation (%)

F

heat-transfer coefficient or pressure drop

factor_Δp

pressure drop multiplication factor (dimensionless)

G

mass flux (kg·m⁻²·s⁻¹)

h

heat-transfer coefficient (W·m⁻²·K⁻¹)

h_fg

enthalpy of vaporization (kJ·kg⁻¹)

HTF

heat-transfer fluid

L

length (m)

p

pressure (kPa)

q

heat flux (kW·m⁻²)

Q

cooling or heating capacity (kW)

Q_vol

volumetric capacity (kJ·m⁻³)

R

heat transfer resistance (K·W⁻¹)

RSF

refrigerant side feature (e.g., microfins, insert)

T

temperature (K, °C)

TPP

thermophysical properties

TTP

total temperature penalization (K)

UA

heat exchanger conductance (W·K⁻¹)

x

vapor quality (decimal fraction)

Δp

pressure drop (kPa)

ΔT_hx

mean effective temperature difference (K)

ΔT

temperature drop (K)

Greek letters

η_s

isentropic efficiency (decimal fraction)

θ

pressure ratio (dimensionless)

λ

thermal conductivity (W·m⁻¹·K⁻¹)

ν

kinematic viscosity (mPa·s)

Π

any parameter of interest

ρ

density (kg·m⁻³)

σ

surface tension (N·m⁻¹)

Subscripts

ave

average

c

critical

cond

condensation

evap

evaporation

hx

heat exchanger

in

inlet

l

liquid

nom

nominal

out

outlet

pred

predicted

r

refrigerant

ref

reference

sat

saturation

tube

tube separating refrigerant and HTF

v

vapor

Appendix: Experimental Data

This Appendix presents a schematic of the test rig and experimental data discussed in Section 5.1, and CYCLE_D-HX inputs and simulation results discussed in Section 5.2. Symbols used in the figures and tables are listed in the Nomenclature at the end of the Appendix.

Figure A1.

Schematic of the experimental apparatus

Table A1(a).

Experimental data–refrigerant-side measurements

	ṁr	Ncomp	P1	P4	P7	P8	P9	P11	ΔPc	ΔPe	ΔPsuc	T1	T3	T4	T7	T8	T9	T11	τcomp
	kg·s−1	rev·min−1	kPa	kPa	kPa	kPa	kPa	kPa	kPa	kPa	kPa	°C	°C	°C	°C	°C	°C	°C	N·m
*	±0.000016	±1	±3.5	±3.5	±3.5	±3.5	±3.5	±3.5	±1.3	±0.8	±0.3	±0.09	±0.09	±0.09	±0.09	±0.09	±0.09	±0.09	±0.33
Cooling A	0.01037	1426	362.8	1105	1076	1076	412.3	373.7	29.7	38.6	10.9	11.74	72.79	70.04	38.70	37.87	9.76	10.81	4.72
	0.01011	1609	370.6	1104	1075	1075	418.4	381.8	29.7	36.7	11.2	14.24	79.15	74.46	38.79	37.91	10.14	13.47	4.08
	0.01101	1810	353.2	1136	1103	1103	412.0	367.4	33.0	44.6	14.2	12.11	81.92	77.06	38.70	37.83	9.70	11.41	4.25
	0.01153	2005	337.5	1145	1108	1108	405.8	353.9	37.2	51.9	16.4	12.79	86.52	81.77	39.77	39.12	9.21	12.16	4.27
	0.01270	2231	307.8	1170	1127	1127	395.5	329.4	42.3	66.2	21.5	10.47	90.44	87.38	40.99	40.80	8.44	9.66	4.99
Cooling B	0.01094	1429	340	896.9	856.3	856.3	396.3	353.3	40.6	43.1	13.2	9.57	63.49	61.21	31.02	30.73	8.58	8.59	4.72
	0.01154	1628	323.8	915.3	869.6	869.6	390.6	340.5	45.8	50.2	16.6	10.51	69.35	66.91	31.56	31.37	8.08	9.64	4.08
	0.01206	1829	308	932.7	883.9	883.9	384.1	327.1	48.9	57.1	19.1	9.63	73.64	71.12	31.78	31.53	7.62	8.78	4.25
	0.01246	2032	295.6	946	894.6	894.6	379.8	317	51.4	62.9	21.4	9.79	77.91	75.27	31.91	31.65	7.28	9.02	4.27
	0.01291	2234	284.9	958	903.7	903.7	377.6	308.9	54.2	68.7	24.0	8.15	81.12	78.46	32.45	32.27	7.11	7.32	4.99
Heating H1	0.008001	1430	293.1	990.8	968	968	329	300.6	22.7	28.4	7.6	8.02	74.28	70.73	36.38	35.42	3.24	6.46	4.72
	0.008433	1628	273.8	1005	979.7	979.7	317.5	284.1	24.9	33.4	10.3	6.80	78.40	74.70	36.66	35.82	2.23	4.98	4.08
	0.009067	1832	264.3	1021	992.8	992.8	315.7	276.5	28.1	39.1	12.3	3.65	81.03	77.40	37.11	36.39	2.05	1.70	4.25
	0.009384	2032	253.7	1032	1002	1002	311.2	267.6	29.9	43.6	13.9	4.19	85.69	81.90	37.33	36.63	1.63	2.40	4.27
	0.009811	2233	246.9	1046	1014	1014	310.5	262.4	31.9	48.1	15.5	2.28	88.75	84.93	37.45	36.76	1.55	0.37	4.99

^*k=2, 95% confidence interval

Table A1(b).

Experimental data–refrigerant-side computed metrics

	COPcool	COPheat	ΔPdis	ηs	ηv	Q̇cool.r	Q̇heat.r	SC	SH	Qvol,cool	Qvol,heat	Ẇcomp.r
	--	--	kPa	--	--	kW	kW	°C	°C	kJ·m−3	kJ·m−3	kW
*	±0.01	±0.01	±0.1	±0.006	±0.006	±0.0035	±0.004	±0.2	±0.3	±30	±40	±0.002
Cooling A	3.33	4.26	1.5	0.520	0.562	1.587	2.032	3.39	3.90	2637	3377	0.477
	3.07	3.96	1.5	0.468	0.481	1.569	2.027	3.27	5.93	2704	3494	0.512
	2.82	3.72	1.7	0.463	0.486	1.693	2.235	4.36	5.00	2567	3388	0.601
	2.62	3.54	1.9	0.457	0.484	1.763	2.378	3.44	6.83	2419	3263	0.673
	2.34	3.31	2.3	0.460	0.524	1.889	2.666	3.39	3.90	2152	3038	0.806
Cooling B	3.95	4.92	2.1	0.508	0.629	1.771	2.202	2.69	3.31	2626	3266	0.448
	3.57	4.54	2.3	0.497	0.618	1.873	2.38	2.71	5.42	2482	3153	0.524
	3.24	4.20	2.5	0.483	0.605	1.949	2.532	3.08	5.70	2349	3051	0.602
	3.02	3.98	2.7	0.475	0.589	2.017	2.663	3.38	6.82	2248	2968	0.669
	2.75	3.72	2.8	0.457	0.573	2.061	2.789	3.21	5.86	2147	2906	0.749
Heating H1	3.04	3.97	1.1	0.521	0.538	1.236	1.615	1.79	5.75	2144	2801	0.407
	2.76	3.70	1.2	0.511	0.533	1.291	1.732	1.95	5.83	1984	2662	0.468
	2.47	3.43	1.4	0.482	0.521	1.356	1.879	1.99	3.29	1893	2624	0.549
	2.33	3.28	1.5	0.473	0.510	1.408	1.985	2.12	4.87	1813	2555	0.605
	2.15	3.11	1.6	0.452	0.495	1.454	2.103	2.42	3.38	1755	2537	0.677

^*k=2, 95% confidence interval

Table A1(c).

Experimental data–HTF-side measurements

	ṁHTF,c	ṁHTF,e	THTF,c,in	ΔTHTF,c	THTF,e,in	ΔTHTF,e
	kg·s−1	kg·s−1	K	C	°C	K
*	±0.00026	±0.00026	±0.6	±0.015	±0.6	±0.015
Cooling A	0.09928	0.1300	33.86	4.625	19.64	4.547
	0.09800	0.1317	33.84	4.713	20.20	4.432
	0.09871	0.1312	33.89	5.158	20.22	4.818
	0.09801	0.1317	33.88	5.572	20.32	4.976
	0.09920	0.1299	33.84	6.092	19.98	5.419
Cooling B	0.09852	0.1300	24.92	5.212	19.72	5.071
	0.09861	0.1300	24.82	5.645	19.86	5.356
	0.09859	0.1299	24.86	6.007	19.81	5.579
	0.09859	0.1299	24.79	6.311	19.90	5.779
	0.09846	0.1299	24.88	6.607	19.89	5.922
Heating H1	0.09941	0.1318	32.00	3.643	11.28	3.377
	0.09875	0.1317	31.94	3.951	10.37	3.510
	0.09878	0.1317	31.97	4.293	10.23	3.688
	0.09872	0.1316	31.91	4.545	10.18	3.847
	0.09873	0.1316	31.90	4.831	10.13	3.976

^*k=2, 95% confidence interval

Table A1(d).

Experimental data–HTF-side computed metrics

	cp,HTF,c	cp,HTF,e	Q̇cool,HTF	Q̇heat,HTF	Q̇ins,HTF,c	Q̇ins,HTF,e
	kJ·kg−1·K−1	kJ·kg−1·K−1	kW	kW	kW	kW
*	±3 %	±3 %	±0.05	±0.05	±10 %	±10 %
Cooling A	4.18	2.59	1.56	2.002	0.081	0.030
	4.18	2.59	1.538	2.013	0.081	0.026
	4.18	2.59	1.660	2.213	0.083	0.023
	4.18	2.59	1.724	2.366	0.082	0.027
	4.18	2.59	1.853	2.613	0.085	0.031
Cooling B	4.18	2.59	1.737	2.178	0.030	0.030
	4.18	2.59	1.838	2.353	0.025	0.036
	4.18	2.59	1.915	2.502	0.024	0.040
	4.18	2.59	1.978	2.631	0.029	0.035
	4.18	2.59	2.025	2.754	0.033	0.034
Heating H1	4.18	2.58	1.218	1.584	0.069	0.071
	4.18	2.58	1.27	1.699	0.067	0.079
	4.18	2.58	1.331	1.842	0.069	0.080
	4.18	2.58	1.385	1.945	0.068	0.082
	4.18	2.57	1.430	2.063	0.069	0.083

^*k=2, 95% confidence interval

Table A2(a).

CYCLE_D-HX simulations–reference run inputs

Heat Exchangers
Type	RSF	THTF,c,in	THTF,c,out	THTF,c,in	THTF,c,out	LMTDc	LMTDe	ΔPc	ΔPe	SC	SH	IDtube	Ltube	#tube,c	#tube,e	#cir
--	--	°C	°C	°C	°C	K	K	kPa	kPa	K	K	m	m	--	--	--
Counter	Enhanced	33.89	39.04	20.22	15.41	8.46	9.08	32.96	44.64	4.36	5.00	0.00846	0.5588	12	10	1

Compressor				Vapor Lines		Auxiliary Power
ηs	ηv	ηm	Q̇cool	ΔTdew,suc	ΔTdew,dis	Ẇfan,indoor	Ẇfan,outdoor	Ẇcontrols
--	--	--	kW	°C	°C	kW	kW	kW
0.46	0.49	1.00	1.69	1.14	0.06	0.00	0.00	0.00

Table A2(b).

CYCLE_D-HX–reference run results

	COPcool	Rtube + RHTF	factorΔP
	--	K·kW−1	--
Condenser	2.794	2.1686	4.329
Evaporator	3.07	4.3507	2.187

Table A3(a).

CYCLED-HX simulations–inputs

		Heat Exchangers						Compressor				Vapor lines		Auxiliary Power
	Ncomp*	THTF,c,in	THTF,c,out	THTF,e,in	THTF,e,out	SC	SH	ηs	ηv	ηm	Q̇cool	ΔTdew,s	ΔTdew,d	Ẇfan,indoor	Ẇfan,outdoor	Ẇcontrols
	rev·min−1	°C	°C	°C	°C	K	K	--	--	--	kW	°C	°C	kW	kW	kW
Cooling A	1426	33.86	38.49	19.64	15.09	3.39	3.90	0.520	0.562	1.00	1.587	0.86	0.05	0	0	0
	1609	33.84	38.56	20.2	15.77	3.27	5.93	0.468	0.481	1.00	1.569	0.88	0.05	0	0	0
	1810	33.89	39.04	20.22	15.41	4.36	5.00	0.463	0.486	1.00	1.693	1.14	0.06	0	0	0
	2005	33.88	39.46	20.32	15.35	3.44	6.83	0.457	0.484	1.00	1.763	1.36	0.06	0	0	0
	2231	33.84	39.93	19.98	14.56	3.39	3.90	0.460	0.524	1.00	1.889	1.90	0.08	0	0	0
Cooling B	1429	24.92	30.13	19.72	14.65	2.69	3.31	0.508	0.629	1.00	1.771	1.10	0.08	0	0	0
	1628	24.82	30.47	19.86	14.51	2.71	5.42	0.497	0.618	1.00	1.873	1.42	0.09	0	0	0
	1829	24.86	30.87	19.81	14.23	3.08	5.70	0.483	0.605	1.00	1.949	1.69	0.10	0	0	0
	2032	24.79	31.11	19.90	14.13	3.38	6.82	0.475	0.589	1.00	2.017	1.95	0.10	0	0	0
	2234	24.88	31.48	19.89	13.97	3.21	5.86	0.457	0.573	1.00	2.061	2.24	0.11	0	0	0
Heating H1	1430	32.00	35.64	11.28	7.902	1.79	5.75	0.521	0.538	1.00	1.236	0.70	0.04	0	0	0
	1628	31.94	35.89	10.37	6.861	1.95	5.83	0.511	0.533	1.00	1.291	1.01	0.05	0	0	0
	1832	31.97	36.26	10.23	6.546	1.99	3.29	0.482	0.521	1.00	1.356	1.23	0.05	0	0	0
	2032	31.91	36.46	10.18	6.336	2.12	4.87	0.473	0.510	1.00	1.408	1.43	0.05	0	0	0
	2233	31.90	36.73	10.13	6.158	2.42	3.38	0.452	0.495	1.00	1.454	1.63	0.06	0	0	0

^*Compressor speed is not an input to the model, but is listed here to help the reader correlate model inputs to experimental data

Table A3(b).

CYCLED-HX simulations–results

	Ncomp*	COPcool	COPheat	Pc,in1	ΔPc	Pe,out2	ΔPe	Q̇cool	Q̇ heat	Qvol,cool	Qvol,heat	Ẇcomp,r
	rev·min−1	--	--	kPa	kPa	kPa	kPa	kW	kW	kJ·m−3	kJ·m−3	kW
Cooling A	1426	3.238	4.238	1118	30.64	369.6	40.92	1.59	2.081	2589	3389	0.4911
	1609	3.025	4.025	1113	29.29	380.0	37.96	1.57	2.089	2673	3557	0.5189
	1810	2.794	3.794	1136	32.96	367.4	44.65	1.69	2.295	2560	3476	0.6049
	2005	2.674	3.674	1146	35.25	360.4	49.24	1.76	2.419	2462	3383	0.6583
	2231	2.414	3.414	1168	40.69	338.4	61.07	1.89	2.672	2227	3149	0.7828
Cooling B	1429	3.967	4.967	901.7	41.32	353.5	43.14	1.764	2.208	2634	3298	0.4446
	1628	3.678	4.678	911.8	44.4	344.2	48.25	1.867	2.375	2526	3212	0.5077
	1829	3.339	4.339	925.1	47.29	334.3	53.34	1.947	2.53	2422	3147	0.5831
	2032	3.151	4.151	932.9	49.49	327.6	57.11	2.017	2.657	2349	3095	0.6402
	2234	2.954	3.954	943.7	51.71	322.1	61.24	2.057	2.753	2269	3037	0.6963
Heating H1	1430	2.924	3.924	1016	21.67	298.0	32.93	1.24	1.664	2103	2822	0.4241
	1628	2.691	3.691	1024	23.29	282.8	37.36	1.29	1.769	1962	2692	0.4795
	1832	2.409	3.409	1038	26.22	274.1	43.61	1.36	1.925	1869	2645	0.5646
	2032	2.295	3.295	1044	27.46	268.2	46.65	1.41	2.024	1814	2605	0.6143
	2233	2.135	3.135	1053	29.14	263.1	50.53	1.45	2.129	1760	2585	0.6792

^*Compressor speed is not an input to the model, but is listed here to help the reader correlate model inputs to experimental data

¹corresponds to P₄ in Figure A.1

²corresponds to P₁₁ in Figure A.1

NOMENCLATURE (APPENDIX)

c_p

specific heat at constant pressure (kJ·kg⁻¹·K⁻¹)

COP

coefficient of performance

factor_Δp

pressure drop multiplication factor (dimensionless)

ID

inner diameter of tube (m)

LMTD

log-mean temperature difference (K)

ṁ

mass flow (kg·s⁻¹)

N

speed (rev·min⁻¹)

P

pressure (kPa)

Q̇

cooling or heating capacity (kW)

Q_vol

volumetric capacity (kJ·m⁻³)

R

heat transfer resistance (K·W⁻¹)

RSF

refrigerant side feature (e.g., microfins, insert)

SC

condenser outlet subcooling (°C)

SH

evaporator outlet superheat (°C)

T

temperature (K, °C)

ΔP

pressure drop (kPa)

ΔT

temperature difference (K)

Ẇ

power (kW)

Ẇ_comp.r

compressor power, computed using the refrigerant mass flow and enthalpy change across compressor (kW)

#

number of (tubes, tube circuits, etc.)

1 to 11

thermodynamic states, see Figure A.1

Greek letters

η

efficiency (decimal fraction)

τ

torque (N·m)

Subscripts

c

condenser

comp

compressor

cool

cooling

controls

heat pump controls

dew

dew-point (saturated vapor point)

dis

discharge line

e

evaporator

fan

fan for indoor/outdoor heat exchanger

heat

heating

HTF

heat transfer fluid, or calculated/measured on the HTF side

in

inlet

indoor

inside the building

ins

heat leak to ambient air through HTF outer tube and insulation

m

compressor motor efficiency

outdoor

outside the building

r

refrigerant, or calculated/measured on the refrigerant-side

s

compressor isentropic efficiency

suc

suction line

tube

tube separating refrigerant and HTF

v

compressor volumetric efficiency

1 to 11

thermodynamic states, see Figure A.1