Abstract
The receptive fields of many auditory cortical neurons are multidimensional and are best represented by more than one stimulus feature. The number of these dimensions, their characteristics, and how they differ with stimulus context have been relatively unexplored. Standard methods that are often used to characterize multidimensional stimulus selectivity, such as spike-triggered covariance (STC) or maximally informative dimensions (MIDs), are either limited to Gaussian stimuli or are only able to recover a small number of stimulus features due to data limitations. An information theoretic extension of STC, the maximum noise entropy (MNE) model, can be used with non-Gaussian stimulus distributions to find an arbitrary number of stimulus dimensions. When we applied the MNE model to auditory cortical neurons, we often found more than two stimulus features that influenced neuronal firing. Excitatory and suppressive features coded different acoustic contexts: excitatory features encoded higher temporal and spectral modulations, while suppressive features had lower modulation frequency preferences. We found that the excitatory and suppressive features themselves were sensitive to stimulus context when we employed two stimuli that differed only in their short-term correlation structure: while the linear features were similar, the secondary features were strongly affected by stimulus stimulus. These results show that multidimensional receptive field processing depends on feature type and stimulus context.
INTRODUCTION
The spectrotemporal receptive fields (STRFs) of auditory cortical neurons have been extensively studied in recent years (Blake and Merzenich, 2002, Elhilali et al., 2004, Gourevitch et al., 2009). The standard approach has been to estimate a single spectrotemporal feature in conjunction with a static nonlinearity (Chichilnisky, 2001). The feature may be seen as a stimulus that drives the neuron to respond, or it may be interpreted as a descriptor of neuronal stimulus processing (Sharpee et al., 2004). The single feature STRF description has provided important insights, though in recent years it has become apparent that many auditory cortical neurons simultaneously encode information about more than one stimulus feature in their spiking activity, and thus the single feature may not reveal the true richness of auditory cortical processing (Atencio et al., 2008, 2009, 2012, Harper et al., 2016, Kozlov and Gentner, 2016).
Multiple stimulus features can be estimated through dimensionality reduction techniques such as spike-triggered covariance (STC) and maximally informative dimensions (MID). STC accounts for pairwise stimulus interactions and can be applied in conjunction with Gaussian stimuli (Paninski, 2003, Samengo and Gollisch, 2013). The STC approach decomposes a spike-triggered stimulus covariance matrix into a set of eigenvectors (or stimulus features), where the contribution of each eigenvector is determined by the corresponding eigenvalue. Each feature can be classified as excitatory (increases neural responsiveness) or suppressive (decreases neural responsiveness) by examining the corresponding eigenvalue (Touryan et al., 2002, Rust et al., 2005, Chen et al., 2007). A more stimulus-robust approach is maximally informative dimension (MID) analysis (Kouh and Sharpee, 2009). MID analysis can be used with any stimulus type, making it useful when analyzing responses to naturalistic stimulation. However, though the MID procedure can account for all stimulus correlations, it is limited to identifying two or a small number of stimulus features due to the limits of data collection in standard physiological experiments (Rowekamp and Sharpee, 2011).
The tradeoff between stimulus type and filter number can be bridged by constraining the neural model. By assuming a functional form for the nonlinear input/output function, and by accounting for a restricted subset of stimulus statistics, an increased number of filters may be estimated. A recently developed approach, the maximum noise entropy (MNE) model, is able to account for the first and second order stimulus correlations that drive a neuron to fire. The MNE model produces an unbiased estimate of stimulus processing because it does not make assumptions regarding the input statistics, and parameter optimization is accomplished using maximum likelihood (Fitzgerald et al., 2011a, Fitzgerald et al., 2011b). For non-specified higher-ordered correlations, the model remains as unbiased as possible. Thus, the MNE model can recover multiple features that account for the linear and pairwise correlations in the stimulus while remaining maximally uncommitted toward other stimulus correlations.
We applied the MNE approach to study the neural coding of auditory cortical neurons. We show that responses of auditory cortical neurons are affected by multiple excitatory or suppressive features and identify a specific relationship between the relevant features. We found that excitatory features encode finer temporal and spectral details compared to the broader contexts encoded by suppressive filters. We further found that the number of identifiable features depended on stimulus context. Thus, our results show that stimulus processing depends on feature type and stimulus context.
MATERIALS AND METHODS
Surgical procedures
All experimental procedures were approved by the University of California, San Francisco Committee for Animal Research under protocol AN086113-01B. The experimental procedures used in this study have been previously described (Atencio and Schreiner, 2010b, a). Briefly, young female adult cats (N=4) were given an initial dose of ketamine (22 mg/kg) and acepromazine (0.11 mg/kg), and then anesthetized with pentobarbital sodium (Nembutal, 15–30 mg/kg) during the surgical procedure. The animal’s temperature was maintained with a thermostatic heating pad. Bupivacaine was applied to incisions and pressure points. Surgery consisted of a tracheotomy, reflection of the soft tissues of the scalp, craniotomy over AI, and durotomy. After surgery, to maintain an areflexive state, the animal received a continuous infusion of ketamine/diazepam (2–5 mg/kg/h ketamine, 0.2–0.5 mg/kg/h diazepam in lactated Ringer solution).
Recording
With the animal inside a sound-shielded anechoic chamber (IAC, Bronx, NY), stimuli were delivered via a closed speaker system to the ear contralateral to the exposed cortex (electrostatic diaphragms, model SRX MK3, from Stax, Japan). The system frequency transfer function was nearly flat (+/− 6dB) for frequencies <= 14 kHz, and attenuated 10 dB/octave for frequencies above 14 kHz.
Extracellular recordings were made using linear multi-channel silicon recording probes, which were provided by Neuronexus (Michigan). We used probes with channel impedances between 2 and 3 MΩ, since these impedances allowed us to resolve single units. Probes were carefully inserted using a microdrive (David Kopf Instruments, Tujunga, CA) into the center of the ectosylvian gyrus, allowing for recording away from the anterior and posterior ectosylvian sulci. The cortical depth position of each recorded neuron was estimated from microdrive readings, which have previously been shown to allow for accurate laminar estimates (Atencio and Schreiner, 2010b).
Neural traces were bandpass filtered between 0.6 and 6 kHz and recorded to disk with a Neuralynx Cheetah A/D system at sampling rates between 18 kHz and 27 kHz. The traces were sorted off-line with a Bayesian spike sorting algorithm (Lewicki, 1994, 1998, Atencio and Schreiner, 2013). The average over the entire recording trace was estimated, and only events in the traces that exceeded the average by 5 RMS noise levels were used in the spike sorting procedure (termed spike events). All recording locations were in AI, as verified through initial multi-unit mapping and determined by the layout of the tonotopic gradient and bandwidth modules on the crest of the ectosylvian gyrus (Imaizumi and Schreiner, 2007).
Stimulation
All neurons were also probed with a broadband (0.5 – 40 kHz) dynamic moving ripple (DMR) stimulus (Escabi and Schreiner, 2002, Atencio et al., 2008). The maximum spectral modulation frequency of the DMR was 4 cyc/oct, and the maximum temporal modulation frequency was 40 cyc/s (Escabi and Schreiner, 2002). The maximum modulation depth of the spectrotemporal envelope was 40 dB. Mean intensity was set at 30–50 dB above the average pure tone threshold. A subset of neurons was probed with a ripple noise (RN) stimulus. The RN is the sum of 16 independently created DMRs, and therefore it has the same carrier structure and modulation depth as the DMR. The RN and DMR differ in short-term, but not long-term, correlations: the DMR has short-term correlations but no long-term correlations, while the RN has neither short-term nor long-term correlations (Escabi and Schreiner, 2002). The duration of each stimulus was either 10 minutes or 15 minutes.
Receptive field estimation and analysis
The stimulus envelope was sampled at 5 ms resolution in time and 6 carriers per octave in frequency. For each neuron, we first chose a set of 25 frequencies and 20 time bins that encompassed the stimulus bandwidth and history to which the neuron responded (500 stimulus dimensions per feature). We then applied the binary noise maximum noise entropy (MNE) analysis described in (Fitzgerald et al., 2011a, Fitzgerald et al., 2011b). The MNE analysis code is available on Github: http://github.com/MarvinT/pyMNE. Briefly, for a given stimulus s, the probability of a spiking response was modeled through a logistic nonlinearity having the form:
The parameters a, h, and J were estimated so that the model matched the experimentally observed mean firing rate, the spike-triggered average (STA) statistics, and spike-triggered covariance (STC) statistics. Maximum likelihood estimation was used to determine a, h, and J while remaining as unbiased as possible otherwise. Compared to a and h alone, including J in the model improved the negative log-likelihood objective function values by approximately 30% (mean=28.9%, SE = 3.3%, N=75) over the population of neurons.
Data was divided into two sets for training and testing. The training set contained 75% of the data, and the test contained 25%. This allowed the MNE model to be estimated four times for each neuron. The final model was the average of the four estimates. The MNE procedure maximizes the noise entropy of the model while satisfying the STA and STC constraints, which is equivalent to minimizing the mutual information between the stimulus and the response, since the model only includes the contributions of the mean firing rate, STA, and STC constraints. After J was estimated, it was decomposed into a set of quadratic features by applying principal components analysis, which produced a set of eigenvalues/eigenvectors. Positive eigenvalues signify excitatory features (increase the response of the neuron), while negative eigenvalues represent suppressive stimulus features (decrease the response of the neuron).
To determine significance, the spike train for each neuron was randomly circularly shifted between 25% and 75% of the stimulus period, and the MNE model was recomputed. Two random shifts were used, resulting in 1000 eigenvalues from the randomization process. The actual eigenvalue distribution was compared to the randomized distribution. Values from the actual eigenvalue distribution that exceeded all eigenvalues from the randomized distribution were deemed statistically reliable and were included in analyses.
The ripple transfer function (RTF) describes the modulation of energy in a filter as a function of temporal (TMF) and spectral modulation frequency (SMF). To obtain the RTF, we first estimated the 2D FFT of the filter, and then folded the result about the TMF = 0 Hz axis. To obtain the temporal modulation transfer function, the RTF was summed across SMF, and the spectral MTF was RTF summed across TMF. The best modulation frequency for an MTF was the peak in the MTF for bandpass MTFs, and it was the midpoint between 0 frequency and the 3 dB cutoff for lowpass MTFs.
To estimate the frequency preference of a filter we calculated the center of mass. Best frequency estimates were not used due to the complex structure of many of the filters. For a filter, negative values were first set to zero. Next, the filter was summed from t=0 to t=50 ms to encompass the excitatory subfields of interest, resulting in a distribution having amplitude as a function of frequency. Last, the center of mass was calculated as , where f(i) is ith frequency, and a(i) is the corresponding amplitude value of the distribution.
Receptive field estimates and statistical measures were compared across the four subjects. No statistically reliable differences were identified between the four populations of neurons from the four subjects (N=13, 5, 14, 43), and therefore the data were combined for the analyses presented in this report.
Analyses were carried out using Matlab 2013a (Mathworks, Inc.) and associated toolboxes. MNE analysis was implemented using custom programs. For statistical analyses, the functions signrank.m, kstest2.m, and corrcoef.m were used for Wilcoxon Signed-rank tests, Kolmogorov-Smirnov tests, and correlation coefficient estimates, respectively.
RESULTS
One of the challenges of sensory neuroscience is to identify the functional sets of inputs that influence a neuron’s responsiveness. A given cortical neuron may receive many inputs, and these will be activated by specific stimulus features (Chen et al., 2011). The goal, then, is to identify the functional consequences of the inputs, where each set of inputs is functionally represented by a stimulus feature, or dimension, that influences neural firing (Chen et al., 2007). It is unlikely that a single functional descriptor, or single STRF, will be adequate to capture the neural processing resulting from the multiple cell types and connectivity patterns that impose themselves on each neuron (Klein et al., 2000, Theunissen et al., 2000, Atencio et al., 2009, Sharpee et al., 2011).
To assess the multidimensional nature of auditory cortical receptive fields, we employed the recently developed maximum noise entropy (MNE) model (Fitzgerald et al., 2011a, Fitzgerald et al., 2011b). The MNE analysis has been verified on model data, showing that the procedure can recover multiple model features from non-Gaussian stimuli (Fitzgerald et al., 2011a, Fitzgerald et al., 2011b). The MNE model allowed us to obtain a linear filter and a covariance matrix that matches the linear and pairwise stimulus interactions that best account for a neuron’s responses. The linear stimulus filter, or stimulus feature, in the model is analogous to the spike-triggered average (STA; the median/median absolute deviation (MAD) correlation between the linear filter and STA was: 0.9923/0.0031). The covariance matrix, which captures the second-order statistics, is analogous to the spike-triggered covariance (STC)(Schwartz et al., 2006, Aljadeff et al., 2013). The covariance matrix can be decomposed into a set of eigenvectors and eigenvalues, where the eigenvectors represent stimulus features and the eigenvalues represent the relative contribution of each eigenvector. Thus, this model of neural processing allows us to identify multiple functional inputs for a given neuron.
To assess the dimensionality of auditory cortical receptive fields, we recorded from 75 neurons in the thalamo-recipient granular layers (600–1000 μm) of cat AI and presented dynamic moving ripple (DMR) stimulation. Across the population, the DMR stimulus drove neurons at approximately 4 Hz (mean/se: 3.8/0.5 spikes/s). Figure 1 shows the complete MNE analysis for a single neuron. The STA-like linear feature shows clear spectrotemporal structure, with oriented excitatory and suppressive subfields that model the frequency sweep selectivity that may be seen in auditory cortical neurons (Fig. 1A). The covariance matrix (Fig. 1B) has eigenvalues that are tightly packed, with the exception of the most negative and most positive eigenvalues (Fig. 1,C). The eigenvalues can be tested for significance (Fig. 1C, red lines correspond to p < 0.002, randomization test) to determine which stimulus features significantly contributed to the neural response. The eigenvectors corresponding to significant eigenvalues are shown Fig. 1 (D,E).
Figure 1.
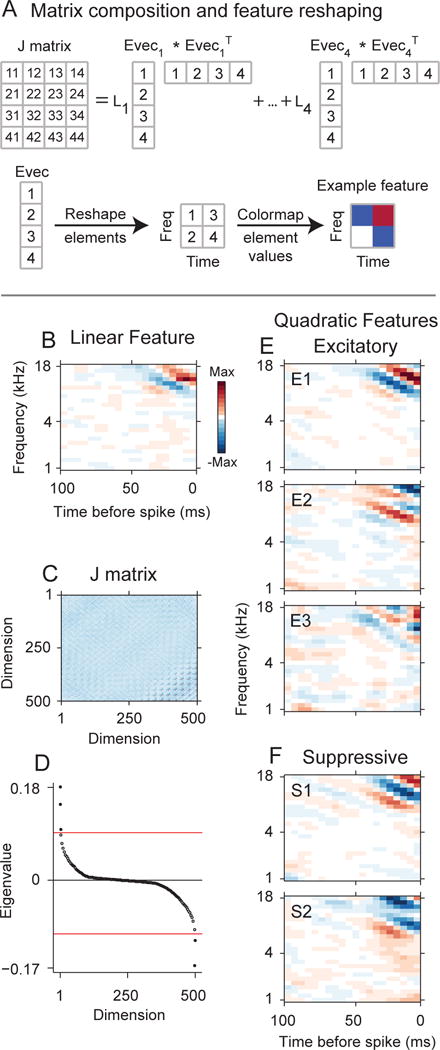
MNE model of a primary auditory cortical (AI) neuron. The model accounts for the linear and quadratic stimulus statistics that account for the response (analogous to the spike-triggered average (STA) and spike-triggered covariance (STC) distributions, respectively). (A) Simplified cartoon showing the composition of the J matrix, which contains the quadratic stimulus interaction that account for the response. In this simplified case sound stimulus spectrograms have 2 frequencies and 2 time bins. (A,Top) The J matrix may be decomposed into a set of eigenvalues (L1, …,L4) and corresponding eigenvectors (Evec1, …, Evec4). Numerals in the matrix and vectors indicate element numbers. Values in J indicate row/column pairs. Example: 32 represents the element at row 3, column 2 in J. (A,Bottom) Each eigenvector may be reshaped into a spectrotemporal stimulus feature. In this simplified example the eigenvector has four elements and is reshaped into a 2×2 matrix. The matrix values are color-mapped to display spectrotemporal structure. (B–F) MNE model for a primary auditory cortical neuron. (B) The linear feature has subfields oriented in frequency and time. (C) The J matrix was decomposed, and (D) five significant eigenvalues (p < 0.01, randomization test, red-line) were found, resulting in five spectrotemporal features that account for the neuron’s response. (E) Three excitatory spectrotemporal features (increase neural responsiveness). E1: most significant excitatory feature, E2: second-most significant feature, etc. (E) Two suppressive spectrotemporal features (decrease neural responsiveness).
A significant advance is that the eigenvectors may be examined for spectrotemporal structure and whether they excite or suppress neural responsiveness. In this context excitation and suppression relate to how the feature affects neuronal responsiveness. While the feature subfields may be classified as excitatory and suppressive, the eigenvector analysis generalizes this to the overall spectrotemporal pattern of the feature, and not just the component subfields. Thus, the eigenvectors in Fig. 1(D,E) have clear spectrotemporal structure, and each may have either an excitatory or suppressive effect on the neuron’s response. Excitatory spectrotemporal features (Fig. 1D) are features that increase the responsiveness of the neuron and they are associated with positive eigenvalues. The frequency extent of the excitatory eigenvector subfields covered a similar range as the linear filter. Comparing the excitatory frequency center of masses for the most significant excitatory quadratic feature to the linear filter revealed a statistically reliable correlation (r = 0.69, p<0.001, d.o.f = 68, t-statistic = 7.84).
Significantly, the eigenvalue analysis can also recover the stimulus features that suppress neural responsiveness (Fig. 1E). Suppressive features have been observed in visual cortex (Rust et al., 2005, Chen et al., 2007), though rarely in the auditory system (though see (Harper et al., 2016, Kozlov and Gentner, 2016). For the neuron in Fig. 1, we recovered two suppressive spectrotemporal features. The suppressive nature applies to the complete spectrotemporal pattern of the feature. Thus, while each feature may have suppressive components, such as suppressive frequency sidebands, it is the complete time-frequency distribution that accounts for the neuron’s decrease in responsiveness. Thus, suppressive spectrotemporal features generalize the standard suppressive subfields of AI neural receptive fields, and the number of features generalizes the one-dimensional single feature STRF that is commonly identified.
Another example also revealed multidimensional feature selectivity (Fig. 2). The linear component or STA-analogous component contains well defined spectrotemporal features, with a main excitatory subfield surrounded by suppressive subfields in both time and frequency. When we diagonalized the quadratic matrix into eigenvalues/eigenvectors, we found eight additional significant spectrotemporal filters. Five of the features were excitatory, and three were suppressive. Thus, for this neuron, an extended set of spectrotemporal features were needed to describe the acoustic processing of the neuron.
Figure 2.
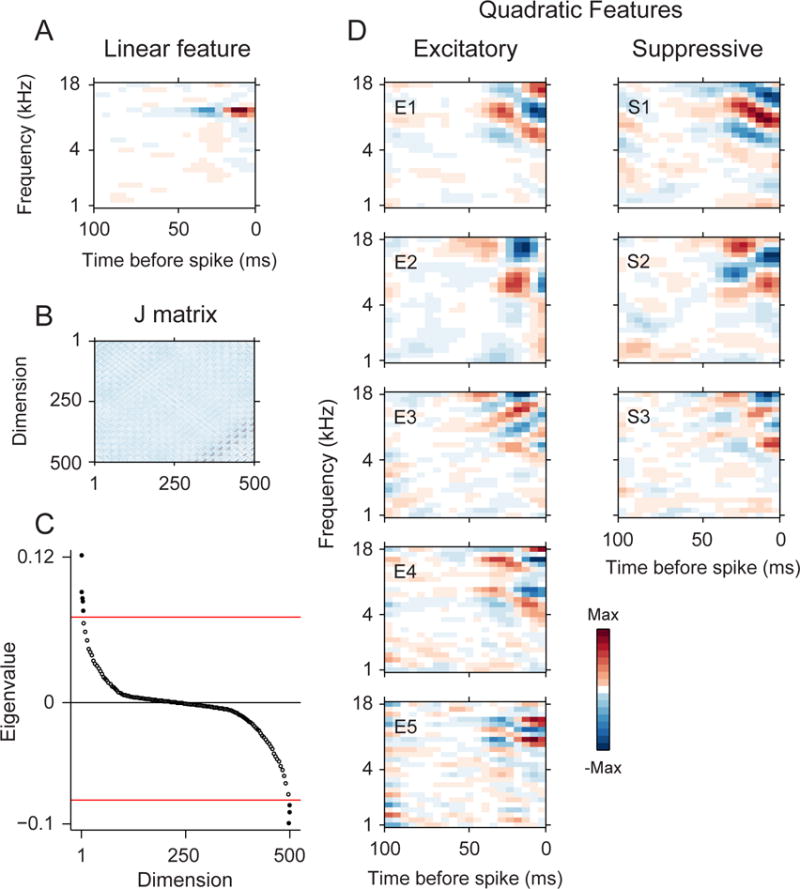
Example MNE model results for AI neuron. (A) The linear feature has circumscribed subfields. (B) The J matrix revealed (C) eight significant eigenvalues (p < 0.01, randomization test). (D) The significant eigenvalues corresponded to five excitatory stimulus features and four suppressive features.
What is the dimensionality of auditory cortical neurons? We determined this by noting the number of significant eigenvectors from the covariance analysis. For our sample of neurons, we identified between 2 and 16 spectrotemporal features that significantly affected the responses of neurons in our data (Fig. 3A; median = 6.0; MAD = 3.0). However, since our stimulus set was restricted, and because our significance level was conservative, the total number of features for cat AI neurons could be even higher. The number of excitatory filters was between 2 and 14, with most between four and eight (Fig. 3B; median = 3.0; MAD = 2.0). For suppressive filters, most neurons had between zero and four filters (Fig. 3D; median = 1.0; MAD = 1.0). Across all neurons, the number of excitatory filters always exceeded the number of suppressive filters (Fig. 3C). Thus, the stimulus selectivity of auditory cortical processing may be described with multiple stimulus features.
Figure 3.
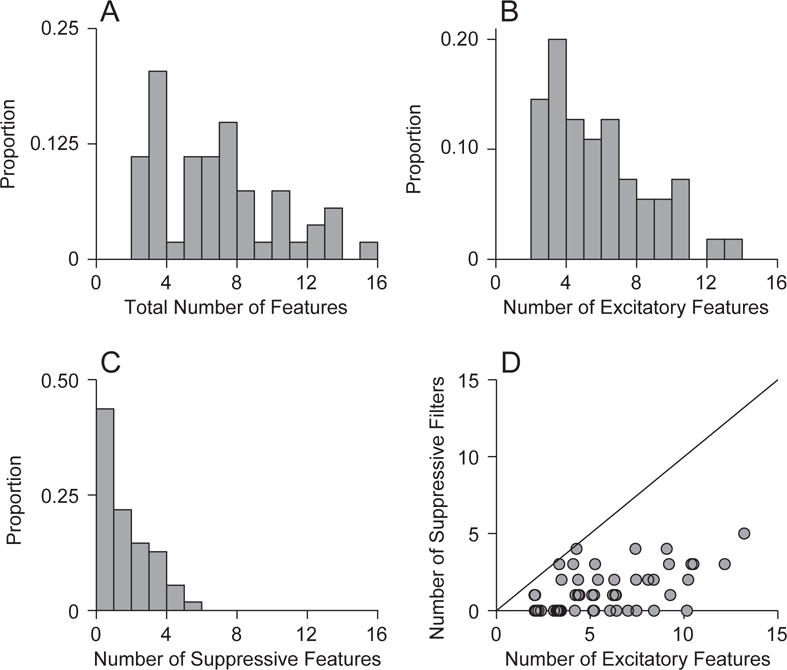
Number of spectrotemporal stimulus features. (A) AI neurons had between two and sixteen features, with the majority having four to ten. (B) Number of excitatory features. (C) Number of suppressive features. (D) The number of excitatory features was greater than the number of suppressive features.
What acoustic information is contained in the excitatory and suppressive features? To address this, for each neuron we examined the modulation processing of each quadratic feature (Atencio and Schreiner, 2010b). For each feature, we first calculated the Fourier transform to obtain the ripple transfer function (RTF). The RTF describes the modulation of energy in the feature as a function of time and frequency (Fig. 4A). We summed across spectral modulation frequency to obtain the temporal modulation transfer function (TMTF), and we summed across temporal modulation frequency to obtain the spectral modulation transfer function (SMTF). Features with well-defined excitatory and suppressive subfields have bandpass TMTFs and SMTFs, from which the best modulation frequency (BMF) may be inferred (Fig. 4A, last two columns, inset values). For neurons with multiple features, MTFs may be estimated for each feature (Fig. 4B). Excitatory features often had TMTFs and SMTFs (Fig. 4C,D) that were shifted to higher modulation frequencies compared to suppressive features (Fig. 4E,F).
Figure 4.
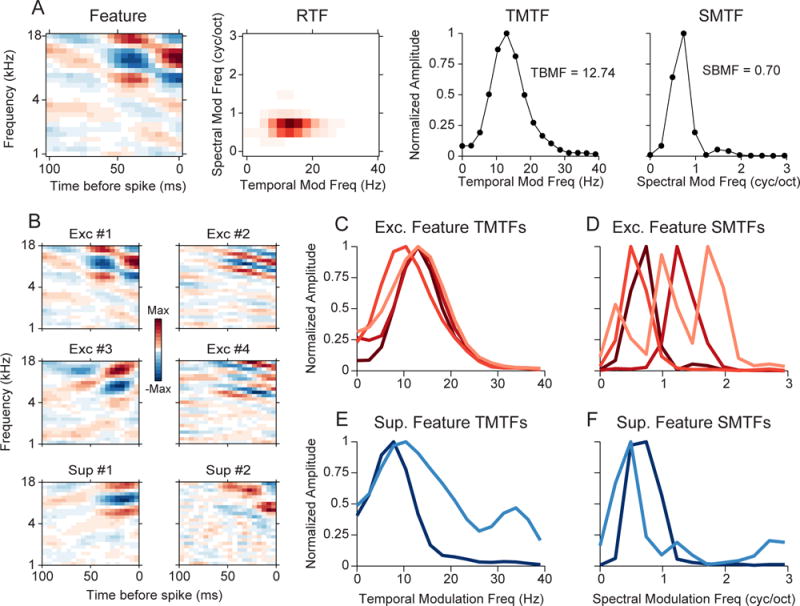
Modulation content of quadratic features. (A) Procedure for characterizing the modulation content of a feature. Each spectrotemporal feature is transformed to a ripple transfer function (RTF). The RTF is summed across spectral and temporal modulation frequency to obtain the temporal and spectral modulation transfer function (TMTF,SMTF), respectively. Best temporal and spectral modulation frequencies are noted in each plot. (B) Quadratic features for a single neuron. (C) TMTFs for the excitatory features in (B). (D) SMTFs for the excitatory features in (B). (E) TMTFs for the suppressive features. (F) SMTFs for the suppressive features.
For each neuron in our distribution, we estimated the TBMF and SBMF for each feature. Across all features, the distribution of TBMFs covered similar ranges for the excitatory and suppressive features. However, though there was a higher proportion of suppressive features that had lower TBMFs (Fig. 5A; p<0.0001, KS-test, KS statistic = 0.334, Nexc filters = 293, Nsup filters = 66). The distribution of SBMFs revealed that excitatory features had consistently higher preferred spectral modulation frequencies (Fig. 5B; p<0.0001, KS-test, KS statistic = 0.315, Nexc filters = 293, Nsup filters = 66).
Figure 5.
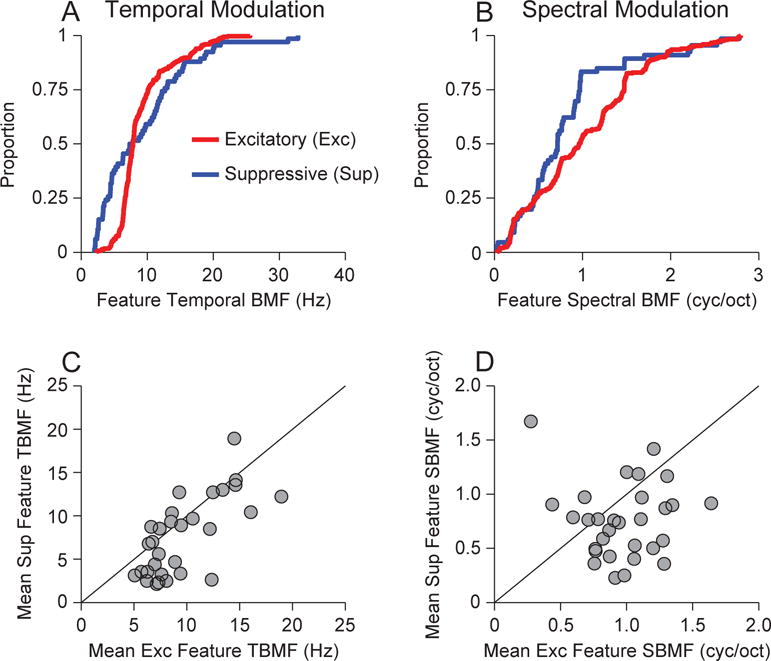
Best modulation frequency for excitatory and suppressive features. (A) Population distribution of best temporal modulation frequencies (TMFs) over all features and neurons. (B) Population distribution of best spectral modulation frequencies (SMFs) over all features and neurons. (C) Mean of best TMFs for excitatory features and suppressive features. Each point represents one neuron, and the value is the mean across all best TMFs. (D) Mean of best SMFs for excitatory and suppressive features.
Since the complete distribution does not maintain neural identity, we compared the BMFs of excitatory and suppressive on an individual neuron basis. For neurons that had both excitatory and suppressive filters we estimated the mean of the BMFs for excitatory features and compared this to the mean of suppressive feature BMFs.
We found that the distributions of temporal BMFs for excitatory and suppressive features were significantly different. On a neuron-by-neuron basis, the mean TBMFs for excitatory features were higher than the mean TBMFs for suppressive features (p = 0.0128, Signed-rank test, signed-rank statistic = 375, N=31). Thus, in aggregate, excitatory features contain faster variations of energy in time; alternatively, suppressive features have longer lasting subfields.
For spectral modulation, the neuron-by-neuron BMF analysis revealed that excitatory features coded spectral modulations that were higher than those for suppressive features (p = 0.0177, Signed-rank test, signed-rank statistic = 369, N = 31). Since spectral modulation correlates with tuning bandwidth (lower spectral modulations correlate with broader tuning), this implies that excitatory features have bandwidths and subfield spacings that are narrower and sharper than those of the suppressive features (Calhoun and Schreiner, 1998, Atencio and Schreiner, 2012). This may also be interpreted as revealing that excitatory features represent fine frequency details, while suppressive features provide a broader contextual analysis of frequency integration.
Does the structure and number of excitatory and suppressive features depend on stimulus statistics? We examined this by presenting two stimuli that had identical long-term statistics and different short-term statistics. For a subset of neurons (N=11), we presented both a dynamic moving ripple (DMR; Fig. 6A) and a ripple noise (RN; Fig. 6B) stimulus. The RN was composed of 16 independently created DMRs added together. Thus, the carrier frequency spacing in the RN is identical to the DMR (Escabi and Schreiner, 2002). However, the DMR contains local correlations while the RN does not. The response strength of the neurons was moderately matched for the two stimuli, with a weakly higher overall rate for the RN stimulus (DMR firing rate mean/se = 10.1/2.1 Hz; RN firing rate mean/se = 14.9/2.3; Signed-rank test: p = 0.0537, signed-rank statistic = 11).
Figure 6.
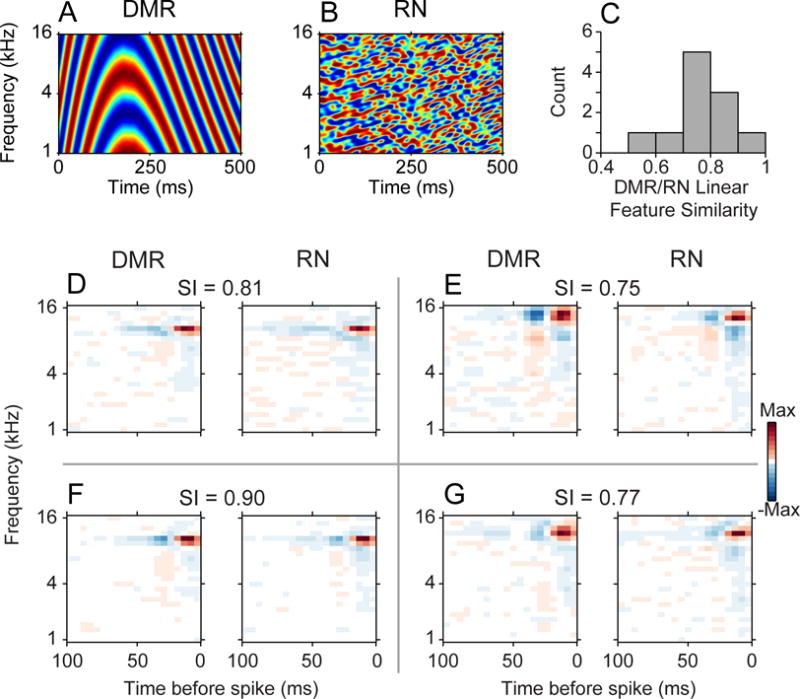
Stimulus distributions and linear stimulus features. Spectrotemporal envelope of (A) Dynamic moving ripple (DMR) and (B) Ripple Noise (RN) stimuli. Both stimuli were both presented to a subset of neurons. (C) Similarity, or correlation, between the linear features for DMR and RN stimuli were high. (D–G) Example linear features for neurons that received both DMR and RN stimulation. The features for each neuron were similar for the two types of stimuli. The similarity index (SI) values indicate the correlation between each pair of DMR and RN linear features.
When we examined the receptive fields of neurons to these stimuli we found that the linear features (analogous to STAs) were largely similar (Fig. 6C). Features derived from the DMR had clear subfields, and features derived from RN had nearly matched subfields. Over the sample of neurons, the correlation between the linear features was always above 0.5, indicating very strong agreement between the spectrotemporal structure of both DMR and RN linear features.
If the linear features are similar, do the DMR and RN statistics induce changes in features derived from the quadratic kernel? We found drastic changes between the features for DMR and RN stimulation. For the example in Figure 7 (top), by using the DMR we were able to reconstruct multiple excitatory (Nexc = 7) and suppressive (Nsup = 3) features. Each feature had subfields that were localized in both time and frequency. In contrast, using the RN we were only able to obtain two excitatory features.
Figure 7.
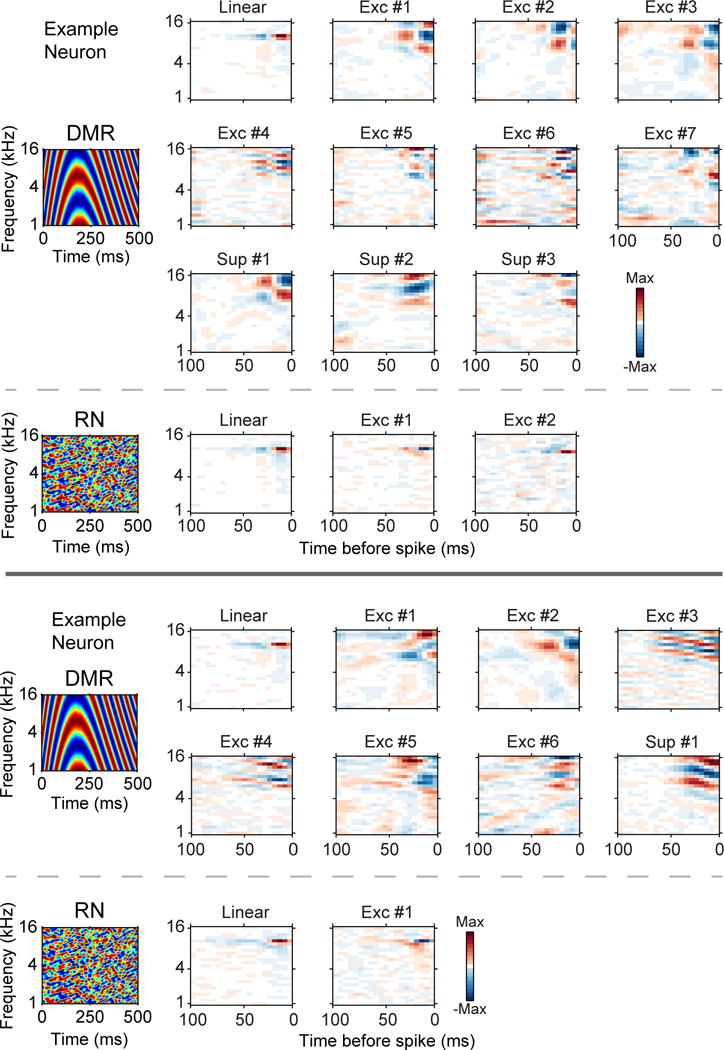
DMR and RN stimulation examples. Receptive field reconstruction for DMR and RN stimulation for two neurons. Top: DMR stimulation allowed 7 excitatory and 3 suppressive filters to be obtained. RN stimulation allowed 2 excitatory filters to be found. Bottom: DMR stimulation resulted in 6 excitatory filters and 1 suppressive filter. RN stimulation produced 1 excitatory filter.
The second example in Figure 7 (bottom) shows similar results. The DMR allowed us to estimate six excitatory features and one suppressive feature, while the RN only allowed us to estimate one excitatory feature. Since the long term statistics of the two sounds were the same, this implies that the short term statistics in the DMR (i.e. local correlations) drive neurons in a different manner than the RN. For DMR, additional functional inputs can be recovered, while for the RN a reduced number, and perhaps different set, of inputs are obtained.
For neurons where we presented the DMR and the RN to the same neuron, the total number of features was higher for DMR stimulation (Fig. 8A). DMR features counts were also higher than RN for both excitatory (Fig. 8B) and suppressive features (Fig. 8C). Across the population of neurons, the total number of features, which is the sum of excitatory and suppressive features, was again larger for DMR than for RN stimulation (Fig. 8D; DMR median = 6.0, DMR MAD = 3.0; RN median = 1.0, RN MAD = 0.0; p < 0.0001, Rank-sum test). For excitatory features, the DMR allowed us to obtain more excitatory features (Fig. 8E; DMR median = 5.0, DMR MAD = 2.0; RN median = 1.0, RN MAD = 0.0; p < 0.0001, Rank-sum test). For suppressive features, we were able to recover more features for DMR than for RN (Fig. 8F; DMR median = 1.0, DMR MAD = 1.0; RN median = 0.0, RN MAD = 0.0; p < 0.0001, Rank-sum test). Thus, feature counts were higher both across the entire population and for the paired stimulus results. Therefore, the differences in local-correlations between the two stimuli allowed us to obtain a much more expansive view of auditory processing with the more naturalistic DMR. In comparison, the RN appears to either suppress the responsiveness of AI neurons, or only partially probe the preferred stimulus regime, and thus reduces the number of functional excitatory and suppressive features that may be captured.
Figure 8.
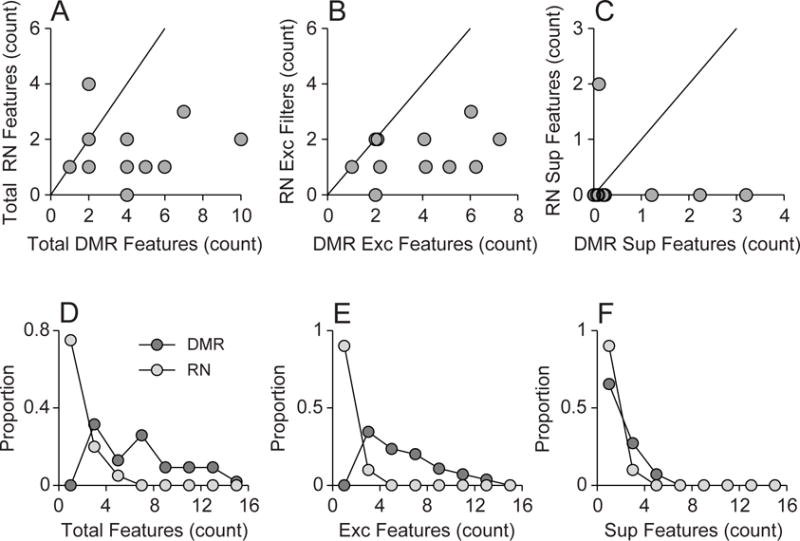
Feature number for DMR and RN stimulation. Top row: for neurons where both DMR and RN stimuli were presented, (A) the total number of filters, (B) the number of excitatory filters, and (C) the number of suppressive filters, was higher for DMR stimulation. Bottom row: Across the population, DMR stimulation allowed (D) more total filters, (E) more excitatory filters, and (F) more suppressive filters, to be recovered.
DISCUSSION
Consistent with earlier work, our study suggests that AI STRFs are based on multiple excitatory and suppressive features (Atencio et al., 2008, 2009, 2012). We identify here a specific relationship between the excitatory and suppressive features and find that the number of relevant features depends on stimulus statistics. Excitatory features encode faster modulation details, while suppressive features process longer contextual variations in time and frequency. Additionally, we showed that stimulus statistics make a substantial difference in identifying the stimulus features that influence a neuron’s response. Thus, feature type (excitatory/suppressive) and feature property (modulation preferences) are influenced by stimulus context.
Previous work
Two previous studies are largely consistent with our work. In the first, the MNE analysis was applied to neurons in a secondary auditory cortex-like center in the songbird (Kozlov and Gentner, 2016). In concord with our results, the authors found multiple excitatory and suppressive features. The total number of features that were found approximated the number that we report in the present study, though songbird non-primary neurons had a higher number of suppressive features. The features themselves were complex in shape and without the typical excitatory/suppressive subfields that are usually seen in more primary regions. When the authors applied a neural network that implemented sparse spiking and divisive normalization, they were able to produce multiple features. Our results differed from theirs in showing clear feature structure, an assessment of modulation processing, and the effect of stimulus statistics on multi-feature receptive field processing.
Harper and colleagues also applied a neural network to estimate a network receptive field (NRF) that models the relationship between natural sounds and ferret primary auditory cortical responses (Harper et al., 2016). They found that many AI neurons had multiple features, and that they could be classified as excitatory or suppressive. They found that the number of features varied between 1 and 7, which is lower than our finding. The individual features coded spectral and temporal information over large extents. Overall, the MNE and neural network approaches provide independent verification that AI neurons possess multidimensional receptive fields. Since the NRF analysis produced fewer features compared to the MNE approach, it is unclear if the NRF is conservative in its estimation, or if this is a difference between ferret and cat AI. Assessing the NRF against model inputs and outputs to ensure the quality of model reconstruction, as previously done for the MNE approach (Fitzgerald et al., 2011a), would help to resolve this issue.
An advantage of the MNE approach is that the linear and quadratic features are naturally incorporated into the neural model. Further, whether a quadratic feature is excitatory and suppressive features may be unambiguously determined by examining the sign of the eigenvalue. Additionally, the spiking output nonlinearity is a logistic function, which bounds the probability of a spiking output between 0 and 1, and therefore eliminates the possibility of non-zero response estimates.
Functional properties of quadratic stimulus features
Because we were able to classify stimulus features as excitatory or suppressive, our results generalize the concept of inhibitory and excitatory sidebands of auditory cortical neurons. Inhibitory frequency sidebands represent regions outside the classical excitatory tuning curve that suppress responsiveness when pure tones are presented at the sideband frequencies (Calford and Semple, 1995, Brosch and Schreiner, 1997, Sutter et al., 1999, Brosch and Schreiner, 2000). These sidebands are experimentally recovered using pure tone, or carrier, stimuli. In our study, receptive fields are derived from the spectrotemporal envelope, which modulates a logarithmically spaced carrier structure. The suppressive stimulus features of the MNE model reduce the responsiveness of a neuron. Thus, suppression is not restricted to specific frequency regions and carrier-like stimuli, but occurs for general spectrotemporal envelope patterns.
By assessing the feature properties of stimulus dimensions, we found that for AI neurons the feature property depends on the feature type. Excitatory features encoded finer temporal and spectral details (shorter durations and bandwidths), while the suppressive features encoded larger-scale envelope variations (longer durations and larger bandwidths). These results align with the results from whole-cell patch recordings, where inhibition was found to be longer lasting and broader in frequency (Tan et al., 2004). For spiking neurons, this phenomenon applies to both frequency integration and to specific spectrotemporal characteristics (Atencio and Schreiner, 2008, Wu et al., 2008).
How could the multiple excitatory and suppressive features enhance auditory processing? No experiment has addressed this question, but parallels to visual cortical cross-orientation suppression may provide clues. In visual cross-orientation suppression, responses to optimally oriented stimuli are suppressed by simultaneously presented stimuli that have an orientation 90 degrees from the optimal orientation (Bonds, 1989). Here the two stimuli overlap in space but differ in their orientations. Visual cortical spike-triggered covariance analyses hypothesized that excitatory and suppressive subunits may help explain the phenomenon due to the different orientation preferences of excitatory and suppressive features (Chen et al., 2007). In the auditory analogy, and if parallels between visual space and auditory spectrum can be maintained, auditory excitatory spectrotemporal stimulus features encode faster spectral modulations, while suppressive features encode slower spectral modulations and integrate over broader frequency regions. Our results predict that presenting both stimulus features simultaneously would lead to reductions in firing rate relative to presenting the excitatory, faster-modulated stimulus feature in isolation. Such a phenomenon would be useful in detecting foreground signals in the presence of background noise, since responses to noise that match the suppressive feature would be decreased (Sharpee et al., 2011).
How might the different context-sensitive spectrotemporal features be a reflection of cortical circuitry? The stimulus features that we recovered for AI neurons are likely a result of coherent subsets of inputs to each neuron. Pioneering two-photon imaging work has shown that auditory cortical neurons receive multiple synaptic inputs that may have different frequency response areas (Chen et al., 2011). Thus, our results may further generalize the two-photon results, since each spectrotemporal stimulus feature may represent a coherent set of functional inputs. A necessary further step is to characterize the spectrotemporal inputs at multiple synaptic sites, and compare the spiking spectrotemporal features to those that can be obtained using appropriate imaging technologies.
Receptive field dimensionality
We note that there is no stereotyped number of features for a cat auditory cortical neuron. While most neurons had multiple features, there was a broad distribution of feature numbers across the neural population. The number likely varies with the location of each neuron in the cortical microcircuit, and will be influenced by columnar, corticocortical, and thalamic inputs (Lee and Winer, 2011). The varying number of functional stimulus features for a given AI neuron finds an analog in the cat primary visual cortex. In cat V1, random stimuli allowed two features to be obtained (Touryan et al., 2002). When naturalistic stimuli were used, a broader set of features were recovered (Touryan et al., 2005). Thus, the stimulus statistics allowed different sets of features to be identified. A difference between the cat V1 studies and our report is that our neurons had STAs, while the cat V1 studies examined complex cells, which have either weak or nonexistent STA (Rust et al., 2005, Touryan et al., 2005, Chen et al., 2007, Fournier et al., 2011, Fournier et al., 2014).
Stimulus context
Finally, stimulus context played an essential role in the types and numbers of stimulus features that we recovered. Different stimulus distributions enabled us to recover vastly different spectrotemporal stimulus features. The differences between features were not evident in the main mode of processing, represented by the linear feature; the linear feature was largely similar for DMR and RN stimuli. The differences were mainly noticeable when we examined the quadratic kernel, which accounts for pairwise stimulus correlations. Thus, the stimulus features reflect the stimulus correlation context, and describe how the functional inputs to AI neurons are engaged, and vary, with stimulus type. The spectrotemporal stimulus features show that local correlations engage AI neurons in a vastly different manner from unstructured stimuli. Thus, the types, varieties, and numbers of functional inputs to AI neurons that may be measured depends on the specific stimulus statistics of the stimulus ensemble (Woolley et al., 2005, David et al., 2009). Therefore, while stimulus context can affect receptive field estimation (Blake and Merzenich, 2002, Gourevitch et al., 2009), we have shown that such context-sensitivity is part of a more general phenomenon. It is reflected in the entire multidimensional nature of auditory cortical receptive fields.
Further considerations: anesthesia and stimulus context
Experimental preparation and stimulus type must also be considered to place our work in. We utilized an anesthetized cat preparation for all recordings. Anesthesia may act to increase response suppression (Cheung et al., 2001, Syka et al., 2005), though the ketamine preparation that we used mitigates some of these effects since it allows greater spontaneous rates and complex firing patterns (Walker et al., 2008, Campbell et al., 2010). Additionally, while thalamacortical oscillations and spindles may be present for short duration stimuli that have strong onsets, our stimuli were continuous, without sharp onsets, and have been shown to maintain auditory cortex in a relatively adapted state (Miller and Schreiner, 2000). Further, this type of stimulation has been shown to reduce spindles (Britvina and Eggermont, 2008). While no study to date describes changes in auditory cortical multidimensional receptive fields under awake and anesthetized conditions, two reports from the visual cortex make it likely that our main conclusions will not be affected. When multidimensional receptive field analysis was performed in the awake and anesthetized macaque monkey, multiple excitatory and suppressive filters were found in both preparations (Rust et al., 2005, Chen et al., 2007).
Our results revealed clear differences between DMR and RN stimulus derived receptive fields. Stimulus context has been previously shown to influence the responsiveness of auditory cortical neurons (Rabinowitz et al., 2011). Ferret AI neurons modulate their gain as stimulus contrast changes (Rabinowitz et al., 2012). This may provide an explanation for the difference in firing rates in response to the DMR and RN stimuli. The decrease in firing rate is consistent with visual cortical work, which revealed increased sparseness for naturalistic stimulation (Vinje and Gallant, 2000, 2002, Haider et al., 2010). In the auditory cortex, while stimulus contrast may induce gain changes, these reports also showed that STRF structure was not affected by changes in stimulus contrast (Rabinowitz et al., 2012). Thus, stimulus contrast effects are unlikely to have affected our results. Additionally, by construction, the envelope contrast of DMR and RN stimuli is similar, further decreasing the likelihood that contrast can account for filter differences.
Synaptic depression has also been found to provide an explanation for STRF stimulus context changes (David et al., 2009). Synaptic depression helped to explain why ferret AI STRFs varied for speech and short-duration ripple stimuli. The changes explained by synaptic depression occurred with respect to the linear STRF. By contrast, we showed that the linear filter in the MNE model was similar for both DMR and RN stimuli. Thus, stimulus context changed our receptive field model with respect to filters that are relatively unexamined in auditory cortical research. While at present it is unknown if a synaptic depression model may be helpful in explaining the DMR/RN multidimensional receptive field changes, it does not appear to be necessary with regard to linear STRF processing.
In summary, we found that under varying stimulus conditions, the linear filter, which is analogous to the STA, did not change. Instead, filters that are not normally examined, and indicate nonlinear stimulus interactions, did change their spectrotemporal properties. Thus, it may be necessary to examine multidimensional receptive fields to assess auditory cortical functional processing.
AI receptive fields are composed of multiple stimulus features
Stimulus features may be excitatory or suppressive
Excitatory and suppressive features have different modulation preferences
Stimulus statistics affect the quantity and characteristics of the features
Acknowledgments
This work was supported by the National Institutes of Health National Institute for Deafness and Communication Disorders grant DC011874, the Coleman Memorial Fund, Hearing Research Inc. (San Francisco, CA), the National Science Foundation (NSF) CAREER award number 1254123 and IOS-1556388, the National Eye Institute of the National Institutes of Health under Award Number R01EY019493, NEI Core grant P30EY019005, and T32EY020503, McKnight Scholarship, and Ray Thomas Edwards Career Award.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
The authors declare no competing financial interests.
References
- Aljadeff J, Segev R, Berry MJ, 2nd, Sharpee TO. Spike triggered covariance in strongly correlated gaussian stimuli. PLoS Comput Biol. 2013;9:e1003206. doi: 10.1371/journal.pcbi.1003206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Schreiner CE. Spectrotemporal processing differences between auditory cortical fast-spiking and regular-spiking neurons. J Neurosci. 2008;28:3897–3910. doi: 10.1523/JNEUROSCI.5366-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Schreiner CE. Columnar connectivity and laminar processing in cat primary auditory cortex. PLoS One. 2010a;5:e9521. doi: 10.1371/journal.pone.0009521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Schreiner CE. Laminar diversity of dynamic sound processing in cat primary auditory cortex. J Neurophysiol. 2010b;103:192–205. doi: 10.1152/jn.00624.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Schreiner CE. Spectrotemporal processing in spectral tuning modules of cat primary auditory cortex. PLoS One. 2012;7:e31537. doi: 10.1371/journal.pone.0031537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Schreiner CE. Auditory cortical local subnetworks are characterized by sharply synchronous activity. J Neurosci. 2013;33:18503–18514. doi: 10.1523/JNEUROSCI.2014-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Sharpee TO, Schreiner CE. Cooperative nonlinearities in auditory cortical neurons. Neuron. 2008;58:956–966. doi: 10.1016/j.neuron.2008.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Sharpee TO, Schreiner CE. Hierarchical computation in the canonical auditory cortical circuit. Proc Natl Acad Sci USA. 2009;106:21894–21899. doi: 10.1073/pnas.0908383106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atencio CA, Sharpee TO, Schreiner CE. Receptive field dimensionality increases from the auditory midbrain to cortex. J Neurophysiol. 2012;107:2594–2603. doi: 10.1152/jn.01025.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blake DT, Merzenich MM. Changes of AI receptive fields with sound density. J Neurophysiol. 2002;88:3409–3420. doi: 10.1152/jn.00233.2002. [DOI] [PubMed] [Google Scholar]
- Bonds AB. Role of inhibition in the specification of orientation selectivity of cells in the cat striate cortex. Vis Neurosci. 1989;2:41–55. doi: 10.1017/s0952523800004314. [DOI] [PubMed] [Google Scholar]
- Britvina T, Eggermont JJ. Multi-frequency auditory stimulation disrupts spindling activity in anesthetized animals. Neuroscience. 2008;151:888–900. doi: 10.1016/j.neuroscience.2007.11.028. [DOI] [PubMed] [Google Scholar]
- Brosch M, Schreiner CE. Time course of forward masking tuning curves in cat primary auditory cortex. J Neurophysiol. 1997;77:923–943. doi: 10.1152/jn.1997.77.2.923. [DOI] [PubMed] [Google Scholar]
- Brosch M, Schreiner CE. Sequence sensitivity of neurons in cat primary auditory cortex. Cereb Cortex. 2000;10:1155–1167. doi: 10.1093/cercor/10.12.1155. [DOI] [PubMed] [Google Scholar]
- Calford MB, Semple MN. Monaural inhibition in cat auditory cortex. J Neurophysiol. 1995;73:1876–1891. doi: 10.1152/jn.1995.73.5.1876. [DOI] [PubMed] [Google Scholar]
- Calhoun BM, Schreiner CE. Spectral envelope coding in cat primary auditory cortex: linear and non-linear effects of stimulus characteristics. Eur J Neurosci. 1998;10:926–940. doi: 10.1046/j.1460-9568.1998.00102.x. [DOI] [PubMed] [Google Scholar]
- Campbell RA, Schulz AL, King AJ, Schnupp JW. Brief sounds evoke prolonged responses in anesthetized ferret auditory cortex. J Neurophysiol. 2010;103:2783–2793. doi: 10.1152/jn.00730.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Han F, Poo MM, Dan Y. Excitatory and suppressive receptive field subunits in awake monkey primary visual cortex (V1) Proc Natl Acad Sci U S A. 2007;104:19120–19125. doi: 10.1073/pnas.0706938104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Leischner U, Rochefort NL, Nelken I, Konnerth A. Functional mapping of single spines in cortical neurons in vivo. Nature. 2011;475:501–505. doi: 10.1038/nature10193. [DOI] [PubMed] [Google Scholar]
- Cheung SW, Nagarajan SS, Bedenbaugh PH, Schreiner CE, Wang X, Wong A. Auditory cortical neuron response differences under isoflurane versus pentobarbital anesthesia. Hear Res. 2001;156:115–127. doi: 10.1016/s0378-5955(01)00272-6. [DOI] [PubMed] [Google Scholar]
- Chichilnisky EJ. A simple white noise analysis of neuronal light responses. Network. 2001;12:199–213. [PubMed] [Google Scholar]
- David SV, Mesgarani N, Fritz JB, Shamma SA. Rapid synaptic depression explains nonlinear modulation of spectro-temporal tuning in primary auditory cortex by natural stimuli. J Neurosci. 2009;29:3374–3386. doi: 10.1523/JNEUROSCI.5249-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elhilali M, Fritz JB, Klein DJ, Simon JZ, Shamma SA. Dynamics of precise spike timing in primary auditory cortex. J Neurosci. 2004;24:1159–1172. doi: 10.1523/JNEUROSCI.3825-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escabi MA, Schreiner CE. Nonlinear spectrotemporal sound analysis by neurons in the auditory midbrain. J Neurosci. 2002;22:4114–4131. doi: 10.1523/JNEUROSCI.22-10-04114.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzgerald JD, Rowekamp RJ, Sincich LC, Sharpee TO. Second order dimensionality reduction using minimum and maximum mutual information models. PLoS Comput Biol. 2011a;7:e1002249. doi: 10.1371/journal.pcbi.1002249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzgerald JD, Sincich LC, Sharpee TO. Minimal models of multidimensional computations. PLoS Comput Biol. 2011b;7:e1001111. doi: 10.1371/journal.pcbi.1001111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier J, Monier C, Levy M, Marre O, Sari K, Kisvarday ZF, Fregnac Y. Hidden complexity of synaptic receptive fields in cat V1. J Neurosci. 2014;34:5515–5528. doi: 10.1523/JNEUROSCI.0474-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier J, Monier C, Pananceau M, Fregnac Y. Adaptation of the simple or complex nature of V1 receptive fields to visual statistics. Nat Neurosci. 2011;14:1053–1060. doi: 10.1038/nn.2861. [DOI] [PubMed] [Google Scholar]
- Gourevitch B, Norena A, Shaw G, Eggermont JJ. Spectrotemporal receptive fields in anesthetized cat primary auditory cortex are context dependent. Cereb Cortex. 2009;19:1448–1461. doi: 10.1093/cercor/bhn184. [DOI] [PubMed] [Google Scholar]
- Haider B, Krause MR, Duque A, Yu Y, Touryan J, Mazer JA, McCormick DA. Synaptic and network mechanisms of sparse and reliable visual cortical activity during nonclassical receptive field stimulation. Neuron. 2010;65:107–121. doi: 10.1016/j.neuron.2009.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper NS, Schoppe O, Willmore BD, Cui Z, Schnupp JW, King AJ. Network Receptive Field Modeling Reveals Extensive Integration and Multi-feature Selectivity in Auditory Cortical Neurons. PLoS Comput Biol. 2016;12:e1005113. doi: 10.1371/journal.pcbi.1005113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imaizumi K, Schreiner CE. Spatial interaction between spectral integration and frequency gradient in primary auditory cortex. J Neurophysiol. 2007;98:2933–2942. doi: 10.1152/jn.00511.2007. [DOI] [PubMed] [Google Scholar]
- Klein DJ, Depireux DA, Simon JZ, Shamma SA. Robust spectrotemporal reverse correlation for the auditory system: optimizing stimulus design. J Comput Neurosci. 2000;9:85–111. doi: 10.1023/a:1008990412183. [DOI] [PubMed] [Google Scholar]
- Kouh M, Sharpee TO. Estimating linear-nonlinear models using Renyi divergences. Network. 2009;20:49–68. doi: 10.1080/09548980902950891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlov AS, Gentner TQ. Central auditory neurons have composite receptive fields. Proc Natl Acad Sci U S A. 2016;113:1441–1446. doi: 10.1073/pnas.1506903113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee CC, Winer JA. Convergence of thalamic and cortical pathways in cat auditory cortex. Hear Res. 2011;274:85–94. doi: 10.1016/j.heares.2010.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewicki MS. Bayesian modeling and classification of neural signals. Neural Comput. 1994;6:1005–1030. [Google Scholar]
- Lewicki MS. A review of methods for spike sorting: the detection and classification of neural action potentials. Network. 1998;9:R53–78. [PubMed] [Google Scholar]
- Miller LM, Schreiner CE. Stimulus-based state control in the thalamocortical system. J Neurosci. 2000;20:7011–7016. doi: 10.1523/JNEUROSCI.20-18-07011.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paninski L. Convergence properties of three spike-triggered analysis techniques. Network. 2003;14:437–464. [PubMed] [Google Scholar]
- Rabinowitz NC, Willmore BD, Schnupp JW, King AJ. Contrast gain control in auditory cortex. Neuron. 2011;70:1178–1191. doi: 10.1016/j.neuron.2011.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinowitz NC, Willmore BD, Schnupp JW, King AJ. Spectrotemporal contrast kernels for neurons in primary auditory cortex. J Neurosci. 2012;32:11271–11284. doi: 10.1523/JNEUROSCI.1715-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowekamp RJ, Sharpee TO. Analyzing multicomponent receptive fields from neural responses to natural stimuli. Network. 2011;22:45–73. doi: 10.3109/0954898X.2011.566303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rust NC, Schwartz O, Movshon JA, Simoncelli EP. Spatiotemporal elements of macaque v1 receptive fields. Neuron. 2005;46:945–956. doi: 10.1016/j.neuron.2005.05.021. [DOI] [PubMed] [Google Scholar]
- Samengo I, Gollisch T. Spike-triggered covariance: geometric proof, symmetry properties, and extension beyond Gaussian stimuli. J Comput Neurosci. 2013;34:137–161. doi: 10.1007/s10827-012-0411-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz O, Pillow JW, Rust NC, Simoncelli EP. Spike-triggered neural characterization. J Vis. 2006;6:484–507. doi: 10.1167/6.4.13. [DOI] [PubMed] [Google Scholar]
- Sharpee T, Rust NC, Bialek W. Analyzing neural responses to natural signals: maximally informative dimensions. Neural Comput. 2004;16:223–250. doi: 10.1162/089976604322742010. [DOI] [PubMed] [Google Scholar]
- Sharpee TO, Atencio CA, Schreiner CE. Hierarchical representations in the auditory cortex. Curr Opin Neurobiol. 2011;21:761–767. doi: 10.1016/j.conb.2011.05.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutter ML, Schreiner CE, McLean M, O’Connor KN, Loftus WC. Organization of inhibitory frequency receptive fields in cat primary auditory cortex. J Neurophysiol. 1999;82:2358–2371. doi: 10.1152/jn.1999.82.5.2358. [DOI] [PubMed] [Google Scholar]
- Syka J, Suta D, Popelar J. Responses to species-specific vocalizations in the auditory cortex of awake and anesthetized guinea pigs. Hear Res. 2005;206:177–184. doi: 10.1016/j.heares.2005.01.013. [DOI] [PubMed] [Google Scholar]
- Tan AY, Zhang LI, Merzenich MM, Schreiner CE. Tone-evoked excitatory and inhibitory synaptic conductances of primary auditory cortex neurons. J Neurophysiol. 2004;92:630–643. doi: 10.1152/jn.01020.2003. [DOI] [PubMed] [Google Scholar]
- Theunissen FE, Sen K, Doupe AJ. Spectral-temporal receptive fields of nonlinear auditory neurons obtained using natural sounds. J Neurosci. 2000;20:2315–2331. doi: 10.1523/JNEUROSCI.20-06-02315.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touryan J, Felsen G, Dan Y. Spatial structure of complex cell receptive fields measured with natural images. Neuron. 2005;45:781–791. doi: 10.1016/j.neuron.2005.01.029. [DOI] [PubMed] [Google Scholar]
- Touryan J, Lau B, Dan Y. Isolation of relevant visual features from random stimuli for cortical complex cells. J Neurosci. 2002;22:10811–10818. doi: 10.1523/JNEUROSCI.22-24-10811.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinje WE, Gallant JL. Sparse coding and decorrelation in primary visual cortex during natural vision. Science. 2000;287:1273–1276. doi: 10.1126/science.287.5456.1273. [DOI] [PubMed] [Google Scholar]
- Vinje WE, Gallant JL. Natural stimulation of the nonclassical receptive field increases information transmission efficiency in V1. J Neurosci. 2002;22:2904–2915. doi: 10.1523/JNEUROSCI.22-07-02904.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker KM, Ahmed B, Schnupp JW. Linking cortical spike pattern codes to auditory perception. J Cogn Neurosci. 2008;20:135–152. doi: 10.1162/jocn.2008.20012. [DOI] [PubMed] [Google Scholar]
- Woolley SM, Fremouw TE, Hsu A, Theunissen FE. Tuning for spectro-temporal modulations as a mechanism for auditory discrimination of natural sounds. Nat Neurosci. 2005;8:1371–1379. doi: 10.1038/nn1536. [DOI] [PubMed] [Google Scholar]
- Wu GK, Arbuckle R, Liu BH, Tao HW, Zhang LI. Lateral sharpening of cortical frequency tuning by approximately balanced inhibition. Neuron. 2008;58:132–143. doi: 10.1016/j.neuron.2008.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]


