Assembling oppositely charged lock and key responsive colloids: A mesoscale analog of adaptive chemistry

Oppositely charged thermoresponsive particles with complementary geometries are assembled into adaptive colloidal molecules.

Abstract

We have seen a considerable effort in colloid sciences to copy Nature’s successful strategies to fabricate complex functional structures through self-assembly. This includes attempts to design colloidal building blocks and their intermolecular interactions, such as creating the colloidal analogs of directional molecular interactions, molecular recognition, host-guest systems, and specific binding. We show that we can use oppositely charged thermoresponsive particles with complementary shapes, such as spherical and bowl-shaped particles, to implement an externally controllable lock-and-key self-assembly mechanism. The use of tunable electrostatic interactions combined with the temperature-dependent size and shape and van der Waals interactions of these building blocks provides an exquisite control over the selectivity and specificity of the interactions and self-assembly process. The dynamic nature of the mechanism allows for reversibly cycling through various structures that range from weakly structured dense liquids to well-defined molecule-shaped clusters with different configurations through variations in temperature and ionic strength. We link this complex and dynamic self-assembly behavior to the relevant molecular interactions, such as screened Coulomb and van der Waals forces and the geometrical complementarity of the two building blocks, and discuss our findings in the context of the concepts of adaptive chemistry recently introduced to molecular systems.

INTRODUCTION

The use of colloids as model atoms or molecules in attempts to investigate various aspects of phase transitions or to fabricate photonic materials has led to enormous progress in the development of model particles with increasing complexity and their assembly into fascinating novel crystalline structures (1–8). Given the limitations in available self-assembled structures for spherical particles with centrosymmetric interaction potentials, the focus has gradually shifted to particles with directional interactions, such as anisotropic colloids, patchy particles, or well-defined colloidal clusters (6–10), where individual particles can additionally be functionalized with DNA strands to also achieve a notion of valency in colloidal self-assembly (5, 11).

Colloid scientists have made a considerable effort to copy various strategies that Nature uses successfully to create complex structures through self-assembly. As an example, in their pioneering work, Sacanna et al. (14) have adapted the concept of a lock-and-key mechanism originally proposed by Fisher (12, 13) for colloidal mixtures of complementary shapes, driven by the use of an additional depletion interaction. Although most studies focus on the use of depletion interactions to direct this specific self-assembly (14–17), alternative approaches have been considered (18–21).

Despite all this effort, in colloid sciences, we are still far from the progress achieved in molecular systems, where concepts, such as supramolecular chemistry, constitutional dynamic chemistry (CDC), and adaptive chemistry pioneered by the Nobel Prize winner Jean-Marie Lehn, have led to enormous progress in creating novel materials. Although classical self-assembly by design strives to achieve full control over the output molecular or supramolecular entity by explicit programming of the building blocks and their interactions, adaptive chemistry provides self-organization with variable selection through the utilization of reversible bonds that allow for a continuous change in constitution by a dynamic reorganization and exchange of building blocks (22).

Here, we show that we can use oppositely charged thermoresponsive core-shell particles with complementary shapes to achieve precisely tunable selectivity and specificity in colloidal self-assembly. We demonstrate that this offers the design of externally tunable and triggerable lock-and-key mechanisms and thus the colloidal analog of supramolecular chemistry. Because of the considerable changes in overall size, local curvature, van der Waals attraction, and surface charge density that can be reached in thermoresponsive core-shell particles with complementary shapes, such as spherical and bowl-shaped particles, we can also attempt to implement the concept of adaptive chemistry or CDC in colloidal suspensions. Here, we successfully use variations in temperature and/or ionic strength to reversibly drive a binary mixture of oppositely charged thermoresponsive particles with complementary shapes (spherical and bowl-shaped) from unstructured dense liquids into well-defined molecule-shaped clusters with variable configurations.

RESULTS

Responsive lock and key particles

Our approach aims to adjust the interactions and size of responsive and soft host and guest particles to control their specific supracolloidal self-assembly with temperature. Here, we use oppositely charged thermoresponsive and soft colloids as dynamic building blocks. The lock and key roles are played by a bowl-shaped composite microgel and a spherical microgel, respectively. Composite polymer microgels are the ideal candidates for implementing this directed self-assembly through externally controllable interactions. As a result of the thermosensitive shell, which undergoes a temperature-induced volume phase transition (VPT) (23), their overall size and the interaction potential can be precisely controlled via temperature (24). We follow a processing route described in our former study to create a bowl-shaped composite microgel consisting of a polystyrene (PS) core and a fluorescent poly(N-isopropylmethacrylamide) (PNIPMAM) shell (25). This system can then be used as a tunable lock particle in the presence of an oppositely charged poly(N-isopropylacrylamide) (PNIPAM) microgel serving as the key particle.

A confocal laser scanning microscopy (CLSM) image of the bowl-shaped core-shell composite microgels is shown in Fig. 1A. The spherical particle synthesis, which is described in Materials and Methods and our previous study (26), leads to monodisperse particles with a PS core that has a radius of 267 ± 20 nm from a statistical analysis of transmission electron microscopy images. CLSM at 20°C evidences the fluorescent shell covalently labeled with rhodamine. At this temperature, the shell thickness is comparable to the core radius as indicated by the hydrodynamic radius of the particle, R_H = 479 nm, measured by dynamic light scattering (DLS). These particles were further postprocessed into bowl-shaped particles following the approach of Im et al. (27), as described in Materials and Methods and our recent work (25). In short, the core-shell particles were swollen with styrene, vitrified in liquid nitrogen, and then equilibrated below 0°C to let the styrene evaporate. A cavity is created at the surface of the particle by styrene evaporation flux. The resulting particles, used as thermoresponsive locks, are monodisperse in size and shape (see Fig. 1A). The lock particles have an overall radius R_L = 497 ± 16 nm measured by CLSM and a slight bowl-shaped anisotropy characterized by an apparent aspect ratio of approximately 1.4 (25). The selected key particles shown in Fig. 1B consist of fluorescently labeled (fluorescein) cross-linked (5 mole percent) PNIPAM microgels with a radius R_K = 443 nm determined by DLS at 20°C. We refer to our former study (28) and Materials and Methods for further details concerning their synthesis and characterization.

Fig. 1. Responsive lock-and-key microgel particle characterization.

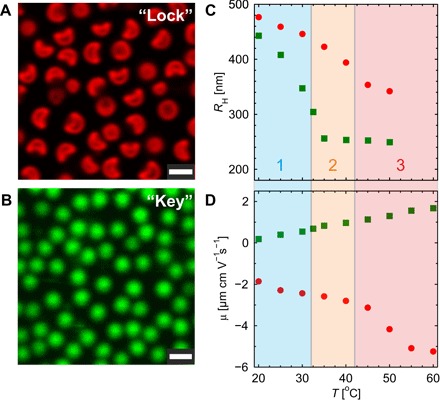
(A) CLSM micrographs of bowl-shaped composite microgels fluorescently labeled in red (rhodamine dye) used as a lock particle. (B) Key particles consisting of cross-linked PNIPAM microgel particles labeled in green (fluorescein), as imaged by CLSM. Scale bars, 1 μm. (C and D) Hydrodynamic radius and electrophoretic mobility measured as a function of temperature: bowl-shaped lock composite microgel (solid circles) and spherical key microgel particle (solid squares). The measurements cross three regions delimited by the VPT temperature of the lock-and-key particles, T_VPT,L and T_VPT,K. In region 1 (T < T_VPT,K), both particles are swollen. In region 2 (T_VPT,K ≤ T ≤ T_VPT,L), lock particles are swollen and key particles are collapsed. In region 3 (T_VPT,L < T), both particles are collapsed.

The swelling behavior of the lock and key particles was characterized using DLS. Here, we follow the evolution of the hydrodynamic radius as a function of temperature. PNIPAM and PNIPMAM microgels respond to temperature with a transition from a swollen to a collapsed configuration with increasing temperature at the VPT temperature, T_VPT. DLS measurements shown in Fig. 1C confirm this feature for the different particles, with a transition at 32°C for the cationic PNIPAM microgels and at about 42°C for the anionic spherical and bowl-shaped PS/PNIPMAM composite microgels. Selecting two responsive polymers with two different T_VPT has the advantage of a fine-tuning of their sizes and interactions, which can be described in three regions, as illustrated in the same figure. Below T_VPT,key in region 1, both components are swollen. Between T_VPT,key and T_VPT,lock in region 2, only the key particles significantly reduce their size, whereas the lock particles maintain a swollen state. For T > T_VPT,lock in region 3, both components are collapsed.

The lock and key particles are oppositely charged, as confirmed by electrophoretic mobility measurements shown in Fig. 1D. The anionic character of the bowl-shaped particles comes from the potassium peroxydisulfate (KPS) initiator and some remaining SDS surfactant, whereas the pure microgel particles are cationic because of the amidine end groups from the 2,2′-azobis(2-methylpropionamidine)dihydrochloride (V50) initiator. The electrophoretic mobility μ is sensitive to temperature and most particularly to the conformation of the microgel. It results in an increase in the effective charge of the particles at higher temperatures with a transition at T_VPT, as documented in the literature (29). For the composite microgels, a similar temperature dependence of the electrophoretic mobility was observed for spherical and bowl-shaped particles. In addition, postprocessing spherical composite microgel into bowl-shaped particles did not strongly affect the swelling behavior, as expected from the slight anisotropy of the bowl-shaped particles and the fact that the postprocessing is almost an isochore transformation (25).

Lock-and-key interaction potential

The extension of the lock-and-key principle to colloids and more complex interaction potentials is based on the idea that interactions are maximized for particles with matching geometries. Combining complementary shape with additional and tunable interparticle interactions then results in an effective pair potential between the lock and key particles that is strongly dependent on the relative orientation and particle dimensions. Moreover, it provides us with an implementation of interaction specificity and selectivity that can be varied through external parameters, such as temperature and ionic strength. For a more generic description of the interactions at play, the lock particle is described by an indented sphere defined by the difference between two equal spheres, where the maximum contact area is $\mathrm{\pi }{\mathit{R}}_{\mathrm{L}}^2$, as shown in Fig. 2A. The electrostatic interactions are treated by considering that the charges are randomly distributed at the surface of the two components and that opposite charges are interacting via a screened Coulomb potential

$${\mathit{V}}_{\text{SC}}(\mathit{r})=-\frac{{\mathit{e}}^2}{4\mathrm{\pi }{\mathrm{ϵ}}_0{\mathrm{ϵ}}_{\mathit{r}}}\frac{{\mathit{e}}^{-\mathrm{\kappa }\mathit{r}}}{\mathit{r}}$$ (1)

where ϵ₀ is the dielectric permittivity of vacuum, ϵ_r is the relative dielectric constant, e is the elementary charge, and r is the distance between the surface charges. κ is the inverse Debye length defined as

$$\mathrm{\kappa }=\mathit{e}{\left(\frac{2{\mathit{N}}_{\mathrm{A}}{\mathit{c}}_{\text{salt}}}{{\mathrm{ϵ}}_0{\mathrm{ϵ}}_{\mathrm{r}}{\mathit{k}}_{\mathrm{B}}\mathit{T}}\right)}^{\frac{1}{2}}$$ (2)

where c_salt is the molar concentration of monovalent salt.

Fig. 2. Calculations of the electrostatically driven self-assembly of oppositely charged lock and key particles.

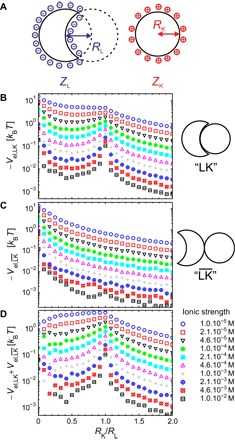
(A) Schematic representation of the oppositely charged lock and key particles used for the modeling of electrostatic interactions. (B) Minimum electrostatic energy in the lock-and-key (LK) configuration as a function of the size ratio, R_K/R_L, calculated for different ionic strengths using R_L = 500 nm, Z_L = −1000e, and Z_K = +100e. (C) Same calculations as in (B) but in the $\overline{\text{LK}}$ configuration. (D) Energy difference between the $\overline{\text{LK}}$ and LK configurations at different ionic strengths (see text for more details).

Calculations were further performed to determine the minimum electrostatic energy, V_el, at contact in either the lock-and-key (LK) configuration (V_el,LK) or the opposite ($\overline{\text{LK}}$) configuration (${\mathit{V}}_{\text{el},\overline{\text{LK}}}$)), as schematically depicted in the insets of Fig. 2 (B and C). These two quantities were first evaluated at 25°C and different ionic strengths as a function of the lock-and-key particle size ratio. The size of the lock particle was fixed to R_L = 500 nm, and the total charges were considered to be constant and equal to Z_L = −1000e and Z_K = +100e. The ionic strength was varied from a fully deionized condition (c_salt = 10⁻⁵ M, κR_L ≈ 5) to the highly screened regime (c_salt = 10⁻² M, κR_L ≈ 164), and the size ratio was varied from 0.04 to 2. As expected from screened Coulomb interactions, the minimum interaction energy strongly depends on the ionic strength. In the optimal configuration corresponding to R_K/R_L = 1, V_el,LK varies from V_el,LK ≈ 4.5 k_BT under deionized conditions to V_el,LK ≈ 0.18 k_BT at c_salt = 2.1 × 10⁻³ M. In comparison, ${\mathit{V}}_{\text{el},\overline{\text{LK}}}$ is more sensitive to the variation of the ionic strength and decreases from ${\mathit{V}}_{\text{el},\overline{\text{LK}}}$ ≈ 1 k_BT to ${\mathit{V}}_{\text{el},\overline{\text{LK}}}$ ≈ 3 × 10⁻³ k_BT. Worth noting is the nonmonotonic dependence of V_el,LK, with an inflexion point around R_K/R_L = 1 at low ionic strengths, which develops to a pronounced maximum as c_salt increases. This is in contrast to the behavior found for ${\mathit{V}}_{\text{el},\overline{\text{LK}}}$, which decreases monotonically with increasing R_K/R_L. These calculations demonstrate that the specificity of the assembly that we define through the difference between ${\mathit{V}}_{\text{el},\overline{\text{LK}}}$ and V_el,LK is maximal for two matching geometries and is promoted at a lower ionic strength, as shown in Fig. 2D.

The total effective charge, Z, and the surface charge density, σ, were evaluated at different temperatures from the measured electrophoretic mobility, μ, and hydrodynamic radius, R_H, assuming Z = 6πηR_Hμ and σ = $\mathit{Z}/(4\mathrm{\pi }{\mathit{R}}_{\mathrm{H}}^2)$. The total charges of the lock and key, Z_L and Z_K, vary with temperature from +98e and −1041e at 20°C to +182e and −1300e at 40°C. This corresponds to a continuous increase of −σ_K/σ_L from about 1/9.25 to 1/2.90 in this temperature range, followed by a decrease to 1/4.26 after the VPT of the bowl-shaped particles at 50°C. These experimental values were further used as input parameters in the model described above to estimate V_el,LK and ${\mathit{V}}_{\text{el},\overline{\text{LK}}}$ at different temperatures, as summarized in Fig. 3A. The difference of the electrostatic energies, $({\mathit{V}}_{\text{el},\text{LK}}-{\mathit{V}}_{\text{el},\overline{\text{LK}}})$, was found to vary from 5 to 11 k_BT between 20° and 40°C to finally reach a value of ≈20 k_BT at 50°C. The specificity of the assembly is strongly related to the surface charge density of the two components considering that V_el is proportional to σ_Lσ_K.

Fig. 3. Minimum electrostatic energy of the specific and unspecific self-assembly between lock and key particles.

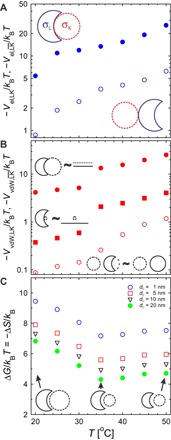
(A) Minimum electrostatic energy determined at c_salt = 10⁻⁵ M from the calculations in the LK (empty circles) and $\overline{\text{LK}}$ (solid circles) assemblies schematically depicted by the insets. (B) Van der Waals interaction contribution determined at a separation distance of 10 nm in three limiting cases illustrated by the corresponding schematic representations: R_L ≈ R_K in LK configuration reducing to a plane-plane approximation (solid circles); R_K << R_L in LK configuration, where the interaction simplifies to a sphere-plane approximation (solid squares); and lock and key particles in $\overline{\text{LK}}$ configuration corresponding to a sphere-sphere approximation (empty circles). (C) Entropy contribution to the free energy at different distances from the ideal contact (see text and the Supplementary Materials). The schematics represent the relative size of the lock and key particles at different temperatures pointed by the arrows.

Van der Waals interactions were estimated for three limiting case scenarios (30). First, in the $\overline{\text{LK}}$ configuration, the interactions simplify to the case of two spheres with their respective Hamaker constants, A_K and A_L, whose surfaces are separated by a distance h

$${\mathit{V}}_{\text{vdW},\overline{\text{LK}}}(\mathit{h})=\frac{{\mathit{A}}_{\mathrm{L}}{\mathit{A}}_{\mathrm{K}}{\mathit{R}}_{\mathrm{L}}{\mathit{R}}_{\mathrm{K}}}{6\mathit{h}({\mathit{A}}_{\mathrm{L}}{\mathit{R}}_{\mathrm{L}}+{\mathit{A}}_{\mathrm{K}}{\mathit{R}}_{\mathrm{K}})}$$ (3)

In the second case, when R_K << R_L in an LK configuration, the interactions are comparable to a sphere interacting with an infinite plane such that

$${\mathit{V}}_{\text{vdW},\text{LK}}(\mathit{h})=\frac{({\mathit{A}}_{\mathrm{L}}+{\mathit{A}}_{\mathrm{K}}){\mathit{R}}_{\mathrm{K}}}{12\mathit{h}}; {\mathit{R}}_{\mathrm{K}}<<{\mathit{R}}_{\mathrm{L}}$$ (4)

Finally, when R_L ≈ R_K in the LK configuration, the interactions can be approximated by two parallel planes having a surface $\mathit{S}=\mathrm{\pi }{\mathit{R}}_{\mathrm{K}}^2$, which results in

$${\mathit{V}}_{\text{vdW},\text{LK}}(\mathit{h})=\frac{({\mathit{A}}_{\mathrm{L}}+{\mathit{A}}_{\mathrm{K}})\mathit{S}}{24\mathrm{\pi }{\mathit{h}}^2}=\frac{({\mathit{A}}_{\mathrm{L}}+{\mathit{A}}_{\mathrm{K}}){\mathit{R}}_{\mathrm{K}}^2}{24{\mathit{h}}^2}; {\mathit{R}}_{\mathrm{L}}\approx {\mathit{R}}_{\mathrm{K}}$$ (5)

We ignored the case where R_K > R_L, which cannot be so easily captured and does not correspond to our simplified model where key particles are always considered smaller than the lock particles. In addition, although the above approximations are valid in most of the configurations, they do not hold when the key particle is in close vicinity of the lock cavity rim.

The microgel particles are highly swollen with water, and their Hamaker constant therefore strongly depends on their degree of swelling. We considered that the polymer volume fraction of the microgel φ_p(T) scales with the overall size of the particles, given by the evolution of their hydrodynamic radii with temperature

$${\mathrm{\phi }}_{\mathrm{p}}(\mathit{T})=\frac{{\mathit{R}}_{\mathrm{H},\text{coll}}^3}{{\mathit{R}}_{\mathrm{H}}{(\mathit{T})}^3}\cdot {\mathrm{\phi }}_{\mathrm{p},0}$$ (6)

where R_H,coll refers to the hydrodynamic radius of the fully collapsed particles, and φ_p,0 refers to the polymer volume fraction in the collapse state. For a core-shell particle with a core radius R_c, a similar calculation can be derived

$${\mathrm{\phi }}_{\mathrm{p}}(\mathit{T})=\frac{{\mathit{R}}_{\mathrm{H},\text{coll}}^3-{\mathit{R}}_{\mathrm{c}}^3}{{\mathit{R}}_{\mathrm{H},\text{coll}}^3-{\mathit{R}}_{\mathrm{c}}^3}\cdot {\mathrm{\phi }}_{\mathrm{p},0}$$ (7)

Following the approach proposed by Rasmusson et al. (31), we can first estimate the Hamaker constant of the swollen microgel for a given temperature T, A_m(T), as

$${\mathit{A}}_{\mathrm{m}}(\mathit{T})={[{\mathrm{\phi }}_{\mathrm{p}}(\mathit{T}){\mathit{A}}_{\mathrm{p}}^{0.5}+(1-{\mathrm{\phi }}_{\mathrm{p}}(\mathit{T})){\mathit{A}}_{\mathrm{w}}^{0.5}]}^2$$ (8)

where A_p and A_w are the Hamaker constants of the microgel (A_p = 6.20 × 10⁻²⁰ J) and water (A_w = 3.7 × 10⁻²⁰ J), respectively (31). An effective Hamaker constant, A_eff(T), can then be estimated for the microgel

$${\mathit{A}}_{\text{eff}}(\mathit{T})={({\mathit{A}}_{\mathrm{m}}{(\mathit{T})}^{0.5}-{\mathit{A}}_{\mathrm{w}}^{0.5})}^2={({\mathit{A}}_{\text{pol}}^{0.5}-{\mathit{A}}_{\mathrm{w}}^{0.5})}^2{\mathrm{\phi }}_{\mathrm{p}}{(\mathit{T})}^2$$ (9)

We can now apply the different calculations to the lock and key particles. A_p was assumed to be the same for PNIPAM and PNIPMAM, and φ_p was determined for the lock particles from the measurements of the spherical core-shell microgels. In addition, because the shell thickness is larger than 100 nm, we have neglected the contribution of the PS core. The different values derived from these calculations are summarized in Fig. 3B. V_vdW was found to vary from 8.7 × 10⁻² to 4.2 k_BT at 20°C and from 1.2 to 25 k_BT at 50°C. Van der Waals interactions are therefore expected to be non-negligible even in the swollen state. However, our model assumes a constant polymer density across the radial density profile at each temperature, which is not the case when the particles are swollen (28, 32). As a consequence, the van der Waals contribution is expected to be negligible at low temperatures because of the fuzzy outer structure of the swollen microgels and to only become effective when at least one of the components is in its collapsed state. In this case, similarly to electrostatic interactions, these simple calculations demonstrate the specificity of the lock-and-key assembly.

Besides electrostatic and van der Waals interactions, there is an entropy loss in the LK configuration. An analytical expression was derived to account for the entropic contribution expressed by the free energy ΔG of hard lock and key particles with different geometrical parameters, as detailed in the Supplementary Materials. For the lock geometry previously discussed, the expression simplifies to

$$\mathrm{\Delta }\mathit{G}(\mathit{d})=\{\begin{array}{cc}-{\mathit{k}}_{\mathrm{B}}\mathit{T} \text{ln}\left(\frac{({\mathit{R}}_{\mathrm{K}}-\mathit{d})({\mathit{R}}_{\mathrm{K}}-2{\mathit{R}}_{\mathrm{L}}+\mathit{d})}{4\mathit{d}{\mathit{R}}_{\mathrm{L}}}\right)& , {\mathit{R}}_{\mathrm{K}}\le \mathit{d}<{\mathit{d}}_{\text{lim}}\\ -{\mathit{k}}_{\mathrm{B}}\mathit{T} \text{ln}(\frac{1}{2}+\frac{1}{2} \text{cos}(\frac{\mathrm{\pi }}{3}+{\text{cos}}^{-1}\left(\frac{{\mathit{R}}_{\mathrm{K}}^2-{\mathit{R}}_{\mathrm{L}}^2-{\mathit{d}}^2}{2\mathit{d}{\mathit{R}}_{\mathrm{L}}}\right)\left)\right)& , {\mathit{d}}_{\text{lim}}\le \mathit{d}\le {\mathit{R}}_{\mathrm{L}}+{\mathit{R}}_{\mathrm{K}}\\ 0& , {\mathit{R}}_{\mathrm{L}}+{\mathit{R}}_{\mathrm{K}}<\mathit{d}\end{array}$$ (10)

where d is the distance between the centers of the lock and key particles and d_lim = ${({\mathit{R}}_{\mathrm{K}}^2-{\mathit{R}}_{\mathrm{K}}{\mathit{R}}_{\mathrm{L}}+{\mathit{R}}_{\mathrm{L}}^2)}^{\frac{1}{2}}$. The minimum distance at contact is R_K when R_K ≤ R_L and $({(4{\mathit{R}}_{\mathrm{K}}^2-3{\mathit{R}}_{\mathrm{L}}^2)}^{\frac{1}{2}}+{\mathit{R}}_{\mathrm{L}})/2$ when R_K > R_L. Detailed calculations of ΔG(d) for different R_K/R_L ratios are provided in fig. S2. The analytical expression was confirmed by Monte Carlo simulation for different R_K/R_L ratios (see fig. S2).

As the entropy diverges at contact, we have evaluated the free energy at a different distance to the “ideal” lock-and-key configuration, d_c = d − R_K, varying from 1 to 20 nm, considering the overall size of the two particles measured from 20° to 50°C. These results, summarized in Fig. 3C, show that for this simplified geometrical model, ΔG varies between ≈10 and 4 k_BT over the temperature range. The maximum value was found at 20°C where R_K/R_L is slightly below unity, whereas the minimum was at 35°C when R_K/R_L is the lowest. In addition, ΔG quickly drops by a few k_BT with increasing d_c. Even so, the entropy contribution is expected to be lower in our experiments particularly at low temperatures, given the soft and deformable nature of the swollen microgel particles. In summary, the proposed model demonstrates that the binding energy could overcome the entropic penalty to bind the key particles in an LK configuration particularly if the surface charges of the two components are properly adjusted.

Lock-and-key responsive assembly

Having established a sound description of the orientation-dependent interaction potential for our lock-and-key mechanism, we now turn to the resulting self-assembly behavior in mixtures of these particles. We first investigate a mixture of lock particles [1 weight % (wt %)] and key particles (0.27 wt %) with increasing ionic strength set by the addition of variable amounts of potassium chloride at 20°C, as shown in Fig. 4. The number density of the microgel particles was estimated from their size in the collapsed state, assuming a polymer volume fraction of 0.8 and using the density of PNIPAM, ρ_PNIPAM = 1.1495 g·cm⁻³ (28). For the core-shell particles, we used the radius and density of the PS core (ρ_PS = 1.054 g·cm⁻³) and the mass ratio between the core and shell from the synthesis conditions (≈0.5) to calculate their number density. This results in a lock-to-key number ratio N_L/N_K ≈ 1.

Fig. 4. Influence of the ionic strength on the lock-and-key self-assembly.

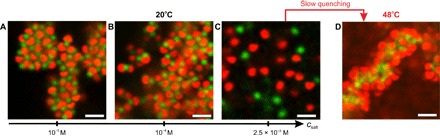
(A to C) 2D CLSM micrographs of the lock and key particles (c_L = 1 wt %, N_L/N_K ≈ 1) recorded at 20°C at various ionic strengths [(A) c_salt = 10⁻⁵ M, (B) c_salt = 10⁻⁴ M, and (C) c_salt = 2.5 × 10⁻³ M]. (D) By slowly rising the temperature from 20° to 48°C at an ionic strength of 2.5 × 10⁻³ M, the key microgel particles become unstable above their T_VPT,key and form a network onto which the lock particles unspecifically adsorb for T ≳ T_VPT,lock. Scale bars, 2 μm.

Figure 4 confirms the electrostatic nature of the self-assembly in these mixtures. At low ionic strength (c_salt = 10⁻⁵ M), the particles associate into dense aggregates where most of the locks were occupied by key particles (see Fig. 4A). Increasing the salt concentration to c_salt = 10⁻⁴ M results in less compact aggregates coexisting with smaller assemblies (see Fig. 4B). Finally, at c_salt = 2.5 × 10⁻³ M, only individual particles were observed (see Fig. 4C). At the highest ionic strength, the weakly charged PNIPAM microgels were unstable above 32°C and built up a loose network, whereas the lock particles were still diffusing freely. However, at 48°C, the lock particles adsorbed on the PNIPAM microgel driven by the increase in the van der Waals interactions (see Fig. 4D).

Next, we investigate the influence of N_L/N_K at constant number density of lock particles (N_L/V ≈ 6.8 × 10⁻² μm⁻³) and low ionic strength (c_salt = 10⁻⁵ M), as shown in Fig. 5. As discussed in the former section, for N_L/N_K ≈ 1, lock and key particles built up dense aggregates by electrostatic interactions, combining specific LK and unspecific $\overline{\text{LK}}$ assemblies (Fig. 5A). At this number ratio, the number of lock particles is insufficient to stabilize the key particles, thus resulting in the formation of large and compact aggregates. Similar observations were made at N_L/N_K ≈ 2 (Fig. 5B), whereas for N_L/N_K ≈ 6, particles rearranged into looser aggregates coexisting with defined tetrahedral assemblies (referred to as tetramers), consisting of a key particle stabilized by four lock particles. The high specificity of the assembly was asserted by counting the fraction of key particles presenting at least one LK association, defined as f(N_LK), which increased from ≈67 to ≈90% with increasing N_L/N_K values (see fig. S3 and the Supplementary Materials for details). It is worth pointing out the dynamic character of lock-and-key assemblies because some lock particles are released from the LK configuration from time to time at 20°C. This is in line with our estimate of a weak interaction potential of about 5 k_BT. The interaction between lock and key particles at this temperature is thus sometimes insufficient to permanently bind all particles in an LK configuration.

Fig. 5. Influence of the number ratio N_L/N_K on the lock-and-key self-assembly.

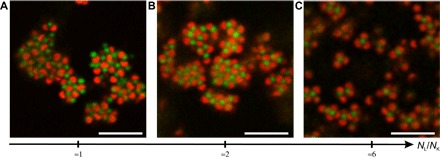
(A to C) 2D CLSM micrographs recorded at 20°C for dispersions prepared at low ionic strength (c_salt ≈ 10⁻⁵ M), with c_L = 1 wt % and different N_L/N_K values [(A) N_L/N_K ≈ 1, (B) N_L/N_K ≈ 2, and (C) N_L/N_K ≈ 6] showing the transition from dense aggregate to colloidal molecules.

The tetrahedral “methane”-like assembly observed at 20°C has to be seen in conjunction with the geometry of the two particles. When both particles are considered as oppositely charged spheres with radii given by their hydrodynamic radii, one would expect a key particle to be stabilized (or decorated) by approximately $4\mathit{K}{({\mathit{R}}_{\mathrm{L}}+{\mathit{R}}_{\mathrm{K}})}^2/{\mathit{R}}_{\mathrm{L}}^2\approx 13$ particles adsorbed to its surface at 20°C, where the prefactor K ≈ 0.9 is the maximum two-dimensional (2D) sphere packing. However, only a maximum of four particles were observed to stabilize the key particles present in an excess of lock particles. In addition, the average distance between the two components, d_LK, was much smaller than the sum of the two hydrodynamic radii, with d_LK ≈ 0.58 μm ≈ 0.63(R_L + R_K). This observation asserts that the particles are almost in contact with the preferential LK configuration, thus explaining the reduced number of particles in the colloidal molecule assembly.

The effect of temperature is then investigated for a constant number ratio of N_L/N_K ≈ 6. Here, T is increased from 20° to 40°C and then from 40° to 48°C, as shown in Fig. 6A. This initially results in a significant shrinkage of the PNIPAM key particles, which are in their fully collapsed state at T = 40°C, whereas the PNIPMAM functionalized lock particles are still highly swollen. As a consequence of the larger size ratio, key particles mostly assemble with two lock particles into a linear “carbon dioxide”–like configuration, which we define as dimers, where d_LK ≈ 0.38 μm ≈ 0.58(R_L + R_K). This assembly was observed in the form of free dimers coexisting with trimers (association with three lock particles) and larger aggregates. The hierarchical self-assembly of the clusters was attributed to the incomplete coverage of the key particles by the lock particles. No dynamic release of particles was observed at this temperature, indicating that the interactions are much stronger, in agreement with the temperature-induced increase in the estimated surface charge density of both components and the additional contribution from van der Waals interactions. Finally, increasing the temperature to 48°C, where both components are in their collapsed configurations, leads to a compact assembly where a key particle is fully enclosed by two lock particles, resulting in d_LK ≈ 0.24 μm ≈ 0.39(R_L + R_K). The small size of the assembly results in a significantly faster Brownian motion, which implies a large uncertainty in d_LK at T = 48°C. The dumbbell shape at this temperature is reminiscent of a “dihydrogen”-like configuration, and we observe mainly individual assemblies coexisting with free lock particles and small aggregates. This temperature-dependent self-assembly thus leads to a reconfigurable formation of colloidal molecules that is thermoreversible, as shown in movie S1.

Fig. 6. Influence of the temperature on the lock-and-key self-assembly into colloidal molecules with adjustable valency.

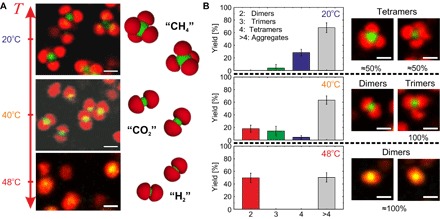
(A) 2D CLSM micrographs of a dispersion (N_L/V ≈ 6.8 × 10⁻² μm⁻³, N_L/N_K ≈ 6) and schematic representations illustrating the specific self-assembly in colloidal molecules with a valency of ≈4 at 20°C (methane, CH₄; top, configuration). Increasing the temperature to 40°C, the key particles exhibit a collapsed state, and the valency of the assembly decreases to ≈2 (carbon dioxide, CO₂; middle, configuration). When both the lock and key particles are in their collapsed state at 48°C, key microgels are confined between two lock particles (dihydrogen, H₂; bottom, configuration). (B) Yield in colloidal molecules relative to the number of key particles determined from various time series recorded at different temperatures. The statistics are supported by typical configurations observed in dispersion together with their relative fractions. Top left: Methane configuration with N_LK = 4. Top right: Tetramer with an unspecific contact and N_LK = 3. Middle left: Carbon dioxide configuration. Middle right: Trimer with an unspecific contact and N_LK = 2. Bottom: Dihydrogen configuration. Scale bars, 1 μm.

The temperature dependence of the assembly specificity was illustrated by the variation of f(N_LK) from ≈90% at 20°C to ≈100% at T ≥ 40°C, in qualitative agreement with our model and the additional contribution of the van der Waals interactions at high temperatures (see fig. S4 and the Supplementary Materials for more details). The yield of the colloidal molecule assembly was determined by counting the number of key particles forming isolated colloidal molecules in respect to those assembled into aggregates, defined as an association including either more than two key particles or more than five lock particles. This was estimated from the number of key particles in the two populations visible in different frames from the 2D micrograph time series. By tracking the colloidal molecules on the movie, we asserted the presence of free dimers, trimers, and tetramers. The statistical analysis shown in Fig. 6B illustrates that the association of the two particles chiefly leads to tetramers with a yield of ≈28% at 20°C. The tetrahedral assembly is characterized by two main states. The ideal case, which we referred to as the methane configuration, where key particles present four LK contacts (N_LK = 4), is roughly representative of 50% of the population and was found to coexist with colloidal molecules where at least one of the contacts is unspecific (N_LK < 4). Figure 6B displays snapshots of the two characteristic assemblies. When the key particles are in their collapsed state at 40°C, mostly dimers and trimers were observed with a respective yield of ≈18 and ≈14%. When the dimers present the ideal carbon dioxide configuration (N_LK = 2), the trimers feature an unspecific lock particle adsorption in all observations (see snapshot in Fig. 6B). Thus, these trimers represent the intermediate configuration of the transition from tetramers to dimers occurring with temperature, as confirmed by the results at 48°C, where only dimers coexisting with smaller aggregates with a large yield of ≈50% were observed. As a general comment, the particles were not index-matched and were imaged about 10 μm away from the surface. Therefore, the estimates for the yield at different temperatures were influenced by the sedimentation of larger aggregates.

DISCUSSION

We have shown that thermoresponsive particles can be processed into complementary geometrical shapes that allow us to implement an externally controllable lock-and-key assembly mechanism. Although colloidal lock and key particles have been described previously, they have mostly been based on “hard” building blocks. This is in contrast to biological systems, which are usually much softer and have the ability to adapt their configuration in response to their local environment, as described by the induced-fit theory formulated by Koshland (33, 34). We foresee that these findings will initiate further studies on more complex colloidal lock-and-key mechanisms using similar soft and responsive colloidal building blocks to study the influence of softness and deformability of the two components and develop the colloidal analogs of the induced-fit theory.

Moreover, our study has demonstrated that responsive and oppositely charged colloidal particles with complementary shapes are ideal building blocks to extend the classical lock-and-key interactions to a highly tunable and dynamic self-assembly process similar to the concept of adaptive chemistry introduced for molecular systems. We can use the combination of electrostatic interactions between complementary shapes, guiding and driving the lock-and-key self-assembly process and the increasing contributions from van der Waals attraction at higher temperatures to create and lock particular configurations. This has allowed us to assemble well-defined colloidal clusters with reconfigurable configurations, mimicking the colloidal analogs of structures, such as methane, carbon dioxide, and dihydrogen. The geometrical complementarity of the particles thus provides us with an association mechanism that implements both selectivity and specificity, whereas the responsive nature of both building blocks results in an exquisite control of these processes.

Adaptive chemistry or CDC provides self-organization with variable selection through the utilization of reversible bonds that allow for a continuous change in constitution by a dynamic reorganization and exchange of building blocks (22). This study has demonstrated that our thermoreversible building blocks allow us to develop colloidal analogs of these systems. We have shown that we can use variations in temperature and/or ionic strength to reversibly drive a binary mixture of oppositely charged thermoresponsive particles with complementary shapes (spherical and bowl-shaped) from unstructured or weakly structured dense liquids into well-defined molecule-shaped clusters with variable configurations. It will be interesting to see whether this approach can be extended to more complex mixtures of responsive particles with carefully designed physical properties (size, shape, charge state, and monomer composition, resulting in different swelling curves as a function of temperature), guided by the theoretical description of the interactions introduced in this study, and investigating the wide range of dynamic system states that we can achieve in this manner. The ability of the lock-and-key colloids to undergo continuous conformational changes and to behave as “shape shifters” allows for adaptive self-organization that is explicitly related to the dynamic exchange and reorganization process into a variety of colloidal molecules, endowing for assemblies capable to adapt to local or external stimuli. We further envision that the association of soft thermoresponsive and oppositely charged key particles with multivalent colloids presenting a defined number of locks per particles (16, 35) could provide the adequate limited valence and tunability necessary to construct and grow well-defined higher-order structures, including non–close-packed crystals.

MATERIALS AND METHODS

Synthesis

Materials

N-isopropylmethacrylamide (Sigma-Aldrich), N-isopropylacrylamide (NIPAM; Sigma-Aldrich), and N,N′-methylenebisacrylamide (BIS; Fluka) monomers and V50 (Fluka), SDS (Fluka), and potassium peroxydisulfate (KPS; Fluka) were used as received. Styrene monomer (BASF) was purified on an Al₂O₃ column before use. Water was purified using reverse osmosis (Milli-RO; Millipore) and ion exchange (Milli-Q; Millipore).

Synthesis of composite PS-PNIPMAM microgel

The core-shell microgel was synthesized and characterized as described in our former contribution, J. J. Crassous et al. (25), as is their postprocessing into bowl-shaped particles. We refer to the J. J. Crassous et al. study (25), which presents the synthesis and characterization of these particles in more detail.

Postprocessing of composite microgels into bowl-shaped particles

The particles were first swollen with styrene and then quickly frozen into liquid nitrogen (−196°C). A void was created at the center of the particles as the styrene solidified from the surface to the center of the PS core. In the next step, the frozen sample was slowly warmed up to let the swollen agent evaporate. The evaporation process was carried out below 0°C under ambient pressure. Because of the presence of an evaporation flux of the styrene, a hole appears in the shell of each hollow particle. We refer to the original work of Im et al. (27) for a more detailed description of the shape transformation mechanism.

Synthesis of the key particles

In a typical procedure, NIPAM (2 g) as monomers, BIS (0.136 g) as the cross-linker, V50 (0.01 g in 10 ml of water) as the initiator, and fluorescein-5-isothiocyanate (2 mg dissolved in 87.8 ml of water) as the dye were polymerized by precipitation polymerization. The reaction was run for 4 hours at 80°C. The reaction mixture was passed through glass wool to remove particulate matter and was further purified by three centrifugation cycles at 10,000 rpm for 20 min, with removal of the supernatant and redispersion between each cycle.

Experimental methods

Confocal laser scanning microscopy

The confocal micrographs were monitored on a Leica SP5 CLSM operated in the inverted mode (D6000I) using a 100×/1.4–numerical aperture immersion objective. The samples were monitored in situ at different temperatures, and an environmental system was used to ensure temperature control with an accuracy of 0.2°C. The suspensions were kept between two cover glasses separated by a 120-μm spacer. A 488-nm Ar ion and a 543-nm He-Ne laser were used to excite the red fluorescence of rhodamine B (543 nm) and the green fluorescence of fluorescein (488 nm), respectively. The cover glass and coverslip were washed with 2 to 5% Decon 90 aqueous dispersion, extensively rinsed with water and dried under nitrogen flow before use.

Dynamic light scattering

DLS was carried out using a light scattering goniometer instrument from LS Instruments equipped with a He-Ne laser (λ = 632.8 nm). The temperature was controlled with an accuracy of 0.1°C. The samples were diluted to 0.01 wt %, preventing interaction effects and multiple scattering. The measurements were performed at scattering angles of 45°, 60°, and 75° for temperatures varying between 20° and 55°C, with an equilibration time of 30 min before data collection. The hydrodynamic radius was derived following a standard angular dependence analysis.

Electrophoretic measurements and effective charge determination

The effective charge, Z_eff, was estimated from the particle electrophoretic mobility, μ, determined with a Zetasizer Nano Z (Malvern) in pure Milli-Q. The dispersions were highly diluted (0.01 wt %) to avoid multiple-scattering effects.

Evaluation of the electrostatic energy

The lock particles were decorated with N_e = 10,000 point charges randomly distributed at their surface. The number of point charges on the key particle was adjusted such that the point charge surface density, defining the mesh size, ρ_L = ${\mathit{N}}_{\mathit{e}}/(4\mathrm{\pi }{\mathit{R}}_{\mathrm{L}}^2)$, was equal on the lock and key particles. The individual charges were then adjusted to match the total charge of the lock and key particles. The electrostatic energy in the LK and $\overline{\text{LK}}$ was then calculated as the sum of pair interactions of the ensemble of opposite charges. The reported results for any given size ratio and ionic strength were derived from the average of five independently generated random charge distributions.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/9/e1700321/DC1

Determination of the entropic contribution for hard lock and key particles

Evaluation of the binding specificity

fig. S1. Geometrical configuration of a particle in a lock-and-key assembly.

fig. S2. Entropic contribution for hard lock and key particles.

fig. S3. Binding specificity dependence of the mixing ratio between lock and key particles.

fig. S4. Binding specificity dependence of the temperature at a constant mixing ratio.

movie S1. Colloidal molecules with tunable valence via lock-and-key self-assembly.