Cooperative deformations of periodically patterned hydrogels

In periodically patterned gels, buckled domains mutually interact and cooperatively deform to minimize total elastic energy.

Abstract

Nature has shown elegant paradigms of smart deformation, which inspired biomimetic systems with controllable bending, folding, and twisting that are significant for the development of soft electronics and actuators. Complex deformations are usually realized by additively incorporating typical structures in selective domains with little interaction. We demonstrate the cooperative deformations of periodically patterned hydrogel sheets, in which neighboring domains mutually interact and cooperatively deform. Nonswelling disc gels are periodically positioned in a high-swelling gel. During the swelling process, the compartmentalized high-swelling gel alternately bends upward or downward to relieve the in-plane compression, but the overall integrated structure remains flat. The synergy between the elastic mismatch and the geometric periodicity selects the outcome pattern. Both experiment and modeling show that various types of cooperative deformation can be achieved by tuning the pattern geometry and gel properties. Different responsive polymers can also be patterned in one composite gel. Under stimulation, reversible transformations between different cooperative deformations are realized. The principle of cooperative deformation should be applicable to other materials, and the patterns can be miniaturized to the micrometer- or nanometer-scale level, providing the morphing materials with advanced functionalities for applications in various fields.

INTRODUCTION

Smart deformations are widespread in nature and significant in both fundamental science and engineering applications (1–5). For example, the Venus flytrap snap closes its leaves to catch insects via a controlled fluid flow between the inner and outer surfaces of the leaf (1). Wheat awns, pinecones, and bean pods show hydration-triggered deformations, which are crucial to the dispersal of seeds (2–4). These deformations are closely related to the typical out-of-plane and in-plane gradient structures or their combinations, which build up internal stresses under external stimuli.

Inspired by Mother Nature, scientists have realized controllable deformations including bending, folding, and twisting (4–12). In a seminal work, Hu et al. developed gels with a bilayer structure (8). Under stimulation, the differential swelling or shrinkage in different layers leads to bending or folding deformations of the composite gels. In recent years, researchers have found that in-plane heterogeneities could also lead to programmed internal stresses and three-dimensional (3D) deformations (13–15). For example, planar hydrogels patterned with different compositions or cross-linking densities buckle into 3D shapes (14, 15). In particular, sheet discs with varying swelling ratios along the radial direction have been investigated both experimentally and theoretically (13, 16–18). A disc buckles into a dome-like shape or develops edge wrinkles when the central part swells more or less, respectively. The embedded structures corresponding to typical deformations are stackable to form an integrated system with programmable complex deformations and elaborate configurations (9, 10, 19, 20), facilitating the tuning of morphing structures and the design of soft actuators toward specific applications (5, 6).

When neighboring units of deformation mechanisms are close enough, the local mode of deformation may be affected by the deformation of neighboring units, and the overall deformation patterns tend to be cooperative. Recently, Mullin et al. (21) have found cooperative pattern transformation in periodic cellular elastomers that were subject to in-plane compression. The circular holes in a square lattice collapse into alternately oriented ellipses due to the cooperative elastic instability, providing the material with negative Poisson’s ratio and iridescent colors (22, 23). Not only do the in-plane deformations of periodic structures tend to influence each other: The out-of-plane buckling of periodically patterned structures is also likely to be cooperative. However, the latter has seldom been studied. In addition to the bending and stretching energies of each individual unit, the elastic interplay among neighboring units, as well as the constraints from geometric symmetry and periodicity, should play a significant role in determining the overall mode of deformation. Moreover, when each buckled unit has several stable or metastable states of equilibrium, the entire structure has a gigantic configuration space. What the overall cooperative buckling mode is and how the modal selection relates to the original planar design are yet to be studied.

Here, we demonstrate the cooperative deformations of 2D periodically patterned hydrogel sheets, which spontaneously deform into 3D alternating concave-convex configurations, as governed by the landscape of total elastic energy. By photolithography, the composite gel sheets are prepared with nonswelling gels that are dispersed in high-swelling ones. The mismatch strain due to the difference in swelling ratio leads to 3D deformations that are highly cooperative. The patterned hydrogels with nonswelling discs in square lattices undergo cooperative deformation, where the compartmentalized square pattern is the basic unit, whereas those with discs in hexagonal lattices exhibit two modes of cooperative deformation, where either the triangular or rhombic pattern is the basic unit. The distinct cooperative deformations only occur when the distance between the nonswelling regions is in a specific range. The selection between triangular and rhombic modes depends on the dimensional parameters and gel properties. The mode of cooperative deformation can also be controlled by tuning the swelling mismatch. By selective preswelling of specific regions, different modes are settled in one patterned gel. Other cooperative deformations and elaborate configurations are developed by tuning the periodic patterns. The principle and approach of cooperative deformations should be applicable to other responsive materials or can be miniaturized down to micrometer or nanometer scales, resulting in morphing structures toward applications in controllable wettability and soft robotics.

RESULTS

Fabrication of patterned gels and their cooperative deformations

The periodically patterned gels are prepared by two-step photopolymerization, as shown for the representative case with discs in a square lattice in Fig. 1. An array of disc gels is fabricated by photolithographically patterning a precursor solution. The photoinitiated polymerization leads to the formation of polyacrylamide (PAAm) gels in the light-exposed regions, whereas no gel forms in the light-protected regions. After the residual solution was removed, another precursor solution was injected into the interspace between the preformed disc gels, followed by photopolymerization without a photo mask, producing poly(acrylamide-co-2-acrylamido-2-methylpropanesulfonic acid) [P(AAm-co-AMPS)] gels surrounding the PAAm disc gels that formed in the first step. The resulting periodically patterned gel sheet consists of regions with distinct swelling capacities, which leads to the buildup of in-plane stress and thus the 3D deformation of the gel upon swelling in water (13, 16). The dispersed PAAm disc gels are nonswelling, whereas the P(AAm-co-AMPS) gels are high-swelling (Table 1). Each compartmentalized P(AAm-co-AMPS) region is surrounded by four PAAm disc gels. The constraint leads to upward or downward buckling of the high-swelling domain. The neighboring domains usually buckle in opposite directions to reduce the curvature at the connection area, thus minimizing the global elastic energy (fig. S1). Under this synergistic interplay, the integrated patterned gel finally deforms into an alternating concave-convex configuration, but the overall morphology remains flat.

Fig. 1. Photolithographic patterning of gel and swelling-induced cooperative deformation.

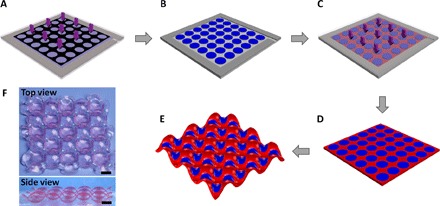
(A) A precursor solution in the reaction cell was exposed to ultraiolet (UV) light irradiation through a mask to produce patterned gels in the light-exposed region. After the residual solution was removed (B), another precursor solution was injected into the interspace between the preformed gels (C). (D) Subsequent photopolymerization without a mask produced an integrated patterned gel. (E) After the periodic patterned gel was swollen in water, it deformed into an alternating concave-convex structure. Blue and red areas correspond to nonswelling and high-swelling gels, respectively. (F) Images of corresponding swollen patterned gel. Scale bars, 1 cm.

Table 1. Swelling ratio in length, λ, and Young’s modulus, E, of the gels.

Gels	λ	E (kPa)
P(AAm-co-AMPS) (as-prepared)	—	48.2 ± 2.1
P(AAm-co-AMPS) (swollen)	1.73 ± 0.02	25.0 ± 1.3
PAAm (as-prepared)	—	40.1 ± 1.8
PAAm (swollen)	1.06 ± 0.01	50.3 ± 2.4

The deformation process of a patterned gel with discs arranged in a square lattice is shown in fig. S2A. The cooperative deformation starts to appear within 1 min and further increases its amplitude with the swelling time until a stable configuration is reached. It appears that the local deformation of each domain is “aware” of the neighboring ones even under a relatively small in-plane stress so that they mutually interplay and cooperatively deform (24).

The alternating convexity does not uniquely determine the deformed profile of a patterned gel, which further depends on the pattern geometry, including periodicity and symmetry. The periodic pattern of gels can be easily tuned by designing the photo masks that are used for photolithography (Fig. 2A). The patterned gels with discs arranged in hexagonal lattices exhibit two distinct cooperative deformations. When the radius of PAAm disc gels, R, is relatively small, the patterned gel shows triangular-mode cooperative deformation, where the basic unit consists of three disc PAAm gels and the central P(AAm-co-AMPS) gel (Fig. 2B). On the other hand, when R is relatively large, the patterned gel shows rhombic-mode cooperative deformation, where the basic unit consists of four nonswelling disc gels and the central high-swelling gel (Fig. 2C). The threefold symmetry is broken, whereas the periodicity is retained. The resultant configuration of composite gel has relatively large undulations along the long axis of the rhombus. The neighboring nonswelling discs have an offset in the vertical direction that is different from the triangular mode, which gives rise to the larger overall amplitude (fig. S3). The deformation processes are similar to those of the patterned gel with a square lattice. The mode of cooperative deformation is determined in the initial 1 min, and the amplitude of buckling gradually increases afterward (fig. S2, B and C). We should note that the alternating concave-convex structure of patterned gels is very stable once it is fully developed. Perturbations, such as pressing one convex domain, do not change the periodic configuration.

Fig. 2. Influence of pattern dimensions on deformations of gels.

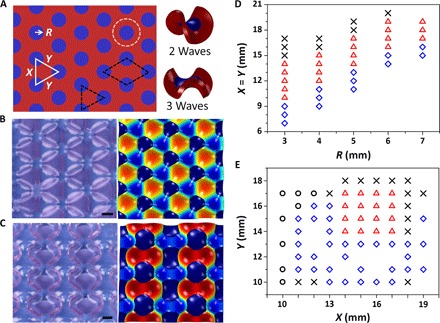
(A) Scheme to show the dimensions of the as-prepared patterned gel. The nonswelling disc gels are arranged in a hexagonal lattice. The black dotted line indicates the base unit of deformation (triangular or rhombic). The orange dotted line indicates the shape of a concentric gel disc, which would deform into different configurations (schematic in the right). (B and C) Representative configurations of the swollen composite gels in water: triangular-mode (B) (X = Y = 15 mm, R = 5 mm) and rhombic-mode (C) (X = Y = 15 mm, R = 6 mm) cooperative deformations. Left: Images. Right: Modeled configurations. Scale bars, 1 cm. (D and E) Phase diagram of the deformations of patterned gels with different dimensions: (D) different R (X = Y) and (E) different X and Y (R = 5 mm). Symbols ◊ and Δ indicate the rhombic- and triangle-mode cooperative deformations, respectively. Symbols ○ and × indicate the rolling and random deformation (without cooperativity), respectively. The thickness of the as-prepared gel is 1 mm.

Principle of cooperative deformations

To understand the principle of the cooperative deformations of the gels, periodically patterned gels with different dimensions are fabricated. The PAAm disc gels are arranged in a hexagonal lattice (Fig. 2A). The interdisc distances (X and Y; center to center), as well as the radius of disc gels, R, are systematically varied to investigate the mode selection of the cooperative deformation. The phase diagrams of deformation modes relative to the pattern dimensions are summarized in Fig. 2 (D and E); representative images are shown in fig. S4. For the lattice with equilateral triangles (X = Y), the patterned gels show rhombic- and triangular-mode cooperative deformations when 2R + 1 ≤ X ≤ 2R + 3 and 2R + 4 ≤ X ≤ 2R + 7, respectively (the unit of X, Y, and R is in millimeters, and the thickness of the as-prepared gel is 1 mm). Evident cooperative deformation is absent when X > 2R + 8 (Fig. 2D). This result indicates that the buckling deformation of compartmentalized domains becomes cooperative at a special distance, termed cooperative distance. Beyond this distance, the localized deformation will not effectively influence the surrounding ones. When R is fixed (R = 5 mm), variations of X and Y also result in similar cooperative behaviors (Fig. 2E). When X = 10 mm, the disc gels in the row connect with each other, and the integrated gels become analogous to the patterned gels with parallel stripes, leading to rolling deformation (15, 25).

On the basis of experimental observations and numerical modeling detailed below, such a phenomenon is mainly determined by elastic mismatch and geometry. Beyond a critical mismatch in swelling, each compartmentalized high-swelling region buckles out of plane (upward or downward) to relieve the in-plane compressive stress. The modes of deformation between the neighboring domains synergistically collaborate to minimize elastic energy. To further understand the principle of cooperative deformation, numerical studies were carried out using a finite element method. The actual swelling process involves concurrent solvent migration and deformation, the direct simulation of which is challenging, especially near the critical points of buckling. To capture the governing physics without going into too much detail, we simplified the model by assuming uniform swelling in each gel and by treating the swollen gels as incompressible neo-Hookean materials (26). The unit cells of the patterned gels are adopted, with symmetric or periodic conditions prescribed on the boundaries. From the deformation fields computed by finite element methods, the total elastic energy of a unit cell is evaluated at the mechanical equilibrium state of each buckling mode, and a comparison among geometrically possible modes suggests the actual mode of appearance. Modeling details are summarized in note S1. The computed profiles of the cooperative deformations in both triangular and rhombic modes are consistent with those in the experiments (Fig. 2, B and C). The difference in elastic energy between the two modes varies with the mismatch strain $\mathsf{ϵ}$, defined as $\mathsf{ϵ}={\mathrm{\lambda }}_{\mathrm{H}\mathrm{S}}/{\mathrm{\lambda }}_{\mathrm{N}\mathrm{S}}-1$, in which λ_HS and λ_NS are the linear swelling ratios of the high-swelling and nonswelling gels, respectively. Typically, the rhombic pattern is energetically more favorable when the mismatch is relatively small (fig. S5A), similar to the results of Euler buckling in which the mode of longer wavelength appears earlier and has lower energy (27). However, under a relatively high swelling mismatch, the triangular mode takes over and energetically becomes more favorable. This is because the stiffer nonswelling discs constrain the large out-of-plane bulging of the high-swelling gels, and the triangular mode involves less deformation in the discs, as shown in Fig. 2B. The energy profile also depends on the distance between neighboring discs and the modulus difference of the gels (fig. S5B). Although the triangular mode should prevail in all cases at relatively large swelling mismatches, the switching from a rhombic mode to a triangular mode needs to overcome an energy barrier. Therefore, the mode selection of cooperative deformations is also affected by the swelling process. The competition between the elastic mismatch and the geometric constraint due to the symmetry and periodicity of the patterns, together with the kinetic swelling process, determines the observed collaborative deformation modes. Nevertheless, the detailed deformation during the transition between the two patterns is still not clear, making it difficult to evaluate the energy barriers. Moreover, the less constrained free edges of the actual gel samples would also affect the energy barriers but are not accounted for in the numerical models.

Controllability of cooperative mode

The cooperative deformations are induced by the swelling and geometric mismatch, which can be directly tuned by the ionic strength of incubated solution that influences the electrostatic repulsion within P(AAm-co-AMPS) (15). The hexagonally arranged patterned gel with R = 5 mm and X = Y = 15 mm shows triangular-mode cooperative deformation when it is directly swollen in pure water, which reversibly transforms into a flat configuration in 0.15 M NaCl solution (Fig. 3A). However, the flat sheet shows rhombic-mode cooperative deformation after the gel was transferred to 0.02 M NaCl solution. After its further transfer to pure water, the gel retains its configuration with increased buckling amplitude. Therefore, an identical patterned gel is programmable to settle to triangular- or rhombic-mode cooperative deformation by controlling the swelling process. Direct transformation between the two modes needs to overcome a large energy barrier and is not feasible. However, indirect transformation via an avenue with saline solution is possible. The different mode of cooperative deformation is related to the different swelling mismatch, which decreases with the increase in NaCl concentration (C_NaCl) of the incubated solution (Fig. 3B). A relatively large mismatch leads to the triangular mode, whereas a small mismatch leads to the rhombic mode, consistent with the modeling results.

Fig. 3. Switching of cooperative mode by controlled swelling process.

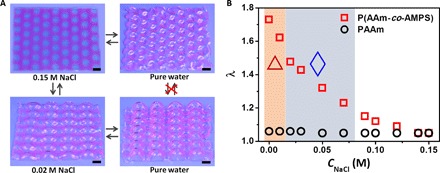
(A) Reversible shape transformation between the triangular- and rhombic-mode cooperative deformation and flat shape with variation in NaCl concentration. Scale bars, 1 cm. (B) Swelling ratio in length λ of PAAm and P(AAm-co-AMPS) gels as a function of saline concentration, C_NaCl. The corresponding modes of cooperative deformation are also shown.

Aside from tuning the cooperative mode of integrated composite gel, manipulating the distinct local regions with the selected mode of cooperative deformations is more challenging. This is achieved by selective preswelling of specific regions before the free-swelling process of the patterned gel (28). The resulting patterned gel with discs in a hexagonal lattice (R = 5 mm, X = Y = 15 mm) was put on a glass substrate, and then a mask with holes was put on top of the gel. Immersing the sample in water for a certain period leads to the local swelling of the gel under the holes, whereas the other regions are protected from swelling. When rhombic holes were put on the prescribed high-swelling region amongst the four nonswelling disc gels, the preswelling led to rhombic-mode cooperative deformation of the gel with controllable orientation after the mask was removed and the patterned gel was swollen subsequently in pure water. Holes with different shapes and positions can be settled in one mask, directing different modes of cooperative deformations in one well-arranged patterned gel (Fig. 4). This approach, together with the shape transformation mediated by saline solution, should facilitate reversible and programmable switching from one complex configuration to another in the same patterned gel.

Fig. 4. Control of cooperative deformations by selective preswelling.

A mask with holes was put on top of the patterned gel to selectively swell the regions under the holes, leading to programmed cooperative deformations after the gel was further swollen in water. (A and B) Mask (A) and the corresponding combined triangular- and rhombic-mode cooperative deformations in one composite gel (B). (C and D) Mask (C) and programmed cooperative deformations with desired mode and direction (D). Scale bars, 1 cm.

Complexity of cooperative deformations

The principle of cooperative deformation is also applicable to other patterns of composite gels to form various configurations (Fig. 5). If the disc PAAm gels are changed to square ones, then the squarely arranged patterned gel shows similar cooperative deformation; however, the localized buckling has a cubic shape (Fig. 5A). When the PAAm gels in the square lattice are inclined ellipses (at 45° with respect to the horizontal direction), the bulged pattern no longer exhibits the cubic shape with a fourfold symmetry (Fig. 5B). When the PAAm gels are ellipses with alternating but orthogonal orientations (at ±45° with respect to the horizontal direction), the bulged pattern appears asymmetric out of plane, that is, the bulging-up and bulging-down domains are in different sizes (Fig. 5C). Frustrated arrangements of nonswelling gels can also be combined into one periodic pattern, such as the square and rhombic arrangements of discs in Fig. 5D. The compartmentalized square and rhombic regions cooperatively bulk upward and downward to form an asymmetric configuration. When the nonswelling disc gels are arranged in a kagome lattice, the compartmentalized, relatively small triangular and large hexagonal domains buckled cooperatively into opposite directions. The modeled configurations of these composite patterned gels coincide with the experimental ones. More complex cooperative deformations and resultant configurations should be obtained by preparing the gels with well-designed patterns (29). The periodic patterns can be miniaturized to the micrometer- or nanometer-scale level (14, 30, 31), providing the gels with versatile functions after cooperative deformation (4, 32).

Fig. 5. Control of cooperative deformations by using different masks.

Periodically patterned gels with square arrangement of square PAAm gels (A), square arrangement of elliptic PAAm gels with identical orientation (B) or orthogonal orientation (C), combined square and rhombic arrangement of disc PAAm gels (D), and kagome arrangement of disc PAAm gels (E). The masks and modeled configurations are above and below the images of deformed patterned gels, respectively. The white and black regions of the mask correspond to nonswelling PAAm gel and high-swelling P(AAm-co-AMPS) gel, respectively. Scale bars, 1 cm.

Multiple shape transformations

The cooperative deformations and resulting configurations are closely related to the dispersion periodicity of the nonswelling gels. The periodicity can be modulated when multiple responsive polymers are incorporated into one composite gel by multistep photolithography (15, 33, 34). Selective actuation of one periodically dispersed gel results in distinct cooperative deformations that are switchable under different stimuli (Fig. 6). As shown in Fig. 6A, pH-responsive poly(acrylic acid) (PAAc) and poly(acrylamide-co-1-vinylimidazole) [P(AAm-co-VI)] disc gels are patterned with different periodicities (that is, in a square lattice but in a different orientation) in the P(AAm-co-AMPS) gel. At pH 2, the PAAc discs are nonswollen, but the P(AAm-co-VI) discs and P(AAm-co-AMPS) gel are highly swollen with similar swelling ratios (Table 2). Therefore, the composite gel cooperatively deforms to form alternating concave-convex configuration (Fig. 6B). At pH 10, the P(AAm-co-VI) discs become nonswollen, whereas the PAAc discs and P(AAm-co-AMPS) gel are highly swollen, leading to cooperative deformation to form another configuration (Fig. 6C). The two pH-responsive disc gels can also be combined to form one periodic pattern (square arrangement), in which PAAc discs have larger periodicity (Fig. 6D). At pH 2, only PAAc discs are nonswollen and the composite gel undergoes square-mode cooperative deformation (Fig. 6E). At pH 7, both PAAc and P(AAm-co-VI) discs are nonswollen; therefore, the structural periodicity of the configuration becomes half of the previous one (Fig. 6F). These shape transformations are reversible in at least three cycles. In principle, more responsive polymers can be patterned to form an integrated composite gel so that shape transformations between more distinct configurations can be achieved. The transformation of cooperative deformations should help in the design of morphing structures.

Fig. 6. Shape transformations of composite gels patterned with multiple responsive polymers.

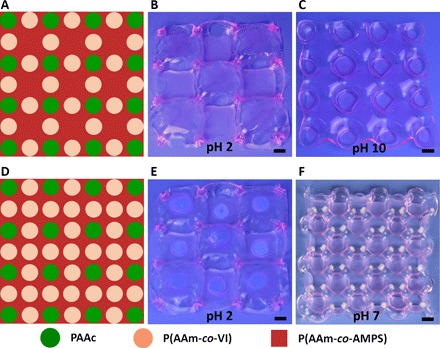
PAAc and P(AAm-co-VI) gel discs positioned in P(AAm-co-AMPS) gel with square arrangement but different orientation (A) or different periodicity (B) and their distinct cooperative deformations under different pH values. Scale bars, 1 cm.

Table 2. Swelling ratio in length, λ, and Young’s modulus, E, of the gels under different pH values.

Gels	λ			E (kPa)
	pH 2	pH 7	pH 10	pH 2	pH 7	pH 10
PAAc	0.96 ± 0.01	1.01 ± 0.02	1.72 ± 0.03	40 ± 4.3	38 ± 4	20 ± 2
P(AAm-co-VI)	1.64 ± 0.02	1.02 ± 0.01	1.11 ± 0.01	30 ± 3	65 ± 5	60 ± 4
P(AAm-co-AMPS)	1.67 ± 0.02	1.75 ± 0.02	1.75 ± 0.02	32 ± 1	25 ± 1	25 ± 2

CONCLUSIONS

Cooperative effects are prevalent in biology and chemistry and have brought astonishing phenomena and functions to them (35). Here, we demonstrate the cooperative deformation of hydrogels with periodic patterns, which results in the formation of alternating concave-convex configuration. The expansion of high-swelling regions is constrained by the nested nonswelling regions, leading to upward or downward buckling of the compartmentalized domains. In the periodically patterned gel, the localized deformations influence the neighboring ones; therefore, cooperative deformation occurs to minimize the elastic energy of the gel, especially at the connection area. Squarely arranged patterned gels show single configuration, whereas hexagonally arranged patterned gels show triangular- or rhombic-mode cooperative deformations. The cooperative deformation only occurs when the distance between the nonswelling regions is in a special range. Both experimental and modeling results indicate that the mode selection of cooperative deformation depends on the pattern dimensions and gel properties. Different modes of cooperative deformations or their transformation can be realized in one identical patterned gel with nonswelling discs that are arranged in a hexagonal lattice by using saline water or selective preswelling to control the initial swelling mismatch. Other cooperative deformations and resultant configurations of patterned gels can be developed by controlling the gel components and periodic patterns. By multistep photolithography, different responsive polymers were patterned in one integrated gel to realize step-by-step cooperative deformations and configuration transformations reversibly triggered by external stimuli. The current work should significantly enrich the possible modes of deformation. The principle of cooperative deformation should be applicable to other materials such as elastomers, shape memory polymers, and hybrid polymer-inorganic materials (36–39), and the dimensions of patterns can be miniaturized to the micrometer- or nanometer-scale level, which might provide deformed sheet materials with versatile physical properties for specific applications in optical devices and soft robotics.

MATERIALS AND METHODS

Synthesis of periodically patterned hydrogels

The patterned gel was fabricated by a two-step photopolymerization, as shown in Fig. 1. A precursor solution containing AAm, N,N′-methylenebis(acrylamide) (MBAA; a chemical cross-linker), and 2-2′-azo-bis-(2-methylpropionamidine) (V-50; a photoinitiator) was poured into a reaction cell composed of two glass substrates separated with a 1-mm-thick silicone rubber spacer. A photo mask prepared by inkjet printing was placed on top of the reaction cell, which was subjected to UV light irradiation (365 nm, 5 mW/cm²) for 90 s. PAAm gels were formed in the light-exposed regions. After the residual solution was removed and the precursor solution containing AAm, AMPS, MBAA, and V-50 was injected into the interspace between the patterned PAAm gels, the sample was immediately exposed to UV light irradiation without a mask for 60 s. The recipes of precursor solutions for gel synthesis are shown in table S1. The resultant composite PAAm/P(AAm-co-AMPS) gel sheet was swollen in a large amount of pure water, which induced 3D deformations. The configurations of swollen patterned gels were recorded by digital camera. To increase the contrast of the PAAm and P(AAm-co-AMPS) gel regions, trace amount of neutral red was added to the second precursor solution.

Multiple responsive disc gels were incorporated into the composite gel sheets by multistep photolithography. The PAAc disc gels were prepared by patterning the precursor solution. After the residual solution was removed and the precursor solution was injected into the reaction cell, the second photolithographic patterning was conducted by using another photo mask, producing P(AAm-co-VI) disc gels beside the PAAc disc gels. After the residual solution was removed, the third precursor solution was injected into the reaction cell, followed by photopolymerization without a mask, which produced the P(AAm-co-AMPS) gel surrounding the preformed disc gels to form an integrated gel sheet. The composite gel sheet was swollen in solution with different pH values, where they deformed into distinct configurations.

Measurements of the swelling ratio and Young’s moduli of gels

The swelling ratio in length, λ, was calculated by dividing the diameter of the gel in the equilibrated and as-prepared states. The Young’s modulus, E, was measured at room temperature by tensile test (Instron 3343 Tester) of the as-prepared and equilibrated gels. The gauge length of the dumbbell-shaped sample is 12 mm, and the tensile rate is 60 mm/min. The value of E was calculated from the slope of stress-strain curves with strain below 10%.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/9/e1700348/DC1

fig. S1. Schematic of the cooperative deformation of composite gels.

fig. S2. Process of cooperative deformations.

fig. S3. Schematic of the configuration via rhombic-mode cooperative deformation.

fig. S4. Representative configurations of the patterned gels after cooperative deformations.

fig. S5. Energy difference between the buckled states of rhombic and triangular patterns.

fig. S6. Schematic of the deformation states of a gel.

fig. S7. The computational unit cell of a composite gel with PAAm gels in a hexagonal lattice.

fig. S8. Elastic energy profile of concentric composite gel as functions of the mismatch strain.

fig. S9. Deformation of concentric composite gels.

table S1. Recipes of precursor solutions for the synthesis of gels.

table S2. Modeled wrinkle numbers of the concentric composite gels with different inner and outer diameters.

table S3. Experimental wrinkle numbers of the concentric composite gels with different inner and outer diameters.

note S1. Detailed theoretical modeling.

Reference (40)