Health care demand elasticities by type of service

Abstract

We estimate within-year price elasticities of demand for detailed health care services using an instrumental variable strategy, in which individual monthly cost shares are instrumented by employer-year-plan-month average cost shares. A specification using backward myopic prices gives more plausible and stable results than using forward myopic prices. Using 171 million person-months spanning 73 employers from 2008–2014, we estimate that the overall demand elasticity by backward myopic consumers is −0.44, with high elasticities of demand for pharmaceuticals (−0.44), specialists visits (−0.32), MRIs (−0.29) and mental health/substance abuse (−0.26), and lower elasticities for prevention visits (−0.02), and emergency rooms (−0.04). Demand response is lower for children, in larger firms, among hourly waged employees, and for sicker people. Overall the method appears promising for estimating elasticities for highly disaggregated services although the approach does not work well on services that are very expensive or persistent.

1. Introduction

This paper revisits the classic issue of price elasticities of demand for health care services, a topic of central importance for understanding moral hazard and optimal insurance plan design, as well as having important implications for health plan choice, access to care, health care cost containment, risk adjustment, and financial risk. Moreover, since modern insurance plans incorporate highly specific benefit plan features in their designs, and these features can be customized for demographic, employment, or geographically-defined groups, understanding demand responses for disaggregated service types is of significant policy interest. In this paper we use a novel instrumental variable technique on a very large sample (171 million person-months) to generate estimates of short-run price elasticities of demand among the privately insured for both aggregated and disaggregated types of services and population subgroups. Many of our elasticities, particularly for services that are not widely used (e.g., MRIs, mental health/substance abuse treatment, lab tests, and ambulance use), are infeasible to estimate on small or modest size samples.

A notable challenge when estimating price elasticities of demand for health care is to control for endogeneity of prices stemming from endogenous health plan choice. Several estimation strategies have been used in previous studies to overcome this difficulty, including randomized control trials (RCTs) (Manning et al. 1987), natural experiments (Duarte 2012; Brot-Goldberg et al. 2017), and instrumental variable strategies (Eichner 1998; Einav et al. 2015; Kowalski 2016; Scoggins and Weinberg 2016). Manning et al. (1987) estimated health care demand responses using RCT data from the RAND Health Insurance Experiment (HIE) conducted in the mid-1970s, with path-breaking results, but the HIE sample size of 6000 individuals limited its ability to generate estimates of demand response other than for broad categories of services and large subpopulations.

Since RCTs are expensive and rare, many studies have exploited natural experiments that induce changes in prices to estimate demand responsiveness. Duarte (2012) is a good recent example: he uses Chilean data with a large number of diverse health plans to study the demand response of both elective (home visits, psychologist visits, physical therapy evaluations) and acute (appendectomy, cholecystectomy, arm cast) health care services when government mandates forced employers to increase their coverage generosity. In the similar spirit, Brot-Goldberg et al. (2017) exploit a natural experiment in health insurance coverage when one large company forced all of its employees to switch to a high-deductible plan. They find a considerable demand response, even among sick people who should expect to exceed deductibles and face low end-of-year prices, suggesting that many people are myopic, and respond strongly to the spot prices at the time of care is received, and not only the more theoretically correct expected end-of-year price.

A final approach for estimating unbiased elasticities is to use instrumental variables to control for the endogeneity of prices (cost shares) within a given year. Eichner (1998) proposes a novel instrument for within-year price variation: the occurrence of accidental injuries (e.g., a broken leg) by dependents as an exogenous event that changes subsequent cost sharing and hence affects the employee’s own demand for medical care. Building on the Eichner framework, Kowalski (2016) uses emergency department spending for injuries by other family members in households with at least four members for her estimation of demand responsiveness, where the instrument (whether a family member incurs spending for an injury) derives its power from the fact that the event increases the likelihood that the family deductible or stop loss can be exceeded, thus reducing the marginal price of care faced by the remaining household members. Einav et al. (2015) use government changes in the Medicare Part D coverage for prescription drugs as an instrument to study consumer responses to cost sharing, while Scoggins and Weinberg (2016) use the plan characteristics as an instrument for the actual observed cost share in claims data. In each case the instrument is based on information that is arguably exogenous to the individual’s own health expenditure experience.

The two main contributions of this paper are its use of a readily-available and powerful new instrument, and its use of extremely large data which gives us the power to estimate elasticities for disaggregated health care services. In our sample, each person contributes twelve monthly observations on endogenous cost sharing and spending decisions. We include person-year fixed effects that also absorb all aspects of the employer, health plan, locality, supply side prices and availability, family, and individual patient health and taste variation from estimation, and then estimate elasticities using monthly data. We also control for seasonality and time trends using monthly dummies. We argue that the remaining variation in individual within-year cost sharing comes only from the effect of nonlinear price schedules in health plans created by deductibles and stoplosses, which we use to estimate the effects of cost sharing on demand. To control for cost sharing endogeneity, we use the employer-, year-, and plan-level “leave out one” average monthly cost share as an instrument for individual cost shares, exploiting the fact that different firms, and different health plans have widely different within-year variation in their cost sharing. We provide evidence that these employer average cost shares at the plan level have considerable power and are very weakly correlated with the average health status of plan enrollees.

We estimate elasticities using commercial claims data from 2007–2014 on 171 million person-months, which allows us to estimate elasticities for very detailed types of health care services, not usually possible due to the low utilization rates for many such services. Understanding how consumers react to changes in cost shares for specific services is important to understand how insurers design their health plans to control for moral hazard and to select services to offer. In that sense, our paper is similar to Einav et al. (2016), which estimates demand elasticities for more than 150 pharmaceutical drugs in Medicare Part D.

We are not aware of any other research studies that have used employer-year-plan level average monthly cost shares as instruments. Our instrument does not rely on any detailed characteristics of health plans, such as the actual value of deductibles, copayments, and coinsurance rates, which makes it a useful instrument for large claims data with few employer, plan, geographic, household, or individual level variables. The method can readily be used to model spending or utilization at any level of aggregation or subsample including at the level of individual procedures and drugs.

A central difference between the approach used here and other papers on health spending demand elasticities is that we focus on price responsiveness due to myopic consumption behavior, which results from changes in spot prices, rather than forward-looking, expected end-of-year prices. A growing literature has shown that consumer myopia is important, whether due to present bias, behavioral errors such as imperfectly understanding ones health plan, or liquidity constraints (Aron-Dine et al. 2015; Brot-Goldberg et al. 2017; Ericson 2017). As discussed further below, our identification strategy relies upon myopia being a significant determinant of demand response.

Let us give a glimpse of our findings before proceeding. We find clear evidence of short run response to within-year variations in cost sharing. We explore two types of price expectations, which we call backward myopic and forward myopic, and argue that they provide upper and lower bounds for the myopic spot prices consumers seem to use when deciding how much to spend on each type of health care service in a given month. Our two myopic prices generate demand elasticities that are quite similar for commonly used services, but backward myopic assumption generates more stable results for rarely used services. We estimate elasticities of −0.44 for backward myopic expectations versus −0.41 for forward myopic expectations. This estimate is consistent with the Manning et al (1987) estimate of −0.2 and the Aron-Dine et al. (2013) reestimation using the HIE data, which is −0.5. We find heterogeneity in the price elasticity of demand across services, health plans, and population subgroups. The highest elasticities are for pharmaceuticals (−0.44), specialty visits (−0.32), and spending on mental health/substance abuse (−0.26), and the lowest elasticities are for prevention visits (−0.02), emergency rooms (−0.04) and mammogram (−0.11). Supporting Einav et al. (2013), we find evidence of not only biased selection but also heterogeneity in price responsiveness, with consumers in health plans that have large changes in cost sharing (e.g., HDHP) yielding higher estimated demand elasticities than HMOs. Demand elasticities also vary modestly by enrollee age, risk scores, time, single versus family coverage, salary versus hourly wage earners, industry, firm size, and firm level average costing.

2. Data

We use IBM/Truven Health MarketScan Commercial Claims and Encounter Database from 2007 to 2014 to identify and extract the claims and enrollment information for all large employers with at least three years of enrollment information and identifiable plan identifiers. We checked for but did not find any employers with annual plan enrollment periods other than the calendar year. We included all individuals, aged 0 to 64, eligible for the full 12 calendar months of the year, and remaining in the same identified health plan, identified using MarketScan’s Plankey, a unique health plan identifier. We require at least one month of eligibility in the year prior to the prediction year, in order to be able to use lagged information for the evaluation (but not estimation) of our results. We sum up total covered payments and out-of-pocket (OOP) payments in each calendar month for various types of services. All dollar amounts were converted into December 2014 dollars by dividing by the appropriate monthly personal consumption expenditure (PCE) deflator for health care costs from the US Bureau of Economic Analysis. Monthly spending was also adjusted for the number of days in the month to remove this minor monthly variation in spending.

For observations in which monthly spending by an individual is positive, we define the cost share as the ratio between out-of-pocket spending and total spending. Negative or less than $1 of spending was reset to zero, as likely reflecting payment adjustments, not actual service provision. Knowing the value of the counterfactual cost share if the individual had positive spending is of considerable interest for studying the decision to seek care, yet there is little information about how such expectations are formed. We discuss below our approach for assigning service specific cost shares (i.e. prices) relevant to consumers for choosing spending levels. We also conduct sensitivity analysis of dropping plans that rely heavily on copayments rather than cost sharing since incentives and responsiveness could potentially be quite different.

Although the plan type of each health plan is not used in our estimation approach, we use plan types to evaluate our results. For this study we included only people enrolled in one of the following six plan types: health maintenance organization (HMO), point of service (POS), preferred provider organization (PPO), comprehensive (COMP), consumer-directed health plan (CDHP) and high deductible health plan (HDHP). MarketScan differentiates the CDHP and HDHP from other plan types not by the size of their deductibles but instead by whether there is a flexible spending account (CDHP), a health savings account (HDHP), or neither (PPO or POS). Some PPO or POS plans have high deductibles, while not all CDHP have high cost sharing.

Our final estimation sample used here has data from 73 employers with 732 plans and information on 14.2 million individual years in six plan types (Table A-1). The mean age is 34.1 years (Table A-2), and average annual total covered spending is $4,648. This large panel enables us to estimate own-price demand elasticities not only for common, but also for relatively rare health care services, as well as for various employee and population subgroups. To illustrate our method, we estimate elasticities for both for broad categories of services (inpatient, outpatient, and pharmacy) as well as for a variety of non-exhaustive specialized types of service (for example, ER, chiropractic, MRIs, PET scans, ambulance). Table 1 display summary statistics for the categories of services modeled here.

Table 1.

Monthly summary statistics on the study variables, by Types of Service (TOS)

Type of Service	Mean Monthly Spending	% Total Spending	Std. Dev	Mean cost share (%)	% obs. Positive spending	Mean spending if positive
All Spending	387	100.00	2,968	31.06	46.35	836
Outpatient	222	57.27	1,397	27.34	32.15	690
Inpatient	80	20.68	2,408	8.62	0.42	19,096
Pharmaceutical	85	22.05	519	40.76	34.24	249
Maternity	12	3.22	433	18.66	0.39	3,232
MH/SA	11	2.84	303	29.77	3.00	366
ER	19	4.97	289	25.09	1.42	1,355
Room and Board	31	8.13	1,497	9.47	0.26	11,920
Non specialty visits	26	6.66	220	28.18	17.14	151
Home visits	1	0.26	108	7.60	0.08	1,219
Prevention	5	1.23	27	4.28	3.48	137
Surgical procedures	8	1.98	538	4.05	0.07	11,554
Surgical supplies/devices	5	1.31	406	4.86	0.06	7,977
Specialty visits	63	16.36	775	30.85	9.58	661
Dialysis	3	0.70	253	4.14	0.03	8,337
PT, OT, speech therapy	9	2.29	114	24.36	2.96	300
Chiropractic	2	0.61	21	37.73	2.49	95
CAT scans	6	1.44	130	18.48	0.60	932
Mammograms	3	0.71	33	6.15	1.13	241
MRIs	7	1.70	123	18.49	0.56	1,176
PET scans	1	0.15	46	7.32	0.02	2,467
Radiology - diagnostic	6	1.65	108	22.70	3.41	188
Ultrasounds	3	0.75	42	22.85	1.12	260
Diagnostic services	11	2.72	236	17.20	2.85	370
DME	2	0.64	89	22.17	0.68	362
Ambulances	2	0.53	165	15.30	0.14	1,464

Note: Table reports summary statistics for the 26 types of services (TOS) identified and constructed from the MarketScan Commercial Claims and Encounter Database. N = 170,963,286 individual months.

3. Methodology

3.1. What prices (or cost shares) matter?

For most goods, a consumer can choose how much to spend without worrying about how her own spending may change the marginal prices paid. Deductibles, coverage ceilings, and stoplosses introduce nonlinearities so that consumers should rationally look ahead when making purchasing decisions. In the path-breaking work by Keeler and Rolph (1988), the appropriate price for consumers to use is the expected end-of-year price.¹ Papers that use an expected end-ofyear price to calculate elasticities include Eichner (1998), Kowalski (2016), Aron-Dine et al. (2015), Einav et al. (2015), and Brot-Goldberg et al. (2017).

Although attractive conceptually, there is considerable evidence that consumer decision making is substantially more myopic than the Keeler and Rolph (1988) models suggest, as they themselves recognized.² Aron-Dine et al. (2015) provide three rationales for why consumers may appear myopic: they may suffer from extreme present bias and ignore future prices; they may suffer from behavioral biases and not understand the nonlinear budget set; or they may be liquidity constrained. Aron-Dine et al. reject the null of perfect myopia, but agree that “individual decisions regarding health care utilization likely reflect responses to both the spot prices and (correctly defined) future price”. They also suggest that two types of elasticities may be relevant, a spot price elasticity and a future price elasticity, with different elasticities mattering in different settings. Brot-Goldberg et al. (2017) make the strongest case that consumers are highly myopic in their responses to high deductibles, with no evidence of learning to respond to the true shadow price in the second year after joining a high deductible plan.

In this paper, we focus on short-run demand responses, namely consumer responses to spot prices captured in the monthly cost shares. Consumer responses to these declining monthly spot prices during the year can occur for two different reasons. One reason is that consumers are myopic, and fail to forecast how their current spending affects future prices. The other reason could be that spot prices react to health care shocks in the same direction as the expected end-of-year price, and hence spot prices can be thought of as an imperfectly measured end-of-year price and we correct for this measurement error using an instrumental variable approach. Although these two mechanisms are conceptually distinct, we do not distinguish or test them here. Instead, we estimate short-run responses and summarize them in elasticities, recognizing that this may underrepresent the long run responsiveness, particularly for foreseeable spending.

To implement our approach, we need a way of calculating the consumer’s spot price, which we model as a response to a cost share. Given that there is no cost share information for months in which a consumer did not have any spending, using the actual cost share is not a sufficient strategy without further assumptions about consumer expectations. Furthermore, our data does not include general plan parameters, such as copayments and deductibles that would allow us to predict what the cost share would be in the absence of spending. Some way of reflecting price expectations is needed to fill in all of the missing prices.

We consider two mechanisms of expectations, which likely provide upper and lower bounds on the relevant spot prices. For the upper bound, we assume “backward myopic” expectations, in which a consumer does not know the price until after spending in a month is complete and cost shares are actually observed (e.g., when the bill is received in the mail). In this case the price relevant is some previously observed or assumed cost share, which is a backward-looking framework. We implement this by using the actual monthly cost share for each subsequent month up until another month with positive spending occurs, after which the backward myopic cost share is again revised. In this backward-looking framework, it is easy to define prices after a visit is made, but an initial price is also needed for each consumer before they make a visit, including those who never make a visit. Here we make the assumption that consumers expect that the cost share for their first visit will be the average of the health plans cost share for all other consumers in their first month of seeking care. (If we knew the actual features of our health plans, we might assume that the initial price in a plan with a deductible was one, but our inference approach leads to nearly that same price.) Specifically, for the backward myopic price, we assign to individuals the average January cost share of those working for the same employer and under the same plan in that year.³

The other price expectations process we model is the “forward myopic” consumer. The forward myopic individual not only knows what the cost sharing will be at the time that services are chosen in a month, but also uses that price to make decisions prior to that first visit. Hence if consumer’s first actual visit with a given type of service happens in March, then we use the actual cost share paid in March for that service as the price for all months January through March. If the year ends with a span of one or more months with no visits, we continue the cost share used in the most recent month for the remainder of the year. To complete this model, we again need to model expectations for consumers who never make a visit. Specifically, we impute for all months the January average of those within the same employer and plan.

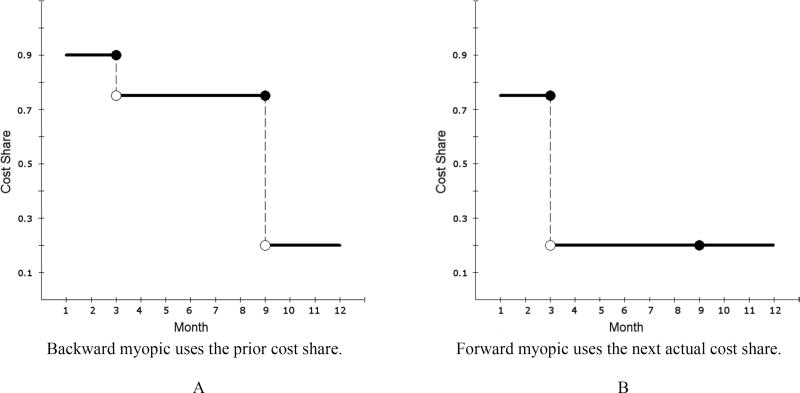
Figure 1 shows a schematic diagram of how prices are assigned for a hypothetical person who makes visits in March and September in a plan with a deductible and followed by stoploss. In panel A, the backward myopic individual made no visits in January, and hence is assigned the average January cost share. The backward myopic consumer uses this same cost share for February and March. In March, this individual obtains care and pays only 75% of the cost, so this new lower cost share is used from April through September. Finally, in October, the consumer observes the 20% cost share from the previous month and adjusts accordingly for the remaining of the year.

Fig. 1. Two models of expectations.

Note: Shown are the backward myopic and forward myopic expected cost shares for a single, hypothetical consumer who makes visits only in March and September, and who experiences an average cost share of .75 in March, and .2 in September. The average cost share for a person making their first visit in January for this employer*year*plan is assumed to be .90. The backward myopic consumer uses this price up through March, then lowers expectations after visits are made in March, and again in October. The forward myopic consumer anticipates the cost shares in March and September and uses them until new information comes along.

In panel B, the forward myopic consumer fully anticipates the March spending even in January. From April onwards, the individual expects the cost share to be what it turns out to be for September, at 20%. Since no further spending occurs for the remainder of the year, this same rate is also used as the forward myopic price through the end of the year. Although the forward myopic consumer is more forward looking than the backward myopic consumer, both are myopic in that they are not forecasting ahead to the end-of-the-year price and instead are using a monthly spot price. Nonetheless, these two prices provide upper and lower bounds on the actual spot prices plausible for each month.

3.2. Estimation equations

We assume health care spending reflects attributes of the individual (i) (which also uniquely defines a household contract), employer (e), whether the plan is for a family or single coverage (f), health plan including its own unique provider network (p), geographic location such as the county or MSA (c), year (y) and a monthly time trend index (t). Using Y for the dependent variable, and CS* to denote the consumer’s cost share (discussed above) relevant for the choice of Y, one strategy would be to directly estimate the following.

$$Y_{\mathit{\text{it}}}=\beta {\mathit{\text{CS}}}_{\mathit{\text{it}}}+{\alpha }_i+{\gamma }_{\mathit{\text{efpy}}}+{\delta }_c+{\lambda }_y+{\gamma }_t+{\epsilon }_{\mathit{\text{it}}}$$ (1)

For this paper we estimate instead the following much simpler specification.

$$Y_{\mathit{\text{it}}}={\alpha \prime }_{\mathit{\text{iy}}}+\beta {\mathit{\text{CS}}}_{\mathit{\text{it}}}+{\gamma }_t+{\epsilon }_{\mathit{\text{it}}}$$ (2)

where ${\alpha \prime }_{\mathit{\text{iy}}}={\alpha }_i+{\gamma }_{\mathit{\text{efpy}}}+{\delta }_c+{\lambda }_y$

This equation estimates the relation between spending and cost share controlling only for individual-year fixed effects and time trend (year-month) fixed-effects, which has the advantage of speeding up computation. Since including individual-year fixed effects controls for all of the individual characteristics that do not vary within the year, we are, in fact, controlling for factors such as age, gender, risk scores, MSA, plans and any other variables that are fixed within a year. The monthly time dummies pick up seasonality, changes in national trends, and the effects of any shocks to the economy (such as recessions). The only covariate over time (in months) is the individual’s monthly cost share.

We now turn to the issue of functional form, and then instrumental variables.

3.3. Functional form

Our dependent variables in model (2) are characterized by a significant fraction of zero spending and a long right tail, a well-known feature of health care spending data. To deal with this using annual data, the convention in the literature is to use the log of annual spending plus one (Aron-Dine et al. 2013, Aron-Dine et al. 2015, Einav et al. 2013, Davis et al. 2016).⁴ Here we modified the convention of adding one to accommodate the fact that we are using monthly rather than annual spending. A priori, we believe using 1/12 makes our results more comparable to other estimated elasticities modeling annual responsiveness and hence chose that as our base specification.

For a sensitivity analysis, we estimated models adding an alternative additive constant within the log specification, a two part model similar to Manning et al (1987) and a specification using the inverse hyperbolic sine transformation (Burbidge et al, 1988). These results are discussed in Section 5 and presented in the appendix.

3.4. Instrumental variables

Since cost shares, including our backwards myopic and forward myopic cost shares, reflect the actual experience of a consumer, they will be endogenous, and using them in OLS for estimation will lead to biased estimates. For a valid instrument, we need our instrument to be correlated with this individual price, but uncorrelated with any demand or supply side shocks that change over time. Note that fixed employer, plan, market or individual characteristics are absorbed by our individual-year fixed effects, so we are looking for instruments that change during the twelve calendar months. The previous studies of Eichner (1998) and Kowalski (2016) used exogenous, individual-level shocks (injuries, and other family member spending decisions) that are time varying. We use instead the monthly average cost shares for consumers in the same employer*year*family/single*plan as our instrument. To purge this measure of direct contamination by a given consumer’s experience, for each person we use the “leave out one” average, which excludes each person’s own contribution when calculating the average. Hence if there are N people in a plan for a given month, we use the average of the N-1 other people in that plan. This measure is exogenous to the individual’s own decisions, but summarizes well the average time path of cost shares due to deductibles, coinsurance and copayments within a given plan. F-tests of the power of our instruments in each first stage regression, which correct for clustered errors, and are discussed in Section 4.⁵

Our IV strategy will lead to unbiased estimates under either of two different assumptions. One assumption is that all consumers are perfectly backward myopic, never anticipating the effect of their own spending in the coming month on the cost share, and hence using a backward view of what the cost share had been in previous months. A second possible condition for unbiasedness is that there is no biased selection, so the health, the degree of foresight, and the demand responsiveness mix of people in every plan is identical. In this case the aggregate average cost share in a plan will also be uncorrelated with errors affecting the individuals own forward looking behavior.

We acknowledge that our instrument is not entirely purged of possible correlation with errors affecting plan choices. For example, if more demand responsive people are more likely to choose high deductible plans (Einav et al 2013), then our elasticity estimate would more closely capture the demand responsiveness of this group rather than that of a random enrollee. The degree to which this might cause bias depends on how much people anticipate their spending behaviors and corresponding effects on health plans’ pricing schedule.⁶ Our study suffers from the problem that any study using natural experiments will suffer from, which is that participation in the experiment is not completely random. In our case the panel data is balanced in that every person is in a single plan for exactly twelve months, but some enrollees face larger declines in spot (and end-of year) prices than others. There is a large literature that has estimated elasticities from such natural experiments.

If people with more foresight or people who are sicker (i.e., have high risk scores) and have chronic conditions are anticipating lower cost shares as well as clustering in more generous health plans, then we should see the average aggregate cost share declining with risk scores. The appendix figure A-1 shows that the average monthly cost sharing is nearly uniformly distributed across different levels of average risk scores, suggesting our data’s approximation to the second assumption.

In sum, we estimate IV linear regression models using the two forms of myopic cost shares as our key variables of interest, while including individual-year and time monthly dummies. We instrument these cost shares with the employer-year-plan “leave out one” average cost shares for the corresponding month. Our dependent variable is log(monthly spending plus 1/12), where 1/12 is chosen to make the elasticity estimates correspond to those from annual data models. Since our model is a log-linear specification, we calculate elasticities from the regression estimates by multiplying the estimated price coefficient by the average cost share for that particular service. Errors are corrected for clustering, assumed to be at the level of the employer-plan-year. Standard errors for the elasticities are generated using the delta method applied to the least squares standard errors.

4. Results

4.1. Graphical results

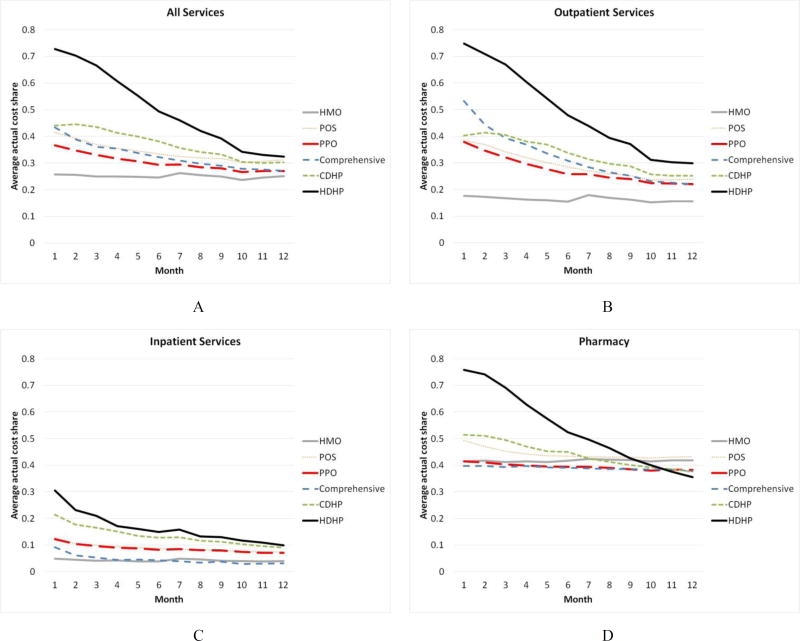
Our identification relies on variation across months in average cost shares as well as variation across health plans in the benefit coverage offered, which are easy to see graphically. Figure 2 shows patterns of average monthly cost shares by plan type. It shows the considerable variation across months, across plan types, and across broad types of service. There is even more heterogeneity in our data in that cost shares vary across employers and over time, which is averaged out in these diagrams. There is also considerable heterogeneity within each single plan type. High deductible plans have the steepest decline in their average cost shares overall, while HMOs have cost shares that remain basically constant. CDHPs, comprehensive plans, PPOs, and POS lie intermediate between the two. Comparing the four panels in the figure, we can see that outpatient spending shows the steepest decline, closely followed by pharmacy spending. Inpatient spending shows a relatively modest decline over months, and is particularly flat for HMOs, as expected since they rely upon supply side controls more than demand side cost sharing to control costs. One surprise is that HMOs have a nearly constant and relatively high cost share for pharmacy spending (reflecting a nearly fixed copayment level) and charge a higher cost share than many other plan types by December.⁷

Fig. 2. Average monthly cost share by plan type, 2008–2014.

Note: Each panel plots the average actual cost share for the services indicated by month, averaged over the seven year period for each plan type for the 73 employer sample. People not using a service in the month are excluded.

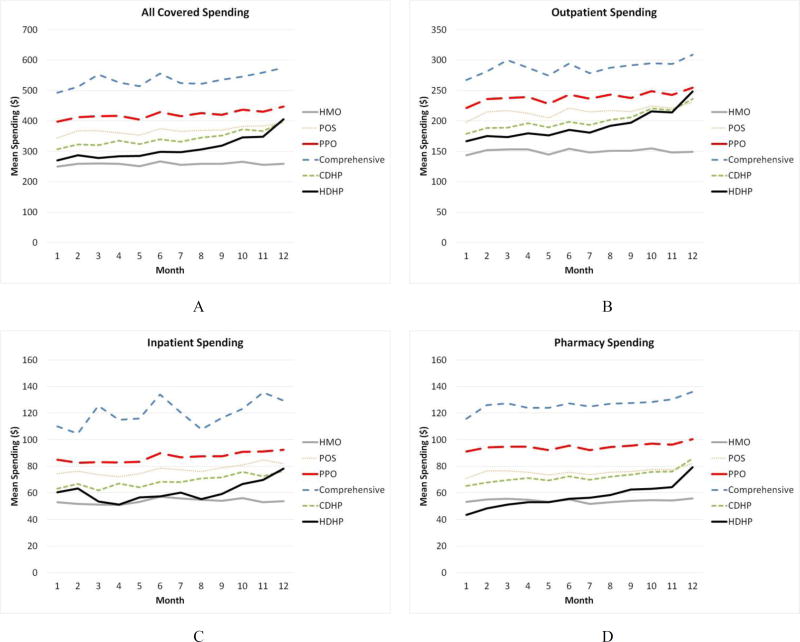
If health care spending is responsive to within-year declines in cost sharing, and spot prices affect spending, then it must be that spending increases during the year. And since cost sharing declines more in the HDHPs, CDHPs, and PPOs than other plan types, this increase should be greater for these plan types than for HMOs. We are not aware of any previous study that has documented this simple prediction. Corresponding to the average cost share by plan in Figure 2A to 2D, Figure 3A–3D presents average monthly spending in each of our six plan types. Each diagram pools across all seven years and all the employers, and since we have a balanced sample with each person in all twelve months for each year in which they are in our analysis, sample means capture growth in spending over time.

Fig. 3. Average monthly spending by plan type, 2008–2014.

Note: Each panel plots the monthly spending for the services indicated by month, averaged over the seven year period for each plan type for the 73 employer sample. People not using a service in the month are included as zero spending.

The immediate pattern in all four plots is that costs are generally increasing in all plan types except for HMOs, where spending per month is nearly flat over time. The lowest line by December in every figure is the one for the HMOs, which is just below that of HDHPs. The line for CDHPs more or less follows the pattern of HDHP, low but strongly increasing. At the other extreme, costs are highest for the comprehensive health plan, which does not manage care, and also has the oldest enrollees and lowest average cost share. PPO spending is generally second highest, but also growing meaningfully over time.

The remaining panels of Figure 3 illustrate that mean costs are also noticeably increasing for outpatient spending and pharmaceutical spending. Spending growth is decidedly lower for inpatient spending, consistent with the slower changing monthly pattern for inpatient cost sharing, yet an upward trend in HDHP is still evident.

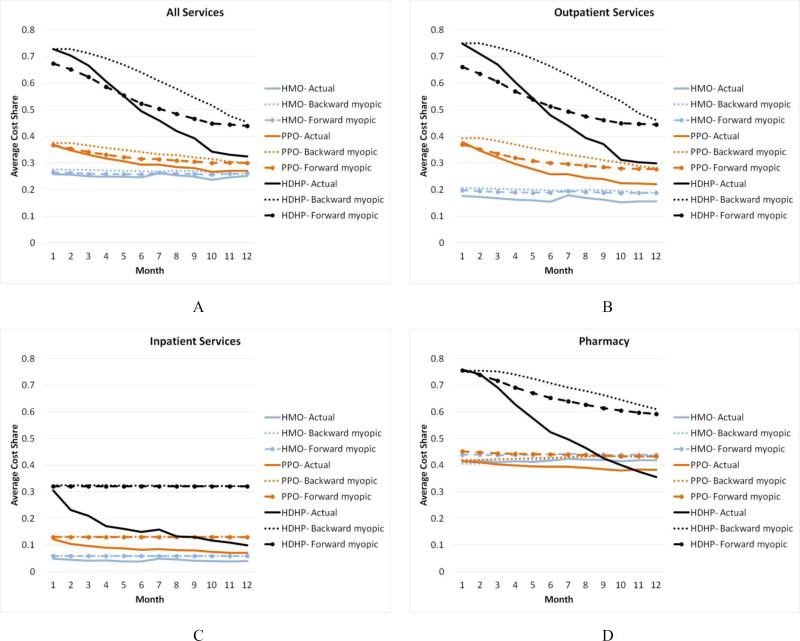
Figure 4 shows empirically the difference in the imputation methodology for three categories of services and three different plan types – HMO, PPO, and HDHP. HDHPs and HMOs are on opposite ends of the spectrum of the monthly cost share variation. Indeed, since the average cost sharing in HMOs is nearly constant from the beginning to the end of the year, the variation is nearly zero, making the imputations very close to the actual values. In sharp contrast, HDHPs have sharply declining actual, backwards and forward myopic prices. Both the backward and forward myopic prices are above the actual values for most of the year. This reflects the mass of individuals that never make a visit and therefore always have a high price expectation. This is particularly striking in the case of inpatient spending, where cost share imputations are nearly constant over time and shows very little variation across the year. The lack of monthly variation within a plan in inpatient cost sharing is a precursor of why we find it difficult to estimate the impact of cost share on inpatient categories such as room and board, and other service categories with precision even in our extremely large sample.

Fig. 4. Cost share imputations for HMOs, PPOs and HDHPs by Type of Service.

Note: Each panel shows the actual, backward myopic, and forward myopic cost shares for three plan types: HMOs, PPOs, and HDHPs. The four panels correspond to All, Outpatient, Inpatient and Pharmacy spending.

4.2. Regression results

Table 2 presents the IV results from estimating model (2) on overall spending, on three broad categories of service (outpatient, inpatient, and prescription drugs), and on 22 finer, not mutually exhaustive, categories of spending, using employer mean cost shares for a month as the instrument. Separate estimates are presented for backward and forward myopic cost shares models.⁸ The overall demand elasticity is estimated to be −0.44 using the backward myopic cost share expectations and −0.41 for forward myopic cost share expectations, which are plausible and consistent with much of the previous literature.⁹

Table 2.

IV regression results showing demand responses to two types of cost share

	Backward myopic cost share			Forward myopic cost share
Model: log(1/12 + Y)	Coefficient	Elasticity	S.E	Coefficient	Elasticity	S.E
All Spending	−1.26	−0.44	0.044	−1.26	−0.41	0.041
Outpatient	−0.86	−0.29	0.034	−0.91	−0.28	0.033
Inpatient	−2.18	−0.30	0.045	−17.37	−2.35	0.357
Pharmaceutical	−1.00	−0.44	0.040	−1.12	−0.51	0.045
Maternity	−0.27	−0.09	0.042	−0.39	−0.12	0.060
MH/SA	−0.62	−0.26	0.046	−0.93	−0.39	0.069
ER	−0.12	−0.04	0.024	−0.51	−0.17	0.102
Room and Board	−1.44	−0.20	0.069	−8.18	−1.14	0.389
Non specialty visits	−0.73	−0.25	0.041	−0.90	−0.28	0.046
Home visits	−0.06	−0.01	0.071	−0.25	−0.05	0.326
Prevention	−0.34	−0.02	0.009	−4.86	−0.29	0.123
Surgical procedures	1.33	0.07	0.098	28.85	1.52	2.139
Surgical supplies/devices	−3.13	−0.22	0.090	−80.88	−5.76	2.318
Specialty visits	−0.80	−0.32	0.033	−1.10	−0.42	0.043
Dialysis	0.17	0.02	0.156	0.31	0.04	0.290
PT, OT, speech therapy	−0.33	−0.15	0.032	−0.60	−0.27	0.057
Chiropractic	−0.36	−0.23	0.065	−0.47	−0.30	0.083
CAT scans	−0.49	−0.15	0.023	−2.64	−0.80	0.123
Mammograms	−1.02	−0.11	0.027	−19.92	−1.97	0.499
MRIs	−0.95	−0.29	0.022	−7.30	−2.21	0.171
PET scans	−1.13	−0.17	0.081	−7.35	−1.13	0.528
Radiology - diagnostic	−0.42	−0.15	0.018	−1.09	−0.38	0.044
Ultrasounds	−0.38	−0.14	0.015	−1.54	−0.56	0.060
Diagnostic services	−0.53	−0.15	0.021	−1.54	−0.42	0.059
DME	−0.39	−0.18	0.038	−1.00	−0.47	0.097
Ambulances	−0.31	−0.07	0.052	−4.75	−1.00	0.806

Note: N = 170,963,286 individual months. Each row is a different regression using the log(spending plus 1/12) as the dependent variable. Each model includes individual*year fixed effects, 12 monthly time dummies and uses employer’s average cost share for that year*plan*family*month, without the own individual, as an instrument. Cluster corrected standard errors use the employer*plan for clusters. Elasticities are evaluated at the mean cost share for that particular type of service, and S.E obtained using the delta method.

The next three rows of Table 2 show heterogeneity between outpatient, inpatient and pharmacy claims. Our model estimates nearly identical elasticities of −0.29 (backward myopic) and −0.28 (forward myopic) models. Pharmacy is more elastic, at −0.44 (backward myopic) and −0.51 (forward myopic). Einav et al. (2016) estimate a mean drug elasticity of −0.24 for a Medicare Part D, a population older than our sample.¹⁰ Inpatient spending is estimated to have a statistically significant elasticity of −0.30 using the backward myopic price versus an implausible −2.35 for the forward myopic price. This instability is a symptom of almost all of estimates of elasticities for relatively rare, inpatient-based services: elasticities are often implausibly large and generally imprecise. As previously pointed out, we believe this occurs because our IV approach fails to find a meaningful within-year variation in prices for these services, which happens invariably when mean monthly spending on a category is high and almost invariably puts a person over their deductible and stoploss. This is a particular problem for the forward myopic prices, so for the most part we focus on the backward myopic results in the remainder of this section.

The remaining rows of Table 2 illustrate elasticities for various services of interest. Emergency room (ER) spending has an extremely low elasticity of −0.04 using backward myopic prices, as does maternity (−0.09), consistent with our expectations. Demand response for mental health and substance abuse (MH/SA) services are of intermediate elasticities (−0.26). This may reflect the current trend that most people getting professional mental health treatment are getting drugs only or receiving MH/SA treatment in primary care (McGuire, 2016), which is consistent with the low level of spending on specialty mental health care observed in our data. Surgical procedures and Dialysis, two very expensive types of services, are of the wrong sign and not statistically different from zero. Other relatively inelastic services (with backward myopic elasticities below −0.1) are prevention and ambulance transport.

Although 171 million observations seems like a very large sample, for infrequently used but expensive services it remains difficult to precisely measure demand response. Table 1 helps identify the services with very low rates of positive spending but high conditional spending: home visits, dialysis, and inpatient surgical procedures are examples of this with high standard errors. Most people with spending on these types of service are likely to be associated with high annual spending, and thus exceed any reasonable deductible or stoploss, and face very little price variation. This is also a good argument for why cost sharing on such services will be an ineffective cost containment tool, since it imposes financial risk with little effect on spending on these services.

Our methodology may also not be reliable for services that are highly chronic since myopic spot prices may be less appropriate. Consider drugs, goods, and services such as statins (for high blood pressure), insulin, oxygen, home health visits for the chronically ill, and long term behavioral, physical, and occupational therapies. Spending on these services is highly predictable for many patients, and when expensive, consumers can readily foresee exceeding their deductibles. Our approach may nonetheless have some power, since even users of these services may have surprises about other types of spending that affect cost shares. Nonetheless, overall our approach will be less reliable for persistent types of spending.

5. Extensions and sensitivity analysis

In this section, we re-estimate the model on various partitions of our sample to consider whether demand response is higher or lower for certain identifiable groups. Since estimated elasticities are sensitive to the average cost shares in each subgroup, which can vary dramatically, we present here only the estimates of the demand curve coefficients on all subgroups, making them comparable. We then conduct a number of sensitivity analyses, examine the robustness of our IVs, and consider alternative functional forms. All of this analysis focuses on the backward myopic formulation of prices.

5.1. Demand responses by selected subsamples

In this section, we examine price coefficients (not elasticities) of total spending and our three broad groups of services for various subgroups of our sample. Table 3 presents the results of our analysis using five different partitions of the individual-years in our estimation sample using the backward myopic price formulation. In broad terms, our data imply the following conclusions. Males and females are not statistically significantly different. Spending on children is less elastic than spending on adults. Pharmacy demand became more elastic from 2008 to 2014. Adults in single versus family contracts are similar in their demand responsiveness, but children are less price responsive. Enrollees at HMOs are less price responsive than enrollees in HDHP for outpatient spending but not pharmacy spending. This last finding about pharmacy has implications for the work of Brot-Goldberg et al. (2017) which focused on changes in demand from a firm that significantly raised its deductibles, and found relatively large demand elasticities. This result is also consistent with the results of Einav et al. (2015) who document heterogeneity in Medicare pharmacy demand.

Table 3.

Estimated demand coefficients by demographic and plan subgroups

Model: log(1/12 + Y), backward myopia expectations, IV results
	% of sample	All spending	Outpatient	Inpatient	Pharmacy
Benchmark	100	−1.26	−0.86	−2.18	−1.00
Gender
Male	48.50	−1.29	−0.83	−1.69	−1.02
Female	51.50	−1.24	−0.88	−2.48	−0.99
Age group
0 to 5	6.39	−0.56	−0.25	−2.03	−0.68
6 to 20	23.67	−0.88	−0.41	−1.19	−0.97
21 to 45	34.87	−1.37	−0.91	−2.90	−0.92
46 to 64	35.07	−1.49	−1.14	−1.82	−1.09
Plan type
HMO	9.97	−1.49	−0.59	0.34	−1.15
PPO	65.51	−1.17	−0.74	−2.59	−0.74
HDHP	1.82	−1.39	−1.34	−3.34	−1.17
Time period
2008–2009	30.67	−0.81	−0.52	−1.98	−0.33
2010–2012	49.74	−1.41	−1.08	−1.98	−1.03
2013–2014	19.59	−1.07	−0.70	−1.95	−1.22
Plan coverage
Single	21.11	−1.47	−1.04	−0.93	−1.13
Family, employee	25.26	−1.61	−1.16	−2.59	−1.08
Family, spouse	19.95	−1.37	−1.01	−2.90	−0.98
Family, child	33.68	−0.83	−0.40	−1.80	−0.89

Note: Table shows the unconditional estimated demand coefficients for all services and for three broad types of services by gender, age group, risk score ranges, selected plan types, time interval and plan coverage. Each coefficient is from a different IV regression. Each IV regression includes individual*year fixed effects and 12 monthly time dummies and uses employer's average cost share for that service in that year*plan*family*month as an instrument for the myopic cost share. Dependent variable is log of spending on that service plus one. Cluster corrected standard errors use the employer*plan for clusters.

Table 4 shows the results by various employment-related groups. We find the following. Enrollees working at a firm in transportation, communications, or utilities have the least price responsive demand curves. Hourly, non-union employees are less responsive than other salary classes. Enrollees in low cost sharing firms have more inelastic demand than those in high cost sharing firms. Demand is less responsive in firms with over 200,000 employees than in firms with 5,000 to 49,999.

Table 4.

Estimated demand coefficients by employment-related subgroups

Model: log(1/12 + Y), backward myopia expectations, IV results
	% of sample	All spending	Outpatient	Inpatient	Pharmacy
Benchmark	100	−1.26	−0.86	−2.18	−1.00
Industry
Services	11.94	−1.52	−1.09	−2.80	−1.67
Manufacturing, Durable Goods	14.18	−1.59	−1.27	−1.66	−0.96
Finance, Insurance, Real Estate	12.78	−1.33	−0.89	−1.62	−1.18
Transportation, Communications, Utilities	13.55	−0.35	−0.15	−4.20	−1.16
Salary class
Union (salaried or hourly)	14.44	−1.24	−0.82	−2.13	−0.93
Salaried, non-union	27.19	−1.22	−0.79	−2.32	−0.86
Hourly, non-union	20.11	−0.95	−0.56	−1.89	−1.02
Employers by level of average cost sharing
Lowest quartile	22.84	−1.08	−0.73	−2.53	−0.89
Second quartile	33.90	−1.06	−0.82	−2.48	−0.81
Third quartile	25.34	−1.66	−0.92	−2.29	−0.85
Highest quartile	17.92	−1.38	−1.65	−1.72	−1.10
Employers by number of employees
2,800 to 49,999	20.31	−1.41	−0.97	−2.12	−1.04
50,000 to 199,999	46.91	−1.20	−0.85	−1.90	−0.97
200,000 or more	32.78	−0.87	−0.41	−3.42	−1.22

Note: Table shows the unconditional estimated demand coefficients for all services and for three broad types of services by industry, salary class, and employer quartiles of costs share. For the last group individuals were divided into four quartiles according to a ranking of the average cost share of their employer in that year, such that the lowest quartile are at employers offering the lowest average cost share. Each coefficient in this table comes from a different IV regression. Each IV regression includes individual*year fixed effects, 12 monthly time dummies and uses employer's average cost share for that service in that year*plan*family*month as an instrument. Dependent variable is log of spending on that service plus 1/12. Cluster corrected standard errors use the employer*plan for clusters.

We present this summary of the effects of cost sharing on diverse population and employer subgroups without attempting to interpret them, primarily as examples of the power of using a readily available instrument in large samples to explore differences in such dimensions. Studies using only survey data or a single employer will not have the power to address such refined issues that may nonetheless be of considerable policy interest.

5.2. Robustness of IVs

One concern about our IV is that cost shares are correlated with the degree of consumer foresight. We therefore generated and examined appendix Figures A-1 for all spending and for our three broad categories of service. The horizontal axis plots intervals of prospective DxCG relative risk scores (RRS) for each person based on prior-year diagnostic information. Here the highest value RRS correspond to being seven times the average spending, while the lowest RRS interval is .1, which is only 10 percent of the population average. The analysis reveals that as expected the backwards myopic and forward myopic prices have a sharp downward slope: sicker people are more likely to exceed any deductibles or stoplosses and pay lower cost shares. But the modestly downward slope for the employer mean actual cost share suggests that overall there is only a weak correlation between our instrument and the average health status of enrollees: The slight downward slope does suggest that enrollees who are sicker tend to work at firms that on average have more generous coverage, so that their average cost share is slightly lower than the population average. Ideally there would be no relationship between the “leave out one” mean cost shares and the RRS. The modest relationship observed implies that our estimated demand elasticities will be slightly too high rather than too low. We interpret this analysis as saying that our IV strategy is strong, although not perfect.

5.3. Alternative functional forms

Appendix Table A-6 reports our estimates using the alterative specification of log(Y+1). Among statistically significant elasticities, using log(Y+1) instead of log(Y+1/12) reduces the elasticities by 20.8 to 38.1 percent.

We also estimated results using a two-part model (Manning et al, 1987), in which the first stage models the binary choice of seeking care and the second stage models the continuous choice of how much treatment to obtain. Given that we rely on a very large number of individual-year fixed effects for identification, non-linear models such as logit or selection models are unattractive or infeasible. Results using a linear probability model are presented in appendix Table A-7. The resulting elasticity estimates are less stable (especially on rarely used services), which we speculate is because the linear probability model does extremely poorly when outcome probabilities are very close to zero. The conditional spending results (appendix Table A-8) predicting log(spending) are also problematic, with both positive and negative price effects detected, as can be expected given the large selection effects at the first stage.

In addition to our log linear and two part models, we also estimate results using the inverse hyperbolic sine function (Burbidge et al, 1988), which provides a different way to accommodate zero spending together with a thick long tail (Table A-5). We find that results are not very different from our initial specification and choose to keep the log model as our preferred specification due to its simplicity.

In sum, we tried three alternative model specifications to our preferred model, and did not find any of them to be preferable. Clearly, finding better specifications for modeling extremely skewed data with a preponderance of zeros using fixed effect methods remains an area needing further research.

6. Conclusions

This paper develops a new IV approach for estimating demand responsiveness using big data and highly disaggregated types of service. We document and take advantage of the considerable within-year variation in cost shares in many health plan types, which when combined with plans that have flat cost sharing creates a nice setting for estimation of demand elasticities. It seems not to be widely recognized that downward cost sharing trends during the calendar year must imply upward spending trends on services if there are unexpected spending shocks, or consumers are myopic. We show that these patterns are strong across many types of service, showing that within-year price responsiveness is significant. We acknowledge that our results represent only US employees working at large firms, but our estimates improve on those coming from only a single large employer. Our results suggest that studies using only a single employer, or using only people who are in high deductible plans may not generalize since they are not representative of the full population of privately insured.

Our IV strategy leads to elasticity estimates that are plausible and consistent with other estimates from the literature for services where a single month of use does not typically put a person over normal deductible levels. Our IV approach works less well for expensive procedures like hospice care, inpatient surgery, room and board spending, and dialysis, where the time of the year matters less since the consumer will almost invariably exceed the deductible. While not perfect, our IV has the advantage of being widely available and easy to use. OLS estimates, in contrast are often in the wrong sign.

An innovation of the paper is that we estimate two different forms of spot prices: backward myopic prices where consumers never anticipate future spending, and forward myopic spot prices, where they fully anticipate actual spending in the current month when making consumption decisions. We find relatively modest differences in our elasticities once we ignore statistically insignificant ones. One hypothesis for this is that our two measures are highly correlated when consumers use a service multiple times per year, and since we use an IV strategy, it corrects for expectation errors.

Our approach holds great promise in potentially providing a new instrument – employer average monthly cost share on a service of interest – which can be used in other studies looking for an instrument for rates of spending or utilization of a service. For example, consider procedure ABC, lab test DEF, or drug GHI that are sometimes used only for a patient with condition 123. If consumers are diagnosed with condition 123 at different times in the year, and face changing cost shares over time, then our approach can be used to generate a reasonable instrument for assessing the effectiveness of each of these procedures, tests, or drugs for treating condition 123. Given how valuable it is to have good instruments, other uses may prove to be as useful as the estimates of demand response that we generate here.