Modeling the Cellular Response of Lung Cancer to Radiation Therapy for a Broad Range of Fractionation Schedules

Abstract

Purpose

To demonstrate that a mathematical model can be used to quantitatively understand tumor cellular dynamics during a course of radiotherapy, and to predict the likelihood of local control as a function of dose and treatment fractions.

Experimental Design

We model outcomes for early-stage, localized non-small cell lung cancer (NSCLC), by fitting a mechanistic, cellular dynamics-based tumor control probability that assumes a constant local supply of oxygen and glucose. In addition to standard radiobiological effects such as repair of sub-lethal damage and the impact of hypoxia, we also accounted for proliferation as well as radiosensitivity variability within the cell cycle. We applied the model to 36 published and 2 unpublished early stage patient cohorts, totaling 2701 patients.

Results

Precise likelihood best-fit values were derived for the radiobiological parameters: α (0.305 Gy^-1; 95% CI: 0.120-0.365), the α/β ratio (2.80 Gy; 95% CI: 0.40-4.40), and the oxygen enhancement ratio (OER) value for intermediately hypoxic cells receiving glucose but not oxygen (1.70; 95% CI: 1.55-2.25). All fractionation groups are well-fitted by a single dose-response curve with a high χ² p-value, indicating consistency with the fitted model. The analysis was further validated with an additional 23 patient cohorts (n=1628). The model indicates that hypofractionation regimens overcome hypoxia (and cell-cycle radiosensitivity variations) by the sheer impact of high doses per fraction, whereas lower dose-per-fraction regimens allow for reoxygenation and corresponding sensitization, but lose effectiveness for prolonged treatments due to proliferation.

Conclusions

This proposed mechanistic tumor-response model can accurately predict over-treatment or under-treatment for various treatment regimens.

Introduction

Until recently, the standard treatment for lung cancer, even localized disease, has been to give 60 Gy total in 30 weekday fractions, with poor resulting local control rates (1,2). However, the ongoing trend towards hypofractionated radiotherapy (called stereotactic body radiation therapy, or SBRT), for early stage disease, has resulted in a range of higher rates of local disease control (3–7), often as high as 95%. In SBRT, advanced imaging localization and immobilization techniques are used to deliver dose distributions that are highly conformal to the disease target volume, while exposure to the surrounding normal tissues is reduced due to the use of multiple converging beams. SBRT is mostly prescribed for localized, early stage tumors requiring limited treatment volumes thereby resulting in tolerable normal tissue damage. However, the precise dose and number of fractions needed have not been well-established and a wide variety of dose-fraction schemes are currently employed.

The goal of this research is to address this need, at once providing a quantitative model to predict the likelihood of local control for different fractionation schemes while also moving towards a more mechanistic radiobiological understanding of tumor response to radiation therapy.

Previous efforts to model the likelihood of local control for early stage lung cancer divide into two categories that can be labeled empirical or mechanistic. Empirical models usually invoke a fitted linear + quadratic dependence on fractional dose (the so-called L-Q model), sometimes adding an empirical proliferation effect (8–11). Empirical models typically yield shallow dose response curves, resulting in limited clinical usefulness. The dispersion of data points around such models is typically large, indicating that the data cannot be drawn from (i.e., “explained by”) the proposed empirical distributions (12). Mechanistic models of the tumor cellular response to radiotherapy have been previously published for multiple tumor sites (13–16). However, none has been fit to extensive clinical datasets.

Our model introduces the driving assumption that hypoxia vs. proliferation is mediated via a local competition for chemical resources (17). Furthermore, we explicitly introduce a category of cells experiencing intermediate levels of hypoxia in which glucose, but not oxygen, is adequately present to provide metabolic viability. Thus, we go beyond the model of Borkenstein et al., who stated: “Intermediate levels of hypoxia, resulting in a gradient in proliferative activity and intermediate OER (oxygen enhancement ratio) values, are not accounted for, even though they are considered to be important for tumor response” (14).

In non-mechanistic models, a repopulation term is sometimes included in the cumulative dose effect calculation based on exponential clonogen repopulation for overall treatment times longer than an ad hoc “kick-off” time, typically fixed as 3-4 weeks (18). This repopulation effect emerges in a natural way in our model, which eliminates the need for the ad hoc assumption.

The ability of the L-Q model alone to describe cell kill at high fraction doses (greater than about 10 Gy), as used in SBRT, has been questioned, leading to proposed modifications of the basic cell kill equations (7,19). However, when only a few fractions are given, our modeling predicts it is the hypoxic cells that are most important in determining response. In this case, the dose effect for hypoxic cells is scaled by 1/OER (20). Thus, if we take into account hypoxia, the L-Q equation can still be used (21–23).

Several important studies support the argument showing that there might be other tumoricidal effects at high fraction size, including direct vascular damage (24,25) and potential immune induction effects (26). Our approach is to leave out these partially understood effects to see if they are required to quantitatively model early stage lung cancer response.

In this study, we apply the previously developed tumor response model with additional cell cycle effect to the extensive clinical outcome data of lung cancer to see if the model based on classical radiobiological effects can accurately predict the tumor response likelihood of the various fractionation schemes.

Materials and Methods

State-driven tumor response model

A previously developed, time evolution state-driven tumor response model was used to simulate a wide range of fractionation regimens (17). The model assumes that a given contiguous fraction of the tumor is fed by a supply of chemical resources, which remains constant over a course of radiotherapy. Cells are distributed between three compartments: proliferating (P), intermediate (I), and (extremely) hypoxic (H) compartments, as shown in Figure 1A. Proliferation takes place in the P-compartment, which is assumed to receive enough oxygen and glucose to support intermittent cell cycle progression. Cell loss takes place in the highly hypoxic H-compartment, which is assumed to receive no oxygen or glucose. In the I-compartment, which recieves glucose but not oxygen, neither proliferation nor cell loss is assumed to take place (27). A fraction of cells in the P-compartment constantly proliferate. Radiotherapy is assumed to doom cells consistent with the L-Q model. This results in “doomed” cells that have lost indefinite proliferation capacity after sterilization. Thus, each compartment also has a doomed cell sub-compartment. As shown in Figure 1B, following the post-mitotic cell death and clearance of proliferating cells, cells in the intermediate compartment begin to receive oxygen and therefore move into the proliferative compartment. At the same time, any surviving hypoxic-compartment cells move into the intermediate compartment (Figure 1C). This naturally results in the process of reoxygenation over a course of radiotherapy, allowing us to evaluate treatment response of various fractionation schemes based on the interplay between hypoxia and proliferation.

Figure 1.

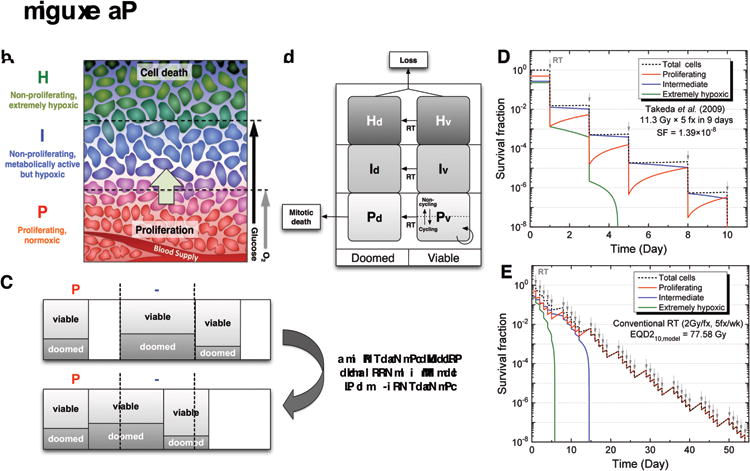
Schematic diagrams of the state-driven tumor response model and the estimation of equivalent dose for non-standard fractionations based on the model. (A) Three different compartments in the model based on the microenvironment of a tumor with respect to the blood supply. Due to a limited blood supply, there are limited supplies of oxygen and the key nutrient, glucose. Cells with adequate oxygen and glucose are actively proliferating, while cells distant from vessels are starving and dying. In the model, theses populations of cells were simplified into three different compartments (P, I, and H), which have different levels of proliferation, hypoxia, cell death, and radiosensitivity. Note that uniform levels of glucose and O₂ were assumed for each compartment. (B) After radiation therapy begins, a fraction of cells in each compartment becomes doomed depending on compartment-specific radiosensitivity and die in an attempt of mitosis in the proliferative P-compartment. (C) Re-compartmentalization and reoxygenation pattern after the post-mitotic death of doomed cells in the P-compartment. As long as cells are available, the P-compartment “tops up” at each time step. (D-E) An example of EQD2_10,model estimation based on two separate simulations, in which the fraction size-dependent radiosensitivity, proliferation, and hypoxia effects are incorporated: (D) after the cell survival fraction was estimated for a SBRT regimen (11.3Gy×5fxs) from Takeda et al. (30), (E) a conventional 2 Gy-fractionation was simulated until the same level of survival fraction was achieved, resulting in EQD2 _α/β,model. (Figures A, B, and C are used with permission). Panel A reprinted from Jeong J, Deasy JO. Modeling the relationship between fluorodeoxyglucose uptake and tumor radioresistance as a function of the tumor microenvironment. Comput Math Methods Med 2014;2014:847162. Panels B and C reprinted from Jeong J, Shoghi KI, Deasy JO. Modelling the interplay between hypoxia and proliferation in radiotherapy tumour response. Phys Med Biol 2013;58:4897–919. © Institute of Physics and Engineering in Medicine. Reproduced by permission of IOP Publishing. All rights reserved.

For the large fraction size in SBRT, known cell cycle variations in radiosensitivity could potentially be important (28,29) and have been added to the model in terms of effective radiosensitivity and effective OER, as described below.

Effective radiosensitivity and OERs based on the cell cycle

The variability of radiosensitivity within the cell cycle has long been recognized (31–35). In general, cells in the S-phase (especially late S-phase) are known to be the most radioresistant, and cells near mitosis (G2/M-phases) are known to be most radiosensitive. Although the radiosensitivity of the early G1-phase can be as high as the S-phase for cells with long G1-phase times, the radiosensitivity of the G1-phase is generally in between those two phases (S and G2/M) (36).

To account for the cell cycle effect on radiosensitivity, the population of proliferating tumor cells is decomposed into three subpopulations (G1, S, and G2/M). The standard L-Q model was used to calculate the survival fraction (SF) as shown in the following equation:

$$\mathit{\text{SF}}=exp(-\alpha d-\beta d^2)$$ [1]

where α and β are the radiosensitivity parameters in the L-Q model and d is the fractional dose.

The total survival fraction for a given fractional dose is obtained as a weighted summation of survival fractions of the three subpopulations, from which the effective radiosensitivity parameters (α_eff and β_eff) can be estimated as shown in equation 2. The effective radiosensitivity is dependent on both the fraction of cells and the radiosensitivity in each cell cycle.

$$\mathit{\text{SF}}=f_{G1}exp(-{\alpha }_{G1}d-{\beta }_{G1}{d}^2)+f_{s}exp(-{\alpha }_{s}d-{\beta }_s{d}^2)+f_{G2/M}exp(-{\alpha }_{G2/M}d-{\beta }_{G2/M}{d}^2)=exp(-{\alpha }_{\mathit{\text{eff}}}d-{\beta }_{\mathit{\text{eff}}}{d}^2)$$ [2]

where, α_eff and β_eff are the effective L-Q parameters, d is the fractional dose, and f_X, α_X and β_X are the fraction of cells, linear parameter, and quadratic parameter for a given cell cycle X (G1, S, or G2/M).

Increased radioresistance of hypoxic cells can be quantified in terms of the OER, which is the ratio of the required dose in hypoxic conditions to the dose in normoxic conditions (37). Carlson, et al. have shown that the dependence of radiosensitivity on alpha and beta coefficients is inversely related to the first and second order of the OER, respectively (20). In the current study, for simplicity, all the hypoxic cells are considered to be in a non-proliferating (quiescent) state (38), and therefore, have constant radiosensitivity. Based on the OER value applied to conventional 2 Gy/fx (OER_ref), the effective OER (OER_eff) can be found as a function of the fractional dose, as given in the following equation:

$${\mathit{\text{SF}}}_{\mathit{\text{hyp}}}=exp(-\frac{{\alpha }_{\mathit{\text{eff}}}}{{\mathit{\text{OER}}}_{\mathit{\text{eff}}}}d-\frac{{\beta }_{\mathit{\text{eff}}}}{{\mathit{\text{OER}}}_{\mathit{\text{eff}}}^2}{d}^2)=exp(-\frac{{\alpha }_{\mathit{\text{ref}}}}{{\mathit{\text{OER}}}_{\mathit{\text{ref}}}}d-\frac{{\beta }_{\mathit{\text{ref}}}}{{\mathit{\text{OER}}}_{\mathit{\text{ref}}}^2}{d}^2)$$ [3]

where SF_hyp is the survival fraction of hypoxic cells, α_eff and β_eff are the effective L-Q parameters derived from the normoxic cells in the cell cycle (Eq. 2), OER_eff is the dose dependent effective OER value, α_ref and β_ref are the reference L-Q parameters at 2 Gy/fx, and OER_ref is the reference OER value at 2 Gy/fx.

Model parameters for lung cancer

A few key variables are fitted to the data, but most model parameters do not have a significant impact on the model fit, and are therefore set once based on other publications or plausibility. In the model, the relative degree of proliferation vs. hypoxia-caused cell death is determined by the initial size of each compartment, derived through exact algebraic relationships with the well-known parameters of initial growth fraction (GF) and initial volume doubling time (T_D). Representative GF and T_D values of 0.25 and 100 days, respectively, were used for the simulation, based on measured data for lung cancer (39,40). The cell cycle time (T_C) was assumed to be two days. The cell cycle distribution was taken as 78%, 12% and 10% for G1-, S-, G2/M-phases, respectively, based on a flow cytometric analysis of 187 surgical specimens of non-small cell lung cancer (41). Because the exact cell cycle-dependent radiosensitivity values are not available for lung cancer, the ratios of radiosensitivity of G1- and G2/M-phases, with respect to the most resistant S-phase, were taken to be 2 and 3, respectively, (α_G1/α_S=2 and α_G2/M/α_S=3), based on the radiosensitivity analysis of synchronized cell populations (32,33). The radiosensitivity of each cell cycle phase was therefore derived from the overall fitted radiosensitivity value (42).

The OER value at 2 Gy/fx for the H-compartment cells was expected to be significantly less than the theoretical maximum of about three, considering the lower OER observed of G0/G1 phase and reduced repair capability of chronically hypoxic cells (43). Parameter values used for the model simulation were summarized in Table 1. The α value, the α/β ratio, and the OER value for intermediately hypoxic cells (OER_I) were derived by fitting the dataset.

Table 1. The parameters used for the model simulation for lung cancer.

Parameters	Values
Growth fraction (GF)	0.25 (40)
Tumor doubling time (TD)	100 days (39)
Cell cycle time (TC)	2 days (37)
Fraction of cells in P-compartment (f P)	50a %
G1-phase in P (f PG1)	28 % (41)
S-phase in P (f PS)	12 % (41)
G2/M-phase in P (f PG2/M)	10 % (41)
Fraction of cell in I-compartment (f I)	27a %
Fraction of cell in H-compartment (f H)	23a %
Ratio of alpha of G1- to S-phase (αG1/αS)	2b
Ratio of alpha of G2/M- to S-phase (αG2/M/αS)	3b
Reference radiosensitivity at 2Gy/fx (αref)	0.35c Gy-1
Alpha-beta ratio (α/β)	10c Gy
OER of I-compartment at 2 Gy/fx (OERI,ref)	2c
OER of H-compartment at 2 Gy/fx (OERH,ref)	1.37 (43)

^aEstimated from GF and TD in the model

^bAssumed parameters based on radiosensitivity analysis of synchronized cell population (32,33)

^cInitially assumed values; various values of these parameters were tested in the sensitivity test

Clinical outcome data

Individual clinical outcome data included in the study of Mehta et al. were reviewed and filtered with the goal of increasing consistency (44). Patient cohorts were separated into three groups: conventional fractionation RT (1.8-3 Gy/fx); SBRT with several fractions (3-10 fxs); and single-fraction SBRT. The cohorts of conventional RT included in Mehta et al.'s analysis exhibit excessively heterogeneous outcomes in a narrow dose range, which makes the comparison with other groups difficult. For consistency within the group, trials were excluded that: used fraction sizes larger than 3 Gy/fx; used twice-a-day fractionation (bid); or used split course RT, as indicated in Table S1. This resulted in nine excluded cohorts. We also included three additional cohorts in the conventional group with two from our institutions. A total of 38 cohorts (2701 patients) were included in the analysis, comprised of 10 conventional, 22 multi-fraction SBRT, and 6 single-fraction SBRT cohorts, as summarized in Table S2.

From each cohort, detailed treatment and outcome information was extracted for model simulation and analysis, including the number of patients, total dose, fractional dose, number of fractions, treatment schedule, dose prescription method, and local control rate. Some cohorts employed multiple fractionation schemes, but reported only the integrated total outcome. For those, separate fractionation schemes were simulated with the model and the population-weighted mean was used to represent the whole cohort. When separate outcomes were available for different fractionation schemes, the patient cohort was divided into separate cohorts.

Since SBRT dose distributions are not uniform, fractional doses at the center and at the PTV margin were averaged and used as the representative dose in the model simulation, which assumed a homogeneously irradiated tumor. For example, when a 10 Gy fractional dose was prescribed to the 80% isodose encompassing the PTV, the maximum dose at the central PTV becomes 12.5 Gy, while the dose at the periphery of the PTV is 10 Gy. The prescribed dose inside the PTV is therefore between 10 and 12.5 Gy and we average these values (11.25 Gy) to represent the dose to the tumor. Analyses in which full dose-volume histograms are available would afford greater accuracy in this regard, but could only be carried out for smaller cohorts and a much more limited range of fractionation schedules.

Model-derived equivalent dose in conventional fractionation

In order to compare the outcomes of various fractionation schemes, the treatment effects of all non-standard regimens were normalized in terms of a model-derived equivalent dose in conventional fractionation (2 Gy/fx, 5 fx/week), for variable α/β ratios, e.g., for a ratio of 10 (EQD2_10,model). The estimation of the EQD2_α/β,model was carried out with two separate model simulations: first, an overall cell survival fraction was estimated based on the fraction size and the fractionation schedule; then, a corresponding conventional 2 Gy-fractionation schedule was simulated to find the dose at which the same level of stem cell surviving fraction would be achieved, resulting in a model-derived equivalent dose at 2 Gy/fx. The process is shown schematically in Figure 1D-E.

Dose-response curves

The maximum likelihood (MLE) method (see below) was used to find the best fit dose-response curve, either for the total group or for separate fractionation groups. The slope of the dose-response curve (γ₅₀) was fixed and assumed to be 1.5, which is known to be a clinically relevant value for NSCLC (42), which was found to adequately describe the data.

In radiotherapy, radiation dose is not the only factor that determines treatment efficacy. In reality, it might be difficult to achieve 100% of tumor control, even with a very high radiation dose, due to the potential to geographically miss a small fraction of occult cells. For example, Chao et al. summarized pathology reports showing the fall off of occult disease with increasing distance from the gross disease boundary (45). We observed empirically that, even at the highest obtained effective doses, local control typically saturated at 95%, which was therefore set as an upper bound in the logistic model (46), as follows:

$$\mathit{\text{TCP}}(D)=\frac{0.95}{1+{(\frac{{\mathit{\text{TD}}}_{50}}{D})}^{4{\gamma }_{50}}}$$ [4]

where TD₅₀ is the tumor dose at which 50% of TCP is expected, γ₅₀ is the slope of the curve at TD₅₀, and D is the total dose of the treatment, which is EQD2_α/β,model in this analysis.

To test the validity of the fit, chi-square tests were performed. A p-value close to unity would indicate the dose-response curve was statistically representative for the fitted data; in contrast, small p-values indicate that the dose-response curve is not statistically drawn from the observed data.

Fitted parameters: α, α/β, and OER_I

Among the parameter values in the model, we found that the simulation results were most sensitive to radiosensitivity-related parameters such as the α value, α/β ratio, and OER_I value. Therefore, data fitting focused on these assumed parameter values, as well as a TD₅₀ value. For possible ranges of these parameter values, simulations were performed to see if the dose responses of the different groups could be fit into a logistic function with a high log likelihood value in the scatter plot of the tumor control rate vs. EQD2_α/β,model. The tests were performed iteratively for α values vs. α/β ratios and α/β ratios vs. OER_I values, until all the values were stabilized with a maximum log likelihood value. The 95% confidence intervals of the parameter estimates were found through the profile likelihood method. Optimal fit values and uncertainty ranges are reported.

MLE method and the estimation of 95% confidence interval of TD₅₀ value

For the m cohorts in each group, the overall log likelihood can be found from the following equation:

$$\sum _{i=1}^{m}In(L_i)=\sum _{i=1}^{m}In(L(p_i|n_i,y_i))=\sum _{i=1}^{m}In(\begin{array}{c}{n}_i\\ y_i\end{array})+y_i\cdot In(p_i)+(n_i-y_i)\cdot In(1-p_i)$$ [5]

where, p_i is the predicted TCP by the logistic fit, n_i is the total number of patients, and y_i is the number of patients with local control in each i^th cohort.

For increasing TD₅₀ values of the logistic curve with a fixed γ₅₀ value of 1.5, the overall log likelihood values were found. The TD₅₀ value that maximizes the overall log likelihood was searched and the 95% confidence interval was found according to the “profile likelihood method” (47,48).

Results

Effective radiosensitivity and OER

For proliferating tumor cells in the P-compartment, the radiosensitivity of each cell cycle phase was estimated from equation 2, based on the relevant cell cycle phase distribution for lung cancer and the assumed ratios of radiosensitivities (α_G1/α_S=2 and α_G2/M/α_S=3). For the reference radiosensitivity of 0.35 Gy^-1 at 2 Gy/fx, the radiosensitivity of each cell cycle was calculated to be 0.376, 0.188, and 0.564 for G1-, S-, and G2/M-phases, respectively.

Using the calculated cell cycle-dependent radiosensitivity values, the surviving fraction of cells in each cycle phase was estimated as shown in Figure 2A, along with the total surviving fraction. As the fractional dose increases, relatively sensitive cells in G2/M- and G1-phases are preferentially killed, followed at higher doses by more resistant cells in the S-phase. Cells in the S-phase become dominant after about 5 Gy/fx and the total surviving fraction in the proliferative (P) compartment is mainly governed by the S-phase surviving fraction. From the overall surviving fraction, the effective alpha value was derived and presented as a function of the fractional dose in Gy as shown in Figure 2B. As the fractional dose increases, the effective alpha values decrease and approach the alpha value of the most resistant S-phase (α_S).

Figure 2.

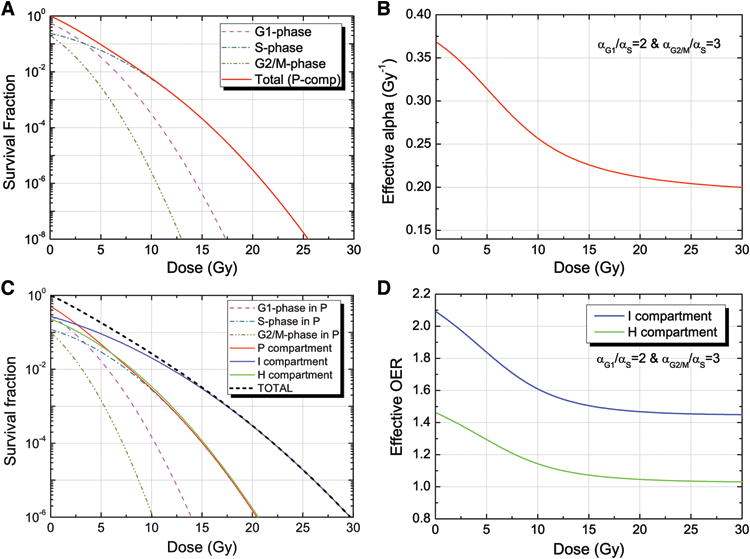
Estimation of the cell cycle-dependent effective radiosensitivity and OER values depending on the fraction size: (A) the surviving fraction (SF) of each cell cycle phase and the total SF for proliferating cells in the P-compartment are computed based on individual radiosensitivities (α_G1/α_S=2 and α_G2/M/α_S=3) assuming an initial cell cycle distribution of [G1: 56%, S: 24% and G2/M: 20%]; (B) the effective alpha value as a function of fractional dose for the assumed cell cycle distribution, resulting in cell cycle dependent radiosensitivities. At 2 Gy/fx, the reference alpha value of 0.35 Gy^-1 was used; (C) the surviving fraction of each compartment, including a cell cycle phase-dependent SF in the P-compartment for the cell cycle distribution and cell cycle-dependent radiosensitivities; (D) the resulting effective OER values for the I- and H-compartments as a function of the fractional dose. As fractional dose increases, the effective radioresistance increases in P-compartment and the effective OERs decrease.

Hypoxia was considered in the model with two hypoxic compartments (I- and H-compartments). Since hypoxic cells were assumed to be only in G0/G1 phase (38,49,50), the surviving fractions of hypoxic compartments are determined by a single radiosensitivity value, while the surviving fraction in the proliferating compartment is composed of three different cell cycle phases (G1, S and G2/M) with different radiosensitivities. The survival fraction of each compartment is estimated as shown in Figure 2C. Due to the relatively resistant S-phase in the P-compartment, the slope of the surviving fraction of the P-compartment becomes shallow as the fractional dose increases, and becomes similar to that of the H-compartment. Although the survival fraction of the I-compartment is still shallower than that of the P-compartment, the relative resistance decreases with the increasing fractional dose. This decreases the effective OER values for the hypoxic compartments, as shown in Figure 2D.

Estimated EQD2_10,model

Because α/β=10 is often quoted as a reasonable parameter for tumors, we included it as a reference. EQD2_10,model values were estimated through model simulation for all the non-standard fractionation schemes. In Figures 1D-E, an example of EQD2_10,model estimation was shown for a SBRT regimen from Takeda et al. (30). The model simulation was performed for the SBRT regimen (11.3 Gy × 5 fxs in 9 days), in which the survival fraction was estimated to be 1.39×10^-8 (Figure 1D). Another simulation with the conventional fractionation (2 Gy/fx, 5 fx/wk) was performed and the same level of survival fraction could be achieved at about 77.6 Gy (Figure 1E), from which the EQD2_10,model of the SBRT regimen was determined.

To compare the evaluated treatment efficacies of SBRT regimens between BED and EQD2_10,model, the ratio of EQD2_10,model/BED was computed with respect to the number of fractions, the treatment duration, and fraction sizes. As shown in Figure S1, the ratio of EQD2_10,model/BED increased with a larger number of fractions, longer treatment duration, and smaller fraction size, due to cell cycle reassortment between fractions and increased reoxygenation with longer schedules. The largest differences were seen for single-fraction regimens, due to the impact of hypoxic cells, with ratios of about 0.5.

Derived dose-response curves

The EQD2_10,model values of the 38 cohorts were computed through model simulation and tumor control rates were fitted on a logistic function via the MLE method for the separate groups or the total group. For comparison, in Figure 3A, we plot results using values of α=0.35 Gy, the commonly quoted value of α/β=10/Gy, and an OER_I value of 2. A grid search was performed to find the best fits. As supported by the resulting small uncertainty intervals, overfitting was not an issue given a dataset this large. Although the different groups follow clear logistic dose-responses, with different TD₅₀ values, we find that combining all the fitted data points into a single logistic dose response curve yields a χ²-test of the fit yielding a p-value of much less than 0.001 (Figure S2A). This indicates that the data could not be drawn from the model with those parameters.

Figure 3.

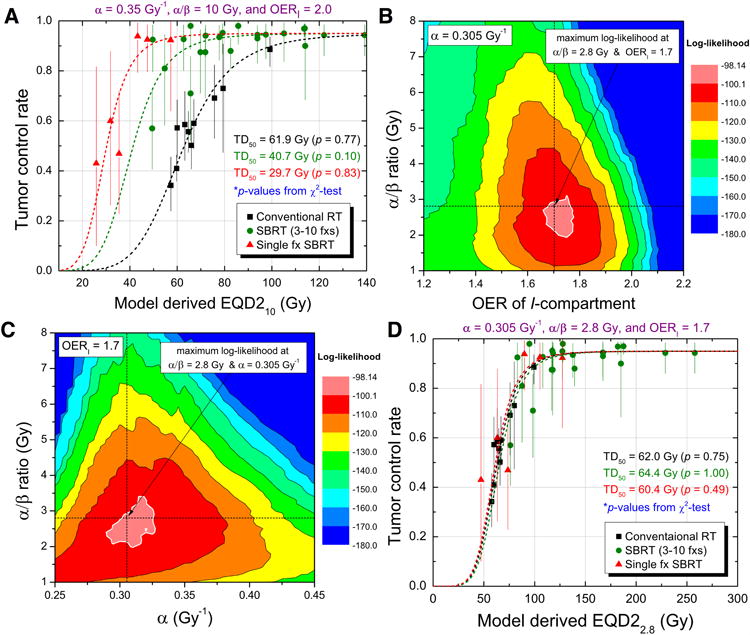
Derivation of best-fit dose-response curves. (A) Dose-response curves estimated from a maximum likelihood method for reference radiosensitivity values (α=0.35, α/β=10, and OER_I=2), with the goodness-of-fit p-values based on Chi-square test. (B-D) Sensitivity test for various values of α, α/β ratio, and OER_I, and the resulting best-fits for the separate groups: (B) best-fit α/β ratio and OER_I values estimated from iterative sensitivity test for the total group; (C) the best-fit α value and α/β ratio estimated from iterative sensitivity test for the total group; and (D) dose-response curves for the separate groups for the best-fit parameter values, which are very close to each other.

Parameter variability effects

Figures 3B and 3C show the landscape of best-fit log likelihood values for varying parameters. As shown in Figure 3D, when we choose optimal values of α, α/β, and OER_I, all the best fit curves from the fractionation groups are closely aligned, which indicates that the fit is not driven by any single group and represents all three groups well. The best fit radiobiological parameters were α=0.305 Gy^-1 (95% CI: 0.120-0.365), α/β=2.80 Gy (95% CI: 0.40-4.40), and OER_I=1.7 (95% CI: 1.55-2.25). In units of EQD2_2.8,model, the TD₅₀ was 62.1 Gy (Figure S2B). Hence, a typical early stage lung tumor had a 50% chance of local control if given 62 Gy in 2 Gy/weekday fractions. As shown in Figure S2B, these parameters result in an excellent fit when using a single curve for all fractionation groups, with a high resulting χ² test p-value (p≈1.00). Through the profile likelihood method, the 95% confidence intervals (95% CI) of the TD₅₀ values were estimated for each group and the total cohorts, as shown in Figure S3.

Effect of dose calculation algorithm and follow-up time

The human lung is a very heterogeneous tissue, which causes secondary electrons set in motion by incident photons to be scattered with disparate distributions (51,52). Simple, ray-trace algorithms are known to misestimate dose as well as underestimate required field widths (53,54). Hence, we might expect that dose calculation algorithms capable of modeling such differences (i.e., the convolution-superposition algorithm family) could provide dosimetric data that produces less residual error. Five cohorts were identified to have used more advanced dose calculation algorithms such as convolution or superposition algorithms. As shown in Figure 4A, those five cohorts showed better agreement with the dose-response curve, compared to other cohorts with a less accurate dose calculation algorithm.

Figure 4.

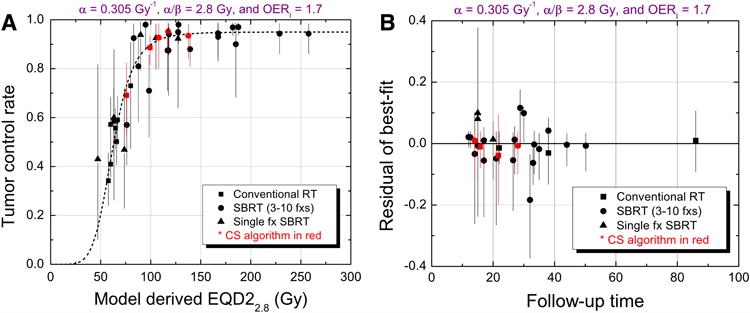
Effect of dose calculation algorithm and follow-up time. (A) Effect of dose calculation algorithm: five cohorts with more accurate convolution or superposition dose calculation algorithms (shown in red) show better agreement with the best-fit dose-response curve. (B) Effect of follow-up time: no discernible pattern was noted for any group and four cohorts with convolution/superposition (CS) algorithm (shown in red) have lower residuals.

To test if differences in follow-up time affected the results, a plot of median follow-up time vs. the residual of the best logistic fit is shown in Figure 4B for 28 cohorts with available follow-up time information. No discernible pattern was noted for all groups, which establishes that ignoring differences in follow-up time was appropriate.

Validation of the model with additional dataset

For validation of the model analysis, more recently published outcome data were reviewed for stage I lung cancer treated with SBRT. Fifteen relevant studies were identified and included into the validation dataset, which is comprised of 23 different patient cohorts with 1628 patients (Table S3). The best-fit parameter values derived from the original datasets were used for the modeling. As shown in Fig 5, the dose response curve derived from the original datasets perfectly fits the validation datasets with the Chi-squared p-value of 1.00.

Figure 5.

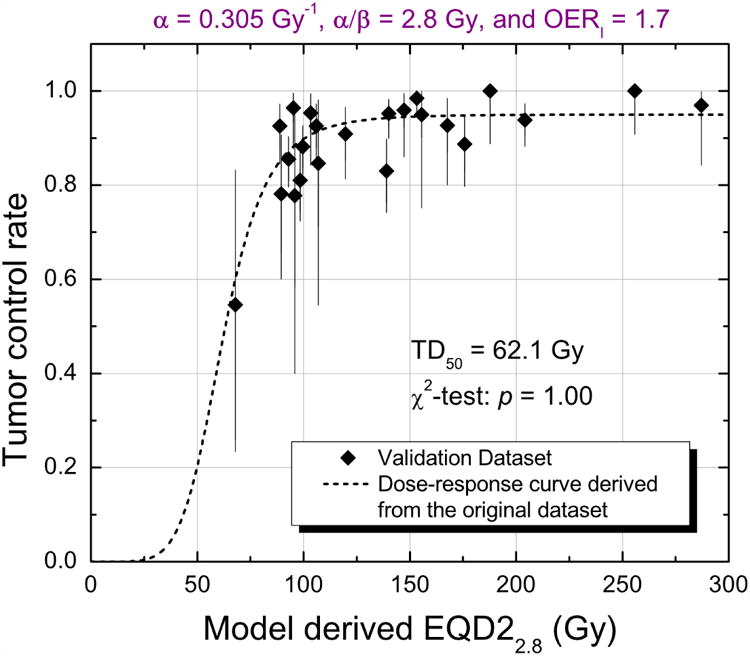
Validation dataset with 23 patient cohorts (n=1628) overlaid with the dose-response curve derived from the original dataset for the best-fit parameter values (α=0.305 Gy^-1, α/β=2.8 Gy, and OER_I=1.7). Chi-square test shows the validation datasets are in great agreement with the dose response curve derived from the original dataset (p=1.0).

Discussion

The motivation of this work is to establish the usefulness of a radiobiological model to describe and predict response to radiotherapy for localized lung cancer. The fitted results show that the model is successful in this regard, despite being an oversimplification of the response of complicated biological entities to non-uniform dose distributions given under widely-varying conditions. Despite this, for the first time, a mathematical model robustly reproduces tumor dose-response across the complete range of clinical fractionation regimens, which has been further validated with additional dataset.

To quantify uncertainty in the resulting dose-response curve for single-fraction SBRT, we plot the change in log likelihood of the overall fit when the TD₅₀ is varied, assuming the other best-fit parameters are still valid. The result is that the 95% confidence interval envelope is relatively wide (53.0-67.3Gy); see Figure S3C. Thus, non-standard “new biology” effects could potentially emerge as a component to the lung dose-response curves, but only with the collection of further single fraction results will be able to clarify this situation. Nonetheless, in the absence of any disagreement between the model and single-fraction clinical results, such effects should be considered theoretical.

The OER of hypoxic cells is a crucial variable in the model. Palcic and Skarsgard found that the OER is dependent on dose (55–57), and others have shown that the dose dependency of OER is a consequence of the variation of OER across cell cycle phases, for example Freyer et al. who showed that the OER of Chinese hamster ovary (CHO) cells was highest in S-phase (2.8-2.9) and lowest in G1-phase (2.3-2.4) (58). As dose increases, the most resistant S-phase cells dominate the surviving fraction; this causes an increase of OER at a higher fractional dose.

Our in situ-derived value (OER_I=1.70) is lower than the commonly quoted maximum of about 3, as measured in vitro, where cell cultures are, typically, briefly exposed to nitrogen or argon gas (55,57). However, there are several reasons to believe that the effective value of OER in a tumor is significantly less than the theoretical maximum of 3. Wouters and Brown discuss the importance of intermediately hypoxic cells, with effective OERs between 1 and 2 (59). In tumors, the vast majority of (chronically) hypoxic cells are thought to be in a quiescent, though metabolically active, phase, and cannot proliferate (38). Similarly, confluent (plateau phase) cell cultures, in which nutrient or space is limited to imitate the in vivo condition of the tumor, consist mostly of cells out of cell cycle (G0/G1-phase), and yields decreased OER values (38,60). Other studies show that cells in G0 might be more sensitive to radiation damage compared to cells in G1 (61,62). It has also been suggested that repair mechanisms for hypoxic cells are less effective than normoxic cells (43,63,64). Perhaps most saliently, cells experiencing chronic hypoxia have been shown to have OER values similar to what we find (65). Hence, our result of an OER of 1.7 for cells receiving glucose, but not oxygen, is consistent with established results.

In the model, the primary determinant of the surviving fraction following SBRT is the fraction of hypoxic cells in the intermediate compartment at the beginning of therapy, whereas 2 Gy/weekday regimens have the advantage of eventual reoxygenation and elimination of the hypoxic component. Because hypoxia reduces the effective dose seen by irradiated cells, departures from the linear-quadratic model that have been proposed to take effect at high doses are seemingly not relevant (66–68).

We freely acknowledge various uncertainties in model parameters. We assumed that a growth fraction of 25% and a tumor doubling time of 100 days would be representative. In fact, this data is not available for most human tumors and, although it is consistent with some publications (39,40), there is also undoubtedly substantial heterogeneity in the parameters, within and between tumors.

Recently, it was argued that SBRT outcomes are consistent as conventional RT (using the L-Q model) without considering hypoxia or proliferation (44). However, we previously addressed this, having shown that the proposed dose-response curve was not a good statistical fit to that dataset (12). Our model p-values show that the available data is entirely consistent with our mechanistic model. Other papers have attempted to model the same or similar datasets (69,70). However, those papers show poor fits overall (with no computed fit p-values), with much wider uncertainties on fitted parameters. When those models were applied to our dataset, both models provided poor fits with very low p-values (p<0.001), as shown in Figure S4.

It has been proposed that vascular endothelial cell damage might play an important role in the SBRT regimen. If this takes place during therapy, blood supply may decrease and the assumption of invariable blood supply would not apply. Although it seems likely that there would be a vascular effect, we do not see it in our data analysis.

Despite the idealized nature of the model, the resulting radiological parameters have reasonable values and small uncertainty bands. The excellent fit results supports the hypothesis that the model, incorporating standard radiobiological principles plus a novel chemical conservation principle, provides a rational basis to understand radiation dose-response for early stage lung cancer across a very wide range of fractionation and dose prescription treatment regimens. The model may be useful in the rational selection of optimized lung cancer radiotherapy protocols, potentially extended even to personalized fractionation schedules and dose prescriptions. As seen in the fitted results, many clinical protocols either over-treat of under-treat early stage lung disease.

In conclusion, we have shown for the first time that a mechanistic mathematical model can quantitatively predict the tremendous differences in response seen in early stage lung cancer across the range of clinical dose and fractionation schemes. Fitting of the model to a large range of reported clinical cohorts results in reasonable radiobiological parameter values with small uncertainty intervals. The model can therefore be used to predict which fractionation schemes over- or under-treat lung tumors.

Translational Relevance.

Modern radiotherapy techniques often utilize a small number of fractions (hypofractionation) rather than the previously standard approach of many daily fractions. However, the tumor sterilization rates for different fractionation schemes vary dramatically in a poorly-understood fashion. This paper applies a detailed mechanistic mathematical model of cellular evolution and response to radiotherapy, including variable microenvironmental conditions, cellular competition for resources, and cell cycle dependent radiosensitivity, that are usually ignored. The resulting prediction model accurately predicts tumor response likelihood for a broad range of fractionation regimens for lung cancer, a result that has not previously been achieved. This cellular response model therefore clarifies the mechanism of radiotherapy action and could be used to avoid over- or under-treatment for a given fractionation schedule.