Abstract
Accurate prediction and validation of the assembly of bioinspired peptide sequences into fibers with defined mechanical characteristics would aid significantly in designing and creating materials with desired properties. This process may also be utilized to provide insight into how the molecular architecture of many natural protein fibers is assembled. In this work, computational modeling and experimentation are used in tandem to determine how peptide terminal modification affects a fiber-forming core domain. Modeling shows that increased terminal molecular weight and hydrophilicity improve peptide chain alignment under shearing conditions and promotes consolidation of semicrystalline domains. Mechanical analysis shows acute improvements to strength and elasticity, but significantly reduced extensibility and overall toughness. These results highlight an important entropic function that terminal domains of fiber-forming peptides exhibit as chain alignment promoters, which ultimately has notable consequences on the mechanical behavior of the final fiber products.
Keywords: protein fibers, terminal domains, coarse-grain modeling, wet-spinning, mechanical properties
Graphical Abstract
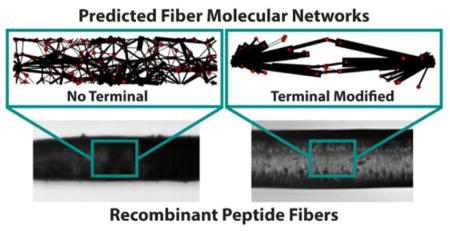
Protein fibers are important physiological structures that assemble from monomers in various ways. In this work, simulation and experimental results are presented that describe a general means by which fiber assembly is facilitated by terminal domains and how resulting fiber mechanical properties are affected. This design process shows promise as a means to investigate and develop materials with desired properties.
1. Introduction
Protein-based fibers represent a large class of biological polymers that serve important physiological roles over a wide range of functional lengths from the nanometer to meter scales. While the expression of the base protein comprising these fibers is well known to be the terminal point of the central dogma, there are still mechanisms that cause mature proteins to form fibers that remain undetermined or poorly understood. Several proteins have specialized assembly processes such as the enzyme-mediated assembly of fibrinogen into fibrin[1] or the ATP driven assembly of actin.[2] However, many protein fibers are made without specific catalysts and, in many cases, their fundamental assembly may be obfuscated by cellular activity, which limits our understanding of the underlying mechanisms that create the fiber network structure. Recent studies on extracellular matrix components fibronectin[3] and collagen[4] have pointed towards alignment-induced interchain exchange at the protein terminals as the means by which mature fiber products are formed. These data suggest that parallel or antiparallel terminal-to-terminal reorientation of the protein strands is a critical step to fiber outcomes. Indeed, terminal domain interactions are believed to play a critical role in many proteins including microfibril assembly of fibrillin,[5] linear connectivity of spider silk,[6] and the formation of amyloid fibers of many proteins.[7] Further, terminal domains of fiber-forming proteins such as these are often highly conserved,[8–11] suggesting an evolutionary advantage is preserved by their inclusion in the sequence. These studies highlight the value of determining the interaction that terminal domains and bulk sequence interactions have on the molecular alignment and coordinated assembly of protein fibers.
Moreover, terminal domains have been used frequently in protein recombination experiments as customizable sequence sites to facilitate purification[12] and fluorescent visualization.[13] Generally, recombinant peptides are processed by expressing characteristic sequences from desired peptides into a simplified sequence that recapitulates some key feature of the source proteins such as specific ligand binding affinities,[14] temperature responsiveness,[15] and strength,[16] which leaves the terminal regions as good targets to promote engineering feasibility without compromising the source sequence. Yet, it has been shown that even small modifications, such as adding a hexa-histidine purification tag, contribute non-negligible pressures on folding[17] and binding capability[18] of the peptides. With this in mind, greater effort is being placed on synergizing the function of the terminal domains with the desired peptide behavior, some examples including therapeutic sequestration in recombinant antibodies[19] and mechanical integration of elastin-like peptides.[20] Specifically in the context of fibrous proteins, Heidebrecht et al.[21] recently documented mechanical advantages conferred by the inclusion of terminal domains to silk-like, diblock peptides and speculate that it is an indirect consequence of improved structure caused by the terminal inclusions. To refine recombinant peptide design further, it will be necessary to gain a fundamental understanding of the molecular behavior of terminally-modified peptides in order to access structure-property explanations that can guide the engineering of novel constructs towards predefined properties and function.
Due to the inherent difficulty in accessing these molecular properties through experimental methods, one possible avenue to describe these characteristics is to use a process combining computational simulation and experimentation to generate a mechanistic explanation that is supported by physical values. By doing so, the model may be able to inform a means by which this natural phenomenon can be more easily reproduced synthetically for engineering purposes. In a previous report,[22] we presented a coarse-grained computational approach using shear to assemble block copolymer peptide sequences into interconnected fibrous networks. In the simulation, interchain assembly is governed by hydrophobic interactions, which are explicitly designed to spontaneously form micelles in solution.[23] The anisotropic alignment induced by the systemic shearing then causes the formation of structured hydrophobic clusters from the core hydrophobic regions of the micelles, which approximates β-sheet secondary structure formation in proteins. Indeed, this mechanism of fiber assembly exhibits significant similarities to the general process ascribed to amyloid fiber formation, which also consistently occurs after micellar aggregation of proteins and independent of specific sequences.[24]
Consequently, this coarse-graining method has shown the capability to describe a known means of fiber formation in peptides and offers good potential as a tool to assess how sequence modification affects fiber outcomes. In this regard, we extend these simulations in this study by modifying the terminal region of the model peptide sequence, by both addition and substitution, in order to observe the effects of terminal sequence modification on the assembly of the fiber molecular network under shear. Additionally, we are able to draw physical correlations to the computational model results by expressing analogous recombinant peptides and investigating their mechanical properties under the constrained conditions of the model environment when spun into fibers, which has not been previously investigated in the context of this simulation system. This combination of modeling and experimentation demonstrates the power of predictive design and validation as a tool to answer difficult research questions and design improved materials.
2. Experimental Section
2.1Computational simulation of block copolymer peptides and varying terminal domains
To investigate the molecular effects of terminal modification, we investigated 3 modeled sequences: a block copolymer base peptide developed from our prior work (H(AB)12)[22] and two new modified variants: one with a hydrophilic terminal substitution (H(AB)10-HST), selected to investigate the effect of changing hydrodynamic behavior with chain length constant, and another with an amphiphilic terminal addition (H(AB)12-AAT), selected to investigate the effect of changing chain length with constant hydrodynamic behavior (Figure 1a). The sequences were modeled using dissipative particle dynamics (DPD) as defined by equations given in Table S1 with additional detail on the method available in the previous report. Each block of the sequences consisted of a specific arrangement of beads that were either classified as entirely hydrophobic (a) or hydrophilic (b) such that neither carried any intrinsic amino acid information and both were equivalent in size. The scale of the coarse graining was such that each bead represented three amino acids. Consequently, the H, A, and B blocks of all sequences consisted of 16 b-beads, 5 a-beads, and 7 b–beads, respectively. The H block represented a cloning and purification sequence, which was incorporated in the model to both improve correlation with the physically expressed peptides and act as a de facto hydrophilic terminal domain for each peptide. The A block represented hydrophobic residues of the peptide generally, which are capable of forming the semicrystalline domains necessary for fiber assembly. The B block represented hydrophilic residues, which lent to the amorphous phase of the peptide structure. The two unique terminal modifications, the hydrophilic substitution (HST) and the amphiphilic addition (AAT) terminals, had bead structures of 24 b-beads for the HST and a predominantly hydrophilic composite structure of b3a3b2a2b11a6bab2ab7a4b, totaling 17 a-beads and 27 b–beads (Figure S1), for the AAT. The determination of the bead permutation sequence of the AAT domain is detailed in section 2.3.
Figure 1. Schematic of the block copolymer sequences.
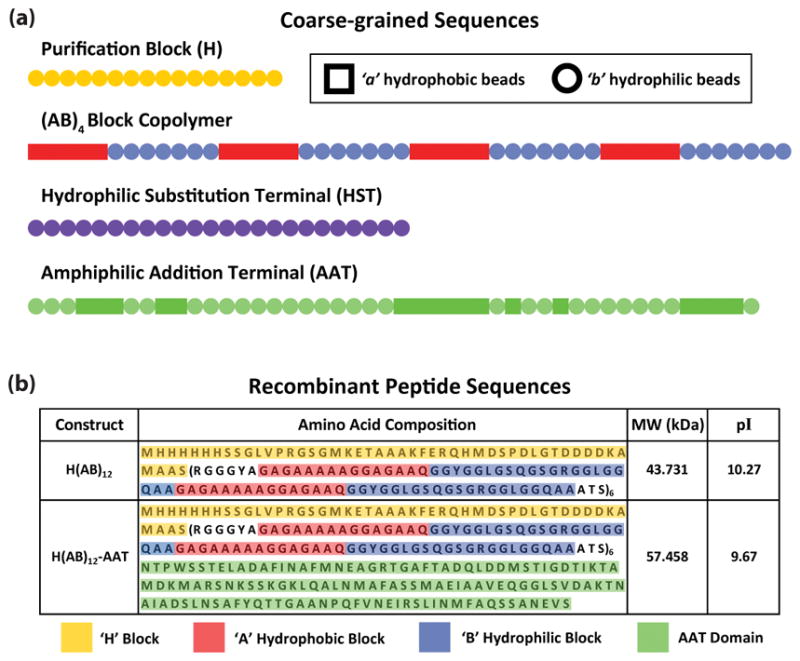
(a) Bead sequences of the major components making up the block copolymer peptides. Each bead represents a triplet of amino acids, which are generalized into a singular behavior of being hydrophobic (a-beads) or hydrophilic (b-beads), shown as square and circle shapes, respectively. The purification block and terminal modifications are shown in their full length. The AB block copolymer is truncated from 12 to 4 repeats for display purposes only. (b) The discrete amino acid sequences of H(AB)12 and H(AB)12-AAT, which were selected for experimentation, are given in terms of how they correlate to the model segments. H(AB)10-HST was not produced experimentally and, therefore, lacks a correlated amino acid sequence. Molecular weights and isoelectric points are provided for reference.
The DPD simulations of the model peptides were performed using the LAMMPS package[25] with explicit water solvent and protein concentrations set to 20% v/v. Every nine water molecules were represented by one hydrophilic w-bead to be consistent with the scale of the coarse-grained beads comprising the peptides.[22] Each simulation consisted of three stages: (I) initial equilibration of the system, (II) application of shear to the system, and (III) equilibration after shear to relax the system. Shearing was applied along the x-axis (xy plane) at a rate of γ̇xy 0.01τ−1 for t = 5000τ where τ = 0.75 ns, which is the characteristic/physical time scale of the DPD model corresponding to the level of coarse-graining that we have applied. The simulation box size was fixed at ( ) where Rc 9.321Å, which is the characteristic/physical length scale of this DPD model. At the start of the simulation, peptide chains were filled in random configurations at random positions. The rest of the box was filled with water beads until the number density of the system reached 3, resulting in 1,512,000 beads in each system. All simulations were performed in a microcanonical ensemble (NVE) with an integration time step of dt = 0.03τ. Molecular simulation of biological systems is usually performed at constant temperature to represent the controlled thermal environment of both biological and experimental systems. The implemented DPD pair style in the LAMMPS code computes conservative, dissipative, and random forces. Temperature effects are calculated as part of the random force, which is kept constant in this ensemble.
2.2 Geometrical analysis of the molecular network
Hydrophobic beads became connected during simulation and created clusters due to a-beads’ capability of forming hydrogen bonds with one another. Two a-beads were assumed to belong to the same cluster if their distance was less than 0.94 Rc. Nodes were defined as the center of mass of a cluster and two clusters were assumed to be tethered by a connection (b-beads) if any number of chains spanning the two clusters contained a-beads in both. Each phase of the simulation was quantified to describe the assembly properties of the chains by determining the number and size of clusters as well as the number and order of connections. From these data, the two sequences with the largest quantified difference in these metrics were selected to clone, express, and test in order to find physical correlations to model outputs from mechanical and structural data.
2.3 Physical cloning, expression, and purification of the recombinant peptides
Modeling results highlighted H(AB)12 and H(AB)12-AAT as the sequences with the greatest difference in their quantified metrics and were selected for further experimentation. The H block region was synthesized using the Novagen (Madison, WI) pET 30a-c(+) vector as a template for cloning and purification purposes. The AB block copolymer region was recapitulated physically based on sequences from major ampullate silk of Nephila clavipes due to the simplicity of its core amino acid composition closely emulating the alternating block copolymer structure (Figure 1b).[26] The AAT domain was based on the N–terminal domain of the same major ampullate silk,[9] which was also the basis for the bead model used in simulation after ranking the amino acid sequence using the Kyte-Doolittle hydrophobicity[27] and coarse-graining triplets of amino acids into singular hydrophobic or hydrophilic beads (Figure S1). This bioinspired method was done to avoid creating an arbitrary permutation of a and b beads to make up the AAT domain.
The genes encoding the recombinant peptides were produced and purified similar to procedures described previously.[28] For large-scale expression, the recombinant strains were grown overnight at 37°C in Luria-Bertani medium under shaking conditions (250 rpm). Afterwards, seeding culture was transferred to yeast extract medium and cultured at 37 °C, pH 6.8 using a New Brunswick BioFlo 3000 bioreactor (New Brunswick Scientific, Edison, NJ). Cells were induced with 1 mM isopropyl-β-D-thiogalactopyranoside (IPTG) (Sigma-Aldrich, St. Louis, MO) when the optical density OD600 reached approximately 10. Once the proteins were produced, purification was performed using immobilized metal affinity chromatography following previously described procedures.[29] The proteins were dialyzed against water using a Slide-A-Lyzer Cassette (Pierce, Rockford, IL) with a molecular weight cut-off of 2,000 Da and lyophilized. The purity of the expressed proteins was verified by sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE) followed by Colloidal Blue staining.
2.4 Fiber production and microscopy
Concentrated solutions were prepared for both H(AB)12 and H(AB)12–AAT by dissolving the proteins in Ultrapure water (Merck Millipore, Billerica, MA) through pipetting and mild vortexing. Pure water was used in order to align with the modeled condition and obtain the best correlations possible. Saturated concentrations were determined by drying leftover solution and measuring the mass of the dried peptide compared to the original solution mass. A simple wet spinning approach was used to create fibers by extruding the peptide solutions vertically through a Hamilton syringe (Hamilton Company USA, Reno, NV), with an inner needle diameter of 0.15 mm, at a spinning rate of 5 μL/min into a collection bath filled with 100% 2-propanol as the coagulation solvent. After fiber formation, the fibers were kept in the coagulation bath for at least 1 h before being tested. No post-spin modifications were performed.
Optical investigations of the fibers were performed using an Olympus IX81 (Center Valley, PA). Images were taken to compare morphology along the length of fibers from which diameters were averaged for use in mechanical properties calculations. Closer investigation of fiber morphology was performed using scanning electron microscopy (SEM) on a Zeiss 55Ultra and a Zeiss Supra (Thornwood, NY). Images were taken of dried fiber on silicon products using InLense and SE2 detectors at 5.00 kV.
2.5 Physical characterization of fibers
Uniaxial tensile measurements of fibers were performed on an Instron Microtester (Norwood, MA) using a 5N load cell with 100 Hz sampling rate. Fiber samples were loaded onto sacrificial custom frames to protect the fibers from breaking before they were loaded onto the testing apparatus. Once the samples were loaded, the sacrificial frames were removed and fibers were pulled at a strain rate of 0.01 s−1 until failure. Force data were collected and normalized to stress values based on respective diameter measurements of each fiber tested.
Infrared spectra of the spun fibers as well as their lyophilized powders were recorded using a Jasco FT/IR-6200 spectrometer (Easton, MD). Spectra were scanned in absorption mode with 4 cm−1 resolution from 4000–400 cm−1. All spectral manipulations were performed with OPUS software (version 5.0) (Mattson Instruments, Madison, WA). Quantification of the secondary structure was done by analyzing the amide I region (1700 – 1600 cm−1) and performing a Fourier self-deconvolution analysis, which has been shown to give structural data consistent with that of x-ray scattering.[30] The average secondary structure composition percentage of the peptides was assessed by integrating the area of each deconvolved curve, and then normalizing to the total area of the amide I peak.
2.6 Statistical Analysis
All results that include statistics are reported as mean ± standard deviation. Significance was assessed based on P-values generated from two-tailed Student’s t-tests in order to compare two sample groups. P–values less than 0.05 were considered significant.
3. Results and Discussion
3.1 Molecular simulations and predictions
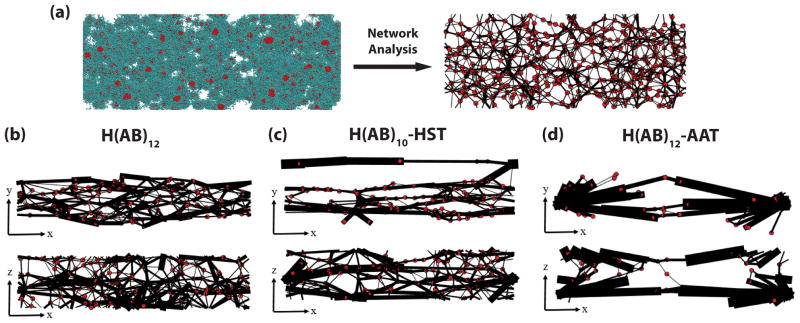
Molecular assembly mechanisms were modeled using DPD at the mesoscale, which provides an approximation of the secondary structure environment of the assembling peptide chain. Triplets of amino acids were generalized as either a hydrophobic (red) or hydrophilic (cyan) bead and organized into chains with differing terminal compositions. Each unique sequence was populated in a simulation space with coarse-grained water as the solvent (Figure 2a). After shearing in the x–direction, crystalline clusters (red dots after network analysis) of the red hydrophobic beads increase in size and connections between clusters, comprised of chains of the cyan hydrophilic beads (black lines after network analysis), begin to strongly bias the shear direction in all three constructs (Figure 2b, c, and d).
Figure 2. Simulation of the network structures of the block copolymer sequences.
(a) Typical simulation snapshot without water molecules shown for the H(AB)12 system. Cyan spheres represent hydrophilic beads and red spheres represent hydrophobic beads. Red bead clusters become red dots after network analysis and cyan beads that connect two clusters together become black lines. Connections and clusters are quantified via network analysis after equilibration. (b–d) Final network maps from two different spatial planes of the three sequences at the end of equilibration after shear. Thickness of the black lines correlates to the size of a connection between red dot nodes.
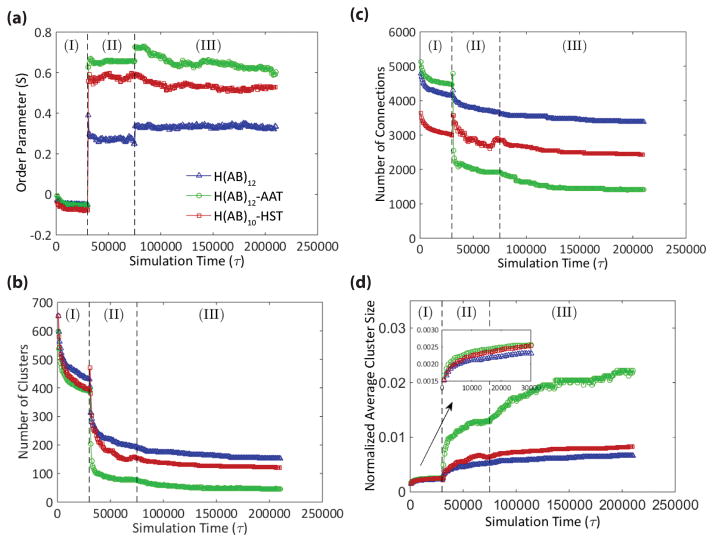
We use an order parameter to describe molecular order and quantify chain alignment, shown in Equation 1, where θ is the angle of the vector connecting two clusters with respect to the shear flow direction and the brackets denote an average over all connections. For completely isotropic connections S = 0, and perfectly aligned connections have S = 1.
| (1) |
In all constructs, S increases significantly with shear (Figure 3a), but separates into a rank of H(AB)12-AAT having the highest order and H(AB)12 having the lowest order. Of note is that the peptides with identical molecular length, H(AB)12 and H(AB)10-HST, show a large difference in alignment preference due entirely to the substitution of the two diblock repeats with purely hydrophilic beads. Continued improvement is observed in the molecular order of H(AB)12–AAT, though this increase is more due to increased molecular length[22] than hydrophilicity. By comparison, H(AB)12 is terminated with the 7 consecutive hydrophilic beads of the final B block and has 28 of its final 48 beads (58%) being hydrophilic. Additionally, the average number of beads in the hydrophilic blocks normalized against the number in the hydrophobic blocks is 1.4, meaning the hydrophilic blocks are 40% longer, on average, than the hydrophobic blocks. The non-repetitive, 44 bead AAT domain shares very similar ratios of hydrophilic content (61%) and hydrophilic/hydrophobic block length (1.36). These values demonstrate that the terminal domains of H(AB)12 and H(AB)12–AAT peptides are very similar in bead composition and distribution of hydrophobic and hydrophilic beads, which points to their difference in chain length as the stronger factor driving alignment.
Figure 3. Quantification of the simulation results.
Each simulation consists of three stages: (I) initial equilibration, (II) shearing, and (III) post-shear equilibration. (a) Tracking the order parameter through the simulation shows that, in all cases, shearing results in greater alignment, or molecular order, in the direction of shear with H(AB)12-AAT aligning to the greatest degree followed by H(AB)10-HST, and lastly H(AB)12. (b, c) Conversely, there is a universal decrease in the number of clusters and connections after shearing with the rank order of the three peptides reversed from that of the order parameter. (d) The decreases in cluster and connection numbers are offset by cluster consolidation, which again follows the order observed for the order parameter. This suggests that molecular order is a means by which semicrystalline domains, modeled by the clusters, are consolidated into larger structures.
These results lead us to speculate that the common element giving rise to improved molecular order from hydrophilicity and molecular weight are respective increases in folded contour length of the peptides in solution following the rank order of their alignment, i.e. H(AB)12 has the shortest contour length while H(AB)12-AAT has the longest. The reason that hydrophilicity would contribute to increased contour length is due to two phenomena: first, replacing the hydrophobic beads of the terminal domain removes its hydrogen bonding capability to interact with the core; and second, the higher number of hydrophilic beads increases the chain susceptibility to entropic reorientation under shear due to their affinity with displacing water. The latter phenomenon is apparent in the total time required after shearing for the system to equilibrate where the construct with the highest hydrophilic content ratio (H(AB)10–HST) was the quickest to equilibrate (Figure S2). For H(AB)12-AAT, the significant increase in its molecular weight, equivalent to 4 diblock repeats, is suspected to be enough added length that, even when folded and lacking a respectively high concentration of hydrophilic beads, it maintains a length advantage over H(AB)10-HST. While the peptide contour length in solution rationalizes the explanations of alignment from two different sources—hydrophilicity and molecular weight—this hypothesis requires further investigation to verify both computationally and experimentally.
Despite improved network order following shear, there is a proportionate decrease in spatial diversity of clusters caused by a fewer total number of clusters (Figure 3b) and connections (Figure 3c) in the networks of both H(AB)10-HST and H(AB)12-AAT compared to that of H(AB)12. Instead, semicrystalline domains consolidate into a smaller total number of larger clusters (Figure 3d) with larger connections between them (represented by the thicker lines seen in Figure 2d). These metrics can be used to inform some qualitative predictions of the mechanical nature of the physical fibers under stretching. The peptide chains, modeled as extensible freely jointed chains,[22] will stretch up to a point of infinite resistance against further elongation first for all connections with the highest degree of order (highest S value) followed by those with lesser order after they are reoriented into the stretching direction. Force will then concentrate on the cluster regions such that the greatest force will be applied to clusters connected by well-ordered connections. As stretching continues, the bonding that holds the clusters together will begin to break under sufficient force allowing molecules to disassociate from the cluster.[31] This pattern of molecular extension, connection reordering, and cluster deconstruction will continue until there is sufficient deformation to disconnect the entire network. The disassociation of molecules from the cluster regions under stretch approximates the phenomenon of protein domain unfolding.
Based on this pattern, it can be expected that H(AB)12-AAT, which has the largest cluster size and greatest alignment, will quickly exhibit high strength at modest strain values and ultimately prove not very extensibility because most of its semicrystalline domains are already aligned in the stretch direction.[32] Conversely, the numerous and diversely aligned connections of the H(AB)12 network should exhibit its strength over a large range of strain because realignment will be necessary for a large number of semicrystalline domains in the network. As such, it is likely that the initially-aligned clusters will begin to unfold prior to the full reorientation of the network, which approximates the behavior of plastic deformation as a consequence of the strain-dependent failure of pre-aligned crystalline domains.[33] In summary, the highly ordered and consolidated H(AB)12-AAT sequence is expected to be much more brittle and acutely strong while the H(AB)12 sequence is expected to be much more plastic and exhibit strength over time.
3.2 Morphology of produced fibers
To test the mechanical effects of terminal modification, the two sequences with the greatest difference in modeled properties, H(AB)12 and H(AB)12-AAT, were processed into fibers using a wet-spinning approach.[34] Concentrated solutions were prepared in deionized water in order to be consistent with the modeled aqueous environment. The maximum aqueous concentrations obtained from the constructs were (Figure 4a) 15.35 ± 1.71% for H(AB)12 and 15.84 ± 1.31% for H(AB)12-AAT, not exhibiting a significant difference between them (P = 0.71). This supports the claim presented in the modeling results that the AAT domain does not contribute to fiber alignment due to improved hydrophilicity of the sequence. Both solutions yielded continuous extrusion of heterogeneous fibers throughout the spinning process (Figure 4c, d) where the average diameters of extruded fibers (Figure 4b) exhibit significant difference (P = 0.019) despite identical spinning conditions.
Figure 4. Microscopic investigation of fiber morphologies.
(a) Maximum aqueous solubility as a percent of mass of the constructs was consistent for both sequences that were processed into fibers (n=20). (b) Average diameter of the extruded fibers shows a statistically significant difference with AAT incorporation. (c, d) Representative light microscopy images of the extruded fibers of H(AB)12 and H(AB)12-AAT, respectively. Fibers showed heterogeneous appearances at the surface with both smooth and rough topographies. Scale bars are 50 μm. * signifies P < 0.05. Error bars represent standard deviations.
SEM investigation of H(AB)12-AAT fibers reveals that micelle-like structures may comprise the fundamental assembly of the fibers (Figure S3), which is consistent with the morphology observed in our previous report for fibers of the H(AB)12 peptide.[22] While further investigation would be needed to validate if this fiber morphology is consistent across numerous fibers of these diblock peptides, this fiber morphology provides support for the model premise that the base building block of the fiber networks are aggregated micelle structures that are assembled and interconnected by shearing. Indeed, we speculate that the difference in each construct’s fundamental micelle/cluster size may be a contributing factor to the statistically significant difference in diameter observed between the constructs. We note that both DLS investigations (Figure S4b) as well as model predictions support the notion of H(AB)12-AAT tending towards larger clusters as building blocks for fiber assembly, whether induced by shearing or occurring spontaneously over time.
3.3 Fiber physical property characterization
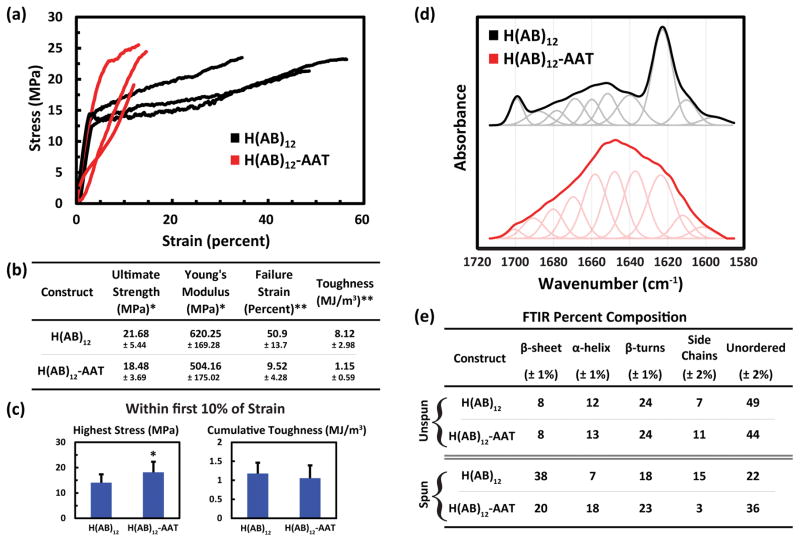
Physical properties were characterized through uniaxial tensile testing and FTIR spectroscopic analysis on spun fibers without any post-spin conditioning to maintain close correlation with the model. Stress-strain relationships with summary statistics of engineering values (Figure 5a, b) were generated from the uniaxial tensile data. All calculated values demonstrated statistical significance; however, ultimate strength, 21.68 ± 5.44 MPa for H(AB)12 and 18.48 ± 3.69 MPa for H(AB)12-AAT (P = 0.045), and Young’s modulus, 620.25 ± 169.28 MPa for H(AB)12 and 504.16 ± 175.02 MPa for H(AB)12-AAT (P = 0.045), were rather slight qualifiers. Indeed, due to the inverse relationship reported between the diameter of polymer fibers and their strength and modulus,[35] the differences between the values of these two constructs can be accounted for by their diameter mismatch as opposed to an intrinsic difference in each construct’s mechanical properties. This signifies that addition of the AAT domain to the repeating diblock core does not have an overall effect on the ultimate strength or Young’s modulus of the resulting fibers.
Figure 5. Physical characterization of the recombinant peptide fibers.
(a) Three representative stress-strain curves of data obtained from uniaxial tensile testing of H(AB)12 and H(AB)12-AAT (n=18, n=20, respectively) shows the general behavior of the materials under extension. (b) Summary statistics of all mechanical data. Failure strengths and Young’s moduli do not vary greatly, while the extensibility, and consequently the toughness, does change considerably. (c) Values of cumulative strength and toughness based on only the first 10% strain for all fibers that stretched that far without failing (n=10 for H(AB)12-AAT). (d) FTIR absorbance in the amide I band for fibers of H(AB)12 and H(AB)12-AAT. Deconvolved peaks of the spectrum are shown below both curve, which correspond to the individual secondary structure contributions of the structure. (e) The resulting relative percentage compositions of secondary structure elements for each sequence, both unspun and spun. * signifies P < 0.05, ** signifies P < 0.001. Error bars represent standard deviation. The spectrum of fibrous H(AB)12 from panel (d) is reproduced with permission[22] from our previous work’s supplemental information. Copyright 2016, Nature Publishing Group.
However, the AAT domain does have a clear negative impact on its fibers’ extensibility. The elongation strain at failure falls from approximately 50% to 10% causing a significant reduction in the total energy the system can endure before fracture, defined as material toughness. This low extensibility agrees with the model predictions, which also predicts high acute strength due to pre-alignment of the chains in the stretch direction of the H(AB)12-AAT peptide. When the material properties of both peptides are observed prior to the 10% strain point (Figure 4c), the toughness difference between the constructs becomes indistinguishable and the maximum strength value of H(AB)12-AAT increases significantly (P = 0.013) compared to that of H(AB)12 fibers. H(AB)12-AAT fibers also achieve a greater stress value relative to their average ultimate strength (98.1%) by that point than the standard AB block copolymer (64.8%). So while the addition of the AAT domain significantly reduces overall extensibility, it does exhibit the acute strengthening effect predicted by the model by eliminating the plastic deformation region seen in H(AB)12 fibers, which was also predicted by the model based on its final molecular network. Taken together, AAT incorporation appears to directly affect the extensile characteristics of the silk-like biopolymers by promoting elasticity and acute strength over greater toughness via greater plastic deformation.
To correlate secondary structures to the model network, FTIR was performed on lyophilized samples of H(AB)12 and H(AB)12-AAT, and on fibers spun from H(AB)12 and H(AB)12-AAT. The wavenumber from 1720 to 1580 cm−1 was investigated closely, as it contains the amide I region (Figure 5d), which correlates to protein secondary structures and can be deconvolved to obtain relative quantities (Figure 5e).[36] In the case of lyophilized powders, FTIR highlights the general lack of β-sheet content in both constructs while helices are the predominant ordered structure prior to spinning. Spinning the solutions into fibers induces the α–helical content of H(AB)12-AAT to increase further, while the same structure decreases in H(AB)12. Both gain significant β-sheet content, but H(AB)12 gains a much larger relative amount than that of H(AB)12-AAT, which correlates positively with the number of clusters modeled parameter (Figure 3b) wherein H(AB)12 maintains a greater number of smaller clusters over H(AB)12-AAT throughout simulation. When the recombinant proteins’ secondary structures are compared with mechanical data, an interesting phenomenon is observed. Despite a near half-fold decrease in β-sheet content and respective doubling of α-helical content in the H(AB)12–AAT, there is not a remarkable change to the strength nor modulus of the fibers when compared to the core region alone. Typically, β-sheet crystallinity is assumed to play the greatest role in the mechanical integrity of silks rather than other structural elements.[37] However, there is evidence from simulation that α-helical structures can contribute large degrees of robustness to the overall material strength at modest strain percentages,[38] which may be the case for H(AB)12-AAT and its relatively low extensibility. This is interesting because it infers that the strength and stiffness of the AAT fibers are determined by a complex interplay of secondary structural elements rather than being determined by the predominance of β-sheets alone.
3.4 Considerations for the model-experimentation correlations
The modeling data demonstrates that increasing terminal hydrophilicity and length causes improved alignment at the molecular level and consolidation of semi-crystalline domains into a fewer number of larger clusters. We correlated these explanations to mechanical properties, which show that the increase in molecular anisotropy results in a more mechanically elastic fiber product. These physical correlations to the model were tested using amino acid sequences that were inspired by specific sequences from spider silk peptides. While this reduces the universality of the physical application to fibrous proteins on a general level, it still serves as a good model system to describe fiber assembly because of the simplicity of the silk peptides. In many models, silk sequences have been the physiological basis to describe peptide analogs of block copolymers consisting of hydrophobic and hydrophilic blocks.[26, 28, 39, 40] This is because the flexible β-strand content of silk, made up largely of alanine or glycine-rich repeats, is offset regularly by flexible, glycine-rich hydrophilic chains with minimal composition contributions from other amino acids.[41] This simple structure thereby facilitates simplification into a model environment as a product of basic interaction forces, as done in this work with hydrophobicity, hydrophilicity, and shear.
The next consideration is whether or not block copolymer peptides are sufficient structures to model other proteins generally, which may have more diverse sequences. While there certainly is information lost in the model by not accounting for some of the amino acid-specific chain-chain interactions observed in many fibrous proteins, such as sulfide bridging of many terminal domains, it is still appropriate to describe protein hierarchical assembly as predominantly a consequence of hydrophobic/hydrophilic interactions. This is because peptide hydrodynamic behavior is a consequence of universally governing thermodynamic events. With respect to fiber formation, our model predicts that physical crosslinking of peptide chains occurs via hydrogen bonding, which are the stabilizing enthalpic contributions derived from the hydrophobic regions of the peptide sequence.[42] This bonding is only possible after alignment of the bonding regions by shear, which is a consequence of the entropic contributions of the peptide chain that derive from its hydrophilicity and length, as we have shown in this work. Simplified to these two events of elongation and bonding, the potential of all peptide sequences to form fibers can then be generalized as a function of their hydrodynamic behavior rather than their specific amino acid sequence, which supports the value of the model predictions from a hierarchical view. Certainly, it has been shown in previous work that peptide β-strands as short as 2 residues are capable of forming stable β-sheet bonding interactions,[43] with the most common number of residues between 5 to 6.[44] Based on this criterion, if the amino acid sequence of any protein of interest is converted to the bead structure of the model using the Kyte-Doolittle hydrophobicity rankings as we have done here, then any site with a mere one or two hydrophobic a-beads in series has potential to form or contribute to a stable semicrystalline domain.
Applying this to proteins in vivo, this simple thermodynamic explanation of fiber formation provides a potential explanation of how numerous native proteins are assembled into fibers. Fibronectin, for example, is assembled by cells into fibers in a process involving secretion of the soluble protein into the extracellular space. Many hypotheses have pointed to the molecule associating with two integrins on the surface of the cell[45] followed by actin remodeling causing the molecule to elongate, priming it for polymerization when ordered with other elongated fibronectin molecules. In the context of our model system, we hypothesize that any environment experiencing shear may cause reordering and alignment of the fibronectin molecules, independent of any specific cell interactions, which is guided and facilitated by entropic contributions of the terminal domains as well as those of the bulk sequence. From this aligned state, spontaneous enthalpic assembly through bonding may then occur without any further input from the cell. Indeed, cell traction measurements show that cells are capable of exerting sufficiently large shear stresses needed to enable such an assembly,[46] which may also receive contributions from other environmental stresses such as fluid shear, muscle contraction, and so forth. Under such a simple assembly model, other fibrous proteins like type I collagen may be organized into fibers similarly through simple environmental shear in tandem with other environmental cues, such as higher local pH or saline concentrations,[47] without necessitating complicated input from cells. This mechanism of assembly via entropic ordering would prove particularly advantageous in environments with high directional stress, such as the synovial space[48] or aortic wall,[49] such that the very stressors degrading the existing matrix would also provide the stimulus for the alignment and formation of new matrix. This hypothesis awaits further investigation, which we believe can be accomplished using the same wet spinning approach on various full-length proteins of interest, including collagen and fibronectin, and observing any potential assembly phenomenon. The shear rate produced in the wet-spinning device is on the order of 425–850 s−1, depending on flow rate, which has been shown to be sufficient to cause conformational elongation in peptides such as von Willebrand factor[50] and the latent TGF-β complex,[51] which leads to functional changes for both. Therefore, it is likely that the shearing caused by the wet spinning device is sufficient to overcome soluble protein folding interactions and cause alignment of the hydrophobic regions to occur for potentially any peptide sequence, especially due to the low number of amino acid residues required for β-strand assembly. Recent work where fibers were generated through wet spinning a blend of silk fibroin with fibronectin is an encouraging result regarding the potential to generate peptide fibers using such a shear approach.[52]
4. Conclusions
Terminal modifications in this work caused significant changes to fiber-forming molecular chains. In a general thermodynamic sense, they are sources of additional molecular weight and hydrophilicity for the peptide strand, which may lend to increases in contour length in order to facilitate alignment and assembly. We have shown that both of these factors improve molecular order in simulation, which consequently consolidates semicrystalline domains while lowering their spatial distribution. When tested experimentally, terminal-modified fibers exhibited larger diameters and experienced a shift in their stress-strain relationship to favor strength and elasticity in the early strain regime at the expense of overall toughness. This is likely a consequence of improved pre-alignment of the semicrystalline domains in the direction of stretch, which also significantly reduces material plasticity. At the structural level, β-sheet content was nearly halved while the α-helical content doubled, yet it proved just as strong as the unmodified control peptide H(AB)12. From a materials design standpoint, this highlights how sequence modification can lead to constructs with very different innate material properties.
In terms of application to native proteins, it is possible that shear-induced alignment in vivo is the means by which β-strand assembly is induced for many fibrous proteins, whether initiated by cells or the environment. We demonstrate that terminal domains of these proteins may play important entropic roles to facilitate the chain-chain orientation necessary to establish the stabilizing enthalpic interactions leading to the formation of insoluble, anisotropic fibers. These findings provide a general context and mechanism for terminals, but does not encapsulate the sequence-specific factors that may also play an important role, including covalent dimerization and charge association. Despite this shortcoming, the coarse-grained model system shows great potential as a means to investigate peptide molecular properties that are difficult to access experimentally. With further correlation to physical properties, it may serve as an in silico screening method to filter new peptide sequences towards developing a throughput system where mechanical properties can be predetermined.
Supplementary Material
Acknowledgments
We thank the NIH (U01 EB014976) for support of this work. We thank N.G. Rim and E.G. Roberts for assistance in mechanical testing of the fibers. We thank M. L. Smith for consultation on the preparation of the manuscript. We thank the Center for Nanoscale Systems of Harvard University for providing access to SEM imaging. The computational resources used for this project have been provided by the National Science Foundation through the Extreme Science and Engineering Discovery Environment (XSEDE) and the Texas Advanced Computing Center under grant numbers TG-DMR140101 and TG-MSS090007.
Footnotes
Supporting Information is available online from the Wiley Online Library or from the author.
Supporting Information is provided as the last section of this submission, containing Table S1 and Figures S1–S4.
Contributor Information
Matthew M. Jacobsen, Department of Biomedical Engineering, Boston University, Boston, MA 02215, USA.
Dr. Olena S. Tokareva, Department of Biomedical Engineering, Tufts University, Medford, MA 02155, USA.
Dr. Davoud Ebrahimi, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dr. Wenwen Huang, Department of Biomedical Engineering, Tufts University, Medford, MA 02155, USA
Dr. Shengjie Ling, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dr. Nina Dinjaski, Department of Biomedical Engineering, Tufts University, Medford, MA 02155, USA
David Li, Department of Biomedical Engineering, Boston University, Boston, MA 02215, USA.
Marc Simon, Department of Physics and Astronomy, Center for Nanoscopic Physics, Tufts University, Medford, MA 02155, USA.
Prof. Cristian Staii, Department of Physics and Astronomy, Center for Nanoscopic Physics, Tufts University, Medford, MA 02155, USA
Prof. Markus J. Buehler, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Prof. David L. Kaplan, Department of Biomedical Engineering, Tufts University, Medford, MA 02155, USA
Prof. Joyce Y. Wong, Department of Biomedical Engineering, Boston University, Boston, MA 02215, USA. Division of Materials Science and Engineering, Boston University, Boston, MA 02215, USA
References
- 1.Weisel JW, Litvinov RI. Blood. 2013;121:1712. doi: 10.1182/blood-2012-09-306639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pollard TD, Blanchoin L, Mullins RD. Annu Rev Biophys Biomol Struct. 2000;29:545. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
- 3.Fruh SM, Schoen I, Ries J, Vogel V. Nat Commun. 2015;6:7275. doi: 10.1038/ncomms8275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sarkar B, O’Leary LE, Hartgerink JD. J Am Chem Soc. 2014;136:14417. doi: 10.1021/ja504377s. [DOI] [PubMed] [Google Scholar]
- 5.Cain SA, Baldwin AK, Mahalingam Y, Raynal B, Jowitt TA, Shuttleworth CA, Couchman JR, Kielty CM. J Biol Chem. 2008;283:27017. doi: 10.1074/jbc.M803373200. [DOI] [PubMed] [Google Scholar]
- 6.Schwarze S, Zwettler FU, Johnson CM, Neuweiler H. Nat Commun. 2013:4. doi: 10.1038/ncomms3815. [DOI] [PubMed] [Google Scholar]
- 7.Fandrich M, Dobson CM. EMBO J. 2002;21:5682. doi: 10.1093/emboj/cdf573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Garcia-Pardo A, Pearlstein E, Frangione B. J Biol Chem. 1983;258:12670. [PubMed] [Google Scholar]
- 9.Rising A, Hjalm G, Engstrom W, Johansson J. Biomacromolecules. 2006;7:3120. doi: 10.1021/bm060693x. [DOI] [PubMed] [Google Scholar]
- 10.Brass A, Kadler KE, Thomas JT, Grant ME, Boot-Handford RP. FEBS Lett. 1992;303:126. doi: 10.1016/0014-5793(92)80503-9. [DOI] [PubMed] [Google Scholar]
- 11.Handford PA, Downing AK, Reinhardt DP, Sakai LY. Matrix Biol. 2000;19:457. doi: 10.1016/s0945-053x(00)00100-1. [DOI] [PubMed] [Google Scholar]
- 12.Chong S, Montello GE, Zhang A, Cantor EJ, Liao W, Xu MQ, Benner J. Nucleic Acids Res. 1998;26:5109. doi: 10.1093/nar/26.22.5109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Griffin BA, Adams SR, Tsien RY. Science. 1998;281:269. doi: 10.1126/science.281.5374.269. [DOI] [PubMed] [Google Scholar]
- 14.Widhe M, Shalaly ND, Hedhammar M. Biomaterials. 2016;74:256. doi: 10.1016/j.biomaterials.2015.10.013. [DOI] [PubMed] [Google Scholar]
- 15.Roberts S, Dzuricky M, Chilkoti A. FEBS Lett. 2015;589:2477. doi: 10.1016/j.febslet.2015.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tokareva O, Jacobsen M, Buehler M, Wong J, Kaplan DL. Acta Biomaterialia. 2014;10:1612. doi: 10.1016/j.actbio.2013.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chant A, Kraemer-Pecore CM, Watkin R, Kneale GG. Protein Expr Purif. 2005;39:152. doi: 10.1016/j.pep.2004.10.017. [DOI] [PubMed] [Google Scholar]
- 18.Khan F, Legler PM, Mease RM, Duncan EH, Bergmann-Leitner ES, Angov E. Biotechnol J. 2012;7:133. doi: 10.1002/biot.201100331. [DOI] [PubMed] [Google Scholar]
- 19.Bernardes GJ, Steiner M, Hartmann I, Neri D, Casi G. Nat Protoc. 2013;8:2079. doi: 10.1038/nprot.2013.121. [DOI] [PubMed] [Google Scholar]
- 20.D’Andrea P, Scaini D, Severino LU, Borelli V, Passamonti S, Lorenzon P, Bandiera A. Biomaterials. 2015;67:240. doi: 10.1016/j.biomaterials.2015.07.041. [DOI] [PubMed] [Google Scholar]
- 21.Heidebrecht A, Eisoldt L, Diehl J, Schmidt A, Geffers M, Lang G, Scheibel T. Adv Mater. 2015;27:2189. doi: 10.1002/adma.201404234. [DOI] [PubMed] [Google Scholar]
- 22.Lin S, Ryu S, Tokareva O, Gronau G, Jacobsen MM, Huang W, Rizzo DJ, Li D, Staii C, Pugno NM. Nat Commun. 2015:6. doi: 10.1038/ncomms7892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sheng YJ, Wang TY, Chen WM, Tsao HK. J Phys Chem B. 2007;111:10938. doi: 10.1021/jp073408s. [DOI] [PubMed] [Google Scholar]
- 24.Dobson CM. Nature. 2003;426:884. doi: 10.1038/nature02261. [DOI] [PubMed] [Google Scholar]
- 25.Plimpton S. Journal of computational physics. 1995;117:1. [Google Scholar]
- 26.Huang WW, Krishnaji S, Hu X, Kaplan D, Cebe P. Macromolecules. 2011;44:5299. doi: 10.1021/ma200563t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kyte J, Doolittle RF. J Mol Biol. 1982;157:105. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 28.Rabotyagova OS, Cebe P, Kaplan DL. Biomacromolecules. 2009;10:229. doi: 10.1021/bm800930x. [DOI] [PubMed] [Google Scholar]
- 29.Tokareva OS, Lin S, Jacobsen MM, Huang W, Rizzo D, Li D, Simon M, Staii C, Cebe P, Wong JY, Buehler MJ, Kaplan DL. J Struct Biol. 2014;186:412. doi: 10.1016/j.jsb.2014.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hu X, Kaplan D, Cebe P. Macromolecules. 2006;39:6161. [Google Scholar]
- 31.Keten S, Buehler MJ. Nano letters. 2008;8:743. doi: 10.1021/nl0731670. [DOI] [PubMed] [Google Scholar]
- 32.Ji BH, Gao HJ. J Mech Phys Solids. 2004;52:1963. [Google Scholar]
- 33.Kikuchi H, Logan JA, Yoon DY. J Appl Phys. 1996;79:6811. [Google Scholar]
- 34.Teule F, Cooper AR, Furin WA, Bittencourt D, Rech EL, Brooks A, Lewis RV. Nat Protoc. 2009;4:341. doi: 10.1038/nprot.2008.250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liivak O, Blye A, Shah N, Jelinski LW. Macromolecules. 1998;31:2947. doi: 10.1016/s0141-8130(98)00085-3. [DOI] [PubMed] [Google Scholar]
- 36.Rabotyagova OS, Cebe P, Kaplan DL. Macromolecular Bioscience. 2010;10:49. doi: 10.1002/mabi.200900203. [DOI] [PubMed] [Google Scholar]
- 37.Keten S, Xu ZP, Ihle B, Buehler MJ. Nat Mater. 2010;9:359. doi: 10.1038/nmat2704. [DOI] [PubMed] [Google Scholar]
- 38.Ackbarow T, Chen X, Keten S, Buehler MJ. P Natl Acad Sci USA. 2007;104:16410. doi: 10.1073/pnas.0705759104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Krishnaji ST, Bratzel G, Kinahan ME, Kluge JA, Staii C, Wong JY, Buehler MJ, Kaplan DL. Advanced functional materials. 2013;23:241. [Google Scholar]
- 40.Rabotyagova OS, Cebe P, Kaplan DL. Biomacromolecules. 2011;12:269. doi: 10.1021/bm100928x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Xu M, Lewis RV. Proc Natl Acad Sci U S A. 1990;87:7120. doi: 10.1073/pnas.87.18.7120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Minor DL, Jr, Kim PS. Nature. 1994;367:660. doi: 10.1038/367660a0. [DOI] [PubMed] [Google Scholar]
- 43.Meier M, Seelig J. J Am Chem Soc. 2008;130:1017. doi: 10.1021/ja077231r. [DOI] [PubMed] [Google Scholar]
- 44.Baker EN, Hubbard RE. Prog Biophys Mol Biol. 1984;44:97. doi: 10.1016/0079-6107(84)90007-5. [DOI] [PubMed] [Google Scholar]
- 45.Schwarzbauer JE, Sechler JL. Curr Opin Cell Biol. 1999;11:622. doi: 10.1016/s0955-0674(99)00017-4. [DOI] [PubMed] [Google Scholar]
- 46.Lemmon CA, Sniadecki NJ, Ruiz SA, Tan JL, Romer LH, Chen CS. Mech Chem Biosyst. 2005;2:1. [PMC free article] [PubMed] [Google Scholar]
- 47.Harris JR, Reiber A. Micron. 2007;38:513. doi: 10.1016/j.micron.2006.07.026. [DOI] [PubMed] [Google Scholar]
- 48.Tsuzaki M, Yamauchi M, Banes AJ. Connect Tissue Res. 1993;29:141. doi: 10.3109/03008209309014241. [DOI] [PubMed] [Google Scholar]
- 49.Vouyouka AG, Pfeiffer BJ, Liem TK, Taylor TA, Mudaliar J, Phillips CL. J Vasc Surg. 2001;33:1263. doi: 10.1067/mva.2001.113579. [DOI] [PubMed] [Google Scholar]
- 50.Kragh T, Napoleone M, Fallah MA, Gritsch H, Schneider MF, Reininger AJ. Thromb Res. 2014;133:1079. doi: 10.1016/j.thromres.2014.03.024. [DOI] [PubMed] [Google Scholar]
- 51.Albro MB, Cigan AD, Nims RJ, Yeroushalmi KJ, Oungoulian SR, Hung CT, Ateshian GA. Osteoarthritis Cartilage. 2012;20:1374. doi: 10.1016/j.joca.2012.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Jacobsen MM, Li D, Gyune Rim N, Backman D, Smith ML, Wong JY. Sci Rep. 2017;7:45653. doi: 10.1038/srep45653. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.