Repeatability of graph theoretical metrics derived from resting-state functional networks in paediatric epilepsy patients

Abstract

Objective:

To measure the repeatability of metrics that quantify brain network architecture derived from resting-state functional MRI in a cohort of paediatric patients with epilepsy.

Methods:

We identified patients with: (1) epilepsy; (2) brain MRI at 3 T; (3) two identical resting-state functional MRI acquisitions performed on the same day. Undirected, weighted networks were constructed based on the resting-state time series using a range of processing parameters including parcellation size and graph threshold. The following topological properties were calculated: degree, strength, characteristic path length, global efficiency, clustering coefficient, modularity and small worldness. Based on repeated measures, we then calculated: (1) Pearson correlation coefficient; (2) intraclass correlation coefficient; (3) root-mean-square coefficient of variation; (4) repeatability coefficient; and (5) 95% confidence limits for change.

Results:

26 patients were included (age range: 4–21 years). Correlation coefficients demonstrated a highly consistent relationship between repeated observations for all metrics, and the intraclass correlation coefficients were generally in the excellent range. Repeatability in the data set was not significantly influenced by parcellation size. However, trends towards decreased repeatability were observed at higher graph thresholds.

Conclusion:

These findings demonstrate the reliability of network metrics in a cohort of paediatric patients with epilepsy.

Advances in knowledge:

Our results point to the potential for graph theoretical analyses of resting-state data to provide reliable markers of network architecture in children with epilepsy. At the level of an individual patient, change over time greater than the repeatability coefficient or 95% confidence limits for change is unlikely to be related to intrinsic variability of the method.

INTRODUCTION

Epilepsy is a common neurological condition that confers a weighty disease-related burden on individuals and families with the condition.^1,2 In children, developmental and other structural lesions are a frequent source of medically intractable seizures.³ Although resection of these epileptogenic lesions can be curative, seizure-free and cognitive outcomes remain variable even in highly selected surgical cohorts.^3,4 The fact that so called “focal” or “localization-related” epilepsies are in many cases associated with global alterations of the cerebral network likely contributes to such inconsistencies.^5–7

Computational methods have been developed with the capacity to model the cerebral network at the whole-brain scale.⁸ In this context, the brain is represented as a collection of anatomical elements, or nodes; connections between pairs of nodes, referred to as edges, are then measured non-invasively. Once constructed, the architecture of the resulting network can be quantified according to graph theoretical principles.⁹ These techniques, therefore, offer the potential to capture physiologically relevant features of the cerebral network. Prototypical network metrics include: (a) clustering coefficient: the tendency of nodes to segregate into relatively independent local neighbourhoods (i.e. the ability to support functional subspecialization within the brain); (b) characteristic path length: the number of edges required to traverse the distance between two nodes (i.e. the ability to support integration of information across the network); and (c) small worldness: the ratio of the clustering coefficient to the path length—a guiding principle in cerebral organization representing a means by which the same network can support both integration and subspecialization.

Resting-state functional MRI (rs-fMRI), a sequence that measures the blood-oxygen-level-dependent (BOLD) signal over time, is one method by which edges in the brain network can be quantified. As this sequence is task free, it offers the potential to measure the functional status of children who are too young or too impaired to co-operate with traditional functional imaging. Elements of the brain that interact in order to support a given function continue to exhibit similar BOLD fluctuations at rest.¹⁰ Hence, the strength of a connection between each pair of nodes can be inferred from the magnitude of correlation between their BOLD signal time courses.

Previous rs-fMRI studies have demonstrated global alterations of the cerebral network in various disease states, including epilepsy.^11–15 Efficient brain network organization, as quantified by graph theory metrics, has even been reported to relate to cognitive function in both adults^6,16 and healthy children.¹⁷ These preliminary results point to the potential for graph theoretical analyses of resting-state data to provide biomarkers of cognitive function in children. Widespread application of this technique, however, will require an understanding of its reproducibility, particularly with regard to its ability to quantify network topology. A further consideration in paediatric populations, especially those with neurological disorders, is the reliance in a significant fraction of the individuals on general anaesthesia during MRI. As anaesthesia is known to alter neurovascular coupling and BOLD synchrony,¹⁸ an assessment of reproducibility in this population should include metrics measured under general anaesthesia. To date, however, the reproducibility of graph theory metrics derived from rs-fMRI has not been widely studied and, in particular, there is very little data from either the paediatric or epilepsy populations.¹⁹ The goal of this study is to measure the repeatability of graph theory metrics derived from functional brain networks in a cohort of paediatric patients with localization-related epilepsy.

METHODS AND MATERIALS

This health insurance portability and accountability act–compliant study was approved by the local institutional review board. Patients were identified retrospectively from the medical record with the following inclusion criteria: (1) paediatric age group (less than or equal to 21 years); (2) clinical diagnosis of localization-related epilepsy; (3) MRI of the brain performed at 3 T; (4) two separate but identical rs-fMRI sequences performed during the same MRI session. Refinements to the above-defined population were based on the following exclusion criterion: any brain surgery performed prior to MRI. Clinical severity of epilepsy for each patient was measured by the childhood epilepsy severity score,²⁰ which includes six measures of epilepsy severity (time period over which seizures occurred; seizure frequency; number of seizure types; occurrence and duration of status epilepticus; number of anticonvulsant medications used; response to treatment).

MRI

All imaging was performed on a 3-T magnet (Philips Achieva^®; Philips Healthcare, Andover, MA) with a 32-channel phased-array coil. The following sequences were obtained: (1) sagittal volumetric T₁ weighted structural image [three-dimensional fast field echo; repetition time/echo time: 7.2/2.9 ms; one acquisition; flip angle: 7°, inversion time: 1100 ms; field of view: 22 cm; voxel (mm): 1 × 1 × 1]. (2) Axial single-shot echo planar functional MRI (fMRI) [repetition time/echo time (ms): 2000/30; flip angle: 80°; one acquisition; voxel (mm): 3 × 3 × 3] performed in the resting state. Two identical resting-state scans, each of 10-min duration, were acquired for each subject during the same imaging session.

IMAGE PROCESSING AND ANALYSIS

Network node definition

Image processing was implemented using MATLAB^® scripts v. 7.13 (MathWorks^®, Inc, Natick, MA) with adapter functions embedded to execute FreeSurfer reconstruction v. 5.3.0 (http://surfer.nmr.mgh.harvard.edu) and tools from the FMRIB Software Library (FSL) suite.²¹ FreeSurfer was used to reconstruct grey–white and pial surfaces using the structural image. This reconstruction includes skull stripping, grey matter segmentation and automated parcellation.^22,23 Cortical surfaces generated in this step were inspected for accuracy using the Freeview software.

Next, a self-developed MATLAB program was used to further subdivide the 75 standard Freesurfer grey matter parcels according to their surface area (as defined on the Freesurfer grey–white surface mesh). Each grey matter parcel was iteratively divided into two new parcels of equal size until the surface area of each output parcel was less than a predefined threshold value. Two different threshold values were used to generate two networks of different sizes in each patient: 350 mm² (fine parcellation) and 600 mm² (coarse parcellation). Each surface parcel was then converted into a volume mask of grey matter at that region. Each resulting grey matter volume of interest formed a node in the brain network. The network, then, consisted of approximately 700 and 400 nodes for the “fine” and “coarse” parcellation thresholds, respectively.

Network edge definition

The first five images in each resting state sequence were discarded to allow magnetization to reach equilibrium. Pre-processing of the functional data sets was performed with FSL Multivariate Exploratory Linear Optimized Decomposition into Independent Components which included motion correction, interleaved slice timing correction, brain extraction, spatial smoothing with a Gaussian kernel of full width at half maximum of 5 mm and high-pass temporal filtering equivalent to 100 s per cycle (0.01 Hz). Noise related to motion and other physiological nuisance was addressed according to an independent component analysis (ICA) technique.²⁴ Non-signal components were removed manually by an expert operator with 5 years' experience using ICA in this patient population. Although the optimal strategies for noise removal in fMRI remain the subject of debate,^25,26 an ICA technique was selected, as it has been shown to minimize the impact of motion on network metrics while at the same time decreasing loss of temporal degrees of freedom and preserving the signal of interest across a variety of resting-state data sets.²⁵ Motion parameters measured during pre-processing were summarized for each patient, as previously described, by the framewise displacement.²⁵ Both of the resting-state image volumes for each patient were registered to that individual's skull-stripped structural T₁ data set using FSL FMRIB's Linear Image Registration Tool. Voxelwise BOLD signal time series were averaged over each node. The strength of an edge between two nodes was defined as the absolute value of the Pearson correlation coefficient between their time series.

Graph construction

Weighted, undirected connection matrices were constructed consisting of the pairwise correlation between BOLD time series over all network nodes. At the completion of this step, four connection matrices (two different parcellation sizes of two separate resting-state acquisitions) were available for each patient. A two-step threshold technique was then applied to each connection matrix. In the first step, non-significant correlations were excluded based on adjusted p-values. In a network with N number of nodes, $\left(N^2-N\right)/2$ correlations were calculated. Therefore, the p-value of each pairwise correlation in the connection matrix was multiplied by $\left(N^2-N\right)/2$ and thresholded at 0.05. In the second step, the graph was further thresholded on the basis of the correlation coefficient. As the optimal cut-off was uncertain, a range of thresholds from 0 to 0.9 (interval: 0.1) was applied. Edges weaker than the threshold were set to zero. At the completion of this step, 40 weighted, undirected connection matrices (two different resting-state acquisitions × 2 different parcellations × 10 different thresholds) were available for each patient.

Network metric calculation

For each weighted connection matrix, MATLAB scripts available from The Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/) were used to compute eight common metrics that summarize global network architecture (Table 1). For the purposes of this article, these will be referred to as “raw” metrics. In a paediatric population, brain volumes change across development, and furthermore, network size can be impacted in a heterogeneous fashion by pathology. To account for differences in network size inherent to this population, a second group of metrics was generated in which the raw metrics for each patient were normalized to the exact same metric computed on a random network of identical size. The random network is generated by the Brain Connectivity Toolbox and, by definition, preserves the degree, strength and weight distributions of the original brain network.²⁷ As such, degree, strength and weight were only considered as raw metrics.

Table 1.

Summary of graph theoretical metrics of brain network architecture

Metric	Description	Range
Degree	Average number of edges associated with each node	[0, N − 1]
Strength	Average weight of edges associated with each node	[0, N − 1]
Density	Fraction of edges that exist out of the total number of possible edges in the network	[0, 1]
Characteristic path length	Minimum number of edges required to traverse the distance between two nodes averaged over the network	[1, ∞]
Global efficiency	Inverse of the shortest path length averaged over the network	[0, 1]
Clustering coefficient	The fraction of a given node's neighbours that are also neighbours of each other	[0, 1]
Modularity	The degree to which the network tends to segregate into relatively independent modules	[0, 1]
Small worldness	Clustering coefficient divided by path length	[0, 1]

N, number of nodes in the graph.

Statistical analyses

All statistical analyses were performed using the R statistical software package v. 3.0.2 (R Foundation for Statistical Computing, Vienna, Austria).²⁸ The Wilcoxon signed-rank test (alpha: 0.05 corrected for multiple comparisons) was used to assess potential differences in repeatability between: (1) patients with structurally normal brains vs those with structural abnormalities; (2) patients undergoing general anaesthesia during MRI scanning vs conscious patients. If no significant differences in repeatability are detected between these subgroups, the cohort will then be considered in aggregate for the remaining analyses.

For each metric, the following statistics were computed: (1) mean and standard deviation; (2) intraclass correlation coefficient (ICC). To be specific, ICC(3,1) was calculated according to the following formula:²⁹

$$\text{ICC}\left(\mathrm{3,1}\right)=\left(\text{BMS}-\text{EMS}\right)/\left(\text{BMS}+\left(k-1\right)\text{EMS}\right),$$

where BMS is the between-subjects mean square, EMS is the error mean square and k is the number of repeated sessions. This calculation was performed using the psych package developed by Revelle.³⁰ According to previous studies,^19,31,32 ICCs between 0.4 and 0.59 were considered fair, those between 0.6 and 0.74 were considered good and those >0.74 were considered excellent. (3) Root-mean-square coefficient of variation. (4) Pearson correlation coefficient.

Finally, to estimate the magnitude of change that would be clinically detectable in an individual child, root-mean-square coefficients of variation were used to calculate the 95% confidence limits for detection of change.⁷ A repeatability coefficient was also calculated as described by Bland and Altman.³³ For an individual patient, changes greater in absolute magnitude than the repeatability coefficient or in fractional magnitude than the 95% confidence limits for change are unlikely to be related to intramethod variability in the measurement of network architecture.

RESULTS

Patients

All imaging was performed from July 2013 to February 2015. 26 patients with localization-related epilepsy (age range: 4–21 years; median: 11 years) comprised the final study group. Of this cohort, 10 patients had structurally normal brains and 16 patients had demonstrable structural abnormalities at MRI, including: focal cortical dysplasia (n = 3), mesial temporal sclerosis (n = 3), encephalomalacia (n = 3), tuberous sclerosis complex (n = 2), Sturge-Weber syndrome (n = 2), low-grade tumour (n = 2) and Rasmussen's encephalitis (n = 1). 16 patients (65%) underwent general anaesthesia during MRI scanning. The degree of patient motion during imaging was not significantly associated with either patient age (p = 0.67) or severity of epilepsy (p = 0.79).

Repeatability

Repeatability across the data set was generally consistent. Specifically, the mean difference between observations in structurally normal brains did not differ from those in brains with structural abnormalities (p-value range: 0.90–0.99). Similarly, there was no significant difference in metric repeatability in patients with vs without the use of general anaesthesia for any metric at any threshold (p-value range: 0.24–0.99). Finally, there was no significant association between repeatability and patient age (p-value range: 0.38–0.99). Hence, the entire cohort was considered in aggregate for the remaining analyses.

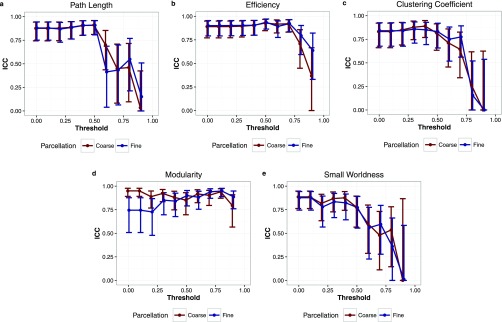
Test–retest estimates for network metrics computed on weighted connection matrices thresholded only by a corrected p-value of 0.05 are presented in Table 2 (coarse parcellation) and Table 3 (fine parcellation). Correlation coefficients demonstrated a highly consistent relationship between repeated observations for all metrics, and ICCs were generally in the excellent range (Tables 2 and 3). Patient level repeatability varied moderately with the specific metric of interest; 95% confidence limits for change in an individual patient ranged from 3% to 21% (Tables 2 and 3). Repeatability in the data set was not significantly influenced by parcellation size. However, trends towards decreased repeatability were observed at higher graph thresholds for both raw (Figure 1) and normalized (Figure 2) metrics. This effect was more pronounced in normalized metrics (Figure 2).

Table 2.

Test–retest estimates of network metrics derived from resting-state functional MRI (coarse parcellation)

Metric	Mean (Std)	Pearson	Repeatability coefficient	ICC (95% CI)	RMS CoV	95% CL change (%)
Degree	277.14 (70.25)	0.92	55.12	0.92 (0.83–0.96)	0.05	13.4
Strength	108.43 (69.61)	0.95	42.27	0.95 (0.9–0.98)	0.10	17.4
Density	0.72 (0.16)	0.90	0.14	0.9 (0.78–0.95)	0.05	13.5
CPL	3.5 (1.05)	0.94	0.74	0.94 (0.87–0.97)	0.06	15.5
CPL (norm)	1.17 (0.08)	0.88	0.08	0.88 (0.74–0.94)	0.02	4.4
Efficiency	0.9 (0.05)	0.89	0.05	0.89 (0.77–0.95)	0.01	4.0
Efficiency (norm)	0.76 (0.14)	0.94	0.10	0.94 (0.86–0.97)	0.04	9.8
Clustering coeff.	0.29 (0.17)	0.96	0.10	0.95 (0.9–0.98)	0.09	15.4
Clustering coeff. (Norm)	1.04 (0.04)	0.83	0.04	0.83 (0.66–0.92)	0.01	2.8
Modularity	0.13 (0.06)	0.87	0.06	0.87 (0.74–0.94)	0.14	18.1
Modularity (norm)	5.4 (1.56)	0.95	1.00	0.95 (0.89–0.98)	0.05	12.9
Small worldness	0.12 (0.14)	0.97	0.07	0.96 (0.92–0.98)	0.14	19.7
Small worldness (norm)	0.89 (0.04)	0.89	0.04	0.89 (0.76–0.95)	0.01	3.1

CI, confidence interval; CL, confidence limit; coeff., coefficient; CPL, characteristic path length; ICC, intraclass correlation coefficient; norm, normalized; Pearson, Pearson correlation coefficient; RMS CoV, root-mean-square coefficient of variation; Std, standard deviation.

Data presented here reflect connection matrices thresholded only by p-value (0.05 corrected).

Table 3.

Test–retest estimates of network metrics derived from resting-state functional MRI (fine parcellation)

Metric	Mean (Std)	Pearson	Repeatability coefficient	ICC (95% CI)	RMS CoV	95% CL change (%)
Degree	441.8 (120.1)	0.93	90.62	0.93 (0.85–0.97)	0.05	14.0
Strength	165.2 (109.0)	0.96	62.90	0.96 (0.91–0.98)	0.10	17.3
Density	0.7 (0.16)	0.90	0.14	0.9 (0.79–0.95)	0.05	14.0
CPL	3.61 (1.04)	0.94	0.73	0.94 (0.87–0.97)	0.05	14.5
CPL (norm)	1.18 (0.08)	0.88	0.08	0.88 (0.75–0.94)	0.02	4.5
Efficiency	0.34 (0.14)	0.96	0.08	0.96 (0.91–0.98)	0.05	15.2
Efficiency (norm)	0.88 (0.06)	0.90	0.05	0.9 (0.79–0.95)	0.01	4.0
Clustering coeff.	0.27 (0.16)	0.96	0.10	0.96 (0.91–0.98)	0.09	15.0
Clustering coeff. (norm)	1.05 (0.04)	0.84	0.04	0.84 (0.68–0.93)	0.01	2.8
Modularity	0.14 (0.06)	0.87	0.06	0.87 (0.73–0.94)	0.12	13.0
Modularity (norm)	6.41 (1.54)	0.76	2.18	0.74 (0.51–0.88)	0.08	21.1
Small worldness	0.1 (0.12)	0.97	0.06	0.96 (0.92–0.98)	0.14	18.3
Small worldness (norm)	0.89 (0.04)	0.88	0.04	0.88 (0.75–0.94)	0.01	3.3

CI, confidence interval; CL, confidence limit; coeff., coefficient; CPL, characteristic path length; ICC, intraclass correlation coefficient; norm, normalized; Pearson, Pearson correlation coefficient; RMS CoV, root-mean-square coefficient of variation; Std, standard deviation.

Data presented here reflect connection matrices thresholded only by p-value (0.05 corrected).

Figure 1.

(a–e) The relationship between intraclass correlation coefficient (ICC) and threshold for raw graph theory metrics. Higher thresholds were associated with less repeatable metrics. Blue, fine parcellation; red, coarse parcellation. Bars denote the 95% confidence interval for the ICC.

Figure 2.

(a–e) The relationship between intraclass correlation coefficient (ICC) and threshold for normalized graph theory metrics. Although similar to results for raw metrics, the impact of thresholding is exaggerated for normalized graph theory metrics. Blue, fine parcellation; red, coarse parcellation. Bars denote the 95% confidence interval for the ICC.

DISCUSSION

Our primary aim was to investigate the test–retest repeatability of graph theoretical metrics derived from rs-fMRI in children with epilepsy. We constructed weighted, undirected networks over a range of technical parameters for two separate resting-state acquisitions in the same patient. We observed excellent repeatability, in terms of the ICC, for all metrics. Furthermore, repeatability coefficients and 95% confidence limits for the detection of change were quantified which allow significance to be attached to changes in these metrics that occur over time in an individual patient.

Second, we observed that the size and number of network nodes did not significantly alter the repeatability of global metrics of network architecture. During network construction, large nodes potentially include adjacent but functionally distinct cortical regions into a single node. The averaged BOLD time course from a large node, therefore, may not accurately reflect the actual time course of any of the functional regions contained therein. Measuring pairwise correlations between such time courses would then be handicapped with respect to their ability to capture the brain's true topology. Hence, higher resolution networks may better capture physiologically meaningful features of the cerebral network. On the other hand, small regions of interest are accompanied by lower signal-to-noise ratios, all other parameters being equal. At some point, parcellation schemes may become noise limited. Hence, optimal parcellation should balance these competing concerns in such a way that global metrics most closely reflect true brain network topology. Our results indicate that a smaller node, at least within a range of sizes commonly seen in the literature,¹⁹ can be used without reducing the reproducibility of global network metrics. It is of interest that Cao et al³² reported better reproducibility of global metrics derived from fMRI using a finer parcellation. However, the parcellation methods in their study differed by more than simply size; the finer parcellation was defined using a functional, rather than an anatomical, atlas. By contrast, our networks were constructed using the same parcellation method only at different resolutions. Other methodological differences between the studies, including performance of a task during fMRI acquisition in Cao et al,³² could also have contributed to the discrepant findings.

Third, we report that more stringent thresholding of the network was associated with poorer reproducibility. In functional networks, edges in the graph are weighted by the strength of correlation between BOLD signal time courses. Thresholds are generally applied to eliminate spurious connections.⁹ As one continues to increase the graph threshold, however, real connections are removed and the network becomes more fragmentary and heterogeneous which contributes to greater variability.³¹ Our results demonstrate that, above some threshold, this heterogeneity can reduce the reliability of global network metrics derived from rs-fMRI. Of note, this effect was exaggerated for normalized metrics. Unlike in normal cohorts, pathological heterogeneity across patients can contribute to significant differences in basic network characteristics such as size. This issue is particularly relevant in paediatric populations, which demonstrate significant additional heterogeneity on the basis of normal development. Although these interpatient differences may not be relevant to brain function, they do impact global metric calculation and, therefore, render comparisons more difficult. To account for such differences between patients, metrics computed from an individual patient's graph can be normalized to the same metrics calculated on a random network of identical sizes.³⁴ As the random networks used in normalization introduce an additional source of variability, it is not surprising that the threshold effects described above are exaggerated for normalized metrics. Our findings with regard to graph threshold are consistent with the work by Telesford et al³⁵ who demonstrated reduced reproducibility of graph metrics at higher thresholds in normal adults. The impact of normalization on metric repeatability in this context has not been previously reported.

Finally, we observed no decrement in repeatability for patients whose imaging was acquired under general anaesthesia. The question of general anaesthesia is a complicated one, as it can be accomplished according to a variety of drug regimens, each of which may have a different effect on resting-state networks.³⁶ Of particular relevance to this study, several groups have reported a relative decrease in connectivity within whole-brain networks during propofol-induced loss of consciousness.^37,38 Our work suggests that, regardless of relative changes that may occur with regard to the intrinsic characteristics of the resting-state signal, graph metrics derived from resting-state functional networks seem to be feasible across a range of states of consciousness. This idea is supported by work in electrocorticography that found large-scale brain networks to be a fundamental aspect of the brain's physiology that does not depend on the state of consciousness.³⁹

To our knowledge, these data represent the first report of the reproducibility of graph-based metrics in either children or in patients with localization-related epilepsy. Our results, however, are comparable to those reported in fMRI studies of healthy adult populations.^35,40 Interestingly, ICCs observed in our study were also similar to those generated based on graph theory analysis of data from magnetoencephalography⁴¹ and near-infra-red spectroscopy.⁴² Finally, our results are comparable overall with similar studies using diffusion tensor imaging, rather than fMRI, to construct cerebral networks.¹⁹ Together, these findings raise the possibility that global network metrics may be robust across a range of patient populations and imaging modalities. It is worth noting, however, that Braun et al³¹ reported lower ICCs in a cohort of healthy subjects. Several methodological differences between their study and ours [including the use of healthy subjects (vs a clinical epilepsy population), the use of binary (vs weighted) networks, the size of network nodes, the use of regression-based denoising techniques (vs ICA-based denoising) and a scanning interval of two weeks (vs same day)] likely account for the discrepant results.

This study has several limitations. First, these data originate from a selected cohort of patients with localization-related epilepsy. Generalization to patients with other types of neurological disorders would require further study. Second, all imaging was performed on the same MR scanner with the same phased-array coil according to the same resting-state fMRI sequence. Further study regarding the reproducibility of these metrics across a wider range of MR hardware would be of great practical value to widespread implementation. Third, although we detected no significant difference in repeatability between patients on general anaesthesia and non-sedated patients, this study was not powered to conclude that repeatability is the same in the two states. Our goal, however, was not to measure systematically the impact of anaesthesia on resting-state networks. Rather, we sought to measure repeatability under conditions that are representative of those experienced by the clinical epilepsy population; this includes anaesthesia in a significant number of patients. Fourth, we studied the reliability of metrics derived from resting-state sequences when performed on the same day in the same session. We selected this design in an attempt to isolate variability of the method from real change over time. Functional networks can change over a very short time scale. In fact, durable alterations in resting-state connectivity have been observed after relatively minor interventions lasting hours^43,44 or even minutes.^45,46 In order to avoid the confounding effect of network reorganization over time, a particular issue in patients with intractable epilepsy, re-testing was performed on the same day. Finally, it is important to note that metrics with the best repeatability are not necessarily the most physiologically meaningful. Optimization of these metrics with regard to their capacity to probe physiologically relevant features of the brain network in paediatric patients with epilepsy will be an important next step.

CONCLUSION

In conclusion, we have quantified the repeatability of graph-based metrics of global network topology in children with epilepsy. ICCs overall were in the excellent range, though reduced at stringent graph thresholds. This work suggests that graph theory analyses of resting-state networks can provide robust markers of brain network architecture despite the influences imparted by brain pathology, normal development with age and the use of general anaesthesia during image acquisition. These data represent a significant advance in our understanding of the reproducibility of these metrics which may one day serve to guide management in patients with localization-related epilepsy.