Disease Progression Modeling: Key Concepts and Recent Developments

Abstract

Disease modeling involves the use of mathematical functions to describe quantitatively the time course of disease progression. In order to characterize the natural progression of disease, these models generally incorporate longitudinal data for some biomarker(s) of disease severity or can incorporate more direct measures of disease severity. Disease models are also often linked to pharmacokinetic–pharmacodynamic models so that the influence of drug treatment on disease progression can be quantified and evaluated. Regulatory agencies have embraced disease progression models as powerful tools that can be used to improve drug development productivity. This article provides a brief overview of key concepts in disease progression modeling followed by illustrative examples from models for Alzheimer’s disease. Finally, recent novel applications in which disease progression models have been linked to cost-effectiveness analysis and genomic analysis are described.

Introduction

Disease progression modeling involves the utilization of mathematical functions as quantitative descriptors of the time course of disease status. Disease models may incorporate biomarkers of disease severity and/or clinical outcomes to characterize the natural progression of disease. In clinical pharmacology, disease models are often integrated with pharmacokinetic–pharmacodynamic models in order to quantify the influence of drug treatment on disease progression. Seminal work in disease progression modeling was published in the early 1990s [1–5], but the field has truly flourished in more recent years, since the US Food and Drug Administration (FDA) embraced such quantitative models as powerful tools that can be used to improve drug development productivity. In 2004, the FDA launched its Critical Path Initiative, which aims to modernize drug development, and disease modeling was promoted as a key opportunity for advancement [6, 7]. Since that time, disease modeling has been widely adopted by the pharmaceutical industry [8]. In addition to encouraging the application of disease progression models to pharmaceutical research and development [6, 7, 9], the FDA has developed and made publicly available models for diseases of public health importance, including Alzheimer’s disease, Parkinson’s disease, bipolar disorder, obesity, and non-small cell lung cancer [10]. This article provides a brief review of the types and components of disease progression models followed by illustrative case studies in the area of Alzheimer’s disease. Finally, recent novel applications of disease progression models to cost-effectiveness analysis and genome-wide analysis are described.

Disease Progression Modeling

Disease progression models can be broadly categorized into three classes: empirical, semi-mechanistic, and systems biology. Empirical models are purely data driven and do not describe underlying biological processes; they serve as mathematical frameworks for interpolation between observed data. At the other extreme, systems biology models of disease progression are physiologically based and incorporate mathematical representations of biological, pathophysiological, and pharmacological processes in as much molecular detail as possible. Semi-mechanistic models fall in between the poles of empirical and systems biology models. Importantly, the appropriate model type depends highly upon the problem at hand. Whereas empirical models are well suited to answering questions that are relatively narrow in scope (e.g., dose selection or clinical trial design and interpretation), the more mechanistic nature of semi-mechanistic and systems models enables application to broader scientific questions (e.g., prediction of effects of drugs with differing mechanisms of action, novel target identification, or risk projection based on biomarker data) [9, 11]. This review will first cover some considerations related to the types of data that can be utilized in disease progression models before discussing these three classes of models in greater detail.

Data

Various types of data can be incorporated into disease progression models [12]. Assessment of disease severity in many areas, especially neurological and mental health disorders, relies upon relatively subjective scoring systems based on patient-reported responses or clinician evaluation. Utilization of subjective measures in disease models poses particular challenges because such data tend to exhibit high variability, and it may therefore be necessary to include many subjects in order to obtain an adequate description of disease progression. Some examples of this type of data that have been used in disease progression models include the Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog) [2, 3, 5, 13], the Hamilton Rating Scale for Depression (HAM-D) [14–16], and the Revised Amyotrophic Lateral Sclerosis Functional Rating Scale (ALSFRS-R) [17, 18]. Although these types of observations are often technically ordinal data, they are generally treated as continuous variables for the purposes of disease modeling because many of these scales comprise relatively wide ranges of possible scores (e.g., 0–70 for ADAS-Cog). Continuous biomarker data are also widely used in disease models. For instance, in a semi-mechanistic bone cycle model, C-terminal telopeptide of type I collagen (CTX) and osteocalcin were incorporated as serum biomarkers of bone resorption and formation, respectively, and bone mineral density was included as a measure of bone mass [19]. Additionally, continuous disease progression models can be linked to discrete clinical endpoints through survival or hazard functions. Approaches for linking disease progression to clinical outcome have been reviewed by Mould [20], and the author provided detailed examples of models linking the time course of chemotherapy-induced myelosuppression to the probability of developing febrile neutropenia [21] and tumor size to survival [22, 23].

Disease models are often developed to characterize chronic diseases that progress slowly, so these models commonly require incorporation of disease severity data that has been collected over extended time periods. Such data is rarely available from a single study, and data from several clinical studies must often be pooled in order to provide sufficient observations for modeling of disease progression. Consequently, model-based meta-analysis is an effective approach for disease modeling. Model-based meta-analysis involves model development using the combined results of multiple previous studies. Unlike traditional model development, which generally utilizes patient-level data from a limited number of clinical studies, model-based meta-analysis may incorporate both summary-level information obtained from literature references and patient-level information obtained from databases and/or available clinical trial data. Importantly, nonlinear mixed-effects modeling, which is widely utilized for empirical and semi-mechanistic disease modeling, can account for differences in study design and subject characteristics to reduce the potential for bias introduced by pooling data from multiple studies. Ahn and French have demonstrated meta-analytic approaches for fitting longitudinal summary-level data with NONMEM software, which is commonly used for nonlinear mixed-effects models of disease progression [24]. They provided illustrative NONMEM code for incorporation of study-level and/or treatment arm-level random effects, both with and without residual correlation, and they used simulated data to evaluate the importance of including these different model components. Mould has also reviewed the application of meta-analysis to disease progression modeling [20] and provided detailed discussion of meta-models for progression of Alzheimer’s disease [25] and Crohn’s disease [26]. Although model-based meta-analysis poses certain challenges, results from such analyses are often statistically stronger and more generalizable than those from single studies [27].

Empirical Models

The empirical approach has commonly been employed in areas where disease severity is routinely assessed via subjective scoring systems. For instance, empirical models have been utilized to model progression of Alzheimer’s disease [2, 3, 5], Parkinson’s disease [28, 29], depression [14, 15], schizophrenia [30, 31], amyotrophic lateral sclerosis [17], and Huntington’s disease [32]. The simplest disease progression model is linear, assuming a constant rate of change for a measure of disease status over time (Equation 1):

$$S(t)=S_0+\alpha \times t$$ (Eq. 1)

where S(t) is disease status at time t, S₀ is the baseline disease status (y-intercept), and α is the rate of change of disease status (slope). A hypothetical linear disease model is depicted in Figure 1. Although this function is quite simple, linear models have been successfully implemented to describe progression of several diseases, including Alzheimer’s disease [2, 3, 5], schizophrenia [30], and Huntington’s disease [32]. For many diseases, however, more complex equations must be used to describe the time course of progression adequately. Details about more complex models, such as asymptotic progress, physiological turnover, and growth and decay models, have been reported in other publications [12, 33]. Mould has also provided example code for implementing such models in NONMEM software [12].

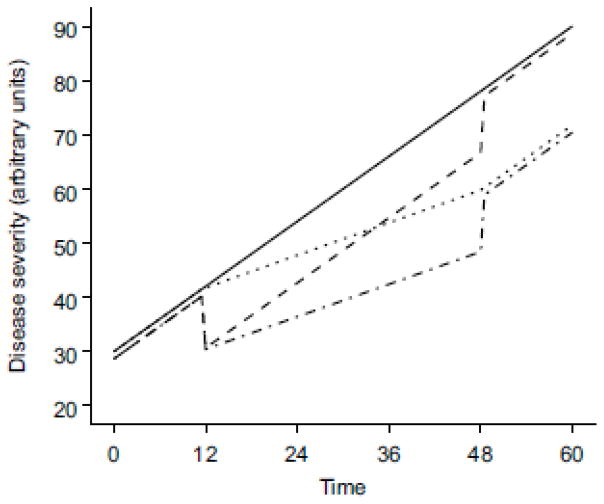
Fig. 1.

A hypothetical empirical disease model with linear progression. The solid line represents disease progression with no treatment, and the other lines represent disease progression with treatment effects that start at time 12 and end at time 48. The dashed line illustrates the effect of a drug that provides symptomatic relief; the dotted line illustrates the effect of a drug that modifies the rate of disease progression; and the dotted-and-dashed line illustrates the combined effects of a disease-modifying drug that also provides symptomatic relief. Note that the lines have been offset slightly to prevent overlap

It should be noted that baseline disease status, S₀, can be a complex parameter in disease progression models. It may be defined as some measure of disease status either at the time a disease started, at the time a disease was diagnosed, or at the time a subject enrolled in a clinical trial. Alternatively, if the disease status, S(t), is defined as the change in a disease measure relative to a baseline value, rather than as the actual value of that measure, then S₀ may be fixed at zero. The precise definition of S₀ can have important implications for how the disease progresses from the baseline time. For instance, in linear models of Alzheimer’s disease progression, baseline disease status is generally defined near the time of trial enrollment, and baseline status has been observed to interact strongly with disease progression rate, which increased with increasing baseline severity [25, 34, 35]. This potential for interaction between baseline disease status and disease progression rate makes baseline severity a crucial factor in clinical trial design and in evaluation of clinical trial and disease model results.

Drug effects can be incorporated into disease models in different ways, and the manner in which a drug effect is included in a disease progression equation has implications for how the treatment influences the disease. For instance, a drug may provide only symptomatic relief. For the linear disease progression example depicted above (Equation 1), a symptomatic drug effect could be incorporated as follows (Equation 2):

$$S(t)=S_0+\alpha \times t+E(t)$$ (Eq. 2)

where S(t) is disease status at time t, S₀ is the baseline disease status (y-intercept), α is the rate of change of disease status (slope), and E(t) is a function incorporating the drug effect. In this case, the drug does not influence the rate of disease progression but merely provides a transient benefit by offsetting the disease severity; when treatment is discontinued, the disease will return to a state that is the same as if the treatment had not occurred (Figure 1). Alternatively, a drug may alter the progression of a disease. For the linear disease progression example depicted above (Equation 1), such a disease-modifying effect could be incorporated as follows (Equation 3):

$$S(t)=S_0+[\alpha +E(t)]\times t$$ (Eq. 3)

where S(t) is disease status at time t, S₀ is the baseline disease status (y-intercept), α is the rate of change of disease status (slope) in the absence of drug treatment, and E(t) is a function incorporating the drug effect. Here, the drug alters the rate of disease progression; when treatment is discontinued, the rate of disease progression returns to that in the absence of treatment (α), but the disease severity will be offset from what it would have been if treatment had not occurred (Figure 1). Methods for incorporating different types of drug effects into more complex disease progression models have been reported in other publications [12, 33] along with example NONMEM code [12].

One critical consideration when comparing drug effects to standard-of-care treatment is the fact that standard of care evolves over time. Improvements in standard of care are likely to be accompanied by changes in the typical time course of disease progression, so disease models and databases must be updated regularly in order to consider the response of disease to novel treatments in an appropriate, current context.

Systems Biology Models

Systems biology models of disease progression incorporate as much molecular detail as possible. Consequently, systems models generally require extensive scientific collaboration and integration of in vitro, ex vivo, in vivo, non-clinical, and clinical data [11]. The complexity of systems disease modeling is evident in work that has been performed in the area of diabetes research. Diabetes is a chronic, complex disease, and a comprehensive model of diabetes progression would incorporate mathematical representations of the molecular pathways involved in glucose homeostasis, diabetes pathophysiology, and the diverse complications associated with hyperglycemia-induced tissue damage. After decades of modeling efforts, researchers are still working toward such a systems model [36]. Ajmera et al. recently reviewed developments in diabetes modeling from the past fifty years and identified challenges that must be addressed in order to achieve a complete description of the relevant regulatory network [37]. Additionally, as a collaborative resource for fellow researchers, Ajmera et al. encoded several key models from the literature in a standard model description language (SBML, systems biology mark-up language [38]) and shared these models via BioModels Database [39], which is an online repository for quantitative models of biological processes.

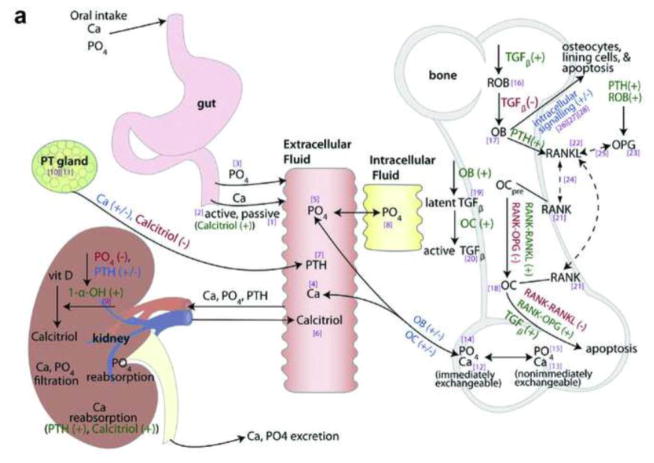
One example of a systems-based disease model is that for calcium homeostasis and bone remodeling published by Peterson and Riggs [40, 41]. The model incorporated relevant molecular pathways in physiological spaces representing the gut, vasculature, intracellular phosphate, kidneys, parathyroid gland, bone, and intracellular osteoblast components [40] (Figure 2a). Although the model contained some empirical elements that could be refined through future experiments, the systems approach enabled adequate description of markers of calcium homeostasis, bone turnover, and bone mineral density under diverse disease states and therapeutic conditions, including hypoparathyroidism, hyperparathyroidism, renal insufficiency, antiresorptive therapy (denosumab), and anabolic therapy (teriparatide) [40, 41]. In 2014, in what has been described as “a watershed moment” for the discipline of quantitative systems pharmacology [42], clinical pharmacologists at the FDA used an open-source version of this model to evaluate the appropriateness of a proposed dosage regimen for a new biologic treatment for hypoparathyroidism [43].

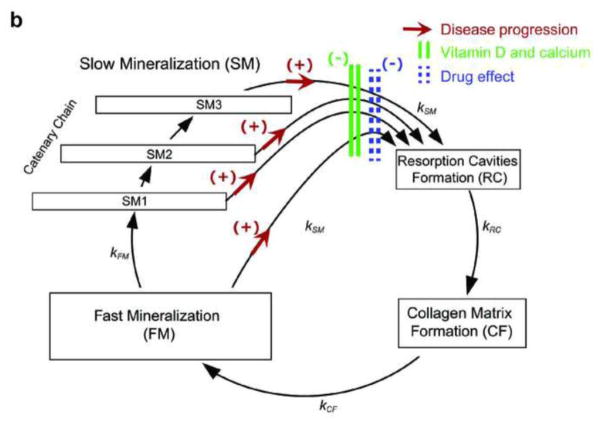
Fig. 2.

a Schematic representation of the systems-based model describing calcium homeostasis and bone remodeling. Solid arrows indicate fluxes, dashed arrows indicate binding effects, dark green plus signs indicate stimulatory effects, red minus signs indicate inhibitory effects, blue plus/minus signs indicate bidirectional effects, and bracketed purple numbers refer to differential equation numbers in the source publication. (Reprinted with permission of Elsevier from [40], copyright 2009) b Schematic representation of the semi-mechanistic bone cycle model. The red arrows between the mineralization and resorption compartments indicate an increased transit rate due to disease progression; the green bars indicate a decreased transit rate due to vitamin D and calcium supplementation; and the dashed blue bars indicate a decreased transit rate due to a drug effect. (Reprinted with permission of Springer from [19], copyright Springer Science+Business Media New York 2015) 1-α-OH 1-alpha-hydroxylase, Ca calcium, OB osteoblast, OC osteoclast, OC_pre osteoclast precursor, OPG osteoprotegerin, PO₄ phosphate, PT gland parathyroid gland, PTH parathyroid hormone, RANK receptor activator of nuclear factor kappa B, RANKL RANK ligand, ROB responding osteoblast, TGF_β transforming growth factor beta, vit D vitamin D

Semi-Mechanistic Models

Like empirical models, semi-mechanistic models are largely data driven, and, like systems models, semi-mechanistic models incorporate knowledge about underlying biological, pathophysiological, and pharmacological processes; however, in contrast to systems models, semi-mechanistic models are not intended to provide comprehensive depictions of molecular pathways. Instead, parsimony is preferred, and mathematical representations of biological processes generally incorporate just enough complexity to describe the relevant data accurately. For instance, van Schaick et al. recently reported a semi-mechanistic model of bone turnover and bone mineral density for evaluating the effects of osteoporosis treatments [19]. The semi-mechanistic approach was implemented because earlier mathematical models of bone remodeling were too complex to characterize adequately the time course of clinical biomarkers of bone turnover and the associated variability observed in clinical studies. Rather than including detailed representation of all molecular and cellular processes involved in bone remodeling, the semi-mechanistic model incorporated assumptions and simplified functions that were thought to capture the most critical aspects of the process. Specifically, the full model consisted of a closed form cyclical model with four compartments representing bone resorption, formation, primary mineralization, and secondary mineralization, a disease progression model representing bone loss in osteoporosis, a vitamin D and calcium supplementation (placebo) model, and a drug model for antiresorptive treatments (Figure 2b). The full model accurately described the short-term (<1 year) and long-term (1 year–10 years) time course of bone turnover biomarkers and bone mineral density in postmenopausal women receiving treatment with either placebo or antiresorptive drugs (bisphosphonate or denosumab). Given the long duration of late-phase osteoporosis trials, incorporation of disease progression was a critical component of the full model. Potential future applications of this model include optimization of dosage regimens, prediction of effects of novel osteoporosis therapeutics, prediction of long-term bone mineral density values in patients based on bone turnover biomarker values observed in short-term phase I trials, and linkage of the model to a discrete clinical outcome, such as the probability of bone fracture.

Case Studies in Alzheimer’s Disease

Alzheimer’s disease is a chronic, neurodegenerative disease that afflicts an estimated 5.3 million Americans and is the sixth leading cause of death in the US [44]. The chronic, degenerative nature of the disease combined with its high prevalence and societal burden have made this area ripe for application of disease progression modeling.

In a pair of companion papers published in 1992, Holford and Peace described the development and evaluation of an empirical disease model for progression of cognitive effects in Alzheimer’s patients treated with the acetylcholinesterase inhibitor tacrine [2, 3]. This work, which proved seminal in the application of nonlinear mixed-effects analysis to disease progression modeling, incorporated data from two clinical trials of the same study design in subjects with probable Alzheimer’s disease. One trial was conducted in the US and the other in France. The design involved an initial, randomized tacrine dose titration phase, a placebo baseline washout phase, a double-blind phase comparing placebo with the best-tolerated tacrine dose in patients who achieved a predefined response, and a blinded, sustained active phase with the best-tolerated tacrine dose in all patients. Patients were blinded to treatment throughout the trials. ADAS-Cog was the primary measure of disease status [13], and the final model successfully described the progression of ADAS-Cog, ADAS-Cog(t), with a linear model that incorporated symptomatic effects for both tacrine and placebo (Equation 4):

$$\mathit{ADAS}-\mathit{Cog}(t)=\mathit{ADAS}-{\mathit{Cog}}_0+\alpha \times t+E_{\mathit{tacrine}}(t)+E_{\mathit{placebo}}(t)$$ (Eq. 4)

where ADAS-Cog₀ is the baseline ADAS-Cog score; α is the rate of disease progression, which was estimated as 6.17 ADAS-Cog units/year; E_tacrine(t) is a function incorporating the drug effect, and E_placebo(t) is a function incorporating the placebo effect. The effect of tacrine shifted the disease progress curve by −2.99 ADAS-Cog units, and there were significant positive correlations between baseline ADAS-Cog score, disease progression rate, and the magnitude of the tacrine effect. Because subjects were blinded to treatment but aware of when changes in treatment occurred, the model included a placebo response at times of treatment change. The placebo model, E_placebo(t), featured a Bateman-type function, which enabled estimation of the onset, offset, and magnitude of the placebo effect. Interestingly, the magnitude of the placebo effect was 76% greater in the French trial compared to the US trial, and the offset of the placebo effect occurred more slowly in the French trial, perhaps reflecting cultural differences in expectations about treatment.

Over the past 25 years, many others have expanded upon the work of Holford and Peace. These efforts have been spurred on by prominent failures in Alzheimer’s disease drug development, which have been partially attributed to inadequate clinical trial design [45]. In several recent publications, generalized logistic functions have been employed to characterize a sigmoidal progression of ADAS-Cog scores in Alzheimer’s patients [46–48]. For instance, Conrado et al. [48] modeled data from the Coalition Against Major Diseases (CAMD) database for control-arm patients (both placebo and stable background Alzheimer’s medication) from randomized, double-blind clinical trials in patients with mild-to-moderate Alzheimer’s disease; the data were adequately described by the Richards function (a generalized logistic function) (Equation 5):

$$\mathit{ADAS}-\mathit{Cog}(t)=\frac{\mathit{ADAS}-{\mathit{Cog}}_0\times 70}{{\left[\mathit{ADAS}-{\mathit{Cog}}_0^{\beta }\times \left({70}^{\beta }-\mathit{ADAS}-{\mathit{Cog}}_0^{\beta }\right)\times e^{-\beta rt}\right]}^{1/\beta }}$$ (Eq. 5)

where ADAS-Cog₀ is the baseline ADAS-Cog score, 70 is the maximum possible observed ADAS-Cog score, r is the intrinsic rate of disease progression, t is time, and β is the shape factor allowing for a non-central inflection point of disease progression. This function describes an asymmetric, S-shaped curve with a non-linear rate of disease progression that increases when ADAS-Cog is below the inflection point and decreases when ADAS-Cog is above the inflection point, which was estimated to occur at a score of 52. Thus, ADAS-Cog scores reach a plateau as they approach the maximum possible value. Compared to earlier linear models, the Richards function more appropriately constrains ADAS-Cog scores to the range of possible values (0–70) and also better characterizes the nonlinear, saturable progression of Alzheimer’s disease, wherein disease scores increase exponentially during the early stages of disease and then the progression rate slows and approaches zero as ADAS-Cog scores approach 70. This plateau in the Richards function is consistent with the ceiling effect that has been observed in clinical practice when patients with severe Alzheimer’s disease experience loss of speech and can no longer perform the tasks required to capture cognitive deterioration via ADAS-Cog. Additionally, in order to completely constrain model predictions to the possible range of ADAS-Cog scores, recent models have incorporated beta-distributed residual variability, which allows for a heteroscedastic error distribution with a variance that approaches zero as ADAS-Cog scores approach the boundaries [46, 48]. Recent modeling efforts have also focused on identification of patient characteristics (i.e., covariates) that appear to influence the rate of disease progression. For instance, age and apolipoprotein E (APOE) genotype have consistently been identified as covariates affecting disease progression rate, with younger age and the presence of the APOEε4 allele associated with faster progression [46–48].

A milestone in Alzheimer’s disease modeling was achieved in the summer of 2013 when the CAMD received regulatory endorsement from both the FDA and the European Medicines Agency (EMA) for its clinical trial simulation tool for mild-to-moderate Alzheimer’s disease [49]. At the core of this simulation tool is a disease progression model that incorporates many of the features described above. Disease progression is described by the longitudinal change in ADAS-Cog score over time, and scores advance along a sigmoidal curve with bounds at 0 and 70 [46]. The placebo effect is incorporated with a Bateman-type function [35], and symptomatic drug effects are described by an overall function offset [49], as illustrated generically in Figure 1 and Equation 2. Although disease-modifying drugs for Alzheimer’s disease are not currently available, the FDA and EMA agreed that claims of a disease-modifying drug effect could be substantiated by evidence of a drug-induced decrease in the rate of disease progression, provided that such a change in progression rate is accompanied by a biomarker change that supports improvement in the underlying pathophysiology [49]. For the purposes of clinical trial simulation, the tool also incorporates covariates, such as age and APOEε4 allele status, which may influence disease progression. The FDA and EMA deemed this tool scientifically sound and fit for purpose in aiding design of future clinical trials in patients with mild-to-moderate Alzheimer’s disease [49], and intended applications include calculation of sample size, determination of optimal trial durations and treatment effect measurement times, identification of optimal data analysis methods, and comparison of the sensitivity of competing trial designs to assumptions about treatment effects [50]. Importantly, such a tool could not have been developed without construction and utilization of a large, collaborative, standardized database [51] that enabled integration of patient-level data with summary-level data from the literature. Similar efforts are currently underway in disease modeling of mild cognitive impairment and pre-symptomatic Alzheimer’s disease [50, 52].

Recent Developments

Integration of Disease Progression Modeling with Cost-Effectiveness Analysis

Widespread concern about rising healthcare costs has made cost-effectiveness analysis an increasingly important component of health technology assessment. At present, cost-effectiveness analyses for pharmaceutical agents primarily rely upon empirical models of disease progression, such as Markov models, to describe probabilistic transitions in the health states of patients over time [53]. Unfortunately, this approach relies on data from late-stage clinical trials and does not allow for model-informed prediction of cost effectiveness during early stages of clinical development. Nevertheless, given the goal of providing effective, safe, and affordable treatment options in a timely fashion, there is increased interest among regulatory agencies, industry representatives, and coverage bodies in early integration of cost-effectiveness analysis with regulatory review [54].

Van Hasselt et al. recently described an integrated simulation framework for eribulin treatment in castration-resistant prostate cancer that included sub-models for disease progression/clinical outcome, eribulin-induced toxicity, dose adaptation, and cost effectiveness [55]. The disease progression/clinical outcome model described the dynamics of prostate-specific antigen and its relationship to overall survival [56]. The models for eribulin-induced toxicity included dose-limiting neutropenia and other graded toxicities (nausea, fatigue, peripheral neuropathy, paresthesia, diarrhea, asthenia, and anemia), and the dose adaptation model incorporated definitions for when and how dose adjustments should be made following toxicities. The hypothetical cost model included direct drug costs and adverse event-related costs. The cost model was only intended to demonstrate proof of concept and was, therefore, relatively simple; however, additional cost considerations, such as those associated with follow-up hospital visits or background mortality rates, could be readily incorporated into such a model. The integrated simulation was conducted in R using the deSolve [57] and MASS packages, and a detailed description of the implementation of cost-effectiveness analysis in R has been previously reported [58]. Using this integrated framework, the authors were able to simulate scenarios with different treatment protocols and patient characteristics and then evaluate the impact of these changes on expected efficacy and cost effectiveness. Thus, the integrated framework successfully linked mechanistic clinical and pharmacological underpinnings to predictions about efficacy and cost. In addition to cancer, diabetes and heart disease are particularly costly therapeutic areas that are currently ripe for application of such integrated disease modeling strategies for cost-effectiveness analysis.

Integration of Disease Progression Modeling with Genomic Data Analysis

To date, the search for genetic variants that influence complex traits and diseases has largely relied upon phenotype data collected from individuals at single time points (i.e., cross-sectional measurements); however, interest has risen in integrating genotype data with longitudinal phenotype data that accounts for the progression of chronic disease [59, 60]. In a recent report, Wu et al. used an empirical nonlinear mixed-effects model to characterize lung function in asthma patients over time and then performed a genome-wide association study to identify genetic contributors to longitudinal phenotypes that were determined from the disease progression model [61]. The authors modeled the time course of forced expiratory volume in 1 second (FEV₁) in children with mild-to-moderate asthma using longitudinal data (FEV₁ recorded every 2–4 months over a 4-year period) collected from 1,041 children as part of the Childhood Asthma Management Program (CAMP) study [62]. FEV₁ was best predicted with an exponential function (Equation 6):

$${\mathit{FEV}}_1=e^{({\theta }_1\times \mathit{age}+{\theta }_2\times \mathit{height}-{\theta }_3)}+{\theta }_{\mathit{drugeffect}}$$ (Eq. 6)

where θ₁ and θ₂ are the rates of change in FEV₁ associated with age and height, respectively, θ₃ is the baseline FEV₁, and θ_drugeffect is the additive (symptomatic) improvement provided by the corticosteroid budesonide. In subsequent genome-wide analysis of a subset of study subjects (581 white patients), the individual-level parameter estimates for baseline FEV₁ (θ₃ in Equation 6) and for rate of change in FEV₁ with age (θ₁ in Equation 6) were used as longitudinal phenotypes, which were tested for association with 473,680 genotyped single nucleotide polymorphisms (SNPs). For comparison, genome-wide association analysis was also performed with a single-time-point phenotype (FEV₁ at 48 months). The genome-wide association study identified seven novel SNPs that were nominally associated with longitudinal lung function phenotypes (six SNPs for baseline FEV₁ and one SNP for rate of change in FEV₁ with age). Additionally, five SNPs that were previously associated with pulmonary function were suggestively associated (p < 0.05) with the longitudinal phenotypes, but the single-time-point phenotype was not associated (p > 0.05) with any of the previously reported SNPs that were considered. Thus, despite sample size limitations, genome-wide association analysis with the longitudinal phenotype appeared to enhance discovery of relevant genetic variants compared to analysis with the single-time-point phenotype [61].

Conclusions

Disease models can be used to synthesize and quantitatively summarize knowledge about disease progression and the influence of drug treatment on disease severity. Models for chronic diseases that progress slowly often require incorporation of data that has been collected from multiple sources over extended time periods. Thus, collaborative research, data sharing, and database standardization are likely to be critical to the continued success of disease modeling endeavors. Recent years have seen notable effective collaborations between industry and regulatory agencies in the area of Alzheimer’s disease modeling and simulation. Novel integration of disease progression modeling with other analyses, such as cost-effectiveness analysis and genomic data analysis, is likely to further expand the utility of this flexible, powerful modeling technique.