Abstract
We present a theoretical model for the nucleation of amyloid fibrils. In our model we use helix-coil theory to describe the equilibrium between a soluble native state and an aggregation-prone unfolded state. We then extend the theory to include oligomers with β-sheet cores and calculate the free energy of these states using estimates for the energies of H-bonds, steric zipper interactions, and the conformational entropy cost of forming secondary structure. We find that states with fewer than ~10 β-strands are unstable relative to the dissociated state and three β-strands is the highest free energy state. We then use a modified version of Classical Nucleation Theory to compute the nucleation rate of fibrils from a supersaturated solution of monomers, dimers, and trimers. The nucleation rate has a non-monotonic dependence on denaturant concentration reflecting the competing effects of destabilizing the fibril and increasing the concentration of unfolded monomers. We estimate heterogeneous nucleation rates and discuss the application of our model to secondary nucleation.
Keywords: aggregation, Amyloid beta-peptides, Biophysics, Fibrous proteins, Protein models
I. INTRODUCTION
Amyloidogenic peptides have been observed in vitro to form a wide array of aggregate morphologies. These experiments are difficult to interpret because it is not clear which aggregation products form under physiological concentrations and which are relevant for disease progression. Insight into the former question can be obtained by mapping out an aggregation phase diagram to understand how the observed aggregation state depends on solution conditions[1,2]. The weakness of these equilibrium approaches is that often kinetic factors prevent the system from reaching equilibrium on experimental or even physiological timescales. A good example of this is the protection against aggregation provided by the natively folded state. Evolutionary pressure has limited the exposure of aggregation prone residues on protein surfaces, so aggregation requires unfolding events in multiple proteins before intermolecular association can occur[3]. Since proteins have folding stabilities on the order of 10 kJ/mol[4], this provides a prohibitive barrier in most cases (the autocatalytic activity of prions is an important exception[5]). Other important kinetic limitations include the nucleation barrier associated with the formation of a new phase and the sequestration of proteins into off-pathway metastable aggregates like oligomers and precipitates[6].
In some cases the timescales associated with the formation of different states are sufficiently separated that pseudo-equilibrium models can predict the system behavior[6]. In other cases, multiple processes can occur on similar timescales requiring elaborate mass-action theories to disentangle the contributions of various pathways. This approach has been instrumental in elucidating the roles of fragmentation and secondary nucleation in the proliferation of fibrils following the initial primary nucleation event [7–10]. However, both of these approaches share a common limitation in that the kinetic predictions are not sensitive to variations in the solution conditions. This is an essential feature when attempting to infer physiological implications from experiments conducted under conditions that greatly accelerate aggregation.
In order to obtain the necessary sensitivity to system conditions, we require a theory that incorporates the microscopic dynamics of aggregation. A pair of useful reaction coordinates for such a theory is the number of intermolecular H-bonds and the alignment, or “registry” between neighboring molecules[11,12]. High resolution structures of mature fibrils show the constituent proteins forming in-register β-sheets resembling one-dimensional crystals[13–15]. To find this highly ordered state, aggregating molecules must sample many different registries, requiring the formation and breakage of many H-bonds[11,12]. This is a slow process, on the order of milliseconds per registry, with the result that aggregation occurs much slower than the formation of secondary structure in the folding of a single protein[12]. This search over registry states has important implications for the influence of solution conditions. At high protein concentrations the diffusion time is faster than the time required for incorrectly aligned proteins to unbind from the fibril. This means that most collisions between monomers and the fibril end cannot lead to successful growth due to the presence of incorrectly bound proteins capping the fibril end. Therefore, weakening the intermolecular bonds, either by increasing the temperature or adding denaturant, will actually increase the rate of aggregation[12]. At low concentration, the diffusion time is slow enough that incorrectly bound proteins can complete the sampling of states before the next molecule attempts to bind to the fibril. In this regime, the dominant effect of weakening the intermolecular bonds is to increase the off-rate of correctly bound molecules giving the intuitive result that fibrils grow faster under conditions where they are more stable.
In a recent paper we used the H-bond reaction coordinate to model the lag times that precede the onset of aggregation[16]. In Classical Nucleation Theory the lag time is a result of the fact that an aggregating cluster must reach a critical size before the favorable energy of binding is able to offset the translational entropy cost of being confined to the cluster[17]. This mechanism is also present in protein fibrils because the cluster must reach a minimum size of four β-strands before incoming molecules can form both the H-bonding and steric zipper interactions found in mature fibrils[18–21]. This means that the second and third β-strands to add to the cluster sacrifice translational entropy without the benefit of the full set of attractive interactions found in a mature fibril. However, in amyloid fibrils a second contribution to the nucleation barrier appears from the conformational entropy cost of extending the peptide backbones into β-sheets[2]. The magnitude of this entropic penalty is such that fibrils must reach a length of ~5 β-strands before the free energy of the fibril is lower than that of the soluble monomers[16].
Our previous theory shows that the dominant nucleation pathway is a compromise between two competing effects[16]. On one hand, pre-nucleation clusters will seek low free energy states that maximize conformational disorder. On the other hand, highly disordered clusters provide a poor binding substrate for new molecules, so highly ordered clusters are more likely to retain newly bound molecules long enough to reach a stable size. As a result, the most probable nucleation pathway goes through states where the cluster is partially ordered. This compromise allows the cluster to avoid the highest free energy states while presenting a binding surface capable of retaining new molecules for an acceptable length of time.
In this paper we extend this work to consider mechanisms that will accelerate or retard nucleation rates relative to this baseline model; the native state of the protein, the search over binding registries, and impurities or interfaces that provide heterogeneous nucleation sites. Under some conditions amyloids have been shown to assemble from pre-formed oligomers[22,23]. However, these oligomers, and the resulting fibrils, are higher in free energy than the fibrils formed via monomer pathways[6]. Moreover, the low concentrations found in vivo are most likely below the critical concentration required for oligomer formation and subsequent assembly[24,25]. Therefore, in the first part of the paper we model a nucleation pathway in which the nucleus grows one molecule at a time. This pathway is the most likely one at low concentration and the model provides insights into the free energy barriers that must be surmounted in any pathway. As an example of more complicated pathways, we include a discussion of heterogeneous nucleation, which shows generically how non-native contacts can alleviate the entropic barrier.
We begin with a free energy analysis of the monomer and initial stages of intermolecular β-sheet formation. These latter states are “oligomers” in the generic sense, but most likely unrelated to the metastable oligomers that have attracted interest for their toxic activity. We believe these oligomers are distinct for two reasons. First, we show that the oligomers in our model are high energy states and do not lie within a free energy basin as required for metastability. Secondly, by design our oligomers lie on the fibril formation pathway and, therefore, are stabilized by contacts that are structurally distinct from those found in toxic oligomers [26–28].
II. MODEL
A. Monomer folding equilibrium
We model the proteins as a solution of α-helix forming peptides, each containing L amino acids. In this context helix-coil theory provides a toy model for a molecule that can adopt an aggregation resistant folded state and an aggregation prone unfolded state. Importantly, the helix-coil model allows for partially unfolded states, but these states are suppressed by the cooperative two-state transitions typical of folded domains[29]. The helix-coil transition is described by two parameters, the propagation parameter, s, and the initiation parameter, σ. We adopt the usual convention where the disordered coil state has a reference free energy of zero. The parameter s is the Boltzmann weight for a peptide unit to join an adjacent helix while σ reflects the entropic penalty required to initiate a helix. The partition function of the helix-coil model can be computed using transfer matrices[30,31]
| (1) |
where L is the length of the protein, the transfer matrix is given by
| (2) |
and λ1 is the largest eigenvalue of the matrix
| (3) |
The free energy of the monomer state is −LkBT ln λ1 and the fraction of amino acids in the helix state is
| (4) |
Since we are interested in the aggregation of unfolded proteins, a more useful parameter is the fraction of amino acids that are not in the folded state ϕ = 1 − δ.
B. Oligomerization and β-sheet formation
After proteins unfold, they become prone to aggregation via the formation of intermolecular β-sheets. In the simplest case each molecule contributes a single β strand to the final aggregate, but more complicated structures have also been observed, ranging from the hairpin motif of Aβ and IAPP[13,32,33] to the β-helix solenoid of the HET-s prion[14]. In the following, we present calculations for the assembly of single β strand and hairpin forming molecules, where the latter case presents the simplest situation where the molecules adopt a conformation allowing the formation of multiple β-strands. Quantities related to these two cases will be denoted with the subscripts “ss” (single strand) or “hp” (hairpin). In both cases we model the fibril as a bilayer consisting of two β-sheets with a steric zipper interface between them.
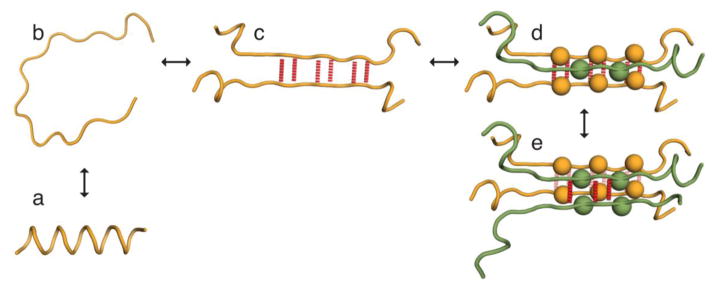
First, we consider the case of single strand molecules. The simplest aggregated species is a dimer which we define by the formation of intermolecular H-bonds (Fig. 1c). These H-bonds constrain a segment of each peptide into the extended β-sheet conformation. The entropic cost of this constraint exceeds the binding energy of the bonds so that the dimer has a net unfavorable free energy[16]. The protein segments not constrained by intermolecular bonds are free to adopt either folded or random coil conformations. We write the partition function for the dimer as
Figure 1.
Cartoon of the aggregation states modeled in our theory. The left panels show the conversion of monomers between (a) an aggregation-resistant folded state that we model as a helix and (b) an aggregation-prone disordered state. (c) A pair of (partially) unfolded proteins forming a dimer through the formation of intermolecular H-bonds. In the figure the dimer is held together by m2 = 6 H-bonds (red dotted lines). (d) A trimer which is held together by H-bonds between the first two molecules (rear) and steric zipper interactions with the third molecule (front). Sidechains participating in the steric zipper are shown as spheres with the remaining sidechains omitted for clarity. The total number of ordered amino acids is 2m2 + m3, m2 from each of the rear molecules plus m3 from the front molecule. In the illustrated conformation there are two sidechains from the front molecule participating in the steric zipper. Since every other sidechain is on the opposite face of the β-strand, this requires at least m3 = 3 amino acids to be in the β-sheet conformation. (e) A tetramer with m2 = 6 β-ordered amino acids on each of the molecules in the rear β-sheet (six yellow H-bonds) and three β ordered amino acids on each strand of the front β-sheet (three red H-bonds).
| (5) |
| (6) |
The summation variable m2 denotes the number of intermolecular H-bonds. Each bond contributes a free energy −kBT ln g2 which accounts for the favorable energy of the H-bond and the loss of conformational entropy from both chains. (L − m2 + 1)2 is the number of ways to select m2 contiguous amino acids from each chain to form the bonds and the factors of λ1 are the contribution from the peptide tails not participating in the H-bonds. The approximation in these formulae, and subsequent oligomer partition functions, comes from employing the long-chain limit for the free tails. The finite sums in these expressions can be evaluated analytically, however, the resulting expressions are unwieldy and contribute little to intuition.
Next, we calculate the free energy of the trimer state. There are two possible trimer states; one where all three molecules are part of a single β-sheet, and a trimer with two molecules in one β-sheet while the third molecule initiates a second sheet and forms steric zipper interactions with the first two. Although the former state has lower free energy (see below), we focus on the latter state since it provides the shortest pathway to a tetramer with two molecules in each β-sheet (rights panels in Fig. 1). This trimer to tetramer transition is the first molecular addition that provides bulk-like interactions with both H-bonds and steric zipper interactions and, therefore, we expect that it is the dominant path toward nucleation.
The partition function for the trimer is
| (7) |
| (8) |
Again, m2 describes the number of H-bonds between the first two molecules and m3 is the number of amino acids in β-conformation on the third molecule. The degeneracy factor in Eq. 8 has additional terms relative to Eq. 6 that describe where the third molecule inserts between the first two and the ways to choose m3 amino acids from the third molecule. The propagation parameter g3 accounts for the loss of conformational entropy from the third molecule as well as the favorable steric zipper interactions. Since the steric zipper requires order in both β-sheets, the summation over m3 is limited to values smaller than the length of the first β-sheet.
For our calculations of the nucleation rate we require the population of trimers that provide a binding surface of exactly m3 amino acids. This is given by
| (9) |
The next largest aggregate is the tetramer. The fourth molecule is the first one that can form both backbone H-bonds and sidechain steric zipper interactions with the existing cluster. Since these are the same interactions present in the growth of a mature fibril, this addition must be thermodynamically favorable. Therefore, this step takes the cluster beyond the nucleation free energy barrier and will be described in the kinetic portion of the theory.
Now we consider the aggregation of hairpin forming molecules. In these systems each molecule contributes two β-strands to the aggregate. This means that half as many molecules need to be recruited to the aggregate in order to reach a stable size. It also means that bulk-like interactions begin with the addition of the second molecule. Therefore, when modeling the equilibrium distribution of pre-nucleation species, we need only consider the conversion of monomers between the folded, unfolded, and hairpin states. While the former two states are described by the helix-coil model, we still require the free energy of the hairpin. We write the partition function for this state as
| (10) |
This expression describes a molecule that forms a steric zipper mhp amino acids in length with the sequences contributing to this zipper separated by a disordered loop of mloop amino acids. The formation of a closed loop incurs a conformational entropy penalty of (3kBT / 2)ln mloop which results in the factor of [34]. The amino acids in the zipper contribute a free energy −mhpkBT ln ghp, which accounts for the loss of conformational entropy and the favorable sidechain interactions. The degeneracy factor accounts for all the possible placements of the zipper along the peptide chain.
Note that the expressions in this section are sequence independent in that they assume that H-bond and steric zipper interactions can form between any pair of amino acids. We consider the opposite limit, that of strict sequence specificity, in section III B.
C. Estimation of parameters
Our model contains six parameters; s, σ, g2, g3, ghp, and the mature fibril propagation constant g4. In this section we constrain the parameter space using estimates of the microscopic interactions contained in these parameters. Following the work of Ghosh and Dill[29], we write the free energy of a helical amino acid as the sum of a H-bond energy and the conformational entropy loss
| (11) |
By fitting thermal unfolding curves, these contributions were found to be fHB/kBT = −1.91 and fCE/kBT = ln (6.83 – 1) = 1.76, which gives a slightly favorable helix free energy of −0.15kBT and a nucleation parameter σ = 0.005kBT[29].
The dimer propagation parameter describes the formation of one H-bond and loss of conformational entropy from two peptide units
| (12) |
Note that this repulsive free energy does not account for the loss of translational entropy, which will be included in the grand canonical treatment in the next section.
The trimer propagation parameter describes the straightening of the third molecule and the formation of steric zipper contacts with the first two molecules (Fig. 1d).
| (13) |
The propagation parameters give the free energy of aggregation per amino acid, however, only half the amino acids in a β-strand participate in steric zipper contacts because the other half remain on the solvent exposed surface. Therefore, fSZ actually represents one-half of the (average) free energy of the steric zipper interaction by a single sidechain. The factor of two in Eq. 13 accounts for the intercalation of the molecule 3’s sidechains between molecules 1 and 2 allowing it to form two sets of steric zipper interactions (Fig. 1d). To estimate the value of g3 we need to know the strength of the steric zipper interactions. This can be obtained from the binding affinity of the fourth molecule.
The fourth molecule can form H-bond contacts with the third molecule while also forming steric zipper interactions with the second molecule in the original dimer
| (14) |
which is the same set of interactions found in mature fibrils. Solubility measurements give ln g4 ≃ 0.5[2,35], so fSZ ≃ −0.35kBT and −ln g3 ≃ 1.06. Finally, the hairpin monomer propagation parameter is −kBT ln ghp = fSZ + 2fCE ≃ 2.87kBT.
This partitioning of energy reduces the original six parameters to just three; fHB, fSZ, and fCE. Next, we need to know how denaturants will affect these binding energies. To obtain this functionality we make two assumptions. First, we assume that the denaturant will have a linear effect on the binding free energy fi(cd) = fi(0) + micd where fi is the negative log of a propagation parameter, cd is the denaturant concentration, and mi is a coefficient describing the effect of the denaturant. Secondly, we assume that the denaturant affects the H-bond and steric zipper interactions such that the m-value is proportional to the non-entropic contribution to the free energy. This gives
| (15) |
for helices, dimers, trimers, and mature fibril contacts, respectively. As a rough check of this analysis we calculate the m-value for mature fibrils. The urea m-value for helices is 0.047 kBT M−1 [29], so for mature fibrils we expect m4 = (fHB + fSZ)ms/fHB = 0.056 kBT M−1. We can obtain an estimate for the effect of GdnHCl by noting that the ratio of Gdn and urea m-values for average proteins is 25/13.1[36]. This gives a Gdn m-value of 0.11 kBT M−1, which is remarkably close to the value 0.12 kBT M−1 obtained by fitting fibril growth rates[12]. We caution that this analysis, at best, applies to average values and, given the number of assumptions made above, this agreement may very well be a coincidence. However, there is less ambiguity to the main conclusion of this section, which is that fibril must achieve a minimum length of 1 + fCE/ln g4 β-strands to pay the entropic penalty of initiating the fibril. This suggests that the minimum length is 4 or 5 strands, in rough agreement with simulation studies[37–39].
D. Equilibrium dimer and trimer concentrations in solutions of single strand molecules
The propagation constants g2 and g3 are both less than unity indicating that the dimer and trimer states are less favorable than disordered monomers. The populations of dimers and trimers are further suppressed by the presence of the favorable helix state and the translational entropy of the monomers. To capture the latter effect we start with the grand free energy of a solution of monomers, dimers, and trimers
| (16) |
where cn is the concentration of a species containing n protein molecules. Here F(n) is the free energy of an oligomer containing n molecules, which we obtain from the partition functions calculated above. In the second term the chemical potential μ serves the usual function of a Langrange multiplier to constrain the total protein concentration. The final terms represent the translational entropy of the oligomers. Taking the derivative with respect to cn we solve for the concentration of each species
| (17) |
which yields
| (18) |
In particular, the expression for c1 yields an expression for the chemical potential in terms of the monomer concentration
| (19) |
Thus the dimer and trimer concentrations are
| (20) |
| (21) |
Since the dimer and trimer are both thermodynamically disfavored, it is an excellent approximation to equate the monomer concentration with the total protein concentration c1 ≃ ct.
In order to obtain the dimensionless concentrations required by Eqs. 20 and 21, we adopt a lattice gas approximation in which the translational degrees of freedom are discretized by the size of a water molecule. Therefore, the dimensionless concentrations are given by the molarity of a given species divided by 55.5 M, the concentration of pure water. Due to this rough approximation, we do not expect a quantitative agreement between our predictions and experimental concentrations.
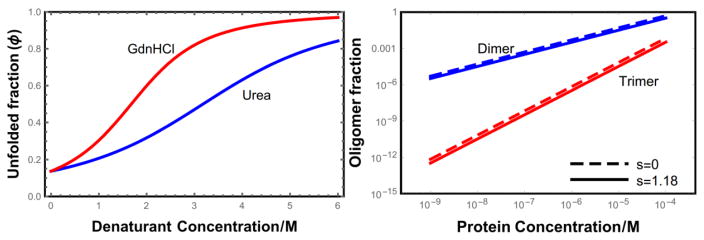
Fig. 2 plots the fraction of proteins in the dimer and trimer states as a function of the total protein concentration. The functional form is a simple power law as seen in Eqs. 20 and 21. Since the interaction energies are net repulsive for oligomers of this size, these states roughly correspond to random collisions and are relatively rare until the concentration reaches 10−4 M. This concentration, which is approximately 1 mg/ml for the L = 100 proteins used in Fig. 2, is the point where the c1 ≃ ct approximation begins to break down. At higher concentrations the oligomer concentration can be determined by using Eqs. 20 and 21 to solve the third order polynomial ct = c1 + 2c2 + 3c3 for c1.
Figure 2.
(a) Denaturant unfolding curves for isolated helices. For the parameters given in the text, helices are ~86% folded in the absence of denaturant. We expect that real proteins will show a more cooperative transition than the helix coil model meaning that they are more folded in the absence of denaturant and the unfolding transition will be more abrupt[29]. (b) Fraction of L = 100 helical proteins in the dimer state (2c2/ct) and in the trimer state (3c3/ct) as a function of the total protein concentration.
Interestingly, the folded helix state has a relatively small effect on the population of oligomers. For s = 1.18 about 86% of the amino acids are in the helical state (Fig. 2a), yet the trimer population is suppressed by less than a factor of 3 and the dimers are only suppressed by about 35%. This finding only applies to equilibrium states; we will soon find that the folded state has a dramatic effect on the kinetics.
E. Nucleation kinetics
We assume that nucleation occurs in a supersaturated solution in which the states occurring before the nucleation barrier have reached a quasi-equilibrium. In the case of single stranded molecules this includes folded and unfolded monomers, dimers, and trimers, while in the case of hairpin molecules it includes monomers in the folded, unfolded and hairpin states. This local equilibrium is possible because of the substantial free energy barrier separating these states from the large aggregates that are the global free energy minimum.
To describe the nucleation time, we modify the rate equation from Classical Nucleation Theory as described previously[16]
| (22) |
Eqs. 22 includes the three ingredients for successful nucleation that are described by Classical Nucleation Theory. First, there needs to be an equilibrium fluctuation large enough to generate the species at the top of the free energy barrier. This is described by the terms c3(m3) and chp(mhp), which give the concentration of clusters in solution that present an ordered binding surface of m3 and 2mhp amino acids, respectively. Using Eqs. 9, 10, and 21 these concentrations are given by
| (23) |
Second, a nucleation attempt begins when an additional molecule binds to the trimer or hairpin causing the cluster to take an initial step downhill in free energy. These attempts are described by the reaction rates konc1c3 or konc1chp. We assume that the rate coefficient kon is limited by the diffusion of the monomers and the probability ϕ that the contact point on the monomer is unfolded (see Eq. 4). Using the rate of reactive particles striking an absorbing sphere, we approximate the collision rate of unfolded molecules as
| (24) |
where α is the radius of the absorbing surface and D is the diffusion constant of the monomers.
Finally, successful nucleation requires that the newly formed clusters continue to grow without dissolving back to a state below the nucleation barrier. In most pre-nucleation solutions (except in cases of extreme supersaturation), the average time required for a new monomer to diffuse to a growing cluster is longer than the average time it takes for a monomer to detach from the mostly disordered cluster. Therefore, successful nucleation requires a succession of unlikely events where either the diffusion time is shorter than average or the residence time is longer than average so that the cluster experiences net growth. The probability of this happening is given by the factor ε1 in Eq. 22, which is conceptually identical to the Zeldovich factor in Classical Nucleation Theory[17,40]. In Eqs. 22 ε1 is written as a function of the number of β-ordered amino acids available for an incoming molecule to bind.
To model the probability of a successful nucleation attempt, we treat the size of the pre-nucleation cluster as a one-dimensional random walk. Forward steps occur when a diffusing monomer binds to the cluster causing it to grow. This occurs with a rate c1kon. Reverse steps happen when a molecule detaches from the cluster. For this to occur, the molecule must break all of the H-bonds holding it to the cluster. If the cluster is highly ordered, the molecules can form more bonds and it takes longer before they are all broken at the same time. As a rough approximation we might expect the residence time of a bound molecule to have a simple Arrhenius dependence , where m is the number of H-bonds to be broken (m = m3 or 2m3 for the single strand and hairpin cases, respectively)[41]. A more careful calculation gives[12]
| (25) |
where νb and Db are the effective drift velocity and diffusion constant of the reaction coordinate describing the number of H-bonds. These are given by
| (26) |
| (27) |
where k + ≃ ns−1 is the timescale for the formation of an H-bond [42] and we have used detailed balance to relate the rates of H-bond formation and breakage (k−) to the free energy of the bonds, k + /k− = g4.
With Eqs. 24 and 25 we can determine the probability that the cluster gains or loses a molecule
| (28) |
where the rate of molecular detachment is . Equations 28 define two concentration regimes for nucleation. When c1kon > kres new molecules generally add to the cluster faster than they fall off. This means that the rate limiting step for nucleation is the formation of the state at the top of the free energy barrier, since this state has a high probability of continuing to grow. On the other hand, at physiological concentrations we expect that the opposite limit c1kon < kres holds. In this regime the cluster is more likely to lose molecules than add them. Therefore, nucleation requires the unlikely event where many molecules add with few detachments. In other words, the cluster size performs a random walk that is biased toward shrinkage events. We define a nucleation attempt to begin when a cluster grows larger than the most unstable size nc. The attempt fails when the cluster returns to nc and succeeds when it reaches the stable size N*. Therefore, the success probability ε1 is the probability of a walk that starts at nc + 1 and reaches N* without returning to nc. If N is the size of the cluster, a convenient reaction coordinate is n = N − nc, the number of molecules above the most unstable size, where nc = 1 or 3 for the hairpin and single strand cases, respectively.
The nucleation probability ε1 probability satisfies the recursion relation[43]
| (29) |
reflecting the fact that a cluster with n molecules evolves to a cluster with n + 1 molecules with probability p + or at n − 1 with probability p−. Eq. 29 can be rewritten as the matrix equation μ(n + 1) = Mμ(n) where
| (30) |
| (31) |
The transfer matrix can be brought into diagonal form with the transformation
| (32) |
| (33) |
By applying the transfer matrix we can generate the success probability for a cluster of any size
| (34) |
| (35) |
| (36) |
where we have used the boundary condition ε0 = 0. By applying the other boundary condition εn* = 1 we arrive at the desired result
| (37) |
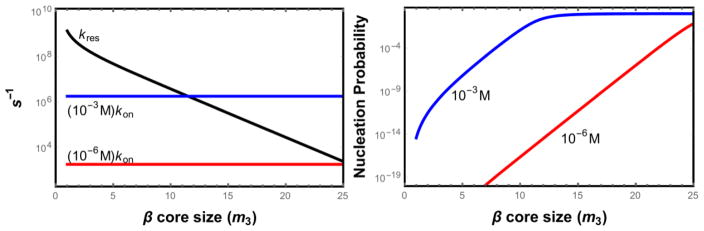
Fig. 3 shows how the nucleation success probability depends on the monomer concentration and the residence time of the bound molecules. At low concentration the detachment rate greatly exceeds the rate of new molecules resulting in prohibitively low success probabilities. The probability increases when either the concentration increases or the nucleating cluster becomes more ordered which increases the residence time of newly bound molecules.
Figure 3.
(a) Comparison of the monomer detachment rate (blue) to the diffusion limited arrival of monomers to the growing nucleus. (b) Probability that a nascent nucleus reaches the stable size as a function of the size of the β core. When the core becomes large enough that newly bound molecules have a residence time comparable to the diffusion time the success probability approaches unity. Both plots assume disordered monomers (s = 0).
The final result for the nucleation rate is given by Eq. 22 with Eqs. 23, 24, and 37.
III. RESULTS AND DISCUSSION
A. Effect of folded state on nucleation
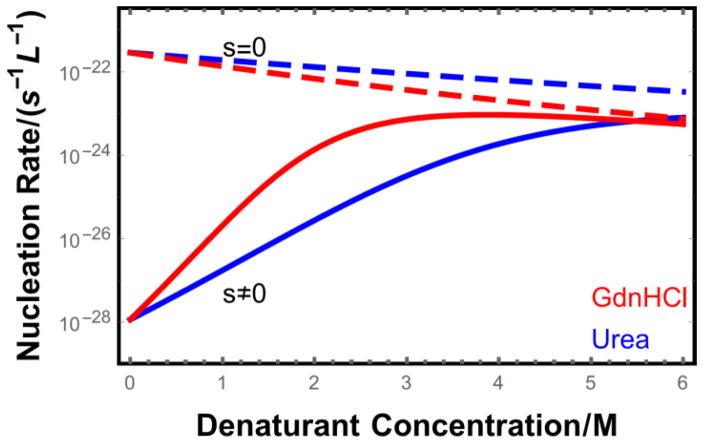
The nucleation rate predicted by Eq. 22 is plotted in Fig. 4 for molecules with (s ≠ 0) and without (s = 0) a stable folded state. In the absence of denaturant the folded state suppresses nucleation by 7 orders of magnitude. Addition of denaturant leads to a rapid increase in the nucleation of the folded protein because the folding equilibrium shifts toward the aggregation-prone unfolded state. However, the denaturant also destabilizes the aggregated state, as seen by the declining nucleation rate of the intrinsically disordered molecules. As a result of these competing effects, the nucleation rate reaches a maximum at about 3 M GdnHCl. At this point the monomeric protein is mostly unfolded and the nucleation rate for the folded and intrinsically disordered cases converge. Urea has a weaker denaturing effect and does not reach a maximum nucleation rate until the concentration is above 6 M. We note that the two order of magnitude enhancement between 2 M and 4 M urea (Fig. 4) is qualitatively consistent with the observation that the lag time for lysozyme aggregation disappears over this range[44].
Figure 4.
Nucleation rate as a function of denaturant concentration for proteins of length L = 100 at a concentration ct = 10−5 M. Intrinsically disordered proteins (s = 0) are monotonically inhibited from nucleating by the addition of denaturant due to the weakening of intermolecular bonds. In contrast, proteins with stable folded states (solid lines) show greatly enhanced nucleation upon denaturant addition because of the increased population of unfolded proteins (s = 1.16 at cd = 0). This trend reverses at high denaturant concentrations since the proteins are mostly unfolded and the dominant effect of further denaturant addition is the destabilization of fibril contacts.
B. Off-register binding
Molecular models of mature fibrils show a striking level of order[13–15]. Most commonly, the molecules form parallel, in-register β-sheets, although anti-parallel structures have also been observed[45,46]. It is an open question whether this perfect alignment of sidechains is representative of all fibrils or simply an artifact of structural techniques that are most sensitive to ordered structures. From a self-assembly perspective, we expect that slow growth conditions will favor more ordered structures while rapid growth conditions will promote the incorporation of defects[12,47]. This would suggest that natural fibrils grown at physiological concentrations would tend to be more ordered (provided only one protein species is incorporated) while the higher concentrations employed in vitro would lead to more disorder.
The nucleation model presented above ignores sequence effects in that all binding states are treated as equivalent. This is the relevant case when considering the aggregation of homopolymers like polyglutamine or very high supersaturations where disordered aggregates are expected to grow. In addition, if the binding selectivity is enforced by steric complementarity more than the chemistry of the sidechains, the small size of the pre-nucleation cluster may allow enough conformational lability to permit promiscuous binding[48]. This would allow for a two-step nucleation process in which cluster formation precedes the onset of crystal order[22,49–51]. A similar decoupling of the density and alignment order parameters is thought to be the nucleation mechanism in protein crystals [52,53].
The opposite limit, where the binding registry is strictly enforced, will modify the theory in two ways. First, it will sharply reduce the concentration of pre-nucleation clusters due to the reduced degeneracy of binding. Eqs. 23 then become
| (38) |
The single strand expression has a degeneracy factor describing the choice of m2 residues out of L for the location of the H-bonds and a second factor to describe where the third molecule inserts its sidechains to form the steric zipper contacts. The hairpin structure, on the other hand, is uniquely determined by the length of the steric zipper interface, mhp and the size of the disordered loop.
Secondly, in-register binding will occur at a much lower rate than off-register binding. If there are L amino acids in each protein, we expect that in-register binding will occur with a probability L−1. This is equivalent to increasing the diffusion time by a factor of L. This has a large effect on ε1, which scales with the diffusion according to (c1kon)2−N*. As a result, the requirement of in-register binding reduces the nucleation rate greatly relative to the promiscuous binding case (Fig. 5).
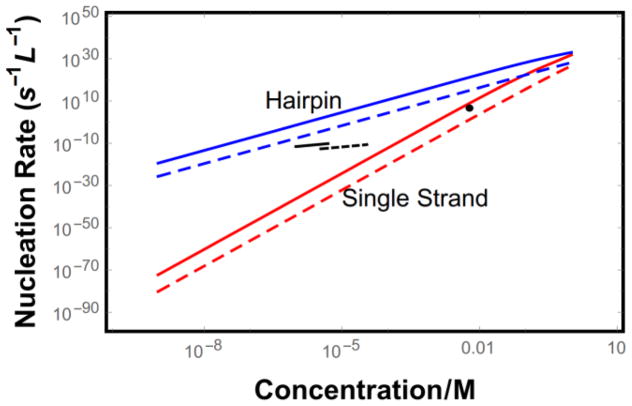
Figure 5.
Predicted nucleation rate for hairpin molecules with L = 40 (blue) and single strand molecules with L = 15 (red). Long dashes represent the case where binding registry is strictly enforced, while solid lines show promiscuous binding. Short black lines show experimentally determined nucleation rates (data were used to fit the proportionality constant and exponent for knuc ∝ cx) for Aβ42 (solid)[54] and Aβ40 (dashed)[55]. The single black dot shows the nucleation rate for insulin[56].
C. Heterogeneous nucleation
Solution impurities can increase nucleation rates by providing binding surfaces for the particles. The energy of binding to the impurity partially offsets the entropic penalty of bringing the particles together, thereby increasing the concentration of critical species. In amyloid systems the nucleation barrier is due to both the translational entropy cost of creating a high density fluctuation and the conformational entropy of stretching the proteins into β-strand conformation. Therefore, heterogeneous binding sites that favor elongated molecules can provide a particularly advantageous pathway to nucleation. A favorable conformational bias can be provided by a surface that is planar on the length scale of the β-strands. Such surfaces include membranes, air-water interfaces, oil droplets, or even the sides of existing fibrils.
To model heterogeneous nucleation we compute the concentration of an assembly of n molecules bound to a heterogeneous site
| (39) |
where chet is the concentration of heterogeneous binding sites and fHn is the free energy of the binding site-oligomer complex. Generalizing Eq. 23 for single stranded trimers we have
| (40) |
Here fhet is the binding energy per amino acid between the proteins and the heterogeneous surface and msurf is the number of amino acids bound to the surface. The binding energy fhet depends strongly on the nature of the heterogeneous binding site with inert surfaces contributing zero binding energy. Depending on whether the protein-surface interaction occurs via sidechains or backbone H-bonds, msurf can be either 2m2 or m2 + m3. Here we assume the protein-impurity interaction is mediated by sidechains so msurf = 2m2. We have also made the assumption that the allowed Ramachandran space is sufficiently limited that binding to a planar surface also restricts the molecules to conformations closely approximating β-strands.
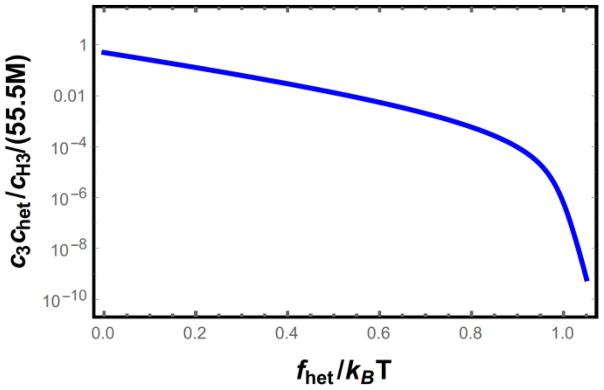
Heterogeneous nucleation will dominate the system when cH3 > c3, therefore, the required concentration of impurity sites for heterogeneous nucleation to be significant is c3chet/cH3. This quantity is plotted in Fig. 6 as a function of the impurity binding energy. The surface binding energy has an exponential effect on the trimer concentration with a marked change in the exponent at fhet ≃ 1 kBT. This value corresponds to the point where free energy of forming the trimer switches from net unfavorable to favorable. When this happens the partition function for the trimer states becomes dominated by the highly ordered terms, leading to the abrupt change in the slope in Fig. 6.
Figure 6.
Required concentration of impurity binding sites needed for heterogeneous nucleation to dominate homogeneous nucleation as the primary nucleation mechanism. There is an abrupt change in the slope when the impurity binding energy, fhet, becomes strong enough to overcome the entropic penalty of straightening the proteins.
A particularly important case of heterogenous nucleation is that of secondary nucleation, where existing fibrils provide the substrate for nucleation events[57]. A recent simulation study showed that Aβ monomers form favorable interactions with hydrophobic sidechains on the fibril surface causing them to extend parallel to the fibril axis[58]. These sidechain mediated interactions are qualitatively similar to steric zipper interactions, yet presumably stronger since the monomer will favor the most attractive sidechains on the fibril surface. This suggests a heterogeneous binding energy on the order of fhet ≃ 2fCE ≃ 1.6 kBT.
IV. CONCLUSION
We have presented a toy model for the nucleation of amyloid fibrils from proteins that have a stable folded state. Experiments have shown that the fibril state is much more stable than the natively folded state, so the folded state represents a deep kinetic trap that helps prevent aggregation[35]. Our calculations show that the native state has a profound effect on nucleation kinetics (Fig. 4) but only a modest suppression on the concentration of unstable oligomers that provide the substrate for nucleation (Fig. 2b). This explains why destabilizing factors, like increased temperature or the addition of denaturants, often lead to rapid aggregation.
Due to the difficulty in disentangling the effects of secondary nucleation and fragmentation from primary nucleation, direct measurements of the primary nucleation rate are sparse. Figure 5 shows three such measurements along with the predictions from our theory. The most direct measurement of the nucleation rate used insulin in micron-scale droplets coated with surfactants to eliminate heterogeneous nucleation[56]. This setup allowed individual nucleation event to be directly resolved, thereby eliminating the complicating factor of secondary nucleation. These experiments yielded a nucleation rate of 5.6×106s−1L−1 at 6 mM protein concentration. This rate is in good agreement with the predicted rate for single stranded molecules, which is surprising because a molecule of the size of insulin would be expected to nucleate using the much faster hairpin mechanism. Unfortunately, the concentration dependence was not investigated in these experiments. This shortcoming was addressed in later studies using Aβ40 and Aβ42 as test systems[54,55]. These works extracted the nucleation rate coefficient by fitting the time dependent fibril concentration to a kinetic theory accounting for secondary nucleation. The obtained rates lie between our predictions for single stranded and hairpin molecules. Assuming that Aβ nucleates via the hairpin mechanism, the experiments are in much better agreement with the theory that assumes that the amino acid alignment is strictly enforced. However, the numerical discrepancy grows to nearly ten orders of magnitude at the upper end of the experimental concentration range. While this is a large number, it is comparable to the discrepancy found in applying nucleation theory to other protein systems[59]. In addition, the strong exponential and power law dependencies inherent to nucleation ensure that small errors are greatly magnified and rough approximations, such as our scaling of concentration units, could be contributing here.
More useful information can be obtained from the concentration dependence. Our theory predicts two power law regimes for the concentration dependence. At high concentrations, where ckon > kres, new molecules bind to the cluster faster than they detach, meaning that the success probability ε1 saturates near unity (Fig. 3). Therefore, the concentration dependence comes from the concentration of unstable clusters and the diffusion rate. This gives a concentration dependence of cnc+1, which results in c2 for hairpin molecules. While this power law agrees with the experimental data for both Aβ systems [54,55], it is surprising that this limit applies to the concentrations where the experiments were conducted. At the μM concentrations explored, the diffusion rates are on the order of ckon ≃ 103 s−1. To achieve a detachment rate slower than this would require an ordered binding surface of ~ 25 amino acids (Fig. 3). Since the entropic cost of ordering amino acids is nearly 2 kBT, we would expect that the system is in the low concentration limit, ckon < kres. In this limit the success probability varies with concentration like cN*, meaning that the overall nucleation rate varies like cN*. The resulting prediction of a nucleation rate proportional to c5 can be ruled out by current experiments (Fig. 5).
How is it that the system is actually in the high concentration regime? The most likely explanation is that nucleation is occurring by a heterogeneous mechanism. Binding to impurity sites will shift the free energy landscape, but will not alter the overall scaling behavior. In this case, binding to an impurity could align the initial molecule enough that the binding surface for subsequent molecules exceeds the 25 amino acids estimated above. We do not believe that a more complicated pathway, for example a two-step mechanism, could explain the observed weak power law because even the smallest disordered cluster, a dimer, would bring a concentration dependence of c2 with subsequent addition events bringing additional powers.
An important caveat is that the nucleation theory presented here uses a one-dimensional reaction coordinate (N). This means that it is unable to capture the displacement of the nucleation flux away from the free energy saddle point[16]. The summation over core sizes in Eq. 22 has a peak flux for clusters with ordered cores of m ≃ 3 at all concentrations. However, intuition suggests that the flux should shift to larger cores at lower concentrations. This is because the increased waiting time will give the system more time to explore ordered states with high free energy. This could also contribute to the overly strong concentration dependence predicted by the model and the discrepancy in the magnitude of the rates.
Another limitation of our model is that the helix-coil model lacks the cooperativity found in proteins with more complicated folds[29]. This, coupled with the rough estimates used in our parameters, means that our predictions are unlikely to be quantitatively accurate. Still, our simple model provides needed insight into the energetics and scaling behavior of fibril nucleation.
Acknowledgments
This work was supported by NIH Grant R01GM107487.
References
- 1.Lee CF. Phys Rev E. 2009;80:31922. [Google Scholar]
- 2.Schmit JD, Ghosh K, Dill KA. Biophys J. 2011;100:450–8. doi: 10.1016/j.bpj.2010.11.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tartaglia GG, Pawar AP, Campioni S, Dobson CM, Chiti F, Vendruscolo M. J Mol Biol. 2008;380:425–36. doi: 10.1016/j.jmb.2008.05.013. [DOI] [PubMed] [Google Scholar]
- 4.Dill KA, Ghosh K, Schmit JD. Proc Natl Acad Sci U S A. 2011;108:17876–82. doi: 10.1073/pnas.1114477108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Prusiner SB. Proc Natl Acad Sci. 1998;95:13363–13383. doi: 10.1073/pnas.95.23.13363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Miti T, Mulaj M, Schmit JD, Muschol M. Biomacromolecules. 2015;16:326–335. doi: 10.1021/bm501521r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Knowles TPJ, Waudby Ca, Devlin GL, Cohen SIa, Aguzzi A, Vendruscolo M, Terentjev EM, Welland ME, Dobson CM. Science. 2009;326:1533–7. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- 8.Cohen SIa, Vendruscolo M, Welland ME, Dobson CM, Terentjev EM, Knowles TPJ. J Chem Phys. 2011;135:65105. doi: 10.1063/1.3608916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cohen SIa, Vendruscolo M, Dobson CM, Knowles TPJ. J Chem Phys. 2011;135:65106. doi: 10.1063/1.3608918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cohen SIa, Vendruscolo M, Dobson CM, Knowles TPJ. J Chem Phys. 2011;135:65107. doi: 10.1063/1.3608918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee CF, Loken J, Jean L, Vaux DJ. Phys Rev E. 2009;80:41906. doi: 10.1103/PhysRevE.80.041906. [DOI] [PubMed] [Google Scholar]
- 12.Schmit JD. J Chem Phys. 2013;138:185102. doi: 10.1063/1.4803658. [DOI] [PubMed] [Google Scholar]
- 13.Lührs T, Ritter C, Adrian M, Riek-Loher D, Bohrmann B, Döbeli H, Schubert D, Riek R. Proc Natl Acad Sci U S A. 2005;102:17342–7. doi: 10.1073/pnas.0506723102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wasmer C, Lange A, Van Melckebeke H, Siemer AB, Riek R, Meier BH. Science. 2008;319:1523–6. doi: 10.1126/science.1151839. [DOI] [PubMed] [Google Scholar]
- 15.Nelson R, Sawaya MR, Balbirnie M, Madsen AØ, Riekel C, Grothe R, Eisenberg D. Nature. 2005;435:773–8. doi: 10.1038/nature03680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang L, Schmit JD. Phys Rev E. 2016;93:60401. doi: 10.1103/PhysRevE.93.060401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kashchiev D. Nucleation. Butterworth-Heinemann; 2000. [Google Scholar]
- 18.Zhang J, Muthukumar M. J Chem Phys. 2009;130:35102. doi: 10.1063/1.3050295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cabriolu R, Kashchiev D, Auer S. J Chem Phys. 2010;133:225101. doi: 10.1063/1.3512642. [DOI] [PubMed] [Google Scholar]
- 20.Auer S. J Phys Chem B. 2014;118:5289–99. doi: 10.1021/jp411370y. [DOI] [PubMed] [Google Scholar]
- 21.Auer S. Biophys J. 2015;108:1176–1186. doi: 10.1016/j.bpj.2015.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Serio TR, Cashikar AG, Kowal AS, Sawicki GJ, Moslehi JJ, Serpell L, Arnsdorf MF, Lindquist SL. Science (80- ) 2000;289:1317–1321. doi: 10.1126/science.289.5483.1317. [DOI] [PubMed] [Google Scholar]
- 23.Hill SE, Robinson J, Matthews G, Muschol M. Biophys J. 2009;96:3781–90. doi: 10.1016/j.bpj.2009.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Seubert P, Vigo-Pelfrey C, Esch F, Lee M, Dovey H, Davis D, Sinha S, Schlossmacher M, Whaley J, Swindlehurst C. Nature. 1992;359:325–7. doi: 10.1038/359325a0. [DOI] [PubMed] [Google Scholar]
- 25.Sengupta P, Garai K, Sahoo B, Shi Y, Callaway DJE, Maiti S. Biochemistry. 2003;42:10506–13. doi: 10.1021/bi0341410. [DOI] [PubMed] [Google Scholar]
- 26.Laganowsky A, Liu C, Sawaya MR, Whitelegge JP, Park J, Zhao M, Pensalfini A, Soriaga AB, Landau M, Teng PK, et al. Science. 2012;335:1228–1231. doi: 10.1126/science.1213151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Apostol MI, Perry K, Surewicz WK. J Am Chem Soc. 2013;135:10202–5. doi: 10.1021/ja403001q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nagel-Steger L, Owen MC, Strodel B. Chem Bio Chem. 2016;17:657–676. doi: 10.1002/cbic.201500623. [DOI] [PubMed] [Google Scholar]
- 29.Ghosh K, Dill KA. J Am Chem Soc. 2009;131:2306–12. doi: 10.1021/ja808136x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zimm BH, Bragg JK. J Chem Phys. 1959;31:526. [Google Scholar]
- 31.Poland D, Scheraga HA. Theory of Helix-Coil Transitions in Biopolymers: Statistical Mechanical Theory of Order-Disorder Transitions in Biological Macromolecules. Academic Press; 1970. [Google Scholar]
- 32.Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. Proc Natl Acad Sci U S A. 2002;99:16742–7. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Luca S, Yau WM, Leapman R, Tycko R. Biochemistry. 2007;46:13505–13522. doi: 10.1021/bi701427q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Doi M, Edwards SF. The Theory of Polymer Dynamics (International Series of Monographs on Physics) Oxford University Press; Oxford: 1988. [Google Scholar]
- 35.Baldwin AJ, Knowles TPJ, Tartaglia GG, Fitzpatrick AW, Devlin GL, Shammas SL, Waudby Ca, Mossuto MF, Meehan S, Gras SL, et al. J Am Chem Soc. 2011;133:14160–3. doi: 10.1021/ja2017703. [DOI] [PubMed] [Google Scholar]
- 36.Ghosh K, Dill KA. Proc Natl Acad Sci U S A. 2009;106:10649–54. doi: 10.1073/pnas.0903995106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zheng J, Ma B, Tsai CJ, Nussinov R. Biophys J. 2006;91:824–833. doi: 10.1529/biophysj.106.083246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.De Simone A, Esposito L, Pedone C, Vitagliano L. Biophys J. 2008;95:1965–1973. doi: 10.1529/biophysj.108.129213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kahler A, Sticht H, Horn AHC. PLoS One. 2013;8 doi: 10.1371/journal.pone.0070521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zeldovich YB. Acta Physicochim URSS. 1943;18:1–22. [Google Scholar]
- 41.Schmit J. n.d [Google Scholar]
- 42.Muñoz V, Thompson Pa, Hofrichter J, Eaton Wa. Nature. 1997;390:196–9. doi: 10.1038/36626. [DOI] [PubMed] [Google Scholar]
- 43.Redner S. A Guide to First-Passage Processes. Cambridge University Press; 2007. [Google Scholar]
- 44.Kumar EK, Prabhu NP. Phys Chem Chem Phys. 2014;16:24076–24088. doi: 10.1039/c4cp02423k. [DOI] [PubMed] [Google Scholar]
- 45.Balbach JJ, Ishii Y, Antzutkin ON, Leapman RD, Rizzo NW, Dyda F, Reed J, Tycko R. Biochemistry. 2000;39:13748–59. doi: 10.1021/bi0011330. [DOI] [PubMed] [Google Scholar]
- 46.Sawaya MR, Sambashivan S, Nelson R, Ivanova MI, Sievers Sa, Apostol MI, Thompson MJ, Balbirnie M, Wiltzius JJW, McFarlane HT, et al. Nature. 2007;447:453–7. doi: 10.1038/nature05695. [DOI] [PubMed] [Google Scholar]
- 47.Whitelam S, Schulman R, Hedges L. Phys Rev Lett. 2012;109:265506. doi: 10.1103/PhysRevLett.109.265506. [DOI] [PubMed] [Google Scholar]
- 48.Cukalevski R, Yang X, Meisl G, Weininger U, Bernfur K, Frohm B, Knowles TPJ, Linse S. Chem Sci. 2015;6:4215–4233. doi: 10.1039/c4sc02517b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Auer S, Meersman F, Dobson CM, Vendruscolo M. PLoS Comput Biol. 2008;4:e1000222. doi: 10.1371/journal.pcbi.1000222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Auer S, Dobson CM, Vendruscolo M, Maritan A. Phys Rev Lett. 2008;101:17–20. doi: 10.1103/PhysRevLett.101.258101. [DOI] [PubMed] [Google Scholar]
- 51.Auer S, Ricchiuto P, Kashchiev D. J Mol Biol. 2012;422:723–30. doi: 10.1016/j.jmb.2012.06.022. [DOI] [PubMed] [Google Scholar]
- 52.Whitelam S. J Chem Phys. 2010;132:194901. doi: 10.1063/1.3425661. [DOI] [PubMed] [Google Scholar]
- 53.Vekilov PG. Cryst Growth Des. 2010;10:5007–5019. doi: 10.1021/cg1011633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cohen SIa, Linse S, Luheshi LM, Hellstrand E, White Da, Rajah L, Otzen DE, Vendruscolo M, Dobson CM, Knowles TPJ. Proc Natl Acad Sci U S A. 2013;110:9758–63. doi: 10.1073/pnas.1218402110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Meisl G, Yang X, Hellstrand E, Frohm B, Kirkegaard JB, Cohen SIa, Dobson CM, Linse S, Knowles TPJ. Proc Natl Acad Sci. 2014;111:9384–9389. doi: 10.1073/pnas.1401564111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Knowles TPJ, White Da, Abate AR, Agresti JJ, Cohen SIa, Sperling Ra, De Genst EJ, Dobson CM, Weitz Da. Proc Natl Acad Sci U S A. 2011;108:14746–51. doi: 10.1073/pnas.1105555108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rubio Ma, Schlamadinger DE, White EM, Miranker AD. Biochemistry. 2015;54:987–993. doi: 10.1021/bi5011442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Barz B, Strodel B. Chem - A Eur J. 2016;22:8768–8772. doi: 10.1002/chem.201601701. [DOI] [PubMed] [Google Scholar]
- 59.Sear RP. J Phys Condens Matter. 2007;19:33101. [Google Scholar]