Abstract
Structural equation modeling (SEM) is a modeling framework that encompasses many types of statistical models and can accommodate a variety of estimation and testing methods. SEM has been used primarily in social sciences but is increasingly used in epidemiology, public health, and the medical sciences. SEM provides many advantages for the analysis of survey and clinical data, including the ability to model latent constructs that may not be directly observable. Another major feature is simultaneous estimation of parameters in systems of equations that may include mediated relationships, correlated dependent variables, and in some instances feedback relationships. SEM allows for the specification of theoretically holistic models because multiple and varied relationships may be estimated together in the same model.
SEM has recently expanded by adding generalized linear modeling capabilities that include the simultaneous estimation of parameters of different functional form for outcomes with different distributions in the same model. Therefore, mortality modeling and other relevant health outcomes may be evaluated. Random effects estimation using latent variables has been advanced in the SEM literature and software. In addition, SEM software has increased estimation options. Therefore, modern SEM is quite general and includes model types frequently used by health researchers, including generalized linear modeling, mixed effects linear modeling, and population average modeling. This article does not present any new information. It is meant as an introduction to SEM and its uses in ocular and other health research.
INTRODUCTION TO STRUCTURAL EQUATION MODELS
Structural Equation Modeling with Latent Variables, SEM,1,2 is most useful for testing complex relationships simultaneously in one model rather than using multiple models. SEM is a confirmatory method that is used to determine whether a model is valid and to test theories of causal relationships. SEM does not let the data determine the best model; models are specified a priori by the researcher. Nevertheless, models are often respecified by the researcher based on model fit assessments using empirical data. SEM is a modeling framework under which several analytic features are combined. First, SEMs allow for the simultaneous estimation of parameters in a system of equations. Within this system, two major submodels are specified: (1) the latent variable model: a model defining the relationships between latent, or unobserved, variables and (2) the measurement model: a model defining the relationships between latent variables and the observed variables which define them.
The combination of the two submodels is one of the major advantages of SEM. This is because the measurement model allows for latent variables to be measured free of random measurement error and this prevents the estimates of association between these variables from bias due to measurement error. Another result is that the reliability, i.e., consistency over repeated observation, of latent variables is perfect since they contain no random measurement error. A second major advantage of structural equation modeling is the simultaneous estimation of coefficients in multiple equations. What this provides is the ability to test associations in the context of a system of associations. Tests involving coefficients across different equations and testing of linear and non-linear combinations of coefficients from multiple equations is possible. These major advantages will be described in more detail in subsequent sections.
SEM models were originally synonymous with “covariance structure models” because estimators were functions of covariances among observed continuous (or quasi-continuous) variables. An assumption about multivariate normality of equation errors, specifically kurtosis that does not deviate from a normal distribution3, were required for correct standard error estimates and chi-square model fit tests. However, standard error estimators and chi-square tests that are robust to excess kurtosis became available.3,4 In addition, methods developed for binary and ordered observed outcome variables, which utilized polychoric or tetrachoric correlations in combination with the robust standard error estimators mentioned above. 3,5 Therefore, classic SEMs offered estimation methods that accommodated the most common types of non-continuous outcomes. More recently, a modeling framework that merges SEM with generalized linear models has developed,6,7 which expands SEM to a include a more general class of linear models. The extension of classic covariance structure models to generalized linear SEM is a major advancement to the method and particularly useful for ocular and medical research that involves the evaluation of count or survival outcomes.
Other extensions have developed in both the literature and in the available software packages, including an expansion in estimation options. One such expansion includes probability weighted point estimators and robust variance estimators such as sandwich estimators.8,9 These estimators are typically applied within a generalized estimation equation (GEE) approach, otherwise known as “population average” or marginal modeling. In contrast to the method of correcting for nesting using GEE approaches, SEM also allows for the explicit estimation of nested correlation structures in random effects.10,11 The random effects estimation capabilities have always been a part of SEM in the form of the estimated variances of the latent variables, but their use as estimates of variance components using multiple level nested data has increased in applications of SEM.12,13
The remainder of this article will describe SEM in the context of modeling ocular health data. The two submodels will be described in more detail with a focus on the utility of these models in practice. Steps in the application of SEM will be described, including model specification, identification of model parameters, traditional estimation methods, and model fit assessment. The merger of SEM with generalized linear models will be presented in the context of an ocular research application. Finally, random effects modeling and GEE modeling approaches within the context of SEM will be discussed.
FOUNDATIONS OF STRUCTURAL EQUATION MODELING
Full structural equation models may be separated into two submodels: the measurement model, which involves the relations between unobserved latent variables with their observed indicators and the latent variable model, which involves the associations between latent variables. Structural equation models require care in their specification. SEM is primarily a confirmatory method that tests theoretical models using empirical data. Therefore, strong theoretical or substantive knowledge should inform SEM modeling and testing. Simplicity should be favored over complexity whenever possible, particularly under small sample size conditions. There are several estimation options for these models, including maximum likelihood and generalized least squares. The models may be evaluated using model fit statistics and indices foremost of which is the chi-square test of global model fit. Bollen1 is the seminal text on classic SEM. Other texts include Hoyle,14 Kaplan,15 Kline,16 and Raykov & Marcoulides,17 among others.
Measurement Models / Confirmatory Factor Analysis
The measurement submodel in SEM is equivalent to a classic confirmatory factor model.18,19 Confirmatory factor analysis (CFA), which is distinct from exploratory factor analysis, is a theoretically based method for defining and testing constructs and has been in use since the mid 20th century mostly in sociology and other social science fields.20 The latent variable or “measurement model” is the model that measures unobserved (latent) variables using multiple observed variables that are proximal indicators of the latent variables.
Many constructs of interest to social scientists cannot be directly measured. For example, identity, solidarity, intelligence, deviance, etc. and their potential multiple dimensions are not directly measurable and are typically measured using proxy observed indicators. However, unobservable constructs are also pervasive throughout the health sciences and the ocular sciences. Consider such constructs as depression, quality of life dimensions, and visual acuity. In fact, the majority of physical diseases are diagnosed using a combination of signs and symptoms that are self-reported by patients to physicians or measured using clinical tests. Physicians then combine those symptoms and their severity to arrive at diagnoses. Many diagnoses are therefore based upon multiple observable symptoms either through social survey of a single respondent, the patient, or clinical measures of symptoms or some combination of these.
Common health and ocular variables also contain random measurement error. This is particularly true for survey data, such as self-reported health status. Even when clinical measures of disease are available, these often have random error with a certain degree of false positive and false negative rates and are often combined with other clinical or non-clinical indicators of a health problem to determine an underlying disease. So, measurement models are an ideal method for health and ocular sciences in measuring underlying disease as well as other behavioral and health traits. To examine the benefits of using latent variables, we will consider measurement of glaucoma as an example.
Glaucoma is typically diagnosed using three indicators: visual field loss, intraocular pressure, and optic nerve damage. Visual field is a subjective test obtained usually with an automated computer perimeter and relies on the responses of the patient. Intraocular pressure is an objective clinical measure. Increase in cupping of the optic nerve head is a hallmark of glaucoma; while cupping traditionally relied on the interpretation of the clinician, increasingly retinal nerve fiber thickness is measured by imaging techniques such as the optical coherence tomography.
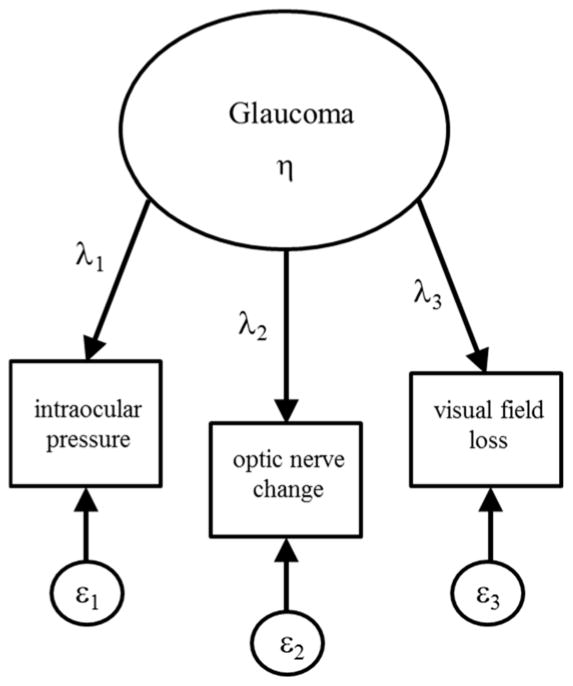
The measurement of each indicator of glaucoma can involve some measurement error as well as error of interpretation on the part of the doctor/observer. Other factors may also cause these measures to vary across individuals (racial/genetic differences) and within individuals (e.g., intra-patient fluctuations during visual field testing). In addition, the timing and compliance of glaucoma eye drop medications may affect the intraocular pressure and cause variability in measured values. A theoretical measurement model for glaucoma is depicted in Figure 1 and the associated equations for this model are given in Equations (1) through (3).
Figure 1.
Measurement Model for Glaucoma
| (1) |
| (2) |
| (3) |
Observations are made for multiple individuals, but for simplicity, subscripts indicating individuals are not included in the equations. In this model, y1, y2, and y3 are the three observed indicator variables: intraocular pressure, optic nerve change, and visual field loss, respectively. The intercepts, v1, v2, and v3 are typically set to zero, but may be estimated. The λ1, λ2, and λ3 are parameters that represent the relationship between the unobserved (latent) variable, η, and the three respective indicators. Here η is glaucoma. The λ are often referred to as factor loadings. One of the λ is typically fixed to 1 to set the scale for the latent variable to a similar scale of one of the indicators. This approach to scaling is preferred when the units of the scaling indicator are intuitive. Alternatively, the latent variable may be set to a standard normal scale by fixing its variance to 1. The εk represent the random measurement error for each of the k indicators and for individuals i (subscript omitted). The latent variable is assumed to be one dimensional, continuous, and normally distributed. We may think of these latent variables as measures of likelihood or severity of a condition where somewhere on the continuum there is a cutoff where we would claim that an individual indeed suffers from glaucoma. (Latent variables may be modeled as discrete or categorical variables,21 but these types of models are not discussed in this article.)
In the model depicted in Figure 1, we are theorizing that glaucoma is not directly observable, but that a patient with glaucoma would have an increased risk of intraocular pressure, increased optic nerve damage, and more visual field loss. The degree to which these three indicators are present in combination determines where on an underlying continuum an individual falls in terms of glaucoma (ranging from no glaucoma to severe glaucoma). The λ parameters may be interpreted like a regression parameter where a one unit increase in the latent variable, glaucoma, is associated with a λk increase in the kth indicator (symptom of glaucoma in this case).
The latent variable, glaucoma, is hypothesized to exist and to explain the association among the three clinical indicators and the uncorrelated components of each of the indicators is estimated as random measurement error, the εk terms in the model. The result of this is that the variation in glaucoma across individuals is measured independent of random measurement error. The random error for a given item is assumed uncorrelated with random error from other items and uncorrelated with the latent variable.
The importance of measuring constructs separated from random measurement error should not be understated.22 It provides reliable measures of constructs and eliminates attenuation bias in bivariate associations, that is, it prevents the estimate of associations from being weaker than the true associations in the population.23 It also eliminates bias in estimates in a multiple regression context. Most traditional regression analyses have an underlying assumption that variables are measured without error. However, often regression models include multiple independent variables with errors, which may result in biased regression coefficients and this bias may be positive or negative depending on the amount of error in measurement and the correlations among the independent variables.1
The glaucoma example above characterizes the typical measurement model. But these models are flexible. Correlations between random errors for two or more items may be estimated and observed indicators may be outcomes of multiple different and distinct latent variables. For example, visual field loss may also be a clinical sign of another disease, e.g., cataract, in the same model. Also, the measurement model depicted in this example is a classic factor model with effect indicators (the indicators are effects of glaucoma), but it may be more appropriate in some cases to use causal indicators (the indicators cause the latent variable).24 For example, in the glaucoma example, it may be appropriate to specify ocular pressure as a cause of glaucoma and optic nerve change and visual field loss as effects of the disease.
There are several examples of the use of confirmatory factor analysis or measurement models in the ocular health literature. An early example is Mayer, Dougherty, and Hu25 who measure the temporal modulation sensitivity function as a latent variable with observed threshold modulation sensitivities at several flicker rates as the indicators of the latent variable. They also provide a nice description of the SEM (“covariance structure analysis”) approach. CFA has also been used to assess the domain structure of the Impact of Visual Impairment (IVI) scale,26 to determine the psychometric validity of the National Eye Institute-Visual Function Questionnaire (NEI VFQ-25) and its subscale structure for use in people with low vision,27 and to identify the content for a vision and quality of life–related utility measure (Vision Quality of Life Index, VisQoL).28
Latent Variable Models, Path Analysis and Simultaneous Equations
The latent variable submodel of SEM is the model of the relationships between latent variables. This includes relationships between latent variables and observed variables that are measured without error (or treated as such in the model). When all variables in this submodel are assumed to be measured without error (i.e., they are directly observable), the latent variable submodel is equivalent to simultaneous regression equation models. 29
Path modeling could be considered the origins of simultaneous equation models. Developed in the early 20th century,30–32 path analysis uses pictorial depiction of relationships between variables, such as those depicted in Figures 1 and 2. In the pictures, straight arrows depict pathways of association between variables with the hypothesized predictor variable at the beginning of the arrow (path) and hypothesized outcome variable at the end of the path. In the figures, circles represent unobserved or latent variables and squares represent observed variables. A two-headed, curved arrow represents a covariance. Path models include multiple and multivariate regression and multivariate ANOVA and ANCOVA as special cases.
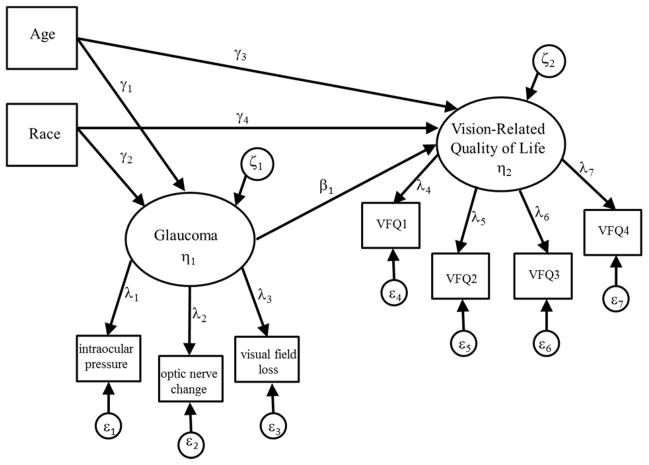
Figure 2.
Model for the Relationship between Age, Race, Glaucoma, and Vision-related Quality of Life
Initially, path model parameters were estimated by writing unknown parameters in terms of the variances and covariances of the observed variables and then plugging in the sample variance-covariance estimates. Modern path analysis involves simultaneous estimation of effects using standard estimation methods such as generalized least squares and maximum likelihood. A primary use of path analysis is the decomposition of effects from various pathways.33 In addition to direct effects of one variable on another, indirect pathways through mediating variables may be calculated as well as total effects, which are effects of one variable on another both directly and through other mediated pathways.34–36
Figure 2 below is a hypothetical example of a path diagram for a model (with latent variables) that includes a mediated relationship. The model defining the relationships between variables excluding the measurement model is given in equations 4 and 5. These equations make up the latent variable submodel.
| (4) |
| (5) |
where x1 represents age and x2 represents race. γ1 is the regression parameter for the effect of age on glaucoma directly, the direct effect, controlling for the effects of race; γ2 is the regression parameter for the direct effect of race on glaucoma controlling for age; γ3 and γ4 are the regression parameters for the direct effects of age and race on visual related quality of life controlling for glaucoma; and, β1 is the parameter for the direct effect of glaucoma on vision related quality of life controlling for the effects of age and race. The γ and β parameters are interpreted as standard regression parameters where a one unit increase in an independent variable in a particular equation is associated with a γ or β increase in the dependent variable for that equation controlling for the other independent variables in that equation. The ζ1 and ζ2 are the equation error for the glaucoma and quality of life outcomes, respectively.
In the model depicted in Figure 2, we are theorizing that age and race are risk factors for glaucoma and also impact an individual’s vision related quality of life (VQAL) both directly as well as through their effect on glaucoma. This model decomposes the effects of age and race on VQAL into three pathways where in a standard regression model, glaucoma would be added as a covariate and we would only have estimates for the direct effects of age and race after accounting for the VQAL variance explained by glaucoma. The indirect effect of age on VQAL through glaucoma is calculated as the product of γ1 and β1. The total effect of age is calculated as the direct effect (γ3) plus the indirect effect (γ1β1). As this example shows, path analysis provides a representation of multifaceted models made up of several equations.
The model depicted in Figure 2 is actually a full structural equation model that combines a measurement model of glaucoma and VQAL using items from the National Eye Institute Visual Functioning Questionnaire (NEI VFQ)37 with the “latent variable model”, which is the model for the relationships among age, race, glaucoma, and VQAL. The measurement model depicted in Figure 1 and defined in equations 1 through 3 is an example where three equations are simultaneously estimated. In the full SEM model depicted in Figure 2, there are seven measurement model equations and two latent variable model equations. The unknown parameters in all of these equations are simultaneously estimated using so called “full information” estimators,38 which will be described in more detail in the next section.
Simultaneous estimation may improve efficiency of parameter estimates when dependent variables are correlated.39 It also allows for variance estimates (standard errors) of linear and non-linear functions of parameters that incorporate the estimated covariances of the parameters involved in the function. An example of a non-linear combination of parameters occurs in mediation testing using a product-of-coefficients method where two parameters from two separate equations are multiplied together.40 For example, for the model in Figure 2 the indirect effect of age on VQAL through glaucoma is γ1β1 with standard error calculated using the delta method:
| (6) |
where σγ1β1 is the covariance between the two coefficients involved in the indirect effect and which are not readily obtained in traditional mediation testing using estimates from regression equations estimated independently. In sum, simultaneous estimation allows for the estimation of new parameters as linear and non-linear functions of individual parameters throughout the system of equations and standard error estimates may be obtained without having to make an assumption of uncorrelated parameters.
Moderation testing is also available in SEM using the traditional method of interactions where the interaction of two variables is a test of moderation.41 Interactions for independent observed variables are estimated in a straightforward way; however, using the interaction method does become difficult when outcomes of some equations are also involved in moderation relationships for other outcomes.42 Latent variables may also be involved in interactions and these methods are more complex.43,44
Moderation testing is also possible and perhaps more flexible using multiple group analysis. Multiple group analysis may be used for a categorical moderator (where the categories are the “groups”). Using multiple group analysis, separate models are specified for each category of the moderator and any parameter in the model may be estimated as the same or different across the categories, including variances of latent and observed variables. For example, we may be interested in testing whether there is a different degree of heterogeneity in glaucoma for black and white subpopulations. Also, it is often of interest to validate measurement invariance across population subgroups by testing for differences in the way a disease (the latent variable) is related to reported symptoms (disease indicators). It may be that the measurement of glaucoma or VRQAL itself differs for different groups.
To a limited extent, path analysis or simultaneous equations methods have been used in the ocular literature. For example, Davidov, et al.45 used a simultaneous equations model to describe the impact of co-morbidities, visual acuity, diabetic retinopathy (DR) grade, and macular edema (ME) on the health-related quality of life (HRQOL) among patients with diabetic retinopathy where several of these variables serve as mediators. Tan, et al.46 used path analysis to calculate indirect effects of narrowed retinal vessel caliber on the long-term incidence of age-related cataract, and Scialfa, Kline, and Wood47 used a SEM model to assess a sensorineural model of contrast sensitivity as a predictor of spatial vision and found a valid two-factor (“two filter”) model.
Full Structural Equation Models: Specification, Identification, Estimation, and Fit
Researchers cycle through several steps when using SEM. The first step is specifying a model and the next step is to ensure that the specified model is identified, that is, that all of the parameters in the model have a unique solution. The model can then be estimated and the adequacy of the model is determined by assessment of the model fit to the data. These steps are repeated until a good fitting model is arrived at. Then parameters from the model may be interpreted as tests of specific causal hypotheses within the model.20,48,49
Model Specification
As described above, a full SEM model combines the measurement model representing the relationship between unobserved (latent) variables and their observed indicators with the structural model of associations between latent variables. Therefore, SEM can account for random errors in construct measurement and evaluate relations between constructs in a system. Comprehensive or “holistic” theories of the multiple relationships involved in visual health can thereby be specified and tested in a single model.
The capability of modeling larger, more complex models that entail many parameter estimates also introduces potential for problems with parameter identification and estimation as well as difficulties with interpretation of specific parameters within the context of the model. Therefore, it is of utmost importance to take care in specifying models. The SEM tradition, including latent construct specification (CFA), involves models developed from a priori theoretical and substantive knowledge. While more exploratory evaluations may be undertaken, it is still important to have an intuitive understanding of what the parameters in the model represent. The researcher ought to be able to interpret every parameter substantively in view of the other parameters in the model. Parsimonious models are favorable for both interpretation and efficiency of parameter estimation, i.e., smaller standard errors. Larger models, models with more estimated parameters, require larger sample sizes to achieve efficiency of parameter estimation. Also, large models are best specified and assessed in stages. For example, specification, testing, and re-specification of measurement models prior to their incorporation into latent variable models help ensure the development of properly specified models.
Parameter Identification
The model specification stage should involve a verification of the identification of the parameters in the model. In classic covariance structure models, model identification means that every unknown parameter being estimated in the model can be defined as a function of the sample variances and covariances of the observed variables. Identification can be established using covariance algebra; however, this is unwieldy for many models of even moderate size. Several identification rules have been established that allow for quick model identification checks of standard models.1 When no rule applies to a model, SEM software will generally detect possible underidentified models, models where at least one parameter cannot be uniquely identified in terms of a combination of sample variances and covariances because the information matrix (see the index of terms for a definition) is not invertible. However, this empirical check is only relevant for local identification, i.e., identification in a particular region of the multidimensional parameter space, where an alternative solution may exist for parameters in a different region. One example where parameter identification is more difficult is in models that are specified with reciprocal relationships. Models of comorbidity would be an example of this, where one might specify that two diseases are directly related to one another. The reciprocal pathways are generally not identified without incorporating instrumental variables, for example, variables that are correlated with each of the diseases in the reciprocal relationship, but not correlated with the other disease in that relationship. Nevertheless, SEM software sometimes provides values for estimates of the underidentified reciprocal effects, which could be mistakenly interpreted as proper estimates of the population parameters. An alternative longitudinal model used to detect reciprocation of two diseases with one another over time is an autoregressive, cross-lagged model.50.
Parameter Estimation
One of the benefits of SEM as described above is the simultaneous estimation of parameters using “full information” estimators. Examples of estimators include maximum likelihood (ML), generalized least squares (GLS), and weighted least squares (WLS) estimators.
The ML estimator is the most commonly used and is given in equation (7).
| (7) |
where S is the covariance matrix of the observed variables in the model, Σθ is the covariance matrix in terms of model parameters that is implied by the specified model, and p is the number of observed variables in the model. For ML, final parameter estimates are obtained when the differences between the observed data covariance matrix elements and the model implied covariance matrix elements are minimized.
A benefit of the full information maximum likelihood estimator (FIML) is that it allows for the estimation of observations with missing information on some of the model variables.51 The method requires a missing at random (MAR) assumption. MAR states that the probability that an item is missing may be a function of the other observed responses in the model but not as a function of the missing responses. This implies missing at random conditioned on the observed responses for variables included in the model.52 The assumption is the same as that required for multiple imputation52,53 where missingness may be a function of the variables in the imputation model. The FIML method for missing data is automated in several SEM software packages and may reduce bias resulting when observations with missing information are omitted from the analysis. Inclusion of those observations using FIML will also increase precision of estimates by retaining a larger sample size.
While there are some advantages to the simultaneous estimation as described above, there are also limitations. For example, misspecification of the relationship among variables in one part of a model may bias estimates in other parts of the model. Therefore, bias can spread throughout the system of equations such that many or perhaps all model estimates are biased. Alternative limited information estimators, such as two-stage least squares (2SLS) may be used to avoid this problem.54,55
Model Fit
One of the great advantages of SEM is the ability to assess the validity of a model using a chi-square model fit test. The test is available for overidentified models only, that is, models where at least one parameter may be written as more than one function of observed variances and covariances. The null hypothesis being tested is HO : Σ = Σθ, where Σ is the population covariance matrix and Σθ is the covariance matrix implied by the specified model. The FML (equation 7) and FGLS fit functions provide the tests where (N − 1)FML and (N − 1)FGLS are χ2 distributions with degrees of freedom where t is the number of parameters to be estimated and p is the number of observed variables in the model. A non-significant chi-square test implies good model fit to the data, i.e., that the model structure imposed on the data is a valid representation. Because a non-significant test is ideal, models estimated using very large samples can result in rejection of the test even when the sample covariance matrix is being closely reproduced.56 In practice, researchers are not specifying perfect models that replicate true models exactly. Rather, they are specifying approximately true models. Under these conditions, very large samples provide statistical power that detects very minor deviations even though the model is approximately true. Because of the statistical power problem, many other descriptive measures of model fit have been developed57–59 to adjust for attributes like model size and sample size. These “global” model fit measures should always be evaluated along with component fit measures such as meaningfulness, size, and statistical significance of individual model parameters. Poor global or component model fit indicates possible misspecification of the model.
EXTENTIONS OF CLASSICAL STRUCTURAL EQUATION MODELS
Generalized Linear Structural Equation Modeling
One limitation of classic SEM is in the assumption of continuous outcomes. One method that developed for binary and ordered categorical outcomes assumes continuous variables underlie the categorical observed outcome variables. The method utilizes poly- and tetra-choric correlations for the S matrix elements and weighted-least-squares (WLS) estimators where the weight matrix, W, is the covariance matrix of the polychoric correlations.5 The polychoric correlations produce unbiased correlation estimates for categorical data and the weight matrix corrects standard error estimates from bias due to non-normal distributions of residual errors.60 This method results in probit parameters for binary and ordered outcomes.61
Classic SEM therefore can handle outcomes encountered in most practical situations including non-normal continuous, dichotomous, ordinal, and censored outcomes. However, the ability to model outcomes with other parametric distributions such as Poisson, gamma, and semi-parametric distributions such as log hazard functions was not traditionally available in SEM. Also, alternative transformations, such as logistic or complementary log-log were not available. A merger of the primary SEM capabilities that include the benefits of both simultaneous equations and measurement models with generalized linear modeling62 has occurred. Generalized linear structural equation modeling (GLSEM)7 allows for the estimation of SEM models with outcomes of varying distributions where parameter estimates for different outcomes (equations) take different forms such as linear, logistic, log-linear, and log-hazard.
Some limitations exist for generalized models relative to classic SEM models. For example, the traditional chi-square model fit test is unavailable for GLSEM. Model fit may be assessed using information criteria measures (AIC, BIC) or log-likelihood ratio tests for nested models.63,64 These test statistics are available in several software packages with SEM capabilities. Maximum likelihood is the primary estimation method, but this method utilizes numeric integration,65,66 which is computationally demanding. Testing linear and non-linear combinations of parameters is not straightforward in GLSEM since these parameters may be in different units due to different linear transformations (“link functions” in the generalized linear framework). For example, evaluating the mediation effect of an independent variable on an outcome through a binary mediator cannot be calculated using the simple product of coefficients method.67,68 Despite these differences and practical limitations, GLSEM is a promising extension to classical SEM and as these models are in early development, more capabilities and improved computational efficiency will likely become available.
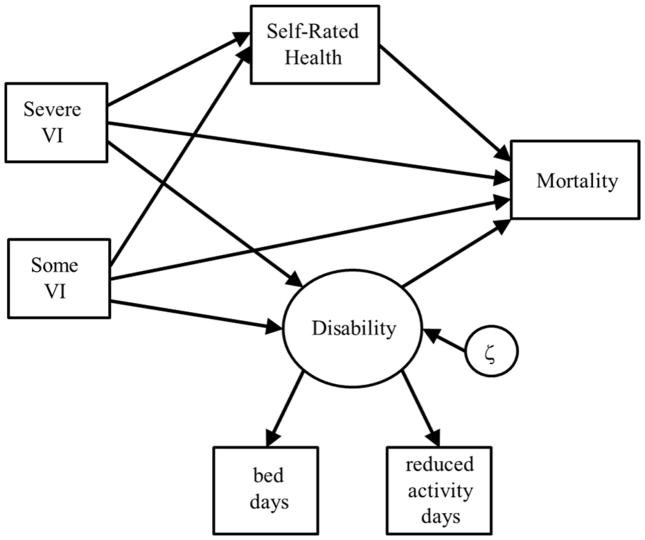
To demonstrate the utility of GLSEM, we present an ocular health example from Christ, Lee, Lam, Zheng, & Arheart.69 Other examples of GLSEM in the ocular literature are Karpa, et al.70 where multiple pathways from visual impairment to all-cause mortality were assessed for older persons and Lam, et al.71 where the direct and indirect effects of visual impairment on suicide mortality were estimated for self-reported health and non-ocular health condition mediators. In Christ, et al.,69 the relationships between visual impairment and mortality through two mediators, self-rated health and disability, were evaluated for a sample of 135,581 adults from the 1986 to 1996 National Health Interview Surveys (NHIS) with mortality linkage through 2002. Figure 3 portrays the model excluding covariate controls. The self-rated health outcome was measured on an ordered scale; therefore an ordered logit link was used for that equation. The equation for the disability latent variable outcome used an identity link since the latent variable itself is continuous and normally distributed, while the paths linking disability to the indicators, number of days in bed and number of days of restricted-activity, use a log link with Poisson distribution. Finally, the equation for the mortality outcome uses a Cox proportional hazards regression. Therefore, four different transformation (link) functions were simultaneously estimated in this model.
Figure 3.
Path Model for Select Portion of the GLSEM for the Relationship Between VI and Mortality. All paths are controlled for covariates with the exception of the paths from disability to its indicators.
Random Effects Estimation in SEM
Latent variable variance estimates in traditional SEM or in GLSEM are random effects estimates. For example, residual equation errors are parameterized as latent variables with a mean of zero and variance ε2 or ζ2. Consequently, latent variables may be used to account for nested structures in the data. As an example, the glaucoma latent variable depicted in Figure 1 may be conceived of as a measure of the degree of nesting of symptoms within patients. Subsequently, within the context of SEM, mixed-effects (or multilevel) models may be specified,12,72 although data structures may differ in the SEM context from other modeling frameworks. In ocular health research, eye care studies evaluating two eyes nested within patient could be accommodated within the SEM framework using latent variables such that variance components for patient and eye level variables would be estimated.
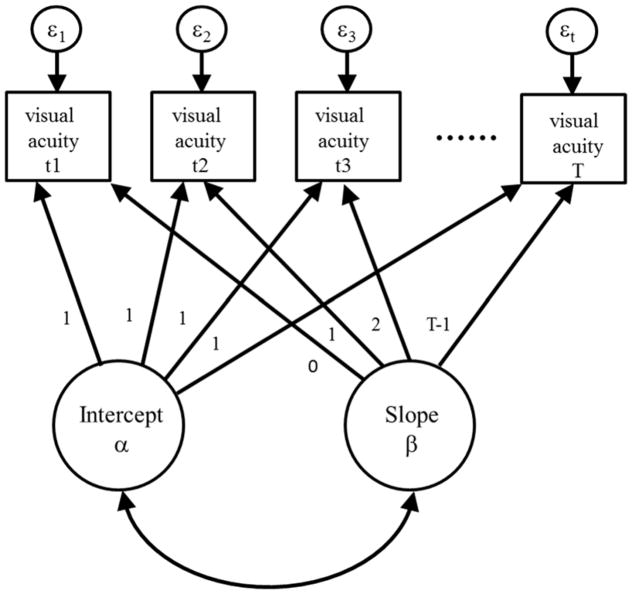
One type of mixed-effects model from traditional SEM that accommodates a nested structure is a trajectory model, which estimates the form and degree of change over time.13 In these models, trajectories are estimated using latent variables where repeated measures are nested within intercept, slope, and quadratic, etc., latent variables. The latent variable mean estimates provide the average of the intercept and slope values (the fixed effects) and the latent variable variance estimates provide the variance of the intercept and slope values (the random effects). Figure 4 depicts a linear trajectory model in the SEM framework. These models may include additional trajectory components (quadratics, cubics, etc.) as well as non-parametric parameterizations such as the free estimation of the time intervals. In SEM, trajectory components (e.g., slopes) may be used as independent or dependent variables in the context of larger models. For example, multiple trajectories and their association with one another may be simultaneously estimated.73
Figure 4.
Example Path Model for a Linear Latent Growth Curve (Trajectory) Model for The Example of Estimating Changes in Visual Acuity Over Time
Another mixed-effects model that has been estimated in a SEM framework is genetics or heritability models using twin and sibling data.74–76 In these models, variance components are estimated for genetic influences, shared environmental influences, and unique environmental influences for a given trait. In fact, this use of SEM is relatively common in the ocular health literature. SEM has be used in twin studies to determine the heritability of central corneal thickness (CCT),77 myopia,78 retinal vessel diameters and blood pressure,79 refractive error,80 peripapillary atrophy,81 and to determine the relative genetic contribution of educational attainment and the shared genetic/environmental factors between education and refraction.82 In their review of the heritability of ocular traits, Sanfilippo, et al.83 found that about 60% of studies used SEM to derive heritability estimates.
Population Average Modeling and GEE
While nested data structures may be estimated explicitly using latent variables to estimate random effects, nesting may also be incorporated into estimation implicitly in population average or marginal models.84 In population average models, the marginal expectation of the outcomes is modeled as a function of explanatory variables and the nesting of data is treated as a nuisance. This approach has traditionally been used in public health and epidemiology fields and also as an approach to estimation of data from complex sampling designs.72,85 Several SEM software packages have included estimation options for dealing with complex samples with nested structures and unequal probabilities of selection. These include weighted point estimates using sampling weights,86 and between-cluster parameter variance estimation.9,87
The estimation used for complex sample designs is a specific example of generalized estimation equations (GEE) where the “working correlation” structure of the nesting (the correlation structure of observations within clusters) is specified as independent. However, the extension to more complex correlation structures such as autoregressive, compound symmetric, and unstructured nesting structures is possible. The advantage of this is that properly specified structures can improve efficiency of parameter estimates, that is, minimize their standard errors. 88,89.
CONCLUSIONS
Structural equation modeling with latent variables has a strong history in the social sciences and has extended to other fields because of its strengths, which include the ability to accommodate measurement of variables that are not directly observable and multifaceted relationships between variables involved in multiple equations. Extensions of the framework, primarily the merger with generalized linear modeling, make the method more favorable to all areas of research, especially the health sciences. However, the strengths may lend themselves to abuses. Model specification is crucial. Well thought out models based on theory and previous research perform the best and prevent multiple testing situations through re-specification and re-estimation of the models using the same data. Where relationships are less well known, model generality is preferable, for example, allowing variables to correlate rather than declaring a direct effect from one variable to the other.
The culmination of structural equation modeling, generalized linear modeling, and mixed-effects modeling together into one modeling framework is documented in the Generalized Linear Latent and Mixed Modeling (GLLAMM) framework.6,7 GLLAMM is a free software that is implemented in Stata.90 Other software available for estimating classical SEM as well as some of the extensions include AMOS,91 EQS,92 LISREL,93 and Mplus.94
While many areas of medical research, public health, and epidemiology are using SEM, it has not been used as much in ocular health research. There are likely opportunities where SEM may serve to enhance research in this area.
Acknowledgments
We acknowledge the following financial support:
R21 EY021187, NEI, Lee (PI)
1R21 EY019096, NEI, Lee (PI)
INDEX OF TERMS
- Attenuation Bias
Bias in regression parameter estimates toward zero.
- Confirmatory Factor Analysis
Analysis of factor or measurement models based on apriori theory about the relationship between latent constructs and observed indicators of the constructs.
- Direct effect
the regression effect of one variable on another through a single pathway.
- Efficiency
In statistics, the degree to which parameter estimates have small(er) variation.
- Factor
Another term for latent variable stemming from factor analysis.
- Full information estimators
Estimators that simultaneously estimate all parameters in a model typically using an iterative procedure. Examples include full-information maximum likelihood (FIML), generalized least squares (GLS), and weighted least squares (WLS)
- Generalized Estimation Equation (GEE)
Estimation method used for parameters of a generalized linear model with a possible unknown correlation between outcomes.
- Identification
A model is identified if all parameters in the model are identified. A parameter is identified if it can be written as a function of known variances and covariances of the observed variables in the model.
- Identity link
In generalized linear models, this is the link function transforming a linear model to a linear model.
- Indirect effect
the effect of one variable on another through an indirect pathway involving additional variables.
- Information Matrix
The second partial derivative with respect to the parameters of the natural logarithm of the likelihood function of the observed variables conditioned on the parameters. Obtaining this matrix is required for calculating the standard errors of model parameters.
- Instrumental Variables
Variables used in limited information estimators such as two-stage least square that are correlated with an independent variable but not with the dependent variable(s).
- Invertible
A matrix is invertible (non-singular) if there exists another matrix that when multiplied by the original matrix results in an identity matrix.
- Kurtosis
A measure of whether the shape of a probability distribution is peaked or flat relative to a normal distribution.
- Latent variable model
The submodel defining the relationships between latent variables, that is, relationships other than those involved in the measurement submodel.
- Latent variable
An unobserved variable measured as a function of multiple observed variables.
- Limited Information Estimators
Estimators such as two- or three-stage least squares that estimate parameters from equations independently of other equations in the model.
- Link functions
In generalized linear models, link functions transform non-linear models into linear models through some specific transformation, for example, a logit transformation.
- Measurement model
The submodel defining the relationships between latent variables and their observed indicators.
- Misspecification
An improper specification of a model such that it does not mimic the population model.
- Mixed-effects models
Models with both fixed and random effects parameters, where the former are standard coefficients for associations and the latter are estimates of variance components.
- Multilevel models
See mixed-effects models
- Observed variable
Variables that are measured.
- Overidentified model
A model is overidentified if at least one model parameter may be written as more than one function of observed variances and covariances.
- Path / Pathway
A pathway in a path model represent an association between a predictor and an outcome variable where the hypothesized predictor variable is at the beginning of the path and the hypothesized outcome variable at the end of the path.
- Path Model / Path Analysis
A path model is used to describe the directed dependencies among a set of variables.
- Random effects
Estimates of variance components.
- Reliability
is the consistency of a set of measurements or of a measuring instrument. Reliability is inversely related to random error.
- Total effect
The effect of one variable on another through all possible pathways, including both direct and any indirect effects.
- Underidentified model
A model is underidentified if at least one model parameter cannot be written as a unique function of observed variances and covariances.
Footnotes
We have no financial disclosures to make. Parts of this paper were presented at the 2012 APHA meetings:
Christ, S.L., et al. (October, 2011). “Holistic Models of Health: A Structural Equation Modeling Framework.” Oral presented at the American Public Health Association 139th Annual Meeting and Exposition. Washington, D.C.
Contributor Information
Sharon L. Christ, Purdue University, Human Development and Family Studies & Statistics
David J. Lee, University of Miami School of Medicine, Epidemiology & Public Health
Byron L. Lam, University of Miami School of Medicine, Bascom Palmer Eye Institute
Zheng D. Diane, University of Miami School of Medicine, Epidemiology & Public Health
References
- 1.Bollen KA. Structural equations with latent variables. New York ; Chichester: Wiley; 1989. [Google Scholar]
- 2.Duncan OD, Goldberger AS Social Science Research Council (U.S.), University of Wisconsin. Social Systems Research Institute. Structural equation models in the social sciences. New York: Seminar Press; 1973. [Google Scholar]
- 3.Browne MW. Asymptotically distribution-free methods for the analysis of the covariance structures. British Journal of Mathematical and Statistical Psychology. 1984;37:62–83. doi: 10.1111/j.2044-8317.1984.tb00789.x. [DOI] [PubMed] [Google Scholar]
- 4.Bollen KA, Stine RA. Bootstrapping goodness-of-fit measures in structural equation models. Sociological Methods & Research. 1992;21:205–229. [Google Scholar]
- 5.Muthén BO. A general structural equation model with dichotomous, ordered categorical and continuous latent indicators. Psychometrika. 1984;49:115–132. [Google Scholar]
- 6.Rabe-Hesketh S, Skrondal A, Pickles A. Generalized multilevel structural equation modeling. Psychometrika. 2004;69:167–190. [Google Scholar]
- 7.Skrondal A, Rabe-Hesketh S. Generalized latent variable modeling : multilevel, longitudinal, and structural equation models. Boca Raton ; London: Chapman & Hall/CRC; 2004. [Google Scholar]
- 8.Hansen MH, Hurwitz WN, Madow WG. Sampling Survey Methods and Theory. New York: Wiley; 1953. [Google Scholar]
- 9.Binder D. On the variance of asymptotically normal estimators from complex surveys. International Statistical Review. 1983;51:279–292. [Google Scholar]
- 10.Goldstein H. Multilevel Statistical Models. 3. London: Arnold; 2003. [Google Scholar]
- 11.Raudenbush SW, Bryk AS. Hierarchical Linear Models. Applications and Data Analysis Methods. 2. Thousand Oaks: Sage; 2002. [Google Scholar]
- 12.Bauer DJ. Estimating multilevel linear models as structural equation models. Journal of Educational and Behavioral Statistics. 2003;28:135–167. [Google Scholar]
- 13.Bollen KA, Curran PJ. Latent curve models : a structural equation perspective. Hoboken, N.J: Wiley-Interscience; 2006. [Google Scholar]
- 14.Hoyle RH. Structural equation modeling : concepts, issues, and applications. Thousand Oaks, Calif ; London: Sage; 1995. [Google Scholar]
- 15.Kaplan D. Structural Equation Modeling: Foundations and Extensions. 2. Vol. 10. SAGE; 2008. [Google Scholar]
- 16.Kline RB. Principles and Practice of Structural Equation Modeling. 3. The Guilford Press; 2010. [Google Scholar]
- 17.Raykov T, Marcoulides GA. A first course in structural equation modeling. 2. Lawrence Erlbaum Associates, Inc. Publishers; 2006. [Google Scholar]
- 18.Jöreskog KG. A general approach to confirmatory maximum likelihood factor analysis. Psychometrika. 1969;34:183–202. [Google Scholar]
- 19.Spearman C. General intelligence, Objectively determined and measured. The American Journal of Psychology. 1904a;15:201–292. [Google Scholar]
- 20.Blalock HM. Making causal inferences for unmeasured variables from correlations among indicators. American Journal of Sociology. 1963;69:53–62. [Google Scholar]
- 21.McCutcheon AL. Latent class analysis. Newbury Park ; London: Sage Publications; 1987. [Google Scholar]
- 22.Rigdon EE. Demonstrating the effects of unmodeled random measurement error. Structural Equation Modeling. 1994;1:375–380. [Google Scholar]
- 23.Spearman C. The proof and measurement of association between two things. American Journal of Psychology. 1904b;15:72–101. [PubMed] [Google Scholar]
- 24.Bollen KA. Indicator methodology. Elsevier Science Ltd; 2001. [Google Scholar]
- 25.Mayer MJ, Dougherty RF, Hu L. A covariance structure analysis of flicker sensitivity. Vision Research. 1995;35:1575–1583. doi: 10.1016/0042-6989(94)00252-h. [DOI] [PubMed] [Google Scholar]
- 26.Lamoureux EL, Pallant JF, Pesudovs K, Rees G, Hassell JB, Keeffe JE. The impact of vision impairment questionnaire: An assessment of its domain structure using confirmatory factor analysis and rasch Analysis. Investigative Ophthalmology & Visual Science. 2007;48:5. doi: 10.1167/iovs.06-0361. [DOI] [PubMed] [Google Scholar]
- 27.Marella M, Pesudovs K, Keeffe JE, O’Connor PM, Rees G, Lamoureux EL. The psychometric validity of the NEI VFQ-25 for use in a low-vision population. Investigative Ophthalmology & Visual Science. 2010;51:2878–2884. doi: 10.1167/iovs.09-4494. [DOI] [PubMed] [Google Scholar]
- 28.Misajon R, Hawthorne G, Richardson J, et al. Vision and quality of life: The development of a utility measure. Investigative Ophthalmology & Visual Science. 2005;46:4007–4015. doi: 10.1167/iovs.04-1389. [DOI] [PubMed] [Google Scholar]
- 29.Goldberger AS. Structural equation methods in the social sciences. Econometrica. 1972;40:979–1001. [Google Scholar]
- 30.Wright S. Correlation and Causation. Journal of Agricultural Research. 1921;20:557–585. [Google Scholar]
- 31.Wright S. The method of path corfficients. Annals of Mathematical Statistics. 1934;5(3):161–215. [Google Scholar]
- 32.Wright S. Path coefficients and path regression: Alternative or Complementary Concepts? Biometrics. 1960;16:189–202. [Google Scholar]
- 33.Alwin DF, Hauser RM. The decomposition of effects in path analysis. American Sociological Review. 1975;40:37–47. [Google Scholar]
- 34.Bollen KA. Total, direct, and indirect effects in structural equation models. Washington, DC: American Sociological Association; 1987. [Google Scholar]
- 35.Brown RL. Assessing specific mediational effects in complex theoretical models. Structural Equation Modeling. 1997;4:142–156. [Google Scholar]
- 36.MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets VA. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mangione CM, Lee PP, Gutierrez PR, Spritzer K, Berry S, Hays RD. Development of the 25-item National Eye Institute Visual Function Questionnaire (VFQ-25) Archives of Ophthalmology. 2001 Jul;119(7):1050–1058. doi: 10.1001/archopht.119.7.1050. [DOI] [PubMed] [Google Scholar]
- 38.Balestra P, Varadharajan-Krishnakumar J. Full Information estimations of a system of simultaneous equations with error component structure. Econometric Theory. 1987;3:223–246. [Google Scholar]
- 39.Greene WH. Econometric Analysis. 5. Prentice Hall; 2002. [Google Scholar]
- 40.MacKinnon DP, Fairchild AJ, Fritz MS. Mediation analysis. Annual Review of Psychology. 2007;58:593–614. doi: 10.1146/annurev.psych.58.110405.085542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Aiken LS, West SG. Multiple Regression : Testing and Interpreting Interactions. Thousand Oaks, CA: Sage; 1991. [Google Scholar]
- 42.Preacher KJ, Rucker DD, Hayes AF. Addressing Moderated Mediation Hypotheses: Theory, Methods, and Prescriptions. Multivariate Behavioral Research. 2007;42:185–227. doi: 10.1080/00273170701341316. [DOI] [PubMed] [Google Scholar]
- 43.Bollen KA, Paxton PM. Interactions of latent variables in structural equation models. Structural Equation Modeling. 1998;5:267–293. [Google Scholar]
- 44.Schumacker RE, Marcoulides GA. Interaction and Non-linear Effects in Structural Equation Modeling. Erlbaum; 1998. [Google Scholar]
- 45.Davidov E, Breitscheidel L, Clouth J, Reips M, Happich M. Diabetic retinopathy and health-related quality of life. Arch Clin Exp Ophthalmol. 2009 Feb;247:267–272. doi: 10.1007/s00417-008-0960-y. [DOI] [PubMed] [Google Scholar]
- 46.Tan AG, Mitchell P, Burlutsky G, et al. Retinal vessel caliber and the long-term incidence of age-related cataract: the Blue Mountains Eye Study. Ophthalmology. 2008 Oct;115(1):1693–1698. doi: 10.1016/j.ophtha.2008.04.005. [DOI] [PubMed] [Google Scholar]
- 47.Scialfa CT, Kline DW, Wood PK. Structural modeling of contrast sensitivity in adulthood. J Opt Soc Am A. 2002 Jan;19(1):158–165. doi: 10.1364/josaa.19.000158. [DOI] [PubMed] [Google Scholar]
- 48.Pearl J. Causal inference in statistics: An overview. Statistical Surveys. 2009;3:96–146. [Google Scholar]
- 49.Pearl J. The causal foundations of structural equation modeling. In: Hoyle RH, editor. Handbook of Structural Equation Modeling. New York, NY: Guilford Press; 2012. pp. 68–91. [Google Scholar]
- 50.Finkel S. Causal Analysis with Panel Data. London: Sage; 1995. [Google Scholar]
- 51.Arbuckle JL. Full information estimation in the presence of incomplete data. Mahwah, NJ: Lawrence Erlbaum Associates; 1996. [Google Scholar]
- 52.Little RJA, Rubin DB. Statistical Analysis with Missing Data. New York: Wiley & Sons; 1987. [Google Scholar]
- 53.Schafer JL. Analysis of Incomplete Multivariate Data. London: Chapman & Hall; 1997. [Google Scholar]
- 54.Bollen KA. An alternative two stage least squares (2SLS) estimator for latent variable models. Psychometrika. 1996;61:109–121. [Google Scholar]
- 55.Bollen KA, Kirby JB, Curran PJ, Paxton PM, Chen F. Latent variable models under misspecification: Two stage least squares (2SLS) and maximum likelihood (ML) estimators. Sociological Methods and Research. 2007;36:46–86. [Google Scholar]
- 56.Bentler PM, Bonett DG. Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin. 1980;88:588–606. [Google Scholar]
- 57.Bentler PM. Comparative fit indexes in structural models. Psychological Bulletin. 1990 Mar;107(2):238–246. doi: 10.1037/0033-2909.107.2.238. [DOI] [PubMed] [Google Scholar]
- 58.Bollen KA, Long JS. Testing Structural Equation Models. Newbury Park, CA: Sage; 1993. [Google Scholar]
- 59.Marsh HW, Balla JW, Hau K. An evaluation of incremental fit indices: A clarification of mathematical and empirical properties. Mahwah, NJ: Erlbaum; 1996. [Google Scholar]
- 60.Satorra A, Bentler PM. Corrections to test statistics and standard errors in covariance structure analysis. Newbury Park: Sage; 1994. [Google Scholar]
- 61.Skrondal A, Rabe-Hesketh S. Structural equation modeling: Categorical variables. Wiley; 2005. [Google Scholar]
- 62.McCullagh P, Nelder JA. Generalized Linear Models. 2. London: Chapman & Hall; 1989. [Google Scholar]
- 63.Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19:716–723. [Google Scholar]
- 64.Schwarz GE. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- 65.Rabe-Hesketh S, Skrondal A, Pickles A. Reliable estimation of generalized linear mixed models using adaptive quadrature. The Stata Journal. 2002;2:1–21. [Google Scholar]
- 66.Rabe-Hesketh S, Skrondal A, Pickles A. Maximum likelihood estimation of limited and discrete dependent variable models with nested random effects. Journal of Econometrics. 2005;128:301–323. [Google Scholar]
- 67.Huang B, Sivaganesan S, Succop P, Goodman E. Statistical assessment of meditational effects for logistic mediation models. Statistics in Medicine. 2004;23:2713–2728. doi: 10.1002/sim.1847. [DOI] [PubMed] [Google Scholar]
- 68.Li Y, Schneider JA, Bennett DA. Estimation of the mediation effect with a binary mediator. Statistics in Medicine. 2007 Aug 15;26(18):3398–3414. doi: 10.1002/sim.2730. [DOI] [PubMed] [Google Scholar]
- 69.Christ SL, Lee DJ, Lam BL, Zheng DD, Arheart KL. Assessment of the effect of visual impairment on mortality through multiple health pathways. Investigative Ophthalmology & Visual Science. 2008 Aug;49:3318–3323. doi: 10.1167/iovs.08-1676. [DOI] [PubMed] [Google Scholar]
- 70.Karpa MJ, Mitchell P, Beath K, Rochtchina E, Cumming RG, Wang JJ. Direct and indirect effects of visual impairment on mortality risk in older persons: The Blue Mountain Eye Study. Archives of Ophthalmology. 2009 Oct;127(10):1347–1353. doi: 10.1001/archophthalmol.2009.240. [DOI] [PubMed] [Google Scholar]
- 71.Lam BL, Christ SL, Lee DJ, Zheng DD, Arheart KL. Reported visual impairment and risk of suicide: The 1986–1996 National Health Interview Survey. Archives of Ophthalmology. 2008 Jul;126(7):975–980. doi: 10.1001/archopht.126.7.975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Bollen KA, Bauer DJ, Christ SL, Edwards MC. An Overview of Structural Equation Models and Recent Extensions. Wiley; 2010. [Google Scholar]
- 73.Lam BL, Christ SL, Zheng DD, et al. et al. Longitudinal relationships among visual acuity and tasks of everyday life: The Salisbury Eye Evaluation Study. Investigative Ophthalmology Visual Science. 2013 doi: 10.1167/iovs.12-10542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Neale CM, Cardon LR North Atlantic Treaty Organization. Scientific Affairs Division. Methodology for Genetic Studies of Twins and Families. Boston/London: Kluwer Academic Publishers; 1992. [Google Scholar]
- 75.Plomin R. Behavioral genetics. 4. New York: Worth publishers; 2001. [Google Scholar]
- 76.Purcell S. Variance components models for gene-environment interaction in twin analysis. Twin Research. 2002 Dec;5:554–571. doi: 10.1375/136905202762342026. [DOI] [PubMed] [Google Scholar]
- 77.Toh T, Liew SHM, MacKinnon JR, et al. Central corneal thickness is highly heritable: The twin eye studies. Investigative Ophthalmology & Visual Sience. 2005 Oct;46:3718–3722. doi: 10.1167/iovs.04-1497. [DOI] [PubMed] [Google Scholar]
- 78.Zhu G, Hewitt AW, Ruddle JB, et al. Genetic dissection of myopia: evidence for linkage of ocular axial length to chromosome 5q. Ophthalmology. 2008 Jun;115(6):1053–1057. e1052. doi: 10.1016/j.ophtha.2007.08.013. [DOI] [PubMed] [Google Scholar]
- 79.Taarnhøj NCBB, Larsen M, Sander B, et al. Heritability of retinal vessel diameters and blood pressure: A twin study. Investigative Ophthalmology & Visual Science. 2006;47:3539–3544. doi: 10.1167/iovs.05-1372. [DOI] [PubMed] [Google Scholar]
- 80.Lopes MC, Andrew T, Carbonaro F, Spector TD, Hammond CJ. Estimating heritability and shared environmental effects for refractive error in twin and family studies. Investigative Ophthalmology & Visual Science. 2009;50:126–131. doi: 10.1167/iovs.08-2385. [DOI] [PubMed] [Google Scholar]
- 81.Healey P, Mitchell P, Gilbert CE, et al. The inheritance of peripapillary atrophy. Investigative Ophthalmology & Visual Science. 2007;48:5. doi: 10.1167/iovs.06-0714. [DOI] [PubMed] [Google Scholar]
- 82.Dirani M, Shekar SN, Baird PN. The Role of educational attainment in refraction: The genes in myopia (GEM) twin study. Investigative Ophthalmology & Visual Science. 2008 Feb;49(2):534–538. doi: 10.1167/iovs.07-1123. [DOI] [PubMed] [Google Scholar]
- 83.Sanfilippo PG, Hewitt AW, Hammond CJ, Mackey DA. The heritability of ocular traits. Survey of Ophthalmology. 2010 Nov-Dec;55(6):561–583. doi: 10.1016/j.survophthal.2010.07.003. [DOI] [PubMed] [Google Scholar]
- 84.Diggle PJ, Heagerty PJ, Liang K-Y, Zeger SL. Analysis of Longitudinal Data. 2. Oxford: Oxford University Press; 2002. [Google Scholar]
- 85.Muthen BO, Satorra A. Complex sample data in structural equation modeling. Sociological methodology. 1995;25:267–316. [Google Scholar]
- 86.Skinner CJ. In: Domain Means, Regression and Multivariate Analysis. Skinner CJ, Holt D, Smith TMF, editors. New York: Wiley; 1989. [Google Scholar]
- 87.Hansen MH, Hurwitz WN, Madow WG. Sampling Survey Methods and Theory. New York: Wiley; 1953. [Google Scholar]
- 88.Zeger SL. The analysis of discrete longitudinal data: Commentary. Statistics in Medicine. 1988;7:161–168. [Google Scholar]
- 89.McDonald BW. Estimating logistic regression parameters for bivariate binary data. Journal of the Royal Statistics Society Series. 1993;B(55):391–397. [Google Scholar]
- 90.Stata Statistical Software [computer program] College Station, TX: StataCorp LP; 2009. [Google Scholar]
- 91.AMOS [computer software] [computer program] Crawfordville, FL: SPSS, Inc; 1983–2009. [Google Scholar]
- 92.EQS [computer software] [computer program] Multivariate Software, Inc; 1994–2004. [Google Scholar]
- 93.LISREL [computer software] [computer program] Lincolnwood, IL: Scientific Software International, Inc; 2006. [Google Scholar]
- 94.Mplus [computer software] [computer program] Los Angeles, CA: Muthén & Muthén; 1998–2007. [Google Scholar]