Modified ideal observer model (MIOM) for high‐contrast and high‐spatial resolution CT imaging tasks

Abstract

Purpose

Although a variety of mathematical observer models have been developed to predict human observer performance for low contrast lesion detection tasks, their predictive power for high contrast and high spatial resolution discrimination imaging tasks, including those in CT bone imaging, could be limited. The purpose of this work was to develop a modified observer model that has improved correlation with human observer performance for these tasks.

Methods

The proposed observer model, referred to as the modified ideal observer model (MIOM), uses a weight function to penalize components in the task function that have less contribution to the actual human observer performance for high contrast and high spatial resolution discrimination tasks. To validate MIOM, both human observer and observer model studies were performed, each using exactly the same CT imaging task [discrimination of a connected component in a high contrast (1000 HU) high spatial resolution bone fracture model (0.3 mm)] and experimental CT image data. For the human observer studies, three physicist observers rated the connectivity of the fracture model using a five‐point Likert scale; for the observer model studies, a total of five observer models, including both conventional models and the proposed MIOM, were used to calculate the discrimination capability of the CT images in resolving the connected component. Images used in the studies encompassed nine different reconstruction kernels. Correlation between human and observer model performance for these kernels were quantified using the Spearman rank correlation coefficient (ρ). After the validation study, an example application of MIOM was presented, in which the observer model was used to select the optimal reconstruction kernel for a High‐Resolution (Hi‐Res, GE Healthcare) CT scan technique.

Results

The performance of the proposed MIOM correlated well with that of the human observers with a Spearman rank correlation coefficient ρ of 0.88 (P = 0.003). In comparison, the value of ρ was 0.05 (P = 0.904) for the ideal observer, 0.05 (P = 0.904) for the non‐prewhitening observer, −0.18 (P = 0.634) for the non‐prewhitening observer with eye filter and internal noise, and 0.30 (P = 0.427) for the prewhitening observer with eye filter and internal noise. Using the validated MIOM, the optimal reconstruction kernel for the Hi‐Res mode to perform high spatial resolution and high contrast discrimination imaging tasks was determined to be the HD Ultra kernel at the center of the scan field of view (SFOV), or the Lung kernel at the peripheral region of the SFOV. This result was consistent with visual observations of nasal CT images of an in vivo canine subject.

Conclusion

Compared with other observer models, the proposed modified ideal observer model provides significantly improved correlation with human observers for high contrast and high spatial resolution CT imaging tasks.

1. Introduction

Hardware and software advances in modern multidetector detector CT (MDCT) provide new means to improve spatial resolution for MDCT systems. The improvement in spatial resolution may benefit many clinical applications that demand high‐spatial resolution, such as the diagnosis of bone fractures or middle and inner ear disease using CT. The High‐Resolution (Hi‐Res) scan mode (GE Healthcare, Waukesha, WI, USA) is a technique to improve spatial resolution in MDCT. It uses in‐plane focal spot deflection, an increased angular sampling rate, and dedicated Hi‐Definition (HD) reconstruction kernels to improve the in‐plane spatial resolution of CT.^{1, 2, 3, 4} However, improved spatial resolution does not necessarily mean improved diagnostic performance, since the ultimate diagnostic performance is jointly determined by spatial resolution, noise power, imaging tasks, and the performance of the image reader. Therefore, to optimally use these new technologies in clinical practice to accomplish a clinical diagnostic task, one must comprehensively study the potential tradeoffs between spatial resolution and noise, as well as their joint impact on the overall diagnostic performance for a specific imaging task. Ultimately, it is the human observer who reads, and infers, diagnostic information from a given image for a given task. Therefore, it would be ideal to evaluate the performance of a new technology for a given task by human observers. However, this is usually a time‐ and resource‐consuming process and thus is not easy to implement for every clinical tasks. To mathematically model the human perception process, mathematical observer models were developed to incorporate the quantitative imaging system characteristics into a single figure of merit (FOM) to predict the performance of human observers. When these observer models are properly validated, they can be used to optimize the needed imaging technologies and the associated scanning parameters for a given clinical tasks. The main purpose of this paper was to develop and validate such an observer model for high‐contrast and high‐spatial resolution discrimination task.

To be more specific, an observer model is a mathematical algorithm that is capable of making decisions about specific visual tasks given an image and a priori statistical information.^{5, 6, 7, 8, 9} Performance of the observer model in decision making can be quantitated by a FOM known as the detectability index d ^′, which can be analytically calculated from the spatial resolution and noise properties of the imaging system as well as the imaging task itself. Compared with other image quality FOMs such as the modulation transfer function (MTF), the observer model‐derived d ^′ has the advantage of being task‐dependent in addition to taking both spatial resolution and noise into account. Therefore, observer models have been widely used in the development and assessment of many imaging modalities, including mammography,^{10, 11, 12} dual‐energy digital radiography,^{13, 14} digital tomosynthesis,^{15, 16, 17, 18, 19, 20} CT,^{21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34} cone beam CT^{17, 18, 31, 35, 36, 37, 38} and differential‐phase contrast CT.^{39, 40}

A variety of observer models have previously been developed, and they differ from each other in the number and nature of hypotheses about the human visual perception that are integrated into the model to obtain a quantitative response variable. Although these observer models have been well validated for low‐contrast imaging tasks, a direct application of these observer models to high‐contrast and high‐spatial resolution discrimination imaging tasks may lead to poor correlation with human observer performance. Therefore, a modified observer model must be developed and validated for high‐contrast and high‐spatial resolution discrimination tasks.

To facilitate reading, the paper is laid out as follows: First, to demonstrate the failure of conventional observer models for the high‐contrast, high‐spatial resolution discrimination tasks, human observer studies were performed in this work, and the results were compared with d′ generated by several popular observer models. Next, a modified observer model with significantly improved correlation with human observers for the high‐contrast and high‐spatial resolution task was presented and validated. Finally, the observer model was used to choose the optimal reconstruction kernel for the Hi‐Res scan mode as a demonstration of its potential application.

2. Methods and materials

2.A. High‐contrast and high‐spatial resolution imaging task

The high‐contrast and high‐spatial resolution CT imaging task used in this work is shown in Fig. 1. The task is to discriminate two hypotheses: the null hypothesis h ₀ is a straight 0.3‐mm‐wide gap in a range‐shaped object (inner and outer diameters are 10 and 17 mm, respectively); for the alternative hypothesis h ₁, a 0.3 × 0.3 mm² component connects a portion of the gap. For both hypotheses, the contrast between the ring and the background is 1000 HU. In the spatial domain, this signal‐known‐exactly, background‐known exactly, and binary discrimination task can be written as

$$t(\mathbf{x})=h_1(\mathbf{x})-h_0(\mathbf{x}),$$ (1)

and the corresponding form in the spatial frequency domain is given by

$$T(\mathbf{k})=\text{FT}[h_1(\mathbf{x})-h_0(\mathbf{x})].$$ (2)

This high‐spatial resolution imaging task was used in both the observer model and human observer studies, so that results of these studies could be directly compared.

Figure 1.

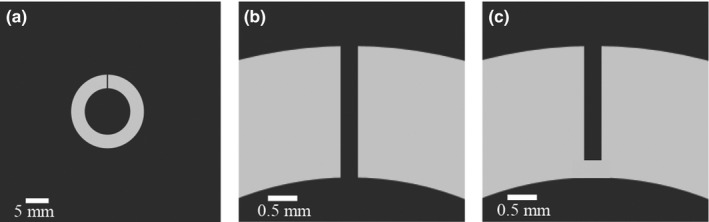
High‐contrast and high‐spatial resolution imaging task used in this work. (a) Null hypothesis (h ₀). (b) Close‐up of the completely disconnected gap in the null hypothesis. (c) Close‐up at the connected region across the gap in the alternative hypothesis (h ₁).

2.B. Human observer studies

2.B.1. Image preparation

To match the experimental conditions between the human observer and observer model studies while having precise control and fine‐tuning of the imaging task, the following image preparation approach was used: Both types of observer studies used the same set of experimental noise‐only CT images. For the human observer studies, the experimental noise‐only images were fused to one of the two hypotheses shown in Fig. 1. For the observer model studies, the experimental noise‐only images were used to measure the noise power spectrum (NPS).

To acquire the noise‐only CT images, a Catphan 600 phantom (Module CTP591, The Phantom Laboratory, Greenwich, NY, USA) was repeatedly scanned using a 64‐slice diagnostic MDCT system (Discovery CT750 HD, GE Healthcare, Waukesha, WI, USA) with the following scan parameters: 120 kV, 400 mAs, axial mode, small focal spot (1.0 × 0.7 mm), large body bowtie filter, and 20 mm detector collimation width. Both conventional and Hi‐Res scan modes were used; for each scan mode, 80 repeated scans were performed. Images acquired using the conventional scan mode were reconstructed using four different kernels, while images acquired using the Hi‐Res mode were reconstructed using five high‐definition (HD) kernels (Table 1). The reconstructed images have a slice thickness of 5 mm, pixel size of 0.1 mm, and a matrix size of 512 × 512. For each scan mode and reconstruction kernel, the ensemble average across the 80 repeated scans was calculated, which was then used to detrend the background and obtain noise‐only images.

Table 1.

Scan modes and reconstruction kernels included in both the human observer and observer model studies

Conventional mode	Hi‐Res mode
Standard	HD Standard
Lung	HD Lung
Bone plus	HD Bone Plus
Edge	HD Ultra
	HD Edge

To prepare images for the reader studies, the imaging task and experimental noise‐only background were fused in the following approach: First, each of the two hypotheses in Fig. 1 was filtered by convolving with a point spread function (PSF), which was experimentally measured using the same scan technique and reconstruction kernel as those used to generate the noise‐only background.⁴¹ This process can be described by

$$h_j^{\prime }\left(\mathbf{x}\right)=h_j\left(\mathbf{x}\right)\otimes \text{PSF}(\mathbf{x}),$$ (3)

where ⊗ denotes the 2D convolution operator, j took values of 0 and 1 for the null and alternative hypothesis, respectively. Next, the filtered hypothesis was added to each (i ^th) of the 80 independent realizations of the noise background, namely

$$g^i\left(\mathbf{x}\right)=h_j^{\prime }+n^i(\mathbf{x}),$$ (4)

where i ∈ [1,80]. This image fusion process was repeated for each of the nine scan model‐kernel combinations listed in Table 1, producing a total of 9 × 80 = 720 images for the human reader studies. Figure 2 shows some examples of these images.

Figure 2.

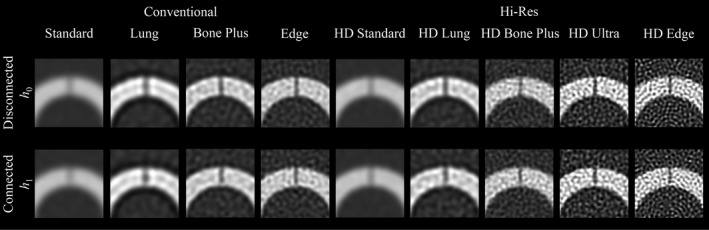
Close‐up images used in the human observer study. One representative image was selected for each of the nine scan mode‐reconstruction kernel combinations and the two hypotheses. The display window and level are 2000 and 300 HU, respectively.

In order to confirm the hybrid images accurately represented true experimental CT images, we compared hybrid and experimental images of a bar pattern in the CTP528 Module of the Catphan 600 phantom, generated with different reconstruction kernels under the conventional scan mode. As illustrated by Fig. 3, for a given reconstruction kernel, the hybrid image closely resembled the true experimental CT image.

Figure 3.

Validation of the hybrid image generation method. The top row shows images of a bar pattern (6 lp/cm) generated by the hybrid method (simulated signal + experimental noise background). The bottom row shows experimental images of the bar pattern. The image display window and level are 2000 and 300 HU, respectively.

2.B.2. Image reading and scoring

Three medical physicists with 7–14 yr of experience in clinical CT research served as human observers in the study. The reading was conducted in a darkened room using a monitor calibrated for clinical diagnosis. The image display window and level were 2000 and 300 HU, respectively. The observers were instructed to keep a viewing distance of approximately 60 cm from the monitor. Each observer first underwent a training session, in which images and the true state of the hypothesis (either 0 or 1) were presented to the observer, so that the observer had a basic idea of how the image looks like for each hypothesis, each scan mode, and each reconstruction kernel. A total of 18 images (two for each scan mode‐reconstruction kernel combination) were used for the training.

After the training session, each observer read a total of 360 images (40 for each scan mode‐reconstruction kernel combination) fetched from the pool of 720 images. To reduce observer bias, the order of the images was randomized, and a black screen was displayed between two consecutive images. The observer scored each image using the 5‐point Likert scale listed in Table 2. The recorded scores were analyzed using a multireader and multicase receiver operating characteristic software (OR‐DBM MRMC 2.5, The University of Iowa).^{42, 43, 44, 45, 46} The interobserver consistency was estimated with the Cohen's kappa coefficient.

Table 2.

5‐point image rating scale used in the human observer study

Score	Criteria
1	The gap is definitely disconnected
2	The gap is probably disconnected
3	Unclear if the gap is disconnected or connected
4	The gap is probably connected
5	The gap is definitely connected

2.C. Observer model studies

2.C.1. Conventional observer models

To demonstrate that conventional observer models have poor correlation with human observers for the high‐contrast and high‐spatial resolution imaging task, a total of five conventional observer models were used to estimate the observer performance for the task.

We first evaluated the ideal observer model, which uses the Bayes theorem to combine all available a priori information with the image data to obtain probabilistic estimates of the correctness of a given hypothesis (signal present or absent).^{6, 7, 47} Its performance can be quantitated, without being dependent on the observer's decision criterion, using the ideal observer detectability index $d_{\mathrm{ideal}}^{\prime }$. The square of $d_{\mathrm{ideal}}^{\prime }$ can be calculated in the Fourier domain as follows:⁴⁷

$$\begin{array}{cc}\hfill {\left(d_{\mathrm{ideal}}^{\prime }\right)}^2& =\int \int \frac{{\left|T(\mathbf{k})\right|}^2{\text{MTF}}^2(\mathbf{k})}{N\left(\mathbf{k}\right)}{\mathrm{d}}^2\mathbf{k}\hfill \\ & =\int \int \frac{{\left|\text{FT}[t(\mathbf{x})\otimes \text{PSF}(\mathbf{x})]\right|}^2}{N\left(\mathbf{k}\right)}{\mathrm{d}}^2\mathbf{k}.\hfill \end{array}$$ (5)

In Eq. (5), k and x are frequency and spatial vectors, respectively, N denote the NPS and was calculated from the ensemble of experimental noise‐only images. A larger $d_{\mathrm{ideal}}^{\prime }$ value indicates better observer performance. In other words, one should expect a strong and positive correlation between $d_{\mathrm{ideal}}^{\prime }$ and human observer performance metrics (such as AUC) if the observer model can accurately predict human observer behavior.

In addition to the ideal observer, several other popular observer models were also used in this work, including prewhitening observer with eye filter and internal noise (PWEi), nonprewhitening (NPW) observer, and nonprewhitening observer with eye filter and internal noise (NPWEi). The eye filter and internal noise used in PWEi and NPWEi take into account of the nonuniform response of the visual system to different spatial frequencies and the internal fluctuation of the visual system. The parameter c in the eye filter formula, E(f) = f exp(−cf), was selected such that the maximum response of E occurred at 4 cycles/deg^{18, 48} for a viewing distance of 70 cm, c = 3.1. The static internal noise was implemented as white noise given by N _int = 0.02N ₀ L ², where L = 0.70 is the viewing distance in meters, and N ₀ is the amplitude of the white noise‐equivalent NPS of the background, given by $N_0=\int \int N(\mathbf{k}){\mathrm{d}}^2\mathbf{k}/\int \int {\mathrm{d}}^2\mathbf{k}$. The induced internal noise was included by multiplying the NPS by a scaling factor of (1+φ), where φ = 0.3.^{7, 10, 49}

2.C.2. Proposed modified ideal observer model (MIOM)

The ideal observer gives the upper bound of human observer detection performance, as it assumes the human observer can perfectly decorrelate (i.e., prewhiten) the image noise. One of the fundamental assumptions behind the ideal observer is that all the spatial components of the input signal contribute with equal weight to the observer's discrimination performance [Eq. (5)]. While this assumption is valid for low‐contrast signal detection tasks, it may be violated for high‐contrast and high‐spatial resolution discrimination tasks, in which the importance of signal recognition may bias certain spatial components of the signal, for example, high‐contrast edges. Therefore, the following modified ideal observer model (MIOM) was proposed in this work:

$${\left(d_{\mathrm{MIOM}}^{\prime }\right)}^2=\int \int \frac{{\left|\text{FT}[t^{\prime }(\mathbf{x})·w(\mathbf{x})]\right|}^2}{N\left(\mathbf{k}\right)}{\mathrm{d}}^2\mathbf{k}.$$ (6)

The weight function w(x) aims to penalize regions of the signal that are likely to have less contribution to the overall observer performance for high‐contrast and high‐spatial resolution discrimination tasks. The proposal is based on two assumptions about the human vision that were previously introduced:^{50, 51} (a) the spatial integration of image information is often limited to a spatial window; (b) the observer generates a tailored discriminator for the signals in question using available information. Throughout the paper this model is referred to as modified ideal observer model (MIOM).

The weighting function used to calculate $d_{\mathrm{MIOM}}^{\prime }$ is shown in Fig. 4(a); it is defined as the alternative hypothesis itself (h ₁) (defined in next subsection) bounded by a rectangular window with softened edges and centered on the task function. Both the width of the window and the degree of edge blurring are optimized, such that the resulting detectability index is as close as possible to the actual human observer performance. The weight function design followed two objectives: (a) to put reduced or zero weight on pixels far away from the task function, since when an actual human observer performs a recognition task, he/she is likely to primarily focus on a region whose size is scaled according to the actual dimensions of the imaging task; (b) to penalize the signal blurring due to the limited spatial resolution of the imaging system, as illustrated in Figs. 4(b)–4(f). The necessity of using this weighting function was confirmed by the results of the human observer experiments in this work.

Figure 4.

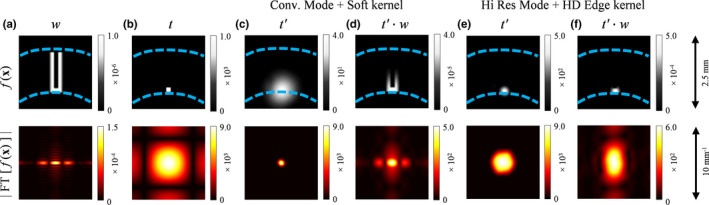
Functions of interest in spatial and frequency domain representations. (a) Weight model used in the proposed MIOM observer. (b) Task function. (c) and (e) show the task function filtered by the PSF, that is, t′, of two different scan modes and reconstruction kernels at the centered position. (d) and (f) show t′ weighted by the function w for two different scan modes and reconstruction kernels at the centered position. The dashed lines in the spatial domain images indicate the position of each function relative to h ₀ and h ₁ (shown in Fig. 1). The units for the spatial domain and frequency domain color bars are HU and HU mm², respectively. [Color figure can be viewed at wileyonlinelibrary.com]

2.D. Quantitation of correlation between human observer and observer model

The correlation between the human observer performance, described by the AUC, and the observer model performance, described by d′, was quantitated using the Spearman rank correlation test, which is a measure of statistical dependence between the ranking of two variables, and it assesses how well the relationship between two variables can be described using a monotonic function, whether their relationship is linear or not.

2.E. Example application of MIOM

After confirming satisfactory correlation between human observer and the proposed MIOM, it was used to select the kernel‐scan mode combination that led to the highest performance for a high‐contrast, high‐spatial resolution CT imaging task. As illustrated by Table 3, the introduction of the Hi‐Res mode to the 750HD MDCT system provides an additional 15 scan mode‐kernel combinations, in addition to the eight kernels provided by previous GE scanner models. Previous studies also demonstrated that the spatial resolution performances of CT systems may also depend on the object position within the scan field of view (SFOV). Optimizing the kernel and scan mode selection for each object position would be time consuming to a human observer. In contrast, the MIOM provides an efficient way to rank the order of kernel‐scan mode combinations for nasal cavity CT imaging. In this work, the ranking was performed for each of the eight object positions shown in Fig. 5. To corroborate ranking provided by the MIOM, an in vivo canine subject (2‐yr‐old 10‐kg male adult beagle) was scanned under an Institutional Animal Care and Use Committee (IACUC)‐approved protocol. Both conventional and Hi‐Res scan modes were used, and other acquisition parameters are listed as follows: tube potential = 80 kV, beam collimation = 20 mm, medium body bowtie filter, axial mode, rotation time = 0.5 s, tube current = 430 mA, and large focal spot. Images were reconstructed with a display field of view of 5 cm, a slice thickness of 0.625 mm, and different reconstruction kernels.

Table 3.

Scan modes and the associated reconstruction kernels provided by the GE Discovery CT750 HD CT system

Conventional mode		Hi‐Res mode
Non‐HD kernels	HD kernels	Non‐HD kernels	HD kernels
Soft		Soft	HD Standard
Standard		Standard	HD Detail
Detail		Detail	HD Lung
Lung		Lung	HD Bone
Chest		Chest	HD Bone Plus
Bone		Bone	HD Ultra
Bone Plus		Bone Plus	HD Edge
Edge		Edge

Figure 5.

The proposed MIOM was used to optimize reconstruction kernel and scan mode selection for eight different off‐centered positions shown in this figure. The ROI used to calculate $d_{\mathrm{MIOM}}^{\prime }$ was indicated by the solid square. [Color figure can be viewed at wileyonlinelibrary.com]

3. Results

3.A. Human observer results

Each observer took approximately 5–10 s per image including both reading and scoring. The measured areas under the ROC curve (AUCs) for individual observer, scan mode, and reconstruction kernels are listed in Table 4. The Cohen's kappa coefficient was found to be κ = 0.22, which indicates “fair” interobserver agreement. The average AUC across the three human observers is plotted in Fig. 6. The error bars indicate standard error. Among the nine scan mode‐reconstruction kernel combinations, the conventional scan mode with the Standard kernel led to the lowest AUC, since it generated the most blurred image as shown in Fig. 2. The AUC was improved by using the combination of the Hi‐Res scan mode and the HD Standard kernel, which improves spatial resolution.⁴¹ Meanwhile, the most aggressive edge‐preserving kernel HD Edge did not generate the highest human observer performance. Instead, its AUC is similar to that of the HD Standard kernel. This is due to the dramatic noise amplification associated with this kernel, despite the fact that it led to the highest MTF.⁴¹ This example shows the importance of taking noise and task‐based overall image quality into account when evaluating the HD kernels, even if they are designed with high‐spatial resolution imaging tasks in mind. Figure 6 also shows that the highest human observer performance was achieved with intermediate kernels such as Bone Plus and HD Lung. These kernels generated higher spatial resolution compared with the Standard (or HD Standard) kernel, and they only led to moderate noise amplification that was still tolerable for the high‐contrast and high‐spatial resolution imaging task (Fig. 2).

Table 4.

Human observer ROC performance for the high‐spatial resolution imaging task. AUC: area under the ROC curve; SE: standard error

Scan mode	Kernel	Observer 1		Observer 2		Observer 3
		AUC	SE	AUC	SE	AUC	SE
Conventional	Standard	0.55	0.03	0.53	0.02	0.69	0.06
Conventional	Lung	0.86	0.05	0.81	0.06	0.90	0.04
Conventional	Bone Plus	0.89	0.05	0.89	0.05	0.92	0.05
Conventional	Edge	0.92	0.04	0.75	0.07	0.72	0.08
Hi‐Res	HD Std	0.81	0.05	0.58	0.06	0.73	0.08
Hi‐Res	HD Lung	0.89	0.06	0.85	0.06	0.92	0.04
Hi‐Res	HD Bone Plus	0.78	0.07	0.69	0.08	0.82	0.07
Hi‐Res	HD Ultra	0.94	0.04	0.75	0.07	0.80	0.07
Hi‐Res	HD Edge	0.69	0.08	0.67	0.07	0.74	0.08

Figure 6.

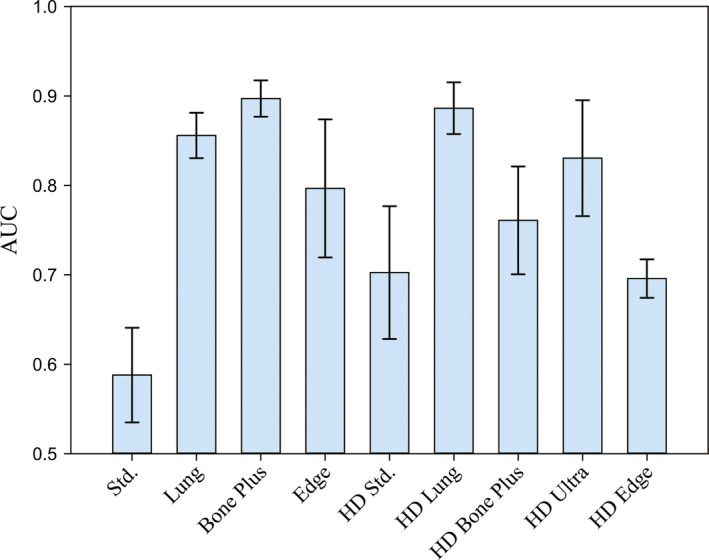
Average human observer AUCs for different reconstruction kernels. [Color figure can be viewed at wileyonlinelibrary.com]

3.B. Correlation between human observers and observer model results

Average AUC values generated by the human observers and the observer models were compared using scatter plots shown in Fig. 7. The ideal observer led to a Spearman's rank correlation coefficient (ρ) of only 0.05 (P = 0.904), and the NPW observer actually generated a weak negative correlation (ρ = −0.18, P = 0.0634). Here, the null hypothesis for the P value is that, the human observer AUC and observer model d′ are not correlated. Correlation coefficients for other conventional observer models are listed in Table 5 and are no greater than 0.30. In comparison, MIOM achieved a much stronger correlation with the human observer (ρ = 0.88, P = 0.003).

Figure 7.

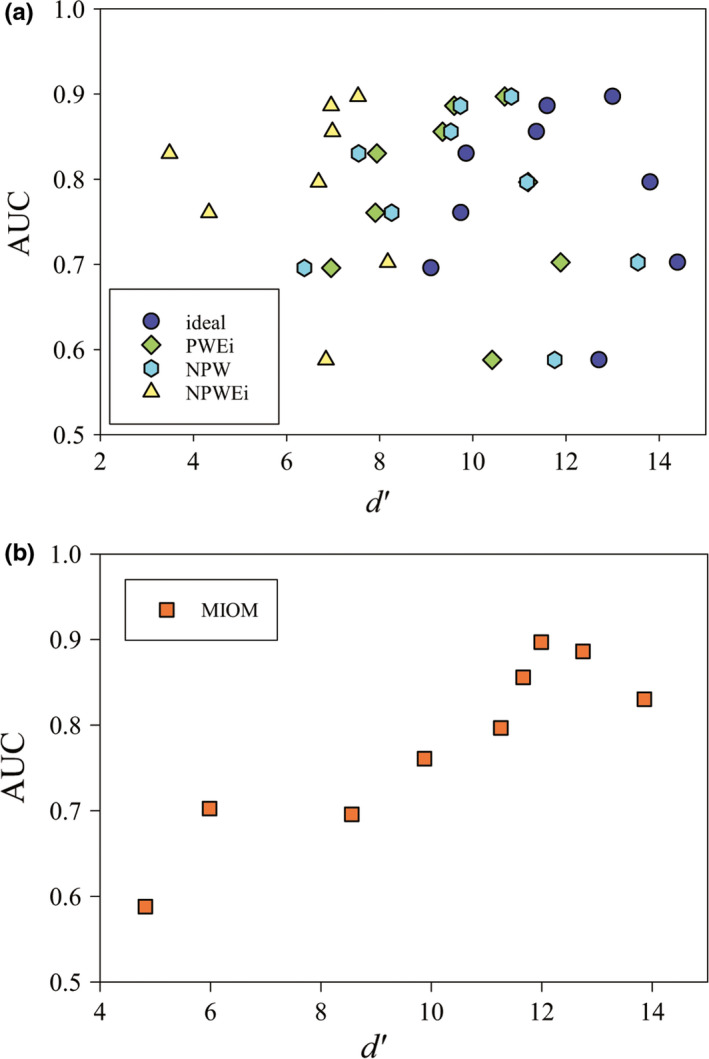
Correlation between human observer and observer models. (a) AUC values paired with d′ for the four conventional observer models. (b) AUC values paired with d′ for the proposed MIOM. [Color figure can be viewed at wileyonlinelibrary.com]

Table 5.

Spearman rank correlation values for different observer models

Observer model	ρ	P
Ideal	0.05	0.904
PWEi	0.05	0.904
NPW	−0.18	0.634
NPWEi	0.30	0.427
MIOM	0.88	0.003

3.C. Example application: optimal kernel selection

Having validated the proposed MIOM observer model, we used it to select optimal scan mode and reconstruction kernel as a function of object positions. Figure 8 provides a map of the measured detectability index ($d_{\mathrm{MIOM}}^{\prime }$) for the imaging task shown in Fig. 1. In general, $d_{\mathrm{MIOM}}^{\prime }$ was very sensitive to the off‐centered position; at severe off‐centered positions, $d_{\mathrm{MIOM}}^{\prime }$ dropped considerably for a given acquisition mode and reconstruction kernel. For the specific imaging task used in this work, the Hi‐Res scan mode combined with the Lung kernel generates the highest $d_{\mathrm{MIOM}}^{\prime }$ values for most off‐centered positions. At the iso‐center, Hi‐Res mode with the HD Ultra kernel generates the highest $d_{\mathrm{MIOM}}^{\prime }$ value, which is consistent with the human observer results. The intermediate edge‐preserving kernels such as Bone Plus and HD Bone Plus showed good balance between spatial resolution and noise. Although the Hi‐Res scan mode with the HD Edge kernel led to the highest spatial resolution in all object positions,⁴¹ the large increase of image noise generated by this scan mode‐reconstruction kernel combination strongly degraded its overall performance for the high‐contrast and high‐spatial resolution imaging task.

Figure 8.

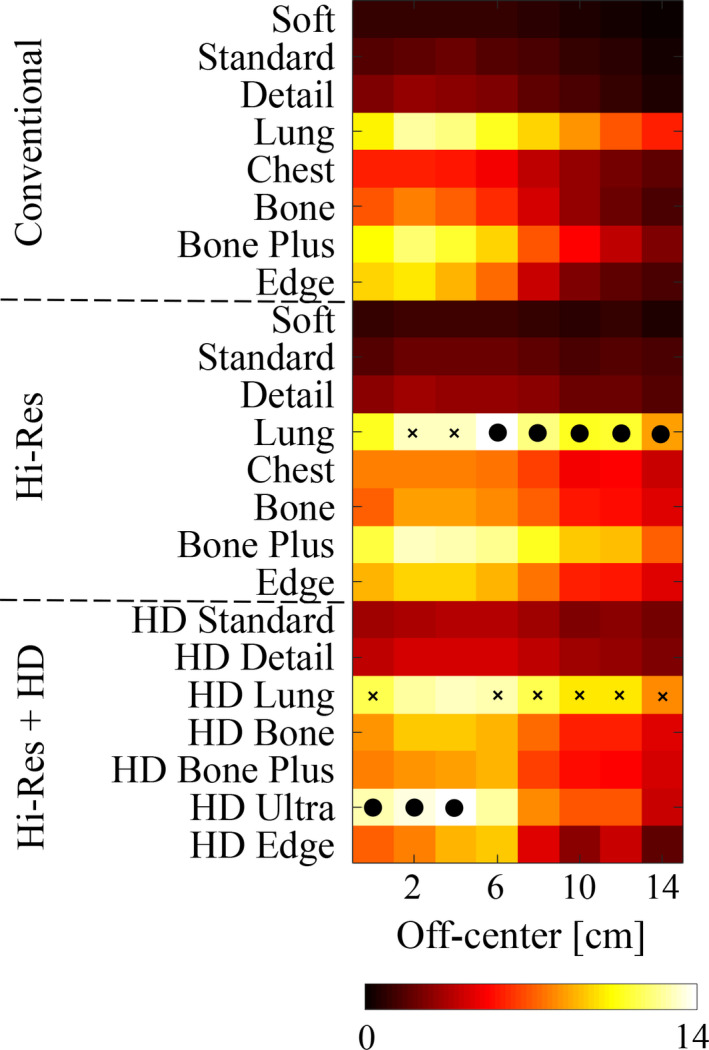
Summary of the detectability index ($d_{\mathrm{MIOM}}^{\prime }$) of the high‐spatial resolution imaging task shown in Fig. 1 for all the scan modes, reconstruction kernels, and object positions. For a given object position, the particular scan mode‐reconstruction kernel combination that achieved the highest detectability was marked with a black dot. The second highest scan mode‐reconstruction kernel combination is also indicated, with a cross. The given color scale corresponds to values of $d_{\mathrm{MIOM}}^{\prime }$. [Color figure can be viewed at wileyonlinelibrary.com]

Images of the nasal cavity of the canine subject generated using the two scan modes (conventional and Hi‐Res) and different reconstruction kernels are shown in Fig. 9. Small nasal ducts (or meatuses) were resolved with different levels of detail in these images. The Hi‐Res scan mode with the HD Ultra kernel allowed one to clearly identify the convoluted cartilage structure of the nasal conchae. Hi‐Res mode with HD Bone Plus kernel also allowed a clear identification of such structures, although with less sharpness. Compared to the Hi‐Res mode with HD kernels, Hi‐Res mode alone (without HD kernels) led to images of slightly lower sharpness. However, noise levels in such images were considerably lower, which resulted in a better balance between spatial resolution and image noise. This was consistent with the optimization results provided by MIOM.

Figure 9.

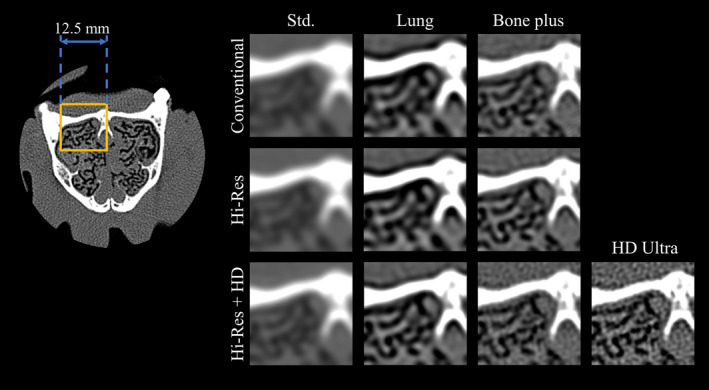
Axial images of the nasal cavity of the canine subject. ROI images are displayed for both conventional and Hi‐Res modes combined with different kernels. The display window and level are 2000 and 300 HU, respectively. [Color figure can be viewed at wileyonlinelibrary.com]

4. Discussion

This work demonstrated that traditional observer models have limited capability in predicting human observer performance for high‐contrast and high‐spatial resolution CT imaging task. Therefore, it is necessary to modify conventional observer models for this type of task. By introducing a weight function to the ideal observer framework, a modified ideal observer model (MIOM) was developed for high‐contrast and high‐spatial resolution task. Experimental results showed the improved correlation between the proposed observer model and human reader performance.

Results of the observer studies showed that even for high‐spatial resolution imaging task, its performance is not entirely determined by spatial resolution, as the kernel with the best MTF did not necessarily lead to the highest observer performance. Noise amplification associated with those kernels may degrade the overall imaging performance. This explains why intermediate kernels such as the Lung and HD Lung kernel generated better performance for the task, since they maintained good balance between spatial resolution enhancement and noise amplification, particularly at off‐centered positions.

An in vivo animal study was included in this work to corroborate predictions made based on MIOM. Results of the animal study were qualitatively consistent with the predictions. However, it is important to recognize that the animal study was only qualitative rather than quantitative, and observations should not be arbitrarily generalized until evaluated with more subjects, imaging tasks, radiation dose levels, and body sizes.

While the use of the MIOM has been justified by the results of the human observer experiments, there are some important limitations that need to be investigated in future studies: First, the proposed modification of the ideal observer was based on empirical assumptions rather than a formal derivation. In particular, the weight function was determined empirically and heuristically, and a more rigorous theoretical modeling of human observer performance for high‐contrast and high‐spatial resolution imaging tasks needs to be performed. Second, the observer model and human observer performances were compared in terms of rank correlation coefficient, which did not strictly describe the quantitative agreement for individual data pair. Third, only a single imaging task and a limited number of readers with non‐clinical training were used in this study. Additional validation studies should include a large number of imaging tasks and physician readers. Fourth, high‐density metal objects such as metal implants may introduce streak artifacts to CT images. Like other observer models, the proposed MIOM does not take these artifacts into account. Finally, the discussion about MIOM assumed linear and shift invariant CT systems with linear reconstruction algorithms and kernels. Nonlinear CT systems, particularly those with iterative reconstruction (IR) algorithms, are beyond the scope of this work. Although IR is gaining popularity for low‐contrast detection tasks, its clinical use for high‐spatial resolution applications is yet to be fully explored. If a high‐spatial resolution clinical application does involve the use of IR, the applicability of MIOM must be reexamined.

5. Conclusions

A modified ideal observer model (MIOM) was developed and validated to predict human observer performance for high‐contrast and high‐spatial resolution CT imaging tasks. Spatial resolution improving technologies such as the Hi‐Res scan mode and the associated HD reconstruction kernels can potentially be better utilized in routine clinical practice under the guidance of MIOM.