Protein Network Construction Using Reverse Phase Protein Array Data

Abstract

In this paper, we introduce a novel computational method for constructing protein networks based on reverse phase protein array (RPPA) data to identify complex patterns in protein signaling. The method is applied to phosphoproteomic profiles of basal expression and activation/phosphorylation of 76 key signaling proteins in three breast cancer cell lines (MCF7, LCC1, and LCC9). Temporal RPPA data are acquired at 48h, 96h, and 144h after knocking down four genes in separate experiments. These genes are selected from a previous study as important determinants for breast cancer survival. Interaction networks are constructed by analyzing the expression levels of protein pairs using a multivariate analysis of variance model. A new scoring criterion is introduced to determine relevant protein pairs. Through a network topology based analysis, we search for wiring patterns to identify key proteins that are associated with significant changes in expression levels across various experimental conditions.

I. Introduction

In cancer, genetic and epigenetic changes are often associated with disease development. Studying epigenetic changes such as protein phosphorylation will greatly aid in understanding the causes and determining effective treatment of cancers and other diseases. With the development of personalized therapeutics for oncology, the systematic and targeted analysis of selected proteins including phosphorylated proteins in tumor tissues is receiving increasing interest [1]. Reverse-phase protein arrays (RPPAs) have emerged as a useful tool for the large-scale analysis of protein expression and protein activation, allowing for the specific detection and quantification of proteins in a reproducible and highly parallelized manner [2]. Besides monitoring differential expression, RPPAs allow the profiling of differential protein modification. Due to the dependency on dot blot compatible antibodies, the number of detectable proteins is limited, but a large number of samples can be profiled due to the reverse array format. Therefore, RPPAs can be used in complex studies, where the impact of multiple experimental factors (e.g., multiple treatments, doses, and time points) on protein expression and cellular signaling is investigated [3].

RPPA data analysis is still a growing area of research. Studies utilizing RPPA data have employed a diverse range of data pre-processing and benchmarking methods, but no single protocol for processing RPPA data has been universally accepted [4–8]. Some of the tools include a web-based data analysis pipeline RPPApipe [3] and an R-package RPPanalyzer [9]. A review of the tools and software approaches developed for RPPA data normalization and data analysis can be found in ref. [10]. In a typical RPPA data analysis, proteins are analyzed individually and expression values are considered to be of primary interest. However, since proteins function in networks and interact with many partners, a network-based approach is desired to analyze the RPPA-based protein expression data. For example, RPPA were used to analyze the expression of 203 proteins in cells taken from acute myeloid leukemia (AML) patients using a network-based approach [11]. Dominant overlapping protein networks between subtypes of AML patients were characterized using a paired t-test and lasso regression analysis. Signaling networks were constructed from the protein pairs that were significantly different. Predicted networks were also compared to known networks from public protein–protein interaction and signaling databases. In a recent study, the levels of 134 proteins measured in 21 breast cancer cell lines stimulated with IGF1 or insulin for up to 48 hours were evaluated by network analysis [8]. Specifically, directed protein expression networks named as time translation models were constructed using lasso regression, conventional matrix inversion, and entropy maximization. The inferred interactions were ranked by differential magnitude to identify pathway differences.

In this study, we introduce a method that performs statistical analysis of protein-pairs to construct protein networks, unlike most studies where proteins are analyzed individually. Instead of taking the ratio of the expression levels of the proteins, we analyze the protein pairs via a multivariate analysis of variance (MANOVA) to test for patterns, where the expression levels of a protein pairs are considered as a bivariate outcome. This approach allows a higher power of identifying significant changes than the ratio comparison. In addition, we introduced a new scoring criterion that utilizes the significance and the correlation of each protein pair, as well as the importance of each protein, for construction of a network. This differs with information-theoretic methods, which constructs networks based on the associations of protein pairs using metrics such as correlation, and mutual information [12–13]. These information-theoretic methods will not work well on this dataset since only limited samples exist for each condition while our proposed method will perform well under this restriction. Another typical network based method is weighted gene co-expression network analysis (WGCNA), which mainly focuses on identifying clusters [14]. This differs with our aim to identify protein markers. In addition, it is unclear how well WGCNA performs under small sample size restrictions. To explore the mechanisms of resistance to therapies targeting estrogen pathways in the treatment of estrogen receptor (ER) positive breast cancer, we previously performed a systemic biological screening of a library of siRNAs targeting an ER- and aromatase-centered network [15]. We identified 46 genes that are dispensable in the estrogen-dependent MCF7 cell lines, but are selectively required for the survival of estrogen-independent MCF7-derived cell lines (LCC1 and LCC9). Based on viability data, we selected four genes: Transducer of ERBB2, 1 (TOB1), Polymerase (RNA) II subunit B (POLR2B), Proteasome 26S Subunit ATPase 5 (PSMC5), and Cysteine Rich Angiogenic Inducer 61 (CYR61). These genes were knocked down individually in each cell line to explore their role in the survival of estrogen-independent ER positive cells and the impact on the signaling architecture of cancer-focused pathways.

We evaluated the proposed computational method using RPPA data derived from breast cancer cells with activation/phosphorylation of 76 key signaling proteins in MCF7, LCC1 and LCC9 cells. Interaction networks between the proteins and phosphorylated proteins were constructed to determine the proteins that significantly changed when a gene was knocked down. The networks were built through the recognition of protein-protein interactions by identifying those pairs of proteins whose expression levels changed in each knockdown at 48h, 96h, and 144h compared to the negative control (without gene knockdown) for cell lines MCF7, LCC1 and LCC9 [11]. A topological analysis of the networks identified key proteins in each network that can play an important role in estrogen-dependent and estrogen-independent cell lines.

The rest of the paper is organized as follows. Section II describes the cell lines, the workflow for the analysis of RPPA data, the proposed MANOVA model for network construction, the protein-protein pair correlative analysis, and topological analysis of the resulting networks. Section III presents the networks generated by the analysis of temporal RPPA data and the key proteins identified for each network. Finally, Section IV summarizes the work and discusses future goals.

II. Materials and methods

A. Reverse phase protein array (RPPA) expression data

To explore the roles of POLR2B, TOB1, CYR61 and PSMC5 genes in the survival of estrogen-independent cells and the impact on the signaling architecture of cancer-focused pathways, basal expression and activation of 76 key signaling proteins in MCF7, LCC1 and LCC9 cells were analyzed using RPPA. MCF7 is an ER positive and estrogen-dependent breast adenocarcinoma cell line and sensitive to treatment with the anti-estrogen (AE) reagents: tamoxifen and fulvestrant. LCC1 is derived from MCF7 and selected in vivo for estrogen-independence, which commonly reflects resistance to aromatase inhibition (AI), but remains sensitive to tamoxifen and fulvestrant. LCC9, further derived by selection from LCC1 cells, is resistant to both tamoxifen and fulvestrant [16, 17].

The four genes for knockdown in each cell line were selected from a previous study [15] that aimed to identify new points of vulnerability in estrogen-independent, AE/AI-resistant breast cancers. The study identified a group of genes with action specifically required for the survival of estrogen independent cells. Tumor suppressor gene TOB1 was identified as a critical determinant of estrogen-independent ER-positive breast cell survival. In addition to TOB1 gene, other 45 genes presented potential function in estrogen-independent growth of ER positive breast cancer. In order to broaden the understanding of the mechanisms of estrogen-independent growth, based on viability data, TOB1 and three genes (POLR2B, CYR61, and PSMC5) were selected for knockdown experiments and RPPA based analysis. These knocked-down genes in the estrogen-independent breast cancer cell lines also demonstrated varying levels of apoptotic activity, and were chosen for RPPA based analysis to compare signaling pathways affected by knockdown of each gene. TOB1, POLR2B CYR61, PSMC5, or negative scrambled siRNAs with a final concentration of 10nM were reverse transfected into cells for 48h, 96h and 144h. Triplicates of each transfection were collected for analysis by RPPA [18]. We used 76 antibodies listed in ref. [15] for acquisition of RPAA data as described previously [19].

B. Protein-protein pair correlation analysis and protein network construction

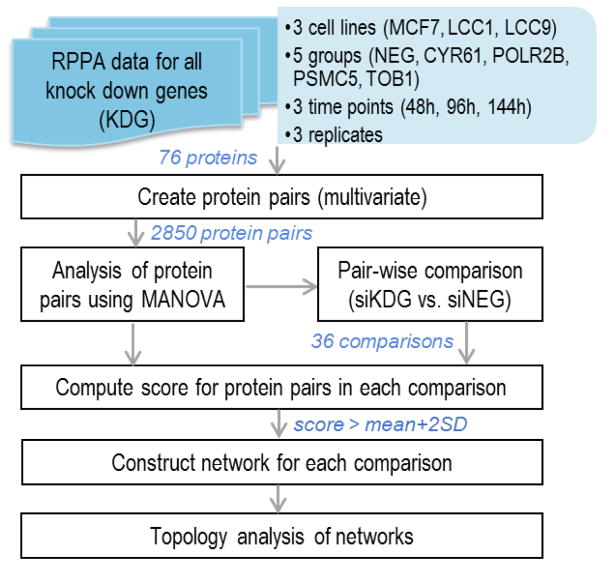
Figure 1 presents the overall workflow for the analysis of RPPA data. Following normalization of the RPPA data, protein pairs were created and the expression levels were analyzed for each protein pair.

Figure 1.

An overview of the workflow for RPPA data analysis.

The expression level of each protein pair was considered as a bivariate outcome to build a three-way MANOVA model with knockdown, time, and cell line as factors, as well as all the possible interactions. Eq. (1) presents the three-way MANOVA model.

$${\mathbf{y}}_{\mathit{ijkl}}=\mathbf{\mu }+{\mathbf{\alpha }}_i+{\mathbf{\beta }}_j+{\mathbf{\gamma }}_k+{(\mathbf{\alpha }\mathbf{\beta })}_{ij}+{(\mathbf{\alpha }\mathbf{\gamma })}_{ik}+{(\mathbf{\beta }\mathbf{\gamma })}_{jk}+{(\mathbf{\alpha }\mathbf{\beta }\mathbf{\gamma })}_{\mathit{ijk}}+{\mathbf{\epsilon }}_{\mathit{ijkl}}$$ Eq. (1)

where

• y_ijkl is the two-dimensional protein pair observation

• μ is the overall mean across all the observations

• α_i is the cell line effects for MCF7, LCC1, and LCC9, such that Σα_i = 0

• β_j is the group effects of siNEG and the knockdown genes POLR2B, TOB1, CYR61, and PSMC5, such that Σβ_j = 0

• γ_k is time point effects at 48h, 96h, and 144h, such that Σγ_k = 0

• (αβ)_ij is the interaction between cell line and group effects, such that Σ_i(αβ)_ij = Σ_j(αβ)_ij = 0

• (αγ)_ik is the interaction between cell line and time points, such that Σ_i(αγ)_ik = Σ_k(αγ)_ik = 0

• (βγ)_jk is the interaction between group and time points, such that Σ_j(βγ)_jk = Σ_k(βγ)_jk = 0

• (αβγ)_ijk is the interaction between cell lines, group, and time points, such that Σ_i(αβγ)_ijk = Σ_j(αβγ)_ijk = Σ_k(αβγ)_ijk = 0

• ε_ijkl is the random error independent and identically distributed from a bivariate normal distribution with mean vector 0, and variance covariance matrix Σ.

For example, y₁₁₁₁ is the first measurement of cell line MCF7 siNEG group at 48h; α₁ is the cell line effect of MCF7; β₁ is the group effect o siNEG; and γ₁ is the effect of time point 48h.

$$\begin{array}{l}{\alpha }_i={\overline{y}}_{i···}-\overline{y}={\frac{1}{n}}_i\sum _j\sum _k\sum _l(y_{\mathit{ijkl}}-\overline{y})\\ {\beta }_j={\overline{y}}_{·j··}-\overline{y}=\frac{1}{n_j}\sum _i\sum _k\sum _l(y_{\mathit{ijkl}}-\overline{y})\\ {\gamma }_k={\overline{y}}_{··k·}-\overline{y}=\frac{1}{n_k}\sum _i\sum _j\sum _l(y_{\mathit{ijkl}}-\overline{y})\\ {(\alpha \beta )}_{ij}={\overline{y}}_{ij··}-{\overline{y}}_{i\cdots }-{\overline{y}}_{·j··}+\overline{y}=\frac{1}{n_{ij}}\sum _k\sum _l(y_{\mathit{ijkl}}-{\overline{y}}_{i\cdots }-{\overline{y}}_{·j··}+\overline{y})\\ {(\alpha \gamma )}_{ik}={\overline{y}}_{i·k·}-{\overline{y}}_{i\cdots }-{\overline{y}}_{··k·}+\overline{y}=\frac{1}{n_{ik}}\sum _j\sum _l(y_{\mathit{ijkl}}-{\overline{y}}_{i\cdots }-{\overline{y}}_{··k·}+\overline{y})\\ {(\beta \gamma )}_{jk}={\overline{y}}_{·jk·}-{\overline{y}}_{·j\mathrm{..}}-{\overline{y}}_{··k·}+\overline{y}=\frac{1}{n_{jk}}\sum _i\sum _l(y_{\mathit{ijkl}}-{\overline{y}}_{·j··}-{\overline{y}}_{··k·}+\overline{y})\\ {(\alpha \beta \gamma )}_{\mathit{ijk}}={\overline{y}}_{\mathit{ijk}·}-{\overline{y}}_{ij··}-{\overline{y}}_{i·k·}-{\overline{y}}_{·jk·}+{\overline{y}}_{i\cdots }+{\overline{y}}_{·j··}+{\overline{y}}_{··k·}-\overline{y}\\ =\frac{1}{n_{\mathit{ijk}}}\sum _l(y_{\mathit{ijkl}}-{\overline{y}}_{ij··}-{\overline{y}}_{i·k·}-{\overline{y}}_{·jk·}+{\overline{y}}_{i\cdots }+{\overline{y}}_{·j··}+{\overline{y}}_{··k·}-\overline{y})\end{array}$$

To control false discovery rate (FDR) in multiple testing, adjusted p-values were calculated following the Benjamini and Hochberg procedure [20]. This is the first step to select the protein pairs that are different across time points, cell lines, or knockdown experiments. To select the protein pairs for the pair-wise group comparisons, we estimated the quantile values of the adjusted p-values of testing α, β, γ, α β, α γ, β γ and α β γ. These protein pairs were then chosen for the pair-wise group comparisons and to construct the networks. This was based on a global test to determine the in- group comparisons, the difference between the negative controls (siNEG) and the knockdown for each gene is compared for all three cell lines at each of the time points, separately. Significant protein pairs were selected based on the Hotelling’s T² test comparing each knockdown vs. negative controls, i.e., to test

$${\mathrm{H}}_0:{\mathbf{\mu }}_{\mathit{ijk}}={\mathbf{\mu }}_{i1k},{\mathrm{H}}_1:{\mathbf{\mu }}_{\mathit{ijk}}\ne {\mathbf{\mu }}_{i1k}$$

where μ_ijk = μ + α_i + β_j + γ_k is the mean of cell line i, group j at time point k, and j=1 denotes the siNEG group. Under H₀, the test statistic

$$\begin{array}{c}{T}_{\mathit{ijk}}^2=\frac{n{v}_E}{2}{\left({\overline{\mathbf{y}}}_{\mathit{ijk}·}-{\overline{\mathbf{y}}}_{i1k·}\right)}^{\mathrm{T}}{\mathbf{E}}^{-1}\left({\overline{\mathbf{y}}}_{\mathit{ijk}·}-{\overline{\mathbf{y}}}_{i1k·}\right)~T^2(2,v_E)\\ F_{\mathit{ijk}}=\frac{v_E-2+1}{2v_E}{T}_{\mathit{ijk}}^2~F(2,v_E-2+1)\end{array}$$

where ȳ_ijk· is the sample mean of cell line i, group j at time point k; E is the error sum of squares matrix; T²(2,v_E) is the Hotelling’s T² distribution with degrees of freedom (2,v_E); F(2,v_E − 2 + 1) is the F-distribution with degrees of freedom (2,v_E − 2 + 1); and v_E = abc(n − 1)is the error degrees of freedom, a = 3 is the number of cell lines, b = 5 is the number of groups, c = 3 is the number of time points, and n = 3 is the number of replicates.

For each knockdown gene, nine comparisons were performed. For example, for the knockdown gene TOB1, the comparisons are siNEG vs. siTOB1 for LCC1, LCC9, and MCF7, at each of the three time points (48h, 96h, and 144h). Each protein pair was then scored based on its significance level in the group comparisons, correlation coefficient, and the number of times each protein is significant in a pair in the three-way MANOVA model. Eq. (2) illustrates how the score was calculated.

$${\mathit{Score}}_{x-y}^{\mathit{ijk}}=\mid {\rho }_{x-y}^{\mathit{ijk}}\mid \times {log}_{10}\left(\frac{\#x\times \#y}{p-{\mathit{value}}_{x-y}^{\mathit{ijk}}}\right)$$ Eq. (2)

where ${\rho }_{x-y}^{\mathit{ijk}}$ is the Pearson correlation coefficient between protein x and protein y in cell line i at time point k of knockdown group j; $p-{\mathit{value}}_{x-y}^{\mathit{ijk}}$ is the p-value of testing H₀: μ_ijk = μ_i1k for protein pairs x and y; and #x and #y are the number of times proteins x and y are significant in the three-way MANOVA analysis, respectively.

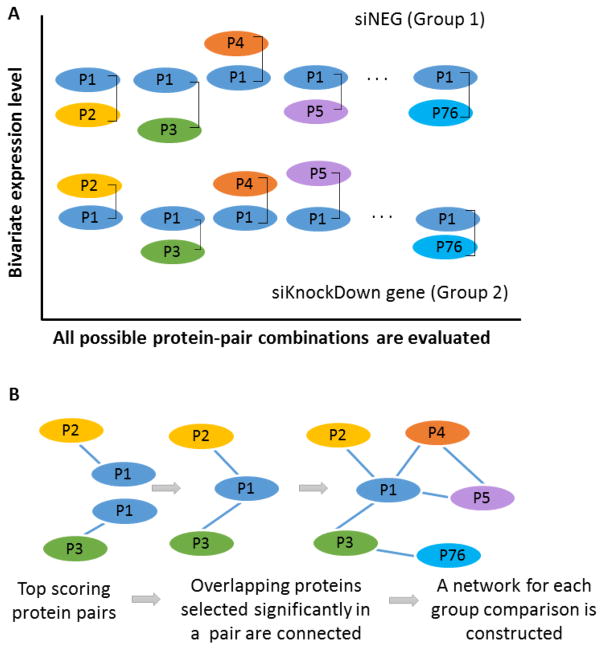
A threshold value was used to select the high scoring protein pairs, with a score > mean + 2SD (SD: standard deviation). This scoring criterion aids in the construction of interaction networks which takes into account the significance as well as the correlation between the proteins. It helps to identify those proteins or phosphorylated proteins that appear in a large number of significant pairs. The prevalence of these proteins in significantly different pairs will make them potential targets or that could be affecting signaling networks. Figure 2A shows a schematic representation of the protein pair analysis using MANOVA. The expression level of each protein pair is represented as a bivariate input to the MANOVA model. For the 76 proteins from our study, 2850 protein pairs will be generated. Figure 2B represents how the top scoring protein pairs that are significantly selected in MANOVA analysis and pair-wise analysis using Eq (2) are used to construct the networks.

Figure 2.

A: a schematic representation of the protein pair analysis using MANOVA. The expression level of each protein pair is represented as a bivariate input to the MANOVA model. B: the construction of protein networks for each group comparison. The top scoring protein pairs that are significantly selected in MANOVA analysis and pair-wise analysis are used to construct the protein networks.

As described above, we considered the paired expression levels as bivariate outcomes instead of taking the ratio for univariate analysis (e.g., the paired t-test). In the following, we discuss one of the shortcomings of constructing a network based on the ratio of a pair of proteins. We assume the case in which the ratio of effect size compared to negative control is the same as the ratio of expression level in the knockdown group, based on the relationship

$$\frac{X}{Y}=\frac{X-X_C}{Y-Y_C}=\frac{X_C}{Y_C}$$

where X is the expression level of protein x in the gene knockdown group and X_C is the expression level in the negative control group. From this, we can conclude that the difference of the ratio comparing the knockdown group and negative control is zero, which is insignificant in the paired t-test. However, the difference in the expression levels X − X_C and/or Y − Y_C can be significant. By conducting tests on the ratio, it may fail to identify this significant change and result in an inflated p-value. Second, for proteins with large effect size, the significance of the ratio may depend on whether it serves as the numerator or the denominator, influencing the times of the protein to be significant in the definition of the score (Eq. (2)). For example, the expression level of the negative control group is (X_C, Y_C) = (2,1), considering two cases of the gene knockdown group: (1) (X₁,Y₁) = (2,1); and (2) (X₂,Y₂) = (22,11). For all three pairs, the ratio is two. If we compare knockdown group with the negative control group, the difference is zero. If we do a bivariate comparison, the difference between knockdown group and the negative control is (1) (X₁,Y₁) − (X_C, Y_C) = (0,0) and (2) (X₂,Y₂) − (X_C, Y_C) =(20,10). For case (1), there is no difference between knockdown and negative control, while case (2) the difference is significant.

C. Topological analysis of the networks

Given a network, topological analysis can help discover hidden patterns to identify key nodes in that network [21]. Common metrics for network topological analysis include node degree, node betweenness, node closeness, node eigenvector centrality, etc. Node degree measures the number of connections for a node. Node betweenness counts how many times a node acts as bridge in the shortest path between two other nodes. Node closeness is defined as the reciprocal of the total distance from one node to all others. For a node located more centrally in the network, its total distance to the others is smaller and thus its closeness is larger. Node eigenvector centrality reveals the importance of a node by assigning relative scores to all nodes based on the idea that connections to high-scoring nodes contribute more to the score than connections to low-scoring nodes. Google’s PageRank algorithm is one variant of the node eigenvector centrality metric [22]. Past studies have used these network topological metrics as complements to individual gene or gene sets as features to build classification models and achieved improved performance in predicting phenotype-gene association in breast cancer [23]. In our analysis, we mainly focus on node centralities for protein marker identification. However, metrics such as node betweenness can also provide meaningful information from edges in the network. Other edge centralities and advanced node centrality metrics such as “party” and “date” hubs can be used for further evaluation and might provide complementary information in addition to the above metrics we used [24].

When multiple networks are available, it is desirable to identify key nodes in each network and compare them across different networks to generate hypothesis for further validation. Selecting the key proteins based on visual observation is one way. But networks can be complicated and visual observation are prone to be biased. Considering this, we prefer to use the metrics mentioned above to select key proteins in each network. In our study, four gene knockdown experiments were conducted (i.e., TOB1, POLR2B, CYR61 and PSMC5). Nine networks were constructed for each gene knockdown experiment involving three cell lines (i.e., MCF7, LCC1 and LCC9) at three time points (i.e., 48h, 96h and 144h). By using node degree, node betweenness, node closeness, and node eigenvector centrality metrics, we identified key proteins that consistently showed up across three time points for each gene knockdown experiment. For each network, we selected the top five proteins according to the above four network topological metrics. Then, we identified proteins that are among the top five for at least three of the four metrics as key proteins for that network. The same procedure was applied to all nine networks for each knockdown experiment.

D. Implementation

The MANOVA code and pairwise comparisons script were written in Matlab (MathWorks). Network representations were graphed in Cytoscape, version 3.5.0-RC2 [25], and DyNet Cytoscape application [26]. Topological analysis was performed by using R package igraph [27]. Programs were run on Windows 7 desktop (i-2600 CPU @ 3.40GHz, 16GB RAM, 64-bit Operating system). The source code and related data used are available at https://github.com/Hurricaner1989/RPPA-Matlab-R-codes.

III. Results and discussion

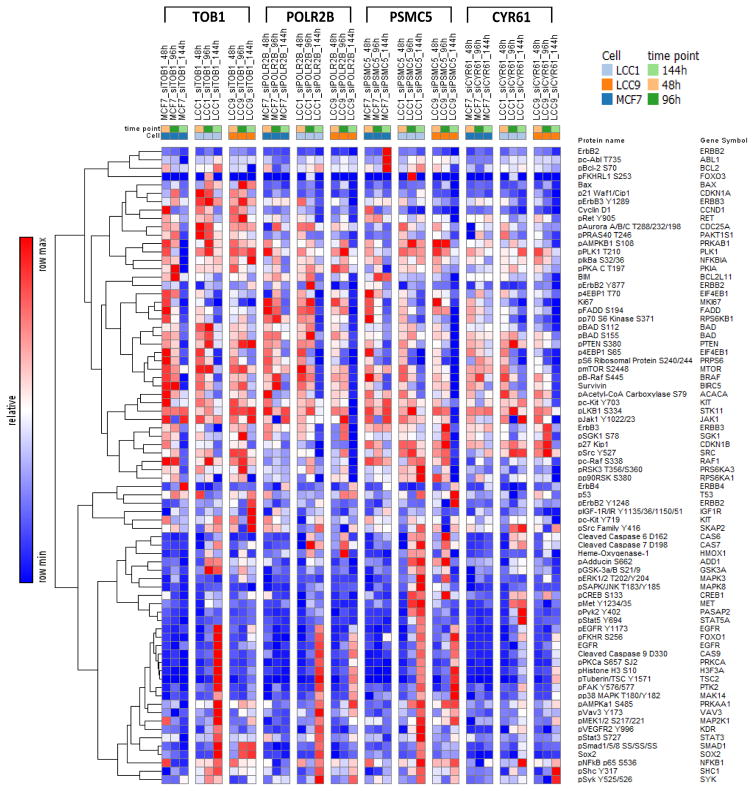
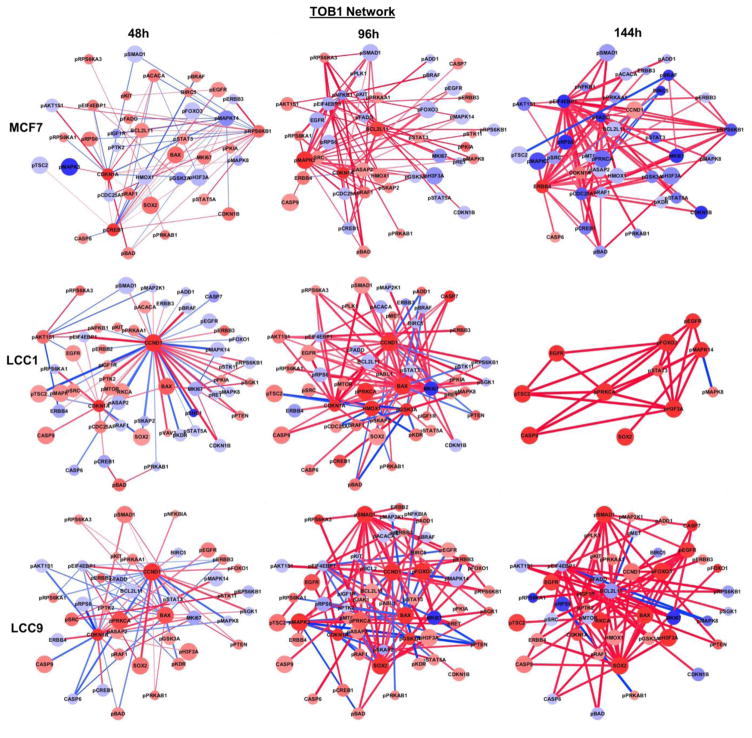
Figure 3 depicts a heatmap of the changes in expression levels of each protein in MCF7, LCC1 and LCC9 for all knock-down experiments compared to it siNEG controls. The figure gives us an overall representation of how a protein has changed its expression for a particular condition (time point and knock-down experiment) when compared to its negative control. Figure 4 shows the nine interaction networks generated for each group comparison when TOB1 was knock-down. Similar networks were constructed for POLR2B, CYR61, and PSMC5 (not shown). Nine group comparisons were performed for each knockdown gene for MCF7, LCC1, and LCC9 cells at 48h, 96h, and 144h against its corresponding siNEG. We focused on the proteins that appear in a large number of significant pairs. The ubiquity of these proteins in significantly different pairs between siNEG and knockdown group will make them potential targets that could broadly affect signaling in the cells. We used Cytoscape to build the networks. Red nodes represent upregulated proteins and blue nodes represent downregulated proteins when compared with siNEG. The node size is proportional to the number of times the protein appears in significant pairs. A red edge in the network depicts positive correlation between the pairs and a blue edge depicts negative correlation. The edge thickness is proportional to the score defined in Eq. (2) for the protein pair. There was no protein pair selected as significant in the comparison against siNEG at 144h for LCC9 when PSMC5 was knocked down. Therefore, no network was constructed for this comparison.

Figure 3.

Heatmap of changes in protein expression for siRNA-transfected MCF7, LCC1, and LCC9 cells at 48h, 96h and 144h for TOB1, POLR2B, PSMC5, and CYR61 knock down genes using the corresponding negative controls (siNEG) as references.

Figure 4.

Protein networks constructed using significant protein-pairs (TOB1 knockdown vs. negative control) for each cell line and each time point.

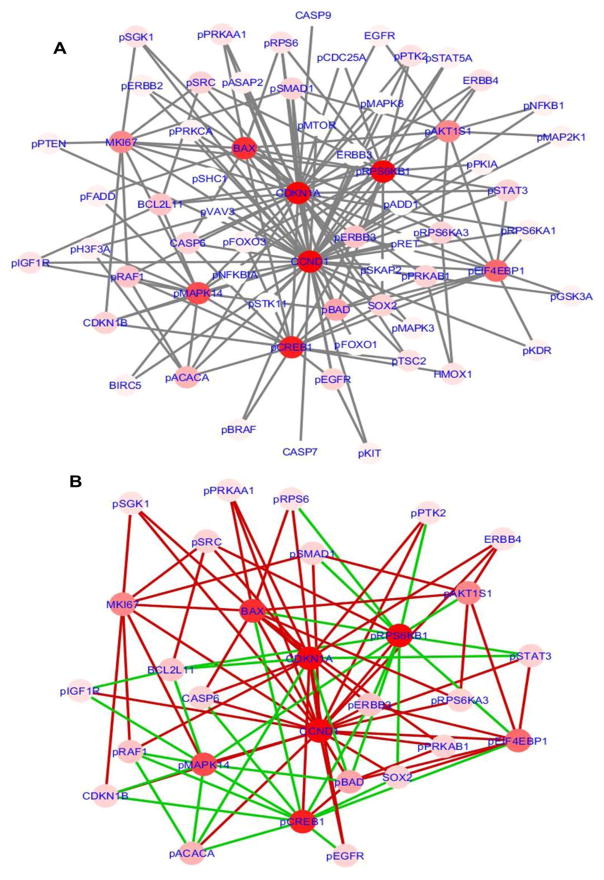
In order to compare the differences between estrogen dependent network (MCF7) and estrogen independent network (LCC1 and LCC9), we combined the interaction networks derived from LCC1 and LCC9 data and compared it against the MCF7 network generated for TOB1 at 48h. Figure 5 shows the networks generated using DyNet to compare MCF7 vs. LCC1-LCC9. To view the networks graphically, we used DyNet, a Cytoscape application to import and compare multiple graph files. A central reference network is generated first from the union of the networks. A pair-wise comparison is then performed by calculating the log₂ fold-change of the attribute value. A score is computed and used to highlight the most variable nodes and edges on the central reference network, using a color gradient (Figure 5A). The D_n-score, is a rewiring metric to support the identification of the most rewired nodes [25]. Figure 5A represents the combined network which shows the most rewired proteins. Figure 5B shows a differential network for MCF7 and LCC1- LCC9 combined network focusing only on the most important nodes. The edges specific to LCC1-LCC9 combined network is colored in red and those unique to MCF7 are colored in green. In this comparison, we can see that CCND1 has more signaling activity in estrogen independent network compared to MCF7, and phosphorylated protein RPS6KB1 and phosphorylated MAPK14 have more activity in MCF7, the estrogen dependent network. These nodes are candidates that can be used to further investigate the differences between estrogen dependent and independent cell lines.

Figure 5.

A: Combined network with most varying nodes and edge changes highlighted for MCF7 vs. LCC1-LCC9. B: Differential network for the most re-wired nodes showing the edge changes in MCF7 vs. LCC1-LCC9.

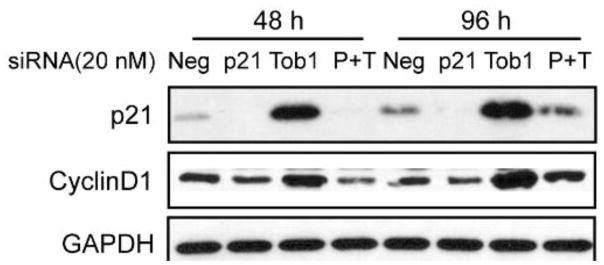
A total of 36 protein networks were generated from all four knock-down experiments. In order to discover hidden patterns and identify key nodes, we performed a topological analysis of these individual networks. Table 1 shows the results of topological analysis of networks for all four gene knock-down experiments (e.g., Figure 4). The table lists the top five proteins from each metric for all nine networks in each gene knock-down experiment. Table 2 presents a summary of the key proteins for each gene knock-down experiment using each cell line across three time points. The unique key proteins for each cell line in each gene knock-down experiment are marked in red. In Figure 5, rewiring proteins are highlighted based on a rewiring score (i.e., D_n-score), defined to represent the variation of that node across multiple networks. The rewiring proteins are specific to one comparison. In contrast, Tables 1–2 selected key proteins in each network. As a complement to network analysis in Figure 5, they can be used to help generate various hypotheses for further validation. For example, in comparing MCF7 vs LCC1 and LCC9, from the networks constructed using protein pair analysis for TOB1 knockdown, we can see that p21 (CDKN1A) and cyclin D1 (CCND1) were inferred as major signaling activation nodes in the TOB1-regulated network of LCC1 and LCC9 cells. Both protein expressions were up-regulated after TOB1 knockdown and experimental data proved that p21 and cyclin D1 were positively correlated (Figure 6). Expression of p21 and Cyclin D1 was both induced by TOB1 knockdown consistent with RPPA analysis. Knockdown of p21 decreased Cyclin D1 level in the absence or presence of siTOB1, which presented a positive correlation between p21 and Cyclin D1. Pathway analysis using Ingenuity Pathway Analysis (IPA) following the network construction inferred p21 and cyclin D1 as major signaling activation nodes in the TOB1-regulated network of LCC1 and LCC9 cells [15]. HMOX1 (Heme oxygenase 1), which is known to be involved in stress responses, was significantly activated at 48h and 96h following transfection of siPOLR2B, siPSMC5 and CYR61, as compared with non-silencing siRNA. We hypothesize that HMOX1 is a key driver in the pro-survival signaling LCC1 and LCC9 cells following transfection with POLR2B and PSMC5 (Tables 1 and 2). pACACA is highly activated after 48h gene knockdown of CYR61 in LCC1 cells. In breast cancer, chromosome 17q, the location of ACACA, has increased copy number in HER2 and luminal A classified breast cancer tumors. ACACA is over expressed in LCC1 compared to MCF7 cells. ACACA is known to be involved in invadopodia formation.

Table 1.

Top five proteins selected based on four metrics from topological analysis of each protein network. Proteins that appeared frequently across different network topological metrics are marked in bold.

		48h					96h					144h
TOB1
		Total # nodes: 48					Total # nodes: 44					Total # nodes: 39
MCF7	Degree	CDKN1A	pRPS6KB1	pCREB1	pMAPK14	pEIF4EBP1	pMAPK3	BCL2L11	pEIF4EBP1	pNFKB1	CDKN1A	pEIF4EBP1	ERBB4	pCDC25A	pFADD	pRPS6KB1
	Betweenness	pCREB1	pRPS6KB1	CDKN1A	pMAPK14	pEIF4EBP1	BCL2L11	pMAPK3	pEIF4EBP1	pNFKB1	CDKN1A	pEIF4EBP1	ERBB4	pRPS6KB1	pFADD	pBRAF
	Closeness	pMAPK14	pRPS6KB1	pCREB1	CDKN1A	pEIF4EBP1	pEIF4EBP1	pNFKB1	pMAPK3	BCL2L11	pSMAD1	pEIF4EBP1	ERBB4	pCDC25A	CCND1	pBAD
	PageRank	pRPS6KB1	CDKN1A	pCREB1	pMAPK14	pEIF4EBP1	pMAPK3	BCL2L11	pEIF4EBP1	pNFKB1	CDKN1A	pEIF4EBP1	ERBB4	pFADD	pCDC25A	pRPS6KB1
		Total # nodes: 54					Total # nodes: 52					Total # nodes: 11
LCC1	Degree	CCND1	CDKN1A	MKI67	pAKT1S1	BAX	CCND1	MKI67	BAX	CDKN1A	pGSK3A	pH3F3A	pMAPK14	pSTAT3	pFOXO3	pPRKCA
	Betweenness	CCND1	CDKN1A	pAKT1S1	pPRKAB1	pEIF4EBP1	pGSK3A	CCND1	pEIF4EBP1	BAX	MKI67	pMAPK14	pH3F3A	pSTAT3	pFOXO3	pPRKCA
	Closeness	CCND1	CDKN1A	pEIF4EBP1	BAX	pPTK2	CCND1	pEIF4EBP1	BAX	CDKN1A	MKI67	pH3F3A	pSTAT3	pMAPK14	CASP9
	PageRank	CCND1	CDKN1A	pAKT1S1	MKI67	pEIF4EBP1	CCND1	MKI67	BAX	pGSK3A	CDKN1A	pMAPK14	pH3F3A	pSTAT3	pPRKCA	pFOXO3
		Total # nodes: 42					Total # nodes: 57					Total # nodes: 45
LCC9	Degree	CCND1	CDKN1A	BAX	pEIF4EBP1	MKI67	pSMAD1	SOX2	CCND1	BAX	pEIF4EBP1	BCL2L11	pEIF4EBP1	SOX2	pSMAD1	pEGFR
	Betweenness	CCND1	CDKN1A	MKI67	BAX	pSRC	pEIF4EBP1	CCND1	pSMAD1	SOX2	BAX	BCL2L11	pEIF4EBP1	SOX2	pSMAD1	pEGFR
	Closeness	CCND1	CDKN1A	BAX	MKI67	pEIF4EBP1	pEIF4EBP1	SOX2	pSMAD1	pKIT	BAX/pEGFR	BCL2L11	pEIF4EBP1	MKI67	pAKT1S1
	PageRank	CCND1	CDKN1A	BAX	pEIF4EBP1	MKI67	pSMAD1	CCND1	SOX2	BAX	pMAPK3	BCL2L11	pEIF4EBP1	SOX2	pSMAD1	pEGFR
POLR2B
		Total # nodes: 43					Total # nodes: 47					Total # nodes: 50
MCF7	Degree	pCREB1	pEIF4EBP1	pCDC25A	pBAD	pMAPK8	pSMAD1	pRPS6KB1	pNFKB1	HMOX1	pBAD	HMOX1	pEIF4EBP1	pFADD	ERBB4	pCDC25A
	Betweenness	pCREB1	pCDC25A	pEIF4EBP1	pBAD	pRPS6KB1	pSMAD1	pRPS6KB1	pNFKB1	HMOX1	pBAD	HMOX1	pEIF4EBP1	pFADD	ERBB4	pCDC25A
	Closeness	pCREB1	pEIF4EBP1	pRPS6KB1	pBAD	pSTAT3/pTSC2	pSMAD1	pRPS6KB1	HMOX1	pNFKB1	pEIF4EBP1	HMOX1	pEIF4EBP1	pRPS6KB1	pSMAD1	CDKN1A
	PageRank	pRPS6KB1	CDKN1A	pCREB1	pMAPK14	pEIF4EBP1	pCREB1	pEIF4EBP1	pCDC25A	pBAD	pRPS6KB1	HMOX1	pEIF4EBP1	pFADD	ERBB4	pCDC25A
		Total # nodes: 28					Total # nodes: 52					Total # nodes: 28
LCC1	Degree	pRAF1	HMOX1	CDKN1B	pCREB1	CCND1	HMOX1	pEIF4EBP1	pRPS6	CASP7	CASP6	CASP9	pFOXO3	pPRKCA	pTSC2	pH3F3A
	Betweenness	pRAF1	CDKN1B	HMOX1	pCREB1	CCND1	HMOX1	pEIF4EBP1	pRPS6	CASP7	MKI67	CASP9	BAX	EGFR	CCND1	pEGFR
	Closeness	pRAF1	HMOX1	CDKN1B	pCREB1	CCND1	HMOX1	pEIF4EBP1	pRPS6	pBAD	BAX	pFOXO3	pPRKCA	pTSC2	CASP9	BAX/pH3F3A
	PageRank	pRAF1	HMOX1	CDKN1B	pCREB1	CCND1	HMOX1	pEIF4EBP1	pRPS6	CASP7	CDKN1B	pMTOR	MKI67	CASP9	pEIF4EBP1/pAKT1S1
		Total # nodes: 42					Total # nodes: 52					Total # nodes: 15
LCC9	Degree	pRPS6	pEIF4EBP1	pAKT1S1	MKI67	pRET	pAKT1S1	HMOX1	pEIF4EBP1	pRPS6	CASP7	pFOXO3	ERBB4	pPRKCA	EGFR	pMTOR
	Betweenness	pRPS6	pEIF4EBP1	pAKT1S1	pBAD	MKI67	pRPS6	HMOX1	pAKT1S1	pBAD	pEIF4EBP1	pPRKCA	pFOXO3	pMTOR	ERBB4	MKI67
	Closeness	pRPS6	pEIF4EBP1	pAKT1S1	MKI67	pRET	HMOX1	pAKT1S1	pEIF4EBP1	CASP7	pBAD	pFOXO3	ERBB4	pPRKCA	EGFR	pTSC2
	PageRank	pRPS6	pEIF4EBP1	pAKT1S1	MKI67	pRET	pRPS6	pAKT1S1	HMOX1	pEIF4EBP1	CASP7	pFOXO3	pPRKCA	pMTOR	ERBB4	MKI67
CYR61
		Total # nodes: 39					Total # nodes: 36					Total # nodes: 47
MCF7	Degree	pMAPK8	pCDC25A	pRPS6KA1	pAKT1S1	pBAD	pEIF4EBP1	pNFKB1	pCDC25A	pKIT	pBAD	pEIF4EBP1	pCDC25A	BIRC5	ERBB4	CCND1
	Betweenness	pCDC25A	pMAPK8	pAKT1S1	pRPS6KA1	pBAD	pEIF4EBP1	pNFKB1	pKIT	pCDC25A	pSMAD1	pEIF4EBP1	pCDC25A	pSRC	ERBB4	pFADD
	Closeness	pBAD	pCDC25A	pMAPK8	pFOXO3	pTSC2	pEIF4EBP1	pNFKB1	pCDC25A	HMOX1	pSMAD1	pEIF4EBP1	pCDC25A	ERBB4	BIRC5	CCND1
	PageRank	pMAPK8	pCDC25A	pRPS6KA1	pAKT1S1	pBAD	pEIF4EBP1	pNFKB1	pCDC25A	pKIT	pBAD	pEIF4EBP1	pCDC25A	BIRC5	ERBB4	pBAD
		Total # nodes: 44					Total # nodes: 40					Total # nodes: 46
LCC1	Degree	MKI67	pRAF1	pFADD	pACACA	pBAD	MKI67	pRPS6	CASP7	pEIF4EBP1	BIRC5	pAKT1S1	MKI67	pASAP2	pEIF4EBP1	pMTOR
	Betweenness	MKI67	pRAF1	pFADD	pACACA		CASP7	MKI67	pEIF4EBP1	pRPS6	pASAP2	pAKT1S1	pEIF4EBP1	BCL2L11	MKI67	pMTOR
	Closeness	MKI67	pRAF1	pFADD	pACACA	pBAD	MKI67	pRPS6	CASP7	pAKT1S	pSMAD1	pAKT1S1	BCL2L11	pEIF4EBP1	HMOX1	MKI67
	PageRank	MKI67	pRAF1	pFADD	pACACA	pBAD	MKI67	pRPS6	CASP7	pEIF4EBP1	BIRC5	pAKT1S1	pASAP2	pEIF4EBP1	MKI67	pMTOR
		Total # nodes: 44					Total # nodes: 48					Total # nodes: 21
LCC9	Degree	pEIF4EBP1	pRPS6	pRPS6KB1	MKI67	pCDC25A	CCND1	pAKT1S1	pEIF4EBP1	pRPS6	pBAD	pH3F3A	pPRKCA	EGFR	MKI67	pFOXO3
	Betweenness	pEIF4EBP1	pRPS6	pRPS6KB1	pCDC25A	MKI67	CCND1	pBAD	pEIF4EBP1	pRPS6	MKI67	pH3F3A	MKI67	pMTOR	pPRKCA	pEIF4EBP1
	Closeness	pEIF4EBP1	pRPS6	pRPS6KB1	pBAD	pGSK3A	CCND1	pEIF4EBP1	pAKT1S1	pRPS6	pACACA	pH3F3A	pPRKCA	EGFR	pFOXO3	CASP9
	PageRank	pEIF4EBP1	pRPS6	pRPS6KB1	MKI67	pCDC25A	CCND1	pRPS6	pAKT1S1	pEIF4EBP1	MKI67	pH3F3A	MKI67	pPRKCA	pEIF4EBP1	pMTOR
PSMC5
		Total # nodes: 44					Total # nodes: 43					Total # nodes: 47
MCF7	Degree	pRPS6KB1	pCDC25A	pCREB1	pMAPK8		pEIF4EBP1	pMAPK8	pCDC25A	BCL2L11	pBAD	pEIF4EBP1	pBRAF	pCDC25A	pFADD	ERBB4
	Betweenness	pRPS6KB1	pCDC25A	pMAPK8	pBRAF	pMAPK14	pEIF4EBP1	BCL2L11	pCDC25A	pMAPK8	pBRAF	pEIF4EBP1	pBRAF	pCDC25A	ERBB4	pFADD
	Closeness	pRPS6KB1	pCDC25A	pMAPK14	pBRAF	pAKT1S1	pEIF4EBP1	pCDC25A	pMAPK8	BCL2L11	pAKT1S1	pEIF4EBP1	pBRAF	pCDC25A	ERBB4	pAKT1S1
	PageRank	pRPS6KB1	pCDC25A	pCREB1	pMAPK8	pMAPK14	pEIF4EBP1	pMAPK8	pCDC25A	BCL2L11	pBAD	pEIF4EBP1	pBRAF	pCDC25A	pFADD	ERBB4
		Total # nodes: 45					Total # nodes: 50					Total # nodes: 32
LCC1	Degree	CDKN1B	HMOX1	pEIF4EBP1	pRAF1	pGSK3A	HMOX1	pRPS6	pASAP2	CASP7	pEIF4EBP1	pPRKCA	pASAP2	pRPS6	CASP9	pH3F3A
	Betweenness	CDKN1B	pEIF4EBP1	HMOX1	pRAF1	pGSK3A	pRPS6	HMOX1	pASAP2	pEIF4EBP1	CASP7	pH3F3A	pRPS6	pPRKCA	pMTOR	pKDR
	Closeness	pEIF4EBP1	CDKN1B	HMOX1	pRPS6KA3	BIRC5	pRPS6	CASP7	HMOX1	pCREB1	BIRC5	pH3F3A	pPRKCA	pEGFR	pFOXO3	pTSC2
	PageRank	CDKN1B	HMOX1	pEIF4EBP1	pGSK3A	pRAF1	HMOX1	pRPS6	pASAP2	CASP7	pEIF4EBP1	pRPS6	pASAP2	pMTOR	pPRKCA	SOX2
		Total # nodes: 52					Total # nodes: 48					Total # nodes: 0
LCC9	Degree	pEIF4EBP1	CCND1	MKI67	pRPS6	CDKN1B	CCND1	pEIF4EBP1	CASP6	HMOX1	CDKN1B	No network constructed
	Betweenness	pEIF4EBP1	pRPS6	CCND1	MKI67	pPRKAB1	pRPS6	CCND1	pMAPK3	HMOX1	pGSK3A
	Closeness	MKI67	pRPS6	CDKN1B	pEIF4EBP1	ERBB4	CCND1	CASP6	HMOX1	pGSK3A	pMTOR
	PageRank	pEIF4EBP1	CCND1	pPRS6	MKI67	CDKN1B	pMAPK3	CCND1	pRPS6	pEIF4EBP1	CASP6

Table 2.

Key proteins for each cell line. Proteins marked in red are unique to a cell line.

	MCF7		LCC1		LCC9
	Key proteins	time point	Key proteins	time point	Key proteins	time point
TOB1	BCL2L11	96h	BAX	96h	BAX	48h, 96h
	CDKN1A	48h, 96h	CCND1	48h, 96h	BCL2L11	144h
	ERBB4	144h	CDKN1A	48h, 96h	CCND1	48h, 96h
	pCDC25A	144h	MKI67	96h	CDKN1A	48h
	pCREB1	48h	pAKT1S1	48h	MKI67	48h
	pEIF4EBP1	48h, 96h, 144h	pEIF4EBP1	48h	pEGFR	144h
	pFADD	144h	pFOXO3	144h	pEIF4EBP1	48h, 96h, 144h
	pMAPK14	48h	pGSK3A	96h	pSMAD1	96h, 144h
	pMAPK3	96h	pH3F3A	144h	SOX2	96h, 144h
	pNFKB1	96h	pMAPK14	144h
	pRPS6KB1	48h, 144h	pPRKCA	144h
			pSTAT3	144h
POLR2B	ERBB4	144h	CASP7	96h	CASP7	96h
	HMOX1	96h,144h	CASP9	144h	ERBB4	144h
	pBAD	48h,96h	CCND1	48h	HMOX1	96h
	pCDC25A	48h,144h	CDKN1B	48h	MKI67	48h
	pCREB1	48h	HMOX1	48h,96h	pAKT1S1	48h,96h
	pEIF4EBP1	48h,144h	pCREB1	48h	pEIF4EBP1	48h,96h
	pFADD	144h	pEIF4EBP1	96h	pFOXO3	144h
	pNFKB1	96h	pRAF1	48h	pPRKCA	144h
	pRPS6KB1	48h,96h	pRPS6	96h	pRET	48h
	pSMAD1	96h			pRPS6	48h,96h
CYR61	BIRC5	144h	CASP7	96h	CCND1	96h
	ERBB4	144h	MKI67	48h, 96h, 144h	MKI67	48h, 144h
	pAKT1S1	48h	pACACA	48h	pAKT1S1	96h
	pBAD	48h	pAKT1S1	144h	pCDC25A	48h
	pCDC25A	48h, 96h, 144h	pBAD	48h	pEIF4EBP1	48h, 96h
	pEIF4EBP1	48h, 96h, 144h	pEIF4EBP1	96h, 144h	pH3F3A	144h
	pKIT	96h	pFADD	48h	pPRKCA	144h
	pMAPK8	48h	pMTOR	144h	pRPS6	48h, 96h
	pNFKB1	96h	pRAF1	48h	pRPS6KB1	48h
	pRPS6KA1	48h	pRPS6	96h
PSMC5	BCL2L11	96h	CASP7	96h	CASP6	96h
	ERBB4	144h	CDKN1B	48h	CCND1	48h, 96h
	pBRAF	144h	HMOX1	48h, 96h	CDKN1B	48h
	pCDC25A	48h, 96h, 144h	pASAP2	96h	HMOX1	96h
	pEIF4EBP1	96h, 144h	pEIF4EBP1	48h, 96h	MKI67	48h
	pFADD	144h	pGSK3A	48h	pEIF4EBP1	48h
	pMAPK14	96h	pH3F3A	144h	pRPS6	48h
	pMAPK8	48h, 96h	pMTOR	144h
	pRPS6KB1	48h	pPRKCA	144h
			pRPS6	96h, 144h
			pRAF1	48h

Figure 6.

P21 positively correlated with cyclin D1 after TOB1 knockdown. 20 nM siRNAs against negative, p21 or TOB1 were transfected in LCC1 cells for 48 h and 96 h. Western blot was used to detect protein expression.

IV. Conclusions

We propose a novel method for statistical analysis of protein-pairs to construct protein networks as an alternative to the typical analysis of individual proteins. This is accomplished by using a multivariate analysis of variance and a new scoring criterion. In contrast to using the ratio between a pair of proteins, our method considers the expression levels of a protein pair as the bivariate outcome, which can yield a higher power of identifying significant changes than the univariate ratio comparison. The method is used to construct networks based on temporal RPPA data acquired from four gene-knockdown experiments in three breast cancer cell lines. Using a topological comparison of the constructed networks, the top five proteins from each network metric are identified. Additional analysis of these proteins helps to select key proteins that are uniquely associated with each cell line, when compared across the three time points. Future work will focus on validation of the key proteins discovered in this study and identification of other proteins that are associated or unique to knockdown genes or the cell lines to help generate new hypotheses.

Highlights.

• A novel computational method is proposed for constructing protein networks based on reverse phase protein array (RPPA) data to identify complex patterns in protein signaling.

• Protein networks are constructed by analyzing the expression levels of protein pairs using a multivariate analysis of variance model.

• A new scoring criterion is introduced to select relevant top protein pairs.

• Key proteins that are associated with significant changes in expression levels across various experimental conditions are identified through network topology analysis.