HOW THE U.S. PRISON BOOM HAS CHANGED THE AGE DISTRIBUTION OF THE PRISON POPULATION

Abstract

This article provides a demographic exposition of the changes in the U.S prison population during the period of mass incarceration that began in the late twentieth century. By drawing on data from the Survey of Inmates in State Correctional Facilities (1974–2004) for inmates 17–72 years of age (N = 336), we show that the age distribution shifted upward dramatically: Only 16 percent of the state prison population was 40 years old or older in 1974; by 2004, this percentage had doubled to 33 percent with the median age of prisoners rising from 27 to 34 years old. By using an estimable function approach, we find that the change in the age distribution of the prison population is primarily a cohort effect that is driven by the “enhanced” penal careers of the cohorts who hit young adulthood—the prime age of both crime and incarceration—when substance use was at its peak. Period-specific factors (e.g., proclivity for punishment and incidence of offense) do matter, but they seem to play out more across the life cycles of persons most affected in young adulthood (cohort effects) than across all age groups at one point in time (period effects).

After nearly five decades of stable incarceration rates, the United States experienced an almost fourfold increase in the size of the state and federal prison population beginning in the mid-1970s (Carson and Golinelli, 2013; Glaze and Herberman, 2013). Spurred by the sheer number of Americans going to prison (Pettit and Western, 2004), social science researchers have worked to understand the causal impact of the incarceration experience on individuals, families, communities, and society at large. More recently, researchers and advocates also have taken an interest in changes to the nature, rather than simply the size, of the prison population itself. This interest has focused prominently on the “graying” of the prison population.¹

The Pew Charitable Trusts (2014) calculated that the number of state and federal prisoners 55 years old or older increased 234 percent (43,300 to 144,500) from 1999 to 2013. Given that the overall prison population increased during this time period, the fact that more older people are in prison is not particularly surprising. However, not only are numbers of older prisoners increasing, but also their rate of increase is much higher than that for the overall prison population. For example, Luallen and Kling (2014) calculated that the proportion of inmates older than 54 years old nearly tripled from 1991 to 2011, from 3 to 11 percent. Furthermore, the population of prisoners older than 44 years old had an 8 percent annual growth rate from 1991 to 2011, which is roughly four times the growth rate of prisoners younger than 35 years old.

These increases in the prevalence of older prisoners matter to policy makers primarily because older prisoners incur substantially higher health-care costs. The poorer overall health of inmates relative to the general population is exacerbated as inmates age (Kim and Peterson, 2014). Luallen and Kling (2014) estimated that inmates 55 years old and older have health-care costs two to three times higher than those of the average inmate.

Given the financial burden of caring for older inmates, it is not surprising that emerging research has been investigating the underlying causes of prison aging. Many reports have implicated longer prison sentences as the main cause (ACLU, 2012; Human Rights Watch, 2012; Kim and Peterson, 2014; Nellis, 2010; Osborne Association, 2014; Reimer, 2008), a focus that has been mirrored by research on the overall increase in the prison population (National Research Council, 2014: 4). Other possible factors could be involved. Prison aging could simply reflect the aging of the general population (Kim and Peterson, 2014). Admission rates may be growing for older individuals in particular (Human Rights Watch, 2012; Pew Charitable Trusts, 2014). And a changing emphasis on certain types of crimes (e.g., drug convictions) may have disproportionately affected older offenders (Pollack, Reuter, and Sevigny, in press). Luallen and Kling (2014) attempted to quantify the contributions of these different factors. By using a simulation approach and admissions data from the National Corrections Reporting Program (NCRP), they reached the unexpected conclusion that the primary driver of prison aging across four states was the increasing admission ages of prisoners. They found little support for the claim that increased sentence lengths or changing offense “mixes” (i.e., more drug convictions) accounted for the observed changes in the prison age distribution.

Luallen and Kling’s (2014) approach relied on a simulated counterfactual in which admissions practices in 2012 were “walked backward” to 2000 to create a world that would have existed if these practices had been used from 2000 through 2012. This counterfactual differs dramatically from the actual outcomes in 2012. Four broad explanations—admissions rate, the age distribution of admission, time served, and offense type—were then examined one at a time to determine whether the counterfactual would change to reflect better the reality as observed in the data. As noted by Luallen and Kling (2014), their simulation approach cannot examine interactions between possible explanations nor can it get at the underlying mechanisms that drive the key factors like changes in the age distribution of the admission. In addition, Luallen and Kling’s analysis was limited to exploring changes from 2000 in four states (South Carolina, North Carolina, New York, and California).

Our estimation-based approach, rooted in demography, focuses on stocks rather than on flows, and makes use of nationally representative data from the Survey of Inmates in State Correctional Facilities for 1974, 1979, 1986, 1991, 1997, and 2004. The nature of our data and approach means that we have the advantage of explaining changes from the well-documented stable regime present in the 1970s (Blumstein and Cohen, 1973) rather than changes from the regime present in 2012.² Our estimation-based approach also allows us to examine the underlying mechanisms for the broad scope of changes observed during this time period and does not force us to examine one explanation at a time. The combination of data with a broader geographic and temporal scope and an estimation-based method that allows for more detailed exploration of underlying mechanisms means that our effort both complements and extends the efforts of Luallen and Kling (2014).

From a demographic perspective, the growth and aging of the prison population can be understood as a period or cohort effect (or some combination of the two). The most common position suggested by prior work is a period effect. The logic of this argument is that the more punitive laws of the 1980s introduced harsher sentencing for certain (violent and drug) offenses, presumably leading to lengthier time behind bars on average and, thus, leading to an older prison population. A second possibility is a cohort effect. The easiest way for this to happen is if a demographic bubble exists, such that there are simply more people in certain birth cohorts than others. In the present case, the overall population is aging with more recent birth cohorts smaller than older birth cohorts, so it is at least possible that this phenomenon will lead to older prison populations. However, this explanation would not be able to account for the rapid increase in the number of prisoners at the same time. A cohort effect can explain both aging of the prison population and growth of prison populations if individuals that come of age during our observation period are incarcerated at higher rates than individuals from earlier birth cohorts. For example, individuals born in the 1960s were at crime-prone ages during the height of the crack-cocaine era (early to mid-1980s), meaning this cohort could be disproportionately drug involved and/or disproportionately affected by the collateral consequences of incarceration (as a result of the crackdown on such crimes in the 1980s), leading to relatively high admission rates for members of this cohort over time.

By using an estimable function approach (O’Brien and Stockard, 2009), we add to the understanding of these phenomena by identifying most of the observed changes in the distribution of offenders in prison as a cohort effect. We find that more recent birth cohorts are becoming involved (and staying involved) with prison at higher rates than earlier cohorts. We then explore the possible reasons driving the high admission rates of these cohorts. By drawing on available survey data, we test whether the associations between cohort and age-specific incarceration rates are mediated by differential treatment (e.g., harsher sentencing), behavior (e.g., substance use and offense type), or background variables that are known risk factors (e.g., family and educational background). We find that the cohort effect is partially attributable to high rates of drug use in certain birth cohorts—in particular, those who “came of age” in the 1980s—rather than to high rates of drug offending or longer sentences.

DEMOGRAPHY OF THE PRISON POPULATION

Although some literature has been devoted to the implications of prison aging for the management of prisons (Williams et al., 2012), little formal demographic understanding exists for how and why the age distribution of prison populations is changing. Part of the reason that demographers have not studied the demography of prison populations is that this approach requires a fundamental reorientation from standard demographic analyses. Formal demography is concerned with the interaction among fertility, mortality, and migration—and how they result in the growth and structure of the population. In this formal demographic sense, the prison population is not a function of fertility or mortality, but it is a function of in-migration (admission) and out-migration (release).³ Since migration is essentially a nuisance and not the main object of demographic study, demographers have not been attracted naturally to the study of prison populations. However, in the absence of formal analysis, there is a tendency to rely exclusively on intuition, intuition that may overlook the complexity of the problem.

The general U.S. population is aging. The prison population, which is drawn from an aging population, could be aging as well (Kim and Peterson, 2014: v). The general correspondence, and hence the intuition, is not a bad one. The median age of the U.S. population increased 8 years from 28 years old in 1974 to 36 years old in 2004.⁴ The median age of a person in the U.S. state prison population also increased 7 years from 27 years old in 1974 to 34 years old in 2004.⁵ If rates of incarceration and release by age are always the same, then the age structure of the prison population would be a constant function of the age structure of the general population. However, rates of incarceration and sentencing patterns have not been constant. At least a quarter-century was characterized by an ever greater proclivity to incarcerate, deny parole, and lengthen sentences. Indeed, as discussed at the beginning of this article, these changes often are pointed to as the best explanations for the “graying” of the prison population.

This late twentieth-century “crack down” hypothesis is intuitive: More time in prison should lead, all else equal, to an older population. Although this intuition may not prove correct, it does usefully suggest a redefinition of mortality in the prison population as not death per se (even though prison deaths do exist) but as an exit from prison (including, occasionally, by death). Under this redefinition, longer prison terms are analogous to longer life expectancy or to lower mortality (chance of exit), hence, an aging population. The redefinition of mortality as an exit provides the key to allowing demographic tools to be applied to this population.

In the same way, increases in the rate of incarceration are akin to increasing fertility, which makes populations younger, not older. Crime is a young person’s game, which means that entries to prison are concentrated at the earliest adult years. The relative constancy of the age–crime curve, with its sharp decline after early adulthood (Gottfredson and Hirschi, 1990; Steffensmeier et al., 1989; Wilson and Herrnstein, 1985), means that most incarceration happens among the young with initial incarcerations after young adulthood being something of a fixed function within cohorts.

In sum, we argue that the age structure of the prison population can be understood by using demographic tools to look at processes analogous to fertility (prison admissions) and mortality (exit from the prison system). However, before delving into our demographic analysis of prison growth and aging, we first review research on the relationship between age and crime, as well as between age and incarceration.

PRISON AGING

The age–arrest curve is an iconic “fact” in the field of criminology (Gottfredson and Hirschi, 1990). Arrest rates rise dramatically from 10 years of age to a peak around 18 followed by a more gradual decline over the life course (Levitt, 1999; Wilson and Herrnstein, 1985) and are fairly constant over time. The age–incarceration curve follows a similar shape, although the sentencing literature has suggested we should expect the peak age to be later. Steffensmeier, Kramer, and Ulmer (1995) showed that among those convicted, a ∩-shaped relationship existed between age and both sentence length and imprisonment decisions. Youth younger than 20 years of age receive comparatively lenient treatment; those in their 20s receive the harshest sentences followed by a fairly steady decline in punitiveness starting in the 30s.

Like Steffensmeier et al. (1989), we think there should be more skepticism regarding the degree of constancy in the shape of these oft-tabulated, age-specific curves. The original statement of the age–invariance hypothesis is at once sweeping—“our thesis is that the age effect is invariant across social and cultural conditions” (Hirschi and Gottfredson, 1983: 560)—and imprecise since the meaning of an “age effect” is vague. The theoretical underpinning is clear enough. The age effect is about a process that occurs across the life course for some combination of social, psychological, and physiological reasons. For that reason, the “age effect” should be apparent within cohorts. Hirschi and Gottfredson (1983) provided an example: the famous age pattern of delinquency in a birth cohort from Wolfgang, Figlio, and Sellin (1972). However, most examples of the age–crime curve tabulate crime rates by age for a specific period with the assumption that the same pattern obtains within cohorts (Hirschi and Gottfredson, 1983). Yet even if the basic shape of the age–crime curve should be apparent and relatively invariant within cohorts, the age patterns may vary across cohorts.⁶ Changes over time in the propensity to incarcerate (National Research Council, 2014) could lead to larger numbers in prison at all ages for birth cohorts who “came of age” during that period (e.g., the 1980s).

If a characteristic “age effect” to incarceration is concentrated in young adulthood and declines thereafter, then much or even most of the secular change in incarceration within the United States should show up statistically in what are known as cohort effects (Smith, 2008): enduring differences over the life cycle (ages) depending on when young men reached adulthood. Certain cohorts may have offended and/or been incarcerated at higher rates during their younger years for any number of historical, political, or sociological reasons. Higher numbers of initial (young-adult–age) incarcerations, which then lead into higher levels of incarceration at later ages—as a result of either continued incarceration within a given sentence or all of the negative judicial, sociological, and criminological sequelae to an early incarceration—will create age patterns of incarceration that are similar in pattern by age within cohorts but may vary in age pattern across cohorts. Such are cohort effects. Period effects, on the other hand, are an alternative way of thinking about what happens when the incidence of offending and/or the propensity to incarcerate is changing over time. They would be observable, in the statistical sense, if changes in offending and/or punishment went up or down without respect to age. More young adults would still be in prison than old adults because young adults offend more and are punished more, whatever the prevailing standards for both crime and punishment. Unlike the cohort perspective, the period effects view of social and criminological change posits no “memory” in the system: That 35-year-olds in 2004 were 22-year-olds in 1991 would be irrelevant; the relevant period-specific age curve would relate their incarceration status to that of 22-year-olds in 2004.

The aging and growth of the prison population often are attributed to tougher sentencing policies adopted in the 1980s, such as “three strikes” laws and the anti-drug abuse acts of 1986 and 1988 (Maschi et al., 2012; Nellis, 2010; Reimer, 2008; Rikard and Rosenberg, 2007). Changes in the sentencing climate may have occurred indiscriminately across cohorts (period effect). However, certain birth cohorts may have been differentially impacted by such policies (cohort effect). For example, if the crackdown on drug crimes in the 1980s disproportionately affected those at peak crime ages (i.e., people born in the 1960s), this might have led to high incarceration rates for this cohort during the 1980s and afterward given high recidivism rates. Once an individual is ensnared by the criminal justice system, extant research has suggested that it is difficult to avoid future contact. For example, a recent study found that 75 percent of former prisoners across 30 states were rearrested within 5 years (Cooper, Durose, and Snyder, 2014). Difficulties staying out of prison are usually attributed to the stigma of a criminal record (Pager, 2003) or to lengthy separations of inmates from the labor market and from outside ties (Apel and Sweeten, 2010; Massoglia, Remster, and King, 2011).

Alternatively, a cohort effect could be driven by differences in background characteristics or behaviors. For example, Pollack, Reuter, and Sevigny (in press) have documented the presence of an aging cohort of drug users who may be relatively “incarceration prone.” They have found that the median age of a new inmate who reported abusing cocaine in the month prior to arrest increased 7 years from 27 years of age to 34 in the time period 1986 to 2004. An aging cohort of drug users also has been evidenced in the general population. In recent years, an increase in drug use has occurred among individuals older than 50 years old or, in other words, those born in the late 1950s and early 1960s (National Institute on Drug Abuse, 2015). It therefore seems plausible that the growth and aging of the prison population is a result of the differential drug involvement of certain cohorts. Indeed, Pollack, Reuter, and Sevigny have also found that little evidence exists that the changes are driven by an increase in sentence length (Pfaff, 2011, 2012, 2013; Raphael and Stoll, 2009, 2013).

Our current study investigates two related questions. First, we examine whether it continues to make sense to think of the age pattern of incarceration as constant and, to the extent that it is not, whether the secular changes that lead to increases and decreases in incarceration are better conceptualized as period or cohort effects. Our results suggest that these changes are more cohort than period effects. Second, we investigate which characteristics differentiate cohorts of inmates and test the extent to which these characteristics, such as sentence length and drug use, mediate the cohort effect that we observe. We present our data, analytic strategy, and results in the following sequence: 1) We first describe our data source, The Survey of Inmates in State Correctional Facilities. 2) We then detail our analytic strategy for estimating the age–period cohort model and the results of that basic model. 3) We then proceed to describe the additional variables and analyses we employ to investigate cohort differences. 4) Finally, we present the results of our second analysis, which suggest that much of prison aging and growth is a result of higher rates of drug use among those born in the 1960s.

DATA

The correctional population is broadly defined as adults on probation, parole, and incarcerated in state or federal prisons and local jails (Glaze, 2010). Ideally, we would want annual data on the population of all people under correctional control in the United States. However, to include all correctional populations poses difficulty as a result of the complexity of jurisdiction and inconsistencies across data sources (Glaze, 2010). The only existing nationally representative surveys for correctional facilities commissioned by the Bureau of Justice Statistics were collected by the U.S. Census Bureau in different years for jails (1972, 1978, 1983, 1989, 1996, and 2002) and state prisons (1974, 1979, 1986, 1991, 1997, and 2004). The Survey of Inmates in Federal Correctional Facilities also was conducted in 1991, 1997, and 2004 but not in the 3 earlier years for which state data exist. Under these circumstances, we focus on state prisons in large part because of their prominence in the overall discussion about mass incarceration, which tends to focus on prisons and not jails. State prisons also hold most prisoners in the United States (87 percent in 2004).⁷ In addition, a key feature of the Survey of Inmates in State Correctional Facilities that is not available in the many censuses of the prison population are the ages of inmates, in single years, at the time of the survey.

A stratified two-stage selection was employed in the sample design. In the first stage, the state prison universe was defined and a representative prison sample was selected by taking into account prison population, facility type, and security level (U.S. Department of Justice, Bureau of Justice Statistics, 1974, 1979, 1986, 1991, 1997, 2004). In the second stage of the sample selection, a random sample was selected based on the list provided by the facility, which included all inmates using a bed the previous night. The sample sizes were 9,008 in 1974, 11,369 in 1979, 14,560 in 1986, 13,931, in 1991, 14,282 in 1997, and 14,459 in 2004. The general content of the survey remained the same over the years with the addition of new background questions in more recent survey instruments.

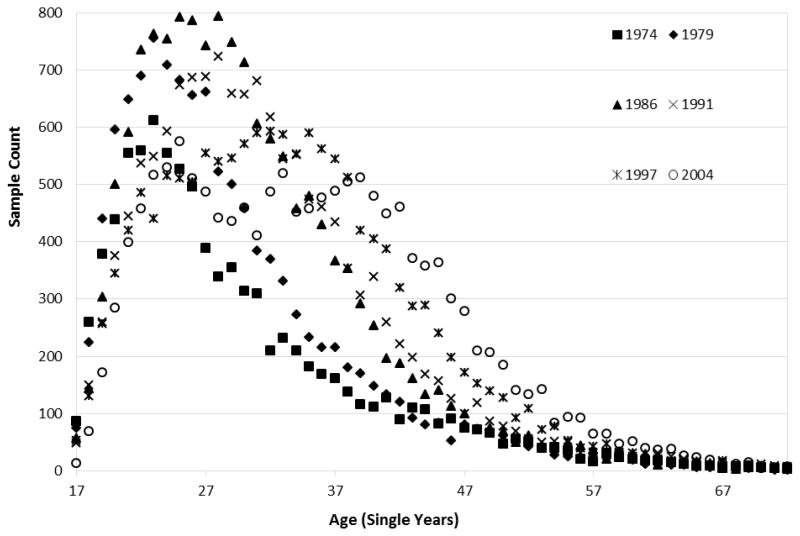
To assess whether sample sizes are large enough to support an age–period–cohort analysis, we consider the estimation of age-specific counts. Let n(a, t) be the number of prisoners age a in year t, where t = 1974, 1979, 1986, 1991, 1997, 2004 and a is a single year of age. As a result of the low numbers of inmates at the tails of the age distribution, we leave out teenagers younger than 17 years of age and truncate older inmates at 72. This makes little or no difference in the age distribution of inmates because few were outside these boundaries. But it does make comparisons across years simpler and is relevant when examining the mean age of the general population as there are many persons a < 17 and a > 72. We estimate n(a, t) as n̂(a, t) = F(s[a,t]); i.e., we do not have a complete count of prisoners but an estimate n̂(a, t) for each sample t, a Horvitz–Thompson estimator ℱ(■) of the age-specific (a) population total based on an observed age-specific sample count, s[a, t]. As figure 1 shows, the density of age-specific counts s[a, t] is high across ages with s[a, t] > 50 in general for a ≤ 50 (and for a < 60 for t = 1997and for a < 60 for t = 2004); and the overall sample size s[t] = Σ_a s[a, t] is of the same order of magnitude across surveys.⁸

Figure 1.

Sample Counts by Single Year of Age: Six Surveys

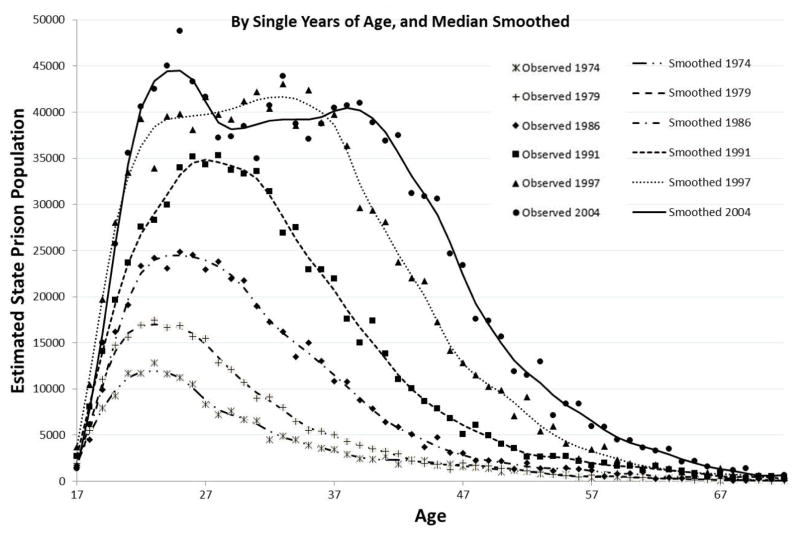
To gain some of the benefits of grouping without losing the single age years, we generate smoothed incarceration counts from the data on a yearly basis rather than thinking of any particular single year of age as a sample independent of the counts of near-neighbors. As shown in figure 2, the surveys through 1991 probably admit to a simple parametric form, where the advantage of a parametric form is that it makes it easier to formalize the reduction in sampling error attendant to the imposition of a “model” (the parametric form). Whatever this parametric form might be, it cannot be sustained for 1997 and 2004. As a result, we chose lowess smoothing ([very] local regressions), as per Velleman (1980), and opted for the 4253H, twice algorithm.

Figure 2.

Estimated State Prison Population from Six Surveys, 1974 to 2004

The theory of the robust median smoothers is that one wants to borrow information where there is support (in the statistical and econometric sense) but not to smooth too much, where “too much” means getting rid of outliers at all costs. Thus, in figure 1, we display the smoothed data and the underlying age-specific estimates. In figure 2, the smoothed data are represented by the lines, whereas the age-specific estimates are shown by symbols. Points near the line are absorbed into it, literally and visually, and all that are left are the outliers. We are not concerned with the effects of smoothing at older ages because the population is sparse there and the sampling error does not much affect our estimate of how many individuals are behind bars.

This also puts more emphasis on 1997 and 2004, the two surveys for prison populations greater than one million. The “jumpiness” in the data by age is not simply a function of comparative population size. The age distribution in 2004 is simply “lumpier” and less regular, and even the smoothed distribution looks the least like the others. If a lot of 22-year-olds entered prison in 1997, some of them with long sentences, and the tendency is not to let people out too early, then ceteris paribus 29 year-olds should be comparatively numerous in 2004. However, in these data, the single ages for which there are peaks in one sample are not always also peaked in the next sample (age plus the time interval between surveys). We believe that single-year peaks (and troughs) are more likely noise and, thus, treat the median-smoothed estimates as our best estimates of the underlying incarceration counts.

ANALYTIC STRATEGY

AGING PRISON POPULATION

As indicated in figure 2, most of the growth in the size of the prison population is through 1997, but the average age of the correctional population increased between 1979 and 2004. Table 1 shows that the average age actually declined between 1974 and 1979 even as the incarceration rate grew. The mean has increased steadily since 1979. The intervals between surveys are only 5 to 7 years, so these are large changes. The distributions are right-skewed, so the median lags the mean (but not by much) and the mode, which is the age at which incarceration is most pronounced, lags both the mean and the median.

Table 1.

Characteristics of the Age–Incarceration Curve, Nonstandardized

Year	Distributional Characteristics							Numbers of inmates (000s)
	Location (Central Tendency)			Spread/Shape			% 40 and older	Ages 17–72	Ages 40 and older
	Mean	Median	Mode	SD	Skew	Kurtosis
1974	29.7	27	23	9.95	1.32	4.59	16%	191	30
1979	29.1	27	23	8.98	1.42	5.26	12%	275	34
1986	30.6	29	24	8.88	1.25	4.95	14%	451	63
1991	31.9	30	27	9.33	1.10	4.48	18%	710	127
1997	33.7	33	33	9.72	0.70	3.38	25%	1,149	290
2004	35.2	34	25	10.43	0.55	2.84	33%	1,221	408

NOTES: The Western age convention is that one is 30 years of age from the time of the 30th birthday up to the day of the 31st birthday. Thus, from the standpoint of “years lived,” reported ages are underestimates by a factor of roughly one half a year. In taking averages of age, it often makes sense to scale them up by a factor of 0.5, but this is not done here because the figures are graphing ages as though 30-year-olds have lived 30 years exactly, and so on. Also, the age distribution is weighted by the smoothed estimates of age-specific totals.

ABBREVIATION: SD = standard deviation.

The extent of the increase in the mean age over fairly short periods is consistent with people staying in prison longer. But new people also are coming in, and although they theoretically could come in at any age, they are more likely to enter at younger ages. As a result, the mean age tends to pull downward as births are what make a general population younger. These processes can be difficult to see in successive cross sections. If we focus, for example, on the age curves in 1979, 1986, and 1991, we see plenty of indication of the general increase in incarceration at all ages. At the same time, the peaks of the distributions are moving to the right, toward older ages, at a rate not too much less than the rate defined by the time between surveys. These are potentially “cohort effects.” Between 1997 and 2004, the cohort pattern is stark: Fairly simple functions map the numbers of inmates at all ages from, for example, 35 years old and older in 1997 onto the corresponding numbers 7 years older in 2004.

Statistical models for the demographic decomposition of aggregated age-by-period data have been used to study related topics in criminology, such as shifts in the age pattern of homicide arrest rates (O’Brien, Stockard, and Isaacson, 1999). Much of the discussion of models with terms for age, period, and cohort concerns the plausibility of identifying restrictions for estimating the coefficients associated with each demographic component (Fienberg, 2013; Held and Riebler, 2013; Luo, 2013; O’Brien, 2013; Yang and Land, 2013b) because otherwise these coefficients are not uniquely identified (Fienberg and Mason, 1979; Searle, 1971; Yang, Fu, and Land, 2004). If a researcher knows an individual’s age in a given period, then he or she also knows cohort (birth year or, perhaps, year attaining adulthood) because a linear combination of any two variables will produce the third variable.

However, the predicted values of the dependent variable are estimable even when specific coefficients corresponding to effects are not, and the fit of the three-effect model can be compared with the effects of models by using only two effects (Mason et al., 1973). O’Brien and Stockard (2009) referred to this as the “estimable function approach” for estimating the effects of age, period, and cohort. Although we cannot estimate (without a linear constraint) the specific age, period, and cohort coefficients when linear terms for all three dimensions of time are simultaneously included in a model, the predicted values for the number of inmates incarcerated will be (under the model) the best linear unbiased estimates of these numbers (O’Brien and Stockard, 2009; Scheffé, 1959; Searle, 1971). Thus, we can 1) compare the fit of any two-factor model (e.g., age–cohort model) with that of the three-factor, age–period–cohort model; and (2) compare predicted with observed values for data arrayed according to any two dimensions (e.g., predicted and observed values by age for each year in which the surveys took place).

Our general equation is a Poisson regression:

$$log{y}_{tj}=\mu +{\mathrm{\alpha }}_i+{\mathrm{\pi }}_j+\sum _{\ell =1}^5{\mathrm{\beta }}_{\ell }f{(k)}^{\ell }$$

The y_ij are the nonparametrically smoothed Horvitz–Thompson estimates of incarceration counts by single year of age (i) and survey year (j) discussed in the previous section. They are logged, and the equations are estimated as Poisson regressions so that predicted numbers of inmates under various models have positive values. Predictor variables are dummies for age and survey years so that α_i is the effect of the ith age and π_j is the effect of the jth period. There are six periods (1974, 1979, 1986, 1991, 1997, and 2004). There are 56 single years of age (ages 17 to 72), and because the surveys span a 31-year (from 1974 to 2004) period, there are 86 potential birth cohorts (k), that is, the birth years of inmates observed across all samples. We employ many terms to fit the age distribution because the details of the age distribution are of great interest. However, as one of our empirical points is the preference for age–cohort models to age–period models even when focusing on the age distribution in any given period, we did not want to give the age–cohort model an arbitrary “advantage” because of the design of the data matrix (many more ages than survey years, hence, many more single-year cohorts [Clayton and Schifflers, 1987: 460–1]). If cohort also were measured as an 80+ category polytomy, the degrees of freedom would differ substantially as between age–period and age–cohort models. Thus, to facilitate comparisons, we have modeled cohort by using five unique parameters.⁹ The five cohort parameters (β_ℓ, ℓ = 1, …, 5) are successive coefficients in a polynomial in which cohort (k) is indexed with values ranging from 1 to 86, where 1 = individuals who were born in 1902, 2 = individuals born in 1903, and so on.¹⁰

When we examine age–period models, then β_ℓ = 0 for all ℓ and it suffices that the coefficient for one category of each factor for age (α_i) and period (π_j be arbitrarily set to zero to identify the equation, as is standard in two-way analysis of variance via dummy variable representations of factors. When we examine age–cohort models, the polynomial representation for cohort renders the equation more like an analysis of covariance (because the cohort terms are continuous) and identification is achieved via a single restriction on the age factors (α_i). However, when we examine age–period–cohort models, the model’s linear terms are not identified pending further restrictions. This has long been recognized when age, period, and cohort are continuous linear variables and/or are represented by factors (or sets of dummy variables) (Fienberg and Mason, 1979; Mason et al., 1973), and it is true when a dimension is represented by a polynomial (Fienberg and Mason, 1985; Yang and Land, 2013a: 66). Setting two nonzero effects for a factor to be equivalent is one solution (Mason et al., 1973); setting the linear polynomial term to zero (β₁ = 0) is another alternative (Fukuda, 2013: 140). The choice of the identifying restriction can have a big effect on estimated parameters (Mason and Smith, 1985), but all just-identified models fit the data equivalently (Fienberg and Mason, 1985: 80; Yang and Land, 2013a: 65–6). In this estimable functions approach, the estimated effects are not of interest. The emphasis is on a comparison of observed data with the fitted values from a given representation of the data (age–period, age–cohort, age–period–cohort). In the next section, we describe the results of this analysis.

PERIOD OR COHORT EFFECT?

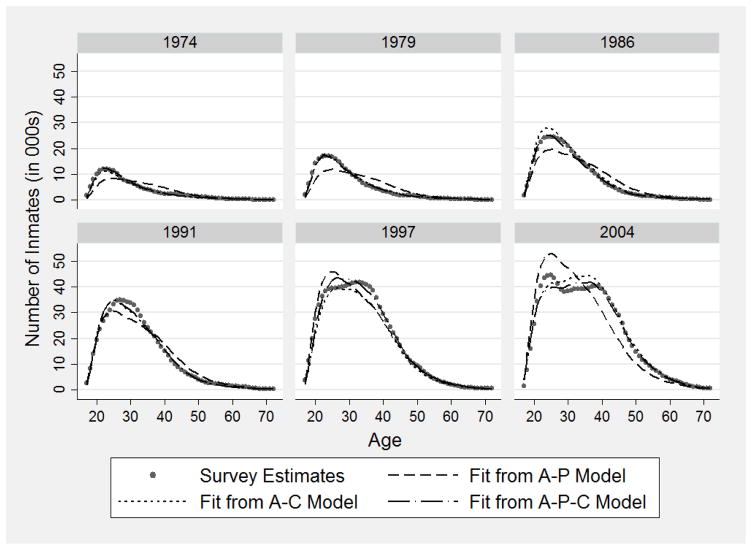
Figure 3 compares the observed counts (under the original sampling estimation and smoothing procedures) with fitted values under the general age–period–cohort model, as well as with restricted age–period (β_ℓ = 0, ℓ = 1, …, 5) and age–cohort (π_j = 0, j = 1, …, 6) cohort models. These are graphed by age for each of the 6 survey years. Because the observed data—the dotted line—are the smoothed estimated inmate population counts, the ever greater number of persons incarcerated, at least through 1997, remains, as per figure 3, the central feature of these data. But the pattern by age within each year does vary, and here the comparison of the age–period (A-P) and age–cohort (A-C) models is instructive. The A-P model, which harkens most closely to the Gottfredson and Hirschi (1990) paradigm—similar shape of age curves over time even as overall levels of offending and/or incarceration change—is often a poor fit to the observed data. This is not surprising because, algebraically, the A-P model is a curve with the same location (mode) in every year, scaled up or down proportionately by a year-specific factor. In contrast, the A-C model provides a better (or equivalent) description of the age pattern of the prison population in all 6 survey years; in 1974 and 1979, the survey estimates cannot be distinguished from the fit under the A-C model, and in no other year is the A-P fit preferable. Nor is this an artifact of overfitting the data: The model has been specified (i.e., the five-term polynomial for cohort) so that the degrees of freedom are the same. There are some occasions when a period (P) factor does improve the fit as in both 1986 and 1997, the A-P-C fitted values are better. In 1997, there does seem to have been an upward effect on imprisonment at all ages even after taking cohort differences into account. In 1986, imprisonment levels were somewhat less than might have otherwise been expected from the growth in imprisonment across successive cohorts.

Figure 3.

Single-Year Age Distribution of Inmates 17 to 72 Years Old in Six Survey Years (N = 336): Smoothed Survey Estimates and Fitted Values under Models for (a) Age and Cohort (A-C), (b) Age and Period (A-P), and (c) Age, Period, and Cohort (A-P-C)

Other things are going on during these years that are not captured by any of these additive age, period, and cohort representations. The fact that a just-identified age–period–cohort (A-P-C) model will not necessarily yield a perfect fit to the data, whereas a standard analysis of variance with interactions for a square table age (A) × period (P) would (i.e., A + P + [A × P]) is a reminder that many potential A × P and/or A × C and/or P × C interactions could still be modeled (Fienberg and Mason, 1985: 71–80). Thus, the deviations of the A-P-C model in figure 3 from the observed data represent potentially omitted interactions. In 1997, in particular, there were many more inmates in state prisons in their 30s than could have been expected from changes in cohort size and intensity of incarceration wedded to a standard age pattern within cohorts; something similar was going on in 1991, albeit at a lesser level. Both of these interactions, along with the double-humped age curve for 2004, may be indicative of the age × cohort (or period × age) interaction implied by Luallen and Kling’s (2014) finding of greater entry at older ages. Since, however, our primary interest is contrasting period-specific with cohort-specific representations of changes in the intensity of imprisonment, we have not attempted to model these interactions explicitly. See Fienberg and Mason (1985: 79–80) for a related perspective.

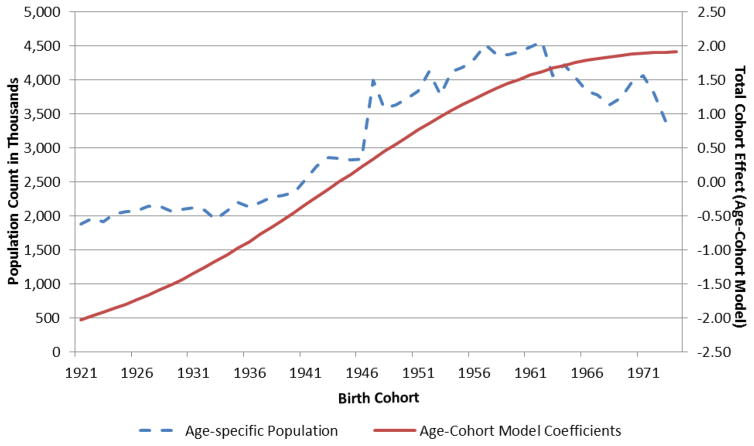
Figure 4 illustrates that the substantial cohort effects that do exist are in some sense the simple size of the successive generations at risk (recall that our outcome is the number of prisoners), but more recently, they reflect period-specific changes in the propensity to incarcerate. We chose to highlight the population figures in 1991 by using cohort effects estimated from the model. We chose 1991 because the cohorts from 1950 to 1975 would be still be largely unaffected by substantial death rates, and therefore, they would best demonstrate the true differences in cohort sizes. The horizontal or x-axis is the age-specific population distribution in 1991, but here it is indexed by birth year (or cohort) rather than by age. The jagged line is, therefore, the number of people from that birth cohort in 1991. It also can be “read backward” as the fertility history of the United States. For example, the largest cohorts correspond to the peak years of the “baby boom” from the mid-1950s through the early 1960s. The smoothed line shows the predicted number of prisoners by a given cohort (listed on the x-axis) from our age–cohort model. The number represents the net effect across the five different polynomial terms for each cohort. As our model is one for the age-specific stocks of inmates (their count or number, not a rate of incarceration relative to the general population), it is not surprising that a good part of the cohort effect is a reflection of changes in the size of the general population. Cohort effects in figure 4 largely track the baby boom, which lasted into the early 1960s. However, even with the onset of the “baby bust,” beginning in the second half of the 1960s, cohort effects continued upward for many years (albeit at a slower rate). This is not a surprise given that the 1980s and 1990s were a period of increasing punishment and incarceration. The social and political factors underlying this change (National Research Council, 2014: 104) were sufficiently strong as to “grow” the prison population even as the general population was receding in the number of young adults.

Figure 4.

Age—Cohort Model Coefficients and U.S. Population Counts Across Birth Cohorts in 1991

What is striking is that these changes can be captured so well by a model that focuses on cohorts. It is true that, in the statistical sense, some period effects add with respect to the cohort effects emphasized here because an age–period–cohort model does explain some additional variation that the age–cohort model alone does not. Also, some higher order interactions exist among age, period, and cohort because there are some years for which even the age–period–cohort model does not provide a tight fit to the data. That said, the age–cohort representation is parsimonious and does describe the data reasonably well. We thus wish to move beyond the designation (based on statistical criteria) of effects as pertaining to “periods” versus “cohorts.” Instead, we point out that the within-cohort age trajectory of incarceration (like the within-cohort age trajectory of criminal behavior) makes period-specific change in laws, social values, public policy, or even the “criminal environment” most likely to work its way through the subsequent age distribution of the prison population in a manner that is associated with factors obtained when the different cohorts composing a population were young adults. Our results highlight the importance of cohort differences, suggesting that period-specific events (e.g., drug epidemics and legislation) may have disproportionately affected different cohorts.

Longer sentence lengths are not the reason for the increase in the average age of prisoners because the same period-specific factors that generate longer prison terms for some individuals concomitantly bring more individuals into prison for offenses with shorter sentences. This basic fact is also why sentence length has played a comparatively small role in the growth of the size of the prison population (Raphael and Stoll, 2009, 2013). What is more germane is the sheer number of persons in prison in young adulthood because even without a cohort-specific increase in the length of sentence of the average prisoner, the cohort is now defined in a way that will contribute to the age distribution of the future prison population. Many incarceration spells are followed by future spells (Cooper, Durose and Snyder, 2014) so that even if a given 22-year-old is no longer in prison when his birth cohort has aged to 27, he is more likely to be back in prison at age 32; hence, ceteris paribus, incarceration in that cohort remains high. We next examine variation across cohorts that might explain this effect.

UNDERSTANDING THE COHORT EFFECT

The Survey of Inmates series includes several items that can be employed to address our second research aim, which is to understand the cohort effect we observe in our first analysis. We exclude data from 1974 as a result of the limited availability of measures at this wave. Variables were then generated at each remaining wave (1979–2004) at the individual level and were aggregated to age-specific mean values. Table 2 provides a description of the variables used in our second analysis.

Table 2.

Survey of Inmates Variable Descriptions (N = 280)

Variable Name	Description	Mean	SD
Demographics
Black	Percent Inmates Black	.418	.131
Hispanic	Percent Inmates Hispanic	.120	.067
Other Race	Percent Inmates Other Race	.042	.036
Male	Percent Inmates Male	.822	.078
Substance Use
Used Cocaine in Month Prior	Percent Used Cocaine/Crack in Month Prior to Arrest	.141	.109
Used Heroin in Month Prior	Percent Used Heroin in Month Prior to Arrest	.071	.055
Used Methadone in Month Prior	Percent Used Methadone in Month Prior to Arrest	.016	.016
Used Marijuana in MonthPrior	Percent Used Marijuana in Month Prior to Arrest	.445	.296
Used Barbiturates in MonthPrior	Percent Used Barbiturates in Month Prior to Arrest	.030	.034
Used Amphetamines in Month Prior	Percent Used Amphetamines in Month Prior to Arrest	.062	.048
Cocaine	Percent Ever Used Cocaine	.291	.195
Heroin	Percent Ever Used Heroin	.181	.127
Methadone	Percent Ever Used Methadone	.075	.057
Marijuana	Percent Ever Used Marijuana	.509	.293
Amphetamine	Percent Ever Used Amphetamines	.170	.121
Barbiturates	Percent Ever Used Barbiturates	.152	.131
Attended Drug Treatment	Percent Attended Drug Treatment Program	.284	.212
Under the Influence of Drugs	Percent Under the Influence of an Illegal Substance at Time of Offense	.206	.142
Under the Influence ofAlcohol	Percent Drinking at Time of Offense	.329	.114
Socioeconomics
Received Public Assistance	Percent Whose Family (or Themselves) Received Public Assistance Prior to Arrest	.265	.151
Employed Prior toIncarceration	Percent Employed at Time of Arrest	.667	.121
Educational Attainment	Average Educational Attainment (0 = less than high school, 1 = some high school, 2 = high-school graduate or GED, 3 = some college, 4 = college graduate)	1.406	.371
Family
Two-Parent Household	Percent Grew Up in Two-Parent Household	.470	.162
Have Children	Percent Who Have Children	.699	.190
Married	Percent Married	.232	.129
Military History
Ever Serve in Military	Percent Ever Served in Military	.258	.194
Years in Military	Average Number of Years Served	.962	1.097
Unfavorable MilitaryDischarge	Percent Received an “Unfavorable” Discharge (includes “other than honorable,” “bad conduct,” and “dishonorable”)	.033	.044
Criminal and Incarceration Background
Property Offense	Percent Incarcerated for Property Offense	.169	.095
Drug Offense	Percent Incarcerated for Drug Offense	.144	.086
Violent Offense	Percent Incarcerated for Violent Offense	.564	.133
Time Served	Average Number of Years Served by Time of Interview	4.312	2.637
Sentence Length	Median Number of Years Sentenced to Serve	10.252	4.029
Age at First Commitment	Average Age of First Incarceration	34.649	12.933
Number of TimesIncarcerated	Average Total Number of Prior Incarcerations	1.015	.471
Percent Sentence Expected	Average Percent Sentence Expected to Serve	82.800	9.268

ABBREVIATION: SD = standard deviation.

We include demographic measures, as well as measures of substance use, family structure, socioeconomic background, and military service. Some cohorts may have been more vulnerable to the popularity and availability of crack in the 1980s or heroin in the 1970s, leading to higher rates of substance use. Other variables, such as employment and marital status, also are established correlates of criminal behavior and may illuminate important differences across inmate cohorts. We also include data on current and past involvement with the criminal justice system to address the possibility that certain cohorts differ in their imprisonment experiences (e.g., longer sentences) or are more likely to be imprisoned for certain crimes (e.g., greater proportion of drug offenders). In addition to drug convictions being pertinent, a recent report noted that the growth rate of older prisoners is faster among violent inmates (Kim and Peterson, 2014).

To assess the total mediation attributable to these variables, we use an elaboration of the product of coefficients method that accounts for multiple mediators and multiple independent variables (Preacher and Hayes, 2008). We first regress the age-specific count on age and cohort variables, excluding prisoners younger than 18 years of age or older than 72 from our analysis as a result of small numbers of inmates in those age groups. We then adjust for our slate of mediators and test the mediation of each variable. The total indirect effect for each mediator is determined by multiplying regression coefficients for 1) the mediating variable (MV) regressed on the independent variables (IV) and 2) the dependent variable (DV) regressed on the MV and IV. Both regressions are estimated by controlling other covariates, including age dummies and other mediators. To compute the total direct effect, we sum the coefficients for the age-specific count regressed on all five cohort measures (coefficients c₁ through c₅). Results include a total indirect effect estimate and the standard error to determine whether the total indirect effect is statistically significant. Once we obtain the total direct and the indirect effects, it is also possible to calculate the percentage of the total effect that is mediated by each variable by using the simple equation: (b_indirect/b_indirect + b_direct).

In model 1 of table 3, estimates are shown for the age–cohort model with no controls. As before, we measure cohort by using five polynomial terms. Coefficients for age categories are not shown for the sake of parsimony. Model 1 is analogous to the age–cohort model used to generate estimates shown in figure 3, albeit excluding data from 1974. Thus, the predicted values are also similar, indicating larger numbers of inmates for birth cohorts in the 1960s. In the second model, we include inmate characteristics and find that cocaine use, heroin use, methadone use, barbiturate use, and drug treatment emerge as significant predictors of the age-specific incarceration count (see table S4-1 in the online supporting information for full results). Overall, we find that most variables are significantly related to age-specific prisoner counts for the time period analyzed. However, statistical significance does not equate to significant mediation.

Table 3.

Age-Cohort Model with Selected Covariates

Variable	b (standard errors)		b (standard errors)
Cohort
Cohort 1	1.165 (.002)	**	1.011 (.010)	**
Cohort 2	−.025 (.001)	**	−.060 (.003)	**
Cohort 3	−.068 (.000)	**	−.034 (.001)	**
Cohort 4	−.001 (.000)	**	.000 (.000)
Cohort 5	.003 (.000)	**	.001 (.000)	**
Substance Use
Lifetime Cocaine Use			−.524 (.029)	**
Lifetime Heroin Use			.207 (.035)	**
Lifetime Methadone Use			.390 (.049)	**
Lifetime Marijuana Use			.764 (.027)	**
Lifetime Barbiturate Use			−.302 (.028)	**
Lifetime Amphetamine Use			.369 (.034)	**
Used Cocaine in Month Prior			.589 (.037)	**
Used Heroin in Month Prior			−.275 (.056)	**
Used Methadone in Month Prior			1.285 (.098)	**
Used Marijuana in Month Prior			−.137 (.011)	**
Used Barbiturates in Month Prior			.559 (.067)	**
Used Amphetamines in Month Prior			−.845 (.048)	**
Drunk at Time of Offense			.102 (.022)	**
Under the Influence at Time of Offense			.545 (.033)	**
Attended Drug Treatment			.269 (.020)	**
Criminal History and Current Incarceration
Property Conviction			−.431 (.037)	**
Drug Conviction			.269 (.037)	**
Violent Conviction			.062 (.033)
Number of Prior Incarcerations			.054 (.006)	**
Years Served			−.044 (.002)	**
Years Sentenced			.002 (.001)	*
vPercent Sentence Expected			−.002 (.000)	**
Age First Admitted to Prison			.006 (.001)	**
Constant	5.706 (.010)	**	5.481 (.052)	**
N	280		280
R2	.97		.98

NOTE: Model 2 controls for the full array of variables presented in table 2. Please see the table S4-1 in the online supporting information for the full model.

^*p < .05;

^**p < .01.

To assess the mediation of each variable, we carry out the product of coefficients method described earlier. Our results indicate that recent cocaine use, recent and lifetime barbiturate use, and lifetime methadone use are significant mediators of the relationship between cohort and the incarceration count.¹¹ These variables account for approximately 30 percent of the total effect. In particular, barbiturate use accounts for 12 percent of the total effect, methadone use for 7 percent, and recent cocaine use for 11 percent. Rather than viewing the effects of these drug variables as separate culprits, they likely reflect a greater tendency of certain cohorts to use drugs in general. For example, most substance users are polyusers, meaning they regularly use more than one drug (Mohler-Kuo, Lee, and Wechsler, 2003).¹² This “high-drug-use” cohort may have been likely to use both cocaine (uppers) and barbiturates (downers) in combination. Taken together, our findings suggest that the cohort effect can be attributed in part to differences in drug use across birth cohorts. This is similar to the results reached by Pollack and colleagues (in press), who have noted that between the 1980s and 2000s, there was an increase in the proportion of inmates who were current drug users and an age shift in the population of drug-using inmates, suggesting an aging cohort of particularly drug-involved offenders. In many ways, our findings complement this work, but we find that the disproportionate drug use of these aging cohorts may actually be driving the aging of the total correctional population. Importantly, differences in drug offending across cohorts do not appear salient, nor do differences in sentence length.

DISCUSSION

This article provides a detailed exposition of changes in the age–incarceration distribution of the U.S. state prison population during the period of mass incarceration from 1974 to 2004. A total of 16 percent of the state prison population was 40 years of age and older in 1974, but 33 percent of the state prison population was 40 years of age and older in 2004. The median age increased from 27 to 34. It is hard to overstate the size and the importance of this shift demographically. For example, according to the National Health and Social Life Survey from 1992, 43 percent of men experience the birth of their first child between the ages of 25 and 34. All else constant, the shift in the age distribution of the prison population means that many more children would experience life with a father in prison even if the size of the prison population stayed constant. Research finding effects of parental incarceration on child inequality (Wakefield and Wildeman, 2013) also have suggested that this “high-incarceration cohort” may lead to a cohort of relatively disadvantaged children. These children warrant further attention. In addition, members of this high-incarceration cohort may be especially likely to be “missing” during their employment years and may put added strain on social security and unemployment programs. Given the link between incarceration and health, this cohort also may present a challenge for health-care providers and programs as they continue to age—in or out of prison.

We investigated the nature of this shift with a very different approach than that suggested by Luallen and Kling (2014). By using an estimable function approach, we estimated an age–period–cohort model to determine to what extent the observed changes in the distribution could be explained by changes in the behavior or treatment of a certain birth cohort. We found that cohort effects explain the observed shifts in the prison population extremely well. Essentially, the younger birth cohorts from the 1980s (e.g., those born in the 1960s) seem to have a high incarceration rate across periods even at older ages in 2004. This finding is consistent with Luallen and Kling’s (2014) conclusion that the aging of the prison population is primarily a result of the changing age distribution of admission. Our finding, like Luallen and Kling’s, contradicts popular wisdom for the growth and aging of the correctional population, which often points to a period effect driven by harsher sentence lengths during the 1980s and 1990s. The fact that our results used an entirely different method than Luallen and Kling, with nationally representative data and a longer time horizon, should lead both researchers and policy makers to reconsider the consensus that changes in the prison population are a result of increased sentence lengths (National Research Council, 2014). If this explanation is flawed or incomplete, policies that focus exclusively on reducing sentence length might not deal effectively with aging. Instead, we see a growing consensus that the massive changes in the prison population have been driven by changes that drive admission (and, relatedly, conviction) rates.

Our method also allows us to go a step beyond Luallen and Kling (2014) and explore the underlying mechanisms driving the changing admission patterns from the stable equilibrium that existed prior to the 1970s. We exploit the micro-data in the inmate survey to adjust the model for the influence of inmate characteristics, including demographics, military service, socioeconomic background, criminal history, and substance use. Interestingly, and surprisingly, our results suggest that the cohort effect is a result of behavioral rather than of treatment differences. These cohorts report relatively high rates of drug use, but differences in sentence length and conviction type were not significant mediators. Again, we do not find support for the hypothesis that longer prison sentences during the late twentieth century were responsible for this shift—even cohort-specific increases in prison sentences. Instead, the shift was explained by sustained increases in prison admissions for the birth cohorts that came of age in the 1980s.

One test of the validity of this insight involves looking for a similar pattern in other parts of the system, including arrest and conviction. A recent Bureau of Justice Statistics study showed that the average age of individuals convicted of felonies in the United States increased by 4 years between 1990 and 2009 (Reaves, 2013). In addition, approximately 1 in 5 convicted felons in 2009 were 40 years of age or older compared with 1 in 10 in 1990. Also in line with our results, there was no increase in the percentage of defendants with a drug charge between time periods. Even at the arrest stage, between 1980 and 2004, the percentage of arrestees between 35 and 44 years of age increased from 10 percent to 19 percent (Arrest Data Analysis Tool, Snyder and Mulako-Wangota, 2015). We see the aging of the convicted and arrested populations as potential evidence of this same cohort effect, although future research should investigate this possibility.

This approach is a “broad brush” that builds on the characteristic age pattern of criminality and connects it not only to changes in the sizes of cohorts entering young adulthood but also to the well-known growth in penalization and incarceration that occurred in the last two decades of the twentieth century. It is focused on stocks and ignores the flows, the age-specific entries and exits that constitute (and reconstitute) the prison population at any point in time. This may seem like a flaw of the analysis—a lot of behaviorism and micro-process is missing—but the broad age contours of the prison population can be captured easily, all the comings and goings aside, by a model that emphasizes incarceration numbers in early adulthood. The implications for prediction of the prison population’s future are strong: Absent period-specific events such as the recent Supreme Court ruling on California state prisons (and the “who” and “how” of release is still undetermined), a model that ties early life-course prevalence to a fairly constant age profile is one that allows us to see fairly far into the future (Wang and Preston, 2009).

One limitation in this article is our incapacity to give demographic decompositions of the various effects as a function of changes in the composition of the population with respect to various individual-level traits (from subgroup membership to previous incarceration histories). Yang and Land (2008) blended macro (age, period, and cohort effects) with micro measures on individuals to estimate age, period, and cohort effects for verbal acuity in the United States, and they explained much of the demographic compositional effect in terms of the changes in the educational distribution of the population. The nature of our data is problematic in this regard. The surveys tell us a great deal about the prison population in any year. But the use of those data to predict incarceration is impossible because, by definition, they are all incarcerated. Whether we might someday be able to match these samples to samples from the general population is a task that lies ahead.

Biographies

Lauren C. Porter is an assistant professor of criminology and criminal justice at the University of Maryland. Her research interests revolve around issues of punishment, with particular interest in the trends and consequences of mass incarceration.

Shawn D. Bushway is a professor of public administration and policy at the University at Albany (SUNY). His current research interests involve understanding changes in the criminal justice system and how the criminal justice system affects the desistance process.

Herbert L. Smith is a professor of sociology and director of the Population Studies Center at the University of Pennsylvania. His ongoing research includes the role of cohorts in social change and forecasting the future, as well as the organization of nursing and its effect on health-care outcomes.

Hui-shien Tsao is the manager of user support at the Center for Social and Demographic Analysis, University at Albany (SUNY). Her research interests involve adaptation of immigrants, often concentrating on residential and work-related experiences, and internal migration.