Abstract
Microbial ecologists are increasingly turning to small, synthesized ecosystems1–5 as a reductionist tool to probe the complexity of native microbiomes6,7. Concurrently, synthetic biologists have gone from single-cell gene circuits8–11 to controlling whole populations using intercellular signaling12–16. The intersection of these fields is giving rise to new approaches in waste recycling,17 industrial fermentation18, bioremediation19, and human health16,20. These applications share a common challenge7 well known in classical ecology21,22; stability of an ecosystem cannot arise without mechanisms that prohibit the faster growing species from eliminating the slower. Here, we combine orthogonal quorum sensing systems and a population control circuit with diverse self-limiting growth dynamics in order to engineer two ‘ortholysis’ circuits capable of maintaining a stable co-culture of metabolically competitive strains in microfluidic devices. While no successful co-cultures are observed in a two-strain ecology without synthetic population control, the ‘ortholysis’ design dramatically increases the co-culture rate from 0% to approximately 80%. Agent-based and deterministic modeling reveal that our system can be adjusted to yield different dynamics, including phase-shifted, anti-phase or synchronized oscillations as well as stable steady-state population densities. The ‘ortholysis’ approach establishes a paradigm for constructing synthetic ecologies by developing stable communities of competitive microbes without the need for engineered codependency.
In order to engineer a stable co-culture of two competitive bacterial strains, we first characterized the dynamics of a small library of quorum sensing (QS) components (Supplementary Fig. 1a–c). This was achieved by evaluating different components of natural quorum sensing systems to identify receptor-promoter pairs and signals (AHL) that yield the desired characteristic upon combination (Supplementary Fig. 1d)23. From a range of possible configurations (Supplementary Fig. 2b), we identified that the Lux and Las systems were suitable for one-way orthogonal signaling, and the Lux and Rpa systems were suitable for two-way orthogonal signaling (Supplementary Fig. 1e–g). We used these components to design synchronized lysis circuits (SLCs)16 in two bacterial strains, whereby each strain is programmed to lyse upon reaching a critical population density.
To understand how an ecosystem harboring the synchronized lysis circuit (SLC) can be altered, we established the range of possible self-limiting dynamics of the circuit (Fig. 1a–b). The circuit exhibits oscillations, characterized by periodic lysis events, which are driven by the activation of the Lux-controlled positive feedback loop upon reaching a quorum threshold of AHL, as was seen in earlier work16. A lysis event reduces the population dramatically, and a few survivors resume the process starting again below the quorum threshold. In microfluidic devices, the fluorescent protein sfGFP reports the activation state of the circuit in this oscillatory state (Fig. 1c, Supplementary Video 1). We also discovered a constant lysis state that is characterized by a steady-state in which growth and lysis are approximately balanced, and the stable ON state of the circuit is evidenced by the constant production of sfGFP (Fig. 1d, Supplementary Video 2). Tuning the degradation efficiency of the activator LuxI by changing its ssrA degradation tag, we demonstrated a bifurcation in lysis dynamics of the population between these two states. In a deterministic model of the circuit (Fig. 1b), lower αq corresponds to stronger enzymatic degradation of LuxI (see Methods section for details). Consistently, the oscillatory lysis behavior was observed for the highest level of activator degradation (Fig. 1e–f), dampened oscillations were observed at a lower level of degradation (Fig. 1g–h), and constant lysis behavior was observed for the lowest levels of degradation (Fig. 1i–j). The SLC therefore exhibited two main modes of dynamics lysis with respect to changes in circuit parameters.
Fig. 1.
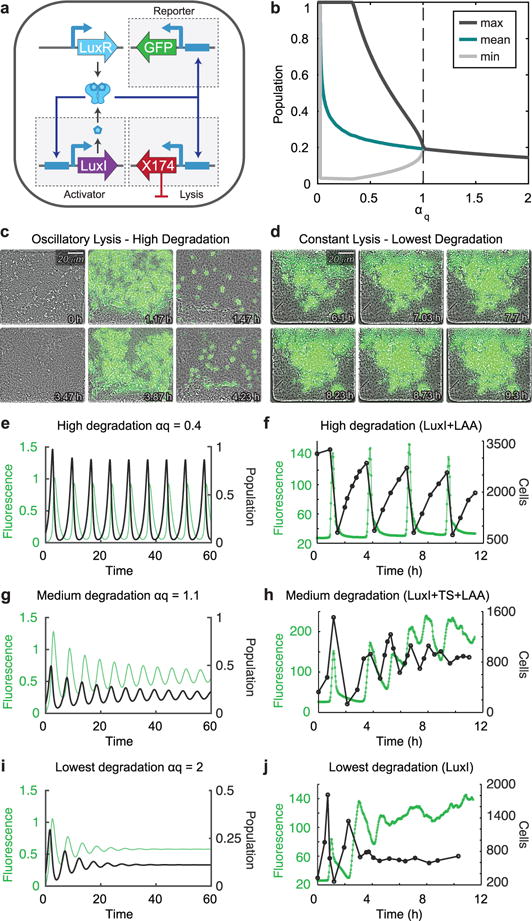
Experimental investigation into the space of population dynamics of a self-communicating synchronized lysis circuit a, Genetic diagram of the synchronized lysis circuit (SLC). The circuit contains a lysis plasmid and an activator/reporter plasmid. Transient production of LuxI eventually leads to an accumulation of AHL above the quorum threshold needed to activate LuxR which begins a positive feedback loop by driving transcription off the PluxI promoters that control production LuxI, GFP, and the lysis gene ΦX174E. LuxR in this system is driven by the native luxR promoter. b, Bifurcation to oscillations in deterministic model of the lysis circuit. Ignoring initial transient behavior, minimum, maximum, and mean population density over time were determined for each parameter value. Lower αq corresponds to stronger degradation (see Methods section for details). c, Video stills showing bacteria harboring the SLC with strong degradation of the LuxI activator (LuxI-LAA) exhibiting oscillations in a microfluidic growth chamber. Oscillations result from repeated cycles of growth, quorum threshold reached, and self-limitation by lysis activation. d, Video stills depicting bacteria harboring the SLC with weaker degradation of LuxI (LuxI with no degradation tag) exhibiting constant lysis. Constant activation of the lysis circuit results in the continual activation of GFP as well as continuous growth and lysis events within the microfluidic chamber. e–j, Changing certain properties, such as the degradation tag of the SLC will result in different population dynamics. e–f, Fluorescence (green) and population (black) over time for cells harboring the SLC with αq=0.4 for the deterministic model (e) and LAA-tagged LuxI for a typical experimental run (f), as seen in c. g–h, Fluorescence (green) and population (black) over time for cells harboring the SLC with αq=1.1 for the deterministic model (g) and TS-LAA-tagged LuxI for a typical experimental run (h). i–j, Fluorescence (green) and population (black) over time for cells harboring the SLC with αq=2 for the deterministic model (i) and untagged LuxI for a typical experimental run (j), as seen in d. The video stills c–d, as well as the fluorescence and population profiles in f, h, and j are all representative of typical microfluidic experiments with these strains.
To build a synthetic ecosystem of two orthogonal SLC strains, we used the previously built circuit based on the Lux quorum sensing system and constructed a new circuit with the Rpa system. The Rpa system had RpaR in place of LuxR and an ssrA tagged RpaI in place of LuxI (Fig. 2a). These strains are called Lux-CFP and Rpa-GFP, respectively, for convenience. Both strains’ gene expression is controlled by the PluxI promoter for consistency, considering pC-bound RpaR can activate PluxI at about 90% the efficiency of AHL-bound LuxR (Supplementary Fig. 2b).23 Although these strains are in the same bacterial host, when started from equal densities in batch culture, Rpa-GFP shows a significant growth advantage over Lux-CFP (Fig. 2b). Because of this growth advantage, a 1:1 mixture of these strains in a batch culture (with or without the lysis gene), is primarily taken over by the faster growing Rpa-GFP strain by the time the strains reach stationary phase (Fig. 2c). However, if the slower growing Lux-CFP strain is enriched 100x more than the green strain, the population stabilizing effects of the lysis circuit becomes evident. Without the lysis gene, the mixture is taken over by the Lux-CFP strain, however with the lysis gene, the population ratio over the initial 10 hours keeps close to a 1:1 ratio. The ‘ortholysis’ strategy thus showed promise in batch co-culture.
Fig. 2.
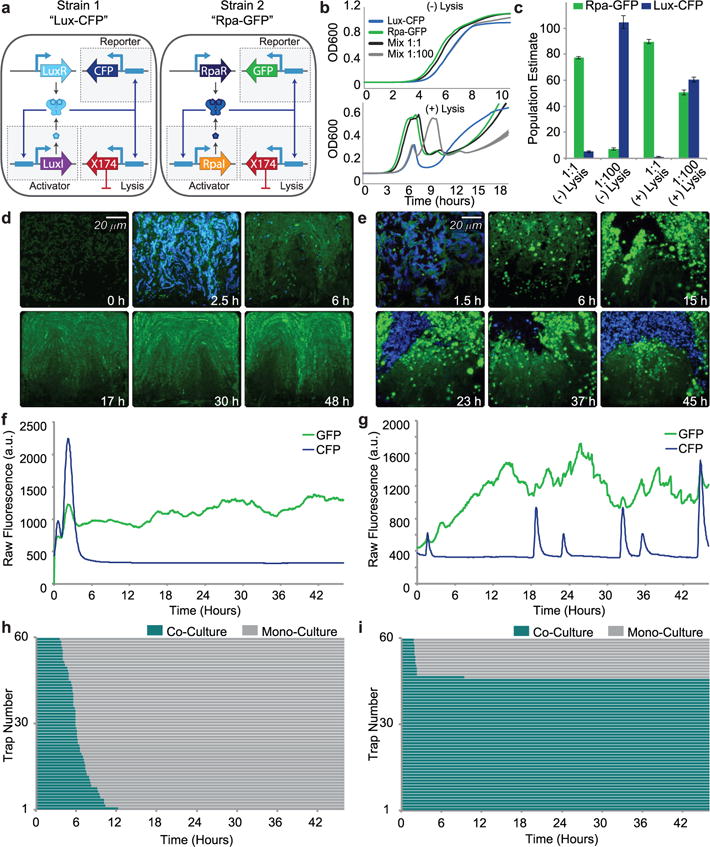
Experimental demonstration of long-term co-culture of competitive species with unequal growth rates using signal orthogonal self-lysis a, Genetic diagram of a two-strain ecosystem of self-lysing Salmonella constructed with two signal orthogonal quorum sensing systems, rpa and lux. b, Batch culture growth curves of the Lux-CFP strain alone (blue), Rpa-GFP strain alone (green), a 1:1 mixture (black), and a 1:100 (Rpa-GFP:Lux-CFP) mixture (gray), both without the lysis gene (top) and with the lysis gene (bottom). All strains were started from the same diluted density and under the same growth conditions. Width of lines represent s.d. (n=3) c, Batch culture population estimates of Lux-CFP and Rpa-GFP co-cultures. Rpa-GFP population estimated as GFP fluorescence (integrated over the full length of the experiment) of the mixture normalized by the time-integrated GFP fluorescence of Rpa-GFP cells alone. Lux-CFP population estimated as CFP fluorescence (integrated over the full length of the experiment) of the mixture normalized by the time-integrated CFP fluorescence Lux-CFP cells alone. Error bars represent s.d. (n=3) d, Video stills of a representative co-culture of non-lysing Lux-CFP and Rpa-GFP strains showing the eventual takeover by the green strain. e, Video stills of a representative co-culture of the Lux-CFP and Rpa-GFP strains with the lysis plasmid. The addition of the lysis plasmid prevents either strain from taking over for the duration of the experiment. f, Time trace of the GFP and CFP Fluorescence of the trap in the video shown in d. g, Time trace of the GFP and CFP Fluorescence of the trap in the video shown in e. h, Graph showing the length of co-culture for each of the sixty traps containing the non-lysing strains. i, Graph showing the length of co-culture for each of the sixty traps containing the strains with the lysis plasmids.
We then grew the strains in microfluidic devices, with a seeding ratio of 1:10 (Rpa-GFP to Lux-CFP) optimized for the new system, in order to examine the long-term dynamics of the co-culture. The microfluidic trap (growth chamber) harboring the two strains without the lysis gene quickly lost its co-culture and was taken over by the Rpa-GFP strain alone (Fig. 2d and Supplementary Video 3). This process was observed for 60 traps, and the time duration of the co-culture was measured over two days. All traps eventually lost their co-culture completely, with an average co-residence time of 6.5 hours (Fig. 2h). However, when the two orthogonal lysis strains were grown together, most of the 60 traps maintained a co-culture for the duration of the two-day experiment (Fig. 2e and Supplementary Video 4); all traps that lost co-culture were completely taken over by the Rpa-GFP strain. Due to differences in the inherent parameters of the two quorum sensing systems, the Rpa-GFP circuit remains in the constant lysis regime and is therefore perpetually producing sfGFP. However, the Lux-CFP strain is in the oscillatory regime and remains dark until it reaches quorum threshold and its lysis events are characterized by a punctuated burst of CFP production (Fig. 2g and Supplementary Fig. 3a–d). The bimodality of the co-residence time (either lost in the first couple hours, or maintained through the end of the experiment) suggests the small volume of these reactors, and the non-deterministic loading conditions, predisposes some wells with very few Lux-CFP cells to stochastic loss of co-culture. Seemingly, depending on the environmental context, oscillatory strains are more susceptible to environmental perturbations than a strain in the constant lysis regime. However, the benefit of using a strain in the oscillatory lysis regime is that it leaves the possibility of engineering dynamic population profiles which may be useful for certain applications like timed delivery of two different payloads. Nevertheless, within our microfluidic device, the ‘ortholysis’ method is rather robust at co-culturing even competitive strains for long periods of time (Fig. 2i).
We used agent-based modeling to visually show how the ‘ortholysis’ strains might behave with different quorum sensing parameters. We first modeled a system where the quorum sensing parameters of the Rpa system were the same as the Lux system parameters used in previous studies16. However, we used the experimental difference in growth whereby the Rpa-GFP strain grows at 110% the rate of the Lux-CFP strain. With the Lux-CFP strain seeded in a 10:1 ratio to the Rpa-GFP strain in the model simulation, the resulting dynamics show anti-phase oscillations (Fig. 3a and Supplementary Video 5). Seemingly due to volume exclusion, as shown by their fluorescence time series, the populations enter an anti-phase pattern where the strains switch off growing and lysing (Fig. 3c).
Fig. 3.
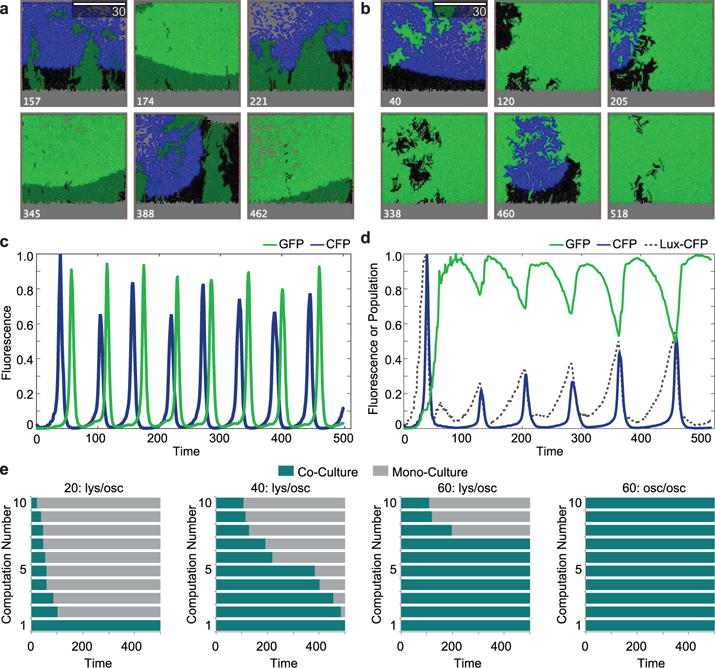
Agent-Based model elucidating experimental dynamics. a, Video stills of a representative, virtual co-culture of two self-lysing strains both in the oscillatory regime of the lysis circuit in a simulated trap of size 60. Scale bar at top, right of micrograph indicates half of the size of the trap. Number at the bottom of the micrographs indicate iteration “Time”. b, Video Stills of representative, model-generated video recreating experimental dynamics. Number at the bottom of the micrographs indicate iteration “Time”. c, Time trace of the GFP (green) and CFP (blue) “Fluorescence” of the trap in a over time. d, Time trace of the GFP (green) and CFP (blue) “Fluorescence” of the trap in b, as well as population of the “Lux-CFP” strain (black, dashed line). e, From left to right: (1) green in constant lysis phase, blue in the oscillatory phase in a trap with size 20. (2) green in constant lysis phase, blue in the oscillatory phase in a trap with size 40. (3) green in constant lysis phase, blue in the oscillatory phase in a trap with size 60. Video in B is in this size trap with these lysing conditions. (4) Both strains in oscillatory phase with trap size 60. Video in a is in this size trap with these lysing conditions.
We then took into consideration the innate differences between the two quorum sensing systems23 by changing several of the Rpa-GFP strain’s quorum sensing parameters in relation to the Lux parameters used. Furthermore, based on observed phenotypic phenomenon the probability of lysing was reduced by 10-fold which allows more AHL to build up and a constant lysis dynamic to develop (Fig. 3b and Supplementary Video 6). The resulting dynamics were similar to the experimental observations, with a constantly lysing Rpa-GFP strain maintaining the majority of the population share, and the Lux-CFP strain intermittently firing and lysing (Fig. 3d). In order to understand how these dynamics and the size of the growth container affect stability, the agent-based model was run many times under different conditions. For conditions where Lux-CFP is oscillating and Rpa-GFP is in constant lysis (lys/osc) or where both are oscillating (osc/osc), ten simulations were done in volumes of 20, 40 and 60 each. As the size of the space increases, so does the average residence time of the co-culture (Fig. 3e), suggesting that, as we expected, larger traps will have fewer issues with losing co-culture to stochastic events.
As evidenced by the agent-based model, our strains demonstrate only one particular dynamic of a wide-range of possibilities facilitated by quorum sensing controlled self-lysing microbes with varying levels of orthogonality. We developed a reduced deterministic model to explore a wider space of possible dynamics achieved through differences in growth rates, QS systems, and lysis circuit regimes. For each case, communication motifs are distinguished and suitable experimental candidate QS systems are chosen to achieve the displayed dynamic. For the two individual lysis circuits, we consider either Non-lysing (no SLC), Lysing (SLC), or Weak Lysing (less effective SLC). With two non-lysing strains, the faster growing strain will eventually dominate the population (Fig. 4a). However, even a single strain equipped with the SLC can stabilize the co-culture, provided the non-lysising strain has the lower growth rate (Fig. 4b). In cases where both strains harbor an SLC, but there is one-way cross-talk, the strain that responds to both signals becomes entrained to the strain that only responds to its own (Fig. 4c–d). An example would be the Lux and Las systems, the Lux can respond to the Las signal, but Las is orthogonal to the Lux signal. The strength of the cross-talk determines the strength and delay of the entrainment, with strong cross-talk (Fig. 4c) exhibiting strong entrainment, and weak cross-talk (Fig. 4d) showing time-delayed entrainment. In cases where each SLC operates independently, by using signal orthogonal QS systems, the most robust co-culturing is achieved where for large ranges of growth rates, the time-averaged population ratio remains around 50/50 (Fig. 4e). If one of the strains exhibits weaker lysing dynamics, in that it has a lower probability of lysing given a quorum threshold, we get dynamics similar to those observed in our experimental system (Fig. 2g and Fig. 4f). As seen in the experiment, the Rpa-GFP strain inhabits most of the space, with blue periodically displacing it until it reaches quorum and self-limits its population. This dynamic, as with the dynamics of each set-up, offers a distinct advantage for certain purposes. For example, a system requiring a constant production of a particular chemical and periodic bursts of a second chemical could appropriate the set-up in Fig. 4f to its advantage.
Fig. 4.
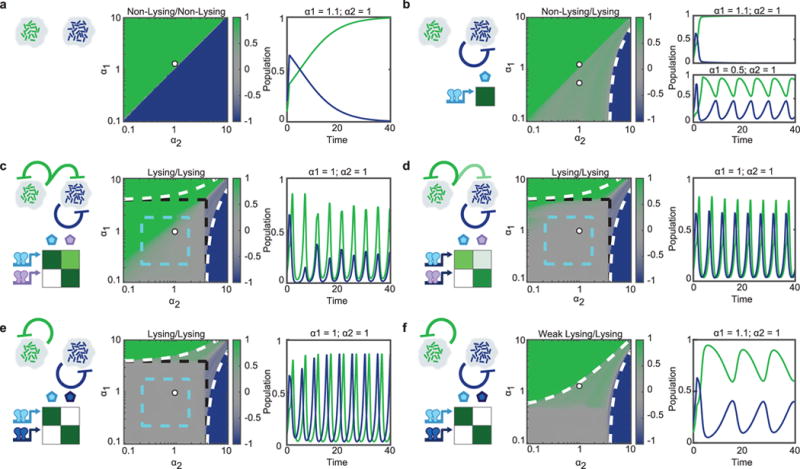
Prediction of synchronized lysis circuit dynamics in a dual strain population using various communication motifs. Model-generated heat maps depicting time-averaged population ratio of green and blue strains in a well-mixed, constant flow co-culture, as function of green’s growth rate α1 against blue’s growth rate α2. Each panel has a particular combination of lysis regimes for each of the strains, either Non-Lysing, Lysing, or Weak Lysing (see Methods Summary for details). On the left of each heat-map is the communication motif it exhibits and experimental candidate QS systems to achieve the desired signaling characteristic. These traits determine the behavior and composition of the co-culture. The white dot on the heat map indicates the growth rate parameters selected for the time-series plots. Time series plots show population of the green and blue strains as a function of time. a, Two non-lysing strains. b, One non-lysing strain and one lysing strain. White, dashed lines indicate the growth rate at which one strain’s growth rate exceeds that of the other one even for maximum lysis activation. c, Two lysing strains with one strain having a strong response to the other’s QS signal. Cyan dashed lines indicate the region where both strains are in the oscillatory regime, black dashed lines mark the area in which strains are self-limiting. d, Two lysing strains with one strain having a weak response to the other’s QS signal. e, Two completely orthogonal lysing strains. The rpa and lux systems could be used for this dynamic as they are signal orthogonal. f, Two completely orthogonal strains with the green strain in the weak lysis regime (leading to constant lysis), and the blue strain in the lysis regime. This is the regime corresponding to our experimental system. Oscillations in the green strain’s population are imposed by the oscillatory blue strain through volume exclusion.
Synthetic biologists have used lysis to control populations before12, but not until recently have populations been engineered to dynamically control their own population without exogenous input16. Since our system relies on DNA parts carried on plasmids, undesired mutations may arise which can hinder the function of the circuit. Bacteria may mutate toxic or burdensome genes, and any possible mutants may gain a selective advantage over non-mutated members of the population. In this regard, strategies to enhance stability of the circuit components inside the host cells would be necessary to ensure long term robustness of the synthetic ecosystem24. Additionally, in the absence of antibiotics, bacteria would encounter a selective pressure to lose the circuit plasmids. This would be problematic when introducing the synthetic ecosystem to an environment without any selective agents. Possible ways this could be addressed are by either integrating circuit components within the genome or using plasmid-stabilizing elements in the circuit. Elements such as toxin/antitoxin systems and actin-like protein partitioning systems have previously been shown to stabilize plasmids in environments without antibiotics25. The emergence of escapees is a direct consequence of strong selection imposed by periodic lysis, and recent evidence also suggests that repeated pruning of a population suppresses beneficial mutations that confer growth advantages unrelated to the lysis circuit26. Therefore, the ortholysis strategy might be an attractive methodology to impose certain population dynamics or types of selection in evolution experiments.
The challenge in maintaining a population of metabolically competitive microbial organisms has long been recognized21. Strategies to maintain the long-term stability of engineered microbial ecosystems that have thus far been investigated mainly consist of mutualistic interactions, such as metabolic interdependencies, or predator-prey type interactions27,28. Recent evidence suggests, however, that competition is likely the dominant interaction in microbial communities29. In this vein, the ‘ortholysis’ system can be viewed as a strategy to stabilize competitive strains without engineering positive and negative interactions between members of the population. Moreover, recent evidence has identified quorum-sensing controlled self-lysis as a naturally occurring phenomenon in Pseudomonas aeruginosa30, which is a relevant example of how the interests of synthetic biologists and microbial ecologists are merging in the field of engineered microbial ecosystems.
With the additional modeling of our circuit it becomes clear that the transition from monoculture synthetic biology to synthetic engineered ecosystems will be marked by an explosion of possibilities. A circuit designed for monocultures, such as the SLC, can have drastically broadened use-cases when expanded into the setting of a community. The ‘ortholysis’ system is immediately applicable for further expansion on the periodic in situ drug delivery system16. However, this phenomenon of stably co-culturing two metabolically competitive strains through orthogonal self-lysing offers the possibility of many unique applications beyond drug delivery where the use of synthetic microbial ecosystems is advantageous.
Methods Summary
Plasmids and Strains
Our circuit strains without the lysis plasmid were cultured in LB media with 50 μg ml−1 kanamycin, in a 37°C incubator. Our circuit strains with the lysis plasmid were cultured in the same way but with 34 μg ml−1 of chloramphenicol as well along with 0.2% glucose. For microscopy and plate reader experiments 1nM of 3-oxo-C6-HSL was added to all media. Plasmids were constructed using the CPEC method of cloning or using standard restriction digest/ligation cloning. The lux activator plasmid (Kan, ColE1) and lux-lysis plasmid (Chlor, p15A) were used in previous work from our group16,31. The RpaR and RpaI genes were obtained via PCR off the Rhodopseudomonas palustris genome obtained through ATCC to create the Rpa-activator and Rpa-lysis plasmids. The lux-sfGFP lysis circuit alone was characterized in E. coli. Co-culturing was performed with non-motile S. typhimurium, SL1344.
The SLC, in both the Lux and Rpa case, is composed of an activator plasmid and a lysis plasmid. For the circuit characterization experiments, there were three variations of the activator plasmid. The first is pTD103LuxI-sfGFP which was used in previous work from our group31. This plasmid contains a LuxI with the ssrA-LAA degradation tag (amino-acid sequence of AANDENYALAA) and sfGFP, a superfolding green fluorescent protein variant32. pTD103LuxI (TS) sfGFP was constructed by adding the TS-linker (amino acid sequence of TS) between the ssrA-LAA tag and LuxI. pTD103LuxI (-LAA) sfGFP was constructed by removing the ssrA-LAA tag from LuxI. For the dual lysis experiments, the Lux-CFP strain used the activator plasmid with the ssrA-LAA tagged LuxI instead with a CFP in place of the sfGFP. The Rpa-GFP strain’s activator plasmid was created by replacing LuxR with RpaR, and the LuxI with an ssrA-LAA tagged RpaI.
The lysis plasmids have a p15a origin of replication and a chloramphenicol resistance marker33 and have been previously described by our group16. The lysis gene, E from the bacteriophage ϕX174, was kindly provided by Lingchong You and was taken from the previously reported ePop plasmid via PCR34. The E gene was placed under the expression of the LuxR-AHL activatable luxI promoter for both the Lux-CFP and Rpa-GFP strains. Most of the construction was done using the CPEC method of cloning35. See Supplementary Fig. 4 and Supplementary Table 1 for maps of the the plasmids used in this study.
Microfluidics and Microscopy
Our group has previously described in depth the microscopy and microfluidics techniques used in this study14. In short, micron-scale features are baked onto silicon wafers using cross-linked photoresist. The microfluidic device resin, PDMS (polydimethysiloxane), is then poured over the wafers and solidified by baking. The PDMS, which contains numerous devices, is peeled off and individual devices are cut out from the whole. Holes are then punched into the device at their input and output where the fluid lines will eventually plug in. After puncturing, the devices are bonded onto glass coverslips via plasma-activation. The devices were then put in a vacuum and the outlet was loaded with cells and the inlet with media. Vacuum pressure loads cells into the traps and media lines are plugged in before the cells can contaminate the upstream section of the device. The flow was then adjusted by changing the relative heights of the syringes, which for all experiments the meniscus of the media was set to one inch above the meniscus of the waste, resulting in a low, constant hydrostatic pressure driven flow.
All microfluidic experiments were done in a side-trap array device as previously described14, and in all cases 0.075% Tween20 was added to the media to deter cells from sticking to the channels and the ports of the device. The bacteria growth chambers were 100μm wide 85μm deep and approximately 1.6μm in height.
For lysis characterization (Figure 1): Cells were cultured until they reached an optical density of approximately 0.1 (Plastibrand 1.5mL cuvettes were used) at which point they were spun-down and loaded via vacuum pressure the chip. Media was LB with Kanamycin and Chloramphenicol. For dual lysis and co-culturing experiments (Figure 2): Cells were cultured until they reached an optical density of approximately 0.1 (Plastibrand 1.5mL cuvettes were used to test OD) and 1.5mL was spun down and resuspended in 50ul of media. This concentrate was used to vacuum load the cells for single strain experiments, or it was mixed at a 10:1 ratio (Lux-CFP:Rpa:GFP) in the co-culturing experiments before loading via vacuum pressure. Media was LB with Kanamycin (and Chloramphenicol for lysis experiments) with 1nM 3OC6 HSL added.
The microscope system used has also been previously described by our group31. In short, a Nikon Eclipse TI epifluorescent microscope with phase-contrast based imaging was used. Our camera is a Photometrics CoolSNAP HQ2 CCD.
The acquisition software used is Nikon Elements. Our microfluidic devices are housed in a plexiglass incubation chamber that is maintained at 37C by a heating unit.
For dual lysis and co-culturing experiments: Phase-contrast images were taken at 20× magnification with 50–200ms exposure times. Fluorescent imaging at 20x was performed at 300ms for GFP, 30% setting on the Lumencor SOLA light source, and 300ms and 35% for CFP. Images were taken every 3 minutes for the course of the experiment (~2 days). Co-culture was determined to be lost if the fluorescence of either CFP or GFP went below background fluorescence, and then was checked manually in cases of the oscillatory lysing CFP strain which can go below threshold between lysis events.
For the lysis characterization (Figure 1), we counted cells using the following strategies: for experiments where the cell population was mostly aggregated together (non-sparse population), we first estimated the average area of an individual bacterial cell and the average void fraction (open space between bacteria in the trap). Taking into account the pixel density of the image, we measured the area of the trap taken up by cells using ImageJ and divided by the average area of a bacterial cell. This value was then multiplied by (1 − void fraction) to yield the total estimated number of cells in the trap. Bacteria that were not close to the main group of cells were counted individually and added to the final number. For experiments where the growing population was sparse (due to the constant lysis regime), we utilized the Trainable Weka Segmentation plug-in for ImageJ to count cells. Plots were generated by using MATLAB.
For co-culture experiments: Co-culture was determined to be lost if the fluorescence of either CFP or GFP went below background fluorescence, and then images were checked manually in cases of the oscillatory lysing CFP strain which can go below threshold between lysis events.
Plate Reader Fluorescence and Population Estimates
For the well-plate experiments the strains were grown in a standard Falcon tissue culture 96-well flat bottom plate with appropriate antibiotics (kanamycin only for non-lysis and kanamycin and chloramphenicol for lysis strains). For consistency with microfluidic experiments, 1nM of 3OC6-HSL was added to all media. We grew the bacterial strains used in Fig. 2b in 4mL cultures to an optical density of 0.15 before adding 10uL of this culture to 10mL of fresh LB with appropriate antibiotics and added HSL. For single strain tests, 200ul of the dilution was distributed into the well-plate. For the 1:1 mixtures, 100ul of each dilution was added to the same well. For the 1:100 mixtures 200ul of the Lux-CFP dilution was added with 2ul of the Rpa-GFP dilution. For all cases there were four technical replicates.
These dilutions were then grown for 10 hours (non-lysing), or 19 hours (with lysis) and their OD600nm, GFP, and CFP levels were measured every 10 minutes in a Tecan Infinite M200 Pro. GFP readings had an excitation of 485nm and emission of 520nm. CFP readings had a an excitation of 433nm and emission of 475nm. The resulting fluorescence curves were used to calculate estimated populations of the co-cultures.
Population estimates in the co-culture mixtures was estimated in the following way. The GFP fluorescence time-series trace of Rpa-GFP alone was integrated and used as a standard for accumulated fluorescence of a culture with 100% of the Rpa-GFP strain. In the same way, the CFP fluorescence time-series trace of Lux-CFP alone was integrated and used as a standard for accumulated fluorescence of a culture with 100% of the Lux-CFP strain. The integrated GFP and CFP fluorescence curves of the mixtures was then divided by the standards to give a population estimate of Rpa-GFP and Lux-CFP, respectively. For all cases, the area of the background fluorescence was subtracted. Additionally, the GFP fluorescence required extra signal normalization because the Tecan’s GFP sensor reads into the CFP emission profile (but not the other way around).
Here are the equations used to calculate the population estimates with appropriate filtering and normalization:
PopulationLux is the population estimate of the Lux-CFP strain in a co-culture.
Area(CFPmix) is the area of the CFP fluorescence time-series curve of a given co-culture. Area(BGCFP) is the area of the background CFP fluorescence time-series line. Area(CFPLux) is the average area of the CFP fluorescence time-series curve in the wells with only the Lux-CFP strain. Area(GFPLux) is the average area of the GFP fluorescence time-series curve in the wells with only the Lux-CFP strain (For this strain the GFP fluorescence should technically be at background, further normalization is done because the Tecan’s GFP sensor reads into the CFP emission profile). Area(BGGFP) is the area of the background GFP fluorescence time-series line. η is the calculated fluorescence emission cross-talk scalar, and is only needed to scale GFP values as the CFP sensor does not read any GFP. The normalized, filtered, GFP value is thus given by GFPReal. Area(GFPmix) is the area of the GFP fluorescence time-series curve of a given co-culture. Area(GFPRpa) is the average area of the GFP fluorescence time-series curve in the wells with only the Rpa-GFP strain. Finally, PopulationRpa is the population estimate of the Lux-CFP strain in a co-culture.
Agent-Based Modeling
For the agent-based model, to simulate bacterial motion, we adapted the mechanical agent-based model developed in our earlier work36,37. Each cell is modeled as a spherocylinder of unit diameter that grows linearly along its axis and divides equally after reaching a critical length ld = 4. It can also move along the plane due to forces and torques produced by interactions with other cells. The slightly inelastic cell-cell normal contact forces are computed via the standard spring-dashpot model, and the tangential forces are computed as velocity-dependent friction.
To describe the intracellular dynamics of each cell, we adapted the ordinary differential equation model from16. Specifically, the intracellular dynamics are
Here the variables Plux, Hi, Ii and Li are the activity of luxI promoter, intracellular AHL, LuxI and lysis protein of the i-th cell. He(xi, t) is the extracellular concentration of AHL at the location of the i-th cell. luxI promoter is induced by AHL. is the production term for AHL. Dm(He(xi, t) −Hi) describes the exchange of intra- and extra-celluar AHL across the cell membrane. CIPlux and γIIi are the production and degradation terms for LuxI. CLPlux and γLLi are the production and degradation terms for lysis protein.
The extracellular AHL concentration He(x, t) is governed by linear diffusion equation
In the simulation, we use 2D finite difference methods to describe the diffusion of AHL.
We implement the model in traps with diffrent side lengths (20, 40 and 60). To simulate the lysis of each cell, we assume that when the concentration of lysis protein Li is above a threshold Lth, the cell has a probability of Pr = pL(Li − Lth) per unit of time to lyse and once a cell lyses, it is removed from the trap.
We chose model parameters to qualitatively fit the experimental results and the parameters H0, m, b, pL were chosen to account for the differences of experimental measurements and dynamic behaviors between Lux-CFP and Rpa-GFP strains. The parameter values for the Lux-CFP strain are α0 = 0.1 (Lux promoter basal production); αH = 2 (Lux promoter AHL induced production); H0 = 1 (AHL binding affinity to Lux promoter); m = 4 (Hill coefficient of AHL induced production of Lux promoter); b = 1.5 (AHL production rate); KI = 1 (Conc. of LuxI resulting half maximum production of AHL); Dm = 10 (Diffusion constant of AHL across cell membrane); CI = 1 (LuxI copy number); γI = 1 (Degradation rate of LuxI); CL = 1 (Lysis gene copy number); γL = 0.5 (Degradation rate of lysis protein); δH = 0.1 (Dilution rate of extracellular AHL); DH = 65 (Diffusion constant of extracellular AHL); pL = 0.3 (Probability of lysing); Lth = 1.6 (Threshold of lysis protein for lysis).
To simulate the constant-lysis Rpa-GFP strain, these parameters have different values: H0 = 0.2, m = 1, b = 0.8, pL = 0.03. Besides, Rpa-GFP strain’s growth rate is 10% larger than Lux-CFP strain.
Deterministic Modeling
Single lysis oscillator strain
We describe the population level mechanisms that lead to oscillations in population size as observed with the synchronized lysis circuit. To gain an intuitive understanding, we use a reduced model that aims to reproduce the observed population level behavior using only the fundamental ingredients of the circuit: Autocatalytic production of quorum sensing agent and quorum sensing agent-induced lysis of cells. The basic equations for a single strain equipped with the lysis circuit are as follows (see Supplementary Fig. 5 for model traces):
| (1a) |
| (1b) |
The cell density is denoted by n. Cells divide with a rate α and die with a maximal rate γ due to lysis. 0 ≤ f (q) ≤ 1 characterizes the promoter under which the QS and lysis proteins are expressed, so it determines the dependence of the death rate on q and the auto-catalyzed production of the QS agent q. αq is the basal production rate of QS agent, which can be increased by the presence of q to a maximum production rate of . q is diluted in the environment with a rate γq. We use a standard Hill function for f (q):
| (2) |
where qc is the concentration of q that results in the half-maximum death rate (and auto-catalyzed production of q) and m is the Hill coefficient.
A linear stability analysis shows that the system (1) has a stable fixed point when
| (3) |
The border of this stability region corresponds to the onset of oscillations. Basal parameters are, unless otherwise mentioned: α = 1, γ = 4, αq = 0.4, , γq = 1, qc = 1, m = 2. These parameters lead to oscillations according to (3). All simulations are carried out using the Runge-Kutta-Fehlberg (RKF45) method. An example trajectory is depicted in Supplementary Figure 5.
While we do not explicitly model individual proteins or enzymes, we can gain an understanding for the influence of LuxI degradation by ClpXP with the model (1) using the following logic: When there is very little LuxI (i.e. the positive feedback loop has not been activated), fast degradation by ClpXP will have a strong influence on the steady-state level of LuxI. LuxI with a strong degradation tag will experience fast degradation by ClpXP leading to a low basal production rate of QS agent (αq), whereas LuxI with a weak degradation tag will have a higher steady-state level and therefore a higher basal procution rate αq. In contrast, once the positive feedback has been activated, the concentration of LuxI (and consequently the parameter of the model) have a much weaker dependence on its degradation tag since an abundance of LuxI produced from a fully activated promoter saturates the limited enzymatic processing capacity of ClpXP and therefore the level of LuxI will be determined mainly by dilution due to cell growth. As seen from (3), decreasing αq by a larger factor than generally brings the system closer to oscillations, which is consistent with the requirement of a strong degradation tag for sustained oscillations demonstrated in Figure 2 of the main text. In summary, we model stronger (weaker) enzymatic degradation of LuxI by a lower (higher) value of αq.
Microfluidic traps and multiple strains
A microfluidic trap is clearly a finite environment, but because nutrients are constantly replenished by diffusion from fresh media in the channel, logistic growth (as is often assumed in other scenarios with finite carrying capacities) would be an unrealistic description of the population dynamics. Instead, we assume that growth is unaffected as long as the population density is below the carrying capacity c of the trap. We then cap the cell density at c, corresponding to any extra cells being washed away by the flow in the main channel (“spillover”). Numerically, we reset the cell density to c after every time step of the simulation if it exceeds c. In all our simulations c = 1. Supplementary Figure 5 shows that the system with standard parameters lyses just before it reaches the carrying capacity of the trap, so it is truly self-limiting.
For simulations of multiple strains, we simulate two copies of the system (1) with variables {n1, q1} and {n2, q2}. Again, we let the system evolve freely as long as n1 + n2 < c. If n1 + n2 exceeds c after any time step, we set n1 and n2 according to
| (4) |
where and correspond to the population densities before the reset. More specifically, this way of limiting the total population density to the carrying capacity c corresponds to assuming a well-mixed environment, such that the relative population densities of the two strains remain unchanged upon spillover.
Consequently, two oscillating strains in one trap that use completely orthogonal quorum sensing systems only interact if the total population density hits the carrying capacity c. As shown in the main text, the strains will eventually lock into an anti-phase pattern where they avoid reaching their peak density at the same time. In order to model cross-talk, we modify the equation of the “receiver” strain (strain 2 in this case) to read
| (5a) |
| (5b) |
where ξ determines how much strain 2 responds to the QS agent of strain 1, i.e. the strength of the cross-talk.
Additional parameters used in the main text
For the parameter scan of a single strain in Figure 1, the model equations were simulated for 2000 time units for different values of the model parameter αq. The last 400 time units were used to determine the minimum, mean and maximum population density. For all parameter scans of two strains, the model equations were simulated for 500 time units and the last 100 time units were analyzed to determine the average cell densities and of the two strains. The “steady-state population ratio” shown in Figure 4 was then calculated as , ranging from −1 (strain 2 dominates) to 1 (strain 1 dominates). For non-lysing strains, the model parameter qc was set to infinity. Cross-talk parameters in Figure 4c and d, are ξ = 0.6 and ξ = 0.12, respectively. Weak lysis (strain 1, Figure 4f) was achieved by reducing the lysis rate of the strain to γ = 0.5.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The modeling code for the agent-based as well as the deterministic numerical simulations is available from the corresponding author upon request.
Supplementary Material
Acknowledgments
This material is based upon work supported by the NIH/NIGMS grant RO1-GM069811 and by the San Diego Center for Systems Biology under NIH/NIGMS grant P50-GM085764. S.R.S. was partially funded by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1144086. P.B. acknowledges support from HFSP fellowship LT000840/2014-C. L.X. and L.S.T. were partially supported by the ONR grant N00014-16-1-2093. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the funding agencies.
Footnotes
Supplementary Information
Supplementary information, including methods, supplementary figures and tables, is linked to the online version of the paper at www.nature.com/nature.
Author Information
The authors declare no competing financial interests. All authors (S.R.S, M.O.D., P.B., L.X., L.S.T., J.H.) contributed extensively to the work presented in this paper.
References
- 1.Gravel D, et al. Experimental niche evolution alters the strength of the diversity-productivity relationship. Nature. 2011;469:89–92. doi: 10.1038/nature09592. [DOI] [PubMed] [Google Scholar]
- 2.De Roy K, et al. Environmental conditions and community evenness determine the outcome of biological invasion. Nature communications. 2013;4:1383. doi: 10.1038/ncomms2392. [DOI] [PubMed] [Google Scholar]
- 3.Tanouchi Y, Smith RP, You L. Engineering microbial systems to explore ecological and evolutionary dynamics. Current opinion in biotechnology. 2012;23:791–797. doi: 10.1016/j.copbio.2012.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wintermute EH, Silver PA. Emergent cooperation in microbial metabolism. Molecular systems biology. 2010;6:407. doi: 10.1038/msb.2010.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Klitgord N, Segre D. Environments that induce synthetic microbial ecosystems. PLoS Comput Biol. 2010;6:e1001002. doi: 10.1371/journal.pcbi.1001002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Little AE, Robinson CJ, Peterson SB, Raffa KF. The Social Biology of Microbial Communities: Workshop Summary. Vol. 62. National Academies Press; 2012. Rules of engagement: Interspecies interactions that regulate microbial communities31; pp. 375–401. [Google Scholar]
- 7.De Roy K, Marzorati M, Van den Abbeele P, Van de Wiele T, Boon N. Synthetic microbial ecosystems: an exciting tool to understand and apply microbial communities. Environmental microbiology. 2014;16:1472–1481. doi: 10.1111/1462-2920.12343. [DOI] [PubMed] [Google Scholar]
- 8.Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 9.Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 10.Hasty J, McMillen D, Collins JJ. Engineered gene circuits. Nature. 2002;420:224–230. doi: 10.1038/nature01257. [DOI] [PubMed] [Google Scholar]
- 11.Endy D. Foundations for engineering biology. Nature. 2005;438:449–453. doi: 10.1038/nature04342. [DOI] [PubMed] [Google Scholar]
- 12.You L, Cox RS, Weiss R, Arnold FH. Programmed population control by cell–cell communication and regulated killing. Nature. 2004;428:868–871. doi: 10.1038/nature02491. [DOI] [PubMed] [Google Scholar]
- 13.Brenner K, Karig DK, Weiss R, Arnold FH. Engineered bidirectional communication mediates a consensus in a microbial biofilm consortium. Proceedings of the National Academy of Sciences. 2007;104:17300–17304. doi: 10.1073/pnas.0704256104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Danino T, Mondragón-Palomino O, Tsimring L, Hasty J. A synchronized quorum of genetic clocks. Nature. 2010;463:326–330. doi: 10.1038/nature08753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen Y, Kim JK, Hirning AJ, Josic K, Bennett MR. Emergent genetic oscillations in a synthetic microbial consortium. Science. 2015;349:986–989. doi: 10.1126/science.aaa3794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Din MO, et al. Synchronized cycles of bacterial lysis for in vivo delivery. Nature. 2016;536:81–85. doi: 10.1038/nature18930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fulget N, Poughon L, Richalet J, Lasseur C. Melissa: global control strategy of the artificial ecosystem by using first principles models of the compartments. Advances in Space Research. 1999;24:397–405. doi: 10.1016/s0273-1177(99)00490-1. [DOI] [PubMed] [Google Scholar]
- 18.Chen Y. Development and application of co-culture for ethanol production by co-fermentation of glucose and xylose: a systematic review. Journal of industrial microbiology & biotechnology. 2011;38:581–597. doi: 10.1007/s10295-010-0894-3. [DOI] [PubMed] [Google Scholar]
- 19.Dejonghe W, et al. Synergistic degradation of linuron by a bacterial consortium and isolation of a single linuron-degrading variovorax strain. Applied and Environmental Microbiology. 2003;69:1532–1541. doi: 10.1128/AEM.69.3.1532-1541.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Petrof EO, et al. Stool substitute transplant therapy for the eradication of clostridium difficile infection:“repoopulating” the gut. Microbiome. 2013;1:1. doi: 10.1186/2049-2618-1-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gause GF. The struggle for existence. Courier Corporation; 2003. [Google Scholar]
- 22.Faust K, Raes J. Microbial interactions: from networks to models. Nature Reviews Microbiology. 2012;10:538–550. doi: 10.1038/nrmicro2832. [DOI] [PubMed] [Google Scholar]
- 23.Scott SR, Hasty J. Quorum sensing communication modules for microbial consortia. ACS synthetic biology. 2016 doi: 10.1021/acssynbio.5b00286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Renda BA, Hammerling MJ, Barrick JE. Engineering reduced evolutionary potential for synthetic biology. Molecular BioSystems. 2014;10:1668–1678. doi: 10.1039/c3mb70606k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Danino T, et al. Programmable probiotics for detection of cancer in urine. Science translational medicine. 2015;7:289ra84–289ra84. doi: 10.1126/scitranslmed.aaa3519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bittihn P, Hasty J, Tsimring LS. Suppression of beneficial mutations in dynamic microbial populations. Physical Review Letters. 2017;118:028102. doi: 10.1103/PhysRevLett.118.028102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Balagaddé FK, et al. A synthetic escherichia coli predator–prey ecosystem. Molecular systems biology. 2008;4:187. doi: 10.1038/msb.2008.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shou W, Ram S, Vilar JM. Synthetic cooperation in engineered yeast populations. Proceedings of the National Academy of Sciences. 2007;104:1877–1882. doi: 10.1073/pnas.0610575104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Foster KR, Bell T. Competition, not cooperation, dominates interactions among culture-able microbial species. Current biology. 2012;22:1845–1850. doi: 10.1016/j.cub.2012.08.005. [DOI] [PubMed] [Google Scholar]
- 30.Zemke AC, Bomberger JM. Microbiology: Social suicide for a good cause. Current Biology. 2016;26:R80–R82. doi: 10.1016/j.cub.2015.12.018. [DOI] [PubMed] [Google Scholar]
- 31.Prindle A, et al. A sensing array of radically coupled genetic/biopixels/ Nature. 2012;481:39–44. doi: 10.1038/nature10722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pédelacq JD, Cabantous S, Tran T, Terwilliger TC, Waldo GS. Engineering and characterization of a superfolder green fluorescent protein. Nature biotechnology. 2006;24:79–88. doi: 10.1038/nbt1172. [DOI] [PubMed] [Google Scholar]
- 33.Lutz R, Bujard H. Independent and tight regulation of transcriptional units in escherichia coli via the lacr/o, the tetr/o and arac/i1-i2 regulatory elements. Nucleic acids research. 1997;25:1203–1210. doi: 10.1093/nar/25.6.1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Marguet P, Tanouchi Y, Spitz E, Smith C, You L. Oscillations by minimal bacterial suicide circuits reveal hidden facets of host-circuit physiology. PloS one. 2010;5:e11909. doi: 10.1371/journal.pone.0011909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Quan J, Tian J. Circular polymerase extension cloning of complex gene libraries and pathways. PloS one. 2009;4:e6441. doi: 10.1371/journal.pone.0006441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Volfson D, Cookson S, Hasty J, Tsimring LS. Biomechanical ordering of dense cell populations. Proceedings of the National Academy of Sciences. 2008;105:15346–15351. doi: 10.1073/pnas.0706805105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mather W, Mondragón-Palomino O, Danino T, Hasty J, Tsimring LS. Streaming instability in growing cell populations. Physical review letters. 2010;104:208101. doi: 10.1103/PhysRevLett.104.208101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.


