Compounding effects of sea level rise and fluvial flooding

Significance

Population and assets in coastal regions are threatened by both oceanic and fluvial flooding hazards. Common flood hazard assessment practices typically focus on one flood driver at a time and ignore potential compounding impacts. Here we outline a unique bivariate flood hazard assessment framework that accounts for the interactions between a primary oceanic flooding hazard, coastal water level, and fluvial flooding hazards. Using the notion of “failure probability,” we also assess coastal flood hazard under different future sea level rise scenarios. The results show that, in a warming climate, future sea level rise not only increases the failure probability, but also exacerbates the compounding effects of flood drivers.

Abstract

Sea level rise (SLR), a well-documented and urgent aspect of anthropogenic global warming, threatens population and assets located in low-lying coastal regions all around the world. Common flood hazard assessment practices typically account for one driver at a time (e.g., either fluvial flooding only or ocean flooding only), whereas coastal cities vulnerable to SLR are at risk for flooding from multiple drivers (e.g., extreme coastal high tide, storm surge, and river flow). Here, we propose a bivariate flood hazard assessment approach that accounts for compound flooding from river flow and coastal water level, and we show that a univariate approach may not appropriately characterize the flood hazard if there are compounding effects. Using copulas and bivariate dependence analysis, we also quantify the increases in failure probabilities for 2030 and 2050 caused by SLR under representative concentration pathways 4.5 and 8.5. Additionally, the increase in failure probability is shown to be strongly affected by compounding effects. The proposed failure probability method offers an innovative tool for assessing compounding flood hazards in a warming climate.

Flooding hazard, characterized by the intensity/frequency of flood events (1), is an important consideration in local level planning and adaptation (2). Coastal cities are especially demanding sites for flood hazard assessment because of exposure to multiple flood drivers such as coastal water level (WL), river discharge, and precipitation (3, 4). Furthermore, dependence among the flood drivers [e.g., coastal surge/tide, sea level rise (SLR), and river flow] can lead to compound events (5) in which the simultaneous or sequential occurrence of extreme or nonextreme events may lead to an extreme event or impact (6). For example, in estuarine systems, the interplay between coastal WL and freshwater inflow determines the surface WL (and hence the flood probability) at subtidal (7) and tidal (8–11) frequencies.

In the United States, flood hazard assessment practices are typically based on univariate methods. For example, procedures for rivers often treat oceanic contributions (e.g., tides and storm surges) using static base flood levels (e.g., ref. 12), and do not consider the dynamic effects of coastal WL (e.g., ref. 13). Similarly, flood hazard procedures for coastal WLs (e.g., ref. 14) do not account for terrestrial factors such as river discharge or direct precipitation into urban areas. Previous studies indicate that univariate extreme event analysis may not correctly estimate the probability of a given hydrologic event (15, 16). This points to the potential importance of multivariate analysis of extreme events in coastal/estuarine systems and consideration of compounding effects between flood drivers (6). Bivariate extreme event analysis has been explored in a coastal context with different variables and in different areas (5, 17–33) (see SI Appendix, Table S2 for more details). Bivariate flood hazard studies have been performed for coasts of the United Kingdom (34–36) and Australia (37, 38); however, they do not consider the impacts of SLR on the estimated flood hazard.

SLR is a well-documented and urgent aspect of anthropogenic global warming (39–46) that threatens coastal communities all around the world. Without flood adaptation, annual losses of 0.3 to 9.3% of global gross domestic product are expected by 2100 (47), while only ∼70% of the coastal landscapes projected to experience future flooding have some capacity to respond dynamically to SLR (48). High-quality sea surface WL data, recorded at tide gauges around the world over the last 100+ y, document a significant globally averaged acceleration in mean SLR of about 0.009 mm⋅y⁻² since 1880 and 0.022 ± 0.015 mm⋅y⁻² between 1952 and 2011, and a globally averaged mean SLR of ∼2.8 mm⋅y⁻¹ between 1993 and 2009 (39, 49–53). Analysis of satellite altimetry records suggests an SLR rate of 3.3 ± 0.4 mm⋅y⁻¹ between 1993 and 2014 (54). The rate of SLR over recent decades is one order of magnitude larger than SLR over the past millennia (55), and projections of SLR over the 21st century, based on current trajectories of anthropogenic activities and greenhouse gases emissions (56), cannot rule out an increase greater than 1 m (55, 57–59).

SLR brings the height of high tides closer to flood stage, and increases the frequency of both nuisance floods (60–64) and destructive flood events (65, 66), such that today’s century-level floods are expected to become decadal by 2050 (67–70). SLR further complicates coastal flood hazard analysis by introducing nonstationarity (71). Physically, SLR adds to the height of future storm tides, reduces pressure gradients that are important for transporting fluvial water to the ocean, and enables greater upstream tide/wave propagation (72, 73).

In this study, we propose a framework that takes the impacts of SLR into account for flood hazard analysis in coastal systems under multiple flood drivers and integrates the concepts of bivariate hazard analysis (74) and nonstationary hazard assessment. We first propose a bivariate flooding assessment approach that accounts for the compounding effects of fluvial flooding and coastal sea level (with future SLR). We then integrate the notion of failure probability to achieve a practical tool for assessing future hazards. Using this framework, we show that ignoring SLR and its compounding impacts may lead to a significant underestimation of future coastal flooding hazard.

Although the framework outlined here is general and can be applied to different regions, for illustration, we focus on the United States, in which over half of the population live in coastal regions (75). Also, 8 out of the 20 most vulnerable cities in terms of average annual losses due to flooding in the globe are located in the United States (2). Using copulas and bivariate dependence analysis (Methods), we quantify increases in flood probabilities caused by SLR based on 2030 and 2050 projections, under representative concentration pathways (RCPs) 4.5 and 8.5. Finally, we evaluate the change in failure probability of compound flood events due to SLR. Note that an inverse analysis for identifying potentially dangerous multivariate occurrences having a fixed level of “acceptable risk,” as clarified in ref. 76, can be carried out by inverting the formulas outlined in Methods. However, this is outside the scope of the present work; for further details please see also refs. 30, 31, 74, and 77.

Here we use three sets of data, available at eight estuarine systems along the coasts of United States (SI Appendix, Fig. S1): (i) hourly WL, (ii) daily freshwater inflow to the lower estuary as a representative of fluvial flow, and (iii) future local SLR projections to describe the impacts of SLR on increased likelihood of flooding by 2030 and 2050. Using these data, we implement univariate and bivariate analysis of coastal flooding for the current and future climate with rising sea levels. In each case, the observation gauges are carefully chosen to make sure that the longest and highest-quality data in that system are analyzed. For extreme WL analysis along tidal rivers, when significant dependence between deriving factors is detected, it is critical to appropriately characterize correlation structure and carefully take the nonlinear interaction between freshwater inflow and upcoming surge tides into account. Otherwise, either large astronomic tidal variabilities may mask the correlation between meteorologically driven components or potential adjustments of WL measured at tide gauge by river discharge may not be appropriately treated.

Coastal WLs resulting from tides and nontidal processes (e.g., storm surge) are taken from hourly coastal WL data at eight tide gauges shown in SI Appendix, Fig. S1 and provided by National Oceanic and Atmospheric Association (https://tidesandcurrents.noaa.gov/). The Galveston and San Francisco records with 70 y and 157 y of data have the shortest and longest available WL series, respectively (see SI Appendix, Table S1 for more information).

The estimated daily freshwater discharges for all of the estuaries are obtained from United States Geological Survey website (waterdata.usgs.gov/nwis/rt), except for San Francisco Bay (SF Bay), for which the Net Delta Outflow Index (NDOI), an output of the California Department of Water Resources Dayflow program (www.water.ca.gov/dayflow/), is used as a proxy for tidally averaged daily river inflow to SF Bay from the Sacramento River delta. NDOI accounts for about 90% of the inflow to SF Bay; and accounts for river inflows, precipitation, agricultural consumptive demand, and California Water Project exports (78, 79). The Columbia River and Buffalo Bayou River, with 660,500 km² (80) and 270 km² watersheds, (waterdata.usgs.gov/tx/nwis) are the largest and the smallest watersheds, respectively, in this study. Size and drainage characteristics of the watershed (e.g., time of concentration) and different forcing mechanisms cause the fluvial flow to occur on different time scales ranging from a few hours (i.e., due to intense local precipitation) to a few days (i.e., rain on snow events) and even weeks (i.e., Spring snowmelt freshets). The case studies investigated here, with relatively long records available, cover a wide range of estuarine systems from moderately (e.g., Hudson River) to strongly (e.g., Potomac River) convergent and from moderately (e.g., Delaware River) to strongly (e.g., Columbia River) dissipative (81); this points to the potential applicability of our proposed approach to many estuarine/coastal systems around the world.

The probability distribution of local SLR projections (F_SLR) at the eight sites of interest, under RCPs 4.5 and 8.5 of Coupled Model Intercomparison Project Phase 5 (CMIP5) scenarios, are provided by ref. 59 in a discrete form by specifying seven quantiles of the following orders: q_i = 0.005, 0.05, 0.17, 0.5, 0.83, 0.95, and 0.995. A continuous version of F_SLR is constructed via a suitable linear interpolation (see SI Appendix for further details).

Results and Discussion

First, we discuss the differences between univariate and bivariate flooding probabilities for three selected estuarine systems along the coasts of United States, where the variables of interest (fluvial flow and coastal WL) are statistically dependent, namely, Philadelphia, PA; San Francisco, CA; and Washington, DC. The results for the rest of the studied estuarine systems, with no significant dependence between variables, are presented in SI Appendix. Here, a direct approach to the hazard assessment is adopted, as clarified in ref. 76. The target is to compute the return periods and/or the failure probabilities associated with observed (and future projected) occurrences.

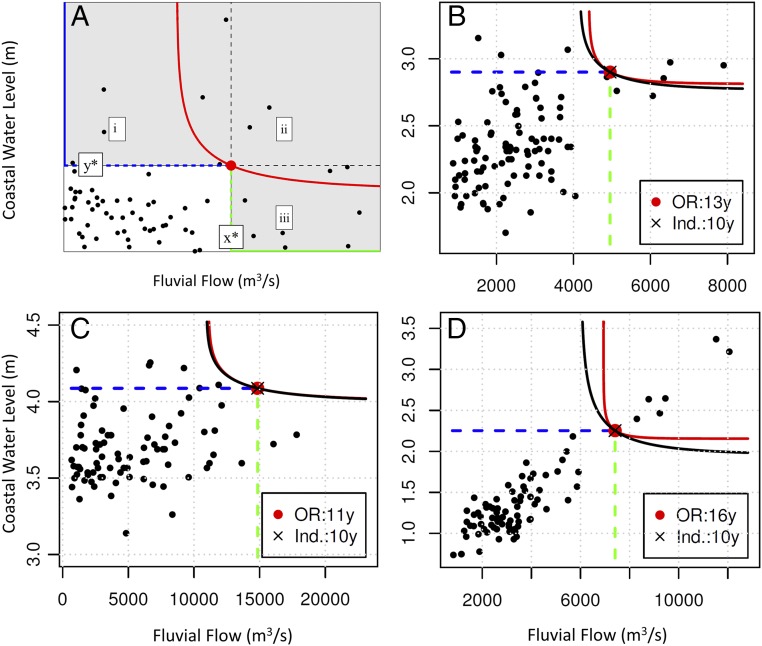
Fig. 1A shows the annual maximum fluvial flow versus the associated maximum coastal WL measured within 1 day of the flood peak (black dots). For the sake of illustration, a reference bivariate occurrence $z^{\ast }=\left(x^{\ast },y^{\ast }\right)$ is chosen, and is indicated by a red circle. Here $x^{\ast }$ and $y^{\ast }$ correspond, respectively, to 20-y return levels of the variables X (fluvial flow) and Y (coastal WL), so that $z^{\ast }$ has marginal univariate return periods (RPs) equal to 20 y (Methods). These univariate hazard scenarios (HSs) for $z^{\ast }$ are shown by a thick green line on the x axis (for X) and a thick blue line on the y axis (for Y). In the bivariate framework, we use copulas to model the compounding effects of fluvial flow and coastal WL (Methods). Here, the HS of interest is the “OR” one, meaning that it is sufficient that either the fluvial flow or the coastal WL or both be large to make a bivariate occurrence hazardous (i.e., the union of the regions i, ii, and iii in Fig. 1A, where either $X>x^{\ast }$, $Y>y^{\ast }$, or both). To highlight the differences between the case of assuming the variables X and Y as dependent or independent within this bivariate framework, in Fig. 1, the red curve indicates the isoline of the actual joint distribution $F_{XY}$ crossing $z^{\ast }$, whereas the black curve indicates the isoline of $F_{XY}$ under the unreasonable assumption of independence between the variables X and Y. Indeed, the more the variables are dependent, the more the two curves are different (e.g., compare Fig. 1 C and D).

Fig. 1.

(A) Illustration of the univariate and bivariate HSs. The black circles represent observed bivariate occurrences, the red circle is the reference occurrence z*, and the red line is the isoline of F_XY crossing z*. The hazardous regions i, ii, and iii are indicated as shaded areas. The estimates of the bivariate OR RPs associated with the occurrence z* are indicated in the legends for (B) Philadelphia, PA, (C) San Francisco, CA, and (D) Washington, DC, with Kendall tau rank correlation coefficients of 0.3, 0.15, and 0.53, respectively. In B–D, the black line shows the isoline of F_XY crossing z*, under the unreasonable assumption of independence between fluvial flow and Coastal WL.

The univariate analysis (i.e., green and blue dashed lines in Fig. 1), however useful for flood events driven only by river discharge (i.e., far upstream in tidal rivers) or only by coastal WL (i.e., at coastal regions not influenced by fluvial flow), may not appropriately characterize the flood hazard at/near estuaries. In estuaries, flood hazard can be influenced by interactions between fluvial flooding and coastal WL (30, 31, 33, 82), and hence a particular hazard level may be more frequent than expected.

For the case of $z^{\ast }$ (indicated by the red circle) with a marginal univariate RP of 20 y, the associated estimates of the bivariate OR RPs are shown in Fig. 1, for Philadelphia, PA (Fig. 1B), San Francisco, CA (Fig. 1C), and Washington, DC (Fig. 1D). In all cases, it is evident that the bivariate OR RP is shorter than the 20-y univariate RP (see also Methods): ∼13 y for Philadelphia, ∼11 y for San Francisco, and ∼16 y for Washington, DC. This indicates that ignoring the compounding impacts of fluvial flow and coastal WLs may inappropriately characterize the coastal flood hazard, and can lead to underestimation of it: Actually, a shorter RP entails a larger frequency of occurrence. The results for 5-, 10-, 20-, and 50-y RPs for all of the studied coastal systems are shown in SI Appendix, Section 5 and Figs. S20–S27.

The dependence between coastal WL and fluvial flow strongly influences the joint flood probability and, in turn, the OR RP. In Washington, DC (Fig. 1D), where the two flood drivers are highly correlated (Kendall tau rank correlation coefficient of 0.53; see also SI Appendix, Figs. S10 and S18), an event with marginal univariate RPs of 20 y, and a ∼10-y OR RP based on the incorrect assumption of independence, becomes a ∼16-y event when the dependence structure is resolved. On the other hand, in San Francisco (Fig. 1C), where the two flood drivers are weakly correlated (Kental tau ∼0.15), an event with a marginal univariate RP of 20 y, and a ∼10-y OR RP based on the assumption of independence, becomes an ∼11-y event. According to the theory of copulas, the marginal univariate RP becomes a better predictor of the OR RP with increasing correlation between the two drivers. Thus, resolving the correlation structure is critical to quantifying the compound OR RP precisely.

A further key question is, to what extent will the flood hazard change as a result of increasing sea levels? With rising sea levels, the likelihood of high WLs at any given time increases. Consequently, the bivariate OR flood hazard necessarily increases as well, and we can quantify the effects of SLR conditions on coastal flooding using a failure probability approach (Methods). The term “failure probability” refers to the probability of observing a potentially hazardous flood event (i.e., lying in a specific HS) at least once in a given design lifetime (e.g., 30 y) (74, 83). Fig. 2 shows the failure probability computed following a univariate approach (black curves), and compounding fluvial flow and coastal WL for current (red curves) and future SLR conditions over a 30-y temporal horizon for 2030 SLR based on RCP 4.5 (purple curves) and 2050 SLR based on RCP 8.5 (green curves). In each case, it is assumed that the WL distribution does not change over the design lifetime.

Fig. 2.

Estimated failure probability due to a 20-y event for a temporal horizon of 30 y. The solid black and red curves show the estimated failure probability computed based on, respectively, the univariate and bivariate OR HSs, according to present climate. Failure probability (and 95% confidence bands) for projected SLR is shown with solid (and dashed) curves for 2030 under RCP 4.5 (purple) and for 2050 under RCP 8.5 (green). In cases with significant correlation between fluvial flow and coastal WL (namely, Philadelphia, San Francisco, and Washington, DC), failure probability under the unreasonable assumption of independence is shown as a blue curve.

Considering the three sites where the dependence is significant [namely, Philadelphia (PA), San Francisco (CA), and Washington (DC)], the plots also show the OR failure probabilities under an unreasonable independence assumption (blue lines in Fig. 2). As a result, these probabilities are always larger than the ones computed using the true copula fitted on the data; in turn, including compounding effects but (falsely) assuming independence may overestimate the hazard (at least in the OR case), suggesting that a correct modeling of the dependencies should always be carried out. Thus, Fig. 2 suggests that (i) neglecting the compounding impacts of flood drivers causes significant underestimation of failure probabilities; (ii) the assumption of independence between variables, when there is significant correlation, results in overestimation of failure probabilities; and (iii) SLR significantly increases the failure probability in the near future/midfuture in all of the cases studied here. For example, we consider New York, NY, which is projected to experience US$174 million per year of loss due to flooding if no further flood management measures are implemented (84). Based on the current conditions, the failure probability at the 20-y return level over a 10-y design life time (e.g., 2017–2026) is expected to be 0.40 based on univariate analysis, and 0.65 based on the bivariate OR analysis. Now considering 2030 sea levels based on RCP 4.5, the failure probability at the same return level based on the bivariate OR analysis increases to 0.95 (0.82 to 1.00 with 95% confidence), a significantly larger value. The situation becomes worse under more-threatening SLRs. At the same return level, 2050 SLR under RCP 8.5, representing the worst-case scenario among the CMIP5 models used for AR5 (85), failure probability increases even more in the following decades. The results suggest that, under this scenario, the failure probability approaches one in six of the study areas (namely, Houston, TX; Los Angeles, CA; New York, NY; Norfolk, VA; Philadelphia, PA; and San Francisco, CA). Similar failure probability figures for different HSs are shown in SI Appendix, Section 6 and Figs. S28–S59.

This increase in failure probability due to SLR is a natural consequence of compounding effects of flood drivers. Given the expected rise in incidence and/or magnitude of high coastal WLs in the coming decades, this bivariate OR approach may be important for assessing socioeconomic impacts on coastal communities. The United States, for example, has two of the three top at-risk coastal cities in terms of assets exposed to flooding, and 17 port cities with populations larger than 1 million (44, 45, 85), and so suffers and will suffer from increased frequency of coastal flooding. However, in addition to the rise in mean coastal WL due to SLR, we expect that other impacts may also affect the frequency of flooding in estuaries, like changes in future fluvial flow regimes, wave−tide interaction, and geomorphic evolution affecting tide/surge propagation along the channel (72, 73, 76, 84, 86–89). In this study, we focus on the interactions between different SLR scenarios and current fluvial flood information, mainly because we have more confidence in the sign of change in future sea levels in a warming climate. The other components of coastal flood hazard (e.g., change in local fluvial flow regimes) are more uncertain and require further in-depth research. Hence, a key issue is developing datasets for coastal communities with contemporaneous measurements of different flood drivers. Nevertheless, the proposed framework can incorporate any combination of two (or even more) flood hazard drivers. It is also able to systematically deal with nonstationarity, and thus it can quantify the change in failure probability in response to the trending nature of drivers/hazards.

Methods

In this work, we consider annual maxima, and use the corresponding block maxima mathematical framework. Robust definition of compound events (3) and the efficient sampling for joint probability analysis (90) are challenging tasks. A desired approach should appropriately represent the information entailed in the data while simplifying the sources data (i.e., refs. 5, 91, and 92). The two variables of interest here are (i) the largest annual freshwater inflow to the lower estuary and (ii) the corresponding largest observed hourly WL within ±1 d. This procedure provides the pairs of interest for any given year (annual bivariate vectors) that can be assumed to be independent for physical reasons.

First, we need to identify suitable HSs that refer to the regions where the values of the variable(s) of interest may be considered as hazardous according to appropriate criteria. An HS is simultaneously characterized by (i) a geometrical component (i.e., a hazardous region, either on the real line in the univariate case or in the real plane in the bivariate case) and (ii) a probabilistic component (i.e., the probability that an occurrence belongs to the hazardous region). This makes it possible to use the HS for both RP and failure probability analyses (74, 77).

In the univariate case, given a critical threshold $x^{\ast }$, the corresponding univariate HS is defined as the set of occurrences such that $\left\{X>x^{\ast }\right\}$. In the bivariate case, given a critical pair $z^{\ast }=\left(x^{\ast },y^{\ast }\right)$, the corresponding bivariate HS is taken to be the inclusive OR one, defined as the set of occurrences such that either $\left\{X>x^{\ast }\right\}$, $\left\{Y>y^{\ast }\right\}$, or both (74). The choice of a bivariate OR approach is a natural one in the present context, since it is sufficient that either the fluvial discharge, the coastal WL, or both be large to produce a potentially hazardous occurrence. This represents a valuable approximation of the dynamics of coastal flooding, in which the combined events due to nonextreme discharges and WLs might also potentially generate hazardous occurrences.

The geometry of the HSs introduced above are illustrated in Fig. 1A, for given critical thresholds $x^{\ast }$ and $y^{\ast }$. The green half-line on the horizontal axis indicates the univariate HS $\left\{X>x^{\ast }\right\}$ corresponding to the variable $X$, and the blue half-line on the vertical axis indicates the univariate HS $\left\{Y>y^{\ast }\right\}$ corresponding to the variable $Y$. The shaded region is the bivariate OR HS corresponding to the pair $\left(X,Y\right)$, where either $X>x^{\ast }$, $Y>y^{\ast }$, or both.

The fundamental difference between a univariate and a bivariate approach lies in the related failure mechanism. In the former case, failure is ruled solely by a single variable, whereas, in the latter, the compounding effects of two variables may result in hazardous occurrences, even if none of the variables take on extreme values. An occurrence may be labeled as hazardous or not, depending on the chosen failure mechanism. For instance, the occurrences in regions ii and iii of Fig. 1A would be considered as hazardous if the ruling variable were the fluvial flow X, but the ones in region iii would not be hazardous according to their WL (since $Y\le y^{\ast }$). Similarly, the occurrences in regions i and ii would be hazardous if the ruling variable were the WL Y, but the ones in region i would not be such in terms of the river flows (since $X\le x^{\ast }$). Instead, all of the occurrences in the regions i, ii, and iii would be hazardous according to the (bivariate) OR criterion. Thus, the OR approach may account for the physically based fact that the combined events of $X$ and $Y$ (even if not extreme) may yield hazardous events.

Univariate and Bivariate Models.

Below, the construction of an appropriate probability model is explained, separately, for the univariate and the bivariate approaches.

Univariate model.

In this case, only one flood driver (either fluvial flow or coastal WL) is considered for hazard assessment. The generalized extreme value (GEV) distribution turns out to adequately fit the available samples of both flood drivers according to the bootstrap p values of the goodness-of-fit tests, which, in all cases, are larger than 5% (SI Appendix, Figs. S2–S9).

Bivariate model.

A variety of parametric and nonparametric methods have been developed for bivariate frequency analysis (93). We use copulas to construct a bivariate model. Copulas offer several advantages for multivariate modeling, such as the following: (i) It is possible to account separately for the marginals and the joint behavior of the variables of interest, (ii) the mathematical formulation is feasible, and (iii) marginal distributions can be freely chosen. Also, copulas allow computing the RPs and the failure probabilities of interest (15, 74, 77). See refs. 94–96 for a theoretical introduction, and see refs. 97–99 for practical descriptions.

According to Sklar’s Theorem (100), the joint distribution F_XY of the pair (X,Y), with marginal distributions F_X and F_Y, for all $(x,y)\in R^2$, can simply be written as

$$F_{XY}\left(x,y\right)=C_{XY}\left(F_X\left(x\right),F_Y\left(y\right)\right),$$ [1]

where the function $C_{XY}:\left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]\to \left[\mathrm{0,1}\right]$ is the bivariate copula of (X,Y) providing the analytical formula of the dependence structure ruling the random joint dynamics of X and Y. Practically, a bivariate model can be constructed by fitting suitable univariate laws on the marginals (in the present context, distributions), and fitting an appropriate copula on the observed pairs (97, 98). To select an appropriate bivariate model, here a thorough statistical analysis was carried out, involving 24 copula models covering a wide variety of dependence structures (see SI Appendix, Section 4).

RP Analysis.

In the present annual-based framework, the RP T associated with a given HS (either univariate or bivariate) can be defined as

$$T=1/P\left\{HS\right\},$$ [2]

where, P{HS} is the probability that an event occurs in the HS of interest (74, 77).

In the univariate case, where the HS is identified via a critical threshold $x^{\ast }$ (or $y^{\ast }$), Eq. 2 reduces to the traditional formula

$$T_X=1/\left(1-F_X\left(x^{\ast }\right)\right),$$ [3]

where $F_X$ is the distribution of $X$, and $1-F_X\left(x^{\ast }\right)$ represents the probability that an occurrence lies on the horizontal green half-line in Fig. 1A (or, equivalently, the probability of the region $ii{\displaystyle \cup }iii$). The same approach can be taken to define the RP $T_Y$ for $Y$ and the region $i{\displaystyle \cup }ii$.

In the bivariate OR case, where the HS is identified via a critical pair $z^{\ast }=\left(x^{\ast },y^{\ast }\right)$ as in Fig. 1A, exploiting the Sklar’s Theorem, Eq. 2 becomes

$$T_{OR}=1/\left(1-F_{XY}\left(x^{\ast },y^{\ast }\right)\right)=1/\left(1-C_{XY}\left(F_X\left(x^{\ast }\right),F_Y\left(y^{\ast }\right)\right)\right),$$ [4]

where, F_XY is the joint distribution of the pair $\left(X,Y\right)$, and $1-F_{XY}\left(x^{\ast },y^{\ast }\right)$ is equal to the probability of X >$x^{\ast }$ OR Y > $y^{\ast }$, i.e., the probability that a bivariate occurrence lies in the shaded region $i{\displaystyle \cup }ii{\displaystyle \cup }iii$ in Fig. 1A. For a thorough mathematical treatment, see refs. 74 and 77.

Since, for all copulas, $C_{XY}\left(F_X\left(x^{\ast }\right),F_Y\left(y^{\ast }\right)\right)\le \min \left\{F_X\left(x^{\ast }\right),F_Y\left(y^{\ast }\right)\right\}$, it turns out that both $T_{OR}<T_X$ and $T_{OR}<T_Y$. Thus, potentially hazardous bivariate OR regions are more frequent than the corresponding univariate ones. Therefore, neglecting the compounding effects of hazard drivers may result in an underestimation of the hazard when the combined action of X and Y plays a significant role.

Failure Probability Analysis.

For a given design lifetime T (typically in years), let (S₁, …, S_T) be a sequence of relevant annual bivariate HSs (in the present case, the OR ones). In general, the corresponding failure probability p_T can be defined as

$$p_T=1-P\left\{\left(X_1,Y_1\right)\notin S_1,\dots ,\left(X_T,Y_T\right)\notin S_T\right\},$$ [5]

equivalent to the complement of the probability that no hazardous event occurs in T years. For an OR HS, identified by a critical pair $z^{\ast }=\left(x^{\ast },y^{\ast }\right)$, in the case of independent identically distributed occurrences, the failure probability is a monotonically increasing function of T, and is given by

$$p_T=1-{\left[C_{XY}\left(F_X\left(x^{\ast }\right),F_Y\left(y^{\ast }\right)\right)\right]}^T,$$ [6]

representing the probability that at least one bivariate OR hazardous occurrence happens during a T-year temporal horizon (see ref. 74 for further details). As explained earlier, since $C_{XY}\left(F_X\left(x^{\ast }\right),F_Y\left(y^{\ast }\right)\right)\le \min \left\{F_X\left(x^{\ast }\right),F_Y\left(y^{\ast }\right)\right\}$, and $F_X\left(x^{\ast }\right)$ and $F_Y\left(y^{\ast }\right)$ represent the probabilities of “safe” univariate X and Y occurrences, it turns out that $p_{T,OR}\ge p_{T,X}$ and $p_{T,OR}\ge p_{T,Y}$ for all Ts, implying that OR occurrences are generally more hazardous than univariate ones.

To integrate the concept of nonstationarity to the proposed bivariate HS and failure probability estimates framework, we perturbed the annual bivariate vectors using Monte Carlo simulations exploiting the projected distribution of SLR. The details are explained in SI Appendix. In Results and Discussion, it is shown how the SLR may increase the failure probability of coastal flood defenses in the future.