Significance
Clustering is a fundamental experimental procedure in data analysis. It is used in virtually all natural and social sciences and has played a central role in biology, astronomy, psychology, medicine, and chemistry. Despite the importance and ubiquity of clustering, existing algorithms suffer from a variety of drawbacks and no universal solution has emerged. We present a clustering algorithm that reliably achieves high accuracy across domains, handles high data dimensionality, and scales to large datasets. The algorithm optimizes a smooth global objective, using efficient numerical methods. Experiments demonstrate that our method outperforms state-of-the-art clustering algorithms by significant factors in multiple domains.
Keywords: clustering, data analysis, unsupervised learning
Abstract
Clustering is a fundamental procedure in the analysis of scientific data. It is used ubiquitously across the sciences. Despite decades of research, existing clustering algorithms have limited effectiveness in high dimensions and often require tuning parameters for different domains and datasets. We present a clustering algorithm that achieves high accuracy across multiple domains and scales efficiently to high dimensions and large datasets. The presented algorithm optimizes a smooth continuous objective, which is based on robust statistics and allows heavily mixed clusters to be untangled. The continuous nature of the objective also allows clustering to be integrated as a module in end-to-end feature learning pipelines. We demonstrate this by extending the algorithm to perform joint clustering and dimensionality reduction by efficiently optimizing a continuous global objective. The presented approach is evaluated on large datasets of faces, hand-written digits, objects, newswire articles, sensor readings from the Space Shuttle, and protein expression levels. Our method achieves high accuracy across all datasets, outperforming the best prior algorithm by a factor of 3 in average rank.
Clustering is one of the fundamental experimental procedures in data analysis. It is used in virtually all natural and social sciences and has played a central role in biology, astronomy, psychology, medicine, and chemistry. Data-clustering algorithms have been developed for more than half a century (1). Significant advances in the last two decades include spectral clustering (2–4), generalizations of classic center-based methods (5, 6), mixture models (7, 8), mean shift (9), affinity propagation (10), subspace clustering (11–13), nonparametric methods (14, 15), and feature selection (16–20).
Despite these developments, no single algorithm has emerged to displace the -means scheme and its variants (21). This is despite the known drawbacks of such center-based methods, including sensitivity to initialization, limited effectiveness in high-dimensional spaces, and the requirement that the number of clusters be set in advance. The endurance of these methods is in part due to their simplicity and in part due to difficulties associated with some of the new techniques, such as additional hyperparameters that need to be tuned, high computational cost, and varying effectiveness across domains. Consequently, scientists who analyze large high-dimensional datasets with unknown distribution must maintain and apply multiple different clustering algorithms in the hope that one will succeed. Books have been written to guide practitioners through the landscape of data-clustering techniques (22).
We present a clustering algorithm that is fast, easy to use, and effective in high dimensions. The algorithm optimizes a clear continuous objective, using standard numerical methods that scale to massive datasets. The number of clusters need not be known in advance.
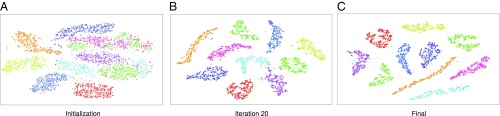
The operation of the algorithm can be understood by contrasting it with other popular clustering techniques. In center-based algorithms such as -means (1, 24), a small set of putative cluster centers is initialized from the data and then iteratively refined. In affinity propagation (10), data points communicate over a graph structure to elect a subset of the points as representatives. In the presented algorithm, each data point has a dedicated representative, initially located at the data point. Over the course of the algorithm, the representatives move and coalesce into easily separable clusters. The progress of the algorithm is visualized in Fig. 1.
Fig. 1.
RCC on the Modified National Institute of Standards and Technology (MNIST) dataset. Each data point has a corresponding representative . The representatives are optimized to reveal the structure of the data. A–C visualize the representation using the t-SNE algorithm (23). Ground-truth clusters are coded by color. (A) The initial state, . (B) The representation after 20 iterations of the optimization. (C) The final representation produced by the algorithm.
Our formulation is based on recent convex relaxations for clustering (25, 26). However, our objective is deliberately not convex. We use redescending robust estimators that allow even heavily mixed clusters to be untangled by optimizing a single continuous objective. Despite the nonconvexity of the objective, the optimization can still be performed using standard linear least-squares solvers, which are highly efficient and scalable. Since the algorithm expresses clustering as optimization of a continuous objective based on robust estimation, we call it robust continuous clustering (RCC).
One of the characteristics of the presented formulation is that clustering is reduced to optimization of a continuous objective. This enables the integration of clustering in end-to-end feature learning pipelines. We demonstrate this by extending RCC to perform joint clustering and dimensionality reduction. The extended algorithm, called RCC-DR, learns an embedding of the data into a low-dimensional space in which it is clustered. Embedding and clustering are performed jointly, by an algorithm that optimizes a clear global objective.
We evaluate RCC and RCC-DR on a large number of datasets from a variety of domains. These include image datasets, document datasets, a dataset of sensor readings from the Space Shuttle, and a dataset of protein expression levels in mice. Experiments demonstrate that our method significantly outperforms prior state-of-the-art techniques. RCC-DR is particularly robust across datasets from different domains, outperforming the best prior algorithm by a factor of 3 in average rank.
Formulation
We consider the problem of clustering a set of data points. The input is denoted by , where . Our approach operates on a set of representatives , where . The representatives are initialized at the corresponding data points . The optimization operates on the representation , which coalesces to reveal the cluster structure latent in the data. Thus, the number of clusters need not be known in advance. The optimization of is illustrated in Fig. 1.
The RCC objective has the following form:
| [1] |
Here is the set of edges in a graph connecting the data points. The graph is constructed automatically from the data. We use mutual -nearest neighbors (m-kNN) connectivity (27), which is more robust than commonly used kNN graphs. The weights balance the contribution of each data point to the pairwise terms and balances the strength of different objective terms.
The function is a penalty on the regularization terms. The use of an appropriate robust penalty function is central to our method. Since we want representatives of observations from the same latent cluster to collapse into a single point, a natural penalty would be the norm (, where is the Iverson bracket). However, this transforms the objective into an intractable combinatorial optimization problem. At another extreme, recent work has explored the use of convex penalties, such as the and norms (25, 26). This has the advantage of turning objective 1 into a convex optimization problem. However, convex functions—even the norm—have limited robustness to spurious edges in the connectivity structure , because the influence of a spurious pairwise term does not diminish as representatives move apart during the optimization. Given noisy real-world data, heavy contamination of the connectivity structure by connections across different underlying clusters is inevitable. Our method uses robust estimators to automatically prune spurious intercluster connections while maintaining veridical intracluster correspondences, all within a single continuous objective.
The second term in objective 1 is related to the mean shift objective (9). The RCC objective differs in that it includes an additional data term, uses a sparse (as opposed to a fully connected) connectivity structure, and is based on robust estimation.
Our approach is based on the duality between robust estimation and line processes (28). We introduce an auxiliary variable for each connection and optimize a joint objective over the representatives and the line process :
| [2] |
Here is a penalty on ignoring a connection : tends to zero when the connection is active () and to one when the connection is disabled (). A broad variety of robust estimators have corresponding penalty functions such that objectives 1 and 2 are equivalent with respect to : Optimizing either of the two objectives yields the same set of representatives . This formulation is related to iteratively reweighted least squares (IRLS) (29), but is more flexible due to the explicit variables and the ability to define additional terms over these variables.
Objective 2 can be optimized by any gradient-based method. However, its form enables efficient and scalable optimization by iterative solution of linear least-squares systems. This yields a general approach that can accommodate many robust nonconvex functions , reduces clustering to the application of highly optimized off-the-shelf linear system solvers, and easily scales to datasets with hundreds of thousands of points in tens of thousands of dimensions. In comparison, recent work has considered a specific family of concave penalties and derived a computationally intensive majorization–minimization scheme for optimizing the objective in this special case (30). Our work provides a highly efficient general solution.
While the presented approach can accommodate many estimators in the same computationally efficient framework, our exposition and experiments use a form of the well-known Geman–McClure estimator (31),
| [3] |
where is a scale parameter. The corresponding penalty function that makes objectives 1 and 2 equivalent with respect to is
| [4] |
Optimization
Objective 2 is biconvex on . When variables are fixed, the individual pairwise terms decouple and the optimal value of each can be computed independently in closed form. When variables are fixed, objective 2 turns into a linear least-squares problem. We exploit this special structure and optimize the objective by alternatingly updating the variable sets and . As a block coordinate descent algorithm, this alternating minimization scheme provably converges.
When are fixed, the optimal value of each is given by
| [5] |
This can be verified by substituting Eq. 5 into Eq. 2, which yields objective 1 with respect to .
When are fixed, we can rewrite [2] in matrix form and obtain a simplified expression for solving ,
| [6] |
where is an indicator vector with the element set to . This is a linear least-squares problem that can be efficiently solved using fast and scalable solvers. The linear least-squares formulation is given by
| [7] |
Here is the identity matrix. It is easy to prove that
| [8] |
is a Laplacian matrix and hence is symmetric and positive semidefinite. As with any multigrid solver, each row of in Eq. 7 can be solved independently and in parallel.
The RCC algorithm is summarized in Algorithm 1: RCC. Note that all updates of and optimize the same continuous global objective 2.
The algorithm uses graduated nonconvexity (32). It begins with a locally convex approximation of the objective, obtained by setting such that the second derivative of the estimator is positive () over the relevant part of the domain. Over the iterations, is automatically decreased, gradually introducing nonconvexity into the objective. Under certain assumptions, such continuation schemes are known to attain solutions that are close to the global optimum (33).
The parameter in the RCC objective 1 balances the strength of the data terms and pairwise terms. The reformulation of RCC as a linear least-squares problem enables setting automatically. Specifically, Eq. 7 suggests that the data terms and pairwise terms can be balanced by setting
| [9] |
The value of is updated automatically according to this formula after every update of . An update involves computing only the largest eigenvalue of the Laplacian matrix . The spectral norm of is precomputed at initialization and reused.
Additional details concerning Algorithm 1 are provided in SI Methods.
SI Methods
Initialization and Output.
We initialize the optimization with and . The output clusters are the weakly connected components of a graph in which a pair and is connected by an edge if and only if . The threshold is set to be the mean of the lengths of the shortest of the edges in .
Connectivity Structure.
The connectivity structure is based on m-kNN connectivity (27), which is more robust than commonly used kNN graphs. We use and the cosine similarity metric for m-kNN graph construction. In an m-kNN graph, two nodes are connected by an edge if and only if each is among the nearest neighbors of the other. This allows statistically different clusters (e.g., different scales) to remain disconnected. A downside of this connectivity scheme is that some nodes in an m-kNN graph may be sparsely connected or even disconnected. To make sure that no data point is isolated we augment with the minimum-spanning tree of the -nearest neighbors graph of the dataset. To balance the contribution of each node to the objective, we set
| [S1] |
where is the number of edges incident to in .
Graduated Nonconvexity.
The penalty function in Eq. 3 is nonconvex and its shape depends on the value of the parameter . To support convergence to a good solution, we use graduated nonconvexity (32). We begin by setting such that the objective is convex over the relevant range and gradually decrease to sharpen the penalty and neutralize the influence of spurious connections in . Specifically, is initially set to , where is the maximal edge length in . The value of is halved every four iterations until it drops below .
Parameter Setting.
The termination conditions are set to maxiterations = 100 and .
For RCC-DR, the sparse coding parameters are set to , , , and . The dictionary is initialized using PCA components. Due to the small input dimension, we set for the Shuttle, Pendigits, and Mice Protein datasets. The parameters and in RCC-DR are computed using , by analogy to their counterparts in RCC. To set , we compute the distance of each data point from the mean of data and set . The initial value of is set to . The parameter is set automatically to
| [S2] |
Implementation.
We use an approximate nearest-neighbor search to construct the connectivity structure (54) and a conjugate gradient solver for linear systems (55).
The RCC-DR Algorithm.
The RCC-DR algorithm is summarized in Algorithm S1: Joint Clustering and Dimensionality Reduction.
Joint Clustering and Dimensionality Reduction
The RCC formulation can be interpreted as learning a graph-regularized embedding of the data . In Algorithm 1 the dimensionality of the embedding is the same as the dimensionality of the data . However, since RCC optimizes a continuous and differentiable objective, it can be used within end-to-end feature learning pipelines. We now demonstrate this by extending RCC to perform joint clustering and dimensionality reduction. Such joint optimization has been considered in recent work (34, 35). The algorithm we develop, RCC-DR, learns a linear mapping into a reduced space in which the data are clustered. The mapping is optimized as part of the clustering objective, yielding an embedding in which the data can be clustered most effectively. RCC-DR inherits the appealing properties of RCC: Clustering and dimensionality reduction are performed jointly by optimizing a clear continuous objective, the framework supports nonconvex robust estimators that can untangle mixed clusters, and optimization is performed by efficient and scalable numerical methods.
Algorithm 1.
RCC
| I: input: Data samples . |
| II: output: Cluster assignment . |
| III: Construct connectivity structure . |
| IV: Precompute . |
| V: Initialize . |
| VI: while or < maxiterations do |
| VII: Update using Eq. 5 and using Eq. 8. |
| VIII: Update using Eq. 7. |
| IX: Every four iterations, update , . |
| X: Construct graph with if . |
| XI: Output clusters given by the connected components of . |
We begin by considering an initial formulation for the RCC-DR objective:
| [10] |
Here is a dictionary, is a sparse code corresponding to the data sample, and is the low-dimensional embedding of . For a fixed , the parameter balances the data term in the sparse coding objective with the clustering objective in the reduced space. This initial formulation 10 is problematic because in the beginning of the optimization the representation can be noisy due to spurious intercluster connections that have not yet been disabled. This had no effect on the convergence of the original RCC objective 1, but in formulation 10 the contamination of can infect the sparse coding system via and corrupt the dictionary . For this reason, we use a different formulation that has the added benefit of eliminating the parameter :
| [11] |
Here we replaced the penalty on the data term in the reduced space with a robust penalty. We use the Geman–McClure estimator 3 for both and .
To optimize objective 11, we introduce line processes and corresponding to the data and pairwise terms in the reduced space, respectively, and optimize a joint objective over , , , , and . The optimization is performed by block coordinate descent over these groups of variables. The line processes and can be updated in closed form as in Eq. 5. The variables are updated by solving the linear system
| [12] |
where
| [13] |
and is a diagonal matrix with .
The dictionary and codes are initialized using principal component analysis (PCA). [The K-SVD algorithm can also be used for this purpose (36).] The variables are updated by accelerated proximal gradient-descent steps (37),
| [14] |
where and . The operator performs elementwise soft thresholding:
| [15] |
The variables are updated using
| [16] |
| [17] |
where is a small regularization value set to .
A precise specification of the RCC-DR algorithm is provided in Algorithm S1.
Algorithm S1.
Joint Clustering and Dimensionality Reduction
| I: | input: Data samples , dimensionality , parameters , , . |
| II: | output: Cluster assignment and latent factors . |
| III: | Construct connectivity structure . |
| IV: | Initialize dictionary and codes . |
| V: | Precompute , , . |
| Vi: | Initialize , , ,, , . |
| VII: | while or < maxiterations do |
| VIII: | Update and using Eq. 5. |
| IX: | Update using Eq. 14. |
| X: | Update using Eq. 12. |
| XI: | Every 4 iterations, update , . |
| XII: | Every 10 iterations, update using Eq. 17. |
| XIII: | Construct graph with if . |
| XIV: | Output clusters given by the connected components of . |
Experiments
Datasets.
We have conducted experiments on datasets from multiple domains. The dimensionality of the data in the different datasets varies from 9 to just below 50,000. Reuters-21578 is the classic benchmark for text classification, comprising 21,578 articles that appeared on the Reuters newswire in 1987. RCV1 is a more recent benchmark of 800,000 manually categorized Reuters newswire articles (38). (Due to limited scalability of some prior algorithms, we use 10,000 random samples from RCV1.) Shuttle is a dataset from NASA that contains 58,000 multivariate measurements produced by sensors in the radiator subsystem of the Space Shuttle; these measurements are known to arise from seven different conditions of the radiators. Mice Protein is a dataset that consists of the expression levels of 77 proteins measured in the cerebral cortex of eight classes of control and trisomic mice (39). The last two datasets were obtained from the University of California, Irvine, machine-learning repository (40).
MNIST is the classic dataset of 70,000 hand-written digits (41). Pendigits is another well-known dataset of hand-written digits (42). The Extended Yale Face Database B (YaleB) contains images of faces of 28 human subjects (43). The YouTube Faces Database (YTF) contains videos of faces of different subjects (44); we use all video frames from the first 40 subjects sorted in chronological order. Columbia University Image Library (COIL-100) is a classic collection of color images of 100 objects, each imaged from 72 viewpoints (45). The datasets are summarized in Table 1.
Table 1.
Datasets used in experiments
| Name | Instances | Dimensions | Classes | Imbalance |
| MNIST (41) | 70,000 | 784 | 10 | 1 |
| Coil-100 (45) | 7,200 | 49,152 | 100 | 1 |
| YaleB (43) | 2,414 | 32,256 | 38 | 1 |
| YTF (44) | 10,036 | 9,075 | 40 | 13 |
| Reuters-21578 | 9,082 | 2,000 | 50 | 785 |
| RCV1 (38) | 10,000 | 2,000 | 4 | 6 |
| Pendigits (42) | 10,992 | 16 | 10 | 1 |
| Shuttle | 58,000 | 9 | 7 | 4,558 |
| Mice Protein (39) | 1,077 | 77 | 8 | 1 |
For each dataset, the number of instances, number of dimensions, number of ground-truth clusters, and the imbalance, defined as the ratio of the largest and smallest cardinalities of ground-truth clusters, are shown.
Baselines.
We compare RCC and RCC-DR to 13 baselines, which include widely known clustering algorithms as well as recent techniques that were reported to achieve state-of-the-art performance. Our baselines are -means++ (24), Gaussian mixture models (GMM), fuzzy clustering, mean-shift clustering (MS) (9), two variants of agglomerative clustering (AC-Complete and AC-Ward), normalized cuts (N-Cuts) (2), affinity propagation (AP) (10), Zeta -links (Zell) (46), spectral embedded clustering (SEC) (47), clustering using local discriminant models and global integration (LDMGI) (48), graph degree linkage (GDL) (49), and path integral clustering (PIC) (50). The parameter settings for the baselines are summarized in Table S1.
Table S1.
Parameter settings for baselines
| Baseline | Parameters |
| GMM | Diagonal covariance: regularization constant = 10−3 |
| Fuzzy | Exponent |
| MS | Flat kernel: estimated bandwidth ’s quantile parameter |
| N-Cuts | Graph construction parameters: order = , |
| AP | Preference = median of similarities, damping factor = 0.9, max iter = 1,000, convergence iter = 100 |
| Zell | Graph construction parameter |
| SEC | |
| LDMGI | Regularization constant |
| GDL | Graph construction parameter |
| PIC | Graph construction parameter |
Measures.
Normalized mutual information (NMI) has emerged as the standard measure for evaluating clustering accuracy in the machine-learning community (51). However, NMI is known to be biased in favor of fine-grained partitions. For this reason, we use adjusted mutual information (AMI), which removes this bias (52). This measure is defined as follows:
| [18] |
Here is the entropy, is the mutual information, and and are the two partitions being compared. For completeness, Table S2 provides an evaluation using the NMI measure.
Table S2.
Accuracy of all algorithms on all datasets, measured by NMI
| Dataset | -means++ | GMM | fuzzy | MS | AC-C | AC-W | N-Cuts | AP | Zell | SEC | LDMGI | GDL | PIC | RCC | RCC-DR |
| MNIST | 0.500 | 0.405 | 0.386 | 0.282 | NA | 0.679 | n/a | 0.609 | NA | 0.469 | 0.761 | NA | NA | 0.893 | 0.827 |
| Coil-100 | 0.835 | 0.832 | 0.828 | 0.750 | 0.739 | 0.876 | 0.891 | 0.843 | 0.965 | 0.872 | 0.906 | 0.965 | 0.970 | 0.963 | 0.963 |
| YTF | 0.788 | 0.779 | 0.774 | 0.846 | 0.680 | 0.806 | 0.758 | 0.783 | 0.273 | 0.760 | 0.532 | 0.664 | 0.684 | 0.850 | 0.882 |
| YaleB | 0.650 | 0.621 | 0.140 | 0.234 | 0.479 | 0.788 | 0.934 | 0.799 | 0.913 | 0.863 | 0.950 | 0.931 | 0.946 | 0.978 | 0.976 |
| Reuters | 0.536 | 0.510 | 0.272 | 0.000 | 0.392 | 0.492 | 0.545 | 0.504 | 0.087 | 0.498 | 0.523 | 0.401 | 0.057 | 0.556 | 0.553 |
| RCV1 | 0.355 | 0.338 | 0.205 | 0.000 | 0.108 | 0.364 | 0.140 | 0.355 | 0.023 | 0.069 | 0.382 | 0.020 | 0.015 | 0.138 | 0.442 |
| Pendigits | 0.680 | 0.695 | 0.695 | 0.703 | 0.526 | 0.729 | 0.813 | 0.647 | 0.317 | 0.742 | 0.775 | 0.330 | 0.467 | 0.850 | 0.855 |
| Shuttle | 0.216 | 0.267 | 0.204 | 0.365 | NA | 0.291 | 0.000 | 0.326 | NA | 0.305 | 0.591 | NA | NA | 0.488 | 0.513 |
| Mice Protein | 0.431 | 0.392 | 0.424 | 0.624 | 0.324 | 0.530 | 0.542 | 0.592 | 0.437 | 0.543 | 0.532 | 0.411 | 0.405 | 0.668 | 0.656 |
| Rank | 7.9 | 9 | 10.2 | 9.4 | 12.6 | 6.6 | 6.5 | 6.7 | 10.4 | 7.6 | 5 | 10 | 10 | 2.7 | 1.9 |
For each dataset, the maximum achieved NMI is highlighted in bold. NA, not applicable.
Results.
Results on all datasets are reported in Table 2. In addition to accuracy on each dataset, Table 2 also reports the average rank of each algorithm across datasets. For example, if an algorithm achieves the third-highest accuracy on half of the datasets and the fourth-highest one on the other half, its average rank is 3.5. If an algorithm did not yield a result on a dataset due to its size, that dataset is not taken into account in computing the average rank of the algorithm.
Table 2.
Accuracy of all algorithms on all datasets, measured by AMI
| Dataset | -means++ | GMM | Fuzzy | MS | AC-C | AC-W | N-Cuts | AP | Zell | SEC | LDMGI | GDL | PIC | RCC | RCC-DR |
| MNIST | 0.500 | 0.404 | 0.386 | 0.264 | NA | 0.679 | NA | 0.478 | NA | 0.469 | 0.761 | NA | NA | 0.893 | 0.828 |
| COIL-100 | 0.803 | 0.786 | 0.796 | 0.685 | 0.703 | 0.853 | 0.871 | 0.761 | 0.958 | 0.849 | 0.888 | 0.958 | 0.965 | 0.957 | 0.957 |
| YTF | 0.783 | 0.793 | 0.769 | 0.831 | 0.673 | 0.801 | 0.752 | 0.751 | 0.273 | 0.754 | 0.518 | 0.655 | 0.676 | 0.836 | 0.874 |
| YaleB | 0.615 | 0.591 | 0.066 | 0.091 | 0.445 | 0.767 | 0.928 | 0.700 | 0.905 | 0.849 | 0.945 | 0.924 | 0.941 | 0.975 | 0.974 |
| Reuters | 0.516 | 0.507 | 0.272 | 0.000 | 0.368 | 0.471 | 0.545 | 0.386 | 0.087 | 0.498 | 0.523 | 0.401 | 0.057 | 0.556 | 0.553 |
| RCV1 | 0.355 | 0.344 | 0.205 | 0.000 | 0.108 | 0.364 | 0.140 | 0.313 | 0.023 | 0.069 | 0.382 | 0.020 | 0.015 | 0.138 | 0.442 |
| Pendigits | 0.679 | 0.695 | 0.695 | 0.694 | 0.525 | 0.728 | 0.813 | 0.639 | 0.317 | 0.741 | 0.775 | 0.330 | 0.467 | 0.848 | 0.854 |
| Shuttle | 0.215 | 0.266 | 0.204 | 0.362 | NA | 0.291 | 0.000 | 0.322 | NA | 0.305 | 0.591 | NA | NA | 0.488 | 0.513 |
| Mice Protein | 0.425 | 0.385 | 0.417 | 0.534 | 0.315 | 0.525 | 0.536 | 0.554 | 0.428 | 0.537 | 0.527 | 0.400 | 0.394 | 0.649 | 0.638 |
| Rank | 7.8 | 8.6 | 9.9 | 9.9 | 12.4 | 6.3 | 6.3 | 8.1 | 10.4 | 7.2 | 4.9 | 9.9 | 10 | 2.4 | 1.6 |
For each dataset, the maximum AMI is highlighted in bold. Some prior algorithms did not scale to large datasets such as MNIST (70,000 data points in 784 dimensions). RCC or RCC-DR achieves the highest accuracy on seven of the nine datasets. RCC-DR achieves the highest or second-highest accuracy on eight of the nine datasets. The average rank of RCC-DR across datasets is lower by a multiplicative factor of 3 or more than the average rank of any prior algorithm. NA, not applicable.
RCC or RCC-DR achieves the highest accuracy on seven of the nine datasets. RCC-DR achieves the highest or second-highest accuracy on eight of the nine datasets and RCC achieves the highest or second-highest accuracy on five datasets. The average rank of RCC-DR and RCC is 1.6 and 2.4, respectively. The best-performing prior algorithm, LDMGI, has an average rank of 4.9, three times higher than the rank of RCC-DR. This indicates that the performance of prior algorithms is not only lower than the performance of RCC and RCC-DR, it is also inconsistent, since no prior algorithm clearly leads the others across datasets. In contrast, the low average rank of RCC and RCC-DR indicates consistently high performance across datasets.
Clustering Gene Expression Data.
We conducted an additional comprehensive evaluation on a large-scale benchmark that consists of more than 30 cancer gene expression datasets, collected for the purpose of evaluating clustering algorithms (53). The results are reported in Table S3. RCC-DR achieves the highest accuracy on eight of the datasets. Among the prior algorithms, affinity propagation achieves the highest accuracy on six of the datasets and all others on fewer. Overall, RCC-DR achieves the highest average AMI across the datasets.
Table S3.
AMI on cancer gene expression datasets
| Dataset | -means++ | GMM | fuzzy | MS | AC-C | AC-W | N-Cuts | AP | Zell | SEC | LDMGI | PIC | RCC | RCC-DR |
| Alizadeh-2000-v1 | 0.340 | 0.024 | 0.156 | 0.000 | 0.021 | 0.101 | 0.096 | 0.232 | 0.250 | 0.238 | 0.123 | 0.033 | 0.000 | 0.426 |
| Alizadeh-2000-v2 | 0.568 | 0.922 | 0.570 | 0.631 | 0.543 | 0.922 | 0.922 | 0.563 | 0.922 | 0.922 | 0.738 | 0.922 | 1.000 | 1.000 |
| Alizadeh-2000-v3 | 0.586 | 0.604 | 0.591 | 0.530 | 0.417 | 0.616 | 0.601 | 0.540 | 0.702 | 0.574 | 0.582 | 0.625 | 0.792 | 0.792 |
| Armstrong-2002-v1 | 0.372 | 0.372 | 0.372 | 0.202 | 0.323 | 0.308 | 0.372 | 0.381 | 0.308 | 0.323 | 0.355 | 0.308 | 0.528 | 0.546 |
| Armstrong-2002-v2 | 0.891 | 0.803 | 0.460 | 0.495 | 0.775 | 0.746 | 0.838 | 0.586 | 0.802 | 0.891 | 0.509 | 0.802 | 0.642 | 0.838 |
| Bhattacharjee-2001 | 0.444 | 0.406 | 0.471 | 0.242 | 0.389 | 0.601 | 0.563 | 0.377 | 0.496 | 0.570 | 0.378 | 0.378 | 0.495 | 0.600 |
| Bittner-2000 | −0.012 | −0.002 | −0.002 | 0.000 | 0.013 | 0.002 | 0.042 | 0.243 | 0.115 | −0.002 | 0.014 | 0.115 | −0.016 | 0.156 |
| Bredel-2005 | 0.297 | 0.208 | 0.297 | −0.000 | 0.324 | 0.384 | 0.203 | 0.139 | 0.278 | 0.259 | 0.295 | 0.278 | 0.468 | 0.466 |
| Chen-2002 | 0.570 | 0.622 | 0.570 | 0.155 | 0.413 | 0.441 | −0.005 | 0.347 | −0.005 | −0.005 | 0.592 | −0.005 | 0.293 | 0.326 |
| Chowdary-2006 | 0.764 | 0.808 | 0.764 | 0.488 | 0.764 | 0.859 | 0.859 | 0.443 | 0.859 | 0.859 | 0.859 | 0.859 | 0.360 | 0.393 |
| Dyrskjot-2003 | 0.507 | 0.532 | 0.503 | 0.063 | 0.332 | 0.474 | 0.303 | 0.558 | 0.269 | 0.389 | 0.385 | 0.177 | 0.359 | 0.383 |
| Garber-2001 | 0.242 | 0.137 | 0.156 | −0.000 | 0.314 | 0.210 | 0.204 | 0.274 | 0.246 | 0.200 | 0.191 | 0.246 | 0.240 | 0.173 |
| Golub-1999-v1 | 0.688 | 0.583 | 0.688 | 0.418 | 0.044 | 0.831 | 0.650 | 0.430 | 0.615 | 0.615 | 0.615 | 0.615 | 0.527 | 0.490 |
| Golub-1999-v2 | 0.680 | 0.730 | 0.708 | 0.571 | 0.642 | 0.737 | 0.693 | 0.516 | 0.689 | 0.703 | 0.600 | 0.689 | 0.656 | 0.597 |
| Gordon-2002 | 0.651 | 0.669 | 0.651 | 0.432 | 0.646 | 0.483 | 0.681 | 0.304 | −0.005 | 0.791 | 0.669 | 0.664 | 0.349 | 0.343 |
| Laiho-2007 | −0.007 | 0.184 | −0.007 | −0.032 | −0.017 | −0.007 | 0.030 | 0.061 | 0.073 | −0.007 | 0.093 | 0.044 | 0.000 | 0.000 |
| Lapointe-2004-v1 | 0.088 | 0.141 | 0.117 | 0.101 | 0.039 | 0.151 | 0.179 | 0.162 | 0.151 | 0.088 | 0.149 | 0.151 | 0.171 | 0.156 |
| Lapointe-2004-v2 | 0.008 | 0.013 | 0.160 | 0.002 | 0.173 | 0.033 | 0.153 | 0.210 | 0.147 | 0.028 | 0.118 | 0.171 | 0.155 | 0.239 |
| Liang-2005 | 0.301 | 0.301 | 0.301 | 0.078 | 0.301 | 0.301 | 0.301 | 0.481 | 0.301 | 0.301 | 0.301 | 0.301 | 0.401 | 0.419 |
| Nutt-2003-v1 | 0.171 | 0.137 | 0.082 | 0.123 | 0.074 | 0.159 | 0.156 | 0.116 | 0.109 | 0.086 | 0.078 | 0.113 | 0.142 | 0.129 |
| Nutt-2003-v2 | −0.025 | −0.025 | −0.025 | 0.000 | −0.025 | −0.024 | −0.025 | −0.027 | −0.031 | −0.025 | −0.027 | −0.030 | −0.030 | −0.029 |
| Nutt-2003-v3 | 0.063 | 0.259 | 0.063 | −0.053 | 0.105 | 0.004 | 0.080 | −0.002 | 0.059 | 0.080 | 0.174 | 0.059 | 0.000 | 0.000 |
| Pomeroy-2002-v1 | −0.012 | −0.022 | −0.012 | −0.000 | 0.105 | −0.020 | −0.006 | 0.061 | −0.020 | 0.008 | −0.026 | −0.020 | 0.111 | 0.140 |
| Pomeroy-2002-v2 | 0.502 | 0.544 | 0.580 | 0.434 | 0.601 | 0.591 | 0.617 | 0.586 | 0.568 | 0.577 | 0.602 | 0.568 | 0.582 | 0.582 |
| Ramaswamy-2001 | 0.618 | 0.650 | 0.636 | 0.009 | 0.511 | 0.623 | 0.651 | 0.592 | 0.618 | 0.620 | 0.663 | 0.639 | 0.635 | 0.676 |
| Risinger-2003 | 0.210 | 0.194 | 0.203 | 0.000 | 0.114 | 0.297 | 0.223 | 0.309 | 0.201 | 0.258 | 0.153 | 0.201 | 0.227 | 0.248 |
| Shipp-2002-v1 | 0.264 | 0.149 | 0.179 | −0.005 | 0.050 | 0.208 | 0.132 | 0.113 | −0.002 | 0.168 | 0.203 | −0.002 | 0.134 | 0.124 |
| Singh-2002 | 0.048 | 0.029 | 0.048 | 0.071 | 0.069 | 0.019 | 0.033 | 0.123 | −0.003 | 0.069 | −0.003 | 0.066 | 0.034 | 0.034 |
| Su-2001 | 0.666 | 0.720 | 0.660 | 0.539 | 0.595 | 0.662 | 0.738 | 0.657 | 0.687 | 0.650 | 0.667 | 0.660 | 0.725 | 0.702 |
| Tomlins-2006-v2 | 0.368 | 0.333 | 0.261 | 0.000 | 0.152 | 0.215 | 0.292 | 0.340 | 0.226 | 0.383 | 0.354 | 0.311 | 0.348 | 0.373 |
| Tomlins-2006 | 0.396 | 0.366 | 0.568 | −0.000 | 0.279 | 0.454 | 0.409 | 0.374 | 0.647 | 0.469 | 0.419 | 0.590 | 0.485 | 0.513 |
| West-2001 | 0.489 | 0.413 | 0.489 | 0.234 | 0.442 | 0.489 | 0.442 | 0.258 | 0.515 | 0.489 | 0.442 | 0.515 | 0.391 | 0.391 |
| Yeoh-2002-v1 | 0.914 | 0.160 | 0.282 | 0.000 | 0.175 | 0.746 | 1.000 | 0.336 | 0.916 | 0.951 | 0.857 | 0.916 | 0.937 | 0.430 |
| Yeoh-2002-v2 | 0.385 | 0.343 | 0.428 | 0.000 | 0.355 | 0.383 | 0.479 | 0.405 | 0.530 | 0.550 | 0.337 | 0.442 | 0.496 | 0.465 |
| Mean | 0.383 | 0.362 | 0.352 | 0.168 | 0.296 | 0.382 | 0.380 | 0.326 | 0.360 | 0.384 | 0.366 | 0.365 | 0.372 | 0.386 |
For each dataset, the maximum achieved AMI is highlighted in bold.
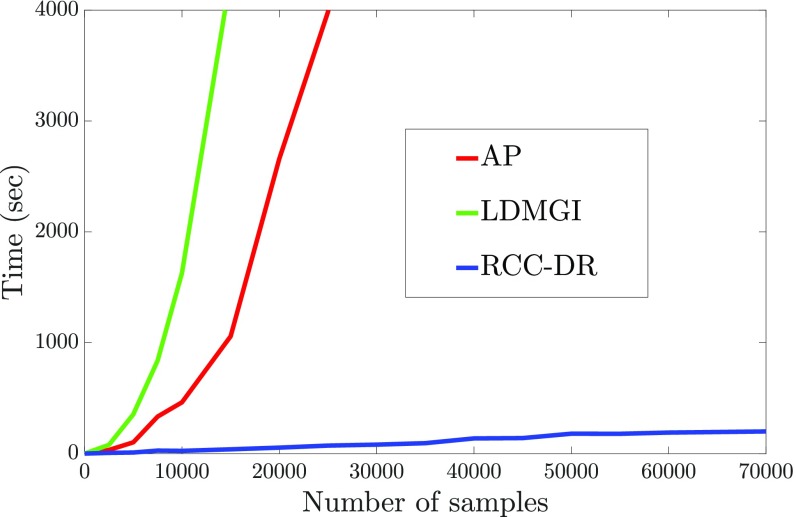
Running Time.
The execution time of RCC-DR optimization is visualized in Fig. 2. For reference, we also show the corresponding timings for affinity propagation, a well-known modern clustering algorithm (10), and LDMGI, the baseline that demonstrated the best performance across datasets (48). Fig. 2 shows the running time of each algorithm on randomly sampled subsets of the 784-dimensional MNIST dataset. We sample subsets of different sizes to evaluate runtime growth as a function of dataset size. Performance is measured on a workstation with an Intel Core i7-5960x CPU clocked at 3.0 GHz. RCC-DR clusters the whole MNIST dataset within 200 s, whereas affinity propagation takes 37 h and LDMGI takes 17 h for 40,000 points.
Fig. 2.
Runtime comparison of RCC-DR with AP and LDMGI. Runtime is evaluated as a function of dataset size, using randomly sampled subsets of different sizes from the MNIST dataset.
Visualization.
We now qualitatively analyze the output of RCC by visualization. We use the MNIST dataset for this purpose. On this dataset, RCC identifies 17 clusters. Nine of these are large clusters with more than 6,000 instances each. The remaining 8 are small clusters that encapsulate outlying data points: Seven of these contain between 2 and 11 instances, and one contains 148 instances. Fig. 3A shows 10 randomly sampled data points from each of the large clusters discovered by RCC. Their corresponding representatives are shown in Fig. 3B. Fig. 3C shows 2 randomly sampled data points from each of the small outlying clusters. Additional visualization of RCC output on the Coil-100 dataset is shown in Fig. S3.
Fig. 3.
Visualization of RCC output on the MNIST dataset. (A) Ten randomly sampled instances from each large cluster discovered by RCC, one cluster per row. (B) Corresponding representatives from the learned representation . (C) Two random samples from each of the small outlying clusters discovered by RCC.
Fig. S3.
Visualization of RCC output on the Coil-100 dataset. (A) Ten randomly sampled instances from each of 10 clusters randomly sampled from clusters discovered by RCC, one cluster per row. (B) Corresponding representatives from the learned representation .
Fig. 4 compares the representation learned by RCC to representations learned by the best-performing prior algorithms, LDMGI and N-Cuts. We use the MNIST dataset for this purpose and visualize the output of the algorithms on a subset of 5,000 randomly sampled instances from this dataset. Both of the prior algorithms construct Euclidean representations of the data, which can be visualized by dimensionality reduction. We use t-SNE (23) to visualize the representations discovered by the algorithms. As shown in Fig. 4, the representation discovered by RCC cleanly separates the different clusters by significant margins. In contrast, the prior algorithms fail to discover the structure of the data and leave some of the clusters intermixed.
Fig. 4.
(A–C) Visualization of the representations learned by RCC (A) and the best-performing prior algorithms, LDMGI (B) and N-Cuts (C). The algorithms are run on 5,000 randomly sampled instances from the MNIST dataset. The learned representations are visualized using t-SNE.
Discussion
We have presented a clustering algorithm that optimizes a continuous objective based on robust estimation. The objective is optimized using linear least-squares solvers, which scale to large high-dimensional datasets. The robust terms in the objective enable separation of entangled clusters, yielding high accuracy across datasets and domains.
The continuous form of the clustering objective allows it to be integrated into end-to-end feature learning pipelines. We have demonstrated this by extending the algorithm to perform joint clustering and dimensionality reduction.
SI Experiments
Datasets.
For Reuters-21578 we combine the train and test sets of the Modified Apte split and use only samples from categories with more than five examples. For RCV1 we consider four root categories and a random subset of 10,000 samples. For text datasets, the graph is constructed on PCA projected input. The number of PCA components is set to the number of ground-truth clusters. We compute term frequency–inverse document frequency features on the 2,000 most frequently occurring word stems.
On YaleB we consider only the frontal face images and preprocess them using gamma correction and DoG filter. For YTF we use all of the video frames from the first 40 subjects sorted in chronological order. For all image datasets we scale the pixel intensities to the range . For all other datasets, we normalize the features so that .
Baselines.
For -means++, GMM, Mean Shift, AC-Complete, AC-Ward, and AP we use the implementations in the scikit-learn package. For fuzzy clustering, we use the implementation provided by Matlab. For N-Cuts, Zell, SEC, LDMGI, GDL, and PIC we use the publicly available implementations published by the authors of these methods. For all algorithms that use -nearest neighbor graphs, we set .
Unlike the presented algorithms, many baselines rely on multiple executions with random restarts. To maximize their reported accuracy, we use 10 random restarts for these baselines. Following common practice, for -means++, GMM, and LDMGI we pick the best result based on the value of the objective function at termination, whereas for fuzzy clustering, N-Cuts, Zell, SEC, GDL, and PIC we take the average across 10 random restarts.
Most of the baselines require setting one or more parameters. For a fair comparison, for each algorithm we tune one major parameter across datasets and use the default values for all other parameters. For all algorithms, the tuned value is selected based on the best average performance across all datasets. Parameter settings for the baselines are summarized in Table S1. The notation (m : s : M) indicates that parameter search is conducted in the range with the step .
Additional Accuracy Measure.
For completeness, we evaluate the accuracy of RCC, RCC-DR, and all baselines, using the NMI measure (51, 52). The results are reported in Table S2.
Results on Gene Expression Datasets.
Table S3 lists AMI results on more than 30 cancer gene expression datasets collected by de Souto et al. (53). The maximum number of samples across datasets is only and for all but one dataset the dimension . Since these datasets are statistically very different from those discussed earlier, for each algorithm we retune the major parameter for the same range as given in Table S1. For both RCC and RCC-DR, we set . For RCC-DR we set and . The author-provided code for GDL breaks on these datasets.
Robustness to Hyperparameter Settings.
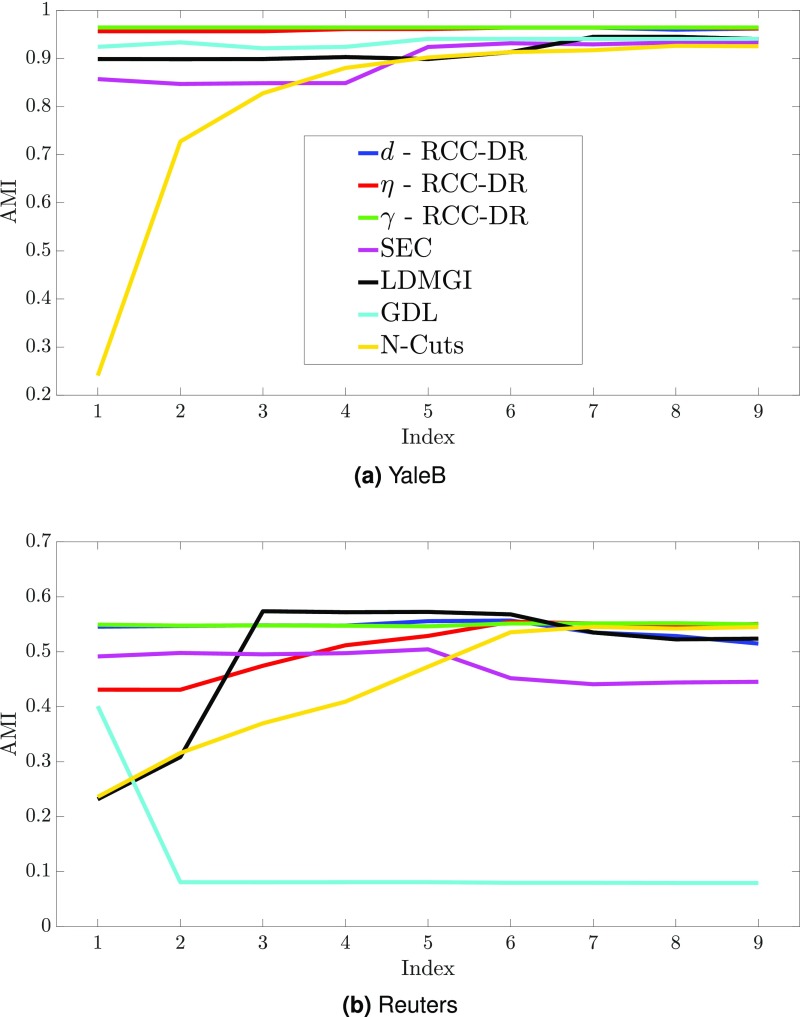
The parameters of the RCC algorithm are set automatically based on the data. The RCC-DR algorithm does have a number of parameters but is largely insensitive to their settings. In the following experiment, we vary the sparse-coding parameters , , and in the ranges , , and . Fig. S1 A and B compares the sensitivity of RCC-DR to these parameters with the sensitivity of the best-performing prior algorithms to their key parameters. For each baseline, we use the default search range proposed in their respective papers. The x axis in Fig. S1 corresponds to the parameter index. As Fig. S1 demonstrates, the accuracy of RCC-DR is robust to hyperparameter settings: The relative change of RCC-DR accuracy in AMI on YaleB is 0.005, 0.008, and 0 across the range of , , and , respectively. On the other hand, the sensitivity of the baselines is much higher: The relative change in accuracy of SEC, LDMGI, N-Cuts, and GDL is 0.091, 0.049, 0.740, and 0.021, respectively. Moreover, for SEC, LDMGI, and GDL no single parameter setting works best across different datasets.
Fig. S1.
(A and B) Robustness to hyperparameter settings on the YaleB (A) and Reuters (B) datasets.
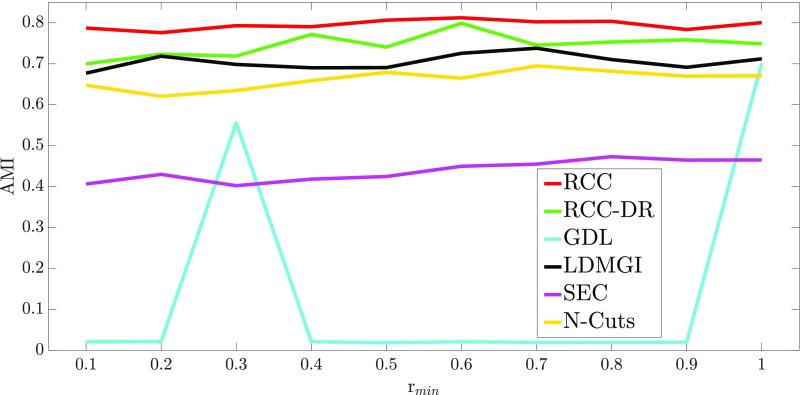
Robustness to Dataset Imbalance.
We now evaluate the robustness of different approaches to imbalance in class sizes. This experiment uses the MNIST dataset. We control the degree of imbalance by varying a parameter between 0.1 and 1. The class “0” is sampled with probability , the class “9” is sampled with probability 1, and the sampling probabilities of other classes vary linearly between and . For each value of , we sample 10,000 data points and evaluate the accuracy of RCC, RCC-DR, and the top-performing baselines on the resulting dataset. The results are reported in Fig. S2. The RCC and RCC-DR algorithms retain their accuracy advantage on imbalanced datasets.
Fig. S2.
Robustness to dataset imbalance.
Visualization.
Fig. S3A shows 10 randomly sampled data points from each of 10 clusters randomly sampled from the clusters discovered by RCC on the Coil-100 dataset. Fig. S3B shows the corresponding representatives .
Learned Representation.
One way to quantitatively evaluate the success of the learned representation in capturing the structure of the data is to use it as input to other clustering algorithms and to evaluate whether they are more successful on than they are on the original data . The results of this experiment are reported in Table S4. Table S4, Left reports the performance of multiple baselines when they are given, as input, the representation produced by RCC. Table S4, Right reports corresponding results when the baselines are given the representation produced by RCC-DR.
Table S4.
Success of the learned representation in capturing the structure of the data, evaluated by running prior clustering algorithms on instead of
| RCC | RCC-DR | |||||||||||
| Dataset | -means++ | AC-W | AP | SEC | LDMGI | GDL | -means++ | AC-W | AP | SEC | LDMGI | GDL |
| MNIST | 0.879 | 0.879 | 0.647 | 0.866 | 0.863 | NA | 0.808 | 0.809 | 0.679 | 0.808 | 0.808 | NA |
| Coil-100 | 0.958 | 0.963 | 0.956 | 0.937 | 0.932 | 0.919 | 0.959 | 0.960 | 0.956 | 0.930 | 0.942 | 0.916 |
| YTF | 0.800 | 0.814 | 0.840 | 0.737 | 0.638 | 0.455 | 0.803 | 0.817 | 0.879 | 0.726 | 0.689 | 0.464 |
| YaleB | 0.960 | 0.964 | 0.975 | 0.957 | 0.872 | 0.566 | 0.967 | 0.967 | 0.974 | 0.958 | 0.872 | 0.541 |
| Reuters | 0.544 | 0.544 | 0.511 | 0.472 | 0.372 | 0.341 | 0.545 | 0.545 | 0.525 | 0.492 | 0.528 | 0.421 |
| RCV1 | 0.460 | 0.425 | 0.368 | 0.461 | 0.301 | 0.018 | 0.488 | 0.474 | 0.384 | 0.455 | 0.209 | 0.026 |
| Pendigits | 0.750 | 0.717 | 0.759 | 0.730 | 0.526 | 0.630 | 0.742 | 0.729 | 0.756 | 0.706 | 0.742 | 0.676 |
| Shuttle | 0.255 | 0.291 | 0.338 | 0.343 | 0.132 | NA | 0.275 | 0.340 | 0.344 | 0.495 | 0.327 | NA |
| Mice Protein | 0.584 | 0.543 | 0.641 | 0.465 | 0.312 | 0.335 | 0.538 | 0.539 | 0.630 | 0.434 | 0.376 | 0.261 |
Left: using the representation learned by RCC as input to prior clustering algorithms. Right: using the representation learned by RCC-DR. Accuracy is measured by AMI. The accuracy of prior algorithms increases substantially when a representation learned by RCC or RCC-DR is used as input instead of the original data. In each case, the maximum AMI is highlighted in bold. NA, not applicable.
The results indicate that the performance of prior clustering algorithms improves significantly when they are run on the representations learned by RCC and RCC-DR. The accuracy improvements for -means++, AC-Ward, and affinity propagation are particularly notable.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1700770114/-/DCSupplemental.
References
- 1.MacQueen J. Some methods for classification and analysis of multivariate observations. Proc Berkeley Symp Math Stat Probab. 1967;1:281–297. [Google Scholar]
- 2.Shi J, Malik J. Normalized cuts and image segmentation. PAMI. 2000;22:888–905. [Google Scholar]
- 3.Ng AY, Jordan MI, Weiss Y. On spectral clustering: Analysis and an algorithm. In: Dietterich TG, Becker S, Ghahramani Z, editors. Advances in Neural Information Processing Systems 14. Vol 2. MIT Press; Cambridge, MA: 2002. pp. 849–856. [Google Scholar]
- 4.von Luxburg U. A tutorial on spectral clustering. Stat Comput. 2007;17:395–416. [Google Scholar]
- 5.Banerjee A, Merugu S, Dhillon IS, Ghosh J. Clustering with Bregman divergences. J Mach Learn Res. 2005;6:1705–1749. [Google Scholar]
- 6.Teboulle M. A unified continuous optimization framework for center-based clustering methods. J Mach Learn Res. 2007;8:65–102. [Google Scholar]
- 7.McLachlan G, Peel D. Finite Mixture Models. Wiley; New York: 2000. [Google Scholar]
- 8.Fraley C, Raftery AE. Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc. 2002;97:611. [Google Scholar]
- 9.Comaniciu D, Meer P. Mean shift: A robust approach toward feature space analysis. Pattern Anal Mach Intell. 2002;24:603–619. [Google Scholar]
- 10.Frey BJ, Dueck D. Clustering by passing messages between data points. Science. 2007;315:972–976. doi: 10.1126/science.1136800. [DOI] [PubMed] [Google Scholar]
- 11.Vidal R. Subspace clustering. IEEE Signal Processing Mag. 2011;28:52–68. [Google Scholar]
- 12.Elhamifar E, Vidal R. Sparse subspace clustering: Algorithm, theory, and applications. Pattern Anal Mach Intell. 2013;35:2765–2781. doi: 10.1109/TPAMI.2013.57. [DOI] [PubMed] [Google Scholar]
- 13.Soltanolkotabi M, Elhamifar E, Candès EJ. Robust subspace clustering. Ann Stat. 2014;42:669. [Google Scholar]
- 14.Ben-Hur A, Horn D, Siegelmann HT, Vapnik V. Support vector clustering. J Mach Learn Res. 2001;2:125–137. [Google Scholar]
- 15.Kulis B, Jordan MI. Revisiting k-means: New algorithms via Bayesian non-parametrics. In: Langford J, Pineau J, editors. Proceedings of the Twenty-Ninth International Conference on Machine Learning. Omnipress; Edinburgh: 2012. pp. 1131–1138. [Google Scholar]
- 16.Friedman JH, Meulman JJ. Clustering objects on subsets of attributes. J R Stat Soc Ser B. 2004;66:815–849. [Google Scholar]
- 17.Tadesse MG, Sha N, Vannucci M. Bayesian variable selection in clustering high-dimensional data. J Am Stat Assoc. 2005;100:602–617. [Google Scholar]
- 18.Raftery AE, Dean N. Variable selection for model-based clustering. J Am Stat Assoc. 2006;101:168–178. [Google Scholar]
- 19.Pan W, Shen X. Penalized model-based clustering with application to variable selection. J Mach Learn Res. 2007;8:1145–1164. [Google Scholar]
- 20.Witten DM, Tibshirani R. A framework for feature selection in clustering. J Am Stat Assoc. 2010;105:713–726. doi: 10.1198/jasa.2010.tm09415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jain AK. Data clustering: 50 years beyond K-means. Pattern Recognition Lett. 2010;31:651–666. [Google Scholar]
- 22.Everitt BS, Landau S, Leese M, Stahl D. Cluster Analysis. 5th Ed Wiley; Chichester, UK: 2011. [Google Scholar]
- 23.van der Maaten L, Hinton GE. Visualizing high-dimensional data using t-SNE. J Mach Learn Res. 2008;9:2579–2605. [Google Scholar]
- 24.Arthur D, Vassilvitskii S. SODA ’07 Proceedings of Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics; Philadelphia: 2007. k-means++: The advantages of careful seeding; pp. 1027–1035. [Google Scholar]
- 25.Hocking T, Joulin A, Bach FR, Vert J. Clusterpath: An algorithm for clustering using convex fusion penalties. In: Getoor L, Scheffer T, editors. Proceedings of the Twenty-Eighth International Conference on Machine Learning. Omnipress; Bellevue,WA: 2011. pp. 1–8. [Google Scholar]
- 26.Chi EC, Lange K. Splitting methods for convex clustering. J Comput Graphical Stat. 2015;24:994–1013. doi: 10.1080/10618600.2014.948181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Brito M, Chávez E, Quiroz A, Yukich J. Connectivity of the mutual k-nearest-neighbor graph in clustering and outlier detection. Stat Probab Lett. 1997;35:33–42. [Google Scholar]
- 28.Black MJ, Rangarajan A. On the unification of line processes, outlier rejection, and robust statistics with applications in early vision. Int J Comput Vis. 1996;19:57–91. [Google Scholar]
- 29.Green PJ. Iteratively reweighted least squares for maximum likelihood estimation, and some robust and resistant alternatives. J R Stat Soc Ser B. 1984;46:149–192. [Google Scholar]
- 30.Marchetti Y, Zhou Q. Solution path clustering with adaptive concave penalty. Electron J Stat. 2014;8:1569–1603. [Google Scholar]
- 31.Geman S, McClure DE. Statistical methods for tomographic image reconstruction. Bull Int Stat Inst. 1987;4:5–21. [Google Scholar]
- 32.Blake A, Zisserman A. Visual Reconstruction. MIT Press; Cambridge, MA: 1987. [Google Scholar]
- 33.Mobahi H, Fisher JW., III 2015. A theoretical analysis of optimization by Gaussian continuation. Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, eds Bonet B, Koenig S (AAAI Press, Palo Alto, CA), Vol 2, pp 1205–1211.
- 34.Wang Z, et al. A joint optimization framework of sparse coding and discriminative clustering. In: Yang Q, Wooldridge M, editors. Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence. AAAI Press; Palo Alto, CA: 2015. pp. 3932–3938. [Google Scholar]
- 35.Flammarion N, Palanisamy B, Bach FR. 2016. Robust discriminative clustering with sparse regularizers. arXiv:160808052.
- 36.Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. Trans Signal Process. 2006;54:4311–4322. [Google Scholar]
- 37.Parikh N, Boyd SP. Proximal algorithms. Foundations and Trends in Optimization. 2014;1:127–239. [Google Scholar]
- 38.Lewis DD, Yang Y, Rose TG, Li F. RCV1: A new benchmark collection for text categorization research. J Mach Learn Res. 2004;5:361–397. [Google Scholar]
- 39.Higuera C, Gardiner KJ, Cios KJ. Self-organizing feature maps identify proteins critical to learning in a mouse model of down syndrome. PLoS ONE. 2015;10:e0129126. doi: 10.1371/journal.pone.0129126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lichman M. UCI machine learning repository. 2013 Available at archive.ics.uci.edu/ml. Accessed December 6, 2016.
- 41.LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86:2278–2324. [Google Scholar]
- 42.Alimoglu F, Alpaydin E. Proceedings of the Fourth International Conference on Document Analysis and Recognition. Vol 2. IEEE Computer Society; Los Alamitos, CA: 1997. Combining multiple representations and classifiers for pen-based handwritten digit recognition; pp. 637–640. [Google Scholar]
- 43.Georghiades AS, Belhumeur PN, Kriegman DJ. From few to many: Illumination cone models for face recognition under variable lighting and pose. PAMI. 2001;23:643–660. [Google Scholar]
- 44.Wolf L, Hassner T, Maoz I. 2011. Face recognition in unconstrained videos with matched background similarity. Proceedings of IEEE CVPR 2011, eds Felzenszwalb P., Forsyth D., and Fua P. (IEEE Computer Society, New York), Vol 1, pp 529–534.
- 45.Nene SA, Nayar SK, Murase H. 1996. Columbia Object Image Library (COIL-100) (Columbia Univ., New York), Technical Report CUCS-006-96.
- 46.Zhao D, Tang X. Cyclizing clusters via zeta function of a graph. In: Koller D, Schuurmans D, Bengio Y, editors. Advances in Neural Information Processing Systems 21. Vol 3. MIT Press; Cambridge, MA: 2008. pp. 1900–1907. [Google Scholar]
- 47.Nie F, Xu D, Tsang IW, Zhang C. Spectral embedded clustering. In: Boutilier C, editor. Proceedings of the Twenty-First International Joint Conference on Artificial Intelligence. Vol 2. AAAI Press; Palo Alto, CA: 2009. pp. 1181–1186. [Google Scholar]
- 48.Yang Y, Xu D, Nie F, Yan S, Zhuang Y. Image clustering using local discriminant models and global integration. IEEE Trans Image Process. 2010;19:2761–2773. doi: 10.1109/TIP.2010.2049235. [DOI] [PubMed] [Google Scholar]
- 49.Zhang W, Wang X, Zhao D, Tang X. Graph degree linkage: Agglomerative clustering on a directed graph. In: Fitzgibbon A, Lazebnik S, Perona P, Sato Y, Schmid C, editors. Proceedings of the Twelfth European Conference on Computer Vision. Vol 1. Springer; Berlin: 2012. pp. 428–441. [Google Scholar]
- 50.Zhang W, Zhao D, Wang X. Agglomerative clustering via maximum incremental path integral. Pattern Recognition. 2013;46:3056–3065. [Google Scholar]
- 51.Strehl A, Ghosh J. Cluster ensembles – A knowledge reuse framework for combining multiple partitions. J Mach Learn Res. 2002;3:583–617. [Google Scholar]
- 52.Vinh NX, Epps J, Bailey J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J Mach Learn Res. 2010;11:2837–2854. [Google Scholar]
- 53.de Souto MC, Costa IG, de Araujo DS, Ludermir TB, Schliep A. Clustering cancer gene expression data: A comparative study. BMC Bioinformatics. 2008;9:497. doi: 10.1186/1471-2105-9-497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Muja M, Lowe DG. Scalable nearest neighbor algorithms for high dimensional data. PAMI. 2014;36:2227–2240. doi: 10.1109/TPAMI.2014.2321376. [DOI] [PubMed] [Google Scholar]
- 55.Guennebaud G, et al. 2010 Eigen v3.3. Available at eigen.tuxfamily.org. Accessed November 28, 2016.