Early history of Neanderthals and Denisovans

Significance

Neanderthals and Denisovans were human populations that separated from the modern lineage early in the Middle Pleistocene. Many modern humans carry DNA derived from these archaic populations by interbreeding during the Late Pleistocene. We develop a statistical method to study the early history of these archaic populations. We show that the archaic lineage was very small during the 10,000 y that followed its separation from the modern lineage. It then split into two regional populations, the Neanderthals and the Denisovans. The Neanderthal population grew large and separated into largely isolated local groups.

Abstract

Extensive DNA sequence data have made it possible to reconstruct human evolutionary history in unprecedented detail. We introduce a method to study the past several hundred thousand years. Our results show that (i) the Neanderthal–Denisovan lineage declined to a small size just after separating from the modern lineage, (ii) Neanderthals and Denisovans separated soon thereafter, and (iii) the subsequent Neanderthal population was large and deeply subdivided. They also (iv) support previous estimates of gene flow from Neanderthals into modern Eurasians. These results suggest an archaic human diaspora early in the Middle Pleistocene.

Around 600 kya, Europe was invaded by large-brained hominins using Acheulean stone tools (1, 2). They were probably African immigrants, because similar fossils and tools occur earlier in Africa. They have been called archaic Homo sapiens, Homo heidelbergensis, and early Neanderthals, yet they remain mysterious. They may have been ancestors of Neanderthals and modern humans (3), or ancestors of Neanderthals only (4, 5), or an evolutionary dead end. According to this last hypothesis, they were replaced later in the Middle Pleistocene by a wave of African immigrants that separated Neanderthals from modern humans and introduced the Levallois stone tool tradition to Europe (6, 7). To address this controversy, we introduce a statistical method and use it to study genetic data of Africans, Eurasians, Neanderthals, and Denisovans.

Our method extends an idea introduced by Reich et al. (8, 9). Their “ABBA-BABA” statistics infer admixture from the frequency with which derived alleles are shared by pairs of samples. As we have shown (10), these estimators have large biases when populations receive gene flow from more than one source. The magnitudes of these biases depend on the sizes and separation times of ancestral populations. Our method avoids bias by estimating these parameters simultaneously.

To accomplish this, our method uses an expanded dataset. ABBA-BABA statistics summarize allele sharing by pairs of samples. We extend this approach to include larger subsets, such as trios of samples, and to use all available subsets. This opens a rich and heretofore unused window into population history.

Nucleotide Site Patterns

Although our method can accommodate complex models, we work here with a four-population model of history (Fig. 1A), which has broad empirical support (11, 12). In this model, Neanderthals ($N$) contribute genes to Eurasians ($Y$) but not to Africans ($X$). The model allows no gene flow from Denisovans ($D$), for reasons explained below. Combinations of uppercase letters, such as $ND$, refer to the population ancestral to $N$ and $D$. Lowercase letters, such as $n$ and $d$, refer to individual haploid genomes sampled from these populations.

Fig. 1.

(A) Population tree representing an African population, $X$; a Eurasian population, $Y$; Neanderthals, $N$; and Denisovans, $D$. The model involves admixture, $m_N$; time parameters, $T_i$; and population sizes, $N_i$. (B) Population tree with embedded gene tree. A mutation on the solid red branch would generate site pattern $yn$ (shown in red at the base of the tree). One on the solid blue branch would generate $ynd$. Mutations on the dashed black branches would be ignored. “0” and “1” represent the ancestral and derived alleles.

The gene tree describes how genes coalesce within the tree of populations. Fig. 1B illustrates one of many possible gene trees. Although closely linked nucleotide sites tend to share the same gene tree, this is not the case for sites farther apart on the chromosome, and any set of autosomal sequence data will encompass a multitude of gene trees.

The gene tree determines opportunities for allele sharing among samples. For example, a mutation on the solid red branch in Fig. 1B would be present in $y$ and $n$ but absent in $x$ and $d$. We refer to this as the “$yn$ site pattern.” Similarly, a mutation on the solid blue branch would generate site pattern $ynd$. In a four-population model, there are 10 polymorphic site patterns, excluding singletons. We can tabulate their frequencies in sequence data and calculate their probabilities given particular population histories. Our program, legofit (described in Section S1), estimates parameters by fitting observed to expected frequencies. Whereas ABBA-BABA statistics use only 2 site patterns (“ABBA” and “BABA”), legofit uses all 10. This allows it to estimate additional parameters and avoid the biases discussed above.

Results

We studied site-pattern frequencies in four populations at a time: an African population ($X$), a Eurasian populaton ($Y$), Neanderthals ($N$), and Denisovans ($D$). We use the high-coverage Altai Neanderthal (14) and Denisovan (12) genomes. The modern samples are from Phase I of the 1,000-Genomes Project (15). We study two African populations, the Luhuya (LWK) of East Africa and the Yoruba (YRI) of West Africa. We also study populations from the eastern and western extremes of Eurasia: Europeans (CEU) and northern Chinese (CHB). To identify different analyses, we use abbreviations such as “LWK.CHB,” which means that the African population ($X$) is LWK and the Eurasian population ($Y$) is CHB. We exclude several populations of great interest—Melanesians, the San, and Pygmies—because they would require a different model of history than that in Fig. 1.

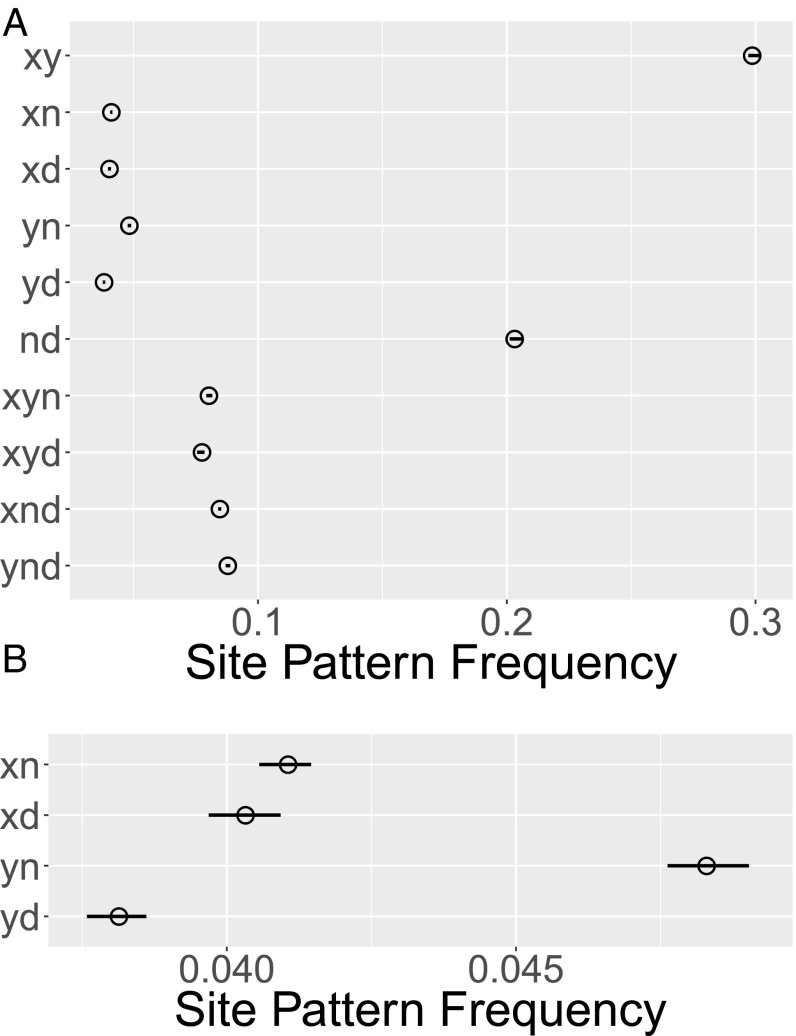
One set of 10 site-pattern frequencies is shown in Fig. 2A. About 30% of the nucleotide sites in these data exhibit the $xy$ site pattern; another 20% exhibit $nd$. Pattern $xy$ is common because $x$ and $y$ are samples from closely related populations and therefore tend to share ancestry. Mutations in these shared ancestors generate the $xy$ site pattern. Shared ancestry also explains the elevated frequency of $nd$.

Fig. 2.

(A) Open circles show relative frequencies (horizontal axis) of nucleotide sites exhibiting each site pattern (vertical axis) in four populations: $X$, YRI; $Y$, CEU; $N$, Neanderthal; and $D$, Denisovan. (B) Expanded view of four site-pattern frequencies, showing 95% confidence intervals, estimated by moving-blocks bootstrap, with 1,000 polymorphic nucleotide sites per block (13).

As noted above, our model of history (Fig. 1A) excludes gene flow from Denisovans into Eurasians. This is not a limitation of our method; it is motivated by the structure of the datasets under study. To see why, consider Fig. 2B. Note first that $yn$ is more common than $xn$—Neanderthals share more derived alleles with Europeans than with Africans. This suggests gene flow from Neanderthals into Europeans (9). More surprisingly, $xd$ is more common than $yd$. The same pattern appears in all four combinations (YRI.CEU, YRI.CHB, LWK.CEU, and LWK.CHB) of African and Eurasian populations in our analysis. This pattern suggests gene flow from Denisovans into Africans, a possibility that we consider in Section S3. It also precludes any estimate of gene flow from Denisovans into Eurasians. For this reason, our base model includes no such term.

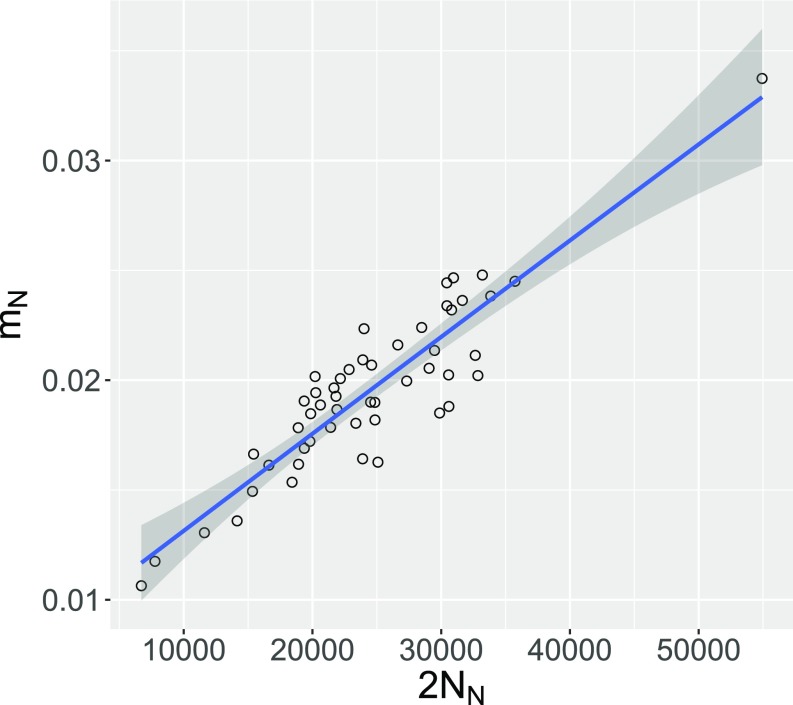
The analysis proceeds in two stages: one to discover dependencies among parameters and a second one imposing constraints to cope with these dependencies. In stage 1, we fit an unconstrained model to the observed data and also to 50 bootstrap replicates. With the data in Fig. 2A, stage 1 revealed strong dependencies among several parameters (Fig. S1). For example, there is a positive relationship between $m_N$, the admixture fraction, and $2N_N$, the Neanderthal population size (Fig. 3). This relationship makes sense: If the Neanderthal population were large, then most introgressing Neanderthal genes would be distantly related to the Altai Neanderthal fossil. It would therefore take more admixture to produce a given effect on the $yn$ site pattern. On the other hand, if the Neanderthal population were small, a little admixture would have a larger effect.

Fig. S1.

Scatter-plot matrix showing associations among pairs of parameters. Each point represents a bootstrap replicate in the YRI.CEU data from Fig. 2A.

Fig. 3.

Covariation of estimates of $m_N$ and $2N_N$ across bootstrap replicates. Data are as in Fig. 2.

Such associations make estimation difficult, because points along the regression line have similar effects on the data. To reduce such issues, stage 2 of our analysis uses associations in the bootstrap data to impose constraints. Each constraint replaces one parameter with its regression on several others, as described in Section S1.4. Because this involves ignoring some of the sampling variation, we do not estimate confidence intervals for constrained parameters.

To calibrate the molecular clock, we use published estimates of $T_{XY}$ and $T_{XYND}$, as explained in Section S2. We assume a generation time of 29 y and a mutation rate of $1.1\times {10}^{-8}$ per generation (16).

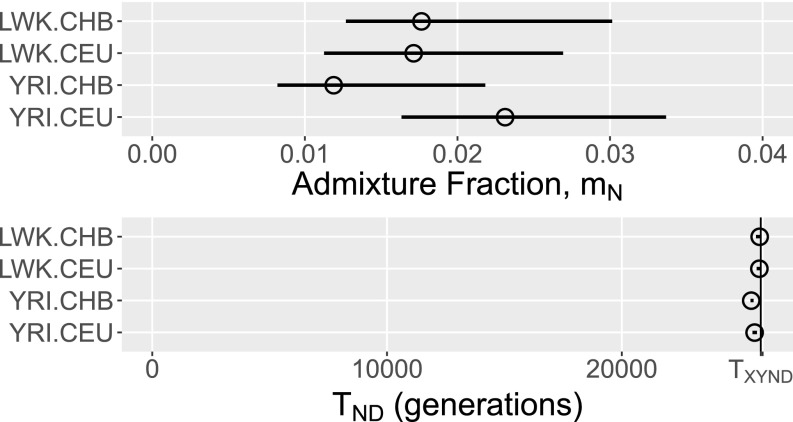
All four analyses—YRI.CEU, YRI.CHB, LWK.CEU, and LWK.CHB—yield similar results. Estimates of Neanderthal admixture ($m_N$) and Neanderthal–Denisovan separation time ($T_{ND}$) appear in Fig. 4. The admixture estimates are 1–3%, in broad agreement with previous results. Our results do not, however, support the view that East Asians carry more Neanderthal DNA than Europeans (12, 14, 17–21). This view may be an artifact of ascertainment bias (17) or of the biases documented by Rogers and Bohlender (10). On the other hand, the East Asian excess may be real, but hidden by the broad confidence intervals surrounding our estimates of $m_N$.

Fig. 4.

Estimates of Neanderthal admixture ($m_N$) and the Neanderthal–Denisovan separation time ($T_{ND}$). The vertical line (Lower) shows $T_{XYND}$. Horizontal lines show 95% confidence intervals based on 50 moving-blocks bootstrap replicates. All point estimates and confidence intervals are based on stage 2 of the analysis.

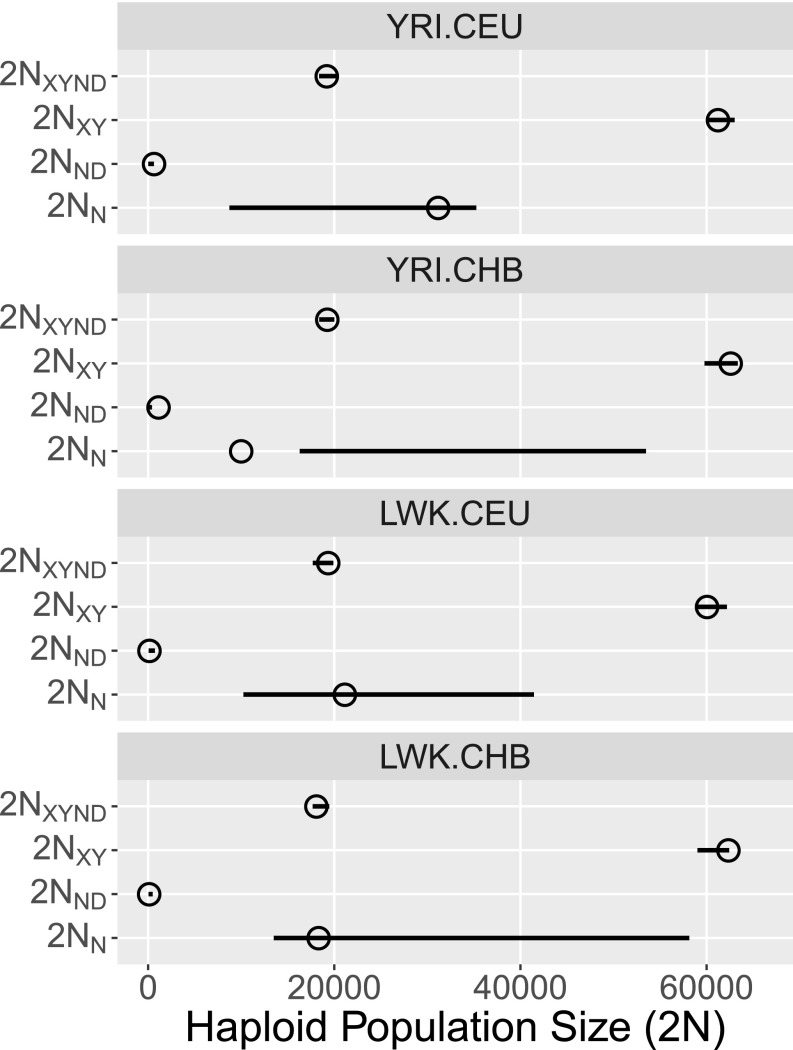
All estimates of $T_{ND}$, the separation time of Neanderthals and Denisovans, are close to 25,600 generations ago—only about 300 generations after the separation of archaics from moderns. Furthermore, this separation time is estimated with high confidence, judging from the narrow confidence intervals in Fig. 4, Lower. During the interval between the two separation events, the ancestral archaic population was apparently very small. Our point estimates of $2N_{ND}$ range from about 100 to about 1,000, with narrow confidence intervals. Following the Neanderthal–Denisovan separation, our results imply a relatively large Neanderthal population, with $2N$ in the tens of thousands. Fig. S3 graphs the history of effective population size of Neanderthals, moderns, and their ancestors, as implied by the YRI.CEU analysis.

Fig. S3.

History of effective size of Neanderthals (solid red lines), moderns (dashed blue lines), and their ancestors, based on estimates in Figs. 4 and 5 for the YRI.CEU analysis.

Could these results be artifacts of a misspecified model? Our model (Fig. 1A) requires that $T_{ND}<T_{XYND}$. Yet our estimates of these parameters barely differ. Furthermore, the confidence intervals for $T_{ND}$ are extremely—perhaps implausibly—narrow. Specification error can produce such effects by pushing all estimates, including those from bootstrap replicates, against the same boundary. The same concern also applies to the narrow confidence intervals for $2N_{ND}$, whose estimates are close to the boundary at zero.

To test this “boundary-compression” hypothesis, we used our simulation program legosim, which is described in Section S1.5. We simulated 50 datasets under the model implied by one set of estimates and then estimated parameters from each simulated dataset. The resulting data (Fig. 6) show how our estimator behaves in the absence of specification error. Our simulation algorithm ignores linkage disequilibrium and may therefore underestimate the widths of sampling distributions. Nonetheless, these widths are similar to those of the confidence intervals in Figs. 4 and 5, suggesting that the bias in our simulations is small. Thus, it is interesting that the spreads of $T_{ND}$ and $2N_{ND}$ are narrow. These narrow distributions imply that we need not invoke specification error to explain the narrow confidence intervals of these parameters.

Fig. 6.

Marginal sampling distributions of legofit estimates, based on 50 simulated datasets. Simulation parameters (shown as red crosses) equal the estimates from the YRI.CEU analysis in Figs. 4 and 5.

Fig. 5.

Population size estimates. All point estimates are based on stage 2 of the analysis. Confidence interval for $2N_{XYND}$ is based on stage 2; other intervals are based on stage 1.

These simulations also show that estimates of $m_N$ and $2N_N$ are not as well behaved as those of the other parameters. They exhibit broad confidence intervals in real data (Figs. 4 and 5). In simulations (Fig. 6), they exhibit broad sampling distributions and bias. Presumably this reflects the association seen in Fig. 3. It is difficult to choose between parameter values that lie along the regression line.

Our base model (Fig. 1A) omits several forms of gene flow that are known or suspected, and these omissions may have introduced bias. We therefore fitted four alternative models, as described in Section S3. None of these explains the surprising features of our estimates. We have found no way to explain these features as artifacts of a misspecified model.

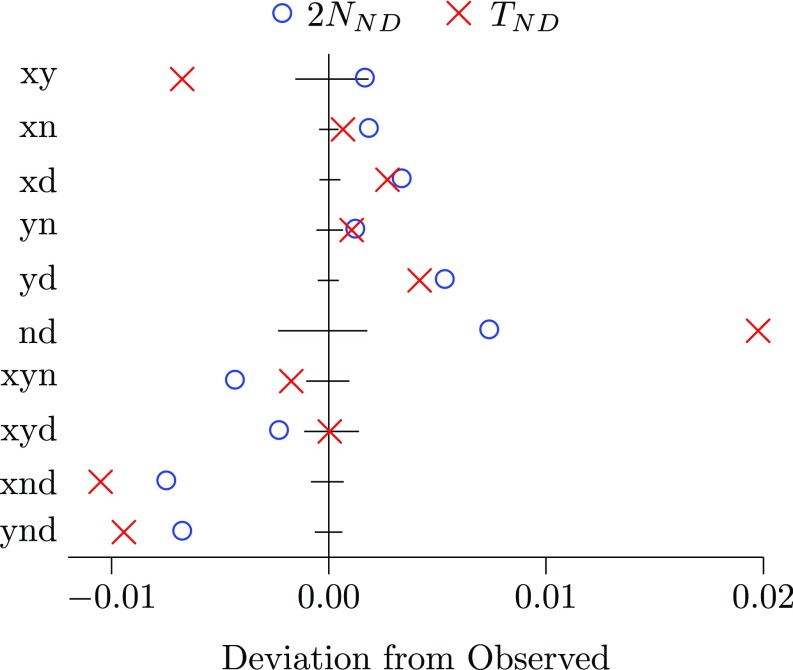
Our estimate of the Neanderthal–Denisovan separation time is surprisingly old. The most recent whole-genome estimate of this parameter is 381 kya (ref. 14, table S12.2), which corresponds to 502 kya or 17,318 generations under our molecular clock. To determine the cause of this inconsistency, we fitted a model in which $T_{ND}$ is fixed at 17,318 generations. The red crosses in Fig. 7 show the difference between fitted and observed site-pattern frequencies under this constrained model. The constrained model predicts too much $nd$ but too little $xnd$ and $ynd$. The predicted points lie well outside the confidence intervals. This, along with the smaller discrepancies seen elsewhere in Fig. 7, refutes the hypothesis that Neanderthals and Denisovans separated as recently as 17,318 generations ago.

Fig. 7.

Poor fit of two constrained models. Horizontal axis shows deviation of fitted from observed site-pattern frequencies under two constraints: $2N_{ND}=10,000$ (blue circles) and $T_{ND}=17,318$ generations (red crosses). Horizontal bars show 95% confidence intervals. Both analyses use the YRI.CEU data.

Our estimate of $2N_{ND}$ is also surprising, because it implies a previously unsuspected bottleneck among the ancestors of Neanderthals and Denisovans. To explore the cause of this result, we fitted a model in which $2N_{ND}$ was constrained to equal a larger value of 10,000. The blue circles in Fig. 7 show the errors implied by this constraint. The constrained model predicts too much $nd$ and $yd$ but too little $xnd$ and $ynd$, and many of the points lie outside the confidence intervals. The data are not consistent with a large value of $2N_{ND}$.

Our own date estimates inherit the uncertainty of the molecular clock. Using the YRI.CEU data, our point estimate of the Neanderthal–Denisovan separation time is 744 kya. Many authors prefer a higher mutation rate of $5\times {10}^{-10}$ per nucleotide site per year. Under this clock, our estimate becomes 616 kya.

Discussion

These results contradict current views about Neanderthal population history. For example, Prüfer et al. (14) estimate that the Neanderthal population was very small—declining toward extinction. This view receives additional support from research showing elevated frequencies of nonsynonymous (and presumably deleterious) mutations among Neanderthals (22–24). This abundance of deleterious alleles implies that drift was strong and thus that population size was small. Yet our estimate of Neanderthal population size is large—in the tens of thousands.

To reconcile these views, we suggest that the Neanderthal population consisted of many small subpopulations, which exchanged mates only rarely. In such a population, the effective size of the global population can be large, even if each local population is small (25). A sample from a single subpopulation would show a misleading signal of gradual population decline, even if the true population were constant (26). Furthermore, there is direct evidence of large genetic differences among Neanderthal populations (22, 27). Finally, the rich and widespread fossil record of Neanderthals is hard to reconcile with the view that their global population was tiny. We suggest that previous research has documented the small size of local Neanderthal populations, whereas our own findings document the large effective size of the metapopulation that contributed genes to modern humans.

This interpretation implies that at least some of the Neanderthals who contributed to the modern gene pool were distant relatives of the Altai Neanderthal. On the other hand, there is also evidence of gene flow from moderns into the Altai Neanderthal (28). This suggests contact between modern humans and at least two groups of Neanderthals: one that was ancestral to the Altai fossil and one or more others whose relationship to Altai was distant.

As discussed above, our results also disagree with previous estimates of the Neanderthal–Denisovan separation time. On the other hand, Meyer et al. (29) show that 430 ky-old fossils from Sima de los Huesos, Spain are more closely related to Neanderthals than to Denisovans. This implies an early separation of the two archaic lineages. Our own estimate—25,660 generations, or 744 ky—is earlier still. It is consistent with the results of Meyer et al. (29) but not with those of Prüfer et al. (14), as discussed above. The cause of this discrepancy is unclear. Prüfer et al. use the pairwise sequentially Markovian coalescent (PSMC) method (30), which may give biased estimates of separation times in subdivided populations (ref. 26, p. 6).

Our results shed light on the large-brained hominins who appear in Europe early in the Middle Pleistocene. Various authors have suggested that these were African immigrants (1, 2). This story is consistent with genetic estimates of the separation time of archaics and moderns (14). Our own results imply that, by the time these hominins show up in European archaeological sites, they had already separated from Denisovans. This agrees with Meyer et al. (29), who show that the hominins at Sima de los Huesos were genetically more similar to Neanderthals than to Denisovans. It also agrees with Hublin (4, 5), who argues that Neanderthal features emerged gradually in Europe, over an interval that began 500–600 kya.

We estimate a small effective size in the population ancestral to Neanderthals and Denisovans. The population may have been small throughout the interval between $T_{ND}$ and $T_{XYND}$, but there are also other possibilities (ref. 31, pp. 109–111). If the population varied in size, its effective size may have been much smaller than its average size. Effective size is also smaller than census size if a few individuals have disproportionate numbers of children. In a structured population, an increase in gene flow may masquerade as a reduction in effective size (26). Nonetheless, our results indicate that at least some of the time, and in at least one sex, a small number of parents produced most of the offspring.

Conclusions

It appears that Neanderthals and Denisovans separated only a few hundred generations after their ancestors left the modern lineage. During the intervening interval, the Neanderthal–Denisovan lineage was small. After separating from Denisovans, the Neanderthal population grew large and fragmented into largely isolated local groups. The Neanderthal metapopulation that contributed genes to modern humans was much larger than the local population of the Altai Neanderthal fossil.

This story is similar to that of modern Eurasians, who also separated from an African population and then experienced a population size bottleneck and split into regional populations. The modern Eurasian diaspora seems to have been foreshadowed by another one, which happened more than half a million years earlier.

Materials and Methods

Vcf files for archaic genomes were downloaded from cdna.eva.mpg.de/denisova/VCF and from cdna.eva.mpg.de/neandertal/altai/AltaiNeandertal/VCF. Ancestral-allele calls are from the Denisova genome.

We filter sites using the Map35_100% criteria (14). The minimum filtered site list was downloaded from bioinf.eva.mpg.de/altai_minimal_filters. We include only SNPs on chromosomes 1–22 that are biallelic across all samples and exclude sites in a CpG context, with systematic errors, or with missing data in any individual.

Statistical methods are described in Sections S1 and S2.

S1 Legofit, A Computer Package for Analysis of Nucleotide Site Patterns

We developed a package of computer programs called legofit, which is available free of charge at https://github.com/alanrogers/legofit. Documentation is at content.csbs.utah.edu/∼rogers/src/legofit/index.html.

S1.1 Site Patterns, Counts, and Their Expectations.

The solid black lines in Fig. 1B show the ancestry of four populations, $X$, $Y$, $N$, and $D$. Within this population tree, we see one of many possible gene trees. A mutation on the solid red branch would generate the $yn$ site pattern; one on the solid blue branch would generate $ynd$. Let $B_{yn}$ and $B_{ynd}$ represent the lengths of these branches, and define analogous $B$ variables for the other site patterns. For this particular gene tree, all other site patterns have branches of zero length: $B_{xy}=B_{xnd}=\mathrm{\cdots }=0$.

Given $B_{yn}$, the number of mutations on the red branch of Fig. 1B is a Poisson random variable with mean $u{B}_{yn}$, where $u$ is the mutation rate per nucleotide site. Although any units might be used, we measure branch lengths in generations and $u$ in units of mutations per nucleotide site per generation.

At any given nucleotide position, the gene tree is a random variable, and so are the various branch lengths. Site pattern $yn$ occurs with an unconditional probability of ∼$uE[B_{yn}]$, ignoring the possibility of multiple mutations. Here, the expectation is with respect to a coalescent process constrained by the population tree. Let $I_{yn}$ denote the count of site pattern $yn$ across all sequenced nucleotide positions. The expected value of this count is

$$E[I_{yn}]=uLE[B_{yn}],$$ [S1]

where $L$ is the number of nucleotide positions in the sequence. The probability that a particular polymorphic site exhibits pattern $yn$ is

$$P_{yn}=\frac{E[B_{yn}]}{{\sum }_{i\in \mathrm{\Omega }}E[B_i]},$$ [S2]

where $\mathrm{\Omega }$ is the set of site patterns under study.

For simple models such as the one in Fig. 1, it is possible to derive analytical formulas for $E[B_{yn}]$, $E[B_{xy}]$, and so on (10). This approach breaks down, however, as the population tree increases in complexity. We therefore adopt a different approach, which estimates these expectations by computer simulation.

The input file of our programs legosim and legofit specifies the population tree and the location of genetic samples within it. It also specifies how population size varies throughout the tree and the times at which populations separate or introgress. These parameters fall into three categories: (i) Free parameters are estimated by legofit, (ii) fixed parameters have values that do not change, and (iii) constrained parameters are specified as known functions of one or more free parameters. These constraints make it possible to model relationships among variables that are implied either by theory or by analysis of variation among replicates generated by simulation or bootstrap.

We use computer simulations to estimate expected site-pattern counts. In each iteration of the simulation, the coalescent algorithm builds a gene genealogy analogous to the one in Fig. 1B. From this genealogy, we calculate the various branch lengths—$B_{yn}$ and so on. We estimate $E[B_{yn}]$ as the average of $B_{yn}$ across simulation replicates. We then use Eq. S2 to estimate $P_{yn}$.

This approach simulates branch lengths but not mutations. For a given level of accuracy, it is orders of magnitude faster than programs that simulate both mutation and recombination. This speed makes it possible to deal with the entire suite of site patterns and with complex models involving tens of populations. We have validated it by comparison with theoretical results in models for which analytical theory is feasible (ref. 10, supplementary materials).

S1.2 Tabulating Site Patterns from Data.

Our analysis is in terms of site-pattern frequencies, which we tabulate from sequence data using our program tabpat. This tabulation does not require phased data. In introducing site patterns above, we assumed that one haploid genome is sampled from each population. Real samples are larger, and a given nucleotide site may contribute to several site patterns. The contribution to a given site pattern is the probability that a subsample, consisting of one haploid genome drawn at random from the larger sample of each population, would exhibit this site pattern. For example, consider a model with three populations, $X$, $Y$, and $N$, and let $p_{iX}$, $p_{iY}$, and $p_{iN}$ represent derived allele frequencies at the $i$th polymorphic site in the samples from these populations. Then site pattern $xy$ occurs at site $i$ with probability $z_i=p_{iX}{p}_{iY}(1-p_{iN})$ (ref. 9, p. S131). Aggregating over sites, $I_{xy}={\sum }_i{z}_i$ summarizes the information in the data about this site pattern. In general, for the $j$th site pattern, we write the analogous summary as $I_j$.

Note that we have just redefined the $I$ statistics. Earlier, they were site-pattern counts in a sample consisting of one haploid genome from each population. Now they have become expected counts in random subsamples drawn from a larger sample.

S1.3 Estimator.

To estimate parameters, we maximize the composite likelihood,

$$L(\theta )=\prod _{j\in \mathrm{\Omega }}{P}_j^{I_j}(\theta ),$$

where $P_j$ is as given in Eq. S2, $\mathrm{\Omega }$ is the set of site patterns under study, and $\theta$ is a vector of free parameters.

We use the method of differential evolution (DE) (32) to maximize $L$. This algorithm maintains a swarm of points—10 times as many as the number of free parameters—distributed across the parameter space. In each generation, these points mutate and recombine to form offspring, which then undergo selection to form the next generation. In our implementation, the objective functions of the points are evaluated in parallel, in separate threads of execution. We begin with 1,000 DE generations during which the objective function is evaluated with modest precision, using 10,000 simulation replicates per function evaluation. We then increase precision, using 2 million simulation replicates per function evaluation. The algorithm is deemed to have converged when neither the maximum objective function value nor the spread of these values has changed in 100 DE generations.

S1.4 Constraints.

There are strong dependencies among several of the parameters in our model. For example, Fig. S1 shows a tight relationship between estimates of $T_{ND}$ and $2N_{ND}$ and a looser one between $m_N$ and $2N_N$. These relationships imply that our statistical problem has fewer dimensions than parameters. We need to reduce the parameter count to get reliable estimates.

To solve this problem, we use legofit’s constraint mechanism. This allows us to define some parameters as polynomial functions of one or more free parameters. These polynomials are estimated by regression analysis across replicates generated by bootstrap or computer simulation.

This analysis proceeds in two stages. In stage 1, we define all parameters as free, except those used to calibrate the clock. This stage generates estimates from each replicate. We then study variation among replicates to identify associations among variables, such as those seen in Fig. S1. Several of the relationships in Fig. S1 are tight, suggesting that we need only bivariate regressions. This appearance, however, is misleading. Much of the scatter in these bivariate graphs is not noise; it is deterministic variation in other dimensions. For this reason, our regressions are usually multivariate.

Based on the results from stage 1, we identify a set of parameters that will be constrained in stage 2 of the analysis. For each constrained parameter, we begin by regressing against all free parameters and use residual dependence plots (33) to evaluate the fit. We then add terms to our model or remove them as needed. For each analysis in the main text, we defined three constrained parameters ($2N_{XY}$, $2N_{ND}$, and $2N_N$) and three free ones ($T_{ND}$, $2N_{XYND}$, and $m_N$).

S1.5 Simulations.

Our simulation program, legosim, ignores linkage disequilibrium and makes use of the fact that a sum of Poisson random variables is itself Poisson. Consider the problem of simulating the number of instances of the $yn$ site pattern in sequence data with $L$ nucleotide sites. The number of sites exhibiting $yn$ is approximately Poisson with mean ${\lambda }_{yn}=uLE[B_{yn}]$, where $u$ is the mutation rate per nucleotide site per generation, and $L$ is the number of nucleotide sites in the sequence, including those that are monomorphic, but excluding those that fail quality-control filters. We use 2 million simulation replicates to estimate $E[B_{yn}]$ and then obtain $I_{yn}$ by sampling from a Poisson distribution with mean ${\lambda }_{yn}$.

We take $L=1,639,253,927$, the number of bases covered by the merged Altai and Denisova bed files, DenisovaPinky.map35_99.MQ30.Cov.indels.TRF.bed.bgz and AltaiNea.map35_99.MQ30.Cov.indels.TRF.bed.bgz, which are available at bioinf.eva.mpg.de/altai_minimal_filters. The product of $L$ with our assumed mutation rate, $u=\mathrm{\hspace{0.17em}1.2}\times {\mathrm{\hspace{0.17em}10}}^{-8}$, is ∼18. Thus, we take $uL=18$ in simulations.

S2 Calibrating the Molecular Clock

We assume generations of 29 y and a mutation rate, $u=\mathrm{\hspace{0.17em}1.1}\times {10}^{-8}$ per nucleotide per generation (ref. 16, box 2), or $0.3793\times {\mathrm{\hspace{0.17em}10}}^{-9}$/y, with 29-y generations.

To calibrate the molecular clock, we must specify the length of one interval within the population tree. Because we ignore singleton site patterns, none of the intervals in our tree extends to the present. Consequently, we base our calibration on two published estimates of population splits.

First, we assume that the archaic and modern lineages separated $T_{XYND}=\mathrm{\hspace{0.17em}25},920$ generations ago. This is based on an average of several PSMC estimates published by Prüfer et al. (ref. 14, table S12.2). The average of their estimates is 570.25 ky, assuming a mutation rate $0.5\times {\mathrm{\hspace{0.17em}10}}^{-9}\cdot {\text{bp}}^{-1}\cdot {\text{y}}^{-1}$. Under our clock, their separation time becomes 751.69 ky or 25,920 generations.

Second, we assume that African and Eurasian populations separated $T_{XY}=\mathrm{\hspace{0.17em}3},788$ generations ago. This is based on Schiffels and Durbin (ref. 34, figure 4), who argue that this split occurred during an interval surrounding 100 kya. They assume a mutation rate of $1.25\times {10}^{-8}$ per generation and a generation time of 30 y, or $0.4167\times {10}^{-9}$/y. Under our molecular clock, their 100,000 y become 109,848 y, or 3,788 generations.

The time, $T_N$, of Neanderthal admixture is fixed at a previously published estimate, 1,897 generations (ref. 35, table 2). The Denisovan fossil was excavated from a layer that has been dated to 50,300 y (ref. 14, p. 43), or 1,734.5 generations. We treat this date as a fixed parameter in legofit. The Altai Neanderthal fossil came from lower in the same level of the excavation and may therefore be older. We treat its date as a fixed parameter with a larger value—1,760 generations. These values are not important, because neither one affects the frequencies of site patterns.

S3 Alternative Models of History

Our estimates (Figs. 4 and 5) of $2N_N$ and $T_{ND}$ are surprisingly large, and our estimate of $2N_{ND}$ is surprisingly small. It is possible that these results reflect factors omitted from our base model of population history (Fig. 1A). To find out, we fitted several alternative models:

Model HtoD assumes that Denisovans received gene flow from a “hyperarchaic” population (14). Specifically, it assumes hyperarchaics introgress into Denisovans 58 kya. The hyperarchaics had separated 1 Mya from other humans. Model XYtoN assumes that the ancestors of modern humans introgressed into Neanderthals 110 kya, before the separation of Africans and Eurasians (28). Model DtoX assumes that Denisovans introgressed into Africans, as suggested by Fig. 2B. Model NtoD assumes that Neanderthals introgressed into Denisovans (ref. 14, pp. 46–47). Each of these modified models adds an additional episode of gene flow, and in each case, the new admixture fraction is fixed at 1%.

Fig. S2 compares estimates under these models to those under the base model. Models HtoD, XYtoN, and NtoD give estimates similar to those under the base model. They therefore provide no alternative explanation for the surprising features of our results. Model DtoX yields an estimate of $2N_N$ that is even larger than that under the base model. This implies that our base model is conservative. Its estimate of $2N_N$ is surprisingly large but may be an underestimate.

Fig. S2.

How estimates respond to various modifications of the base model. Key: base, model in Fig. 1A; DtoX, gene flow from Denisovans into Africans; HtoD, gene flow from hyperarchaics into Denisovans; NtoD, gene flow from Neanderthals to Denisovans; XYtoN, gene flow from early moderns into Neanderthals. All estimates are based on the YRI.CEU dataset.

In summary, we are unable to explain our main results in terms of an alternative model. This suggests that these results are not artifacts of a misspecified model.