Adaptive-illumination STED nanoscopy

Significance

We demonstrate DyMIN (Dynamic Intensity Minimum), a versatile illumination concept for coordinate-targeted superresolution fluorescence imaging. Dynamically adapting the illumination (and therefore resolution) for the probing of molecular signals to local structural features entails major reductions in the light dose applied to the sample over the duration of the image scan. The resulting strong photobleaching reduction benefits signal and image contrast, as well as resolution, in biological nanoscale imaging. We show DyMIN stimulated emission depletion nanoscopy of different challenging samples in two and three dimensions.

Abstract

The concepts called STED/RESOLFT superresolve features by a light-driven transfer of closely packed molecules between two different states, typically a nonfluorescent “off” state and a fluorescent “on” state at well-defined coordinates on subdiffraction scales. For this, the applied light intensity must be sufficient to guarantee the state difference for molecules spaced at the resolution sought. Relatively high intensities have therefore been applied throughout the imaging to obtain the highest resolutions. At regions where features are far enough apart that molecules could be separated with lower intensity, the excess intensity just adds to photobleaching. Here, we introduce DyMIN (standing for Dynamic Intensity Minimum) scanning, generalizing and expanding on earlier concepts of RESCue and MINFIELD to reduce sample exposure. The principle of DyMIN is that it only uses as much on/off-switching light as needed to image at the desired resolution. Fluorescence can be recorded at those positions where fluorophores are found within a subresolution neighborhood. By tuning the intensity (and thus resolution) during the acquisition of each pixel/voxel, we match the size of this neighborhood to the structures being imaged. DyMIN is shown to lower the dose of STED light on the scanned region up to ∼20-fold under common biological imaging conditions, and >100-fold for sparser 2D and 3D samples. The bleaching reduction can be converted into accordingly brighter images at <30-nm resolution.

Fluorescence nanoscopy (1, 2), also known as superresolution microscopy, has continuously gained momentum in recent years. This is because of its unique and growing capabilities in imaging biological structure at nanometer resolutions, well beyond the optical diffraction limit. Intact whole cells, both fixed and alive, can be analyzed at resolutions typically in the range of 20 nm to 60 nm.

A widespread implementation of laser-scanning stimulated emission depletion (STED) nanoscopy (3–6) superposes the excitation focal spot with a doughnut-shaped spot of STED light. The presence of STED light of a certain fluorophore-dependent threshold intensity I_S and higher serves to transiently switch off the fluorescence ability of fluorophores by stimulated emission everywhere but in the proximity of a central intensity zero point. Right in the center, where the intensity is below the threshold, fluorophores experience little or no STED light and can thus fluoresce. In contrast, markers located farther out encounter an increasingly high flux of STED light photons and are forced to remain in their ground state with higher probability until, at a certain distance from the doughnut center, the fluorescence of the molecules is essentially switched off. Since the switch-off effect is governed by a largely exponential function, this distance cannot be exactly pinpointed, but it has been generally agreed that an advantageous specification is to where the fluorescence is reduced by half. This yields a widely used resolution measure, namely the full width at half maximum (FWHM) of the resulting “effective” point spread function (PSF).

Photobleaching, and more specifically the bleaching of organic fluorophores induced by the high intensity at the overlap of doughnut crest and excitation spot, has so far prohibited STED microscopy from reaching its theoretically molecular resolution. At the crest, the intensity can be orders of magnitude higher than the threshold intensity. In other words, the intensity of the STED beam is locally much greater than what is actually needed to effectively switch a fluorophore off. This excess of STED photons is a major source of photobleaching, and a number of schemes have been conceived with the goal of either reducing the exposure of fluorophores to the doughnut crest or protecting them from the detrimental effects of it. One of the latter concepts is known as “multiple off-state transitions” (7) nanoscopy and uses a second type of (low light level) fluorophore transition that shields the dye from the effects of high intensities required for the first one, thereby allowing the recording of an increased number of images of the same region (7). Another concept, termed MINFLUX (nanoscopy with minimal photon fluxes) (8), has attained molecular resolution by probing the position of individually on/off-switched molecules with a doughnut minimum of excitation light. MINFLUX therefore avoids subjecting the fluorophores to high intensity. An approach termed RESCue (reduction of state transition cycles) (9), related to controlled light exposure microscopy (10), reduces the light dose impinging on the sample by using STED to briefly probe for empty nanoscale regions. Illumination of subdiffraction regions devoid of fluorophores nonetheless causes photobleaching at neighboring regions. In RESCue, judgment of a region to be empty is followed by immediate shutdown of all beams at scan positions that are not occupied by fluorophores. Finally, a method called MINFIELD (11) was recently presented, which works by limiting the scan field to a region of about the same size as the doughnut minimum “valley.” This avoids scanning the high-intensity crests over the fluorophores, significantly reducing their bleaching. At the fluorophores, MINFIELD therefore applies no switching (STED) light more intense than is needed for the off-switch required for their separation. It enables the recording of many more frames of the respective sample region and/or imaging at higher resolutions, since a higher STED intensity can be applied, albeit at the expense that neighboring areas are potentially negatively affected (11).

Here, we present a versatile illumination concept for sample-responsive superresolution fluorescence imaging called Dynamic Intensity Minimum (DyMIN). This concept follows the same fundamental rationale as MINFIELD, but evades the application of unnecessary off-switching (STED) photons without limiting the field of view to a small region. To explain the concept, we consider two fluorophores spaced closer than the diffraction limit (Fig. 1A). We start the scan away from the fluorophores without STED light, i.e., at confocal resolution. As the dye molecule is approached by the flank of the Gaussian excitation spot, the detected signal starts to increase, at which point the STED beam power is increased just enough that the fluorophore remains “off” given the new, enhanced resolution. At one of the next scan positions, the fluorophore emits again, and the STED power is further increased, and so on, until the desired STED power (i.e., resolution) is reached. Similarly, continuing the scan and moving away from the second fluorophore on the other side, the STED power is reduced to avoid scanning the crest across the fluorophore again. The fluorophores in DyMIN scanning therefore experience lower STED light doses than they would in a conventional scan, since the STED beam is not set to full power all of the time. Indeed, the highest power is applied at the scan positions centered at fluorophores and their vicinity. But the fluorophores, as they are located near the minimum, do not experience the high intensity of the doughnut crest. This is exactly the rationale behind MINFIELD (11), but here the dynamic probing and adjustment of the STED intensity lifts the limitation of small scan fields, while it still avoids scanning a full-power doughnut over the whole sample.

Fig. 1.

Nanoscopy with DyMIN adaptive illumination. (A) Concept illustrated for two fluorophores spaced less than the diffraction limit. Signal is probed at each position, starting with a diffraction-limited probing step (P_STED = 0, Top), followed by probing at higher resolution (P_STED > 0). At any step, if no signal indicates the presence of a fluorophore, the scan advances to the next position without applying more STED light to probe at higher resolution. For signal above a threshold (e.g., T₁, Upper Middle), the resolution is increased in steps (Lower Middle), with decisions taken based on the presence of signal. This is continued up to a final step of P_max (full resolution where required). For the highest-resolution steps, directly at the fluorophore(s), the probed region itself is located at the minimum of the STED intensity profile (Bottom). (B) Simulations of conventional vs. DyMIN scanning for a sample with many fluorophores (Top). Due to different STED powers applied (Middle), different dosages result during the respective scans (Bottom). In conventional scanning, the full STED power P_max is applied throughout. In DyMIN, large parts of the sample are scanned with no STED light, or with STED at low powers, with the cumulative dose reduced 45-fold at the fluorophores shown.

Results

Basic Considerations of DyMIN Scanning.

Crucially, with more fluorophores present in a more realistic specimen, DyMIN can still significantly reduce the light exposure, because fluorophores are not subjected to high STED intensity everywhere. The exposure is also typically much lower compared with RESCue, where fluorophores experience the full-power STED profile during the probing step, albeit not for the full duration of the pixel dwell time. In practice, scanning is performed in discrete pixels, and the STED intensity is also changed in discrete levels, as fluorophores are approached during the scanning process. We can therefore formalize a practical implementation of DyMIN as follows: At each pixel, we sequentially conduct i = 1, 2, … N imaging steps, where we probe for signal over a time t_i with a Gaussian excitation spot and a STED profile of power P_i from the ordered list {P₁ = 0, P₂,…, P_N = P_max}. If we detect no emission at step i, we stop the registration of counts for the rest of this pixel, and we blank both the excitation and the STED laser. Only if the detected emission exceeds a predefined threshold T_i at step i do we continue with step i + 1, i.e., we wait for emission for a time t_i+1 with increased STED power P_i+1, until either P_max is reached or we fail to detect sufficient photons. The illumination decision (mask) m(x) at each step i, where the STED power P_i has been applied, can then be written as

$$m_1=1\forall \mathit{x},m_{i+1}\left(\mathit{x}\right)=\theta \left[s\left(\mathit{x}\right)\otimes h_i^{\text{eff}}\left(\mathit{x}\right)-T_i\right],$$

where s is the object (distribution of fluorescent markers), $h_i^{\text{eff}}$ is the effective resultant PSF at step i, $\theta$ is the Heaviside step function, and $\otimes$ is the convolution operator. The total cumulative STED light dose at position x is

$$D_{\text{tot}}\left(\mathit{x}\right)={\displaystyle \sum _i}{m}_i\left(\mathit{x}\right)\otimes h_i^{\text{STED}}\left(\mathit{x}\right)\cdot t_i,$$

with $h_i^{\text{STED}}$ as the spatial profile of the STED light. The two expressions are evaluated in tabular form in Table S1. Clearly, it is crucial for an implementation of DyMIN to arrive at favorable sets {t_i}, {T_i}, and {P_i}. This is presumably strongly dependent on the unknown sample and the way in which STED beam power translates to bleaching, but general observations can be made. First, note that the spatial extent of $h_i^{\text{eff}}$ and the total power in $h_i^{\text{STED}}$ are strongly related by a square-root dependence on the intensity (power) of the STED beam, meaning that, starting from $h_1^{\text{STED}}=0,$ the initial application of STED power translates into a comparatively large increase of resolution. For DyMIN, this means that choices of P_i from where the power−resolution curve has a steep slope are an efficient way of probing the structure, in that a lot more information can be obtained with only little additional STED power. Consequently, a large subset of {P_i} should be from this range, and this includes a confocal probe step at P₁ = 0. Second, and somewhat counterintuitively, since additional steps act at smaller spatial domains, they reduce the total STED light dose D_tot compared with a scan with fewer steps at higher STED power applied at more of the pixels. This reduction of D_tot when N is increased slows down asymptotically (Fig. S1); a reasonable number of steps is likely a small number.

Table S1.

Calculation of STED light dose applied in DyMIN scanning

Step	Mask creation	STED light dose
$\text{Step}1$	$h^{\text{eff}}\left(P_1=0\right)\otimes \text{Struct}\to {\text{Mask}}_2$	${\text{Dose}}_1=0={\text{Mask}}_1\otimes h^{\text{STED}}\left(P_1=0\right)\cdot t_{\text{dec}}\left(P_1\right)$
$\text{Step}2$	$h^{\text{eff}}\left(P_2\right)\otimes \text{Struct}\to {\text{Mask}}_3$	${\text{Dose}}_2={\text{Mask}}_2\otimes h^{\text{STED}}\left(P_2\right)\cdot t_{\text{dec}}\left(P_2\right)$
$\text{Step}3$	$h^{\text{eff}}\left(P_3\right)\otimes \text{Struct}\to {\text{Mask}}_4$	${\text{Dose}}_3={\text{Mask}}_3\otimes h^{\text{STED}}\left(P_3\right)\cdot t_{\text{dec}}\left(P_3\right)$
$\text{Step}N$		${\text{Dose}}_N={\text{Mask}}_N\otimes h^{\text{STED}}\left(P_N\right)\cdot t_{\text{Img}}$
$\text{Total}$		${\text{Dose}}_{\text{tot}}={\text{Dose}}_2+{\text{Dose}}_3+\dots +{\text{Dose}}_N$

Mask_i corresponds to m_i in the main text; Dose corresponds to D. t_Img: dwell time for imaging.

Fig. S1.

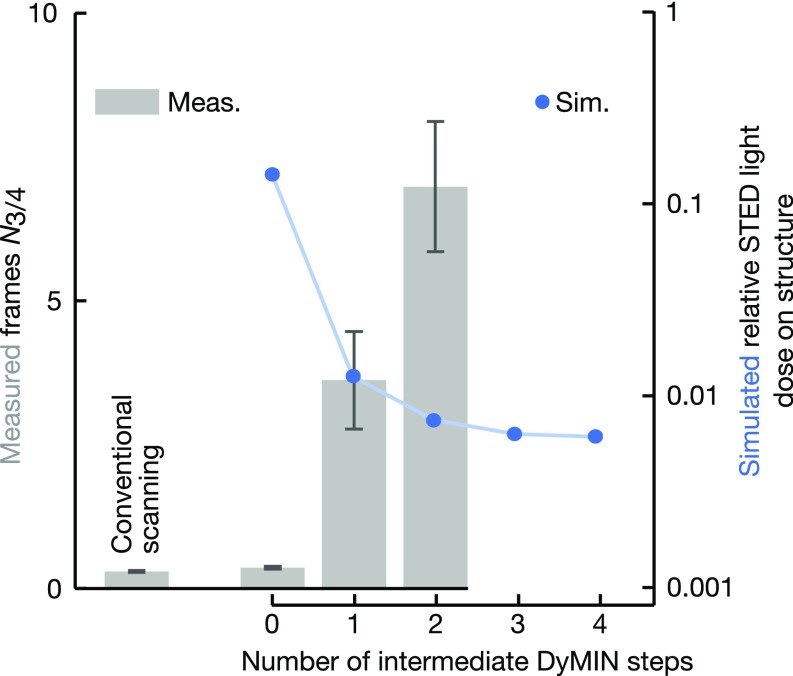
Effect of the number of intermediate DyMIN steps on signal increase. Measured number of frames N_3/4 before signal reduction by 25% (gray bars) vs. number of intermediate DyMIN steps (excluding the initial confocal resolution probing step and the final step at the final resolution of 50 nm). The sample consisted of fluorescent nanoassemblies (Bead R; GattaQuant). The pixel dwell time was 100 µs. The simulated STED light dose on the structure for these acquisition parameters and the observed density of beads vs. the number of intermediate DyMIN steps is shown as blue circles. The blue line is a guide to the eye. The STED light dose approaches a minimum for greater than three intermediate steps and is expected to rise again for larger numbers of steps.

To assess the best DyMIN strategy and to analyze how it fares compared with other methods, we conducted simulations to arrive at the average STED light dose experienced per marker fluorophore and by the specimen as a whole with DyMIN, RESCue, and conventional scanning for a range of realistic sample types (Fig. S2). To this end, in a square region with 5-μm side length, we modeled specimens with random distributions of (i) points with different average distances; (ii) crossing lines (mimicking cytoskeletal filaments); and (iii) circles, resembling subdiffraction-sized structures like virus particles, nuclear pore complexes (NPCs) or vesicles. For each specimen, we simulated the imaging (i.e., the scanning process) as follows: For standard STED, we obtained the light dose at each pixel by convolving the STED illumination profile of power P_max with each pixel of the sample, accounting for the duration of the illumination. For DyMIN, we sought the optimal parameter set for each sample by numerically minimizing the average dose of STED light on the fluorophores (SI Materials and Methods) to obtain the best intermediate probe powers.

Fig. S2.

Simulations of applied STED light dose on random structures of different geometries. For a discussion, see Materials and Methods (simulated final resolution: 25 nm). (A−C) (Left) Point-like structures (20 points per square micrometer). (Middle) Linear structures. (Right) Ring structures. (A) Underlying distributions of fluorophores. (B) Different STED powers applied. At each pixel, the color indicates the highest STED power that would be applied here. As discussed in Basic Considerations of DyMIN Scanning, the respective high STED intensity is not experienced by fluorophores at the specific pixel, but by fluorophores at pixels farther away (doughnut crest). (C) Different dosages at the fluorophores result during the respective scans. The illumination is nonuniform, and strongly reduced compared with standard scanning with the STED intensity necessary to achieve the same final resolution. (D) Relative STED light dose on structures vs. resolution applied at step 2 in a three-step DyMIN implementation for point-like structures (dots), linear structures (lines), and rings. For all three types of structures, a global minimum in STED light dose is observed, suggesting an optimal resolution at DyMIN step 2. For the dots, this optimum is 46 nm; for the lines, it is 40 nm; and, for the rings, it is 39 nm.

We note that our framework allows us to view RESCue as a method with a single probe step at P_max, permitting us to evaluate it along with variants with additional DyMIN intermediate probing steps. Already, a simple three-step DyMIN process with STED powers {0, P_max/4, P_max}, i.e., a confocal resolution step, a step at half the final resolution, and a final step at full resolution (Fig. 1B), reduces the average light dose per marker molecule by up to 45× compared with standard STED and by about 14× compared with RESCue STED. As anticipated, the simulations indicate that a higher number of DyMIN steps tends to increase light savings, albeit at diminishing gains for higher step numbers (Fig. S1).

The detailed impact of this large reduction of light exposure, in practice, depends not only on the sample and DyMIN parameters but, especially, on the bleaching behavior of the particular dye in use, which is possibly nonlinear and dependent on prior illumination. Nevertheless, it is to be expected that the optimal DyMIN parameters found by minimizing the STED light dose will also provide optimal bleaching reduction. We found, by simulation (Fig. S1), that more than four DyMIN steps provide diminishing additional reductions. Additionally, the confidence in the step decision strongly increases with the number of photons available at each step and therefore disfavors later steps recorded at higher resolutions. More DyMIN steps mean more decision-taking, and the risk of a wrong decision—i.e., a prematurely aborted pixel although signal would have been present—increases.

Experimental Assessments of DyMIN.

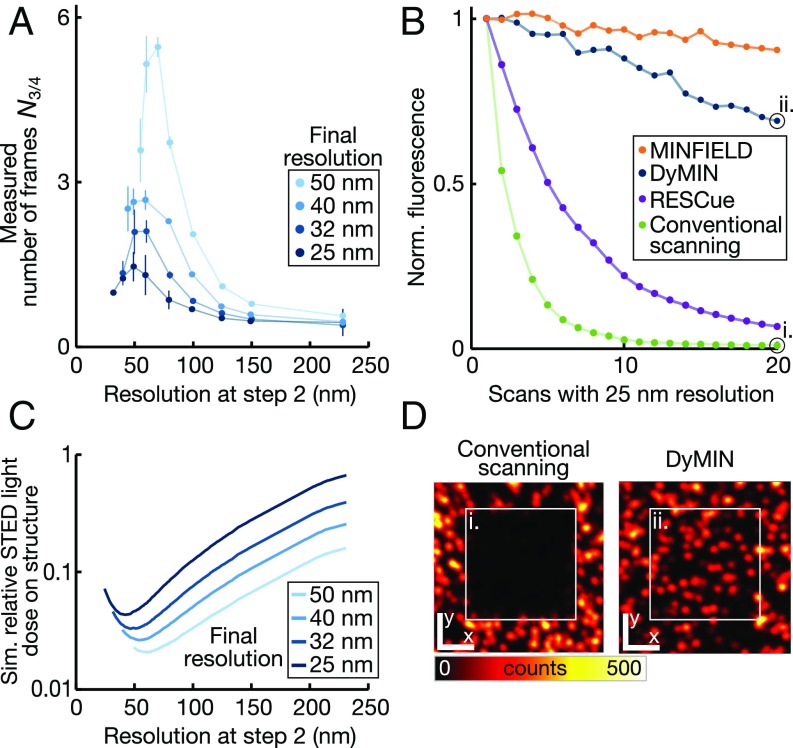
We investigated the photobleaching behavior of dispersed fluorescent beads under three-step DyMIN, MINFIELD, RESCue, and conventional STED scanning conditions (Fig. 2). Fig. 2A shows the number of frames N_3/4 after which the total intensity in the image has dropped to 75% of the original value vs. the applied power in step 2 (P₂) for a range of final resolutions between 25 nm and 50 nm. The peak of each curve corresponds to a value of P₂ that minimizes bleaching and maximizes signal. This peak occurs roughly at the same values of P₂ (Fig. 2C) found by our numerical algorithm (SI Materials and Methods), indicating that our simulations capture the effects of dose reduction. DyMIN is a general concept, and its application is not limited to 2D imaging. It can be applied also to a resolution enhancement along the optic axis z. We tested DyMIN for 3D STED, where the optimal strategy again consists of a confocal probing step and a probing step at half the final resolution, followed by the final step at the highest resolution (Fig. S3). In Fig. 2B, the fluorescence of 40-nm-diameter fluorescent beads (shown in Fig. 2D and dataset in Fig. S4) is plotted vs. the number of recorded frames. Importantly, these results are expected to hold not only for individual molecules (11) but also for small dense clusters and therefore also for, e.g., antibodies or nanobodies labeled with multiple markers, or small cellular structures composed of several macromolecules. They apply for all localized structures positioned in otherwise unlabeled regions, such as filaments, membranes, or mitochondria. Only for dense clusters or vast planes of homogeneously labeled structures is RESCue expected to be the better choice (Fig. S5). For very high fluorophore densities, the DyMIN advantage vanishes, as fluorophores cannot be separated at the resolution of the intermediate probing step(s).

Fig. 2.

Bleaching reduction with DyMIN. The advantages of DyMIN scanning depend on the choice of the intermediate signal probing steps (step 2 and higher). (A) The resolution applied at the second step of three-step DyMIN scanning affects the numbers of frames N_3/4 before the signal has dropped to 75% of its original level. Shown is N_3/4 vs. resolution at step 2, measured for ∼23-nm-sized fluorescent nanoassemblies (Bead R; GattaQuant). Measurements for different final resolutions (50 nm, 40 nm, 32 nm, 25 nm) are shown with identical scan parameters (pixel size, 15 nm; decision time, 10 µs). Lines are guides to the eye. (B) Signal reduction over time due to photobleaching vs. number of frames imaged at 25-nm resolution for MINFIELD (150-nm field), three-step DyMIN, RESCue, and conventional scanning. Fluorescence is normalized to the initial frame. The sample consisted of dispersed 40-nm fluorescent nanobeads. For MINFIELD, the curve is a median of 10 experiments on single beads. (C) Simulations of the experiments in A (SI Materials and Methods) quantify the relative STED light dose on the structure for choices of step 2 resolution. The signal maximum for the step 2 resolution of about half the final resolution (2× its value) is shown to correspond to a minimum in the applied STED dose. (D) Confocal images of scanned regions after the 20th acquired frame of C: conventional scanning (Left) vs. DyMIN scanning (Right). [Scale bar (x, y): 1.5 µm.]

Fig. S3.

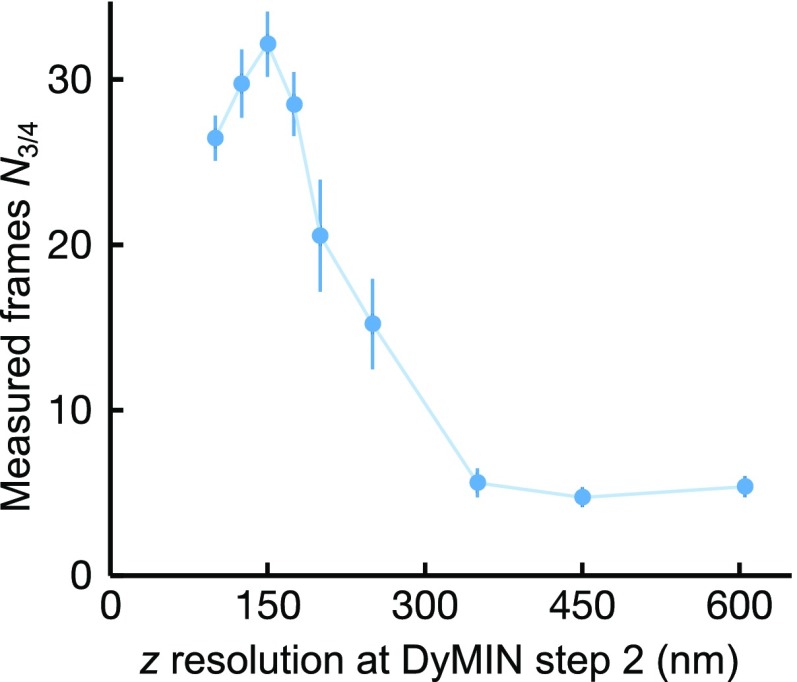
Signal increase vs. resolution applied at the second step (three-step DyMIN): 3D DyMIN STED. The resolution applied at the second step of DyMIN scanning affects the numbers of frames N_3/4 before the signal has dropped to 75% of its original level. N_3/4 vs. axial (z) resolution at step 2 was measured for ∼40-nm-sized fluorescent nanobeads (Crimson; Molecular Probes). Pixel size was 30 nm, and decision time was 20 µs.

Fig. S4.

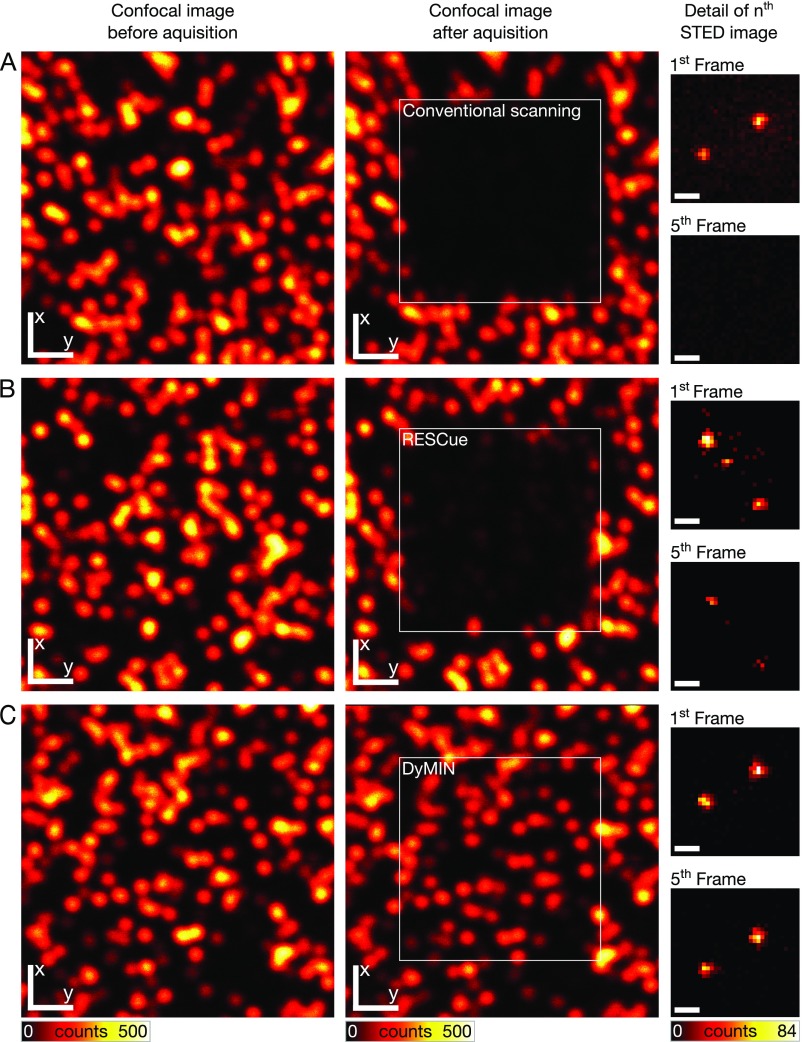
Signal reduction over time due to photobleaching for conventional scanning, RESCue and DyMIN (data in Fig. 2 B and D). (Left) Confocal fluorescence images before acquisition. (Middle) Confocal fluorescence images after acquisition. (Right) STED image details in first and fifth acquired frame. The sample consisted of dispersed fluorescent nanobeads (Crimson beads; Molecular Probes) of nominally 40-nm diameter. (A) Conventional scanning, (B) RESCue, and (C) DyMIN. [Scale bars: 1 µm (Left and Middle), 100 nm (Right).]

Fig. S5.

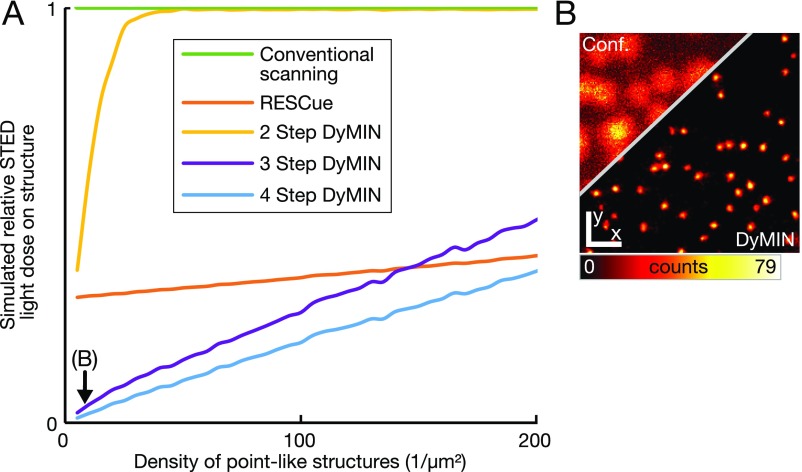
DyMIN effectiveness in dependence of sample density. (A) Relative STED light dose on structure vs. density of markers, simulated over two orders of magnitude of densities (25-nm final resolution): conventional scanning; RESCue; and DyMIN with two steps, three steps, and four steps. For densities commonly observed in biological imaging, DyMIN scanning reduces the dosage by well above an order of magnitude. Where applicable, the optimal resolutions for the intermediate steps were calculated for a density of 20 per square micrometer. (B) Nuclear pores (∼7 per square micrometer) imaged by DyMIN STED nanoscopy. The image was smoothed with a Gaussian of width 1.5 pixels. [Scale bars: 500 nm (x, y).]

Subsequently, we applied three-step DyMIN to a range of biological samples with varying density and homogeneity. To illustrate the DyMIN performance on a known structure, we imaged the exquisite periodic organization of betaII spectrin along the distal axon in neurons (Fig. 3A), which was initially revealed by stochastic optical reconstruction microscopy and has tighter spacing than the diffraction limit (12, 13). The DyMIN approach leads to a threefold increase in the brightness of the betaII spectrin scaffold compared with conventional scanning. We further focused on other cellular compartments that benefit from superresolution microscopy due to their small sizes, namely synapses (14). In particular, we focused on gephyrin, a scaffolding protein of inhibitory synapses that exhibits a monocluster or multicluster organization (15–17). Here, we used our pixelwise three-step DyMIN process to automatically prelocalize the structure twice with low resolution and low STED powers in each pixel, followed by a local recording at full resolution. The DyMIN recordings (Fig. 3B, Right) were performed at a pixel dwell time of 100 µs, which is the dwell time that maximizes signal for the final resolution of ∼25 nm (SI Materials and Methods and Fig. S6). Conventional scan recordings at this light dose (i.e., pixel dwell time multiplied by intensity) were not possible, and we therefore reduced the dwell time to 10 µs to arrive at the light dose that results in the best possible signal for standard STED with the same resolution as with DyMIN before (Fig. 3B, Left). DyMIN enabled us to image gephyrin clustering at superior contrast (Fig. 3B, Right), whereas with standard STED at this high resolution, the gephyrin clusters were drowned in noise (Fig. 3B, Left). Alternatively, the reduction of the light dose provided by DyMIN could have been converted to about 42% improved resolution (according to Eq. S5 and SI Materials and Methods) at the same signal level.

Fig. 3.

Improved image brightness and structural definition in DyMIN STED nanoscopy. STED recordings at the highest resolution levels are challenged by bleaching. The bleaching reduction by DyMIN can be converted to higher resolution and increased signal from fine structures. (A) Periodic spectrin-II cytoskeleton (indirect immunofluorescence) along the axon of rat hippocampal neurons resolved by STED with conventional scanning (Left) and DyMIN with 29-nm resolution (Right). To take advantage of the lower bleaching compared with conventional scanning, DyMIN recordings should use accordingly longer pixel dwell times (SI Materials and Methods, here: 40 µs vs. 100 µs). (B) Nanoscale morphology of gephyrin clustering at inhibitory synapses of rat hippocampal neurons (indirect immunofluorescence), with ∼ninefold signal increase, on average, for 24-nm resolution DyMIN (10 µs vs. 100 µs dwell time). Shown is conventional scanning (Left) vs. DyMIN scanning (Right). (C) Quantifications of the signal increase of images as shown in B. (>100 clusters in both cases, sourced from six separate measurements analyzed). Data are mean ± 1 SD of the mean fluorescence signals). [Scale bars: 500 nm (A), 200 nm (B).]

Fig. S6.

Limits to the attainable fluorescence signal in STED imaging: dependence on pixel size, dwell time, and resolution. Photobleaching dictates the maximum signal that can be reached for a given resolution. (A) In single-point-scanning nanoscopy, the following considerations apply under steady-state conditions for pixel sizes much smaller than the extent of the optical focus: half of the (off-)switching light dose that drives photobleaching has already been applied at the target coordinate before fluorophores at this coordinate are read out. D_F, final dosage; D_A = 0.5 D_F, dosage up to completion of readout (acquisition). (B) Assuming an exponential photobleaching kinetic of the fluorescence, fluorescence levels F_A and F_F are reached at the time of readout and after completion of the linear scan, respectively. (C) Measured signal vs. dwell time, for two final resolutions, 40 nm (blue) and 44 nm (orange), sampled with 15- and 17-nm pixels, respectively. The sample was ∼23-nm-sized fluorescent nanoassemblies (Bead R; GattaQuant) as used for experiments shown in Fig. 2A. The fits shown are to Eq. S4 (SI Materials and Methods).

We used the simulation framework (SI Materials and Methods) to calculate the reduction of STED light photons acting directly at the structures of interest, and on the sample at large within the scanned field. For the axonal segment of Fig. 3A, a threefold reduction of the STED light dose at the structure was inferred, while the images of gephyrin clustering featured a DyMIN-based dose reduction of ∼13-fold at the structures and ∼25-fold for the full region imaged. The calculated dose savings on the structures quantitatively agree with the realized signal gains: an ∼threefold brighter image was recorded with DyMIN in Fig. 3A, and the structures in Fig. 3B were ∼9 times stronger in signal (quantification in Fig. 3C). A full list of the imaging parameters used in all experiments is provided in Table S2.

Table S2.

Parameters used in imaging experiments

Figure	Pixel/voxel size, nm	Step 1	Step 2	Step 3	Step 4
Fig. 2A	Pixel, 15
Excitation power, μW		18	18	18	—
STED power, mW		0	0–108	43–185	—
Decision/dwell time, μs		10	10	100	—
DyMIN threshold (counts)		10	5	—	—
Fig. 2C (DyMIN)	Pixel, 15
Excitation power, μW		9	9	9	—
STED power, mW		0	65	301	—
Decision/dwell time, μs		10	10	100	—
DyMIN threshold (counts)		10	5	—	—
Fig. 3A	Pixel, 13
Excitation power, μW		2.5	15	15	—
STED power, mW		0	22	172	—
Decision/dwell time, μs		10	10	100	—
DyMIN threshold (counts)		14	7	—	—
Fig. 3B	Pixel, 13
Excitation power, μW		2.5	15	15	—
STED power, mW		0	26	258	—
Decision/dwell time, μs		10	10	100	—
DyMIN threshold (counts)		18	13	—	—
Fig. 4B	Voxel, 30
Excitation power, μW		1	9	9	—
STED power, mW		0	43	215	—
Decision/dwell time, μs		10	10	80	—
DyMIN threshold (counts)		16	9	—	—
Fig. 5B (lamina)	Pixel, 25
Excitation power, μW		4.5	4.5	4.5	—
STED power, mW		0	43	301	—
Decision/dwell time, μs		10	17	80	—
DyMIN threshold (counts)		40	20	—	—
Fig. 5B (NPCs)	Pixel, 25
Excitation power, μW		3	12.5	12.5	—
STED power, mW		0	30	344	—
Decision/dwell time, μs		10	10	80	—
DyMIN threshold (counts)		39	30	—	—
Fig. 6B	Pixel, 8
Excitation power, μW		12	12	21	21
STED power, mW		0	11	64	450
Decision/dwell time, μs		10	10	13	150
DyMIN threshold (counts)		10	9	7	—

Pushing Signal in 2D and 3D Nanoscopy for Superior Contrast and Structural Definition.

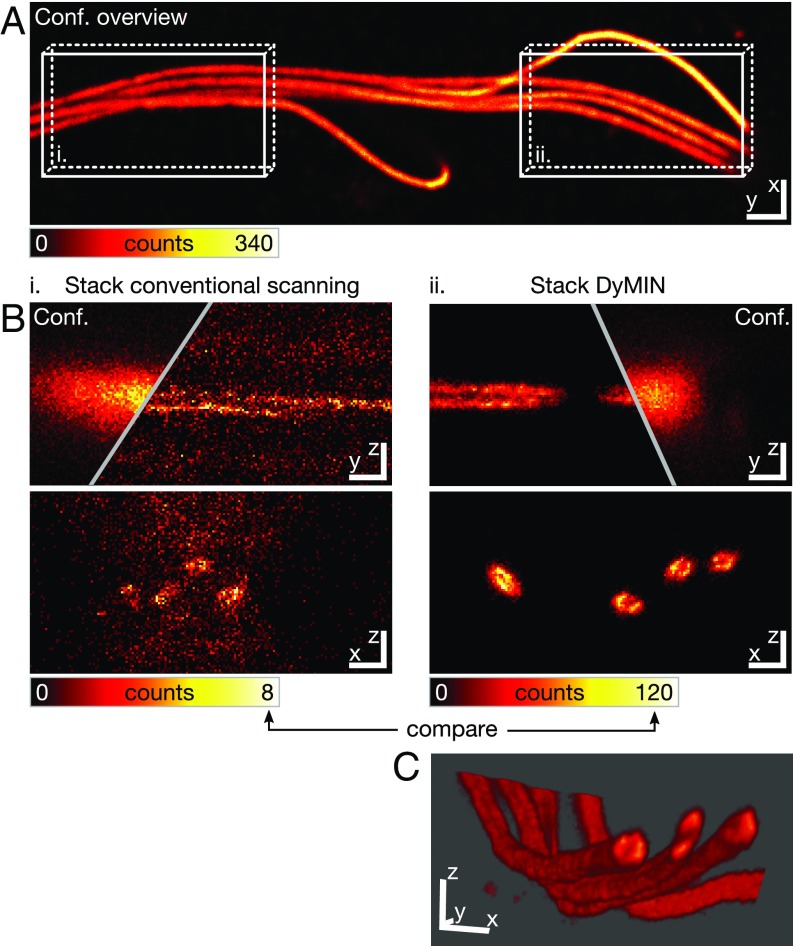
Photobleaching is often the factor limiting signal and/or resolution in 3D STED. We therefore applied DyMIN to 3D STED recordings to assess the bleaching reduction by DyMIN in practice. Fig. 4 shows results for mature mouse spermatozoa (confocal impression in Fig. 4A). Their axonemes are known to contain a tube-like structure with a diameter of ∼100 nm, composed of nine microtubule doublets with another central doublet. We perform immunofluorescence labeling of microtubules in fixed mouse sperms and recorded xzy stacks with 3D STED (Fig. 4B), both with (i) standard STED and (ii) DyMIN STED, with the respective dwell times optimized for signal. The nonoptimized standard STED recording shows strong photobleaching, to the point where a meaningful image is out of reach and the tubular structure of the sperm tail cannot be appreciated. The dosage-optimized standard STED recording with greatly reduced dwell time also shows virtually no useful signal. A remedy here would be to reduce the STED power to lower the total light dose and further increase signal, at the expense of resolution. DyMIN, however, permits the recording of a full stack at high STED powers, at the voxels containing structures, by reducing dosage ∼22-fold over the full stack and allowing ∼14-fold brighter images compared with the best conventional STED image.

Fig. 4.

Pronounced signal increase in DyMIN STED nanoscopy enables 3D visualization of tubulin in the axonemes of mouse spermatozoa. The ‘empty’ voxels surrounding the fluorophores of interest often make up a substantial fraction of 3D volumes scanned, as illustrated here for mouse spermatozoa axonemes, tube-like structures based on tubulin (indirect immunofluorescence, SI Materials and Methods). (A) Confocal overview recording of the spermatozoa. (B) The yz and xz slices through the tube taken from xzy stacks (fastest scan axis: x) recorded with 3D STED at an isotropic resolution of ∼70 nm, both with conventional and DyMIN scanning. The voxel (30 nm × 30 nm × 30 nm) dwell times were 6 µs and 80 µs, respectively, with the signal increased ∼14-fold for DyMIN. (C) The higher signal-to-noise ratio enables identification of isosurfaces and volume rendering from the DyMIN data. The coordinate bars in C represent 1 µm × 1 µm × 1 µm, with the positive y axis pointing toward the reader. [Scale bars: 3 µm (xy) (A), 500 nm (xz and yz) (B).]

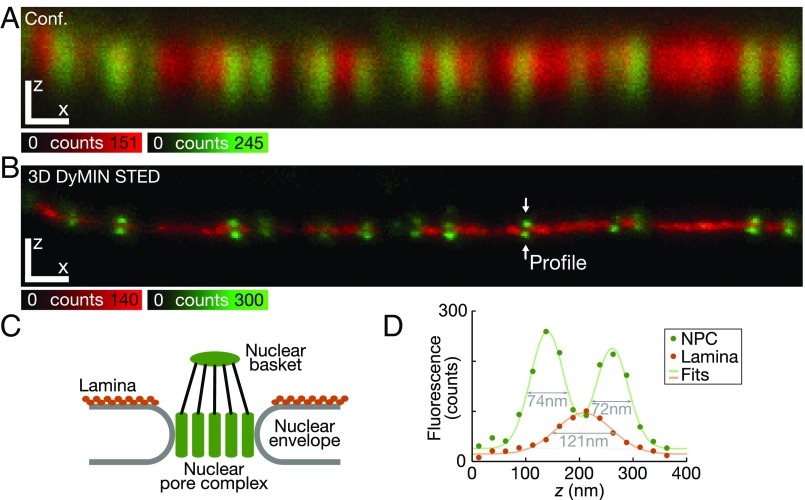
DyMIN can readily be applied to multichannel recordings using dyes at different wavelengths (6). Ideally, but not necessarily, each dye channel is imaged at its own characteristic STED power for best results (18). Fig. 5 shows NPCs and lamina recorded with 3D DyMIN STED. The resulting resolution is about 60 nm for the NPC labeling and slightly lower for the lamin staining. We used an antibody that is known to target several types of NPC proteins (SI Materials and Methods), and DyMIN enabled us to clearly resolve two distinct domains formed in the basket and close to the central channel and membrane ring, with the lamin roughly halfway in between, below the nuclear membrane. To further reduce photobleaching here, we imaged the redder dye (NPCs) first, immediately followed by the greener dye (lamin). This avoids unnecessary state cycling of the dye attached to the lamin, since it is not excited during the first recording of the red dye. DyMIN, implemented with four steps, enables resolution of dye-labeled DNA origami structures (19) at excellent contrast (Fig. 6). The chosen origami consisted of two closely packed groups of ∼15 ATTO647N fluorophores each, separated center-to-center by nominally 30 nm, with a gap of 10 nm. This is an example where the additional intermediate step makes a substantial difference, enabling an ∼173-fold dose reduction at the structures for the chosen image acquisition parameters.

Fig. 5.

Dual-color isotropic nanoscopy of nuclear pore components and lamina with DyMIN STED. (A) Confocal and (B) 3D DyMIN STED recordings of NPCs (shown in green) and lamina (red). We used antibodies that are known to target several different NPC proteins and different lamins (SI Materials and Methods). DyMIN resolves two distinct domains of the NPC (nuclear basket and close to the central channel and membrane ring) along the axial direction z with high contrast (pixel size 25 nm × 25 nm, dwell time 80 µs in both channels). (C) Schematic representation of labeled structures in A and B. (D) A line profile of signal intensity along z quantifies the resolved structures with superior image brightness and resolution. Lines show fits of a linear combination of two Gaussians (NPC) and a single Gaussian (lamina). [Scale bars: 500 nm (A and B).]

Fig. 6.

DyMIN STED imaging of DNA origami structures (fluorophore assemblies with 30-nm separation) at high signal-to-noise ratio. (A) Confocal and (B) DyMIN STED recordings of DNA origami-based nanorulers (GATTAquant) with nominally 30-nm separation (10-nm gap) of groups of ∼15 ATTO647N fluorophores, on average, each. (C) Schematic of nanorulers imaged. (D) Intensity profile along connecting line of the fluorophore groups. The fit (blue line) represents a combination of two Gaussians (22.1- vs. 24.2-nm widths), with their peak-to-peak separation determined as 30.0 nm (in agreement with the nominal value). Accounting for the known ∼20-nm extent of the fluorophore groups (compare C), the widths of the Gaussians imply an effective PSF of ∼17 nm (FWHM). [Scale bars: 200 nm (A and B).]

Raw Data

All image data are in photon counts registered, without further processing unless otherwise indicated. Linear lookup tables as indicated, from 0 to maximum counts in the respective image, are used for representation of all image data.

Powers Stated

Powers stated are powers in the focal plane, measured with a slide power sensor head (S170C; Thorlabs).

Comparisons of DyMIN to MINFIELD, RESCue, and Conventional Scanning

In all of these comparisons, the same excitation power (for confocal and STED) was used. The STED powers in MINFIELD, RESCue, and conventional scanning corresponded to P_max of DyMIN (final step). The dwell times were adjusted as stated for the individual recordings shown.

Dwell Times and Decision Times

The times spent probing at a given step i < N of the DyMIN scanning are referred to herein as decision times. The time spent accumulating signal at the final step N is referred to as the dwell time of the recording. The total time spent at each pixel/voxel is the sum of all decision times and the dwell time and rise/fall times of beam controls (see Optical Setup).

Optical Setup

The microscope design followed a previously described optical setup (11), with a confocal pinhole at ∼0.75 Airy units. Deviating from the setup described in detail in “Three-dimensional STED microscopy” of SI Materials and Methods of ref. 11, we here used a pulsed excitation laser at 635 nm with a pulse width of 120 ps (Abberior Instruments). For the fast probing of fluorescence signals, the signal from the avalanche photodiodes was analyzed by a field-programmable gate array (FPGA). A custom-written FPGA program based on count thresholds and decision time intervals decided whether to abort the step list of powers or advance to higher power (next step). In the case of abort, the STED and respective excitation laser beams were switched by an acoustooptic modulator (AOM) (AA Opto Electronic) to not reach the sample. Custom electronics allowed to quickly change the analog voltage at the AOM with subdwell time delay (∼10 µs), allowing the setting of up to three predefined STED powers and two excitation powers. These powers were applied within submicrosecond times (minimal rise/fall time of the AOM), after the additionally required digital signals to disable blanking were applied. Rise and fall times added less than 1% of total dose at the typical imaging parameters in this work.

Simulations

Simulation Framework of DyMIN Scanning (See also Table S1).

For each step i, the object structure (rendered by discrete dots) was convolved with the respective effective PSF $h^{\text{eff}}$ for a STED power $P_i$ [Fast Fourier Transform (FFT) Convolution]. The dependence of the effective PSF on power P had been experimentally determined. The result of this convolution was mapped onto the image pixels and, using a threshold of $1/e$, pixels were set to 0 or 1. This binary pixel representation then served as the “illumination mask” ${\text{Mask}}_i$. The next illumination in step i+1 occurred only in the pixels of value 1 of ${\text{Mask}}_i$ with the doughnut $h^{\text{STED}}$($P_{i+1})$ for the duration of the decision time $t_{\text{dec}}\left(P_{i+1}\right)$, with t_dec determined as described in Decision Time for Resolution at Step i. The spatially dependent dose (due to the extended doughnut intensity profile) in the pixelated image is then the Convolution (FFT) of ${\text{Mask}}_i$ and the spatially distributed light exposure $h^{\text{STED}}\left(P_i\right)\cdot t_i$. In the final step, the sample illumination is computed at the locations of the ${\text{Mask}}_{N-1}$ with final doughnut $h^{\text{STED}}\left(P_N\right)$ for the dwell time $t_{\text{Img}}$ (final step). To determine the (spatially dependent) ${\text{Dose}}_{\text{tot}}$, all dosages ${\text{Dose}}_{i=2}$ up to ${\text{Dose}}_N$ are summed.

For easier reference, the above procedure is summarized in tabular form for N steps in Table S1.

The simulated relative STED light dose on the structure was evaluated as the mean value of all dosages Dose_tot at the set of dots making up the simulated structure. The DyMIN dose is always normalized to the dose for conventional STED scanning.

As described, in a DyMIN scan, the list of powers is stepped through at each pixel and either aborted at an appropriate step or continued to the end. The respective last step reached is assigned to each pixel, yielding a mask. It is evident that, for step i+1, steps i and earlier had been applied. The map of the respective last step in each pixel therefore contains all information on prior illuminations.

Decision Time for Resolution at Step i.

Decision times were based on reasonable choices of the decision times for two relevant resolutions, 30 µs for a resolution of 25 nm (to match the RESCue experiments) and 10 µs for a nominal resolution nRes of 50 nm (as a resolution at or close to the important step 2 resolution). Based on these two parameter pairs, the following relation accounting for the geometrical dependence of the expected signal was used for the decision time t_dec (in microseconds) for choices of resolution res:

$$t_{dec}=a\frac{\text{n}{\text{Res}}^2}{{\text{res}}^2}+b,$$ [S1]

where nRes = 50 nm, a = 2/300,000, and b = 1/300,000.

Simulations of Different Types of Structures.

Simulations (Fig. S2) were carried out for three basic structures: points (dots, Fig. S2A, Left), rings (Fig. S2A, Middle) and linear structures (lines, Fig. S2A, Right). These structural features mimic basic geometries observed in biological imaging, such as nuclear pores (points), virus particles, gephyrin, clathrin, etc. (rings), and tubulin, vimentin, etc. (lines). Rings and lines were represented by individual points with mutual separations far closer than the final resolution of the last DyMIN step, yielding quasi-continuous structures. The spatial distribution of structures was randomly generated. Identical recording parameters were simulated for all structures: final resolution (step N) of 25 nm and dwell time of the last step 100 µs. The decision time t_dec in simulations of RESCue was chosen as 30 µs, a realistic value under typical signal conditions for 25-nm resolution.

We first examined the effect of varying the resolution of the intermediate step (step 2) in three-step DyMIN on the dose during acquisition (Fig. S2D). This intermediate resolution was varied in increments of 1 nm from values corresponding to the final resolution (25 nm) to confocal resolution (230 nm). The dependence of STED light dose on the resolution at step 2 is shown for the three types of structures.

For the lowest dose, the sample-dependent dose is shown in Fig. S2C. For all three basic structures, the dose exhibits a global minimum with respect to step 2 resolution. The optimum is not sharply defined, meaning that the step 2 resolution does not have to be precisely adjusted but should fall near the dose minimum. This minimum occurs often at about half the final resolution (twice its numerical value). The shown curves were calculated with the parameters above, which are realistic (useful) for STED nanoscopy. Combinations of parameters do exist which yield no minimum, for example, very short dwell times at the final step: These would not produce useful images in practice.

In general, the lower (further right in Fig. S2D) step 2 resolution for the same dose should be chosen. This allows DyMIN to maintain a clearance area around the structure, to ensure it is completely contained within the imaged area.

Fig. S5 shows the total dose for a range of densities of emitters, with randomized distributions of points as the sample structure. The density was varied from 0 to 200 points per square micrometer, and the STED dose was simulated for conventional scanning, two-step DyMIN, three-step DyMIN, four-step DyMIN, and RESCue. The simulation parameters were as outlined above for Fig. S2, with resolutions for this study of the density dependence (Fig. S5) as follows: two-Step DyMIN, res1 = 230 nm; three-Step DyMIN, res1 = 230 nm and res2 = 50 nm; and four-Step DyMIN, res1 = 230 nm, res2 = 105 nm, and res3 = 35 nm. These optimal resolutions were determined by simulations for a density of 20 per square micrometer. Note that DyMIN, for a sample of a different density, will require different resolution to achieve lower relative dose than shown here.

It becomes apparent that three-step DyMIN has a significant advantage over RESCue, especially at realistic densities (compare Fig. S5B). The reason for this is the high baseline exposure in the RESCue mode that comes from the relatively long fixed decision time with the high intensity of the state transfer light acting. Four-step DyMIN has a conceptual and practical advantage, especially for small structures.

Use of the Framework for the Analysis of 2D Experimental Data.

Combined with dwell times and corresponding STED powers, the masks contain the complete information on the illumination. For experimental measurements, the masks were directly saved and allow later dose calculations over entire scanned fields or on the structures themselves, defining all imaged pixels as the structure.

Basic Considerations (Extended): Fluorescent Signal with STED and How It Depends on Pixel Size, Dwell Time, and Resolution

Without photobleaching of dyes, molecular resolution is conceptually well within reach for STED nanoscopy. However, photobleaching limits the signal that can be extracted from a structure at a certain resolution. In point-scanning nanoscopy, the following considerations apply for pixel sizes much smaller than the extent of the optical focus under steady-state conditions. At the inner part of the scan, each dye molecule sees the same dose of illumination inducing bleaching. Half of the dose has already been applied at the target coordinate before fluorophores at this coordinate are read out (Fig. S6A). Assuming an exponential photobleaching kinetic of the fluorescence (Fig. S6B), fluorescence levels F_A and F_F are reached at the time of readout and after completion of the linear scan, respectively. While the integration of signal at the detector proceeds linearly with time, the fluorescence follows the nonlinear decay due to photobleaching. In other words, long dwell times at some point will no longer lead to higher signal, since the fluorescence has been bleached by the higher dose before it could contribute to the signal (Fig. S6C). The following considerations apply.

In general, a fluorophore will be able to undergo a certain number of cycles between ground state and excited state, while it is being scanned over. We assume that, for each cycle, there is a finite probability that it will irreversibly photobleach (no recovery). We further assume, for simplicity, that bleaching is primarily induced by STED light photons (11) when they interact with the fluorophore while it is in the excited state. Consequently, the probability density function of the number of photons that can be collected from a fluorophore follows a geometric distribution or an exponential distribution in the continuous limit (many fluorophores). The signal S which can be extracted from a sample scales with an initial fluorescence F₀ (depending on the number of fluorophores present) and has an optimum for a certain dwell time.

We can compute the number ${\displaystyle \sum N}$ of STED photons that induce bleaching at a pixel before it has been reached in the scan,

$${\displaystyle \sum N}=t_d\cdot I\cdot \sigma \frac{1}{E_{ph}}\cdot \frac{n}{2},$$ [S2]

with the dwell time $t_d,$ the STED intensity $I,$ a bleaching cross-section $\sigma$, the energy of a STED photon $E_{\text{ph}},$ and the number of pixels $n=A/a^2$ enclosed by the doughnut. $A$ is the area of the STED doughnut, and $a$ is the edge length of a scanned pixel. With this, we can write the residual signal fraction as

$$S=t_d\cdot e^{-C{\displaystyle \sum N}}=t_d\cdot e^{-C{t}_{d}I\cdot \frac{1}{a^2}},$$ [S3]

where we have combined the constant terms into $C.$ Now, $a$ has an inverse proportional dependence on the resolution increase $\rho =d_{CONF}/d_{\mathit{STED}}=\sqrt{1+I/I_s}$, namely, $a=d_{conf}/\rho \cdot \nu$; $d_{CONF/STED}$ are the respective resolutions (given, for example, as the FWHM), $I_s$ is the threshold intensity, and $\nu$ is a pixel oversampling factor. Combining these expressions, we find

$$S=t_d{e}^{-C\cdot t_d\cdot {\rho }^2\left({\rho }^2-1\right)}.$$ [S4]

Again, some constants have been combined into $C.$ We can see that, as one wishes to move on very high resolutions, an increase in resolution $\rho$ leads to a sharp decrease in the available signal, as more pixels have to be scanned at higher STED intensities. For similar reasons, $\nu$ should be kept as low as possible above the Nyquist criterion to maximize the signal. Finally, when plotted over t_d, S has a maximum at $t_d=1/\left[C\cdot \left({\rho }^4-{\rho }^2\right)\right]$, i.e., there exists an optimal pixel dwell time, which is different for each resolution. The maximally attainable signal is

$$S_{\text{max}}=\frac{1}{e\cdot C\cdot \left({\rho }^4-{\rho }^2\right)}.$$ [S5]

In other words, the only chance to increase $S_{\text{max}}$ for a given resolution is to lower $C.$ There are only a few options to achieve this. A reduction of the bleaching cross-section would be beneficial, but, for a given dye and imaging system, by far the easiest and most promising approach is to reduce the amount of light ${\displaystyle \sum N}$ a dye molecule sees. Reducing ${\displaystyle \sum N}$, i.e., the principle of adaptive illumination, is the rationale of DyMIN. For example, if the number of STED photons is reduced by a factor $x$, $S_{max}$ will immediately increase by the same factor. Likewise, the gain in signal can be invested in a resolution that is approximately $\sqrt[4]{x}$ better at the same signal level as before.

The dependencies shown in Fig. S6C were fit by Eq. S4, where, for both datasets, the only fitting parameter was C and F₀. C and F₀ agreed within 1%, as extracted by independent fitting of both curves. This suggests that our model captures the important effects in this system.

Sample Preparation

Mouse Sperm.

Mouse spermatozoa were collected in PBS from the epididymis of 12-wk-old CD1 mice and frozen in liquid nitrogen. After thawing, spermatozoa were incubated on poly-l-lysine (cat. P8920; Sigma-Aldrich) coated coverslips for 1 h at 37 °C. Samples were then rinsed in PBS and fixed in cold methanol for 10 min, rehydrated in PBS, and blocked in PBS supplemented with 1% BSA for 30 min. Both the primary and secondary antibody incubations were performed in PBS for 1 h at room temperature. Samples were mounted in Mowiol.

Neuronal Cell Culture and Immunolabeling.

Cultures of hippocampal neurons were prepared from Wistar rats of mixed sex at postnatal day P0–P1 in accordance with the Animal Welfare Law of the Federal Republic of Germany (Tierschutzgesetz der Bundesrepublik Deutschland, TierSchG) and the regulation about animals used in experiments (August 1, 2013, Tierschutzversuchsverordnung). For the procedure of sacrificing rodents for subsequent preparation of any tissue, all regulations given in section 4 of TierSchG were followed. Since killing of animals is not an experiment on animals according to section 7 Abs. 2 Satz 3 TierSchG, no specific authorization or notification was required. Cells were plated on coverslips coated with 100 μg/mL of polyornithine (cat. P3655; Sigma-Aldrich) and 1 μg/mL of laminin (cat. 354232; BD Bioscience). Neuronal cultures were maintained in Neurobasal medium (cat. 21103049; Gibco) supplemented with 2% B27 serum-free supplement (cat. 17504044; Gibco), 2 mM l-glutamine (cat. 25030; Gibco), and pen/strep (100 units/mL and 100 μg/mL, respectively, cat. A2213; BiochromAG). On the day after plating, 5 μM cytosine β-d-arabinofuranoside (cat. C1768; Sigma-Aldrich) was added to the cultures. For immunostainings, cells (20–30 days in vitro) were washed with PBS and fixed in 4% PFA in PBS (pH 7.4) for 20 min at room temperature, quenched with ammonium chloride and glycine (100 mM each) for 5 min, permeabilized with 0.1% Triton X-100 for another 5 min, and blocked in PBS supplemented with 1% BSA for 30 min. Both the primary and secondary antibody incubations were performed in PBS for 1 h at room temperature. Samples were mounted in Mowiol supplemented with 1,4-diazabicyclo[2.2.2]octane.

Antibodies.

The antibodies used in this study were anti-Gephyrin (cat. 147 011, 1:200 dilution; Synaptic Systems), anti-beta-Tubulin (cat. T5201, 1:200 dilution; Sigma-Aldrich), and anti-betaII spectrin (cat. 612563, 1:200 dilution; BD Biosciences); sheep anti-mouse (515-005-003; Dianova) was labeled with STAR635P (cat. 1-0101-007-6; Abberior).

Mammalian Cell Culture and Immunolabeling.

Vero cells were grown and labeled as described before (11), using antibodies against NUP153 and Lamin B1 (both Abcam). These primary antibodies were detected using secondary antibodies (Dianova) custom labeled with the fluorescent dyes Abberior STAR 635P (Abberior) and Alexa Fluor 594 (Thermo Fisher Scientific), respectively.

Crimson Fluorescent Nanobeads.

Beads were diluted from the stock solution in water (1: 5,000), binding to a cleaned standard coverslip (#1.5) surface prepared with undiluted poly-l-lysine for 5 min. The sample was mounted in Mowiol (Abberior).

Fluorescent Nanoassemblies (Bead R; GATTAquant).

Individual assemblies in this DNA origami sample were of nominally 23-nm size, containing ∼80 ATTO647N fluorophores with low variability in number.

Nanoruler (Custom-Supplied; GATTAquant).

This DNA origami template specified two ensembles of ∼15 ATTO647N fluorophores each, with their centers separated by a nominal distance of 30 nm. According to the manufacturer’s instructions, dyes in each of the ensemble occupy an area of 13 × 20 nm². DNA nanorulers are based on the DNA origami technology. Base structures are rigid multihelix bundles which offer single-stranded extensions (docking sites) to bind complementary dye-labeled oligos (yellow marks). Since the binding efficiency is not 100%, some docking sites remain unstained (gray marks).

Discussion and Conclusions

We have demonstrated how dynamically probing structures with adaptive resolutions increases fluorescent signals by minimizing the application of excess intensity of the state transfer light. In a point-scanning implementation of STED nanoscopy, more than 10-fold brighter images have been recorded under typical immunofluorescence sample conditions. DyMIN is a concept which facilitates the highest final resolutions at robust, strong signal for biological STED nanoscopy, as shown here by record axial resolutions (∼60 nm FWHM) for the single-lens 3D STED approach (Fig. 5). The demonstration of lateral separation of dye-based structures at 30-nm separation with unprecedented signal contrast (∼100 counts in peak, Fig. 6D) further demonstrates the importance of applying DyMIN.

We optimized the probing strategy using simulations and imaging experiments. A 10-fold signal increase can, given sufficient signal, be alternatively converted into ∼42% increased resolution. The superior performance of DyMIN results from avoiding scanning STED light over the sample at high power where this is not needed for fluorophore separation, with illumination curtailed as much as the structure allows. Clearly, sparse specimens exhibit the strongest advantage. While sparse structures could be imaged with almost the same resolution/signal with MINFIELD, the latter requires picking individual small scan fields, which then have to be precisely approached by a more involved scanning system, in contrast to the dynamical and self-adjusting DyMIN method. Denser specimens experience a drastic reduction of incident STED light with DyMIN scanning, too. As long as one or more probe steps, each at a different resolution, can be executed in between (clusters of) fluorophores, DyMIN uses these steps to prelocate denser structures, thus avoiding scanning across them at full power.

Compared with RESCue, its dynamical generalization further reduces photobleaching, with additional advantages. As DyMIN initializes the pixel-based probing with a confocal step in “empty” sample regions farther away from the structure, increasing resolution as the structure is approached, there is no hard inherent cutoff of structures as seen with RESCue. There, already, the first probing step is executed with the highest STED power and resolution, and therefore necessarily also close to the structure. Additionally, the Poissonian statistics of threshold detection can lead to noise-induced artifacts at abrupt transitions between background and actual signal. In a way, DyMIN creates a clearance area around regions containing fluorophores, instead of unflexibly probing each pixel with the highest light dose. Additionally, the low-power probe steps ensure high fluorescence fluxes, and, therefore, decisions can be made in shorter time, further reducing the accrued light dosages.

By now, the on/off principle (1, 3, 20, 21) is firmly established as the cornerstone of feature separation in far-field fluorescence nanoscopy. Whether fluorophores indeed need to be in different states further depends on their relative distance in the sample, given a certain resolution. Adaptions of the illumination applied for on/off state transfer are therefore a logical consequence of optimization of this general principle. DyMIN can be viewed as a sample-adapted implementation of this on/off strategy for feature separation. In STED nanoscopy, it limits the impact of the finite probability of photobleaching per on/off cycle by reducing—ideally minimizing—the number of cycles fluorophores need to undergo. The consequences of this versatile strategy will have to be explored for other coordinate-targeted nanoscopy variants, such as reversible saturable/switchable optical linear (fluorescence) transitions (20) and ground state depletion (GSD) (21) nanoscopies.

While this initial demonstration featured predefined pixel dwell times for each signal-probing step, more light could be saved by aborting any of the steps early once a confident decision on presence or absence of fluorophores can be taken. More advanced development directions will take DyMIN to conceptual limits. One might, for example, envision a STED nanoscope which scans more elaborate spatial sequences. An initial lower-resolution impression of the fluorescent structures could then successively inform all further scan coordinate, illumination, and resolution choices, also allowing the saving of time by skipping regions without fluorophores. Extremely fast (electrooptic) beam positioning will prove to be very effective in this regard. A limitation of the present initial experimental demonstration is the spatially dependent bleaching evident in some examples imaged (Fig. S7A), for which signal accumulation from numerous fast, repeated frames (22) with little bleaching will improve spatial homogenization. In addition, the decisions at each of the adaptive resolution steps could incorporate information from the collective of all pixels (“frame steps,” not “pixel steps”), not just the one pixel analyzed at a time. This knowledge could also be used to correct dark pixels originating from false decisions at any step, or enable floating decision thresholds to address larger signal variabilities within a specimen (Fig. S7B). We therefore anticipate that intelligent, multiadaptive illumination schemes, based on DyMIN and further advancements, will play a major role in the future. These schemes will allow convenient recording of nanoscopic images with superior resolution, lower illumination dose, and higher signal-to-noise.

Fig. S7.

Limitations of the initial DyMIN implementation with pixel steps. (A) An extended sharp edge of a structure, when approached by DyMIN with pixel steps (as in this initial demonstration), can result in uneven bleaching. For example, the top edge here is imaged brighter than the bottom edge. The shown structure is the periodic betaII spectrin lattice, oriented orthogonally to the slow scan axis. Accumulating several frames, and incorporating knowledge obtained by lower-resolution probing steps, possibly in elaborate scan patterns, is a promising direction toward developing the general DyMIN concept to homogenize bleaching. (B) DyMIN scanning as applied here, with suitable choices of fixed parameters, does not always capture very large signal variabilities, resulting, for example, from defocus [here, clusters fragmented by a few nonimaged pixels (encircled)]. In a “frame-step” implementation (i.e., probing an entire image frame for a DyMIN step), the knowledge about the structure at this step could be incorporated to ensure that all fluorophores are captured. Sample: Gephyrin clusters. [Scale bars: 200 nm (A and B).]

Materials and Methods

Detailed descriptions of the optical setup, image acquisition, and sample preparation including immunofluorescence labeling, as well as simulations of DyMIN performance, are provided in SI Materials and Methods. The 2D and 3D DyMIN STED fluorescence nanoscopy was demonstrated with a microscope setup extended from the one previously described in ref. 11. For sample preparation of rat hippocampal neurons (Fig. 3), all regulations given in section 4 of the Animal Welfare Law of the Federal Republic of Germany (Tierschutzgesetz der Bundesrepublik Deutschland, TierSchG) and the regulation about animals used in experiments (August 1, 2013, Tierschutzversuchsverordnung) were followed for the procedure of sacrificing rodents. Since sacrificing of animals is not an experiment on animals according to section 7 Abs. 2 Satz 3 TierSchG, no specific authorization or notification was required.