Investment in secreted enzymes during nutrient-limited growth is utility dependent

Significance

Bacteria secrete enzymes into the environment to digest macromolecules into smaller molecules that can be used as nutrients for growth. Secreted enzymes have potential benefits but also entail costs in the form of biomass and energy. How do bacteria determine how much of them to make? Using a system in which nutrient acquisition requires production of secreted enzymes, we infer that bacteria produce secreted signals in proportion to the benefit they would receive from the action of secreted enzymes. Investment in secreted enzymes is adjusted according to the magnitude of those signals. Our model provides a framework that can be applied to bacterial growth in many environments from contaminated food to microbial communities within a host.

Abstract

Pathogenic bacteria secrete toxins and degradative enzymes that facilitate their growth by liberating nutrients from the environment. To understand bacterial growth under nutrient-limited conditions, we studied resource allocation between cellular and secreted components by the pathogenic bacterium Pseudomonas aeruginosa during growth on a protein substrate that requires extracellular digestion by secreted proteases. We identified a quantitative relationship between the rate of increase of cellular biomass under nutrient-limiting growth conditions and the rate of increase in investment in secreted proteases. Production of secreted proteases is stimulated by secreted signals that convey information about the utility of secreted proteins during nutrient-limited growth. Growth modeling using this relationship recapitulated the observed kinetics of bacterial growth on a protein substrate. The proposed regulatory strategy suggests a rationale for quorum-sensing–dependent stimulation of the production of secreted enzymes whereby investment in secreted enzymes occurs in proportion to the utility they confer. Our model provides a framework that can be applied toward understanding bacterial growth in many environments where growth rate is limited by the availability of nutrients.

Nutrient acquisition is essential for the proliferation of all forms of life. Organic nutrients such as amino acids, nucleic acids, and sugars are often present in the environment as large oligomers that must be partially digested outside the cell to be imported. Many bacteria are capable of secreting hydrolytic enzymes that perform these functions. Secreted enzymes play critical roles in many microbe-associated processes including pathogenesis, as digestion and uptake of nutrients are essential for a pathogen to proliferate within a host (1–6).

How do bacteria regulate the production of enzymes involved in degradation of extracellular macromolecules? We do not understand bacterial growth kinetics in environments with polymeric nutrient sources despite over a century of research on bacterial growth because the regulation of secreted hydrolytic enzyme production is not well understood (7). Production of many secreted proteins is affected by the production and sensing of secreted small molecules called autoinducers in a diverse group of processes known as quorum sensing. Disruption of quorum-sensing systems often inhibits the production of secreted proteins, resulting in the inability to metabolize extracellular nutrients (8, 9). Although the qualitative reliance of secreted enzymes on quorum sensing is well established, a quantitative understanding of the relationship between bacterial growth and protein secretion is lacking.

We sought to understand how bacteria regulate investment in secreted enzymes by studying growth of the ubiquitous bacterial pathogen Pseudomonas aeruginosa in a medium where nutrient acquisition requires extracellular digestion of a protein substrate. We measured bacterial density, substrate degradation, and secreted protease activity of cultures growing under nutrient limitation. Our results indicate that P. aeruginosa increases its investment in secreted proteases as the perceived utility of secreted proteases increases due to the cell density dependence of the nutrient acquisition rate. We construct a mathematical model of bacterial growth under nutrient-limiting conditions based on measurable parameters, providing a general framework for the analysis of bacterial growth on macromolecular substrates.

Results

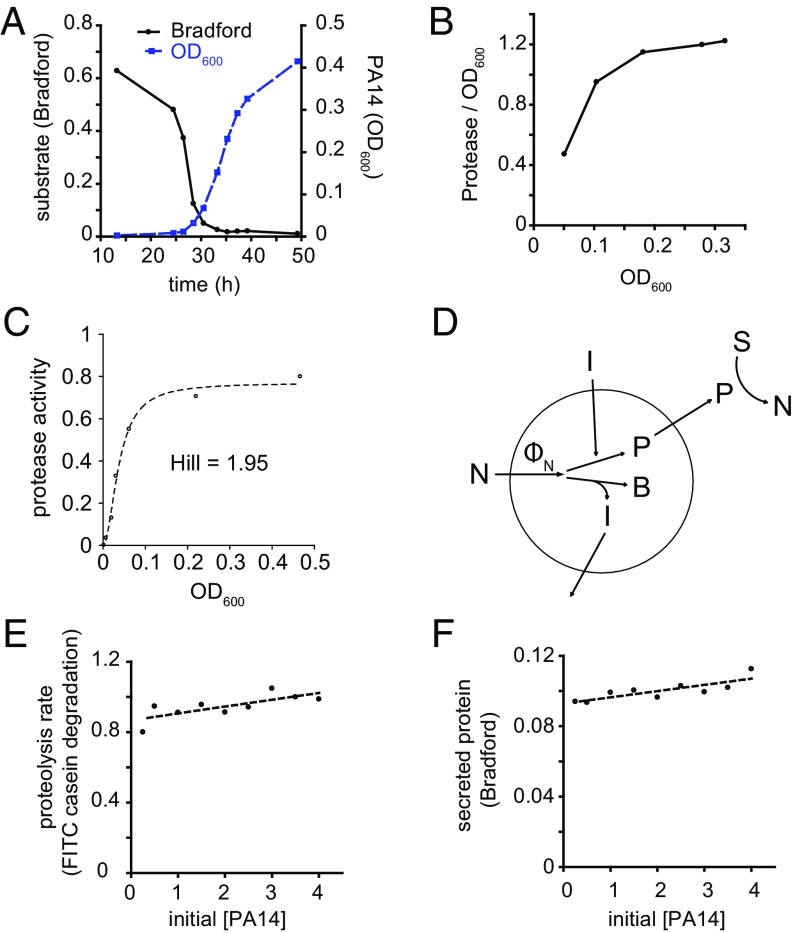
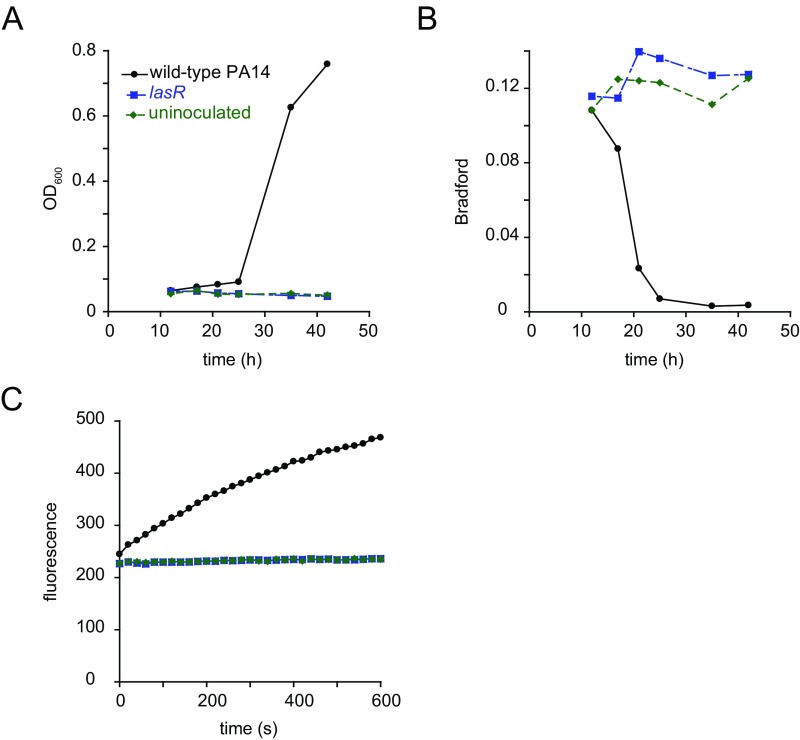
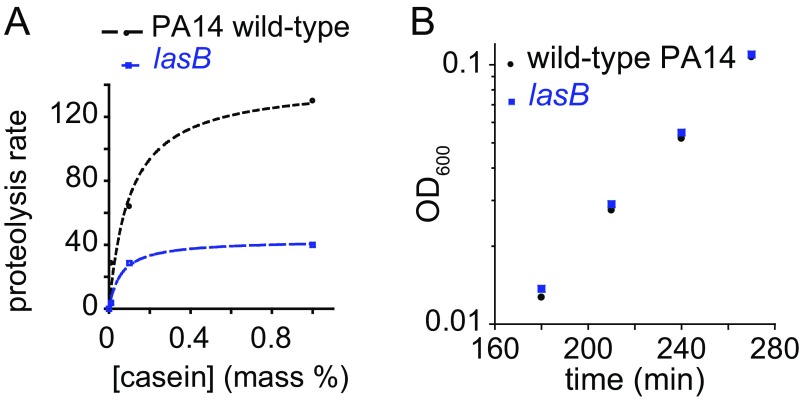
We began by examining the growth kinetics and protease secretion of P. aeruginosa strain PA14 (hereafter simply PA14) in a medium in which milk casein proteins serve as the sole source of carbon and nitrogen. In the absence of exogenous proteolytic activity, secretion of proteases is required for P. aeruginosa to use proteins as a nutrient source because large undigested proteins are not imported (9). We monitored degradation of casein in the media by Bradford staining supernatants after pelleting cells by centrifugation. During PA14 growth in casein, the loss of Bradford staining initially occurred slowly, with the rate increasing over time until a majority of the signal was lost (Fig. 1A). Loss of the majority of the Bradford signal preceded the rapid growth of bacteria by several hours. Throughout the course of growth, we also measured the activity of soluble proteases in the culture. Proteolytic activity per unit biomass increased over time, suggesting that the bacteria invested a greater fraction of their resources in secreted proteases as the culture grew (Fig. 1B). These observations are consistent with quorum-sensing control of secreted protease production (8, 10, 11). Deletion of the lasR gene, which encodes a quorum-sensing transcription factor (8, 12), greatly reduced the production of secreted proteases by PA14 and inhibited growth in casein (Fig. S1). We were interested in understanding why protease production is regulated by quorum sensing and sought to establish a quantitative basis for the regulation of secreted protease production that would allow for the modeling of bacterial growth on polymeric substrates.

Fig. 1.

PA14 growth and secreted protease production under different conditions. (A) Growth kinetics of PA14 in 1% casein medium and degradation of substrate. (B) Activity of soluble proteases per unit biomass increases as cell density increases. (C) Secreted protease activity as a function of cell density at saturation. PA14 was grown in media limited by different concentrations of tryptone (x axis). Proteolytic activity of supernatants was measured after bacteria grew to saturation under all tryptone concentrations. The data were fit to the Hill equation [y = y_max × xⁿ/(kⁿ + xⁿ)], where n is the Hill coefficient. The data fit to n = 1.95. (D) Model of autoinducer-regulated production of secreted protease during nutrient-limited growth. Autoinducer (I) is produced in proportion to nutrient flux (Ф_N) that is channeled toward cellular biomass (B). Total biomass production by cells in the environment is reflected by the total autoinducer concentration, which determines the proportion of each cell’s nutrient flux that is devoted to secreted protease production (P). The remaining nutrient is invested in cellular biomass (B). Secreted proteases cleave substrate (S) into smaller peptides (N) that can be taken up by the cell. (E) Proteolytic activity of supernatants of different concentrations of PA14 after exposure to a pulse of importable nutrients (CAAs). PA14 concentration is represented as multiples of saturated culture of PA14 in M9 without NH₄Cl containing 1% CAA. Data fit to a line with slope of 0.039 and Y intercept of 0.87. (F) Secreted protein produced by different concentrations of PA14 after exposure to a pulse of CAAs. Data fit to a line with slope of 0.0035 and Y intercept of 0.093.

Fig. S1.

lasR quorum-sensing mutant growth in casein. (A) Growth of wild-type PA14 and a PA14 lasR mutant in M9 without NH₄Cl plus 1% casein. (B) Levels of casein degradation as measured by Bradford staining throughout the course of bacterial growth. (C) Proteolytic activity of culture supernatants. Supernatants of cultures were collected after 35 h of growth. Proteolytic activity was measured using the FITC casein assay.

We considered the rationale for the increase in protease production per cell during growth in casein. It is expected that greater production of secreted proteases would result in greater release of nutrients from protein sources in the environment, provided that such sources are present. However, bacteria must balance the production of secreted factors with investment in their own maintenance and growth. We therefore considered the production of secreted proteases as a problem of optimization of nutrient flux into the bacteria under conditions in which bacteria have limited information about the environment. Because proteases are typically produced by P. aeruginosa when nutrients are depleted or limiting (13), we considered the rate of nutrient consumption of a population of bacteria growing under limiting nutrient. Specifically, we postulate that nutrient flux (Ф_N) can be modeled as a function of the concentration of bacteria (B) and the concentration of nutrient (N):

$${\mathrm{\Phi }}_N={\mu }_{\max }\frac{B•N}{K_S+N},$$ [1]

where μ_max is the maximum growth rate of the bacterium using a particular nutrient and K_S is the concentration of nutrient at which the growth rate is one-half of the maximum. Eq. 1 follows Monodʼs description of bacterial growth at different substrate concentrations (14). Here, we describe nutrient flux, whereas Monod described growth rate, but the relationships are analogous.

At high nutrient concentrations (N >> K_S), nutrient uptake approaches its upper limit for a given bacterial density. These conditions result in exponential growth at the maximum rate for a particular nutrient composition. At high nutrient concentrations, liberating additional nutrients from the environment will not serve to increase the uptake of nutrients by the bacteria. It is likely for this reason that bacteria growing in batch culture containing importable nutrients do not begin to secrete proteases in earnest until their growth is restricted by nutrient limitation (15). At low nutrient concentrations (N << K_S), the nutrient flux equation becomes the following:

$${\mathrm{\Phi }}_N={\mu }_{\max }\frac{B•N}{K_S},$$ [2]

and therefore,

$$\frac{\partial {\mathrm{\Phi }}_N}{\partial N}={\mu }_{\max }\frac{B}{K_S},$$ [2a]

which describes nutrient uptake that is dependent on both the cell density and the nutrient concentration. Under these conditions, the growth rate will be less than the maximum growth rate due to the growth-limiting rate of nutrient consumption. Under these conditions, the change in nutrient flux with respect to nutrient concentration is proportional to the cell density. These conditions describe a nutrient-limiting environment that stimulates secretion of proteases and other soluble diffusible enzymes. The linear dependence of nutrient flux on the external nutrient concentration means that there is also a linear dependence of growth rate on the external nutrient concentration. Thus, if additional nutrients can be liberated from the environment, there will be an increase in the nutrient flux and therefore an increase in the growth rate.

Because the utility derived from investing in increasing the nutrient concentration varies under nutrient-limited growth depending on the cell density, producing a fixed amount of secreted protease per unit biomass is not optimal in every environment (16–18). The linear dependence of the change in flux with respect to nutrient on B from Eq. 2a suggests that, at low nutrient concentrations, cells should invest a larger fraction of their resources in secreted proteases as cell density increases to increase the rate of nutrient uptake. We define γ as the fraction of nutrient flux devoted to secreted protease (P) and hypothesized that there is a Michaelis–Menten type relationship between γ and the cell density:

$$\gamma =\frac{\frac{dP}{dt}}{{\mathrm{\Phi }}_N}={\gamma }_{\max }\frac{B}{K_{\gamma }+B}.$$ [3]

At low cell density, γ is proportional to B. At high cell density, the fractional investment in P levels off at a maximum value (γ_max). The introduction of γ_max is necessary because otherwise cells could devote all of their resources to the production of secreted proteases, which would prevent them from growing. The cell density at which the culture devotes one-half of the maximal amount of resources to secreted protein is characterized by K_γ. Because γ is a ratio of time-dependent quantities, it is challenging to measure. We therefore chose to relate the predicted behavior of γ to total protease and cell density:

$$\begin{array}{l}\text{For}\hspace{0.17em}B<<K_{\gamma },\hspace{0.5em}\hspace{0.5em}\gamma =\frac{{\gamma }_{\max }}{K_{\gamma }}•B,\\ \text{and}\hspace{0.17em}\text{for}\hspace{0.17em}\gamma <<1,\hspace{0.5em}\hspace{0.5em}{\mathrm{\Phi }}_N\approx \frac{dB}{dt};\\ \text{therefore},\hspace{0.17em}\hspace{0.5em}\gamma \approx \frac{\frac{dP}{dt}}{\frac{dB}{dt}}=\frac{dP}{dB}=\frac{{\gamma }_{\max }}{K_{\gamma }}•B,\\ \text{and}\hspace{0.5em}{\displaystyle \int dP}\approx {\displaystyle \int \frac{{\gamma }_{\max }}{K_{\gamma }}•BdB,}\\ \text{resulting}\hspace{0.17em}\text{in}\hspace{0.17em}P\approx \frac{{\gamma }_{\max }}{2K_{\gamma }}•B^2.\end{array}$$ [4]

This indicates that for values of B that are sufficiently small, the amount of protease secreted is hypothesized to be proportional to the square of the cell density. To test the prediction that secreted protease production scales with the square of cell density for low cell densities, we grew PA14 to saturation in a medium that does not require the action of extracellular proteases for nutrient acquisition. We measured secreted protease activity when cultures reached saturation in the presence of different limiting concentrations of tryptone (Fig. 1C). The data were fit to the Hill equation with a Hill parameter approximately equal to 2 (1.95), suggesting that secreted protease levels are proportional to the square of the cell density at low densities.

We considered how cells might sense and respond to the overall cell density via quorum sensing. At the most basic level, it is possible that cells secrete a substance in proportion to their biomass growth that reflects the amount of resources invested in cellular biomass. Then, the cells in the environment can regulate production of secreted proteases in proportion to the concentration of that signal. We propose a regulatory strategy whereby cells report on the net benefit they receive (i.e., nutrient flux less investment in secreted products) during nutrient-limited growth by producing diffusible autoinducers (Fig. 1D). Greater amounts of autoinducers correspond to greater benefit from secreted protease production in the form of a higher rate of cellular biomass accumulation. Protease production levels are then adjusted based on the sensed concentration of autoinducers (19). Thus, as secretion of proteases becomes more useful, an increasing fraction of available resources is devoted to secreted protease production:

$$\frac{d\gamma }{dt}\approx \frac{{\gamma }_{\max }}{K_{\gamma }}•\frac{dB}{dt}.$$

Under this model, the rate of change of the fraction of cellular resources devoted to secreted protease production increases in proportion to the benefit they confer during nutrient limited growth. Higher rates of biomass accumulation will result in a more rapid increase in γ.

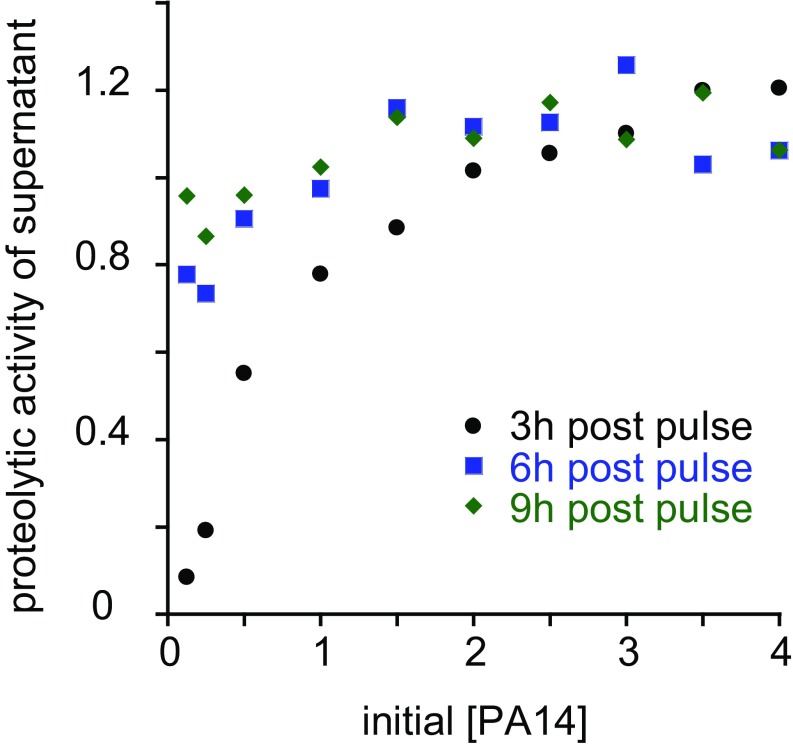
To test this theory, we considered what would happen if we decoupled cell density and total benefit by exposing different concentrations of stationary-phase cells to a pulse of importable nutrient. We took saturated overnight cultures of PA14, washed the cells in buffer to remove diffusible autoinducers, and resuspended them at different concentrations in fresh buffer. We then added an identical quantity of casamino acids (CAAs) to each sample and monitored secreted protease production. Protease activity measurements were taken at time intervals after nutrient addition to measure the combined kinetics of protease production and protease inactivation (Fig. S2). Higher initial [PA14] resulted in more rapid increase in secreted protease activity. Based on the stability of protease activity over several hours at high initial [PA14], we deduced that protease inactivation over several hours is negligible under these conditions.

Fig. S2.

Secreted protease activity over time after nutrient pulse. Secreted protease activities of different concentrations PA14 after exposure to a pulse of importable nutrients (CAAs) for 3, 6, or 9 h. PA14 concentration is represented as multiples of saturated culture of PA14 in M9 without NH₄Cl containing 1% CAA.

Because the prospective benefit is determined by the size of the nutrient pulse, it is identical for all of the samples at different initial cell densities. Thus, according to our theoretical model, we expected that under these conditions the output of secreted protease would be independent of the initial cell concentration. Alternatively, if cells were to secrete proteases in a manner independent of the nutrient taken up after the pulse, we would expect the level of secreted protease to be proportional to the initial biomass. When we plotted secreted protease level as a function of initial cell density, we observed that the slope of the best fit line (0.039) was only slightly positive, with a Y intercept of 0.87, 88% of the value for the highest initial cell density (Fig. 1E). The expected fit line under the alternative hypothesis above would intercept the origin, resulting in a slope of ≈0.25 based on the level of secreted protease at the highest initial concentration of PA14 tested. Moreover, we observed that total secreted protein production, as measured by Bradford staining, was also nearly independent of the cell density. The slope of the best-fit line (0.0035) was considerably smaller than 0.028, which would be expected if the best-fit line passed through the origin (Fig. 1F).

Based on the cell density-dependent production of secreted proteases, we constructed a model for the growth of PA14 in casein. We modeled substrate (S), nutrient flux (Ф_N), protease concentration (P), bacteria concentration (B), and nutrient concentration (N) as a function of time. The rate of change of substrate with respect to time was modeled by Michaelis–Menten kinetics of degradation of the substrate by secreted proteases: $dS/dt=\hspace{0.17em}-V_{\max }\hspace{0.17em}•\hspace{0.17em}P\hspace{0.17em}•\hspace{0.17em}S/\left(K_m+S\right)$. P. aeruginosa secretes several different proteases. Rather than model each protease individually, we modeled the entire suite of secreted proteases as a single “metaprotease.” We measured the secreted protease activity against the casein substrate as a function of casein concentration. We found that the activity of secreted proteases as a function of casein concentration can be modeled well by the Michaelis–Menten equation with a K_m of ≈0.29 mass % (Fig. 2A). V_max was approximated based on the rate of degradation of casein upon addition of exudates from PA14 cultures grown in 1% CAA medium. We used an approximate value of 1 (mass% substrate)⋅(mass% enzyme)⁻¹⋅min⁻¹. This value is likely to be lower than the actual cleavage rate of casein by secreted proteases. However, not every cleavage event results in a peptide that is small enough to be imported. Early in the time course when most of the molecules are uncleaved, many cleavage events distant from both termini are expected to result in both products being too large to be imported.

Fig. 2.

Modeling of PA14 growth in casein based on flux-dependent investment. (A) Activity of secreted proteases against casein. Fit is to the Michaelis–Menten equation with K_m = 0.29%. (B) Growth of PA14 in 1% CAA medium. Fit is to exponential growth function with μ = 0.023 min⁻¹. (C) Results of growth simulation of PA14 in 1% casein. Bacterial biomass (B) and protease biomass (P) increase monotonically. Substrate concentration decreases monotonically. Importable nutrient concentration (N) increases through most of the growth and begins to fall as the culture approaches saturation. (D) The ratio of secreted protease to biomass increases during the simulated growth of PA14 in casein.

Nutrient flux into cells was modeled based on Monodʼs model of bacterial growth as a function of nutrient concentration: ${\mathrm{\Phi }}_N=\hspace{0.17em}{\mu }_{\max }\hspace{0.17em}•\hspace{0.17em}N\hspace{0.17em}•\hspace{0.17em}B/\left(K_S+N\right)$. We calculated μ_max in casein based on the exponential growth rate of PA14 in CAA medium (Fig. 2B). The doubling time is ≈30 min, yielding μ_max = (ln 2)/30 min, which is ≈0.023 min⁻¹. K_S is difficult to measure (20, 21), especially for a nutrient source such as caseinolytic peptides, which are not homogeneous and whose average composition could change over the course of PA14 growth in casein. We used a K_S value of 0.01 mass % based on preliminary data fitting.

The rate of change of nutrient concentration is the negative of the rate of degradation of substrate minus the rate of nutrient flux into cells: $dN/dt=\hspace{0.17em}-dS/dt-{\mathrm{\Phi }}_N=V_{\max }\hspace{0.17em}•\hspace{0.17em}P\hspace{0.17em}•\hspace{0.17em}S/\left(K_m+S\right)-{\mu }_{\max }\hspace{0.17em}•\hspace{0.17em}N\hspace{0.17em}•\hspace{0.17em}B/\left(K_S+N\right)$.

The rate of change of extracellular protein is defined by γ: $dP/dt=\gamma •{\mathrm{\Phi }}_N$, where γ is the fraction of nutrient taken up that is devoted to secreted protein. We modeled the investment in secreted proteases using Eq. 3. We set K_γ based on the cell density at which the half-maximal ratio of secreted protease to cell density was achieved in tryptone medium. Because protein constitutes approximately one-half of cellular biomass, we set γ_max equal to one-half the fraction of protein secreted vs. cellular protein based on Bradford assays. Based on the results of the secretion of proteases by PA14 in different tryptone concentrations (Fig. 1C), we took the initial concentration of protease to be proportional to the square of the initial cell density.

The rate of change of cellular biomass is equal to the proportion of nutrient uptake not devoted to secreted protease: $dB/dt=\left(1-\gamma \right)•{\mathrm{\Phi }}_N$. This model assumes that all nutrient is converted to biomass (i.e., biomass yield is equal to 1), which is an approximation, as the nutrient used for energy production is neglected. We note, however, that the model can be generalized to any biomass yield, so long as the yield is constant during the course of growth and across the different conditions tested (22).

Simulations were performed by numerical integration of the differential equations describing the rates of change of S, N, B, and P. Simulations showed an increasing growth rate over time, which agreed with the experimental results (Fig. 2C). The simulations also exhibited an increasing ratio of secreted protease to cell density over the course of growth (Fig. 2D), which is consistent with measurements. We detected what appeared to be an inconsistency between our simulations and the observations with respect to the degradation of substrate. Bradford staining indicated that substrate is degraded several hours before bacterial levels reach saturation (Fig. 1A). This suggests that, in the intervening time, there exist high levels of accumulated nutrient. At such high levels of nutrient, PA14 would be expected to grow at its maximum rate, as it would not detect any sort of nutrient limitation. Although the growth rate of PA14 increases significantly after the Bradford signal has been depleted, the bacteria are still growing several times slower than the maximum growth rate. The most likely explanation of the apparent discrepancy between the Bradford signal and the growth of PA14 is that, although the Bradford signal initially decreases linearly with protease cleavage, not all of the early cleavage products result in peptides small enough to be imported. Thus, when the Bradford signal is depleted, the majority of peptides must still undergo further digestion to be imported. Our model predicts that the proteolysis rate measured by Bradford signal should be proportional to the rate of importable nutrient production when the substrate is mostly undigested. Another possible explanation for this discrepancy is that K_S is actually much higher than in the model, approaching or even exceeding 1% nutrient. Because this is far higher than values typically observed for bacteria (21, 23), this explanation seems less likely.

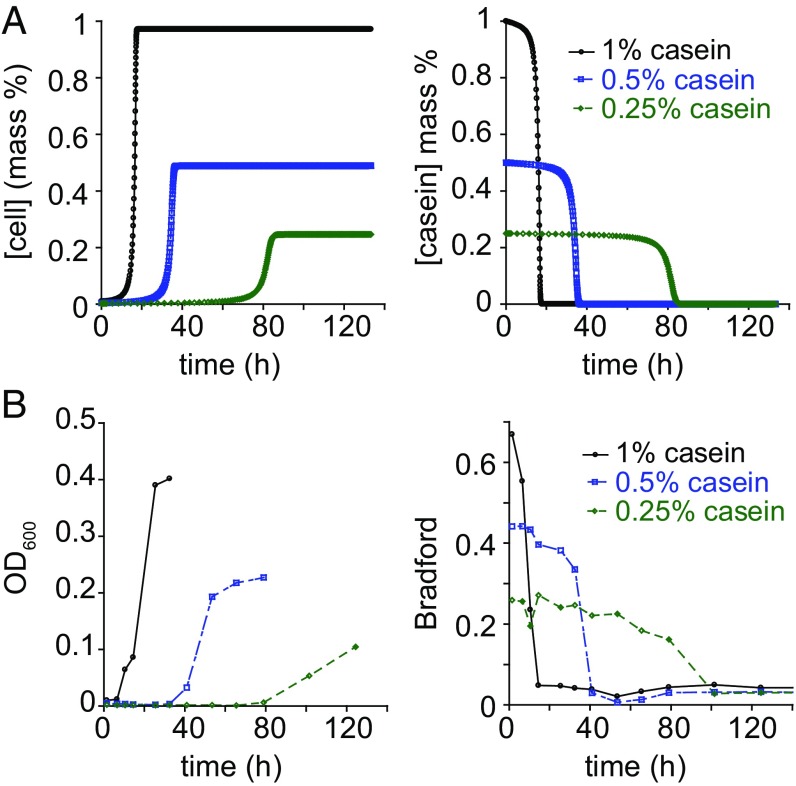
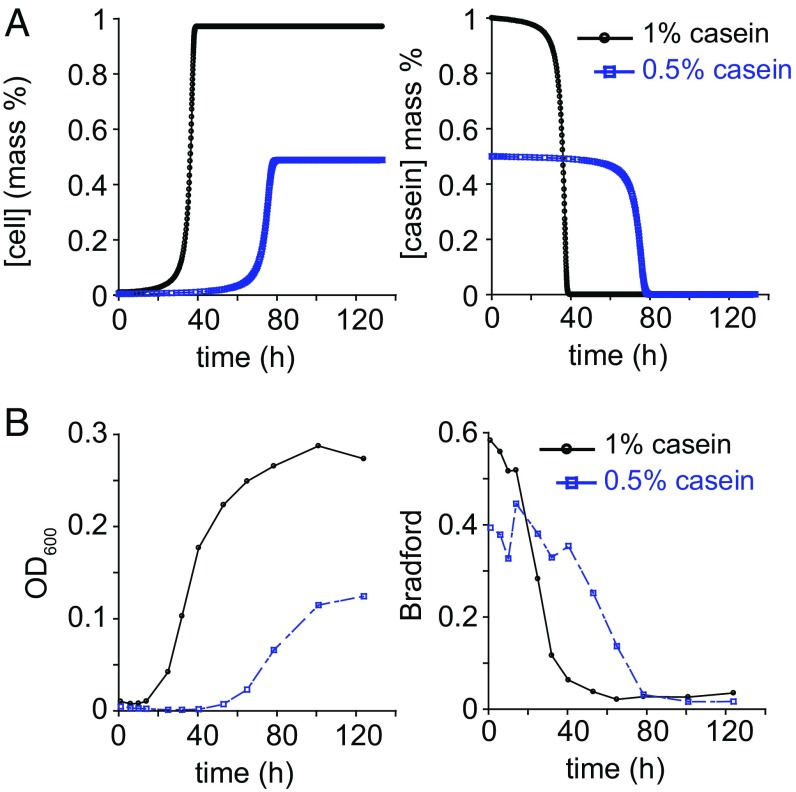
We sought to test our theory by modeling and measuring bacterial growth under different conditions. When we adjusted various parameters in the model and ran corresponding simulations, we noticed that the concentration of substrate had a large effect on the time to saturation of the culture (Fig. 3A). This phenomenon could be attributed to the combination of two factors. A minor contribution is due to the K_m of the protease mixture. This contribution is minor because the casein concentrations used were near or above the measured K_m, meaning that changes in substrate concentrations resulted in less-than-proportional changes in proteolysis rate. At much lower casein concentrations this factor is expected to play a larger role. The other more significant factor is that the initial concentration of bacteria in the simulation is proportional to the casein concentration. With a smaller initial cell density, lower concentrations of casein result in lower initial contributions to protease production and therefore a lower rate of growth. The model predicts an approximately reciprocal relationship between casein concentration and time to saturation. We tested this prediction by growing PA14 in media with different concentrations of casein and found that the relationship predicted by the model was corroborated by experiments (Fig. 3B).

Fig. 3.

Predicted and observed dependence of growth on nutrient concentration. (A) Simulated growth of PA14 and substrate degradation in media containing different concentrations of casein. (B) Observed casein concentration dependence of PA14 growth and substrate degradation.

Pseudomonas aeruginosa secretes a suite of proteases, of which LasB is the most abundant and has the greatest proteolytic activity against casein. The caseinolytic activity of secreted proteases of a lasB mutant were characterized by a V_max ≈ 29% of wild-type PA14 and K_m ≈ 60% of wild-type PA14 (Fig. S3A). The dominant role of LasB in the degradation of casein left open the possibility that only the production of LasB protease is regulated in a utility-dependent manner. To test the applicability of our model to other proteases secreted by PA14, we simulated the growth of a lasB mutant in a manner similar to wild-type PA14, changing only the V_max and K_m parameters for secreted proteases. Intrinsic growth parameters of the lasB mutant (i.e., μ_max and K_S) were identical to those of wild type (24) (Fig. S3B). The predicted kinetics of growth of the lasB mutant remained dependent on nutrient concentration but were slower than for wild-type PA14 (Fig. 4A). The measured values were consistent with the rate of growth of lasB mutant in casein (Fig. 4B). These results suggest that the utility-dependent production of secreted proteases is broadly applicable to the suite of proteases secreted by PA14 and is therefore likely to be a general regulatory strategy for secreted products.

Fig. S3.

Properties of a lasB mutant. (A) Proteolytic activity of lasB mutant culture supernatant compared with wild-type PA14 culture supernatant against different concentrations of casein. (B) Growth of lasB mutant in M9 without NH₄Cl plus 1% CAA.

Fig. 4.

Predicted and observed kinetics of growth of a secreted protease mutant in casein. (A) Simulated growth kinetics of lasB mutant in casein and substrate degradation. (B) Observed growth and casein substrate degradation by lasB mutant.

Discussion

During periods of nutrient scarcity, cells adjust their allocation of resources based on their metabolic state and information obtained about the environment. Prior theoretical studies of microbial growth on macromolecular substrates have typically assumed either a constant output of secreted proteases per unit biomass or a constant fraction of nutrient influx devoted to secreted proteases under nutrient-limited growth conditions (21, 24–26). Our study suggests that a more complex mode of regulation of secreted proteases is required to capture the natural physiological regulation of secreted products for P. aeruginosa. Specifically, our model suggests that bacteria initially grow more slowly than expected on a polymeric substrate compared with prior models. Over time, however, the growth rate on a polymeric substrate is expected to increase more rapidly according to our model than in prior models due to increasing investment in secreted products with increasing cell density.

Aspects of secreted protein regulation uncovered here are reminiscent of the regulation of the lac operon in Escherichia coli. Both secreted protein production and lac operon expression entail a cost to cells that activate them. For the lac operon, costs include the production of the response proteins LacZYA, as well as the energetic cost associated with the activity of LacY, which serves to import lactose (27, 28). For secreted protein, there is the cost of production of the proteins as well as the energy required to secrete them. To avoid expression of the lac operon in the absence of lactose, the lac operon is induced by titration of the lac repressor off of the lac operator in the presence of allolactose (29). Allolactose is a minor product of the action of the β-galactosidase enzyme LacZ on lactose. Because allolactose is not used as a nutrient by the cell, its levels can serve as an indicator of the potential for lactose-based metabolism without interference by the rates of other metabolic processes that may influence the utility of measuring the level of substrate or major products of the LacZ-catalyzed reaction. If the intracellular allolactose concentration is a function of LacZ activity, then the allolactose concentration can serve as a signal indicating the cell’s metabolic capability of breaking down lactose. In effect, allolactose acts like an intracellular version of autoinducers for secreted protein production.

Our results indicate that the production of secreted proteases by P. aeruginosa is dependent on the projected utility that they would confer to the bacteria that produce them. Under nutrient-limited growth conditions, the benefit is proportional to the cell density. Therefore, it is logical that secreted protease production is controlled by quorum sensing. We suggest that this rationale is generally applicable for secreted products, many of which are regulated by quorum sensing (30, 31). It is worth noting, however, that other strategies may be used to regulate the production of secreted enzymes. When Rosenberg et al. (32) studied the growth of Myxococcus xanthus in casein, they did not observe large differences in the amount of secreted protease produced per unit biomass under the different conditions, suggesting a fundamentally different mode of regulation than in P. aeruginosa. When feeding, M. xanthus cells move together in groups, or swarms. It was suggested that this behavior increases the rate of uptake of nutrients obtained from secreted hydrolytic enzymes. Experiments in yeast suggest that grouping can be a favorable strategy while secreting hydrolytic enzymes (33). Indeed, an aggregation strategy could be preferable to a density-controlled secretion strategy if the affinity for the importable nutrient is low (as was observed for M. xanthus) because increasing the local cell density also limits the rate of loss of hydrolytic products. Thus, quorum sensing is an important method, but not the only method, by which secreted products may be regulated.

Xavier and colleagues (34, 35) have put forth a theory of the regulation of production of rhamnolipid, another product secreted by P. aeruginosa. Because rhamnolipids are carbon rich, the opportunity cost of producing them is lower when carbon is in excess. The principle of “metabolic prudence,” whereby the quantity of rhamnolipid secreted by cells is dependent on the availability of excess carbon in the cell, limits the resources devoted to rhamnolipid production during carbon starvation. Our study suggests an extension to metabolic prudence. We posit that secreted enzyme production is dependent on both utility and cost, as determined by nutrient uptake and biomass production. This strategy allows bacteria to expand their production of secreted products when they are useful, and to ration their investment in secreted products that contain scarce nutrients.

Our model of secreted protease production does not account for mechanisms by which bacteria might reduce their investment in secreted proteases if nutrient import rates were to rise or fall abruptly. An abrupt rise in nutrient import could effectively allow the bacteria to grow at a rate independent of nutrient concentration. Under such conditions, secreted protease production would be scaled back due to catabolite repression (36). An abrupt decline in nutrient import could lead to scaling back of investment in secreted proteases as a result of autoinducer degradation, which can occur by spontaneous hydrolysis or by autoinducer-degrading enzymes produced by P. aeruginosa or other organisms in the environment (37–41). Moreover, it has been demonstrated in an autocrine signaling model that the combination of signal degradation and positive feedback can result in a bimodal activation response (42), implying the coexistence of secreting and nonsecreting cells. Indeed, phenotypic heterogeneity of virulence factor production has been observed in other pathogenic bacteria in a host environment (43, 44).

In summary, we have shown that it is possible to understand the growth of bacteria on a polymeric substrate using a utility-dependent model for the quorum-sensing regulation of secreted proteases. Proteases are a subset of the molecules secreted by P. aeruginosa (31, 45). The mechanism of control of secreted proteins we propose does not require a detailed accounting for the costs and benefits of all secreted products. Several studies suggest that there are additional regulatory mechanisms relating to the metabolic state of the cell that control the fraction of individual components of the total secretome (34, 35, 46–49). A combination of regulatory feedbacks could allow bacteria to tailor the composition of their secretomes to specific features of the environment to facilitate growth (7). Our analysis of the growth of P. aeruginosa on casein opens up the possibility of quantitative study of other secreted products with respect to the environment to better understand and predict the rate of growth of bacteria in more complex and diverse environments containing different types of polymeric substrates. Understanding which autoinducers or combinations of autoinducers relay information about the benefits and costs of different potential secreted products will be an important step in the development of quorum-sensing inhibitors targeted against specific secretion profiles associated with virulence in different environmental niches (49, 50).

Materials and Methods

Strains, Media, and Growth Conditions.

P. aeruginosa UCBPP-PA14 (51), lasB MAR2xT7 transposon insertion mutant PA14 (52), and an unmarked in-frame lasR deletion mutant of PA14 (from Eliana Drenkard, Department of Pediatrics, Massachusetts General Hospital, Boston) were grown at 37 °C in 15-mL glass tubes placed 16 cm from the axis of rotation on a rotary drum (New Brunswick Scientific; M1053-0450) spinning at 60 rpm.

M9 media lacking NH₄Cl were made by mixing 5× M9 salts lacking NH₄Cl (240 mM Na₂HPO₄, 110 mM KH₂PO₄, 43 mM NaCl) with casein, CAA, or tryptone, followed by the addition of MgSO₄ (1 M stock) and CaCl₂ (1 M stock). Final concentrations of M9 components in media were 48 mM Na₂HPO₄, 22 mM KH₂PO₄, 8.6 mM NaCl, 2 mM MgSO₄, and 100 µM CaCl₂.

Stocks of nutrient sources were prepared as follows: 2% (wt/vol) casein (sodium caseinate; Sigma; C8654) was dissolved in water and autoclaved at 100 °C for 20 min; 10% (wt/vol) CAAs (AMRESCO; J851) was dissolved in water and autoclaved at 120 °C for 20 min; 10% (wt/vol) tryptone (BD; 211705) was dissolved in water and autoclaved at 120 °C for 20 min.

Three-milliliter starter cultures in LB medium were inoculated with freshly streaked bacteria from LB plates. After 14–16 h of growth, cultures were centrifuged at 13,500 × g for 1 min and resuspended in M9 media without NH₄Cl or carbon source. Resuspended cultures were diluted 100-fold in M9 media without NH₄Cl or carbon source. Casein growth experiments were initiated by inoculating casein growth medium with 1/100 vol of the 100-fold diluted resuspended cultures.

For Bradford measurements, samples were removed from the culture and centrifuged at 13,500 × g to pellet cells. Supernatants were transferred to new tubes and frozen at −20 °C for the duration of the experiment. All samples were then thawed and protein concentrations were measured using the Bio-Rad protein assay.

Turbidity Measurements.

Bacterial growth was halted by fixing culture samples with equal volumes of 10% formalin in PBS. For growth experiments, fixed samples were stored at 4 °C for the duration of the time course. Turbidity (OD₆₀₀) for all time points was measured after completion of the experiment by resuspending the fixed cells, transferring them to a flat-bottom 96-well plate, and recording the optical density at 600 nm in a microplate reader (SpectraMax M5).

Protease Assays.

The Pierce Colorimetric Protease Assay kit (Thermo Fisher Scientific; 23263) was used to measure the proteolytic activity of supernatants against casein. Lyophilized succinylated casein was resuspended in M9 without NH₄Cl to a concentration of 2 mg/mL. Supernatants containing protease were diluted 100-fold in M9 without NH₄Cl. Fifty microliters of diluted supernatant was added to 100 µL of succinylated casein and incubated at 37 °C for 1 h in a microtiter plate. Fifty microliters of 0.033% TNBSA were added, and samples were incubated for 20 min at room temperature. Absorbance at 450 nm was measured in a microplate reader and corrected by subtracting a control containing buffer instead of supernatant. In addition, measurements were taken for samples containing supernatant with buffer instead of succinylated casein and corrected by subtracting a control sample of buffer in place of both succinylated casein and supernatant. The final reading was calculated by subtracting the corrected succinylated casein without supernatant signal from the succinylated casein-plus-supernatant signal.

The FITC casein protease assay was performed using FITC-labeled bovine casein (Sigma; C0528). Ten microliters of supernatant was added to 190 µL of FITC-conjugated casein (2.5 µg/mL) in M9 without NH₄Cl in a microtiter plate. Fluorescence emission of fluorescein at 520 nm was measured after excitation at 480 nm at 20-s intervals. Proteolysis rates were calculated by linear fitting of the first five time points.

Protein Concentration Measurement.

Protein concentrations were measured using the Bio-Rad protein assay (Bio-Rad; 500-0006) in a microtiter plate. At higher protein concentrations, where Bradford measurements of undiluted samples fell outside the linear range of the assay, samples were diluted 10-fold in PBS before performance of the Bradford assay. Signal for diluted samples was scaled accordingly.

Growth Modeling.

Modeling was performed using MATLAB (MathWorks), version 9.1.0.441655 (R2016b). Differential equations were solved numerically using ODE45. Data and MATLAB code will be provided upon request.

We observed, as others have observed previously (53, 54), that for P. aeruginosa growing in casein, there is an early growth phase (phase I) that is independent of secreted protease production. The existence of phase I is presumably due to the presence of small molecular-weight species that constitute a minor fraction of commercially available casein. Saturated cultures of a secreted-protease deficient mutant in different concentrations of casein indicated that the fraction of bacteria at the end of phase I is ≈1% of the total available biomass. Our model applies to the protease-dependent growth phase (phase II), treating the concentration of bacteria at the end of phase I as the initial bacterial concentration.

Initial values were set as follows: S₀, initial substrate concentration (mass %); B₀, ≈1% of initial substrate concentration (based on cell density after phase I of growth); N₀, assumed to be zero at the end of phase I, before secreted protease production; P₀, initial amount of protease produced at the end of phase I, calculated based on B₀:

$$P_0=B_0•\gamma \left(B_0\right)={\gamma }_{\max }•\frac{B_0^2}{K_{\lambda }+B_0}.$$