Abstract
Outbreaks of infectious diseases such as influenza are a significant threat to human health. Because there are different strains of influenza which can cause independent outbreaks, and influenza can affect demographic groups at different rates and times, there is a need to recognize and characterize multiple outbreaks of influenza. This paper describes a Bayesian system that uses data from emergency department patient care reports to create epidemiological models of overlapping outbreaks of influenza. Clinical findings are extracted from patient care reports using natural language processing. These findings are analyzed by a case detection system to create disease likelihoods that are passed to a multiple outbreak detection system. We evaluated the system using real and simulated outbreaks. The results show that this approach can recognize and characterize overlapping outbreaks of influenza. We describe several extensions that appear promising.
Keywords: Influenza, Outbreak Detection, Outbreak Characterization, Bayesian Modeling
Graphical abstract

1. Introduction
Influenza is a contagious viral disease that spreads around the world in seasonal epidemics. It causes 3–5 million severe illnesses and 250,000–500,000 deaths annually. It also causes considerable health care costs and lost productivity [1]. There is a clear need for accurate, timely predictions of influenza outbreaks for hospitals, public health officials, and business [2].
This paper describes a Multiple Outbreak Detection System (MODS) that detects and characterizes overlapping outbreaks of influenza. MODS is part of a framework for disease surveillance developed by our group [3, 4, 5]. In this framework, a natural language processing system extracts signs and symptoms from the full text of emergency department (ED) patient care reports. These extracted features are combined with laboratory values and passed to a Case Detection System (CDS) that infers a probability distribution over the diseases each patient may have. For each patient, this distribution is expressed as a set of likelihoods of the patient’s data. MODS searches a space of outbreak models and scores each model according to the probability of the findings of each patient in the ED given the model. Models are weighted and combined to make predictions. See Figure 1.
Figure 1.
End-to-end framework for outbreak detection and characterization.
There has been significant prior work in the detection and characterization of outbreaks of influenza [6, 7, 8, 9, 10]. The work reported here differs from much of the prior work in three important ways. First, we address the problem of detecting and characterizing multiple, overlapping outbreaks. These are commonly due to separate type A and type B infections, but may also be caused by multiple introductions of the same influenza strain, the spread of an influenza strain in different demographic groups, or different strains of influenza [1, 11, 12, 13, 14]. Second, we do not rely on simple counts. Instead, for each patient, CDS produces a set of likelihoods of that patient’s evidence given the diseases he or she may have. This is more robust than a posterior probability. While the posterior probabiliy of influenza given fever and cough in a particular patient will change if it is summer, the peak of an influenza outbreak, or the days following an anthrax attack [15], the likelihood of fever and cough given influenza is relatively stable. Finally, we explicitly account for Non-Influenza Influenza-Like Illnesses (NI-ILI) which are clinically similar to influenza and can also display outbreak activity.
2. Material and Methods
2.1. Evidence
As stated above, MODS is part of an end-to-end system that starts with the full text of emergency department patient care reports. These reports contain a record of the patient assessment, past medical history, and history of present illness. To model outbreaks of influenza, these can be more informative than just chief complaints [16]. In this section, we describe how these reports are processed to support outbreak detection and characterization.
The text of each patient care report is parsed to extract 79 findings (such as abdominal pain, cough, fever, etc.) that were deemed by experts to be relevant to the diagnosis of influenza and influenza-like illnesses. Thus, each report is converted into a set of 79 features. Each feature can take the values present (the corresponding finding is explicitly mentioned, e.g. “the patient is cyanotic.”), absent (the finding is denied, e.g. “the patient denies chest pain.”), or missing (the finding is not mentioned in the text). Four pre-coded features, age, respiratory panel ordered, laboratory result available, and laboratory positive influenza are then added to the text-based 79 findings. Thus, each report is converted to a set of 83 features. These features are listed in Table 1.
Table 1.
Features extracted from reports with NLP plus precoded findings. Precoded findings are in italics. “AC” or “SLC” indicate if finding was used in CDS for Allegheny County or Salt Lake City.
| abdominal distress | lab testing ordered (influenza) (AC) |
| abdominal pain | lab testing ordered (rsv) (SLC) |
| abdominal stress | lab testing ordered (panel) (SLC) |
| abdominal tenderness | malaise |
| abnormal chest radiograph findings | myalgia (AC) |
| acute onset | nasal flaring |
| anorexia | nausea |
| apnea (SLC) | nonproductive cough (AC) |
| arthralgia | non-specific cough (other cough) (AC, SLC) |
| barking cough | other abnormal breath sounds |
| bilateral acute conjunctivitis | other pneumonia (AC) |
| bronchiolitis (AC) | paroxysmal cough |
| bronchitis | pharyngitis diagnosis |
| cervical lymphadenopathy | pharyngitis on exam |
| chest pain | poor feeding |
| chest wall retractions | poor antipyretics response |
| chills | productive cough |
| conjunctivitis | rales |
| crackles | reported fever (AC, SLC) |
| croup | respiratory distress (SLC) |
| cyanosis | rhonchi |
| decreased activity | rigor |
| diarrhea | runny nose |
| dyspnea | seizure |
| grunting | sore throat |
| headache | staccato cough |
| hemoptysis | streptococcal pharyngitis |
| highest measured temperature (SLC) | stridor |
| hoarseness | stuffy nose |
| hypoxemia (AC, SLC) | tachypnea (SLC) |
| ill-appearing (AC) | toxic appearance |
| infiltrate | upper respiratory infection |
| influenza-like illness (AC) | viral pneumonia |
| lab order (nasal swab) (AC, SLC) | viral syndrome (AC) |
| lab positive adenovirus | vomiting |
| lab positive enterovirus | weakness or fatigue |
| lab positive hmpv | wheezing |
| lab positive influenza (AC, SLC) | age (AC, SLC) |
| lab positive parainfluenza | respiratory panel ordered (AC, SLC) |
| lab positive rhinovirus | laboratory result available (AC, SLC) |
| lab positive RSV | laboratory positive influenza (AC, SLC) |
| lab positive strep A |
Two site-specific case detection systems were built, one for Allegheny County and one for Salt Lake City. Each case detection system was automatically constructed from training data using a machine learning algorithm that performs feature selection followed by the construction of a Bayesian network using the selected features. Based on this process, the Bayesian network for Allegheny County contains 17 of the original 83 features, and the network for Salt Lake City contains 15. (The selected features are marked in Table 1 with “AC” or “SLC.”) Each case detection system is a Bayesian network that represents the conditional probability distribution of findings and disease state (flu, NI-ILI, or other). This distribution can provide the probability of that patient’s findings given their assumed disease state. That is, P(E(p, d)|flu), P(E(p, d)|NI-ILI), and P(E(p, d)|other) where E(p, d) denotes the findings for patient p on day d. (Note that E(p, d) consists of 17 findings for a patient in Allegheny County and 15 findings for a patient in Salt Lake City due to feature selection.) These likelihoods— P(E(p, d)|flu), P(E(p, d)|NI-ILI), and P(E(p, d)|other) for each patient—are passed to MODS.
Note that MODS does not classify patients as flu, NI-ILI, or other, and does not use simple evidence counts. Rather, it derives likelihoods that represent the extend to which a patient’s findings are more or less likely given flu, NI-ILI, or other. This is in keeping with our Bayesian approach which seeks to build a model that best explains the data.
To summarize, we start with the full text of ED patient care reports. We use NLP to extract 79 features from each report, add four additional pre-coded features (including the result of a laboratory test), to represent each patient as a set of 83 features. We then use a case detection system to produce three likelihoods (P(E(p, d)|flu), P(E(p, d)|NI-ILI), and P(E(p, d)|other)) for each patient. Thus, the dataset given to MODS after preprocessing consists of three likelihoods for each patient. Additional details are provided in Appendix A.
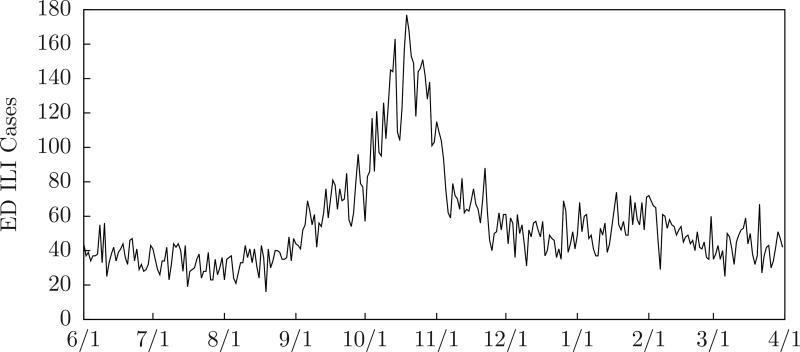
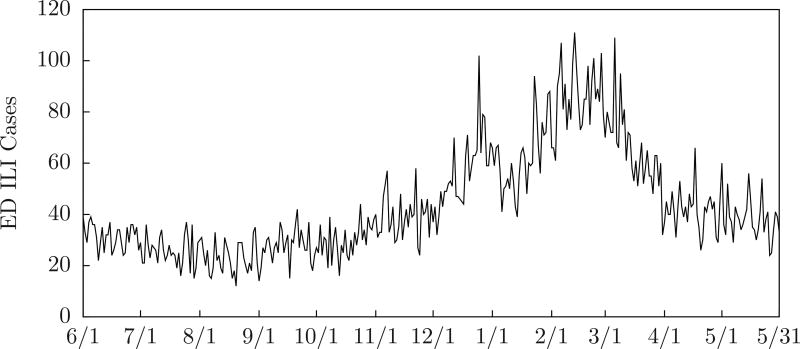
Although MODS does not categorically classify patients, we can count ILI (influenza-like illness) patients by selecting cases with findings that include fever and (cough or sore throat). Although MODS does not use this information, it can provide a convenient way to visualize the data. Figure 2 shows the number of emergency department ILI cases counted in this way for Allegheny County during the 2009–2010 influenza season, and Figure 3 shows the number for Sale Lake City during the 2010–2011 influenza season. We include this plot on graphs in this paper.
Figure 2.
ED ILI cases for Allegheny County 2009–2010 influenza season.
Figure 3.
ED ILI cases for Salt Lake City 2010–2011 influenza season.
2.2. Modeling Outbreaks
An outbreak of influenza is a chain of infections that starts when a few individuals infect the general population, the infection spreads evenly and steadily through the population until the number of infected individuals reaches a peak, then decreases and finally trails off. More generally, an outbreak may be caused by different strains of influenza that are introduced into different demographic groups at different times. That is, multiple chains of infection, each with its own start time.
2.2.1. SEIR Models
A SEIR model [17] divides the population into four compartments: Susceptible individuals who have no immunity to the disease, Exposed and Infected individuals who are not yet contagious, Infectious individuals who have the disease and can transmit it, and Recovered individuals who are immune. When an outbreak begins, every individual is assigned to one compartment and move from compartment to compartment according to difference equations.
A SEIR model is defined by seven parameters. R0 (the Basic Reproduction Number) is the average number of people an infectious person would infect if they were introduced into a population of totally susceptible individuals, Latent Period is the average time from initial contact with an infected person to when a person becomes infectious, and Infectious Period is the average time an individual is infectious and can transmit the disease. Also, Initial Susceptible, Initial Exposed, Initial Infectious, and Initial Recovered are the initial numbers of people assigned to the corresponding compartments on the first day of the outbreak when the population is initially infected.
Given the parameters of a SEIR model, we can compute the number of people in the Susceptible, Exposed and Infected, Infectious, and Recovered compartments each day using a set of difference equations [17].
2.2.2. Modeling Multiple Outbreaks of Influenza
MODS includes three kinds of influenza models corresponding to no outbreak, one chain of infections, and two chains of infections:
A Zero Outbreak Model is defined by b, a baseline level of infectious influenza cases in the general population. We denote the zero outbreak model with 〈b〉.
A Single Outbreak Model is defined by a baseline level of infectious influenza cases in the general population, a start day, and a SEIR model. Given a baseline level of infectious influenza cases b, a start day s, and a vector of SEIR parameters λ̅, we denote the single outbreak model with 〈b, s, λ̅〉. Note that 〈b, s, λ̅〉 has a total of nine parameters: a baseline level of influenza, the start day, and the vector λ̅ of seven SEIR parameters.
A Double Outbreak Model is defined by a baseline level of infectious influenza cases in the general population, a start day and SEIR parameters for the first outbreak, and a start day and SEIR parameters for the second outbreak. Given a baseline level of infectious influenza cases b, a start day s and a vector of SEIR parameters λ̅, and a second start day t and vector of SEIR parameters γ̅, we denote the double outbreak model with 〈b, s, λ̅, t, γ̅〉. Note that 〈b, s, λ̅, t, γ̅〉 has a total of seventeen parameters: the baseline level of infectious influenza cases, two start days, and two vectors of seven SEIR parameters each.
A single outbreak model 〈b, s, λ̅〉 is intended to model the introduction on day s of an infection that spreads according to the SEIR model defined by the parameters λ̅. Likewise, a double outbreak model 〈b, s, λ̅, t, γ̅〉 is intended to model the introduction on day s of an infection that spreads according to the SEIR model defined by the parameters λ̅, and a second infection introduced on day t that spreads according to the SEIR model defined by the parameters γ̅. We often denote an influenza model by ℐ rather than write out 〈b〉, 〈b, s, λ̅〉, or 〈b, s, λ̅, t, γ̅〉.
If ℐ is a zero, single, or double outbreak model of influenza, it determines ℐ(d), the number of infectious influenza cases in the general population on day d, in the following ways:
If ℐ is a zero outbreak model 〈b〉, then ℐ(d) = b is constant.
If ℐ is a single outbreak model 〈b, s, λ̅〉, then ℐ(d) is b plus the number of infectious influenza cases in the general population on day d predicted by the SEIR model λ̅ starting on the start day s.
If ℐ is a double outbreak model 〈b, s, λ̅, t, γ̅〉, then ℐ(d) is b, plus the number of infectious influenza cases in the general population on day d predicted by the SEIR model λ̅ starting on its start day s, plus the number of infectious cases in the general population on day d predicted by the SEIR model γ̅ starting on its start day t.
That is, we compute ℐ(d) by adding b, plus the number of infectious influenza cases predicted by the first SEIR model (if there is one), plus the number of infectious influenza cases predicted by the second SEIR model (if there is one). The number of infectious influenza cases predicted by each SEIR model is the number of cases in its Infectious compartment, which can be computed with a set of difference equations, as mentioned above. Note that we make the simplifying assumption that there is a constant, baseline level of infectious influenza cases (b) in the general population.
2.2.3. Influenza in the General Population and the Emergency Department
MODS searches a space of outbreak models. For each model ℐ considered, ℐ(d) is the number of infectious influenza cases in the general population on day d predicted by the model. However, only a fraction of these cases go to an ED. We rely on the scaling factor θ which is the probability that someone who is infectious with influenza will actually go to a emergency department (ED) on any given day. In general, we do not know θ exactly, so we integrate over a range of values. However, we do assume it is constant for the duration of an outbreak.
2.2.4. Accounting for Non-Influenza Influenza-Like Illness
Clinically, it is difficult or impossible to distinguish influenza from a variety of Influenza-Like Illnesses (ILI). Most kinds of ILI are viral—such as respiratory syncytial virus (RSV) and parainfluenza—but some other diseases and toxic exposures also cause influenza-like symptoms. In most years, influenza is present in only a minority of ILI cases, but may account for 50–60% of ILI cases at the peak of an epidemic [18]. Because some kinds of ILI are contagious and exhibit outbreak activity [17], it is important to distinguish them from true influenza in order to accurately predict and characterize outbreaks of influenza. We rely on the use of laboratory tests, such as the polymerase chain reaction (PCR) test, to distinguish influenza from NI-ILI. Because laboratory tests are ordered for relatively few patients, we have developed a technical approach to calculate 𝒩(d), the expected number of NI-ILI cases in the ED on each day d. The details of our method are described in Appendix B.
2.2.5. Evaluating Models
Let E be all of the evidence available to the system, E(d) the evidence from day d, E(1 : d) the evidence from days 1 through d, and E(p, d) the evidence from patient p on day d. CDS represents the joint probability distribution of findings and diseases, so we can find P(E(p, d)|flu), P(E(p, d)|NI-ILI), P(E(p, d)|other), the probability of a patient’s findings given influenza, NI-ILI, or some other diagnosis (such as appendicitis, trauma, etc.).
We evaluate a model ℐ by how well it explains the data—that is, the probability of the data given ℐ. Since ℐ predicts the number of influenza cases in the population—but the data is drawn from hospitals—θ (the fraction of people infectious with influenza who will go to an ED) plays a role. We do not know θ precisely, but our belief in its value is uniform over an interval [θl, θu]. Thus, given data E(1 : d), we evaluate a model ℐ with:
| (1) |
We also need to account for the effect of NI-ILI on the data. Appendix B shows how to construct a function 𝒩(d) that estimates the number of NI-ILI patients in the ED each day d and shows:
| (2) |
ℐ(d′) is the number of cases of infectious influenza in the general population predicted by the model ℐ on day d′. Section 2.2.2 describes how ℐ(d′) is computed. 𝒩(d′) is the number of NI-ILI patients in the ED given by the model of NI-ILI. If we assume that given ℐ, 𝒩, and θ the probability of each patient’s evidence is independent of the other patients, we have:
| (3) |
Putting all of this together gives:
| (4) |
We estimate the probability that an arbitrary ED patient has influenza as θ · ℐ(d)/|pts(d)| and the probability he has NI-ILI as 𝒩(d)/|pts(d)| (where pts(d) is the number of ED patients on day d), so:
| (5) |
Although Equation 4 is a closed-form equation involving only the variable θ, we have no practical way to integrate it. However, given values for ℐ(d), 𝒩(d) and θ, we can evaluate the expression inside the integral, so we approximate the integral with:
| (6) |
where θ1, …, θn are randomly and uniformly drawn from [θl, θu].
2.3. Detection and Characterization
2.3.1. Detecting Outbreaks
Let Z, S, and D be the propositions that zero, one (single), or two (double) outbreaks of influenza will occur during the year (365 days starting from day 1). Let Zd, Sd, and Dd be the propositions that zero, one, or two outbreaks of influenza start on or before day d. We want to find P(Zd|E(1 : d)), P(Sd|E(1 : d)), and P(Dd|E(1 : d)). That is, the probability that zero, one, or two influenza outbreaks have already begun given the evidence so far. Using Bayes Rule we obtain:
| (7) |
| (8) |
| (9) |
where P(E(1 : d)) is the standard normalizing term.
First, we will derive P(Zd), P(Sd), and P(Dd). Zd claims that no outbreak will start on or before day d, but zero, one, or two may start later. If f(s) is the probability that an outbreak will start on day s, then:
| (10) |
| (11) |
The first term expresses the fact that the probability that no outbreaks start on or before day d given no outbreaks start at all is one. The second term expresses the fact that the probability that no outbreaks start on or before day d given one outbreak will occur during the year is the probability that outbreak begins after day d. The third term expresses the fact that the probability that no outbreaks start on or before day d given two outbreaks will occur during the year is the probability that both outbreaks begin after day d.
Dd claims that two outbreaks of influenza start on or before day d. This logically rules out Z and S. Since there are exactly two outbreaks and both begin on or before day d we have:
| (12) |
| (13) |
Finally, by simple probability theory, we know P(Sd) = 1 − (P(Zd) + P(Dd)).
We introduce some notation that we will need here and in the next section. Given a baseline level of influenza b, there is exactly one zero-outbreak model, which we denote by 〈b〉. A baseline level of influenza b, a start day s, and SEIR model parameters λ̅ specify a one-outbreak model, which we denote by 〈b, s, λ̅〉. A baseline level of influenza b, start days s and t, and SEIR model parameters λ̅ and γ̅ specify a two-outbreak model, which we denote by 〈b, s, λ̅, t, γ̅〉.
Now, we will derive P(E(1 : d)|Zd), P(E(1 : d)|Sd), and P(E(1 : d)|Dd). We assume that the baseline level of influenza b is fixed. There is only one zero-outbreak model 〈b〉 so P(E(1 : d)|Zd) = P(E(1 : d)|〈b〉). For each start day d, we need to integrate over a continuum of one-outbreak outbreak models:
| (14) |
Likewise, we need to integrate over two-outbreak models to obtain:
| (15) |
In these equations, p(·) is a probability density function over SEIR model parameters. Note that we assume the double outbreak start dates are independent of one another, although this assumption can be relaxed.
If we assume that start days and SEIR model parameters are uniformly distributed over their ranges, we can estimate the integrals in Equations 14 and 15 as follows:
| (16) |
| (17) |
where N is a large integer to determine enough points to estimate the integral, and the λ̅n and γ̅n are randomly and uniformly selected from their ranges.
These two equations perform model averaging. Consider Equation 16 to estimate the probability of E(1 : d) given the assumption of one outbreak. For each possible start day, it randomly selects N single-outbreak models and computes the posterior probability of the evidence for each of those models and averages their predictions. We perform similar operations for zero and two outbreaks and combine the results using Equations 7, 8, and 9 to find the probability of zero, one, or two outbreaks given E(1 : d).
2.3.2. Characterizing Outbreaks
Given evidence E(1 : d), MODS predicts zero, one, or two outbreaks have started by day d depending on whether P(Zd|E(1 : d)), P(Sd|E(1 : d)), or P(Dd|E(1 : d)) (derived in the previous section) is greatest.
We also want to know the expected number of influenza cases on day d′ given E(1 : d). In general, d′ > d since we want to project into the future beyond the evidence we have already collected. (We can have d′ ≤ d, however, if we want to assess what has happened to date.) If flu(d′) is the number of influenza cases on day d′, then:
| (18) |
That is, we can find the expected number of influenza cases predicted by the zero-outbreak model, one-outbreak models, and two-outbreak models separately and combine them in a weighted sum.
We already know how to compute P(Zd|E(1 : d)), P(Sd|E(1 : d)), and P(Dd|E(1 : d)). The other terms can be expanded as follows:
| (19) |
| (20) |
| (21) |
where 〈b〉(d), 〈b, s, λ̅〉(d) and 〈b, s, λ̅, t, γ̅〉(d) are the number of influenza cases predicted by each of the models on day d. Of course, 〈b〉(d) = b is a constant function.
Finally, if we apply Bayes’ rule, assume all start days are equally likely, assume the density functions are uniform, then we can approximate the integrals in Equations 20 and 21 with:
| (22) |
| (23) |
where the λ̅n λ̅m, γ̅n, and γ̅m are randomly and uniformly selected.
Again, these equations perform model averaging. Consider Equation 22 to estimate the number of infectious on day d given E(1 : d) and the assumption of one outbreak. For each possible start day s ≤ d it randomly selects N single-outbreak models. For each of these models, it computes the number of infectious people predicted by the model times the probability of the model, then it computes the expected number of infectious on day d over these models that start on day s. The outer sum computes the expected number of infectious on day d over all the possible start days. We perform similar operations for zero and two outbreaks and combine the results using Equation 18 to find the expected number of infectious.
2.4. Algorithmic Methods
2.4.1. Prior Probabilities and Parameters
Population is the number of people in the region being monitored. S, E, and I are the initial values of Susceptible, Exposed, and Infectious. Latent Period and Infectious Period are expressed in terms of days. We set the prior probabilities for zero, one, or two outbreaks in the next year to be 0.1, 0.8, and 0.1, respectively. To generate a SEIR model of influenza we randomly and uniformly select parameters from Table 2. We also eliminate models with duration more than 180 days.
Table 2.
SEIR parameter ranges.
| Parameter | Minimum Value | Maximum Value |
|---|---|---|
| S | 0.5 * population | 1.0 * population |
| E | 0 | 0 |
| I | 1 | 100 |
| R0 | 1.1 | 3.0 |
| Latent Period | 1 | 4 |
| Infectious Period | 1 | 8 |
2.4.2. Implementation
We now descibe the overall operation of MODS. Given evidence E(1 : d) for days 1 through d, MODS creates the baseline model, 10, 000 single-outbreak models with start day on or before day d, and 10, 000 double-outbreak models with start days on or before day d. MODS then computes the probability of E(1 : d) given each of these models. It then computes the posterior probability of zero, one, or two outbreaks given E(1 : d). It uses the same models to compute the expected number of infectious on each day through the rest of the year. Note that models are evaluated using evidence from on or before day d to find their probabilities given E(1 : d). The models are then projected into the future and their predictions combined according to how well they performed on evidence in the past. The complexity and runtime of MODS are described in Appendix C.
3. Results
3.1. Experiments with Real Outbreaks
We applied MODS to clinical data from patient care reports in Allegheny County, Pennsylvania during the 2009–2010 influenza year and reports from Salt Lake City, Utah during the 2010–2011 influenza year. The ED data we monitor capture about 62% of patients in Allegheny County and 55% of patients in Salt Lake City. We estimated that approximately 1% of people infectious with influenza in the general population will visit an ED [4]. Baseline levels of influenza, NI-ILI, and other diseases were estimated from the summer months when there were no outbreaks.
We evaluated MODS’ predictions both locally and regionally. Locally, we compared MODS’ predictions to a seven day central moving average of the daily number of positive PCR tests in the monitored ED’s. We will refer to the peak day of this moving average as the “local peak.” Regionally, we compared MODS’ predictions to the weekly totals of laboratory confirmed cases of influenza reported by the CDC’s FluView system [19] for HHS Region 3 which includes Pennsylvania and HHS Region 8 which includes Utah.1 We will refer to the Wednesday of a week with a maximum number of confirmed cases as the “regional peak.” (We selected a specific day of the week in order to compare the local and regional peaks.)
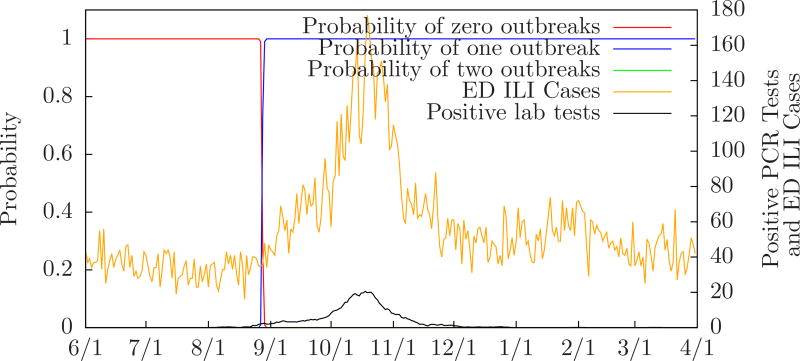
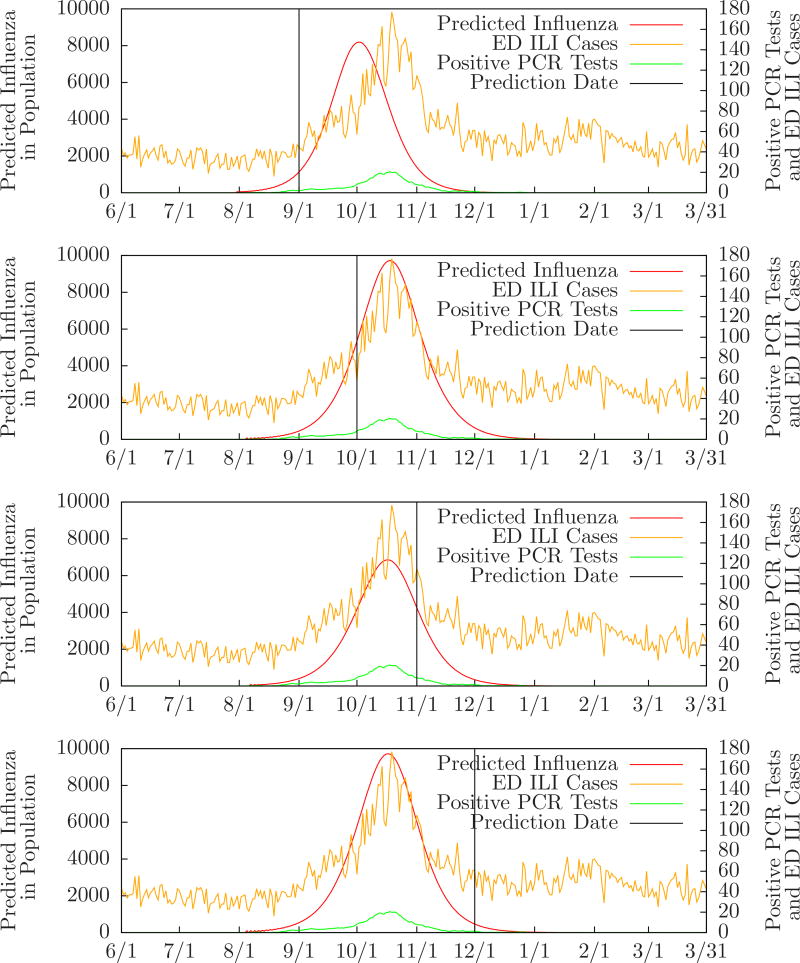
Figure 4 shows the probability of zero, one, or two outbreaks compared to the number of positive PCR tests performed in the monitored ED’s, and the expected number of influenza cases, for Allegheny County from June 1, 2009 to March 31, 2010. Table 3 compares MODS’ predictions to the local and regional peaks for Allegheny County during the same period. For instance, the row labeled “10/1/2009” means that on October 1 MODS predicted one influenza outbreak with a predicted peak three days after the local peak and one day after the regional peak. (There was a single local peak on October 18 and a single regional peak on October 20. These are essentially identical since the regional dates have only one week of precision.) Figure 5 shows MODS’ predictions on September 1, October 1, November 1, and December 1 with local PCR counts for comparison.
Figure 4.
Probability of zero, one, or two outbreaks for Allegheny County 2009–2010 influenza season.
Table 3.
Predictions for Allegheny County and HHS Region 3 2009–2010 season.
| Date | Predicted Number of Outbreaks |
Local Peak Offset | Regional Peak Offset |
|---|---|---|---|
| 8/1/2009 | zero | ||
| 9/1/2009 | one | −13 | −15 |
| 10/1/2009 | one | +3 | +1 |
| 11/1/2009 | one | +2 | 0 |
| 12/1/2009 | one | +2 | 0 |
| 1/1/2010 | one | +5 | +3 |
| 2/1/2010 | one | +4 | +2 |
| 3/1/2010 | one | 0 | −2 |
| 3/31/2010 | one | +6 | +4 |
Figure 5.
Evolution of predictions for Allegheny County 2009–2010 influenza season.
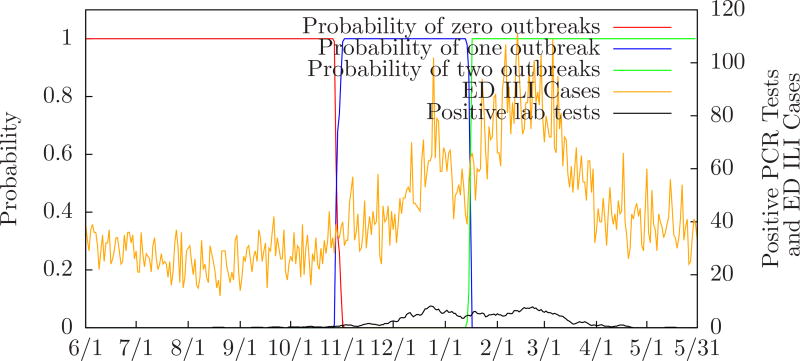
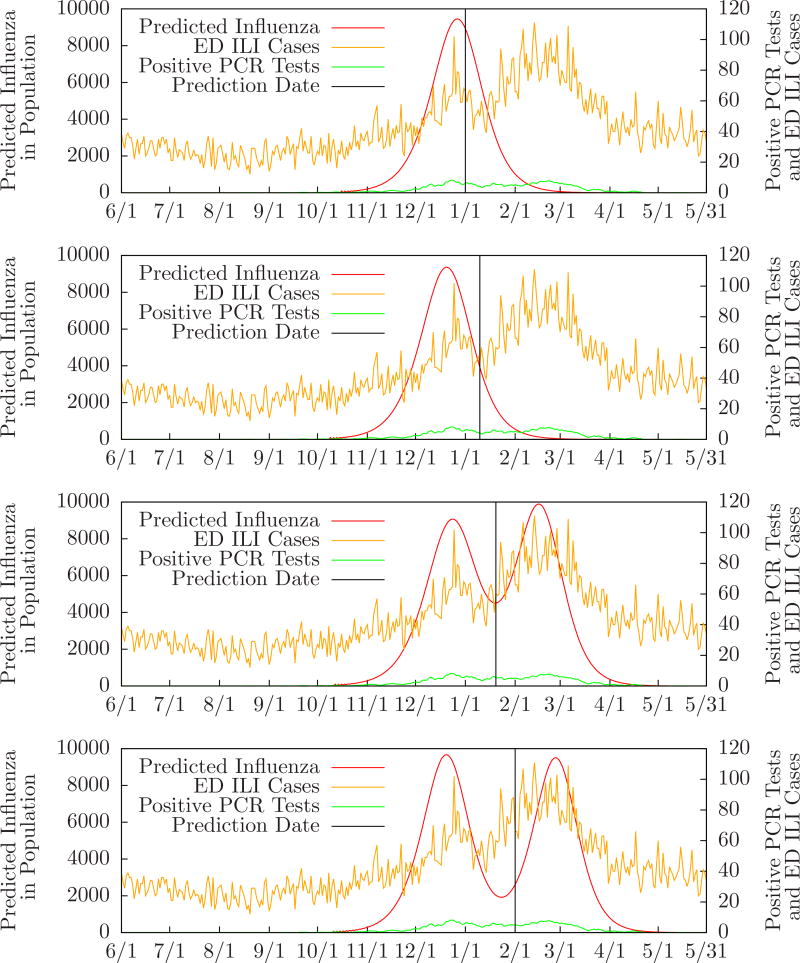
Figure 6 shows the probability of zero, one, or two outbreaks compared to the number of positive PCR tests performed in the monitored ED’s for Salt Lake City from June 1, 2010 to May 31, 2011. Table 4 compares MODS’ predictions to the local and regional peaks for Salt Lake City during the same period. For instance, the row labeled “2/1/2011” means that on February 1 MODS predicted two influenza outbreaks. The first predicted peak was two days before the first local peak and the second predicted peak seven days after the second local peak. Also, the first predicted peak was five days before the first regional peak and the second predicted peak four days after the second regional peak. (There were two local peaks on December 25, 2010 and February 19. 2011, and two regional peaks on December 28, 2010 and February 22, 2011. These are essentially identical since the regional dates have only one week of precision.) Figure 7 shows how MODS’ predictions evolve during the month of January when it first detects a second outbreak.
Figure 6.
Probability of zero, one, or two outbreaks for Salt Lake City 2010–2011 influenza season.
Table 4.
Predictions for Salt Lake City 2010–2011 season.
| Date | Predicted Number of Outbreaks |
First Local Peak Offset |
Second Local Peak Offset |
First Regional Peak Offset |
Second Regional Peak Offset |
|---|---|---|---|---|---|
| 8/1/2010 | zero | ||||
| 9/1/2010 | zero | ||||
| 10/1/2010 | zero | ||||
| 11/1/2010 | one | −17 | −20 | ||
| 12/1/2010 | one | −8 | −11 | ||
| 1/1/2011 | one | +6 | +3 | ||
| 1/10/2011 | one | −2 | −5 | ||
| 1/20/2011 | two | −6 | −3 | −9 | −6 |
| 2/1/2011 | two | −2 | +7 | −5 | +4 |
| 3/1/2011 | two | −4 | +2 | −7 | −1 |
| 4/1/2011 | two | +3 | +12 | 0 | +9 |
| 5/1/2011 | two | +6 | +1 | +3 | −2 |
| 5/31/2011 | two | +6 | +7 | +3 | +4 |
Figure 7.
Evolution of predictions for Salt Lake City 2010–2011 influenza season.
3.2. Experiments with Synthetic Outbreaks
Simulated outbreaks were generated by instantiating models of influenza outbreaks in the population with data from actual patient cases. To populate these simulated datasets we relied on the results of the polymerase chain reaction (PCR) test, a definitive indicator of influenza, to create three sets of patients:
Influenza patients with a positive PCR test. Patients for this set were selected based on a positive PCR test result, but that test result was not included in the findings or computation of the likelihood.
NI-ILI patients with a high probability of ILI but a negative PCR test. Again, patients for this set were selected based on the negative PCR test result, but that test result was not included in the findings or computation of the likelihood.
Other patients from summer months with a low probability of ILI and no PCR test ordered.
Note that some patients in the Influenza set have a higher likelihood of NI-ILI and some patients in the NI-ILI set have a higher likelihood of influenza since the only definitive piece of information (the result of the PCR test) has been excluded. This reflects the fact that influenza and NI-ILI patients can have similar presentations.
We instantiate a model by assuming that each infectious case of influenza in the model goes to an ED with probability 0.01 (based on our estimate that 1% of the population with influenza will visit an ED). Thus, for each infectious case of influenza in the model we add a random element of Influenza to the test data with probability 0.01. Likewise, we assume that each day there are 10, 000 NI-ILI cases and 50, 000 other cases, each of whom go to a monitored ED with probability 0.01. Thus, for each of these cases we add a random element of NI-ILI or Other to the test data with probability 0.01. For instance, if a model predicts 1, 000 infectious influenza cases on day d, then the instantiation will contain approximately 10 Influenza, approximately 100 NI-ILI, and approximately 500 Other cases for day d as determined by binomial distributions.
Thus, these simulated outbreaks are simulated in the sense that the set of cases with influenza was determined by a model, but real in the sense that each patient case used real data from a confirmed case of influenza.
Table 5 summarizes the performance of MODS on 100 randomly generated single-outbreak datasets. We generated 100 single-outbreak models by randomly and uniformly selecting parameters from Table 2, instantiated each model as described above, and ran MODS on each one for each day from the start of the outbreak to its peak. The row starting with “0.100” represents the performance of MODS on the day when 0.100 of the total outbreak cases have occurred. This day will vary since the outbreaks were randomly generated, but the average number of days to the peak was 18, the average probability an outbreak was occurring was 1.00, and the mean error of estimating the peak was +10 (ten days after the actual peak).
Table 5.
Results of evaluation on 100 simulated single outbreaks.
| Fraction of Outbreak Cases That Have Occurred |
Mean Number of Days Until Peak |
Mean Posterior Probability an Outbreak is Occurring |
Mean Error of Estimating Peak Day |
|---|---|---|---|
| 0.001 | 55 | 0.09 | −146 |
| 0.010 | 38 | 0.93 | 0 |
| 0.100 | 18 | 1.00 | +10 |
| 0.250 | 9 | 1.00 | +8 |
| 0.500 | 0 | 1.00 | +6 |
To understand MODS’ ability to recognize a second peak we conducted a set of experiments with two identical outbreaks with peaks that ranged from 5 to 65 days apart. Table 6 summarizes the results of these experiments. For instance, column 35 says that for a synthetic double outbreak with peaks 35 days apart, MODS began to predict with probability ≥ 0.50 a second future peak 0.56 of the distance from the first peak to the second (about twenty days after the first peak and fifteen days before the second peak). MODS was unable to distinguish peaks only five days apart.
Table 6.
Discriminating one or two outbreaks.
| Days Between Peaks | 5 | 15 | 25 | 35 | 45 | 55 | 65 |
| Tipping Point | - | 1.00 | 0.66 | 0.56 | 0.56 | 0.54 | 0.55 |
3.3. IRB Approval
The research protocol was approved by both institutional IRBs (University of Pittsburgh PRO08030129 and Intermountain Healthcare 1024664). All the research patient data were de-identified.
4. Discussion
4.1. Experimental Results
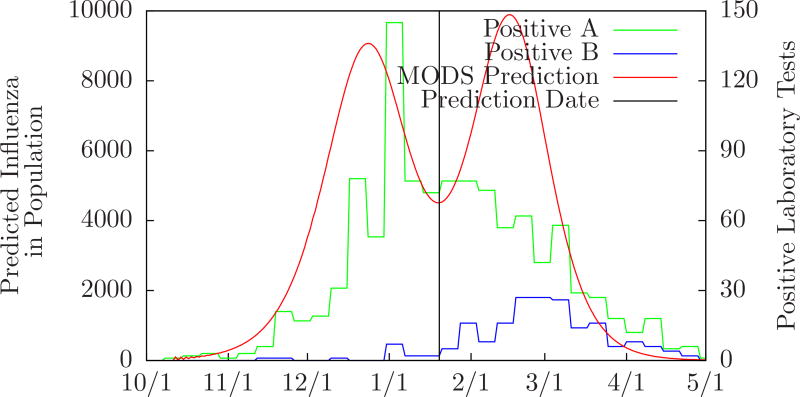
Tables 5 and 6 demonstrate how well MODS was able to predict actual single and double outbreaks. MODS’ ability to predict single influenza outbreaks is consistent with our prior work [4]. The double peak predicted by MODS from the Salt Lake City 2010–2011 data is intriguing. The Utah Public Health Laboratory tracks positive influenza laboratory tests broken down by type. Positive influenza A tests peaked around January 1 and positive influenza B tests peaked around February 26 [20]. These dates are close to the peaks predicted by MODS as shown in Figure 8. This is noteworthy given that MODS did not have test information that distinguished A from B, but was able to recognize separate A and B outbreaks.
Figure 8.
Comparison of MODS’ prediction on January 20 to positive influenza A and B laboratory tests in Salt Lake City 2010–2011. (Data from Utah’s Unified State Laboratory: Public Health.)
4.2. Limitations
The work reported here has several limitations. These stem from our basic assumptions, our use of SEIR models, and computational limitations.
We assume there is a constant, baseline number of influenza cases, b, in the general population throughout the year. We derive this number using data from summer months. However, the baseline varies daily and throughout the year. We could avoid this assumption by integrating over the range of values of b in Equations 14 and 15 each day. However, we do not believe this will affect the results since the baseline level is very small compared to outbreak levels.
We assume that the basic context of an outbreak remains fixed for its duration. However, in reality, weather and humidity, immunization programs, and shifting populations can affect how an outbreak proceeds [21]. These concerns can be addressed by allowing the basic parameters of models to change over time. We also assume that θ (the probability that a person in the general population who has influenza will go to an ED) is constant throughout the outbreak. In fact, it can change daily based on several factors, such as media reports. We can address this by integrating over a range of values for θ each day in Equation 4 instead of just once over the entire outbreak period (essentially by moving the integral to after the daily product). However, we would want to model some dependency in θ from one day to the next.
We rely on the mass action principle that any two individuals in the population are equally likely to come in contact with each other. Although this is a common simplifying assumption, it ignores the fact that children are more likely to contact other children in the classroom and adults are more likely to contact adults at work. We can address this assumption by using stratified models [17] that maintain separate compartments for different demographic groups. More generally, since our framework only relies on specifying a model of influenza by a set of numeric parameters, we can explore different kinds of models (including stochastic models) that better capture the dynamics of actual outbreaks.
Although the theory described above can be extended to any number of outbreaks, we have limited MODS to only two, primarily due to computational limitations. Although the two-outbreak restriction is sufficient to model the type A and type B waves of influenza that often occur, it ignores more complicated situations with multiple introductions of single or multiple strains. The size of the search space grows exponentially with the number of outbreaks considered. The simple Monte Carlo algorithm used here is unlikely to scale to the larger, more complex search space (although we might be able to handle three outbreaks by using a high-performance computer and switching to SIR models to eliminate some variables). Properly addressing this will require more sophisticated search algorithms.
4.3. Further Work
The approach to outbreak detection and characterization described in this paper is flexible. We will briefly describe several possible extensions.
Incorporating Different Sources of Data
Emergency department patient care reports are a rich source of information about outbreaks in the general population, but they are limited. Only a small fraction of people with influenza seek care in an emergency department, the hospitals we monitor are urban and suburban so many rural areas are invisible to us, and different demographic groups may seek ED care at different rates, skewing our data. Although no single source of data is without limitations or bias, we can correct for some of their individual shortcomings by combining them. The Bayesian framework described here provides a principled way to do this. Suppose that our evidence consists of two sets of data, E1 and E2. For instance, E1 may be emergency department reports and E2 may be daily counts of internet searches related to influenza [9]. If we assume that E1 and E2 are independent given the level of ILI in the population, we have P(E1E2|ℐ,𝒩) = P(E1|ℐ,𝒩)P(E2|ℐ,𝒩). The first term can be evaluated using Equation 4. The second term can be evaluated similarly if we know how many people with ILI will search for information about influenza on the internet each day. We can get a first-order approximation to that quantity by relying on previous serological studies to determine the total number of people affected by influenza during one season [22] and internet search records to determine the number of influenza-related searches during an outbreak and non-outbreak periods.
Modeling Influenza A and B Separately
MODS first detected a second outbreak in the Salt Lake City 2010–2011 data on January 20. However, positive influenza B laboratory tests began to appear much earlier. MODS can be extended to recognize the second outbreak much sooner than it did. CDS can model influenza A and B as separate diseases. The presence of a subtyped laboratory test can distinguish A or B definitively and clinical presentation can also help distinguish them [23]. Given separate likelihoods for influenza A and B, MODS can model them as separate outbreaks. With these changes, we believe that MODS will be able to recognize the second outbreak much sooner than it did.
Efficient Computational Methods
The theory described here can be extended to any number of outbreaks. However, building a practical system that can model complex multiple outbreaks will require more sophisticated algorithms.
Robust Prediction of the Effect of an Intervention
MODS does not select a single most likely model and base its predictions on it. Rather, it entertains a set of plausible models, assigns a probability to each of them, then computes the expected trajectory of an outbreak based on a combination of the probabilities and predictions of all of the models. It is noncommittal. However, when public health officials are faced with an outbreak they often commit to a model they believe best describes the outbreak and design an intervention based on it [11, 12, 24, 25]. This is fraught with danger since they must make a decision with huge public health, economic, and political risk based on limited evidence early in an outbreak [2]. We propose a different approach: instead of picking a single outbreak model, use all of the models, project the effect of an intervention against each model in the set, and predict the interventions’ efficacy with the expected outcome based on the models’ probabilities that were computed before the intervention.
5. Conclusions
We described a framework for the detection and characterization of multiple, overlapping outbreaks of influenza from ED patient care reports. We also described the implementation and evaluation of a system capable of detecting and characterizing two overlapping outbreaks. We believe that the results reported here show that the approach we describe is sufficient to detect and characterize overlapping outbreaks. Further work will includes investigating more sophisticated models of multiple outbreaks, data that can distinguish separate outbreaks, and more efficient computational methods.
Highlights.
We describe a system to model and predict multiple overlapping outbreaks of influenza.
Clinical findings are extracted from patient-care reports using natural language processing.
These findings are analyzed by a case detection system to create disease likelihoods that are passed to a multiple outbreak detection system.
We evaluated the system using real and simulated outbreaks. The results show that this approach can recognize and characterize overlapping outbreaks of influenza.
Acknowledgments
This work was supported by NIH grant R01 LM011370 on Probabilistic Disease Surveillance. John Aronis was supported by the National Library of Medicine Training Grant T15LM007059 to the University of Pittsburgh. Part of this work was done on the Olympus High Performance Compute Cluster located at the Pittsburgh Supercomputing Center at Carnegie Mellon University, which is supported by National Institute of General Medical Sciences Modeling Infectious Disease Agent Study (MIDAS) Informatics Services Group grant 1U24GM110707.
Appendix A
CDS
The data consist of the full text of emergency department patient care reports collected at two sites: the University of Pittsburgh Medical Center in Allegheny County (AC), Pennsylvania and Intermountain Healthcare in Salt Lake City (SLC), Utah. There are approximately 300–600 patient care reports each day at each site. A patient care report may consist of the union of several separate documents filed during the patient’s stay in the ED or shortly thereafter. We ignore administrative delays and assume the entire set of documents is available when the patient is discharged from the ED.
Each report is processed by a site-specific parser to extract a set of 79 findings that were identified by expert clinicians as potentially relevant to influenza like illness. The parsers are implemented using Topaz 2.0 [5] and apply pattern-matching and deduction rules to extract clinical findings. The input to each parser is a patient care report. The output is a set of clinical findings. Findings that are not found and extracted from the text are given the value “M” for missing. After the text of the report has been processed, the patient’s age and three laboratory results are added to the set of findings, for a total of 83 findings. (See Table 1.)
Two site-specific case detection systems were created for AC and SLC using the following procedure at each site [26]. Training datasets were created at each site using ED encounters between January 1, 2008 and May 31, 2010. Cases with a positive influenza lab test were labeled flu, cases with a negative influenza lab test were labeled NI-ILI, and other cases were labeled other. Features were selected based on information gain. Then, a Bayesian network (CDS) was constructed for each site using the K2 algorithm [27]. Thus, each CDS is a Bayesian network that represents the conditional probability distribution of the findings and disease state (influenza, NI-ILI, or other). Given the findings of a particular patient, E(p, d), the appropriate CDS (AC or SLC) can produce likelihoods P(E(p, d)|flu), P(E(p, d)|NI-ILI), and P(E(p, d)|other). That is, the likelihood of that patient’s findings given they have influenza, non-influenza influenza-like illness (NI-ILI), or some other condition (such as appendicitis, trauma, etc.). MODS uses these likelihoods to evaluate models.
Table 1 shows the 79 features parsed from the text of patient care reports, plus age and the added laboratory variables. The annotation “AC” means that the feature was used in the CDS for Allegheny County, and the annotation “SLC” means that the feature was used in the CDS for Salt Lake City.
Appendix B
Modeling NI-ILI
We model NI-ILI with a Bayesian time-series. On the first day, we start with a prior probability distribution over the fraction of ED patients with NI-ILI P(NI-ILI1 = x) for x = 0.00, 0.01, 0.02, …, 1.00. (For instance, P(NI-ILI1 = 0.20) is the probability that 20% of the ED patients on day 1 have NI-ILI.) Each day, d, we update our probability distribution for NI-ILI with the available lab results using the following equation:
| (B.1) |
where ⊕d and ⊖d are the number of positive and negative tests on day d. It is likely that clinicians are more or less likely to order a lab test for a given patient as an outbreak progresses, so we simply assume that the relative rate of lab tests given influenza or NI-ILI, P(lab ordered|flu)/P(lab ordered|NI-ILI), is a constant c. Estimating the number of influenza patients in the ED with θ · ℐ(d), we have (by the binomial theorem):
| (B.2) |
That is, P(⊕d, ⊖d|NI-ILId = x) is the probability that ⊕d of the lab tests ‘hit’ influenza patients and ⊖d of the lab tests ‘hit’ NI-ILI patients. Then, each day we update our beliefs by P(NI-ILId+1 = x) = P(NI-ILId = x|⊕d, ⊖d). Finally, we define 𝒩(d) to be the expected number of NI-ILI patients in the ED on day d:
| (B.3) |
Note that 𝒩 is computed day-by-day, updating our beliefs each day using only laboratory tests from the previous day and earlier, so 𝒩(d) depends only on E(1 : d − 1).
Given data E(1 : d), we need P(E(1 : d)|ℐ, θ) to evaluate a model ℐ, where θ is the fraction of infectious influenza cases we expect to go to an ED on any given day. We can expand this as follows:
| (B.4) (B.5) |
However, each day d E(d) does not depend on all of the evidence from previous days or the entire model ℐ, but only 𝒩(d) and ℐ(d), so we have:
| (B.6) |
Appendix C
Complexity and Runtime
The overall operation of MODS is to generate a model of influenza, create its corresponding model of NI-ILI, and evaluate the pair against the data. Then, repeat this for several thousand models. After the models have been created and evaluated, the expected number of infectious cases each day is computed. To generate a model of influenza, MODS randomly and uniformly selects parameters from the ranges in Table 2. A model can then be generated in O(D) time where D is the number of days in the dataset being analyzed. Generating NI-ILI models requires a preprocessing step to count the number of positive and negative lab tests each day. This is done once in time O(DP), where P is the average number of patients per day. For each model of influenza, creating its corresponding NI-ILI model requires us to evaluate Equation B.1 for each day and each value of n. This can be done in time O(Dcnct) where cn is the number of values of n and ct is the average number of lab tests administered each day. Finally, we compute 𝒩(d) from Equation B.3 in time O(D). Thus, generating M influenza/NI-ILI models takes time O(DP + M (D + Dcnct)). We can evaluate an influenza/NI-ILI model in time O(cθDP), where cθ is the number of discrete values of θ and P is the average number of patients per day, by implementing Equation 6 in the obvious way. We speed this up by precomputing and cacheing values of P(E(d)|i, n) where i and n are discretized fractions of ED patients with influenza or NI-ILI. If cd is the number of discrete values we can precompute the cache in time then evaluate each model in time O(D). Thus, scoring M models takes time. After all the models have been created and evaluated we update the expected number of influenza cases in time O(MD) for M models. Putting all of this together, a single run of MODS takes Typically, D is 365, P is about 500, cd is 400, M is about 100,000, cθ is three to five, cn is 100, ct is about 100. Creating the caches for the Allegheny County and Salt Lake City takes about six hours for each dataset, and running MODS takes about four hours on each dataset, when run on a single 1.6GHz processor. The synthetic experiments were run on a high-performance cluster of 64 2.3GHz processors with shared memory. It took about twelve hours to create and analyze 100 simulated single outbreaks, and about five hours to create and analyze 60 simulated double outbreaks.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Region 3 is composed of Delaware, District of Columbia, Maryland, Pennsylvania, Virginia, and West Virginia. Region 8 is composed of Colorado, Montana, North Dakota, South Dakota, Utah, and Wyoming.
References
- 1.World Health Organization. Influenza fact sheet. 2003
- 2.Lipsitch Marc, Riley Steven, Cauchemez Simon, Ghani Azra C, Ferguson Neil M. Managing and reducing uncertainty in an emerging influenza pandemic. New England Journal of Medicine. 2009;361(2):112–115. doi: 10.1056/NEJMp0904380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wagner Michael, Tsui Fuchiang, Cooper Gregory, Espino Jeremy, Harkema Hendrik, Levander John, Villamarin Ricardo, Voorhees Ronald, Millett Nicholas, Keane Christopher. Probabilistic, decision-theoretic disease surveillance and control. Online Journal of Public Health Informatics. 2011;3(3) doi: 10.5210/ojphi.v3i3.3798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cooper Gregory F, Villamarin Ricardo, Rich Tsui Fu-Chiang, Millett Nicholas, Espino Jeremy U, Wagner Michael M. A method for detecting and characterizing outbreaks of infectious disease from clinical reports. Journal of Biomedical Informatics. 2015;53:15–26. doi: 10.1016/j.jbi.2014.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tsui Fuchiang, Wagner Michael, Cooper Gregory, Que Jialan, Harkema Hendrik, Dowling John, Sriburadej Thomsun, Li Qi, Espino Jeremy, Voorhees Ronald. Probabilistic case detection for disease surveillance using data in electronic medical records. Online Journal of Public Health Informatics. 2011;3(3) doi: 10.5210/ojphi.v3i3.3793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Viboud Cécile, Boëlle Pierre-Yves, Carrat Fabrice, Valleron Alain-Jacques, Flahault Antoine. Prediction of the spread of influenza epidemics by the method of analogues. American Journal of Epidemiology. 2003;158(10):996–1006. doi: 10.1093/aje/kwg239. [DOI] [PubMed] [Google Scholar]
- 7.Ong Jimmy Boon Som, Mark I, Chen Cheng, Cook Alex R, Lee Huey Chyi, Lee Vernon J, Lin Raymond Tzer Pin, Tambyah Paul Ananth, Goh Lee Gan. Real-time epidemic monitoring and forecasting of H1N1-2009 using influenza-like illness from general practice and family doctor clinics in Singapore. PloS One. 2010;5(4) doi: 10.1371/journal.pone.0010036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shaman Jeffrey, Karspeck Alicia. Forecasting seasonal outbreaks of influenza. Proceedings of the National Academy of Sciences. 2012;109(50):20425–20430. doi: 10.1073/pnas.1208772109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ginsberg Jeremy, Mohebbi Matthew H, Patel Rajan S, Brammer Lynnette, Smolinski Mark S, Brilliant Larry. Detecting influenza epidemics using search engine query data. Nature. 2009;457(7232):1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- 10.Hall IM, Gani R, Hughes HE, Leach S. Real-time epidemic forecasting for pandemic influenza. Epidemiology and Infection. 2007;135(3):372–385. doi: 10.1017/S0950268806007084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Greenhalgh David. Control of an epidemic spreading in a heterogeneously mixing population. Mathematical Biosciences. 1986;80(1):23–45. [Google Scholar]
- 12.Handel Andreas, Longini Ira M, Antia Rustom. What is the best control strategy for multiple infectious disease outbreaks? Proceedings of the Royal Society of London B: Biological Sciences. 2007;274(1611):833–837. doi: 10.1098/rspb.2006.0015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mills Christina E, Robins James M, Bergstrom Carl T, Lipsitch Marc. Pandemic influenza: Risk of multiple introductions and the need to prepare for them. PLoS Med. 2006;3(6) doi: 10.1371/journal.pmed.0030135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Prosper Olivia, Saucedo Omar, Thompson Doria, Torres-Garcia Griselle, Wang Xiaohong, Castillo-Chavez Carlos. Modeling control strategies for concurrent epidemics of seasonal and pandemic H1N1 influenza. Mathematical Biosciences and Engineering. 2011;8(1):141–170. doi: 10.3934/mbe.2011.8.141. [DOI] [PubMed] [Google Scholar]
- 15.Centers for Disease Control and Prevention. Considerations for distinguishing influenza-like illness from inhalational anthrax. 2001 doi: 10.1001/jama.286.20.2537-jwr1128-2-1. [DOI] [PubMed] [Google Scholar]
- 16.Elkin PL, Froehling DA, Wahner-Roedler DL, Brown SH, Bailey KR. Comparison of natural language processing biosurveillance methods for identifying influenza from encounter notes. Annals of Internal Medicine. 2012;156 doi: 10.7326/0003-4819-156-1-201201030-00003. [DOI] [PubMed] [Google Scholar]
- 17.Vynnycky Emilia, White Richard. An Introduction to Infectious Disease Modelling. Oxford University Press; 2010. [Google Scholar]
- 18.Centers for Disease Control and Prevention. Flu activity and surveillance. 2016 [Google Scholar]
- 19.Centers for Disease Control and Prevention. FluView Interactive. 2016 [Google Scholar]
- 20.Utah Department of Health. Utah MMWR week 20 of 2011. 2011 [Google Scholar]
- 21.Shaman Jeffrey, Pitzer Virginia E, Viboud Cécile, Grenfell Bryan T, Lipsitch Marc. Absolute humidity and the seasonal onset of influenza in the continental United States. PLoS Biology. 2010;8(2) doi: 10.1371/journal.pbio.1000316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Reed Carrie, Katz Jacqueline M, Hancock Kathy, Balish Amanda, Fry Alicia M. Prevalence of seropositivity to pandemic influenza A/H1N1 virus in the United States following the 2009 pandemic. PloS One. 2012;7(10) doi: 10.1371/journal.pone.0048187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kaji Masahide, Watanabe Aya, Aizawa Hisamichi. Differences in clinical features between influenza A H1N1, A H3N2, and B in adult patients. Respirology. 2003;8(2):231–233. doi: 10.1046/j.1440-1843.2003.00457.x. [DOI] [PubMed] [Google Scholar]
- 24.Gani Raymond, Hughes Helen, Fleming Douglas, Griffin Thomas, Medlock Jolyon, Leach Steve. Potential impact of antiviral drug use during influenza pandemic. Emerging Infectious Diseases. 2005;11(9):1355–1362. doi: 10.3201/eid1109.041344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Longini Ira M, Nizam Azhar, Xu Shufu, Ungchusak Kumnuan, Hanshaoworakul Wanna, Cummings Derek AT, Halloran M Elizabeth. Containing pandemic influenza at the source. Science. 2005;309(5737):1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
- 26.Ye Ye, Wagner Michael M, Cooper Gregory F, Ferraro Jeffrey P, Su H, Gesteland P, Haug Peter J, Millett Nicholas E, Aronis John M, Nowalk Andrew J, Ruiz Victor M, Pineda Arturo L, Shi Lingyun, Van Bree Rudy. A study of the transferability of influenza case detection systems between two large healthcare systems. PLoS ONE. 2017;12(4) doi: 10.1371/journal.pone.0174970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cooper Gregory, Herskovits Edward. A Bayesian method for the induction of probabilistic networks from data. Machine Learning. 1992;9 [Google Scholar]