Multithreaded Stochastic PDES for Reactions and Diffusions in Neurons

Abstract

Cells exhibit stochastic behavior when the number of molecules is small. Hence a stochastic reaction-diffusion simulator capable of working at scale can provide a more accurate view of molecular dynamics within the cell. This paper describes a parallel discrete event simulator, Neuron Time Warp-Multi Thread (NTW-MT), developed for the simulation of reaction diffusion models of neurons. To the best of our knowledge, this is the first parallel discrete event simulator oriented towards stochastic simulation of chemical reactions in a neuron. The simulator was developed as part of the NEURON project. NTW-MT is optimistic and thread-based, which attempts to capitalize on multi-core architectures used in high performance machines. It makes use of a multi-level queue for the pending event set and a single roll-back message in place of individual anti-messages to disperse contention and decrease the overhead of processing rollbacks. Global Virtual Time is computed asynchronously both within and among processes to get rid of the overhead for synchronizing threads. Memory usage is managed in order to avoid locking and unlocking when allocating and de-allocating memory and to maximize cache locality. We verified our simulator on a calcium buffer model. We examined its performance on a calcium wave model, comparing it to the performance of a process based optimistic simulator and a threaded simulator which uses a single priority queue for each thread. Our multi-threaded simulator is shown to achieve superior performance to these simulators. Finally, we demonstrated the scalability of our simulator on a larger CICR model and a more detailed CICR model.

1. INTRODUCTION

The human brain may be viewed as a sparsely connected network containing approximately 10¹⁴ neurons. Each neuron receives inputs into thousands of dendrites and sends outputs to thousands of other neurons by means of its axon.

The neural membrane has ion channels which selectively control flow of various species – primarily sodium, potassium, and calcium. Movements of ions through these channels follow the concentration gradient from higher to lower. Additionally, there are pumps which depend on energy to move ions against the gradient. Electrical models for neurons [Lytton 2002] can be constructed using the well-known laws of electricity (Ohm, Kirchkoff, capacitance). However, these electrical models only provide a limited view of neuronal activity since calcium, as well as many other species (nucleotides, peptides, proteins, etc) diffuse in the cytoplasm (the inside of the cell) and function as information messengers. In order to develop realistic models of neurons, it is necessary to develop models which account for the movement and functioning of these messengers.

The combination of chemical reactions within a cell, the flux of ions through the membrane, and the diffusion of ions in the cytoplasm can be modeled as a reaction-diffusion system and can be simulated by (parabolic) partial differential equations [McDougal et al. 2013]. However, such a continuous model is not appropriate when there are a small number of molecules, e.g. < 1000 molecules. In these cases, a stochastic model will provide a more realistic and accurate representation [Sterratt et al. 2011; Ross 2012; Blackwell 2013]. Generally the concentration of calcium in cytosol is very low, between 50–100 nM [Foskett et al. 2007], where M is a concentration unit used in biochemistry and 1 M = 1 mol/Liter. These low concentrations mean small numbers of ions with different localized concentrations of cytosolic calcium that can play an important role in intracellular dynamics.

It is well known that a system consisting of a collection of chemical reactions can be represented by a chemical master equation, the solution of which is a probability distribution of the chemical reactants in the system [Sterratt et al. 2011]. In general, it is very difficult to solve this equation. In [Gillespie 1977] a Monte Carlo simulation algorithm called the Stochastic Simulation Algorithm (SSA) is described. Under the assumption that the molecules of the system are uniformly distributed, the algorithm simulates a single trajectory of the chemical system. Simulating a number of these trajectories then gives a picture of the system. The Next Subvolume Method (NSM) [Elf and Ehrenberg 2004] is an extension of the SSA which incorporates the diffusion of molecules into the model.

Because the size of a realistic simulation of a network of neurons is immense, it is necessary to make use of a parallel or distributed architecture. The NSM partitions space into cubes called sub-volumes. In PDES these sub-volumes can be represented as Logical Processes (LP) [Wang et al. 2011]. The diffusion of ions between neighboring sub-volumes is represented as events.

Communication latency is the main bottleneck of PDES systems [Fujimoto 1999]. The emergence and widespread use of multi-core processor significantly reduces this cost by using fast channels among cores on a multi-core chip. Alam [Alam et al. 2006] observed a significant benefit (approximately 8% to 12%) when communicating between processes running within a multi-core processor as opposed to between cores on different processors.

In a multi-threaded program, each thread has its own execution flow, and all of the threads share the same memory space. This feature makes it quite attractive to develop multi-threaded PDES systems to achieve better performance-messages can be transferred among threads directly within a process. However this can also lead to contention, e.g. on the Pending Event Set of each thread [Chen et al. 2011; Dickman et al. 2013], resulting in a great deal of overhead to deal with the contention.

NTW-MT was developed as part of the NEURON project (www.neuron.yale.edu). NEURON [Carnevale and Hines 2013; 2006] is a widely used simulator in the neuroscience community. It makes use of deterministic simulators for reaction-diffusion [McDougal et al. 2013] and electrical models. NTW-MT is intended to provide a more realistic picture of smaller populations of molecules and will be connected to NEURON.

The remainder of this paper is organized as follows. Section 2 describes background and related work, section 3 is devoted to the architecture and algorithms in our simulator, and section 4 describes our experimental results. The conclusion and future work are presented in section 5.

2. BACKGROUND AND RELATED WORK

2.1. Stochastic Simulation

There are two types of tools that have been used for stochastic simulation in neurons, particle-based methods and lattice-based methods [Blackwell 2013]. In particle-based methods, the state of the system is the number and location of particles in the subcellular space. The location of a particle and the system time are governed by probability distributions, e.g. the distribution in [Blackwell 2013]. Particles engage in a reaction when they are close enough. MCell [Bartol Jr et al. 1991], Smoldyn [Andrews et al. 2010] and CDS [Byrne et al. 2010] are particle-based simulators. NSM is a lattice-based simulation, in which space is partitioned into mesh grids. Reactions can happen between molecules in the same grid and molecules can diffuse to adjacent grids. MesoRD [Hattne et al. 2005] is an implementation of NSM, STEPS [Hepburn et al. 2012] is a spatial extension of the SSA, and NeuroRD [Blackwell 2013] are based on a spatial extension of the Gillespie tau-leap algorithm. However, these tools focus on developing serial versions, while our intention is to produce parallel simulation capable of large scale simulations.

2.2. Process-based PDES and XTW

In PDES, LPs are assigned to a collection of Processing Elements (PE)s, each of which is implemented by a process. A PE executes the events at the LPs in non-decreasing simulation time order. This is done in order to guarantee local causality. A pending events set in each PE is used to sort and store pending events. Many process-based PDES have appeared, including TWOS [Jefferson et al. 1987], GTW [Das et al. 1994], the CTW family [Avril and Tropper 1995; Xu and Tropper 2005; Patoary et al. 2014], Parsec [Bagrodia et al. 1998], ROSS [Carothers et al. 2002], μsik [Perumalla 2005], JAMES II [Himmelspach and Uhrmacher 2007] and YH-SUPE [Yao and Zhang 2008].

As to the selection of the synchronization protocol, [Dematté and Mazza 2008] points out that a conservative synchronization algorithm for a stochastic simulator will perform poorly because of the zero-lookahead property of the exponential distribution and the fact that a dependency graph of the reactions is likely to be highly connected and filled with loops. This indicates that an optimistic synchronization algorithm such as Time Warp [Jefferson 1985] is preferable. [Wang et al. 2009] presents an experimental analysis of several optimistic protocols for the parallel simulation of a reaction-diffusion system. [Jeschke et al. 2008] uses NSM in an optimistic simulation along with an adaptive time window. [Jeschke et al. 2011] compares the performance of spatial τ-leaping with that of NSM and Gillespie’s Multi-particle Method (GMPM) in terms of speedup and accuracy.

We previously developed a process based simulator, Neuron Time Warp (NTW) [Patoary et al. 2014], which makes use of a multi-level queue. We verified and examined its performance on a calcium buffer model and a predator-prey [Schinazi 1997] model. The queueing structure described in this paper and the one in [Patoary et al. 2014] are outgrowths of the multi-level queue described in XTW [Xu and Tropper 2005].

2.3. Multi-threaded PDES

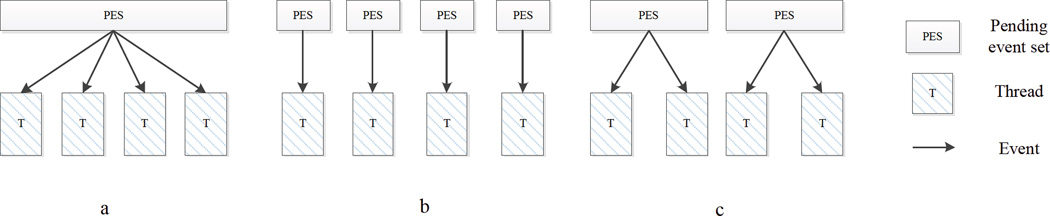
In a multi-threaded PDES simulator, a PE is implemented by a thread which can be assigned to a process. We do not distinguish between a PE and a thread in the following. To date there are two main schemes for storing and sorting the pending events for each thread, a global queue and a separated (distributed) queue. In a global queue scheme, as shown in part (a) of Fig. 1, a number of threads share a single priority queue. This scheme attempts to achieve load sharing at the expense of contention at the queue. Threaded WARPED [Miller 2010] adopted this architecture. The main drawback of this scheme is that there is too much contention at the global queue, as demonstrated by Chen [Chen et al. 2011]. This results in excessive overhead caused by locking operations-up to 50%–90%. Because threads have to wait for the output from the global queue the scalability is poor. Moreover, it is possible to have several events at the same LP processed by several threads simultaneously, thus a lock on each individual LP must be employed in order to preserve consistency.

Fig. 1.

Three scheme for storing and dispatching pending events to thread.

In a separated queue scheme, as shown in part (b) of Fig. 1, each worker thread has its own priority queue and only processes events from that queue, thereby eliminating contention at the queue. However, there are still concurrent operations on the priority queues arising from other threads in the same process. In order to avoid locking the contents of individual LPs, each LP is mapped to only one thread. This may lead to a load-imbalance, so it is necessary to balance the workload for each thread and process. [Chen et al. 2011] adopts the separated queue scheme and proposes a global scheduling mechanism to balance the workload between the threads in the same process. However, a global schedule still allows simultaneous processing of events at individual LPs, necessitating a locking mechanism. ROSS-MT [Jagtap et al. 2012] also employs a separated queue and uses an input queue to store the events sent from other threads. Contention on the input queue remains high. A hybrid scheme [Dickman et al. 2013] combines the above two schemes by creating several priority queues within one process and mapping a subset of the threads to a single queue, as shown in part (c) of Fig. 1.

ROOT-Sim [Vitali et al. 2012] makes use of interrupts to cope with synchronization. It considers the concurrent access (arrival of new event) to LPs to be an interrupt. The response to this interrupt consists of two steps: (1) place the interrupt (and associated parameters) in a queue and (2) process and remove the interrupt from the queue. This approach can lead to high memory usage.

2.4. GVT algorithms for multi-threaded PDES

In Time Warp, Global Virtual Time (GVT) is used to eliminate events and states via fossil collection which are not necessary to effect a rollback. In a distributed platform, Mattern’s [Mattern 1993] and Samadi’s [Samadi 1985] algorithm can be used. Both of them compute GVT by two rounds of message passing. Mattern’s algorithm does not require acknowledgements for each message, thereby resulting in better performance. Fujimoto [Fujimoto and Hybinette 1997] proposed an efficient algorithm for shared memory multiprocessors. In this algorithm, if p processes participate in a simulation, any process can trigger GVT computing by setting a variable GVTFlag to p. Other processes periodically check this variable, report their local simulation time and decrease GVTFlag by 1. GVT is computed when GVTFlag equals to zero. However this algorithm requires all of the processes to reside within one shared memory cluster, which constrains the scale of simulation. In [Pellegrini and Quaglia 2014] the authors propose a wait-free GVT computing algorithm by splitting the GVT computing phase in [Fujimoto and Hybinette 1997] into three phases. Better performance is achieved than Fujimoto’s original algorithm.

In order to compute GVT in multi-threaded PDES systems, Ross-MT [Jagtap et al. 2012] uses an optimized barrier to block all of the threads at wall clock time T. This can result in long waiting times if the duration for processing a single event is long. Each thread in [Chen et al. 2011] can receive and send messages, thus Mattern’s algorithm is applicable. In Threaded WARPED [Miller 2010], a manager thread is responsible for calculating the local GVT at a threaded Warped node. When a GVT compute message arrives at a node, the manager thread suspends all of the simulation objects in that node (to make sure new messages are not created within that node) and then sets the Least Time-Stamped Event (LTSE) to be the local GVT of that node. The computing of local GVT in Threaded WARPED still operates with a barrier. Overall, the present GVT computing algorithms are suitable for either pure distributed or pure shared memory platform. Our simulator, NTW-MT is a hybrid of shared and distributed memory platform and needs hybrid algorithms.

3. ARCHITECTURE AND ALGORITHMS

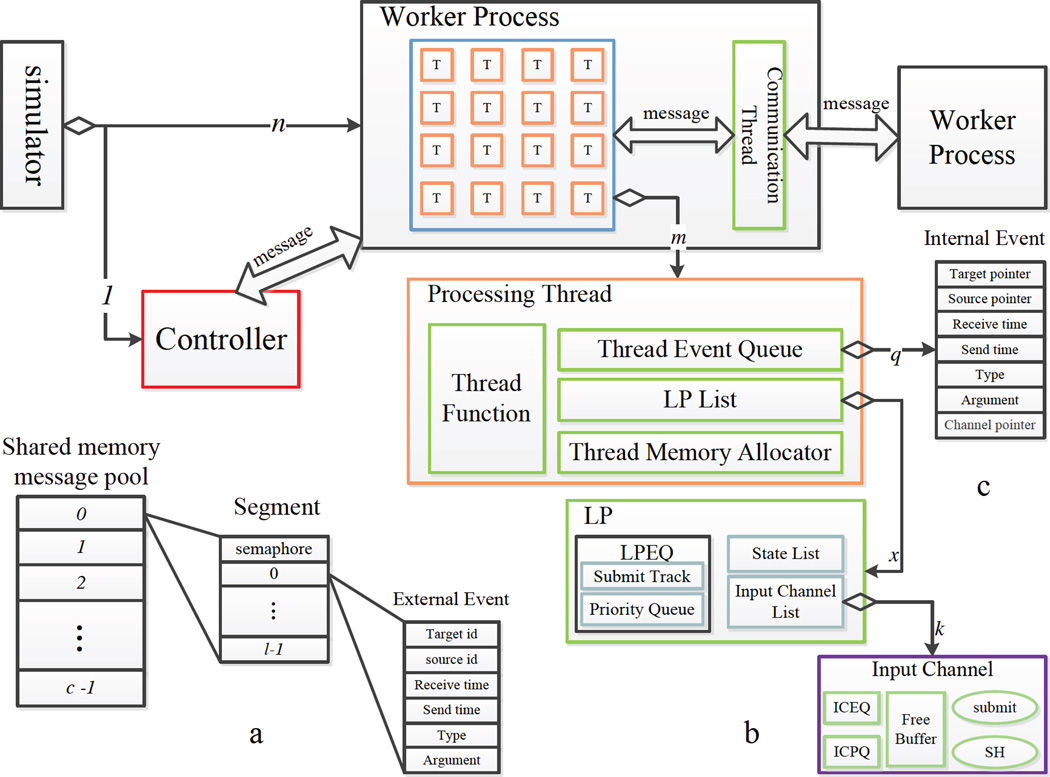
We employ a separated priority queue scheme in our architecture. The simulator architecture is depicted in Fig. 2. One of the processes is a controller, exercising global control functions (GVT computation and load balancing). The remaining processes are worker processes which process the events at the LPs that reside in the process. Each worker process contains a communication thread and several processing threads. All of the worker processes have the same number of threads.

Fig. 2.

Architecture of NTW-MT simulator.

The communication thread sends and receives messages for the process which hosts this communication thread. Processing threads can neither send nor receive messages. After initialization, the communication thread receives messages from shared memory, in which case the the message is from a family process residing in the same node (see section 3.5) or via MPI from remote nodes. Control messages are the first messages to be processed. LPs then schedule external events by placing them into the send buffer of the communication thread. To avoid contention for this buffer, it is partitioned into m segments, where m is the number of processing threads. The ith processing thread can write only into the ith segment. The communication thread scans the segments in the buffer and then sends out the messages. At present, the communication thread sends only one message per segment (a fairness policy).

LPs are partitioned into m × n subsets, where n is the number of worker processes and m is the number of processing threads. Each subset is mapped to a processing thread. Each processing thread includes a LP List which stores the LPs associated with the thread, a Thread Event Queue (TEQ) used in Multi-Level Queuing (MLQ) algorithm presented in section 3.1, a Thread Memory Allocator which is involved in the Memory Management presented in section 3.3 and a Thread Function. The Thread Function is responsible for processing the events, and is presented in algorithm 1, where LVT refers to Local Virtual Time.

ALGORITHM 1.

Processing sequence of a PE

while simulation is running do

Dequeue an event e from Thread Event Queue;

% RB-messages are special messages used for roll-back, see section 3.2.

if e.type != RB-message then

if e.receiveTime < e.targetLP.LVT then

e.targetLP rolls back to a time point prior to e.receiveTime according to algorithm 2;

end

e.targetLP advances Local Virtual Time to e.receiveTime and processes e;

else

Process e according to RB-message-processing algorithm 3;

end

Fetch an event from e.targetLP according to Multi-Level Queuing algorithm;

end

An event has two timestamps, the receive time and the send time [Jefferson 1985]. The events in the priority queue are sorted by their receive time. There are two types of events: internal events which are scheduled by internal processing threads and external events from external processing threads. As the processing threads share the same memory space, internal events use a pointer to identify LPs. A PE can use this pointer to access the LP directly. External events use an integer identifier to represent LPs. They are converted into internal events upon receipt by a communication thread and are then inserted into LPs.

3.1. Multi-Level Queuing

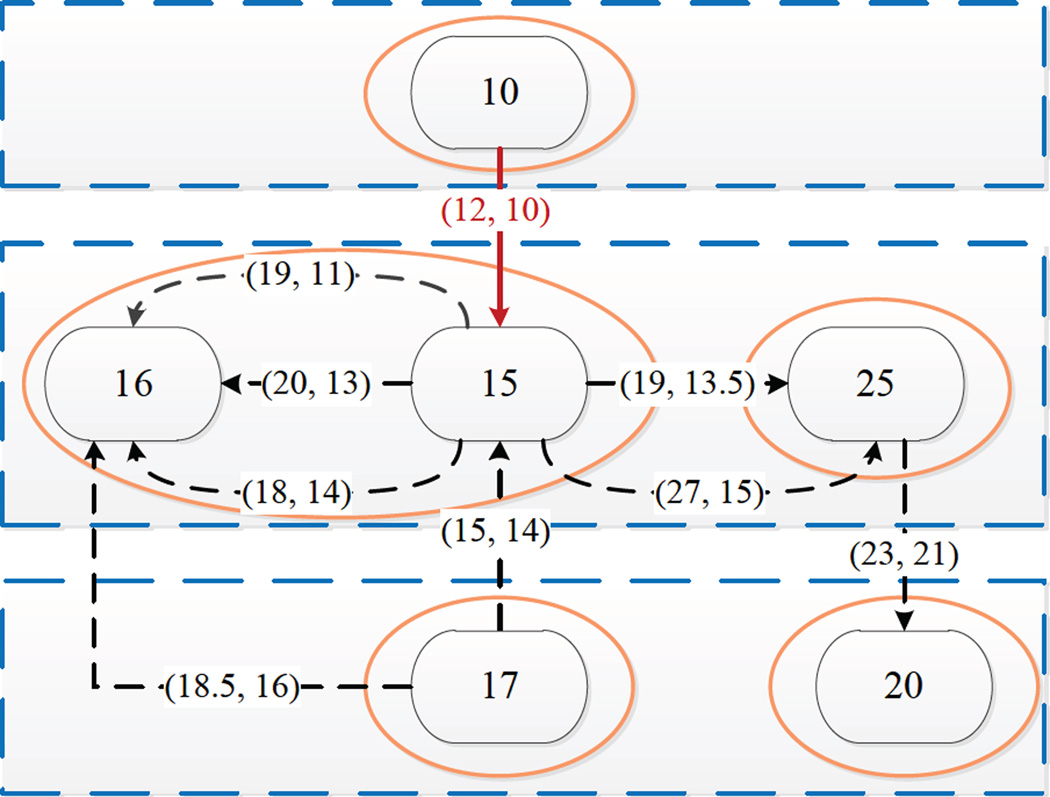
Every thread in a process can access any priority queue in the same process, which can cause excessive contention [Dickman et al. 2013]. To further aggravate matters, during a roll-back processed events with a timestamp greater than the receive time are re-enqueued in the priority queue. Two ways are used to alleviate this contention (1) decreasing the probability by which a few threads access the same queue simultaneously and (2) decreasing the cost of a single operation on a queue. In a stochastic neuronal simulation, the virtual time increment can vary from 0 to a large value. Consider the example in Fig. 3.

Fig. 3.

This example shows 6 LPs (rounded rectangles) which are distributed over three processes (dashed rectangles). Some are located in the same processing thread (an ellipse). The number in each LP is the local virtual time of the LP, and is also used to identify the LP. Each arrow indicates an event. The number on each arrow is the timestamp of the event (receive time, send time). Some LPs and events are omitted.

In Fig. 3 event (12,10) is a straggler at LP 15, and the dashed-lined-events at LP 16 are pending events. LP 16 has four pending events which would be stored in a queue. One may notice that it is not necessary to store and sort all four events in the TEQ-only event (18,14) needs to stay in the TEQ. There are several reasons for this: (1) some insertions in the TEQ can be omitted, decreasing the probability of contention. (2) the size of the TEQ can be controlled and the cost of an operation eliminated. Events (20,13) and (18,14) would be cancelled due to the roll-back of LP 15, hence sorting them is wasteful. (3) to cancel an event which would not access the TEQ decreases the probability of contention. Suppose that (1) a PE holds x LPs, numbered from 0 to x − 1 (2) S_i is the Pending Event Set (PES) of LP_i and that the events in S_i are in non-decreasing order in receive time. The minimum pending event of LP_i is minPE_i. It is easy to prove that minPE in PES is equal to the min{minPE_i, i = 0, 1, ⋯, x−1}. Therefore the PE only needs to compare each minPE_i to find minPE. This indicates that any LP only needs to have one representative event in TEQ. The remaining events are stored in the LP Event Queue (LPEQ). Each LP has a LPEQ and all the LPEQs are linked to the corresponding TEQ.

In a three-dimensional environment, space is partitioned by a mesh grid, resulting in a maximum of 6 neighbors for each LP. Molecules diffuse through channels (in this paper, channels refer to a path for diffusion between neighbouring sub-volumes, and they are not biological channels.) between these neighbors. We use an input channel to receive events from a neighbor and store them in an Input Channel Event Queue (ICEQ). All of the ICEQs are linked to the corresponding LPEQ.

To control the size of a queue, a lower level queue can only submit an urgent event (definition 1) to an upper level queue. A lower level queue records the unprocessed events which have been submitted to an upper level queue, and checks to see if an event is urgent when it receives it. Every input channel has a variable submit of event pointer which refers to the lower bound of unprocessed events that have been submitted to its LPEQ. Every LPEQ has a stack structure submitTrack which traces the unprocessed events which have been submitted to its TEQ. At the input channel level, urgency is checked by comparing the receive time of event e_x and submit of this channel. Because a LPEQ receives events from several input channels, it may submit several events to the TEQ, and there may be several pointers in submitTrack, hence urgency is checked by comparing the receive time of event e_x and the top element of this stack. In a reaction-diffusion simulation an event can have smaller receive time than a predecessor, thereby leading to the creation of an urgent event (see the example below).

Definition 3.1

An event $e_x^i$ in a queue $q_x^i$ at level i is urgent if its receive time is less than the receive time of any events $e_y^j$ in its upper level queue $q_y^j$ at level j (j > i).

At this point, we have three level queuing architecture, as shown in part (b) of Fig. 2. The access to TEQ, LPEQ and ICEQ is mutually exclusive and we use mutexes to prevent concurrency problems on them, whereas only the host LP can access ICPQ (Input Channel Processed event Queue), thereby no concurrency problem on ICPQs. The queuing works as follows.

• —In the initialize phase, the TEQ, LPEQ and input channels are constructed, submitTrack of LPEQ is empty and submit of input channel is set to 0. Each LP schedules an initial event to itself and adds it to its TEQ and then add the initial event to submitTrack.
• —
  Any processing thread and communication thread can insert events into a LP. To insert an event e, a thread first identifies the target LP_x by routing and checks if it is located in the same process. If not, this event will be added to the send buffer of the communication thread. If so it is inserted in the target LP as follows.

  1. Apply memory, find the target LP LP_x, fill in the Targetpointer field of this event by the pointer to LP_x.
  2. Determine the input channel channel_x, fill in the Channel Pointer field of this event by the pointer to channel_x, check whether it is urgent. If it is not urgent, insert it into ICEQ. Otherwise submit it to the LPEQ and update submit.
  3. At the LPEQ level, check urgency. If it is not urgent, insert it into LPEQ. Otherwise submit it to TEQ and insert its pointer to the top of submitTrack.
  4. At the TEQ level, insert this event into the TEQ.
• —After processing an event from input channel channel_s, a PE fetches an event from channel_s to make sure that there is a representative in the LPEQ, updates submit of channel_s, then inserts the new event in the LPEQ. At the level of the LPEQ, this PE checks submitTrack and the smallest event in LPEQ at that time to determine whether to submit an event to the TEQ or not.

In the example in Fig. 3, LP 16 has two neighbors LP 15 and 17. Event (19, 11) comes from LP 15, arriving at channel [16, 15] (a channel is marked in the format [host LP, source LP]), finds submit of this channel to be 0, and is submitted to the LPEQ of LP 16, submit is set to (19, 11); submitTrack of LPEQ 16 is empty. Then this event is submitted to TEQ, the pointer to (19, 11) is pushed at the top of submitTrack and the insertion of (19, 11) now ends. It is in the TEQ, where it at time T1. Then event (20, 13) arrives at channel [16, 15]. It is not urgent and thus stays in ICEQ. This insertion ends at time T2. Event (18, 14) arrives, and is found to be urgent for channel [16, 15], then it is submitted to the LPEQ; it is also urgent for LPEQ 16, and is submitted to the TEQ. The top of submitTrack becomes the pointer to event (18, 14) at time T3. Event (18.5, 16) from LP 17 arrives at channel [16, 17], finds submit to be 0, and is submitted to LPEQ 16. submit is set as a pointer to (18.5, 16) at time T4. The successive insertions depend upon the relationship of the above time points.

• —T4 < T1, this implies this event arrives before any events from LP 15. (18.5, 16) will be submitted to TEQ, (19, 11) will stay at LPEQ 16, (18, 14) will be submitted to TEQ, (20, 13) stays at ICEQ [16, 15]. top of submitTrack is pointer to (18, 14) followed by pointer to (18.5, 16).
• —T1 < T4 < T3, event (18.5, 16) is urgent and will be submitted to TEQ. Event (18, 14) is also urgent when it arrives at LPEQ 16. In this case, there are three events, (18, 14), (18.5, 16) and (19, 11), in TEQ.
• —T3 < T4, event (18.5, 16) is not urgent when it arrives at LPEQ 16, thus stays at LPEQ 16. Two event, (19, 11) and (18, 14) are submitted to TEQ.

3.2. RB-massage and Roll Back

XTW [Xu and Tropper 2005] uses one RB-message to cancel incorrect events instead of sending a series of anti-messages, eliminating the need for an output queue at each LP thereby reducing the overhead of a roll-back.

When a LP receives a straggler, it rolls back to a time point in prior to the straggler and then processes the straggler, as shown in algorithm 2. A LP does not store the processed events which were scheduled by itself. Processed events scheduled by other LPs are stored in the appropriate Input Channel Processed Queue (ICPQ).

ALGORITHM 2.

Steps for roll-back caused by stragglers, head is the smallest event in any queue, rt (st) is receive time (send time) of an event

Input: Roll-back time rbt (receive time of the straggler message), straggler message straggler.

Output: The next event smallest of this LP.

Search the latest valid state s prior to rbt with timestamp t1;

Recover LVT of this LP to t1, recover state to s;

counter = 0;

for channel ch in input channel list do

Recover events with receive time greater than t1 to ch.ICEQ from ch.ICPQ;

if ch.ICEQ.head.rt < ch.submit.rt then

Submit the smallest event to LPEQ from ch.ICEQ and update ch.submit;

counter++;

end

if ch.scheduleHistory ≥ LVT then

Send a RB-message (RB_PRIORITY, LVT) to ch.neighbour;

ch.scheduleHistory=LVT;

end

end

if counter > 0 then

Re-enqueue straggler into LPEQ;

Dequeue the smallest event from LPEQ as smallest;

else

Return straggler as the smallest event;

end

In the above example, the message (12, 10) sent by LP 10 to LP 15 is a straggler, so LP 15 should roll back to a point in time before time 12. Suppose a state at 11.5 is found, and the states with timestamp greater than 11.5 are released. After that, LP 15 recovers processed events with timestamp greater than 11.5, finds the smallest event and sends RB-messages to its neighbors, LP 16 and LP 25. However, it is not really necessary to send a RB message to every neighbour; we use a variable ScheduleHistory (SH) [Patoary et al. 2014] in the input channel in Fig. 2. SH records the upper bound of the send times of events sent to a LP. The use of SH can avoid sending unnecessary RB messages, see the example below.

RB-messages have a higher priority RB_PRIORITY, a negative real constant, than other normal events, the send time of RB-message is set as the present LVT of the LP that sends it. A RB-message (RB_PRIORITY, t_rb) sent from LP x to LP y announces that LP x has rolled back to t_rb, then the pre-sent events with send time greater than t_rb becomes invalid. LP y follows the steps in algorithm 3 to process RB-messages.

ALGORITHM 3.

Steps for processing a RB-message, tail refers to the element with the greatest timestamp in a queue

Input: The RB-message rb

if rb.channel.ICPQ.tail.st < rb.st then

Remove events with send time greater than or equal to rb.st in ICEQ and LPEQ;

for event es in SubmitTrack do

if es.channel == rb.channel & es.st ≥ rb.st then

Remove es in TEQ;

end

end

if rb.channel.submit.st ≥ rb.st then

rb.channel submits its smallest event to upper level queue and updates submit;

end

else

Search cut-point ecut in rb.channel.ICPQ;

rbt = −1;

if ecut is not NIL then

rbt = ecut.rt;

else

rbt = rb.st;

end

rb.targetLP rolls back to a time point prior to rbt according to algorithm 4;

end

smallest = the smallest event in LPEQ;

if submitTrack is empty | smallest.rt < submitTrack.top.rt then

Submit smallest to TEQ and push it to submitTrack;

end

The processing of a RB-message depends upon whether or not invalid events have been processed.

• —The invalid events have not been processed. These events are removed and submit event to upper level queue if necessary. In the above example, a RB-message (RB_PRIORITY, 12) will be sent by LP 15 to LP 16. Events (20, 13) and (18, 14) become invalid, while event (19, 11) is valid. The invalid events are removed from the queue in LP 16. This kind of RB-message does not interfere other LPs, for no successive rollback is triggered, thus we call it friendly RB-message.
• —The invalid events have been partly or totally processed. A roll-back is triggered, thus we call it aggressive RB-message. The send time of the RB-message is used to find the cut-point in the ICPQ, such that all events with a send time larger than the send time of the RB-message are after the cut-point. The LP sets the rollbacktime equal to the receive time of the first event after the cut − point. In the above example, a RB-message (RB_PRIORITY, 12) will be sent by LP 15 to LP 25, the events (19, 13.5) and (27, 15) become invalid while (19, 13.5) has been processed. A secondary roll-back is triggered and LP 25 follows steps in algorithm 4 to handle the roll-back.

ALGORITHM 4.

Steps for roll-back triggered by a RB-message

Input: Roll-back time rbt, the RB-message rb

Output: the number of events recovered to LPEQ nRecovered

Search the latest valid state s prior to rbt with timestamp t1;

Recover LVT of this LP to t1, recover state to s;

nRecovered = 0;

for channel ch in input channel list do

if ch == rb.channel then

Remove all ordinary events with send time greater than or equal to rb.st in ch.ICEQ,

ch.ICPQ, LPEQ and TEQ;

Recover events with receive time greater than t1 to ch.ICEQ from ch.ICPQ;

if ch.submit.st ≥ rb.st & ch.ICEQ is not empty then

Submit the smallest event in ch.ICEQ to LPEQ and update ch.submit;

nRecovered++;

end

else

Recover events with receive time greater than t1 to ch.ICEQ from ch.ICPQ;

end

if ch.ICEQ.head.rt < submit.rt then

Submit the smallest event in ch.ICEQ to LPEQ and update ch.submit;

nRecovered++;

end

if ch.scheduleHistory ≥ LVT then

Send a RB-message (RB_PRIORITY, LVT) to ch.neighbour;

Set ch.scheduleHistory to LVT;

end

end

The basic operation of RB-rollback is the same as that of a roll-back triggered by a straggler, except for the recovery of processed events. The input channel which received the RB-message removes all of the events with a send time greater than the send time of the RB-message. Otherwise it moves the processed events with receive time greater than rollback time from ICPQ to ICEQ. Sending a RB-message is necessary for either type of roll-back. The ScheduleHistory of channel [25, 20] is 21. Suppose that the first event after the cut−point is (22, 10.5). LP 25 will roll back to time 22, because 22 > 21 and no RB-message will be sent from LP 25 to LP 20. If the rollback time is 19, a RB-message (RB_PRIORITY, 19) will be sent to LP 20 by LP 25, and LP 20 applies the above steps to process this RB-message again. Our use of multi-level queue and RB-message is an extension of [Xu and Tropper 2005].

3.3. Memory Management

There are two problems that are important to focus on when designing a memory management system for PDES. First, PDES involves frequent memory allocations and deallocations, resulting in frequent locking and unlocking of memory. Second, sending data from one LP to another leads to cache misses if the target LP is located far from the sender LP. These problems led us to try and eliminate locking when allocating and de-allocating memory and to try to maximize cache locality.

In order to process an event e, both e and the LP which processes e, say LPx, should be in cache. Also, when an LP, say LP y, schedules an event e₂, there will be fewer write misses if e₂ is near LP y.

To achieve the first goal, assigning each thread a memory buffer is enough, LPs in that thread can allocate memory from this buffer when they schedule events. However this scheme will increase cache misses because the buffer is shared by all of the LPs in the thread, and an event from this buffer can be far from a LP. When scheduling inter-thread messages, both the sender LP and the receiver LP may be far from the scheduled event.

A simple approach is to split the buffer into slices and to assign a slice to each LP, requiring that an LP only allocate memory from its private slice. Hence each LP owns a private buffer that is near to its data and there will be fewer write misses when an LP schedules an event.

When a LP x deallocates an event e, it can return e to the sender LP y or to its own buffer. However it is not wise to return e to the sender LP y, because LP y may be in another thread, and be allocating memory for another LP at that time (otherwise we need a lock on the buffer of any LP). LP x can return e to its own buffer and there would be no need for a lock. Once an event e has been deallocated, it can be reused by LP x. Now suppose that LP x schedules an event for LP z, and that this event uses the memory from e (note that e is from the buffer of LP y), e is far from both LP x and z.

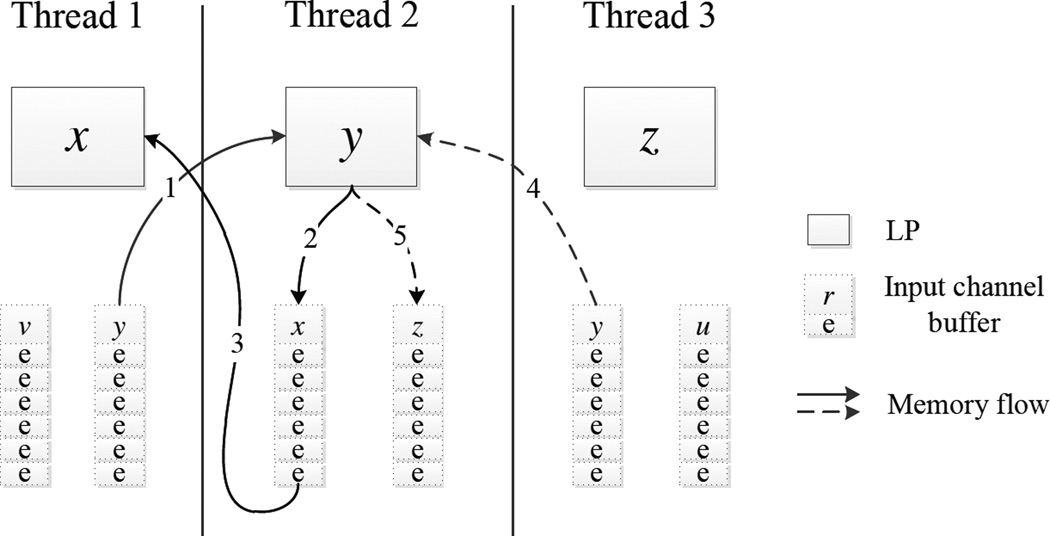
The connection of LPs is static in our reaction diffusion simulations. Hence we can split the buffer of each LP into slices and bind each slice to an input channel. Memory is then allocated and deallocated to the slice. In this way we can achieve the two goals, as we see in the example in Fig. 4.

Fig. 4.

An example of memory allocation of events. The style of arrows is used to mark sender LP, and the number on each arrow tells the sequence number of that operation.

Fig. 4 shows three LPs which are distributed to three threads, and they schedule events and allocate memory as follows.

1. LP x schedules an event for LP y, and the memory is allocated from the channel buffer allocated to LP y. This event is nearby LP x, thus there are fewer write misses. Note that LP x is in cache.

2. LP y returns this memory to the channel buffer allocated to LP x. LP y has exclusive access to this buffer, thus no locks are needed.

3. LP y allocates events for LP x from the corresponding channel. This event is nearby LP x, hence there are fewer read misses when LP x processes this event.

We see that the memory for events is near either the sender or the receiver LP, and no lock is needed. It is possible for an event to be near both the sender and receiver LPs if the two LPs are in the same thread.

We use on-the-fly fossil collection [Fujimoto and Hybinette 1997]. There is no explicit fossil collection (otherwise we traverse all of the LPs to reclaim memory). The allocation of events is as follows:

1. A LP inserts any processed events into corresponding ICPQ after processed.

2. The pre-allocated memory is pushed into a free buffer in each channel after initialized, and a LP allocates memory from this free buffer first.

3. If there is no free event available in the free buffer, it checks available event memory in ICPQ (any processed event with a timestamp less than GVT becomes available).

4. A processing thread also has a memory allocator (see Fig. 2), and a LP uses this allocator to get event memory if the above steps failed.

3.4. Asynchronous GVT Computing

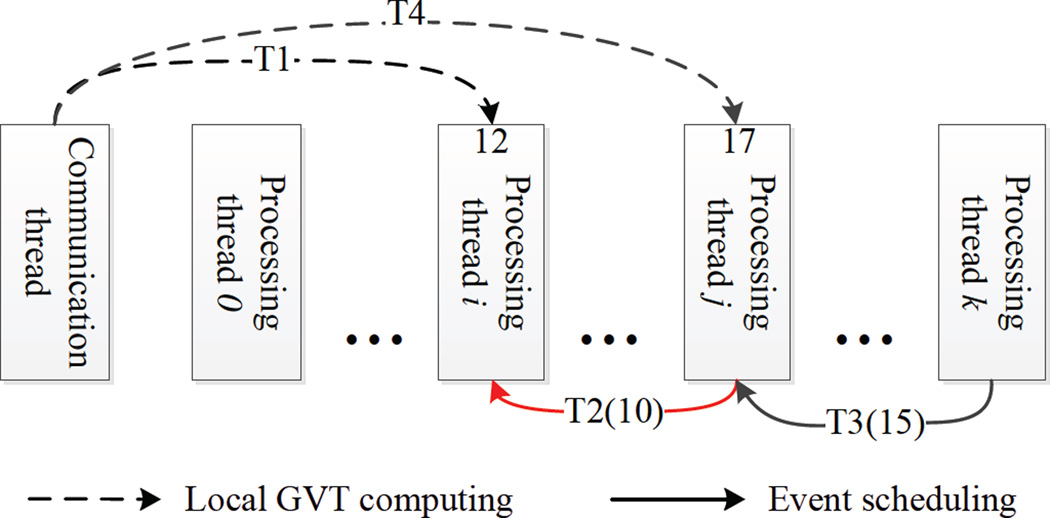
Since a processing thread can neither send nor receive external events directly, it is not aware of external message passing. Additionally there is simultaneous reporting problem in GVT computing as Fig. 5 shows.

Fig. 5.

An example of simultaneous reporting problem within a worker process.

In Fig. 5, in order to compute a local GVT [Fujimoto 1999] the communication thread begins to check TEQ_i at wallclock time T₁ and leaves TEQ_i at wallclock time $T_1^{\prime }$. It then checks TEQ_j at wallclock time T₄, $T_1<T_1^{\prime }<T_4$. Processing thread j schedules an event with timestamp10 to thread i at wallclock time T₂ and thread k schedules an event with timestamp15 at thread j at wallclock time T₃. Suppose these time points satisfy the order $T_1<T_1^{\prime }<T_2<T_4$ (this circumstance happens due to arbitrary order of locking and unlocking TEQs), then the event with timestamp 10 is not accounted for, resulting in an incorrect local GVT value, say 12. The point is that events sent between threads during a GVT computation in a process must be accounted for.

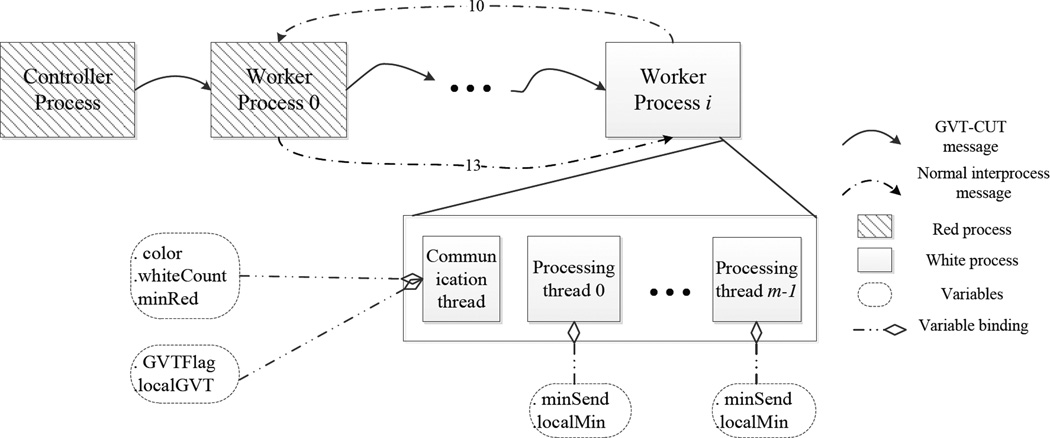
The message flow and corresponding data structure for computing GVT is depicted in Fig. 6. Each worker process holds two sets of variables for the GVT computation; (color, whiteCount, minRed), which is used for interprocess communication, and (GVTFlag, localGVT) which, along with the minSend and localMin variable in each processing thread is used to find local GVT in each worker process.

Fig. 6.

Message flow and data structure of asynchronous GVT computing.

In Mattern’s algorithm, a process can be either red or white. At the beginning, all processes are white. A white process becomes red when it receives a GVT-CUT message, while a red process becomes white when it receives a GVT-broadcast message notifying it of the latest GVT value. Messages take on the color of the sending process. A GVT-CUT message is used to notify all worker processes to start a GVT computation. A cut message has two fields (tempGVT, count), where tempGVT is the the latest GVT and count is the number of white messages sent but not received since the last GVT. The controller process triggers a GVT computation by sending a GVT-CUT message (∞, 0) to the first worker process every T_GVT seconds. Upon receiving an external message, a worker process counts the number of white messages received since the last GVT. It follows the steps in algorithm 5 to receive a GVT-CUT message. In Fujimoto’s algorithm, a process checks the GVTFlag variable before processing an event and updates its local GVT if GVTFlag is greater than zero. A process computes GVT if that process is red. It then inserts a GVT-CMP message into the TEQ of each processing thread. A GVT-CMP message is a special control message which requires each processing thread to report its local GVT. Hence each processing thread only modifies the GVTflag and updates its local minimum timestamp once during a GVT computation.

ALGORITHM 5.

Steps for communication thread receiving an external event

Input: External event e received via shared memory or MPI

if e is a non-control message then

if e.color == WHITE then

whiteCount−;

end

else

% Only the GVT-computing-related message is described here

if e.type == GVT-CUT then

Set color of this process to RED;

Set localGVT to e.tempGVT, cache e.count;

% write lock on GVTFlag

Set GVTFlag to the number of processing threads m;

for processing thread T in the same process do

Insert a GVT – CMP message into the TEQ of T;

end

end

end

A processing thread reports its local GVT value while processing a GVT-CMP messages in its TEQ, as depicted in algorithm 6, and records this value in its localMin variable. The local GVT value in a processing thread is the minimum of the smallest receive time of the pending events in the TEQ and the smallest send time of the RB-messages in the TEQ. Note that the current event being processed by this thread is the GVT-CMT event, thus there are no partially processed ordinary events in this thread. The processing thread updates the localMin value and decreases GVTFlag by 1. When the GVTFlag equals zero all of the processing threads in a process have reported their GVT values. The processing thread that decreases the GVTFlag to zero inserts a GVT-CUT message into the send buffer of the communication thread in order to indicate that the local computing is finished. The steps are shown in algorithm 6. When a processing thread schedules normal events to other processing threads within the same process, it checks GVTFlag and updates its minSend variable if GVTFlag is greater than zero, as presented in algorithm 7. Here we can see simultaneous access and modification to GVTFlag by threads in the same process, necessitating concurrency protection on it. Note that GVTFlag can be accessed when a thread schedules internal events and modified only when that process is computing GVT, which indicates that read access is much more than write access. Based on this observation, we use a read-write spin lock on GVTFlag to improve performance in our simulator, and the lock operations are marked in algorithm 5, 6 and 7.

ALGORITHM 6.

Steps for processing threads processing a GVT – CMP message

Set t1 to the smallest receive time of ordinary events in TEQ;

Set t2 to the smallest send time of RB-messages in TEQ;

Set localMin to min(localMin, t1, t2);

% write lock on GVTFlag

GVTFlag−;

% read lock on GVTFlag

if GVTFlag == 0 then

Insert a GVT – CUT message in the send buffer of the communication thread;

end

ALGORITHM 7.

Steps for processing threads scheduling internal events

Insert event e to target LP by Multi-Level Queuing algorithm;

% read lock on GVTFlag

if GVTFlag > 0 then

if e.type == RB-message then

minSend=min(minSend, e.st);

else

minSend=min(minSend, e.rt);

end

end

A communication thread follows the steps in algorithm 8 to compute its local GVT when sending inter-process messages. For ordinary messages, it counts the number of white messages sent and received since the last GVT and updates the minimum among receive time (send time of RB-message) of red messages sent since the latest round of GVT computing. The final value of the local GVT in a process is calculated when the communication thread sends out a GVT-CUT message. The localGVT value is the minimum among localGVT and localMin, minSend in each processing thread. Then it forwards a GVT-CUT message (localGVT, count) to the next worker process, resets count to zero and localMin, minSend in each processing thread to ∞.

GVT-CUT messages are passed from one worker process to another and eventually return to the controller process. The controller process checks whether the count field in the received GVT-CUT message equals zero. If it does, a new GVT value tempGVT in the received GVT-CUT message is obtained and the controller process broadcasts this value to all of the worker processes. Otherwise (some transient messages were missed in this round) the controller process forwards this GVT-CUT message to the first worker process and triggers a new round.

ALGORITHM 8.

Steps for communication thread sending external events

Input: External event e to be sent

if e is a non-control message then

if e.color == WHITE then

whiteCount++;

else

if e.type == RB-message then

minRed=min(minRed, e.st);

else

minRed=min(minRed, e.rt);

end

end

else

if e.type == GVT-CUT then

for processing thread T in the same process do

localGVT=min(localGVT, T.localMin, T.minSend);

end

Set count to the sum of whiteCount and cached count;

whiteCount=0;

localGVT=min(localGVT, minRed);

Forward a GVT-CUT message (localGVT, count) to the next process;

end

end

A worker process becomes white when it receives a GVT broadcast message. It then updates its GVT value to the received value and resets color to white, minRed to ∞, and whiteCount to zero.

A correctness proof to this asynchronous GVT algorithm can be found in online appendix.

3.5. Hybrid Communication

We call the worker processes located in the same node a family. In part (a) of Fig. 2, assume that there are c processes in a node. The shared memory is partitioned into c segments, numbered 0, 1, ⋯, c − 1, Each process uses one of the segments as its receive buffer. Each segment has a semaphore associated with it to control access to the segment. For example, when process 0 is about to send data to its family member process 2, process 0 needs to hold the semaphore for process 2, after which it releases the semaphore when it is finished writing. When receiving data, process 0 must hold the semaphore.

Together, we have three-level communication mechanism, communication between threads within same process is completed by pointers, to shared memory for processes in the same node, and by MPI for remote processes.

4. EXPERIMENTS AND RESULTS

4.1. Platform

We use two platforms. One machine (PEPI) is a cluster node with 4 Intel(R) Xeon(R) E7 4860 2.27 GHz, 10 cores per processor, 1 TB memory, with Linux 2.6.32-358.2.1.el6.x86 64, Red Hat Enterprise Linux Server release 6.4 (Santiago). The other is the SW2 node (of Guillimin at McGill HPC center), consisting of two Dual Intel(R) Sandy Bridge EP E5-2670 2.6 GHz CPUs, 8 cores per processor, 8 GB of memory per core, and a Non-blocking QDR InfiniBand network with 40 Gbps between nodes. The node runs Linux 2.6.32-279.22.1.el6.x86_64 GNU/Linux.

4.2. Verification

Free calcium is buffered by intracellular buffers (e.g. calmodulin or parvalbumin) and is therefore unavailable. However, it can escape from these buffers, resulting in an almost constant concentration of cytosolic calcium. This observation can be used to verify our simulator. The buffer model includes two reactions as follows.

$$\text{Composition}:{\text{ Ca}}_{\mathit{\text{cyt}}}^{2+}+\text{Buf}\stackrel{k_f}{\to }\text{CaBuf},\text{Decomposition}:\text{ CaBuf}\stackrel{k_b}{\to }{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}+\text{Buf}$$

We executed this buffer model using the deterministic NEURON simulator on a ”Y” shaped geometry which consists of three cylinders (10 µm long, 1 µm diameter, and a sketch can be found in [Patoary et al. 2014]). To show spatial effects, we initialize high concentration of free calcium in one cylinder and low concentration in the remaining two cylinders, and then trace the evolution of the molecules. The initial high and low concentration of Ca²⁺ is set to 1.0 mM and 0.1 mM, while the concentration of Buf and CaBuf is set to 0.5 mM and 0.001 mM everywhere. The reaction rates k_f and k_b are set to 0.06 and 0.01. In NTW-MT, the geometry is partitioned into 2766 sub-volumes, and the length of each subvolume is 0.25 µm. High concentration of Ca²⁺ is initialized in the first 922 sub-volumes (922/2766=1/3) by setting 10 molecules in each of those subvolumes, while 1 calcium molecule is set in each of the remaining 1844 sub-volumes. The initial numbers of Buf and CaBuf molecules in each subvolume are set to 5 and 0, respectively. From Fig. 7, we can see that the stochastic approach exhibits a similar behavior to the deterministic approach.

Fig. 7.

Deterministic NEURON simulation vs. stochastic NTW-MT simulation, Ca H and Ca L refer to high and low concentration of calcium in respective region in deterministic and stochastic simulation.

4.3. Calcium waves

Calcium plays a very important role in regulating a great variety of cellular processes, from fertilization through gene transcription, muscle contraction to cell death. Calcium for signaling is sourced from both extracellular calcium that enters through the cell membrane, and from intracellular sources [Berridge 1998]. Some major intracellular sources are accessed though Ca²⁺-induced-Ca²⁺-release (CICR) [Berridge 1998; Roderick et al. 2003]. A brief introduction to the intracellular CICR dynamics is given in the online appendix. CICR can happen spontaneously at a local spot within cells even without any external stimulation [Ross 2012], this kind of localized CICR event is observed and called as ”spark” [Cheng et al. 1993] or ”puff” [Parker and Ivorra 1990]. This type of local event occurs stochastically in both temporal and spatial dimensions. In reproducing such events, a stochastic simulation should be employed.

4.4. Calcium wave model

A deterministic CICR model has been developed in NEURON [Neymotin et al. 2015]. Based on this model we developed a discrete event model and simulated it. In our experiments we only take the Inositol 1,4,5-triphosphate (IP₃) and Ca²⁺ into account. Because the real CICR model is complex and we cannot use the differential equations directly, we simplified it by assuming (1) the IP₃ receptor opens when the concentration of IP₃ and Ca²⁺ are both higher than some respective threshold and (2) an opening IP₃ receptor channel will close for a period of time determined by an exponential distribution. To be more specific, once when the two thresholds are reached in a subvolume, the IP₃ receptor opens in that subvolume opens immediately and will close in a duration 10 × ln(u), u ~ U(0, 1). The reactions include:

$$\mathrm{E}\mathrm{R}\text{ Release}:{\text{ Ca}}_{er}^{2+}\stackrel{k_{\mathit{\text{release}}}}{\to }{\text{Ca}}_{\mathit{\text{cyt}}}^{2+},k_{\mathit{\text{release}}}={\nu }_{IP3R}{m}^3{n}^3([{\text{Ca}}_{er}^{2+}]-[{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}])$$

$$\mathrm{E}\mathrm{R}\text{ Leak}:{\text{ Ca}}_{er}^{2+}\stackrel{k_{\mathit{\text{leak}}}}{\to }{\text{Ca}}_{\mathit{\text{cyt}}}^{2+},k_{\mathit{\text{leak}}}={\nu }_{\mathit{\text{leak}}}([{\text{Ca}}_{er}^{2+}]-[{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}])$$

$$\mathrm{S}\mathrm{E}\mathrm{R}\mathrm{C}\mathrm{A}\text{ Pump}:{\text{ Ca}}_{\mathit{\text{cyt}}}^{2+}\stackrel{k_{\mathit{\text{pump}}}}{\to }{\text{Ca}}_{er}^{2+},k_{\mathit{\text{pump}}}=\frac{{\nu }_{SERCA}{[{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}]}^2}{k_{SERCA}^2+{[{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}]}^2}$$

where ${\text{Ca}}_{er}^{2+}$ refers to Ca²⁺ in Endoplasmic Reticulum (ER), ${\text{Ca}}_{\mathit{\text{cyt}}}^{2+}$ refers to Ca²⁺ in cytosol, [•] refers to the concentration of the corresponding species •, m = [IP₃]/([IP₃]+k_IP3), $n=[{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}]/([{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}]+k_{\mathit{\text{act}}})$, k_IP3, k_act, ν_IP3R, ν_leak, ν_SERCA and k_SERCA are given constant parameters, the value can be found in [Neymotin et al. 2015] and listed in online appendix. ${\text{Ca}}_{er}^{2+}$ can only diffuse within ER, cytosolic Ca²⁺ and IP₃ can only diffuse within cytosol.

The initial concentrations of Ca²⁺ (in the ER and cytosol) and IP₃ are set to 9.511765 µM, 0.1 µM and 0.1 µM respectively. In each subvolume, 17% of the volume is the ER while the remaining 83% is cytosol. The threshold for controlling the channel opening is 0.2 µM and 2 µM for cytosolic Ca²⁺ and IP₃, respectively.

We made use of the following scenario. In the beginning both the concentrations of cytosolic Ca²⁺ and IP₃ are less than their respective threshold. At some time point, we inject IP₃ molecules into the middle 8 sub-volumes by adding 50 µM IP₃ molecules to those sub-volumes to trigger the release reaction in those sub-volumes. We ran this simplified model on a one-dimensional geometry to give an example, the figures are shown in the online appendix. As those appended figures show, this simplified model can produce a calcium wave as expected.

4.5. Geometry

We simulate the intracellular Ca²⁺ wave in a CA1 hippocampal pyramidal neuron [Ishizuka et al. 1995]. The hippocampal pyramidal neuron used in our experiment is taken from NeuroMorpho.Org [Ascoli et al. 2007] (NO. c91662), and a three-dimensional view of this neuron is given in online appendix. The neuron is partitioned into mesh grids, and each grid is taken to be a subvolume. In general, the topology of a network of cells can play an important role as, for example, it can be difficult to partition the space into cubes. Algorithms from computer graphics, such as the marching cubes algorithm, can be employed to deal with this issue. We select 14749 sub-volumes with a distance of less than 50 µm from soma (a three-dimension view of the selected region is also given in online appendix.), and the length of each subvolume to be 0.5 µm. The sub-volumes are evenly distributed among the processing threads.

4.6. Performance

The performance of NTW-MT is compared to two other versions. One is a process-based parallel simulator which uses a controller process to calculate GVT. Memory operations employ the standard new and delete mechanism. A thread+SQ version uses threads but does not use the MLQ algorithm. Each thread uses a single priority queue to hold the pending events. We know from [Xu and Tropper 2005] that RB messages result in superior performance when compared to anti-messages and do not compare the simulator to one with anti-messages.

In the thread+SQ case, when 32 processing threads are used, a roll-back avalanche occurs. This phenomenon is much more serious for the process-based version, which essentially cannot get beyond 8 processes. We consider these results inaccurate in terms of performance and do not include them.

The placement of threads is an important issue, it affects the memory usage and communication. We consider three placements- (1) within process in which all of the processing threads are in the same process, thereby no interprocess events; (2) within node in which processes exchange messages via shared memory; (3) hybrid respectively which makes use of MPI for remote processes and the preceding techniques otherwise.

4.6.1. within Process Mode

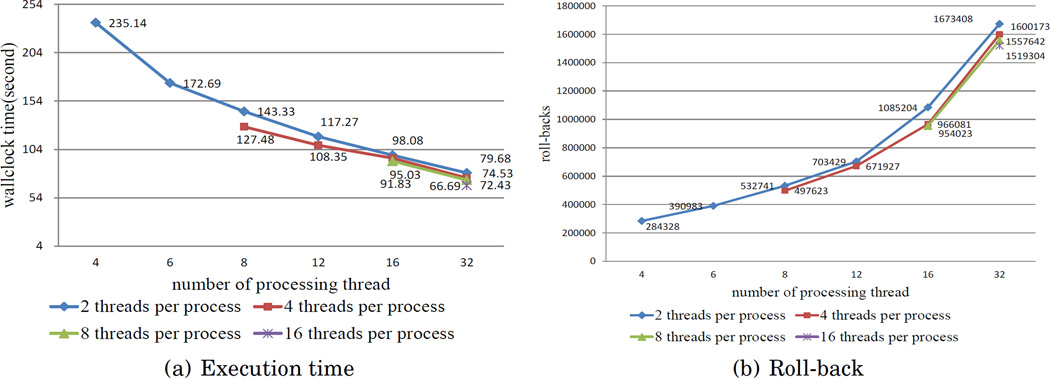
We run this experiment in the PEPI machine by starting up two processes, one controller and one worker process, and creating the processing threads within the worker process. The results are shown in Fig. 8.

Fig. 8.

Execution time and roll-back with all of the processing threads running within one process in the PEPI machine.

From Fig. 8(a), we can see that the execution time decreases with an increase in the number of processing threads. The process-based version is slowest because each process receives and sends events in the main processing loop and communication is time-consuming.

When fewer than 8 processing threads are involved in the simulation, the thread+MLQ version is slower than the thread+SQ version. The greatest difference (about 13%) occurs when one processing thread is used. Because the essence of MLQ is the dispersion of contention on a single queue, it is of no use if there is no contention.

rollbacks increase for all of the versions in Fig. 8(b). The process-based version suffers more rollbacks (25%–35%) than the other two versions. The roll-back of the two thread version is almost same in the few thread cases, while the MLQ version experienced fewer (around 18%) rollbacks than the SQ version. The events are inserted into thread queue directly in the SQ version resulting in a greater delay.

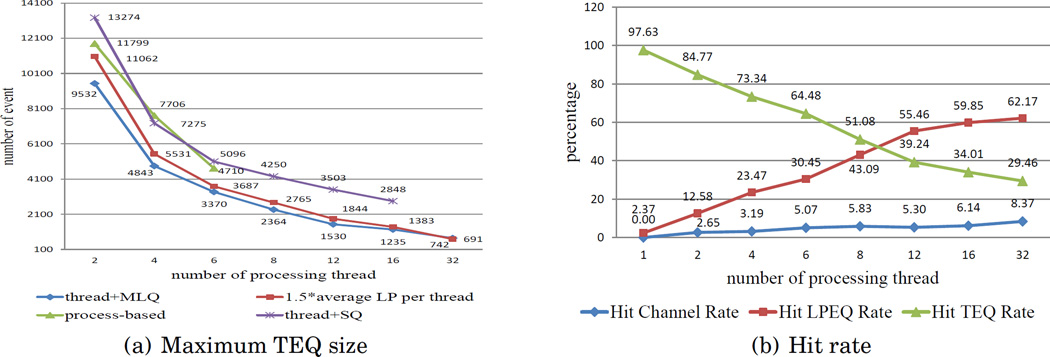
The size of the TEQ scales well-it contains no more than 1.5 times the average number of LPs per processing thread. Hence the access time for the TEQ is well controlled, see Fig. 9(a). In the MLQ algorithm, an event insertion may end at different levels of the queuing system-the input channel, the LPEQ and the TEQ. Define the hit rate of a level to be the proportion of insertions ending at each level. In the process-based and thread+SQ version, all of the events are inserted into the thread queue. From Fig. 9(b), we can see that most insertions end at the LPEQ when more than 8 threads are used, suggesting that the contention is dispersed.

Fig. 9.

Maximum size of TEQ and hit rate in within process mode in the PEPI machine.

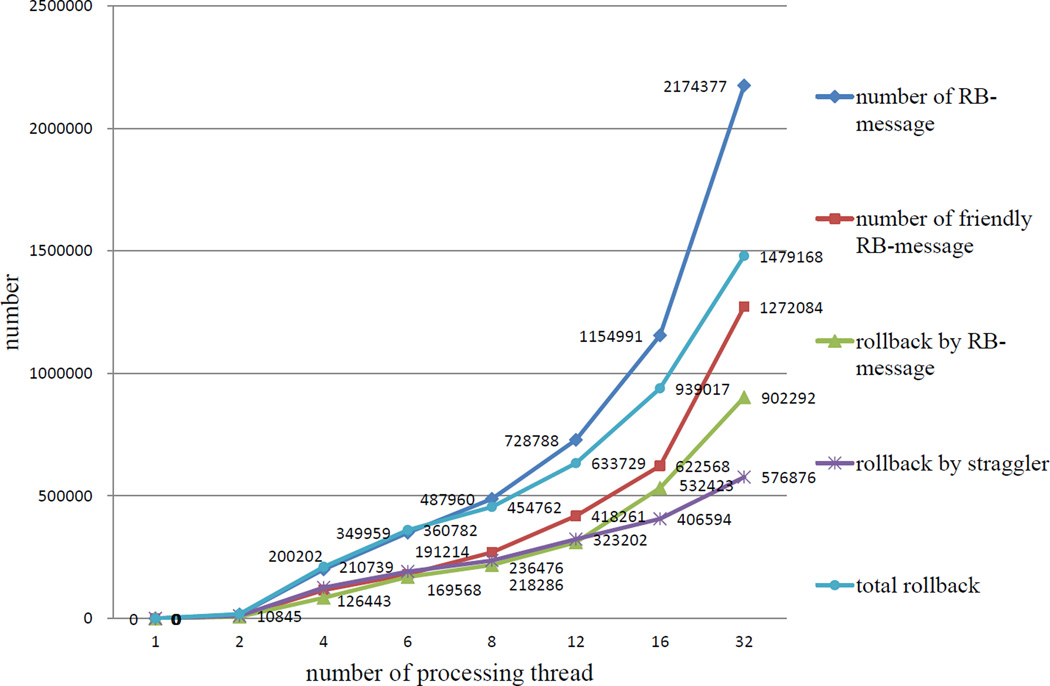
A roll-back is caused by either a straggler or an anti-message. In our implementation, we replace a sequence of anti-messages by a single RB-message, which decrease the number of events in the whole system. In Fig. 10, let r, r_p and r_s denote the total number of roll-back, roll-back caused by straggler, and roll-back caused by RB-messages. Let rm, rm_f and rm_a denote the total number of RB-messages, the number of friendly RB-messages and the number of aggressive RB-messages, then we have r = r_p + r_s and rm = rm_f + rm_a.

Fig. 10.

Detailed analysis of rollback of NTW-MT in within process mode in the PEPI machine.

From Fig. 10, we can see that when all of the processing threads are in the same process, the roll-back triggered by a straggler shows a gradual increase. This is because event insertion is done by pointer and contention on priority queues is dispersed, thus communication delay is negligible.

There are three obvious crossover points in Fig. 10. The first one happens between the total roll-back and total RB-message curves. Before the crossover the two curves are similar, implying that a roll-back causes a RB-message. However, after the crossover a roll-back can result in several RB messages due to imbalanced execution of processing threads. The second one happens between the number of friendly RB-message and roll-back by straggler curves. Before the crossover the number of friendly RB-messages is low, which implies that most RB messages are triggered by secondary rollbacks. Both of the crossover points take place when 7 processing threads are involved. The explanation for this is as follows. In a three-dimensional grid one subvolume can have no more than 6 adjacent sub-volumes, resulting in at most 7 threads inserting events at an individual LP simultaneously. Let μ = number of processing threads/7 as the mean concurrency at a LP, if μ ≤ 1, a LP receives one event in an event-processing cycle on average and sends only one RB-message on average once it rolled back (see the usage of the ScheduleHistory variable in section 3.2); in contrast a LP sends more than one RB-message during rolling back if μ > 1. The third one happens between the roll-back by straggler and the roll-back by RB-message curves. Before the crossover, roll-back triggered by a straggler dominates, while roll-back by RB-message increases after the crossover point. Note that after the third cross point, a LP can receive twice the number of events in an event processing cycle on average, thus the roll-back by RB message exhibits a sharp increase.

4.6.2. within Node Mode

All of the processes reside in the same node and transfer external messages via shared memory. This experiment was done on the PEPI machine.

From Fig. 11(a), we see that placing more threads in the same process results in better performance. This is reasonable because less interprocess communication is used. However, comparing these results to those obtained by placing all of the processing threads in the same process, we do not see a great difference. The combination of communication threads and shared memory results in a short latency.

Fig. 11.

Execution time and roll-back with shared memory communication in within node mode.

4.6.3. Hybrid Mode

The number of threads is limited by the number of physical cores in a node. The obvious conclusion is that several nodes must be employed in a large scale simulation. We conducted such a hybrid experiment on the Guillimin machine and used the MPI option ppn (process per node) to dispatch worker processes to nodes.

The Guillimin machine uses a well-optimized infiniBand for remote communication. From the results in Fig. 12(a), we again see that placing all of the processing threads in the same process results in the best performance. When remote communication is involved, performance decreases and the number of rollbacks increases.

Fig. 12.

Execution time and roll-back with hybrid communication, ppn refers to process per node.

In the purely remote communication case, the send buffer of the communication thread overflows when more than 8 threads are in the same process. One communication thread cannot accommodate 8 or more processing threads. This indicates the importance of determining the number of processing threads in one worker process.

4.6.4. Scalability

To determine the scalability of NTW-MT for larger geometries, we increase the total number of LPs in the simulation. This is done by selecting subvolumes in a larger region around the soma of the CA1 neuron. There are 23547 subvolumes within a radius 120 μm from the soma of the CA1 neuron. We ran the model with same scenario in Guillimin in hybrid mode; the results are depicted in Fig. 13.

Fig. 13.

Execution time and rollbacks of the simplified model in bigger geometry.

Comparing Fig. 12(a) and 13(a), the total number of LPs increases, resulting an increase in total execution time, whereas the two curves show similar shape. The number of rollbacks is low when 2 threads are used, so their role in estimating their contribution to the execution time can be ignored. Note that there is almost no contention when one thread is used, hence we do not use the execution time of one thread case to make estimates. Since the initial condition, scenario parameters and end condition are same in the two runs, we assume that the mean computational cost of an individual LP during the simulation is approximately the same, and that the execution consists of two parts-a computational part (t_c) and an overhead part (t_o). Let θ be the ratio of number of LPs in the two geometries, θ = 23547/14749 ≈ 1.6. When 2 threads are used, the bigger geometry has an execution time of about 1.9 times the execution time of the small geometry, t^b = 1.9t^s (the superscript b refers to bigger geometry), $t_c^b=1.6t_c^s,t^b=t_c^b+t_o^b,t^s=t_c^s+t_o^s$, then $t_o^b=t^b-t_c^b=1.9t^s-1.6t_c^s=0.3t_c^s+1.9t_o^s$. We see that the overhead in the bigger geometry plays a bigger role than in the smaller geometry. There are four major reasons for this: (1) more events were scheduled in the bigger geometry, leading to more time spent in allocating memory for events and writing events; (2) the LPEQ and ICEQ are protected by mutexes (section 3.1), there are more locking and unlocking operations when more LPs are involved; (3) the size of the TEQ increases with the number of LPs (the size of the LPEQ and the ICEQ depends on the number of neighbors (6), and has little to do with the total number of LPs). As a result it takes more time to operate on the TEQs (we use STL multiset). The STL multiset is implemented as a Red-Black tree. The cost of a single operation is proportional to log₂(q), where q is the number of elements in the queue. From the analysis in section 4.6.1, the size of the TEQ is about 1.5 times as the number of LPs in a thread, then η = log₂(1.5 × 23547/2)/log₂(1.5 × 14749/2) ≈ 1.05. (4) more LPs consume more memory, which may lead to more cache misses.

When 16 threads are used the execution time for the bigger geometry is about 2.45 times that of the smaller one. When using either 2 or 16 threads the number of rollbacks for the larger geometry is much higher than for the smaller geometry. This is because rollbacks in the bigger geometry have longer ”rollback chains”. A rollback chain is a list of LPs such that a primary rollback of the header LP leads to secondary rollbacks at the successive LPs in the list. In a bigger geometry, because there are more LPs which cover a wider spatial region, a rollback can spread further.

4.6.5. CICR Model + Channel State Transition Model

An IP₃R channel is a tetramer of four IP₃R molecules [Foskett et al. 2007]. Each IP₃R molecule is a linear amino acid sequence. The four molecules have a pore in their center, allowing Ca²⁺ to flow through the pore when the channel is open. In each IP₃R molecule (subunit), there are three sites: one binds with IP₃ for activation, another binds with cytsolic Ca²⁺ for activation while the last binds with cytsolic Ca²⁺ for inactivation. A subunit is activated if both activation sites are bound and the inactivation site is not bound. An activated subunit becomes inactivated when the inactivation site is bound. The conductance of an IP₃R channel is proportional to the number of activated subunits, and a channel is considered as open if three of the four subunits are activated [De Young and Keizer 1992]. Since the binding and unbinding rate of activation sites is much faster than the inactivation site (on the order of 2000 and 10 respectively [Li and Rinzel 1994]), we assume that the two activation sites are in a dynamic steady state (the number of bound sites is almost constant) before the inactivation site is bound. More details can be found in the online appendix.

The binding and unbinding rate of the inactivation site is related to the concentration of the cytosolic Ca²⁺. From [Neymotin et al. 2015] we know that an inactivation site is bound with Ca²⁺ at a rate k_b=(1−h_inf)/τ, and is unbound at a rate k_u=h_inf/τ, where h_inf is computed as $K_{\mathit{\text{inh}}}/(K_{\mathit{\text{inh}}}+[{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}])$, K_inh and τ are given constant. An inactivation site can be in a bound (1) or an unbound (0) state. Hence an individual IP₃R can be in one of the 8 states s_ijk, where i, j, k is 0 or 1, and only the state s₀₀₀ allows Ca²⁺ to flow from the ER to the cytosol. As a result, there are 12 bidirectional reactions for the state transition of an individual IP₃R as follows.

$$s_{0jk}+{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}\underset{k_u}{\overset{k_b}{\rightleftharpoons }}{s}_{1jk},s_{i0k}+{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}\underset{k_u}{\overset{k_b}{\rightleftharpoons }}{s}_{i1k},s_{ij0}+{\text{Ca}}_{\mathit{\text{cyt}}}^{2+}\underset{k_u}{\overset{k_b}{\rightleftharpoons }}{s}_{ij1}$$

As a (sanity) check for the state transition of the subunits, we initialize 8 × k IP₃R channels in each subvolume (k channels in each state), use 200 sub-volumes in a linear geometry, inhibit release, leak and pumping reactions in each subvolume, i.e. only the state transition reactions can occur. The ctysolic Ca²⁺ concentration is initialized as 9.6 × 10⁻⁵ mM, τ is 400 ms, and the simulation lasts 5 virtual seconds (5s ≫ 400 ms). We count the number of subunits in each state, as displayed in table I, h = [3 × s₀₀₀ + 2 × (s₀₀₁ + s₀₁₀ + s₁₀₀) + (s₀₁₁ + s₁₀₁ + s₁₁₀)]/(200 × 3 × 8 × k). K_inh = 0.0019 mM, $h_{\mathit{\text{inf}}}=K_{\mathit{\text{inh}}}/(K_{\mathit{\text{inh}}}+[\mathrm{c}{\mathrm{a}}_{\mathit{\text{cyt}}}^{2+}])=0.0019/(0.0019+9.6\times {10}^{-5})=0.951903808$. We see that h converges to h_inf as k → ∞.

Table I.

Number of activated subunits with various initial number of IP₃R channel

k	s000	s001	s010	s011	s100	s101	s110	s111	h
10	13803	714	706	32	670	30	42	3	0.951937
5	6870	351	353	19	370	18	17	2	0.9505
1	1392	67	68	2	62	4	5	0	0.9548

In total, there are 27 reactions (along with the 3 reactions in the simplified model) and 11 species (3 species in the simplified model and IP₃R channel in each state s_ijk). We call this model the 8-states model. With the same configuration, we run the 8-states model with 14749 LPs on PEPI and show the results in Fig. 14.

Fig. 14.

Execution time and rollbacks of the 8-states model.

Comparing Fig. 11(a) and 14(a), we see that NTW-MT scales well for the complex model (8-states model). Its execution time is about 1.8 times that of the simplified model. The roll-backs do not exhibit a significant difference between Fig. 11(b) and 14(b). The complex model involves more computation for processing events. LPs spend extra time in (1) saving more states (a state copy consists of 11 integers in the 8-states model) and (2) computing the propensity of the reactions- the complex model contains more reactions, thereby taking more time to compute the propensity of the reactions.

5. CONCLUSIONS AND FUTURE WORK

This paper is concerned with the development of a parallel discrete event simulator for reaction diffusion models used in the simulation of neurons. To the best of our knowledge, this is the first parallel discrete event simulator oriented towards stochastic simulation of chemical reactions in a neuron. The research was done as part of the NEURON project (www.neuron.yale.edu).

Our parallel simulator is optimistic and is thread based. It makes use of the NSM algorithm [Elf and Ehrenberg 2004]. The use of threads is an attempt to capitalize on multicore architectures used in high performance machines. Communication latency is minimized by self-adaptive communication which selects the proper communication method (i.e. pointer, shared memory and MPI) upon the location of receiver. It makes use of a multi-level queue for the pending event set and a single roll-back message in place of individual anti-messages to disperse contention and decrease overhead of roll-back. Memory management avoids locking and unlocking when allocating and deallocating memory and maximizes cache locality. The GVT is computed asynchronously both within and among processes to reduce the overhead for thread synchronization.

We verified our simulator by comparing the result to that of the deterministic solution in NEURON on a calcium buffer model. To examine its performance, we simulated a discrete event model for calcium wave propagation in a hippocampal pyramidal neuron and compared it to the performance of (1) a process based optimistic simulator and (2) a threaded simulator which uses a single priority queue for each thread. NTW-MT exhibited superior performance when all of the threads were in the same process. The effects of shared memory and MPI based communication were investigated; the multilevel queue simulator proved to be scalable. Finally, we we demonstrated the scalability of our simulator on a larger CICR model and on a more detailed CICR model which included channel state transition.

The need for load balancing algorithms and for window control was made clear during the course of our our experiments. We are introducing window control and load balancing techniques based on the use of techniques from artificial intelligence [Meraji and Tropper 2012]. The need to optimize state saving, e.g. by using reverse computation, was also indicated by our experiments.

Although NTW-MT was developed for the simulation of stochastic reaction and diffusion models of neurons, the techniques that we developed can be more widely applied. For one, NTW-MT is applicable to general reaction-diffusion systems. Its multithreaded architecture, asynchronous GVT algorithm and its use of hybrid communication are, in actuality, general-purpose mechanisms for PDES.