Abstract
A key step in genomic studies is to assess high throughput measurements across millions of markers for each participant’s DNA, either using microarrays or sequencing techniques. Accurate genotype calling is essential for downstream statistical analysis of genotype-phenotype associations, and next generation sequencing (NGS) has recently become a more common approach in genomic studies. How the accuracy of variant calling in NGS-based studies affects downstream association analysis has not, however, been studied using empirical data in which both microarrays and NGS were available. In this article, we investigate the impact of variant calling errors on the statistical power to identify associations between single nucleotides and disease, and on associations between multiple rare variants and disease. Both differential and nondifferential genotyping errors are considered. Our results show that the power of burden tests for rare variants is strongly influenced by the specificity in variant calling, but is rather robust with regard to sensitivity. By using the variant calling accuracies estimated from a substudy of a Cooperative Studies Program project conducted by the Department of Veterans Affairs, we show that the power of association tests is mostly retained with commonly adopted variant calling pipelines. An R package, GWAS.PC, is provided to accommodate power analysis that takes account of genotyping errors (http://zhaocenter.org/software/).
Keywords: genome wide association test, genotyping, genotyping error, sequencing, statistical power
1 INTRODUCTION
Genome-wide association studies (GWASs) have identified many common variants that are associated with disease susceptibility, and have revealed previously unknown disease mechanisms (Hindorff et al., 2009; Hirschhorn & Daly, 2005). A variable portion of the heritability can be explained by the identified variants to date, however, possibly due to the presence of rare variants that predispose people to disease (Cirulli & Goldstein, 2010; Manolio et al., 2009; Yang et al., 2010). To study rare variant associations, next generation sequencing (NGS) has become commonly employed in genomic studies due to reduced cost, improved accuracy, and mature analysis pipelines (Michaelson et al., 2012; Need et al, 2012; O’Roak et al., 2011). Variant calling and postcalling quality control in NGS data have been extensively studied and benchmarked (Challis et al., 2012; DePristo et al., 2011; Koboldt et al., 2009; Li et al, 2009), but genotyping error can still be a major attributor to the relatively low power of rare variant association test. The importance of quality control and the impact of genotyping error of high-throughput genotyping platforms in association test is widely recognized (Pluzhnikov et al., 2010; Yan et al., 2016).
In this paper, and linked to the Million Veteran Program (Gaziano et al., 2016) being conducted by the U.S. Department of Veterans Affairs, we evaluate the statistical power of association tests in the presence of variant calling errors from NGS data. The Million Veteran Program is a mega-biobank that combines data from questionnaires, electronic health records, and biospecimens; the current research is based on a corresponding alpha-test project (see Section 2). In support of the program, we considered it important to understand genotyping errors and their impact on the power of association testing, thereby identifying the best genotyping strategy. More specifically, we consider the power from both single-marker association tests, and multiple rare marker association tests, while accounting for genotype-specific error rates.
In the alpha-test project, we have genotyped a group of subjects by two different genotyping platforms, NGS and genotyping microarrays. There are noticeable discrepancies in the genotyping results of the two platforms, suggesting the existence of genotyping errors. The question we are interested in is as follows: how the genotyping errors would affect the association test? Historically, Mote and Anderson (1965) discussed the loss of asymptotic power in chi-square test for contingency tables when misclassification is ignored. In the statistical genetics literature, it is well known that the statistical power to detect risk loci is reduced if the genotyping error is ignored in association tests (Gordon & Finch, 2005). For association test of rare variants, substantial power loss was also observed (Powers, Gopalakrishnan, & Tintle, 2011). The loss of power depends on several factors, including the type of genotyping error and the statistic of association test. Kang and colleagues quantified the cost of genotyping errors by the fraction of increased sample size that is necessary to maintain power of 2 × 3 χ2 test of independence, and found that misclassification of the common homozygote genotype as the less common homozygote or heterozygote is the most costly (Kang, Gordon, & Finch, 2004). In particular, the cost is more protruding when the minor allele frequency goes to 0. This work was later extended to a genetic model-based framework, which studies the change of %MSSN (percentage of minimum sample size necessary) with each type of genotyping error at specified mode of inheritance and level of linkage disequilibrium (Kang, Finch, Haynes, & Gordon, 2004). The findings are consistent when the linear trend test is used for association test (Ahn et al., 2006).
In view of the impact of genotyping errors, association tests that can account for genotyping errors have been proposed, which usually rely on accurate estimation of genotype frequency and genotyping error rates. Assuming two instruments (devices, platforms) are available for classifying units, one less expensive but more error prone, and the other one more expensive but more accurate, Tenenbein (1970, 1971) proposed a double sampling scheme to correct bias in estimation of binomial parameter in a cost-effective manner. The work was later extended to multinomial case (Tenenbein, 1972). On top of the double sampling scheme, likelihood ratio test (Gordon et al., 2004) and linear trend test (Gordon, Haynes, Yang, Kramer, & Finch, 2007) were adapted to incorporate genotyping error in association tests. In another study, assuming that several Centre d’Etude du Polymorphisme Humain pedigrees are genotyped by an automated platform, the genotyping error rates were estimated via a maximum likelihood method by considering pedigree information (Gordon & Ott, 2001). Rice and Holmans (2003) also suggested using “external validation” study to estimate the genotyping error rate in GWAS studies. In the alpha-test project, the less expensive platform is more accurate (see Section 3), but sequencing platform has other benefits, such as better coverage of rare variants and potentially functional variations. Nevertheless, Tenenbein’s assumption is not valid here.
In the literature mentioned above, only nondifferential genotyping error was considered. In other words, the genotyping error rates in the case group and the control group are assumed to be the same in those approaches. However, differential genotyping error, which means the genotyping error rates in the case group and the control group are different, is more problematic because it causes inflation in type I error (Cook, Benitez, Fu, & Tintle, 2014; Moskvina, Craddock, Holmans, Owen, & O’Donovan, 2006). Differential genotyping error is more protruding in large-scale studies, where cases and controls are likely to be genotyped at various sites with imbalanced proportion. Mayer-Jochimsen, Fast, and Tintle (2013) examined the impact of this type of errors on type I error of association test of rare variants by simulation. They found that the inflation of type I error increases with sample size and the number of variants, and the pattern is consistent for all five test statistics examined (Mayer-Jochimsen et al, 2013). Kim et al. (2012) extended the linear trend test to allow for differential genotyping error in association analysis of single marker and multiple markers. Their proposed test maintains type I error rate and the power is at least comparable to other methods. Instead of modeling differential error, Garner used a quality control parameter, depth, as a covariate in regression analysis to account for differential genotyping error in each individual (Garner, 2011), and the inflation of type I error was reduced.
In support of the MVP (Million Veteran Program) program, we considered it important to understand genotyping errors and their impact on the power of association testing. More specifically, we consider the power from both single marker association tests, and multiple rare marker association tests, while accounting for genotype-specific error rates. Our novel contributions in this manuscript are (1) to provide an empirical dataset with practically relevant estimates of genotyping error rate of NGS technology; (2) to build a statistical framework for power analysis by considering different model of genotyping error and adjusting for the inflation of type I error when applicable; and (3) to provide a software of power analysis functions. Our results have important implications for genomic study designs. In addition, the analytical framework enables us to study how the statistical power varies as a function of genotype-specific error rates, which in turn can inform the selection of quality control strategies in NGS variant calling.
The remainder of the manuscript first describes the framework to calculate the statistical power of association tests for given genotype-specific error rates. We then explore how the error rates observed in the alpha-test datasets affect the statistical power, and thus the sample size needed to achieve desired thresholds of statistical power. We find that in single marker analysis for common single nucleotide polymorphisms (SNPs), the loss of power due to genotyping errors is modest. The difference of genotyping error between cases and controls is not severe, and would not inflate the type I error much. We also demonstrate that the power of burden test is sensitive to the specificity of genotyping results.
We believe that the proposed framework will help geneticists better design NGS-based human genomic analyses, and also optimize quality control strategies in variant calling to retain power in subsequent association tests.
2 METHODS
2.1 Materials
In conjunction with the Million Veteran Program (Gaziano et al., 2016), the Department of Veterans Affairs (VA) is conducting Cooperative Studies Program (CSP) Project #572, “Genetics of Functional Disability in Schizophrenia and Bipolar Illness” (Harvey et al., 2014) to detect genetic associations for the development of, and functional disability from, major mental illness. As participants (total N = 9,356 with valid phenotypes) were being enrolled, a substudy population of 576 Veterans, composed of 188 schizophrenia (SCZ) patients, 191 bipolar (BP) patients, and 197 healthy controls (CTRL), were analyzed by both genotyping arrays and exome sequencing. (Although N = 200 patients in each category were identified, samples for 24 patients were not available at the time of the analysis.) The DNA materials were analyzed via whole exome sequencing (WES) and genotyping arrays at the Yale Center of Genome Analysis. The NimbleGen Seq-Cap EZ human exome library v2.0 was used for library preparation, and the samples were then sequenced on the Illumina HiSeq platform. The specimens were also genotyped on the Illumina genotyping array HumanOmni2.5Exome-8 Bead-Chip. For genotype calling from microarray data, the image files were loaded into Illumina’s GenomeStudio software, and genotypes were generated by the GenCall algorithm.
To analyze the WES data, the sequencing reads were mapped to the reference genome b37 by BWA (Li & Durban, 2009). The mappable reads were then filtered by multiple steps: (1) PCR duplicates were removed by Picard; (2) reads with mapping quality lower than 30 were excluded; (3) off-target reads were discarded; and (4) sequencing reads without matched pair were removed. After quality control, the remaining reads were realigned and recalibrated in GATK (DePristo et al., 2011). The recalibrated reads were used for variant calling. The GATK haplotype module was used for variant calling. Afterwards, the variant calling results were recalibrated via the GATK VQSR (Variant Quality Score Recalibration) module. We further used the depth of coverage and Fisher strand bias as filters to remove potentially low-quality variant calls.
2.2 Genotyping error rates in NGS studies
Genotypes of N = 575 patients were inferred by both genotyping arrays and WES; one sample (male, healthy control) was unusable from the DNA materials sent for sequencing. We denote the genotyping results from genotyping arrays and WES, respectively, as Array genotypes and WES genotypes. We compared the WES genotypes to Array genotypes, and summarize the concordant and discrepant results in Table 1, with “A” as the major allele, and “a” as the corresponding minor allele.
TABLE 1.
Comparisons of genotyping results
| Array Genotype | WES Genotype | Total | |||
|---|---|---|---|---|---|
| aa | Aa | AA | NA | ||
| aa | n11 | n12 | n13 | n10 | n1 |
| Aa | n21 | n22 | n23 | n20 | n2 |
| AA | n31 | n32 | n33 | n30 | n3 |
For example, n12 in this table represents the number of sites with Array genotype aa and WES genotype Aa; n33 represents the number of sites that both Array genotype and WES genotype are AA; and n10 is the number of sites with Array genotype aa and no calls in WES dataset. The sites with no calls in genotyping arrays were not included in the analysis. For markers with the most discrepancies of the genomic results between the two platforms, we manually checked the genotyping quality of Array genotype by looking at the clusters formed in genotyping arrays (see supplementary Fig. S1 and S2). For both common SNPs and rare SNPs, two or three clear clusters were found in genotyping arrays, demonstrating that the Array genotypes have high quality. Moreover, the allele frequencies estimated by Array genotypes are closer to the frequencies documented in the 1000 Genomes Project. Variant calls from the WES platform assigned different genotypes to patients who fell into the same cluster, however, suggesting higher error rates for WES-based variants. Thus, in the following section, we assume that the Array genotypes are accurate, and the genotype specific error rates of the WES platform can be estimated by , for i ≠ j.
2.3 Metrics of genotyping quality
We consider two previously used metrics (DePristo et al., 2011) to define genotyping quality of the WES platform. The first is sensitivity (equation (2.1)), which is defined as the proportion of nonreference genotypes that are identified through WES. The second metric is nonreference discrepancy (equation (2.2)), defined as the proportion of discrepant genotypes among nonreference genotypes inferred from the two platforms.
| (2.1) |
| (2.2) |
2.4 Power for single marker analysis
For case-control studies, we use logistic regression for genotype-phenotype association analysis (equation (2.3)), where x is the genotype of a marker, coded as 0, 1, and 2 copies of the nonreference allele, and Y is the disease status (equation (2.4)).
| (2.3) |
| (2.4) |
Under the null hypothesis of no association, H0: β = 0, the null deviance approximately follows chi-square distribution with 1 degree of freedom. Under the alternative hypothesis, the null deviance follows a noncentralized chi-square distribution , where λ is the noncentrality parameter. The power of the association test is given by . To assess the power of association tests, it suffices to evaluate the noncentrality parameter.
Let the risk allele frequency be p. Under Hardy-Weinberg equilibrium, the genotype frequencies in the population are P (X = 2) = p2, P(X = 1) = 2p(1 − p), and P (X = 0) = (1−p)2. We assume multiplicative genetic effects for disease-associated SNPs and the relative risk is denoted as r, such that
| (2.5) |
Given the disease prevalence pD, the penetrance of the reference genotype can be derived as:
| (2.6) |
Thus, the genotype distribution in cases and controls can be inferred, respectively, via a Bayesian rule (see equations (2.7) and (2.8)). The noncentrality parameter can be derived by fitting a logistic regression.
| (2.7) |
| (2.8) |
Next, we consider the observed genotype distribution with genotyping errors. We assume that conditional on the true genotype, the inferred genotypes from WES, denoted as XWES, follow a multinomial distribution (see equation (2.9)). Please note that there is a fourth genotype category in the inferred genotypes from WES, NA, other than all the possible true genotypes, 0, 1, and 2. NA indicates no-calls (not applicable) through WES. Inclusion of “NA”s in the model gives us the flexibility to account for sample size loss when applying more stringent quality control strategies. For a marker with minor allele frequency p and relative risk r, we can calculate the probability of observing WES genotype i in cases and controls accordingly (see equations (2.10) and (2.11)).
| (2.9) |
| (2.10) |
| (2.11) |
2.5 Power for multiple variant analysis
For rare variant analysis, we consider the burden test (Li & Leal, 2008) to evaluate the association between multiple rare variants and the disease phenotype. Suppose there are M rare variants in a genomic region of interest, {SNPi, i = 1, 1, M}, and the minor allele frequencies are {pi, i = 1, ⋯, M}, respectively. Let Yi be defined as follows:
We make the following assumptions:
The disease status of one subject is attributed to only one rare variant, that is, and P (Yi = 1, Yj = 1) = 0.
Each rare SNP has a multiplicative effect on disease risk.
Under the above assumptions, cases can be divided into M subgroups, with group i corresponding to patients attributed to SNPi. Let the penetrance of variant i be , and for genotypes 0, 1, and 2, respectively. Let the relative risk of SNP i be ri. From equation (2.5), the disease prevalence attributed by variant i is . The term can be derived by further assuming that the penetrance of the reference genotype is identical across different rare variants (see equation (2.12)). The proportion of diseased subjects attributed to SNPi is denoted as πi. The genotype distribution of SNPi in cases is derived in equation (2.13). The entity Pr(Xi = x|Yi = 1) can be similarly derived as in equation (2.7). The genotype distribution of SNPi in controls is derived in equation (2.14).
| (2.12) |
| (2.13) |
| (2.14) |
In the burden test, the frequencies of subjects with rare alleles, ϕcase and ϕcontrol are compared between cases and controls (see equations (2.15) and (2.16)). The noncentral parameter of the chi-square test can be calculated as equation (2.17). Thus, the power of the burden test can be calculated by equation (2.18).
| (2.15) |
| (2.16) |
| (2.17) |
| (2.18) |
In practice, the measured genotypes may differ from true genotypes due to typing errors. We assume that variant calling/genotyping errors are characterized by a probability matrix Z. Compared to the error models for common SNPs, the genotypes Aa and aa are collapsed as nonreference genotypes because they are not distinguished in the burden test described in Section 2.5. In this context, z11 is the sensitivity defined in equation (2.1), and z00 is the specificity of identifying homozygous reference genotypes, .
| (2.19) |
Based on the above definitions, we can derive the statistical power of the burden test, considering the discrepancies in the observed genotypes and the true genotypes as shown in equations ((2.20) and (2.23)). The power of the burden test is calculated by equations ((2.16) and (2.17)).
| (2.20) |
Xi1,i2,⋯,ik denotes the variables Xi1, ⋯, Xik, and X−(i1,i2,⋯,ik) denotes all the variables other than Xi1, ⋯, Xik.
| (2.21) |
| (2.22) |
| (2.23) |
2.6 Differential genotyping error
When the genotyping error rates differ between the case group and the control group, the observed genotype of a null variant may show cryptic association with disease status, causing inflation of type I error. Fortunately, it is straightforward to infer the null distribution in the presence of differential genotyping error in our framework. Two multinomial distributions are used to characterize the conditional distribution of observed genotype in cases and controls separately given the true genotype (equations (2.24) and (2.25)). The parameters and are the conditional probabilities in cases and controls.
| (2.24) |
| (2.25) |
The distribution of the null deviance in single marker analysis is a noncentralized chi-square distribution, and the non-centrality parameter can be calculated similarly as described in Section 2.5 (see equations (2.26) and (2.27)).
| (2.26) |
| (2.27) |
In the multiple marker analysis, by setting the relative risk ri to 1 in equation (2.12), and distinguish the conditional distribution of WES genotype in cases and controls, the noncentrality parameter can be derived as described in Section 2.5.
3 RESULTS
We first report a quality assessment of WES-based calls from a Million Veteran Program related substudy. We then apply the results of the power analysis to evaluate the impact of errors in genotype calls on statistical power to detect association signals.
3.1 Quality assessment of WES genotypes
In the VA substudy, the DNA materials of 575 patients were analyzed by both genotyping arrays and WES, and we used the GATK (Genome Analysis Toolkit) best practice pipeline for variant calling. 221,578 SNPs were identified from WES, and among them 30,704 were also genotyped on the genotyping arrays. We also applied a postcalling filter that removed variants with sequencing depth less than a given threshold.
Two metrics, sensitivity and nonreference discrepancy (see Section 2.3 in Section 2), were used to assess the genotyping quality while the threshold of the depth filter was varied. Given that allele frequency is an important factor of genotyping quality in both genotyping arrays and WES, we evaluated the genotyping quality for common variants (minor allele frequency ≥ 0.05) and rare variants (minor allele frequency ≤ 0.01) separately (Fig. 1). Regardless of variant frequency, the sensitivity decreased when a more stringent depth filter was applied.
Figure 1.
Quality assessment of the whole exome sequencing genotypes in CSP572 substudy
The nonreference discrepancy decreased when the depth filter threshold was increased, and the decrease became modest when the depth filter was greater than 5. When we used a depth filter of 5, the sensitivity of common and rare variants was 94.30% and 91.44%, respectively, and the corresponding nonreference discrepancy was 1.47% and 0.61%, indicating accurate variant calling in WES to detect nonreference genotypes. The distribution of depth of coverage at each variant calling site, broken down by allele frequency and sample status can be found in supplementary Figure S1.
3.2 Evaluation of statistical power for common variants
In addition to considering the quality metrics discussed above, we evaluated the genotype-specific error rates of the WES genotype. Due to the errors in inferring genotypes through WES, the distribution of the observed genotypes (i.e., the proportion of AA, Aa, and aas in case subjects and control subjects) will deviate from the true distribution, leading to reduced statistical power to detect associations.
In single marker association analysis, we used logistic regression to model the genotype-phenotype relationship, and test the significance of the regression coefficient. The power of the test is affected by sample size, effect size, and type I error rate. Under the alternative hypothesis, the test statistic approximately follows a noncentral chi-square distribution, and the noncentrality parameter is sufficient to characterize the power of the test (see Section 2.5 in Section 2). Another advantage of studying the noncentrality parameter instead of the statistical power itself is that the interpretation of the noncentrality parameter is independent of the type I error rate, which can vary by experimental design.
The influence of genotyping error in single marker association test has been intensively studied in the literature (see Section 1). Here, we focus on quantifying the loss of power incurred by the genotyping error in the CSP572 substudy. A hypothetical study was used to investigate the impact of genotype-specific error rate on statistical power. We considered the power of a GWAS with 10,000 cases and 10,000 controls, and a disease prevalence of 10%. The genotype-specific error rates estimated from the substudy were applied to model the distribution of WES genotypes. For common variants, the loss of power is minimal, even without stringent filtering (see Fig. 2). Applying a more stringent depth filter does not significantly increase the noncentrality parameter. The pattern is consistent across different allele frequencies and relative risks. To put the value of noncentrality parameter into perspective, at genome-wide significance level (P-value cutoff is 5 × 10−8), the power is roughly 0.8 when the noncentrality parameter is 40.
Figure 2.
Power analysis of single marker association test with multiplicative inheritance mode. The relative risk of the SNP is 1.2 and the minor allele frequency is 0.1. (Left) The noncentrality parameter with varying depth filters. Dashed line: the power of association test using true genotypes. Solid line with crosses: the power of association test when plugging in the empirical genotyping error rates with varying depth filter in the CSP572 substudy (right) The minimum sample size to achieve statistical power of 0.8 at varying depth filters
We focused on SNPs with minor allele frequency 0.1 as an example to explain the effect of genotyping errors. Adequate power generally exists to detect SNPs with relative risk no less than 1.3, even in the presence of genotyping errors. For an SNP with relative risk 1.2, the minimum sample size needed to achieve the power of 0.8 is 12,059 when we apply a depth filter of 5, compared to 9,863 when there is no genotyping error (see Fig. 2). Therefore, it is important to consider the genotyping quality in experimental design, but the sample size needed to compensate the power loss is modest. The results for dominant and recessive modes of inheritance are shown in supplementary Figures S4 and S5.
3.3 Statistical power for rare variant analysis
The single-marker analysis is underpowered to study rare variant association. In particular, in the presence of genotyping error that fails to detect the reference genotype, the minimum sample size needed to maintain power increases indefinitely when the minor allele frequency approaches zero (Kang et al., 2004). To boost power, collapsing methods—in which the genotypes across multiple rare variants in a gene/region are collapsed—are frequently used. Here, we use the burden test to study the power of identification of multiple rare variant association. In the burden test, suppose there are multiple rare variants in a gene/region, and the frequencies of samples with at least one rare allele in cases (ϕcase) and that in controls (ϕcontrol) are compared (see Section 2). The theoretical power of burden tests can be inferred by estimation of ϕcase and ϕcontrol. In practice, the power of the test can be compromised due to the difference of the inferred genotypes and the true genotypes. In particular, the inaccurate inference of genotypes of multiple rare variants in a gene/region can collectively bias the estimation of ϕcase and ϕcontrol. As a result, the power of downstream association test in a GWAS is affected.
Genomic studies that use the WES platform for genotyping are geared to identify rare variant associations. With several assumptions (see section 2.5 in Section 2), the statistical power of burden tests that accounts for assay quality can be evaluated analytically. We first used a hypothetical examples to show how statistical power changes with the assay quality. Then, we used the quality metrics of the VA CSP572 substudy to evaluate the impact of quality on association tests.
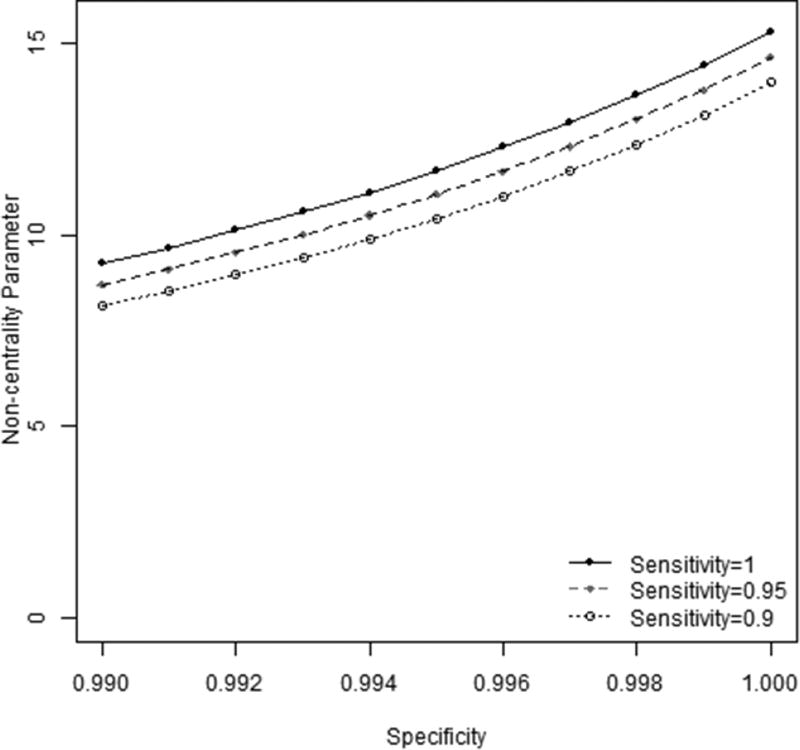
The hypothetical example was designed to investigate the influence of specificity on the statistical power of the burden test. We considered a gene with 20 rare variants, each with allele frequency 0.01 and with relative risk set to 3. The numbers of cases and controls were set to 10,000. The sensitivity was fixed at three different levels, 0.9, 0.95, and 1, and the specificity varied between 0.99 and 1.0. We referenced the CSP572 substudy to select the range and magnitude of changes of sensitivity and specificity. When specificity changes at magnitude of 0.01 and sensitivity was fixed at either 0.9, 0.95, or 1, the change in noncentrality parameter was around 6 (see Figure 3). On the contrary, the change of sensitivity from 0.9 to 1 only increased the noncentrality parameter at around 0.6, when the specificity was kept constant between 0.99 and 1 (see Figure 3). These results suggest that the power of burden test is more sensitive to the changes in specificity. In practice, sensitivity and specificity usually change together, perhaps at different magnitude. We have created an R package, “GWAS.PC,” which calculates power with different combinations of parameters. The best variant calling pipelines can be identified by computing and comparing statistical power of each pipeline.
Figure 3.
The influence of genotyping quality on the statistical power of burden test analysis
Next, we used the genotyping quality of variant calling to evaluate the statistical power to identify rare variant association in sequencing based genomic analyses. In particular, we showed how the power of association test changes with varying depth filters. When a more stringent depth filter was used, there was power loss in association tests (see Figure 4). Thus, although we can make more accurate variant callings for nonreference genotypes when more stringent filters are applied (Fig. 1), the statistical power is decreased due to the drop of the specificity parameter. Given this observation, we propose an imputation step that assigns all sites with no calls to the reference genotype. This proposed step can significantly increase the specificity, which in turn will increase the statistical power of association tests (see Figure 4). For example, for a gene with 20 rare variants, with a minor allele frequency of 0.01 and a relative risk of 3.0, the power to identify an association at a significance level of P = 0.0001 is 0.51. When considering genotyping errors, the power is 0.22 when variant callings with depth less than one are filtered out. With the proposed imputation step, however, the statistical power is increased to 0.33. Thus, in the context of genotyping quality at the level observed from the current substudy data, most of the statistical power can be retained.
Figure 4.
The power of burden test in the CSP572 substudy
3.4 Inflation caused by differential genotyping error and the adjusted power analysis
Differential genotyping error refers to the situation where the genotyping error is different in cases and controls. It is important to consider this type of error because it inflates type I error, and decreases power to association test. We evaluated the extent of differential genotyping error in our dataset. The subjects naturally fall into three categories, BP, SCZ, and CTRL. We first compared the genotype-specific error rate of BP versus CTRL, and SCZ versus CTRL, and calculated the noncentrality parameter of the null distribution (Tables 2 and 3). The shift of noncentrality parameter from the centralized chi-square distribution is small, and the corresponding inflation of type I error is ignorable. Nevertheless, our method can be applied to adjust for inflation caused by differential error in general situations. Kim et al. (2012) also studied the effect of differential error. However, in their model, the error refers to sequencing error instead of genotyping error as discussed here. Sequencing error is the probability of reading nucleotide A as B in sequencing reads, and only part of the genotyping error is attributed to sequencing error.
TABLE 2.
The inflation in single marker test caused by differential genotyping error in CSP572 substudy
| Depth Filter | SCZ vs. CTRL | BP vs. CTRL |
|---|---|---|
| 1 | 7.70 × 10−2 | 4.64 × 10−3 |
| 2 | 6.75 × 10−2 | 1.64 × 10−3 |
| 3 | 7.09 × 10−2 | 5.16 × 10−3 |
| 4 | 5.93 × 10−2 | 4.91 × 10−3 |
| 5 | 5.64 × 10−2 | 6.09 × 10−3 |
| 6 | 5.52 × 10−2 | 6.40 × 10−3 |
| 7 | 4.57 × 10−2 | 8.83 × 10−3 |
| 8 | 4.11 × 10−2 | 1.11 × 10−3 |
| 9 | 3.71 × 10−2 | 1.50 × 10−2 |
| 10 | 3.33 × 10−2 | 2.29 × 10−2 |
TABLE 3.
The inflation in multiple marker test caused by differential genotyping error in CSP572 substudy
| Depth Filter | SCZ vs. CTRL | BP vs. CTRL |
|---|---|---|
| 1 | 0.77 | 3.89 × 10−5 |
| 2 | 0.68 | 9.99 × 10−5 |
| 3 | 1.01 | 2.68 × 10−3 |
| 4 | 0.76 | 1.85 × 10−2 |
| 5 | 1.07 | 1.26 × 10−2 |
| 6 | 0.90 | 1.54-× 10−4 |
| 7 | 1.15 | 1.03 × 10−2 |
| 8 | 1.15 | 2.581 × 10−4 |
| 9 | 0.84 | 1.12 × 10−2 |
| 10 | 1.02 | 7.51 × 10−5 |
4 DISCUSSION
Statistical power is important in genomic study designs, and a number of factors are commonly considered in performing such analyses, including allele frequency, relative risk, and model of inheritance. In this report, we have further considered the impact of genotyping and sequencing errors on statistical power for association analysis. We have demonstrated that assay quality is an important factor to consider in power analysis, both for single marker and multiple marker analysis. In multiple rare variant analysis, the power of the burden test is very sensitive to the specificity that reference genotypes are called. Therefore, it is important to consider genomic assay quality when designing genomic studies. Our power analysis framework can be applied to association studies when preliminary data are available to assess the genomic assay quality of the study. It can also be used to calculate the sample size needed to achieve targeted power, especially when additional samples may be needed to compensate for the power loss due to imperfect genotyping. With high-quality variant calling results, such as those estimated from the CSP572 substudy, errors will likely have minimal effect on the power to detect both common and rare variant association. Moreover, the proposed framework can be extended to study the power of other types of statistical association tests.
For a new sequencing study when no array-based genotyping is available, in order to do power analysis, we have the following suggestions. First, include at least one reference sample (e.g., a HapMap sample with known genotype) in every sequencing batch. The reference sample can be used to estimate genotyping error rate. Second, compare the depth information in cases and controls. If there is substantial difference, choose the “differential genotyping error” mode in power analysis.
Our study can also inform the selection of quality control parameters. Our results suggest that less stringent filters are recommended in the pursuit of power in GWAS studies, although this approach may not be relevant in other situations. (For example, stringent filters should be applied in the study of Mendelian disease to distinguish heterozygous and homozygous nonreference genotypes.) This work was conducted in the context of the VA Million Veteran Program, specifically as part of an alpha-test project assessing genetic influences on SCZ and BP disorder. From a broader perspective, the Million Veteran Program is aligned with the Precision Medicine Initiative (Collins & Varmus, 2015), a U.S. Health and Human Services initiative. With these and similar efforts worldwide, it will be important to examine methodological approaches for analyzing the results of genotyping and sequencing laboratory assays.
In summary, we have considered an analytical framework for power analysis that accounts for genotyping quality of GWAS data. More specifically, we studied the impact of errors in genomic assays on the power of association tests for single marker and multiple rare markers, using the data quality estimated from data collected from an ongoing genomic study of SCZ and BP disorder. For common variant analysis, the power loss is minimal. For rare variant analysis, we found out that it is important to ensure a high specificity in variant calling. Here, we focused on assessing the genotyping quality and its impact on power of association test, however, the value of the dataset is not limited by the scope of this paper. As suggested by Borchers et al., the duplicated genotype data can be modeled to increase power of association test (Borchers, Brown, McLellan, Bekmetjev, & Tintle, 2009; Tintle, Gordon, Bruggen, & Finch, 2009). Our general framework can help human geneticists in developing genomic study designs, and it also provides a basis to optimize variant calling pipelines to maximize statistical power for downstream association analysis.
Supplementary Material
Acknowledgments
This research was supported by the VA Office of Research and Development (Cooperative Studies Program #572 and Million Veteran Program #G002). The authors thank staff members on the corresponding projects, Sandra Augustitus for assistance with the manuscript, and especially participants who previously served their country and agreed to enroll in these studies. Dr. Harvey has served as a consultant to Boeheringer-Ingelheim, Forum Pharma, Lundbeck, Otsuka-America, Sanofi, Sunovion, and Takeda, and he has received a research grant from Takeda; these activities are not related to the content of this paper. Support from the VA Office of Research and Development included input from Drs. Grant Huang, Jennifer Moser, Sumitra Muralidhar, Ronald Przygodzki, and Timothy O’Leary.
Footnotes
Additional Supporting Information may be found online in the supporting information tab for this article.
References
- Ahn K, Haynes C, Kim W, Fleur RS, Gordon D, Finch S. The effects of SNP genotyping errors on the power of the Cochran-Armitage linear trend test for case/control association studies. Annals of Human Genetics. 2006;71:249–261. doi: 10.1111/j.1469-1809.2006.00318.x. [DOI] [PubMed] [Google Scholar]
- Borchers B, Brown M, McLellan B, Bekmetjev A, Tintle N. Incorporating duplicate genotype data into linear trend tests of genetic association, methods and cost-effectiveness. Statistical Applications in Genetics and Molecular Biology. 2009;8(1):1–20. doi: 10.2202/1544-6115.1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Challis D, Yu J, Evani US, Jackson AR, Paithankar S, Coarfa C, Yu F. An integrative variant analysis suite for whole exome nect-generation sequencing data. BMC Bioinformatics. 2012;13(1):8. doi: 10.1186/1471-2105-13-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cirulli ET, Goldstein DB. Uncovering the roles of rare variants in common disease through whole-genome sequencing. Nature Review Genetics. 2010;11(6):415–425. doi: 10.1038/nrg2779. [DOI] [PubMed] [Google Scholar]
- Collins FS, Varmus H. A new initiative on precision medicine. New England Journal of Medicine. 2015;372:793–795. doi: 10.1056/NEJMp1500523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook K, Benitez A, Fu C, Tintle N. Evaluating the impact of genotype errors on rare variant tests of association. Frontiers in Genetics. 2014;5:62. doi: 10.3389/fgene.2014.00062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo MA, Banks E, Poplin R, Garimella KV, Maguire JR, Hartl C, Daly MJ. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nature Genetics. 2011;439(5):491–498. doi: 10.1038/ng.806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garner C. Confounded by sequencing depth in association studies of rare alleles. Genetic Epidemiology. 2011;35:261–268. doi: 10.1002/gepi.20574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaziano M, Concato J, Brophy M, Fiore L, Pyarajan S, Breeling J, O’Leary TJ. Million veteran program (MVP): A mega-biobank to study genetic influences on health and disease. Journal of Clinical Epidemiology. 2016;70(2):214–223. doi: 10.1016/j.jclinepi.2015.09.016. [DOI] [PubMed] [Google Scholar]
- Gordon D, Finch S. Factors affecting statistical power in the detection of genetic association. Journal of Clinical Investigation. 2005;115(6):1408–1418. doi: 10.1172/JCI24756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon D, Haynes C, Yang Y, Kramer P, Finch S. Linear trend test for case-control genetic association that incorporate random phenotype and genotype classification error. Genetic Epidemiology. 2007;31:853–870. doi: 10.1002/gepi.20246. [DOI] [PubMed] [Google Scholar]
- Gordon D, Ott J. Assessment and management of single nucleotide polymorphism genotype errors in genetic association analysis. Pacific Symposium on Biocomputing. 2001;6:18–29. doi: 10.1142/9789814447362_0003. [DOI] [PubMed] [Google Scholar]
- Gordon D, Yang Y, Haynes C, Finch S, Mendell N, Brown A, Haroutunian V. Increasing power for tests of genetic association in the presence of phenotype and/or genotype error by use of double-sampling. Statistical Applications in Genetics and Molecular Biology. 2004;3(1):1–32. doi: 10.2202/1544-6115.1085. [DOI] [PubMed] [Google Scholar]
- Harvey PD, Siever LJ, Huang GD, Muralidhar S, Zhao H, Miller P, Concato J. The genetics of functional disability in schizophrenia and bipolar illness: Methods and initial results for VA cooperative study #572. American Journal of Medical Genetics Part B: Neuropsychiatric Genetics. 2014;165 B(4):381–389. doi: 10.1002/ajmg.b.32242. [DOI] [PubMed] [Google Scholar]
- Hindorff LA, Sethupathy P, Junkins HA, Ramos EM, Mehta JP, Collins FS, Manolio TA. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proceedings of the National Academy of Science of the United States of America. 2009;106(23):9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirschhorn JN, Daly MJ. Genome-wide association studies for common diseases and complex traits. Nature Review Genetics. 2005;6(2):95–108. doi: 10.1038/nrg1521. [DOI] [PubMed] [Google Scholar]
- Kang SJ, Finch SJ, Haynes C, Gordon D. Quantifying the percent increase in minimum sample size for SNP genotyping errors in genetic model-based association studies. Human Heredity. 2004;58:139–144. doi: 10.1159/000083540. [DOI] [PubMed] [Google Scholar]
- Kang SJ, Gordon D, Finch SJ. What SNP genotyping errors are most costly for genetic association studies? Genetic Epidemiology. 2004;26:132–141. doi: 10.1002/gepi.10301. [DOI] [PubMed] [Google Scholar]
- Kim W, Londono D, Zhou L, Xing J, Nato AQ, Musolf A, Gordon D. Single-variant and multi-variant trend tests for genetics association with next-generation sequencing that are robust to sequencing error. Human Heredity. 2012;74:172–183. doi: 10.1159/000346824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koboldt DC, Chen K, Wylie T, Larson DE, McLellan MD, Mardis ER, Ding L. Varscan: Variant detection in massively parallel sequencing of individual and pooled samples. Bioinformatics. 2009;25(17):2283–2285. doi: 10.1093/bioinformatics/btp373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Durbin R. Fast and accurate short read alignment with burrows—Wheeler trans-form. Bioinformatics. 2009;25(14):1754–1760. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N 1000 Genome Project Data Processing Subgroup. The sequence alignment/ map format and samtools. Bioinformatics. 2009;25(16):2078–2079. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: Application to analysis of sequence data. American Journal of Human Genetics. 2008;83(3):311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, Visscher PM. Finding the missing heritability of complex diseases. Nature. 2009;461(7265):747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer-Jochimsen M, Fast S, Tintle N. Assessing the impact of differential genotyping errors on rare variant tests of association. PLoS ONE. 2013;8(3):e56626. doi: 10.1371/journal.pone.0056626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaelson JJ, Shi Y, Gujral M, Zheng H, Malhotra D, Jin X, Sebat J. Whole-genome sequencing in autism identifies hot spots for de novo germline mutation. Cell. 2012;151(7):1431–1442. doi: 10.1016/j.cell.2012.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moskvina V, Craddock N, Holmans P, Owen MJ, O’Donovan M. Effects of differential genotyping error rate on the type I error probability of case-control studies. Human Heredity. 2006;61:55–64. doi: 10.1159/000092553. [DOI] [PubMed] [Google Scholar]
- Mote VL, Anderson RL. An investigation of the effect of misclassification on the properties of χ2 tests in the analysis of categorical data. Biiometrica. 1965;52:95–109. [PubMed] [Google Scholar]
- Need AC, McEvoy JP, Gennarelli M, Heinzen EL, Ge D, Maia JM, Goldstein DB. Exome sequencing followed by large-scale genotyping suggests a limited role for moderately rare risk factors of strong effect in schizophrenia. American Journal of Human Genetics. 2012;91(2):303–312. doi: 10.1016/j.ajhg.2012.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Roak BJ, Deriziotis P, Lee C, Vives L, Schwartz JJ, Girirajan S, Eichler EE. Exome sequencing in sporadic autism spectrum disorders identifies severe de novo mutations. Nature Genetics. 2011;43(6):585–589. doi: 10.1038/ng.835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pluzhnikov A, Below JE, Konkashbaev A, Tikhomirov A, Kistner-Griffin E, Roe CA, Cox N. Spoiling the whole bunch: Quality control aimed at preserving the integrity of high-throughput genotyping. American Journal of Human Genetics. 2010;87:123–128. doi: 10.1016/j.ajhg.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers S, Gopalakrishnan S, Tintle N. Assessing the impact of non-differential genotyping errors on rare variants tests of association. Human Heredity. 2011;72:152–159. doi: 10.1159/000332222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice KM, Holmans P. Allowing for genotyping error in analysis of unmatched case-control studies. Annals of Human Genetics. 2003;67:165–174. doi: 10.1046/j.1469-1809.2003.00020.x. [DOI] [PubMed] [Google Scholar]
- Tenenbein A. A double sampling scheme for estimating from binomial data with misclassifications. Journal of the American Statistical Association. 1970;65(331):1350–1361. [Google Scholar]
- Tenenbein A. A double sampling scheme for estimating from binomial data with misclassifications: Sample size determination. Biometrics. 1971;27:935–944. [Google Scholar]
- Tenenbein A. A double sampling scheme for estimation from misclassified multinomial data with applications. Technometrics. 1972;14(1):187–202. [Google Scholar]
- Tintle N, Gordon D, Bruggen DV, Finch S. The cost effectiveness of duplicate genotyping for testing genetic association. Annals of Human Genetics. 2009;73:370–378. doi: 10.1111/j.1469-1809.2009.00516.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan Q, Chen R, Sutcliffe JS, Cook EH, Week DE, Li B, Chen W. The impact of genotype calling errors on family-based studies. Scientific Report. 2016;6:28323. doi: 10.1038/srep28323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Visscher PM. Common SNPs explain a large proportion of the heritability for human height. Nature Genetics. 2010;42(7):565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.