The influence of respiratory motion on dose delivery in a mouse lung tumour irradiation using the 4D MOBY phantom

Abstract

Objective:

During precision irradiation of a preclinical lung tumour model, the tumour is subject to breathing motion and it can partially move out of the irradiation field. This work aimed to perform a quantitative analysis of the impact of respiratory motion on a mouse lung tumour irradiation with small fields.

Methods:

A four-dimensional digital mouse whole body phantom (MOBY) with a virtual 4-mm spherical lung tumour at different locations in both lungs is used to simulate a breathing anaesthetized mouse in different breathing phases representing a full breathing cycle. The breathing curve is determined by fluoroscopic imaging of an anaesthetized mouse. Each MOBY time frame is loaded in a dedicated treatment planning system (small animal radiotherapy-Plan) and is irradiated by a full arc with a 5-mm circular collimator. Mean and time-dependent organ doses are calculated for the tumour, heart and spinal cord.

Results:

Depending on the location of the lung tumour, an overestimation of the mean tumour dose up to 11% is found. The mean heart dose could be both overestimated or underestimated because the heart moves in or out of the irradiation field depending on the beam target location. The respiratory motion does not affect the mean spinal cord dose. A dose gradient is visible in the time-dependent tumour dose distribution.

Conclusion:

In the future, new methods need to be developed to track the lung tumour motion before preclinical irradiation to adjust the irradiation plan. Margins, collimator diameter and target dose could be changed easily, but they all have their drawbacks. State-of-the-art clinical techniques such as respiratory gating or motion tracking may offer a solution for the cold spots in the time-dependent tumour dose.

Advances in knowledge:

A suitable method is found to quantify changes in organ dose due to respiratory motion in mouse lung tumour image-guided precision irradiation.

INTRODUCTION

Small animal models are increasingly used in preclinical cancer radiobiology research to investigate the characteristics of cancer, e.g. tumour progression, metastases or hypoxia.¹ The combinational use of precision kilovolt X-ray irradiators and high-resolution cone-beam CT imaging systems provides an improvement of the accuracy in small animal image-guided radiotherapy.² Respiratory motion in small animals during image-guided precision irradiation is mentioned as a concern which has not been investigated in the literature yet.² Some organs could change position in the mouse as a function of time owing to breathing, which is not taken into account in currently available small animal precision irradiators and associated treatment planning software.

While irradiating a mouse with a lung tumour in small animal precision radiotherapy, the tumour can partially move out of the small irradiation field such that certain regions of the tumour will not be irradiated for a small period of time. During the whole irradiation treatment, there are multiple breathing cycles where the tumour can partially or completely move out of the irradiation field. This issue is caused by the breathing motion and is more severe in small animals than in human patients. First, because mice can be irradiated with precision beams using small margins between beam and target. Secondly, because the relative displacement of the lung tumour will be larger in a mouse than that in a human. Currently, commercially available image-guided small animal radiation research systems³ such as the Xstrahl Ltd (Camberley, UK) small animal radiation research platform or the Precision X-ray Inc. (North Branford, CT) X-Rad small animal radiotherapy (SmART) do not provide an option to perform four dimensional (4D) CT imaging. Therefore, we cannot perform dose calculations on each 4D CT time frame. In this work, we estimate the influence of breathing motion on the mean dose and the time-dependent dose in a mouse lung tumour irradiation in a mathematical phantom.

METHODS AND MATERIALS

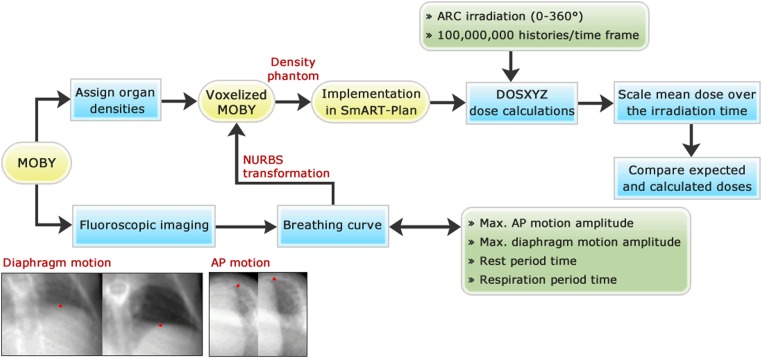
Figure 1 describes the workflow which will be explained in the following sections.

Figure 1.

Flow diagram of the procedure to estimate lung tumour dose over time: the computer programs are shown in the rounded yellow rectangles, the methods in the blue rectangles and the parameters or settings in the partially rounded green rectangles. The red dots in the fluoroscopic images are the most extreme diaphragm and anteroposterior (AP) position. The maximum motion amplitudes are determined by taking the difference between these most extreme points. MOBY, digital mouse whole body phantom; NURBS, non-uniform rational B-splines.

Four-dimensional digital mouse whole body

Figure 2 displays the digital mouse whole body phantom (MOBY), which is used to create a realistic and versatile respiratory model of the mouse anatomy.⁴ Raw 32-bit binary output files are generated using the “activity mode”, where radionuclide activities for the various organs can be assigned in the input file. Instead of assigning activities, we assigned tissue densities to the organs listed in the activity mode. Owing to the lack of small animal tissue data, human tissue densities and compositions^5,6 are assigned to the organ activity values. This assignment results in a MOBY consisting of tissue densities.

Figure 2.

Lateral view of the digital mouse whole body phantom⁴ and its Cartesian coordinate system, with several organs segmented (used with permission of W Paul Segars).

Originally, the breathing curve of a tidal breathing mouse without a resting phase was implemented in MOBY by the developers. This curve was obtained by monitoring time-dependent volume changes of a tidal breathing human, scaled to the dimensions of a mouse.⁴ In preclinical research, the mouse will be irradiated under the influence of anaesthesia whereby the resulting breathing pattern will be slower and deeper; hence, a new breathing curve must be obtained.

The respiratory motion of the phantom is modelled by a breathing curve which can be characterized by determining four parameters defined in the originally implemented curve: the (i) maximum diaphragm motion amplitude, (ii) maximum anteroposterior (AP) motion amplitude, (iii) rest period time and (iv) respiration period time. No left–right motion is modelled.

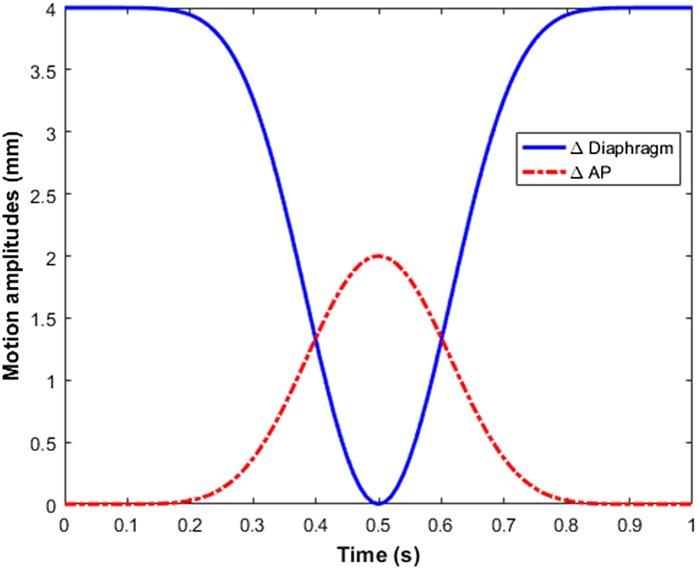
Fluoroscopic X-ray imaging (30 frames per second, 80 kVp, 4.0 mA) of a deeply anaesthetized mouse (isoflurane) is performed using the onboard imaging panel of the X-RAD 225Cx irradiator (Precision X-ray Inc., North Branford, CT) to determine the four parameters described above. Figure 3 illustrates a breathing curve derived from these fluoroscopic imaging measurements. Both motion curves are obtained by using the image-processing toolbox available in MATLAB^® v. R2012b (The MathWorks Inc., Natrick, MA). The diaphragm and AP motion amplitudes are tracked at the most extreme points on the transition from lung to surrounding tissue. A visualization of this tracking method is added to the Supplementary Materials. The observed rotation in this visualization is due to the rotation of the onboard imaging panel.

Figure 3.

The diaphragm and anteroposterior (AP) motion amplitudes as a function of time obtained by fluoroscopic X-ray imaging of an anaesthetized breathing mouse: the long resting phase due to the use of anaesthetic gas (isoflurane) can be noticed. A breathing digital mouse whole body phantom is visualized on the basis of these two parameters and is added to the Supplementary Materials.

The maximum AP amplitude, maximum diaphragm amplitude, rest period time and respiration period time are found to be 2.0 mm, 4.0 mm, 2.2 s and 0.6 s respectively. The diaphragm motion amplitude starts at 4.0 mm owing to the negative z diaphragm movement during inspiration according to the coordinate system in Figure 2. Following the same reasoning, the AP motion amplitude curve starts at the origin owing to the positive y movement during the inspiration phase.

The full breathing curve is converted in non-uniform rational B-splines (NURBS) allowing the curve to be implemented in MOBY. NURBS are preferred to model the respiratory motion because the curve parameters can be spline-interpolated in time to create a 4D phantom for any time interval.

As a final step, the MOBY software samples the NURBS lung volume of the phantom in time frames consisting of 256 × 256 × 101 voxels with an isotropic size of 0.2 mm. The cubic voxel size determines the resolution of the resulting voxelized phantom. In correct sequential order, 56 output frames represent a full breathing cycle of 2.80 s, in which each frame represents a time interval of 50 ms.

Digital mouse whole body phantom simulation cases

A total of eight different MOBY breathing simulation cases are divided equally into two main series: the right and left lung series. The two series are created by placing the lung tumour at four different z positions in each lung, while the x and y initial coordinates of the lung tumour are fixed throughout the creation of each series. The centre of the 4-mm sphere lung tumour is displaced 2 mm in the positive z direction for each following MOBY simulation case in the series.

Figure 4 shows eight average MOBY breathing phases obtained over the whole breathing cycle. Especially in the first and second case of both series, the tumour movement in the negative y and z directions due to breathing can be clearly seen as a blurred tumour on the average motion images. This blurring, due to organ motion, is also visible in the average left lung images with respect to the heart.

Figure 4.

The average motion images over the whole 2.8-s breathing cycle of the eight digital mouse whole body phantom simulation cases in left (L, bottom) and right (R, top) lungs taking into account the derived breathing curve of an anaesthetized mouse: the tumour is shown as a white sphere in all cases; the heart can be seen only in the left lung series as white structure situated under the tumour. The white colour of both the tumour and heart is used only for visualization purposes; correct tissue values are assigned in the simulation.

Small animal radiotherapy-Plan

SmART-Plan⁷ (PXi, North Branford, CT) is a dedicated SmART treatment planning system (TPS) developed for use in preclinical research. It is preferred over a clinical TPS considering the small voxel sizes, small irradiation beams and kilovoltage X-rays employed for irradiation. Currently, SmART-Plan does not allow dose calculations in moving mouse geometries.

SmART-Plan is modified using MATLAB to perform dose calculations on all MOBY time frames constituting one breathing cycle. For each simulation case, the new automated SmART-Plan script loads each voxelized MOBY time frame in the computer memory, whereby structure delineation is performed based on the organ densities assigned in the voxelized dense MOBY. The preset irradiation treatment is planned on the memorized time frame and a Monte Carlo (MC) dose calculation is started. These automatic delineation, planning and calculation processes are repeated for all the MOBY time frames constituting one breathing cycle of 2.8 s. When the dose calculations of one simulation case are terminated, a rescaling of the mean structure doses is performed, which will be further explained in following paragraphs. A more detailed explanation is added in Appendix B.

Full arc irradiations are performed to deliver an 8-Gy target dose to the lung tumour. In each case, the beam is centred on the initial position of the tumour. By making use of SmART-Plan, MC DOSXYZnrc dose calculations⁸ are executed on all MOBY time frames of each single case, taking into account the parameters listed in Table 1.

Table 1.

Treatment and calculation settings of small animal radiotherapy (SmART)-Plan combined with the digital mouse whole body phantom (MOBY) parameters to perform Monte Carlo dose calculations

SmART-Plan settings		MOBY parameters
Irradiation plane	360° arc	Time resolution (∆t)	50 ms
Beam diameter	5 mm	Tumour diameter	4 mm
Planned target dose	8 Gy	Breathing curve	Anaesthetized mouse (Figure 3)
Histories per frame	100,000,000

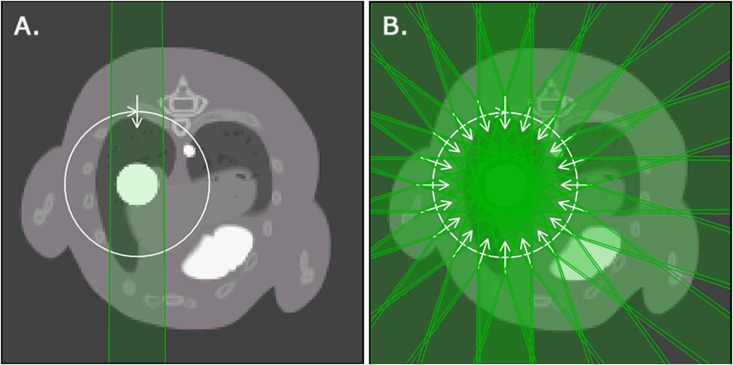
The final organ doses are determined in two different approaches (Figure 5): (i) the mean organ doses and (ii) the time-dependent organ doses. The organs for which dose is reported are the tumour, heart and spinal cord. Owing to the changes in lung volume, it is challenging to calculate mean and time-dependent lung doses.

Figure 5.

The axial view of the digital mouse whole body phantom integrated in small animal radiotherapy-Plan is showing the two different dose calculation methods: (a) a full 360° arc irradiation is used to obtain the mean organ doses for each discrete time frame in the whole breathing cycle and (b) 20 equally spaced beams are used in each time frame to represent a full arc irradiation and to obtain time-dependent organ doses.

Mean organ doses

Every static MOBY time frame is loaded separately in SmART-Plan. Each time frame is treated as a static geometry. Mean organ doses are determined in each time frame; hence, a rescaling of the obtained mean organ doses is required to achieve dynamic mean organ doses taking into account the respiratory motion.

The rescaled value of the final mean organ dose D_organ is calculated according to following equation:

$$D_{\text{organ}}=({\displaystyle \sum _{i=1}^N\frac{D_{\text{organ},i}}{t_{\text{irr},i}}·\Delta t·)C_{\text{br}}}\hspace{0.17em}\text{,}$$ (1)

where N is the total number of MOBY time frames in one breathing cycle, D_organ,i is the mean organ dose in time frame i, t_irr,i is the total irradiation time corresponding to each loaded time frame i estimated by SmART-Plan, ∆t is the time interval of one MOBY time frame (50 ms) and C_br is the total number of breathing cycles during the irradiation beam on time.

Time-dependent organ doses

This method to determine the dose distribution is more complicated because of the dynamic interplay between the motion of the gantry and the phantom. MC dose calculations are performed on the same eight MOBY simulation cases to obtain a more realistic dose distribution in the tumour, taking into account both breathing motion and gantry rotation. The SmART-Plan settings and the MOBY parameters remain the same, with the exception of the irradiation plan. The original 360° arc is now divided into 20 beams rotated 18° relative to each other.

The respiratory period of the MOBY occurs only during the breathing peak of 600 ms, which is represented by 13 MOBY time frames including the starting point. Each of these MOBY time frames are loaded in SmART-Plan as a static geometry and are treated according to the modified irradiation plan. Dose calculations are performed for each beam of each MOBY time frame, which results in a total number of 260 dose distributions. A time-dependent dose distribution of the tumour, heart and spinal cord can now be calculated by making use of these dose distributions in combination with the interrelationship between the organ displacement caused by breathing, the beam number and the MOBY time frame at specific time intervals.

RESULTS

Lung tumour displacement

The displacement of the centre of mass of the lung tumour due to breathing is quantified for all MOBY simulation cases. The maximum three-dimensional lung tumour displacement (Table 2) is calculated with the maximum y and z tumour displacement compared with the tumour position in the first MOBY time frame, ∆y_max and ∆z_max, respectively. There is no measurable tumour displacement in the x direction all cases in both lungs.

Table 2.

Maximum lung tumour displacements of all digital mouse whole body phantom (MOBY) simulation cases in the Cartesian coordinate system (TD_max² = y² + z²)

Cases	R series (mm)			L series (mm)
	∆ymax	∆zmax	TDmax	∆ymax	∆zmax	TDmax
Case 1	−1.4	−3.9	4.1	−1.4	−3.9	4.1
Case 2	−1.0	−2.7	2.8	−1.2	−3.4	3.6
Case 3	−0.3	−0.9	1.0	−0.2	−0.2	0.3
Case 4	0.1	−0.1	0.1	0.1	−0.1	0.1

∆y_max, maximum y tumour displacement compared with the tumour position in the first MOBY time frame; ∆z._max, maximum z tumour displacement compared with the tumour position in the first MOBY time frame.

TD-tumour displacement.

Mean organ doses

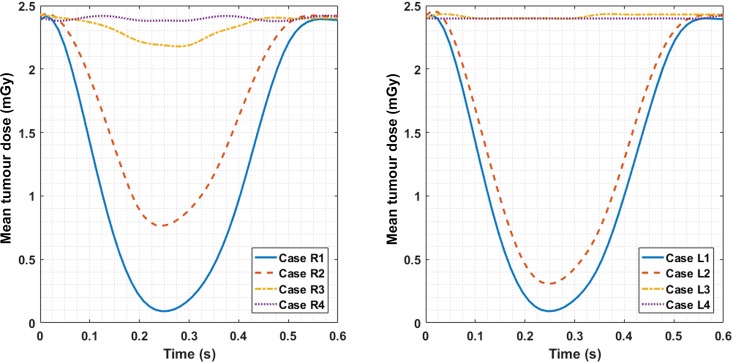
During the arc irradiation in the 600-ms breathing peak, the mean tumour dose delivered in each MOBY time frame (50 ms) is shown in Figure 6. Only the breathing peak time interval is shown in the graph because the mean doses delivered in the rest phase do not change with time.

Figure 6.

The spline-interpolated mean tumour dose delivered to each time frame of 50 ms during the breathing peak of 600 ms (Figure 3) for both right and left lung simulation cases.

These obtained mean organ doses delivered to each MOBY time frame are averaged to a final mean organ dose over the full irradiation according to Equation (1). Table 3 lists the rescaled mean organ doses delivered to the tumour, heart and spinal cord. The obtained mean and expected mean doses are considered in a breathing and a non-breathing MOBY, respectively. Relative differences are determined between the obtained and expected mean organ doses. This provides an insight into the percentage overestimation (−) or underestimation (+) of the mean organ dose due to respiratory motion.

Table 3.

The expected (static) and obtained (moving) mean dose for the tumour, heart and spinal cord of all simulation cases in both right (R) and left (L) lungs. The beam on time calculated by small animal radiotherapy-Plan is shown between brackets to the right of the simulation case number, this value could be used to calculate mean dose rates and rotation speeds

Organs	Expected (Gy)	Obtained (Gy)	Difference %	Expected (Gy)	Obtained (Gy)	Difference %
	Case R1 (165.5 s)			Case L1 (165.0 s)
Tumour	7.93 ± 0.03	7.09 ± 0.05	−11	7.92 ± 0.03	7.09 ± 0.05	−11
Heart	0.40 ± 0.01	0.52 ± 0.01	30	0.51 ± 0.01	0.64 ± 0.01	25
Spinal cord	0.69 ± 0.05	0.69 ± 0.05	0	0.70 ± 0.04	0.70 ± 0.05	0
	Case R2 (163.1 s)			Case L2 (163.2 s)
Tumour	7.91 ± 0.03	7.40 ± 0.03	−6	7.91 ± 0.03	7.22 ± 0.04	−9
Heart	1.18 ± 0.01	1.15 ± 0.02	−3	1.46 ± 0.01	1.40 ± 0.02	−4
Spinal cord	0.80 ± 0.05	0.81 ± 0.05	1	0.78 ± 0.04	0.78 ± 0.04	0
	Case R3 (164.6 s)			Case L3 (164.6 s)
Tumour	7.95 ± 0.03	7.89 ± 0.03	−1	7.95 ± 0.03	7.94 ± 0.05	0
Heart	1.30 ± 0.02	1.15 ± 0.02	−12	1.55 ± 0.03	1.36 ± 0.03	−12
Spinal cord	0.99 ± 0.05	0.99 ± 0.05	0	0.90 ± 0.05	0.90 ± 0.04	0
	Case R4 (165.8 s)			Case L4 (164.7 s)
Tumour	7.96 ± 0.03	7.96 ± 0.03	0	7.94 ± 0.03	7.93 ± 0.03	0
Heart	0.51 ± 0.03	0.44 ± 0.03	−14	0.58 ± 0.04	0.50 ± 0.02	−14
Spinal cord	1.22 ± 0.05	1.21 ± 0.05	−1	1.02 ± 0.04	1.02 ± 0.04	0

Time-dependent organ doses

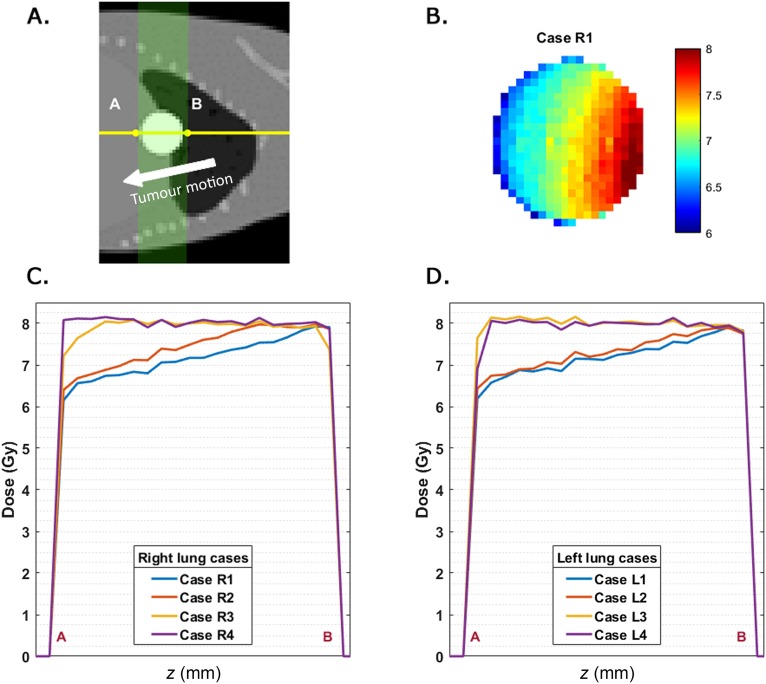
A dose profile along the line A–B in Figure 7a is determined in the time-dependent dose distribution at the position where the spherical tumour has its maximum diameter. These dose profiles were extracted for each case in the right and left lung series; the results are shown in Figure 7. Only the dose gradient of Case R1 is shown (Figure 7b) to obtain a better understanding of the time-dependent dose profiles in Figure 7c,d. Underdosage in the tumour of up to 23% can be seen in the volume that will move out of the irradiation field first. This difference will decrease if the tumour moves out of the irradiation field for a shorter period of time. The dose gradients for both lung series in the y, z plane are shown in Figure 7c,d.

Figure 7.

(a) The A–B dose profile line across the lung tumour is displayed on top of a digital mouse whole body phantom simulation case. The tumour motion is indicated by the arrow; the green area shown in the sagittal slice is covered by the 20 equally spaced beams. (b) The time-dependent dose distribution of the tumour in a y, z plane including the dose profile line A–B. (c, d) The A–B time-dependent tumour dose profiles of all simulation cases in right (c) and left (d) lungs.

DISCUSSION

The breathing motion amplitude of the mouse lung tumour strongly depends on its position in the lung. This amplitude is larger at tumour locations near the diaphragm and smaller at tumour locations near the top of the lung. For the two superiorly placed cases of the left and right lung series, the tumour displacement and tumour dose difference are sufficiently small to be ignored. This is caused by a combination of the tumour diameter (4 mm), circular field diameter (5 mm) and small motion amplitudes (approximately 0.1 mm), ensuring the radiation field encompasses the tumour at all times. In this study, motions only in the y and z directions are modelled, in accordance with mouse breathing measurements. Therefore, no motion in the x direction is modelled.

When the static dose calculation is compared with the one taking into account motion, the former overestimates the mean tumour dose by up to 11%. This adverse overestimation of the mean tumour dose due to breathing increases at lower tumour positions in the lung. In case of the heart, the relative difference of the mean heart dose strongly depends on the lung tumour position (range −14 to +30%). The tumour movement is smaller at higher lung tumour positions, although the heart displacement remains the same in all simulation cases. No cardiac pulses are modelled in the heart; the displacement of the heart is caused by breathing only in this model. Depending on the lung tumour and therefore the target position, the heart moves in or out of the small radiation beam. Mainly in the superior lung tumour positions, the heart moves out of the radiation beam, which results in an overestimation in the mean heart dose. The relative differences of the mean organ doses are consistent for both lungs taking into account the absolute tumour displacement, although the mean heart doses are larger when the tumour is situated in the left lung. In all simulation cases, the mean spinal cord dose remains constant during the irradiation treatment.

The time-dependent tumour dose distribution has the advantage that cold spots are visualized, which was not feasible with the mean dose rescaling method. A gradient in the z direction is noticeable in the dose section lines of the slice with a maximum tumour diameter. A steeper dose gradient is present when the tumour is located near the diaphragm, which decreases when the tumour is located higher in the lung. When the tumour is located at the top of the lung, the dose distribution is almost homogeneous. Cold spots are first visible in the region where the tumour starts to move out of the irradiation field. The dose reduction in a tumour voxel is proportional to the time it is out of the irradiation field.

A higher target dose can be set so that the whole lung tumour volume receives a minimum dose, although a resulting dose gradient due to breathing cannot be avoided in this way. The dose gradient can be avoided by irradiating the tumour with a collimator size equal to the tumour radius plus the maximum tumour displacement. A drawback of this approach is that the dose delivered to the surrounding organs will be increased significantly (Appendix A).

Using state-of-the-art techniques such as respiratory gating⁹ or motion tracking allows for the delivery of uniform dose distributions to the tumour without delivering higher doses to surrounding normal tissues. These techniques and related breathing mouse phantoms are not yet available in commercial image-guided small animal radiation research platforms, although they are currently being investigated.⁹ Studies like ours can provide guidelines for treatment margins to avoid underdosing target structures.

All the results in this work are obtained using one derived breathing pattern of an anaesthetized mouse and one irradiation plan with different tumour positions in the left and right lungs. It should be noted that the results will depend on the species, type of anaesthesia, tumour position and irradiation plan.

CONCLUSION

Usage of the mathematical motion MOBY in combination with a small animal TPS SmART-Plan provides a suitable method to quantify the dose reduction due to respiratory motion in a mouse lung tumour irradiation, based on mean doses.

Some differences between the expected and obtained mean tumour doses are large enough to take into account in small animal treatment planning of lung tumours. Especially in cases where the lung tumour is located near the diaphragm of the mouse, because the tumour displacement will be larger.

We recommend assessing the tumour motion of animal specimens using, for e.g., fluoroscopic imaging under treatment anaesthesia, before performing small animal precision irradiation. In the absence of gating or tracking techniques, the use of a suitable target volume margins is recommended.

Appendix A

The mean organ doses are calculated using the same MOBY settings and SmART-Plan parameters with the exception of a larger circular collimator of 10 mm instead of 5 mm.

Table A1.

The obtained mean organ doses, in case of a breathing MOBY phantom, are calculated using a 10-mm circular collimator instead of 5 mm, which was used in previous mean organ dose calculations. The absolute differences (in Gy) are calculated between the obtained doses using a 5-mm and a 10-mm collimator diameter

Organs	Obtained (Gy) Dcoll = 5 mm	Obtained (Gy) Dcoll = 10 mm	Absolute difference (Gy)	Obtained (Gy) Dcoll = 5 mm	Obtained (Gy) Dcoll = 10 mm	Absolute difference (Gy)
	Case R1			Case L1
Tumour	7.09 ± 0.05	7.84 ± 0.08	0.75	7.09 ± 0.05	7.83 ± 0.08	0.74
Heart	0.52 ± 0.01	2.58 ± 0.02	2.06	0.64 ± 0.01	3.16 ± 0.01	2.52
Spinal cord	0.69 ± 0.05	2.81 ± 0.07	2.12	0.70 ± 0.05	2.76 ± 0.06	2.06
	Case R2			Case L2
Tumour	7.40 ± 0.03	7.95 ± 0.08	0.55	7.22 ± 0.04	7.90 ± 0.08	0.68
Heart	1.15 ± 0.02	3.38 ± 0.02	2.23	1.40 ± 0.02	4.09 ± 0.01	2.69
Spinal cord	0.81 ± 0.05	3.50 ± 0.06	2.69	0.78 ± 0.04	3.34 ± 0.06	2.56
	Case R3			Case L3
Tumour	7.89 ± 0.03	7.98 ± 0.08	0.09	7.94 ± 0.05	7.97 ± 0.08	0.03
Heart	1.15 ± 0.02	3.30 ± 0.02	2.15	1.36 ± 0.03	3.95 ± 0.02	2.59
Spinal cord	0.99 ± 0.05	4.30 ± 0.05	3.31	0.90 ± 0.04	3.78 ± 0.05	2.88
	Case R4			Case L4
Tumour	7.96 ± 0.03	7.99 ± 0.08	0.03	7.93 ± 0.03	7.97 ± 0.08	0.04
Heart	0.44 ± 0.03	2.39 ± 0.03	1.95	0.50 ± 0.02	2.81 ± 0.02	2.31
Spinal cord	1.21 ± 0.05	4.94 ± 0.04	3.73	1.02 ± 0.04	4.18 ± 0.04	3.16

Dcoll, Collimator diameter.

The overestimation of the tumour dose can be avoided by using a larger collimator diameter which covers the maximum tumour displacement plus the tumour radius. As a drawback, the mean doses delivered to the surrounding tissues are much larger.

Appendix B

The dose calculations are performed using two different approaches. This appendix explains the mean and time-dependent dose calculations in more detail. Both approaches are influenced by time, but the mean doses are scaled only after calculation and the time-dependent dose distributions are calculated cumulatively over the irradiation time. The following detailed method description is performed fully automatically:

• (a) MOBY phantom creation

  • ▪ Eight mathematical 4D phantoms are created using the activity mode of the MOBY phantom. The organs are related to their density assigned in the activity mode.

  • ▪ In addition, eight 4D lung tumours phantoms are created using the MOBY spherical lesion generator that will create 4D phantoms of only the lung tumours.

  • ▪ The one-dimensional binary 32-bit output time frames (without header) of the MOBY density and tumour phantom are put together and rescaled to the correct dimensions in a 3D matrix using MATLAB. Each voxel in this matrix represents a density value of a specific organ.

• (b) Load the MOBY phantoms in SmART-Plan (one MOBY time frame at a time).

  • ▪ A 3D MOBY phantom time frame is loaded in SmART-Plan using the correct pixel spacing, pixel positions and image dimension. This volume is cropped to reduce the calculation time by eliminating unnecessary air voxels surrounding the phantom.

  • ▪ Based on the assigned organ densities and the known organ positions, automatic organ delineation and Electron Gamma Shower (EGS) material allocation is performed for each time frame. This allows us to automatically create an EGS phantom without time-consuming organ delineation.

  • ▪ A preset irradiation plan is planned on the initial lung tumour target position. This 3D target position is found automatically by calculating the centre of mass of the initial sphere lung tumour volume and is then used as target location in any following time frame of the simulation case. The used treatment plan depends on the chosen approach: (i) mean organ doses and (ii) time-dependent dose distributions.

  • ▪ The dose calculation is performed using the irradiation plan and the EGS phantom. When the dose calculation is terminated, mean organ doses are calculated in each time frame for the tumour, heart and spinal cord.

  • ▪ The SmART-Plan case is saved.

  • ▪ This automatic subprocess is performed for all time frames constituting one breathing cycle in one specific simulation case.

• (c) Rescaling of the mean doses over the irradiation time

  • ▪ The mean organ doses are calculated for each time frame assuming it was a full treatment; hence, a rescaling is applied using the total irradiation time or BOT provided by SmART-Plan. This total irradiation time is different for each MOBY time frame because the geometry of the phantom is changing owing to breathing.

  • ▪ Equation (1) can be translated into words. The mean organ dose in a time frame is divided by the BOT of the corresponding time frame to obtain a mean dose value per second. This value is then multiplied by the time resolution of a time frame (50 ms) to obtain a mean organ dose delivered in 50 ms. This calculation is performed for each time frame constituting one breathing cycle (2.8 s) and the doses are summed to obtain a mean organ dose delivered in one breathing cycle. The mean organ dose over the irradiation treatment is then determined by multiplying the mean organ dose in one breathing cycle by the total number of breathing cycles during the irradiation.

• (d) Calculate the cumulative dose distribution over the irradiation time

  • ▪ 20 equally spaced beams (360° arc) are placed on each MOBY time frame within the respiration period. For each of these 13 time frames, 20 separate dose distributions are calculated. This method results in 260 dose distributions, which have to be scaled with the total irradiation time of each beam.

  • ▪ A cumulative dose distribution can be calculated with a time resolution ∆t of 50 ms to obtain the time-dependent dose distribution as a final step. In this cumulative dose distribution, both the collimator rotation and the breathing motion are considered in the calculations.

  • ▪ While the mouse is breathing at time t, the 3D position of the tumour and its related dose distribution will be different at t + ∆t. A 3D translation of the dose volume has to be performed for each ∆t, based on the translated binary mask of the tumour volume. A 3D translation of the dose volume is necessary at each 50 ms while the mouse is breathing.

  • ▪ The dose volumes at different time intervals can be added using the method described above.

  • ▪ The final step of this calculation gives the time-dependent doses shown in the article.

Appendix C

A new non-realistic sinusoidal breathing curve y = A sin⁸ (πt) is implemented in the four left lung simulation cases.

This breathing curve should be interpreted in the same way as the previous curve, but note the exclusion of the rest period.

Figure C1. The non-realistic sinusoidal breathing curve in order to investigate the influence of the breathing curve on the dose calculations.

Table C1.

The expected (static) and obtained (moving) mean dose for the tumour, heart and spinal cord of all simulation cases in the left (L) lung. The beam on time calculated by small animal radiotherapy-Plan is shown between brackets to the right of the simulation case number; this value could be used to calculate mean dose rates and rotation speeds

Organs	Expected (Gy)	Obtained (Gy)	Difference %
	Case L1 (165.0 s)
Tumour	7.92	6.27	−21
Heart	0.52	0.79	52
Spinal cord	0.71	0.70	−1
	Case L2 (163.5 s)
Tumour	7.92	6.55	−17
Heart	1.46	1.36	−7
Spinal cord	0.79	0.79	0
	Case L3 (164.5 s)
Tumour	7.98	7.97	0
Heart	1.55	1.14	−26
Spinal cord	0.92	0.92	0
	Case L4 (164.5 s)
Tumour	7.97	7.96	0
Heart	0.57	0.38	−33
Spinal cord	1.04	1.03	−1