Optimizing dual energy cone beam CT protocols for preclinical imaging and radiation research

Abstract

Objective:

The aim of this work was to investigate whether quantitative dual-energy CT (DECT) imaging is feasible for small animal irradiators with an integrated cone-beam CT (CBCT) system.

Methods:

The optimal imaging protocols were determined by analyzing different energy combinations and dose levels. The influence of beam hardening effects and the performance of a beam hardening correction (BHC) were investigated. In addition, two systems from different manufacturers were compared in terms of errors in the extracted effective atomic numbers (Z_eff) and relative electron densities (ρ_e) for phantom inserts with known elemental compositions and relative electron densities.

Results:

The optimal energy combination was determined to be 50 and 90 kVp. For this combination, Z_eff and ρ_e can be extracted with a mean error of 0.11 and 0.010, respectively, at a dose level of 60 cGy.

Conclusion:

Quantitative DECT imaging is feasible for small animal irradiators with an integrated CBCT system. To obtain the best results, optimizing the imaging protocols is required. Well-separated X-ray spectra and a sufficient dose level should be used to minimize the error and noise for Z_eff and ρ_e. When no BHC is applied in the image reconstruction, the size of the calibration phantom should match the size of the imaged object to limit the influence of beam hardening effects. No significant differences in Z_eff and ρ_e errors are observed between the two systems from different manufacturers.

Advances in knowledge:

This is the first study that investigates quantitative DECT imaging for small animal irradiators with an integrated CBCT system.

INTRODUCTION

Dual-energy CT (DECT) imaging is now commonly used for a wide range of radiological purposes and shows potential for improving various parts of the radiotherapy workflow.¹ It has already been shown that DECT imaging can improve the accuracy of tissue segmentation and Monte Carlo dose calculations in the kilovoltage energy range,^2–8 which is promising for small animal radiotherapy. However, for preclinical imaging and small animal radiotherapy purposes, DECT imaging is still largely unexplored. Previous research in the field of small animal DECT imaging focused on using nanoparticle-based contrast agents to investigate atherosclerotic plaques, tumour vasculature and cardiac injury.^9–13

For DECT imaging, two images are acquired with two different X-ray spectra, which can be obtained by applying different X-ray tube voltages and/or different filters. The resulting CT number images can be decomposed into effective atomic number (Z_eff) images and relative electron density (ρ_e) images.^14,15 The current small animal irradiators with an integrated cone-beam CT (CBCT) system are not able to acquire the two different images simultaneously. However, the images can be acquired consecutively.

To achieve the typical submillimetre voxel sizes in small animal imaging, a relatively high imaging dose is required, which is generally one or two orders of magnitude higher than that in human imaging.^16,17 Although higher dose levels lead to better image quality, the imaging doses should always be as low as reasonably achievable to ensure the welfare of the animal and to avoid compromising the biological processes of interest. Tumour growth can be affected by doses exceeding 1 Gy;¹⁸ so, when two CT images are acquired for DECT imaging, the dose level for each acquisition should be below 50 cGy.

The aim of this work was to investigate whether quantitative DECT imaging is feasible for small animal irradiators with an integrated CBCT system. The optimal imaging protocols were determined by analyzing different energy combinations and dose levels. The influence of beam hardening effects and the performance of a beam hardening correction (BHC) were investigated. In addition, two systems from different manufacturers were compared in terms of errors in the extracted Z_eff and ρ_e for phantom inserts with known elemental compositions and relative electron densities.

METHODS AND MATERIALS

Mini phantoms

A series of measurements and simulations were performed using two mini phantoms each with 12 cylindrical inserts that have a 3.5-mm diameter (SmART Scientific Solutions, Maastricht, Netherlands). Figure 1 shows the phantom layout and Table 1 lists the Z_eff and ρ_e reference values provided by the manufacturer. One phantom, containing parts of tissue-equivalent inserts of a Gammex RMI 467 phantom (Gammex, Middleton, WI), was used for calibration. The other phantom, containing parts of CIRS 002ED inserts (CIRS, Norfolk, VA) plus other materials with known Z_eff and ρ_e, was used for validation. The water insert was created by filling a nuclear magnetic resonance (NMR) sample tube (Wilmad-LabGlass, Vineland, NJ) with distilled water. The inserts are contained in a Gammex CT Solid Water casing with a 3-cm diameter and a 1-cm width.

Figure 1.

Phantom layout. Numbers 1–12 relate to Table 1.

Table 1.

Effective atomic number (Z_eff) and relative electron density (ρ_e) reference values provided by the manufacturer

Calibration phantom				Validation phantom
Number	Insert name	Zeff	ρe	Number	Insert name	Zeff	ρe
1	Gammex AP6 Adipose	6.21	0.928	1	Gammex BR12 Breast	6.93	0.956
2	Gammex CT Solid Water	7.74	0.992	2	Teflon	8.46	1.860
3	Gammex IB3 Inner Bone	10.42	1.086	3	Lucite	6.53	1.146
4	Gammex SR2 Brain	6.09	1.047	4	Air	7.71	0.001
5	Gammex CB2-30% CaCO3	10.90	1.276	5	PMMA	6.53	1.156
6	Gammex BR12 Breast	6.93	0.956	6	Paraffin Wax	5.48	0.959
7	Air	7.71	0.001	7	Water	7.48	1.000
8	Water	7.48	1.000	8	CIRS Muscle	7.59	1.041
9	Gammex B200 Bone Mineral	10.42	1.103	9	Air	7.71	0.001
10	Gammex LV1 Liver	7.74	1.064	10	Air	7.71	0.001
11	Gammex SB3 Cortical Bone	13.64	1.695	11	CIRS Adipose	6.44	0.956
12	Gammex CB2-50% CaCO3	12.54	1.469	12	CIRS Bone	11.90	1.507

Imaging protocols

For the first set of measurements, the mini phantoms were imaged using an X-RAD 225Cx system (Precision X-ray, North Branford, CT).¹⁹ The images were acquired for a series of X-ray tube voltages ranging from 40 to 100 kV in 10-kV increments. Each of the seven X-ray spectra were filtered with 2 mm of aluminium. The acquired images were reconstructed into a 328 × 311 × 591 matrix with a 103 × 103 × 103-µm³ voxel size using a Feldkamp back projection algorithm.²⁰ To achieve an equivalent dose level of 30 cGy for each energy (60 cGy for any combination of two energies), the exposures (product of tube current and exposure time) listed in Table 2 were used. To verify the dose level for each energy, measurements using a TN30012 Farmer-type ionization chamber (PTW, Freiburg, Germany) were performed according to the AAPM TG-61 protocol for kilovoltage X-ray beam dosimetry to determine the absorbed dose to water at the surface of the phantom.²¹ The dose inside the phantom is considerably lower than the surface dose.

Table 2.

Exposures for the different X-ray tube voltages

Tube voltage (kV)	Exposure (mAs)
40	1111.2
50	670.8
60	477.0
70	369.6
80	300.0
90	249.6
100	213.6

For all 21 energy combinations, a separate calibration and validation were performed.

To investigate the influence of the dose level on the mean error and standard deviation for Z_eff and ρ_e, the total dose level of 60 cGy for the optimal energy combination was reduced to 45 and 30 cGy. New images were acquired using the X-RAD 225Cx system and a new calibration and validation were performed for each dose level.

The influence of beam hardening effects was investigated by performing simulations using ImaSim.²² Seven different X-ray spectra, equivalent to the ones used for the measurements, were generated with SpekCalc.^23–25 These spectra were used to simulate images of both the calibration and validation phantom with different diameters of 3, 5 and 7 cm, as shown in Figure 2. The image reconstruction was performed with and without ImaSim's built-in BHC, which is based on water attenuation properties. Assuming that the imaged object is cylindrical and made of water, an ideal projection is calculated as the weighted sum over the real projection and the linear attenuation coefficient of water which is a function of the X-ray spectrum and path length through the cylinder. As a final step, the back projection is performed using the ideal projections instead of the real projections.

Figure 2.

Simulated CT images (50 kVp) of the phantoms with different diameters: 3, 5 and 7 cm (top row: calibration phantom, bottom row: validation phantom).

The accuracy of the simulations was evaluated by comparing the Z_eff and ρ_e values that were extracted from the ImaSim simulations to the Z_eff and ρ_e values that were extracted from the X-RAD 225Cx acquisitions. A good correspondence was found; the mean difference between the simulated and measured values equals 1.5% for Z_eff and 1.0% for ρ_e (Appendix A) (Figure A1).

The results for the X-RAD 225Cx system were compared with the small animal radiation research platform (SARRP) (Xstrahl, Camberley, UK).²⁶ Also for the SARRP, images of both mini phantoms were acquired for a series of X-ray tube voltages ranging from 40 to 100 kV in 10-kV increments. Each of the seven X-ray spectra were filtered with 1 mm of aluminium. The acquired images were reconstructed into a 512 × 512 × 512 matrix with a 103 × 103 × 103-µm³ voxel size using a Feldkamp back projection algorithm.²⁰ For both systems, the same exposures (listed in Table 2) were used, which leads to a higher dose level for the SARRP (1-mm aluminium filtration; 43 cGy for each energy) than that for the X-RAD 225Cx system (2-mm aluminium filtration; 30 cGy for each energy). The slices were acquired in the radial direction of the phantoms; so, for the X-RAD 225Cx system with the rotating gantry and fixed table, the phantom's cylindrical axis was positioned horizontally. For the SARRP with the rotating table, the phantom's cylindrical axis was positioned vertically.

Extracting the effective atomic number and relative electron density

Z_eff was extracted using the tissue substitute method described by Landry et al,¹⁴ which is based on a parameterization of the ratio of high- and low-energy linear attenuation coefficients. The ratio is defined as ${\mu }_{\text{ratio}}=\frac{{\mu }_{\text{LowEnergy}}}{{\mu }_{\text{HighEnergy}}}$ and is calculated for each individual voxel. The mean μ_ratio for each insert was calculated in a circular region of interest in the four central slices of the calibration phantom. The mean μ_ratio for the different inserts was plotted as a function of the reference Z_eff. The following calibration curve was fitted through these points. In this equation, both μ_LowEnergy and μ_HighEnergy are relative to the linear attenuation coefficient of water and A, B, C, D, E, F, n and m are fit parameters.

$${\mu }_{\text{ratio}}=\frac{{\mu }_{\text{LowEnergy}}}{{\mu }_{\text{HighEnergy}}}=\frac{A+B\cdot {{\displaystyle Z_{\text{eff}}}}^{n-1}+C\cdot {{\displaystyle Z_{\text{eff}}}}^{m-1}}{D+E\cdot {{\displaystyle Z_{\text{eff}}}}^{n-1}+F\cdot {{\displaystyle Z_{\text{eff}}}}^{m-1}}$$

For the validation, Z_eff was solved separately for each voxel by calculating μ_ratio from the corresponding voxels in the images that were acquired with the low- and high-energy X-ray spectra. The mean Z_eff for each insert was calculated in a circular region of interest in the four central slices of the validation phantom and then compared with the reference value that is provided by the manufacturer.

It is not possible to solve for Z_eff when μ_ratio is below the minimum of the calibration curve. For example, in the case of the 50- and 90-kVp combination, which is shown in Figure 3, the minimum μ_ratio is indicated by the dashed line and equals approximately 0.68. All voxels to which no Z_eff value could be assigned were excluded from the analysis (generally <0.01% of the voxels in the regions of interest). Most of the excluded voxels are located at sharp transitions between air and the solid water casing. This might be caused by partial volume effects; air and solid water both partially fill the voxel and are combined into a voxel with a CT number that corresponds to neither air nor solid water.

Figure 3.

Effective atomic number (Z_eff) − μ_ratio calibration curve [50- and 90-kVp combination; X-RAD 225Cx (Precision X-ray, North Branford, CT)]. The dashed line indicates the minimum μ_ratio for which a Z_eff value can be assigned.

ρ_e was extracted using a method described by Saito et al,¹⁵ which is based on a single linear relationship between a weighted subtraction of CT numbers and ρ_e. The weighted subtraction of CT numbers is defined as $\Delta \text{HU}=\left(1+\alpha \right)\cdot {\text{HU}}_{\text{HighEnergy}}-\alpha \cdot {\text{HU}}_{\text{LowEnergy}}$, in which α is the weighting factor. The mean HU_LowEnergy and HU_HighEnergy for each insert were calculated in a circular region of interest in the four central slices of the calibration phantom. The reference ρ_e was plotted as a function of the mean HU_LowEnergy and HU_HighEnergy for the different inserts. The following calibration curve was fitted through these points. In this equation, a, b and α are fit parameters.

$${\rho }_{\text{e}}=a\cdot \frac{\left(1+\alpha \right)\cdot {\text{HU}}_{\text{HighEnergy}}\mathrm{-}\alpha \cdot {\text{HU}}_{\text{LowEnergy}}}{1000}+b$$

For the validation, ρ_e was solved separately for each voxel by calculating ΔHU from the corresponding voxels in the images that were acquired with the low- and high-energy X-ray spectra. The mean ρ_e for each insert was calculated in a circular region of interest in the four central slices of the validation phantom and then compared with the reference value that is provided by the manufacturer.

RESULTS

Optimal energy combination

The mean Z_eff and ρ_e error for different energy combinations (X-RAD 225Cx) are shown in Figure 4. The largest errors were found close to the diagonal, i.e. for similar X-ray tube voltages. This can be explained by the fact that these X-ray spectra have a large spectral overlap, meaning that the image acquired with the second spectrum does not add much information. Combinations with the 100-kVp spectrum also showed inferior results. With this exception, all combinations with well-separated X-ray spectra (≥20-kVp difference) produced acceptable results with a mean Z_eff error ≤0.33 and a mean ρ_e error ≤0.030. The smallest errors were obtained for the 50- and 90-kVp combination. For this combination, Z_eff and ρ_e can be extracted with a mean error of 0.11 and 0.010, respectively. The relative errors are 1.6% for Z_eff and 0.8% for ρ_e. The maximum Z_eff insert error was obtained for the paraffin wax insert and equals 0.25. The maximum ρ_e insert error was obtained for the polymethyl methacrylate (PMMA) insert and equals 0.034. The errors for each individual insert are shown in Figure 8 (to be discussed below) and the fit parameters are shown in Appendix C (Table A1).

Figure 4.

Mean effective atomic number (Z_eff) and relative electron density (ρ_e) error for different energy combinations [X-RAD 225Cx (Precision X-ray, North Branford, CT)].

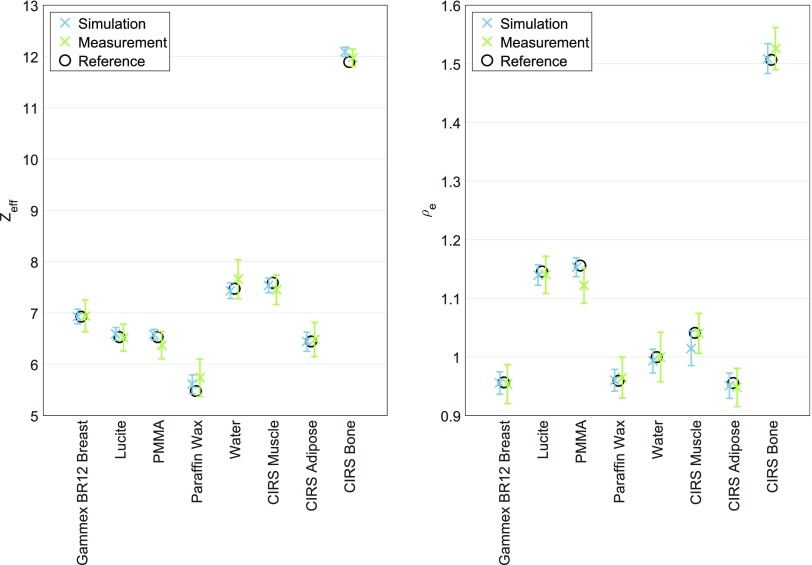
Figure 8.

Measured vs reference effective atomic number (Z_eff) and relative electron density (ρ_e) (50- and 90-kVp combination).

Different dose levels

Figure 5 shows the mean error and standard deviation for Z_eff and ρ_e for different dose levels (50- and 90-kVp combination, X-RAD 225Cx). A decrease in dose leads to an increase in both the error and the standard deviation in quantitative DECT imaging. For the lower dose levels, less photons at the level of the source result in less photons at the level of the imaging panel. This generates a lower signal, which leads to relatively more noise. The results show that this noise also propagates into Z_eff and ρ_e.

Figure 5.

Mean error and standard deviation for effective atomic number (Z_eff) and relative electron density (ρ_e) for different dose levels [50- and 90-kVp combination; X-RAD 225Cx (Precision X-ray, North Branford, CT)].

Beam hardening effects

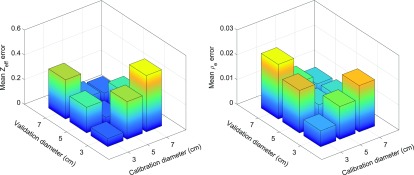
The mean Z_eff and ρ_e errors for the different phantom sizes (50- and 90-kVp combination, ImaSim simulations, no BHC applied) are shown in Figure 6. The smallest errors were found close to the diagonal, i.e. for matching sizes of the calibration phantom and validation phantom. The larger errors for the different (non-matching) phantom sizes are caused by beam hardening effects; a thicker object increases the mean energy of the X-ray spectra by filtering out the low-energy photons. This change in mean energy is not accounted for in the calibration when the calibration is performed with a phantom that has a different size. The mean Z_eff and ρ_e errors are not symmetric with respect to the diagonal, meaning that the errors for the 3-cm calibration combined with the 7-cm validation are different than the errors for the 7-cm calibration combined with the 3-cm validation.

Figure 6.

Mean effective atomic number (Z_eff) and relative electron density (ρ_e) error for the different phantom sizes [50- and 90- kVp combination, ImaSim simulations, no beam hardening correction (BHC) applied].

Beam hardening correction

Figure 7 shows the simulated Z_eff and ρ_e with and without BHC (50- and 90-kVp combination, ImaSim simulations). The simulations were performed for one of the worst cases, in which the calibration phantom has a diameter of 3 cm and the validation phantom has a diameter of 7 cm. This is equivalent to performing a quantitative DECT analysis on a rat with a 7-cm diameter when the calibration was performed using the phantom with the 3-cm diameter. Without BHC, Z_eff and ρ_e can be extracted with a mean error of 0.32 and 0.022, respectively. When applying a BHC in the image reconstruction, Z_eff and ρ_e can be extracted with a mean error of 0.12 and 0.019, respectively. Especially for Z_eff this is a large increase in accuracy, but also for ρ_e there is a slight increase in accuracy. The relatively large ρ_e error for the CIRS Bone insert can be explained by the fact that the BHC is based on water attenuation properties, which are more appropriate for soft tissues than for bone tissues.

Figure 7.

Simulated effective atomic number (Z_eff) and relative electron density (ρ_e) with and without beam hardening correction (50- and 90-kVp combination; ImaSim simulations).

X-RAD 225Cx vs small animal radiation research platform

The optimal energy combination of 50- and 90-kVp for the X-RAD 225Cx system was also determined to be the optimal energy combination for the SARRP. In Figure 8, the measured Z_eff and ρ_e for the two systems are compared. Both systems produced values close to the reference values. For the SARRP, Z_eff and ρ_e can be extracted with a mean error of 0.16 and 0.014, respectively. The relative errors are 2.4% for Z_eff and 1.3% for ρ_e. The maximum Z_eff insert error was obtained for the PMMA insert and equals 0.34. The maximum ρ_e insert error was obtained for the CIRS Adipose insert and equals 0.023. The X-RAD 225Cx system produced slightly smaller mean errors than the SARRP. A Wilcoxon signed-rank test showed that there are no significant differences in Z_eff (p = 0.313) and ρ_e (p = 0.195) errors between the two systems. However, it should be stated that a higher dose level was used for the SARRP (approximately 86 cGy; 43 cGy for each energy) than for the X-RAD 225Cx system (approximately 60 cGy; 30 cGy for each energy). Examples of CT, Z_eff and ρ_e images for both systems are included in Appendix B (Figure A2).

DISCUSSION

This work shows that Z_eff and ρ_e can be extracted with a mean error of 0.11 and 0.010, respectively. Such a high level of accuracy can be obtained only when the two images that are acquired with two different X-ray spectra overlap perfectly geometrically. A small misregistration between the images can cause two non-corresponding voxels to be combined in the analysis, leading to an incorrect μ_ratio and ΔHU, which in turn yields incorrect values for Z_eff and ρ_e. Therefore, breathing motion might cause a decrease in the accuracy of quantitative DECT imaging. A potential solution to this problem could be the implementation of respiratory gating, i.e. excluding projections for a certain breathing phase from the image reconstruction. Another option is to implement fast kilovoltage switching to obtain very short intervals of projections with different X-ray spectra. Separate image reconstructions are then performed for the projections that are acquired with the low- and high-energy spectra.

In the simulations, beam hardening influenced the accuracy of the extracted Z_eff and ρ_e values. The best results are obtained when the size of the calibration phantom matches the size of the imaged object. This leads to the conclusion that for the imaging of larger animals, such as rats or rabbits, a larger calibration phantom is required. To limit the contribution of beam hardening effects, a circular phantom in which the X-rays travel through the same amount of material for each projection is preferred. The X-RAD 225Cx system with the rotating gantry and fixed table acquires slices in the transverse plane of the mouse; so, the X-rays travel through the same amount of material for each projection. The SARRP with the rotating table acquires slices in the coronal plane. For some angles, the X-rays travel through the long (craniocaudal) axis of the animal and for other angles, the X-rays travel through the short (lateral) axis of the animal. This implies that for the SARRP, a decrease in the accuracy of quantitative DECT imaging can be expected for animals and other non-circular objects. Applying a BHC in the image reconstruction showed to increase the accuracy of the extracted Z_eff and ρ_e values. At the moment, however, neither the X-RAD 225Cx system nor the SARRP have a BHC implemented in their image reconstruction software.

To achieve a high accuracy in tissue segmentation and Monte Carlo dose calculations, it is important to reduce Z_eff and ρ_e errors. Quantitative DECT imaging can be further optimized by, for e.g., applying different levels of filtration to the low- and high-energy X-ray spectra to improve the spectral separation. Simulation models are a useful tool to explore different kinds of optimization possibilities.

CONCLUSION

It can be concluded that quantitative DECT imaging is feasible for small animal irradiators with an integrated CBCT system. To obtain the best results, optimization of the imaging protocols is required. Well-separated X-ray spectra (≥20-kVp difference) and a sufficient dose level (approximately 60 cGy; 30 cGy for each energy) should be used to minimize the error and noise for Z_eff and ρ_e. When no BHC is applied in the image reconstruction, the size of the calibration phantom should match the size of the imaged object to limit the influence of beam hardening effects. No significant differences in Z_eff and ρ_e errors are observed between the X-RAD 225Cx system and the SARRP.

Appendix A

In Figure A1, the Z_eff and ρ_e values that were extracted from the ImaSim simulations are compared with the Z_eff and ρ_e values that were extracted from the X-RAD 225Cx acquisitions. The simulations and measurements were performed for the 50- and 90-kVp combination at a total dose level of 60 cGy. No BHC was applied in the image reconstruction. The calibration and validation were performed separately for the simulations and measurements using the phantoms with a 3-cm diameter. The mean difference between the simulated and measured values equals 1.5% for Z_eff and 1.0% for ρ_e.

Figure A1. Simulated vs measured Z_eff and ρ_e (50- and 90-kVp combination).

Appendix B

Examples of CT, Z_eff and ρ_e images for both systems are shown in Figure A2. The images in the top row were acquired using the X-RAD 225Cx system and the images in the bottom row were acquired using the SARRP. For both systems, the Z_eff and ρ_e images were acquired using the 50- and 90-kVp combination. All voxels to which no Z_eff value could be assigned are marked with a red colour. The three circular red areas contain air.

Figure A2. CT, Z_eff and ρ_e images of the validation phantom (50- and 90-kVp combination) (top row: X-RAD 225Cx, bottom row: SARRP).

Appendix C

Table A1 shows the fit parameters for the Z_eff − μ_ratio calibration (A − F, n, m) and ρ_e − ΔHU calibration (a, b, α). The fit parameters for the optimal energy combination of 50 and 90 kVp are listed together with the minimum and maximum values that were found for the 21 energy combinations (X-RAD 225Cx).

Table A1. Fit parameters for the Z_eff − μ_ratio calibration (A − F, n, m) and ρ_e − ΔHU calibration (a, b, α)

Parameter	50 and 90 kVp	Minimum value	Maximum value
A (×10−1)	4.98	1.53	5.68
B (×10−3)	5.59	1.62	11.55
C (×10−5)	1.45	0.61	2.77
D (×10−1)	7.34	2.35	7.89
E (×10−3)	2.96	1.34	11.24
F (×10−7)	8.35	3.74	10.00
n	3.20	2.85	3.20
m	4.16	4.07	4.45
a	0.94	0.57	1.07
b	1.01	0.97	1.03
α	1.32	0.77	10.06

CONFLICTS OF INTEREST

FV, PG and SvH are the founders of SmART Scientific Solutions (Maastricht, Netherlands). In addition, FV, PG and SvH declare that they have received research funding from Precision X-ray (North Branford, CT) and have commercial interests with this company.