Robust bent line regression

Abstract

We introduce a rank-based bent linear regression with an unknown change point. Using a linear reparameterization technique, we propose a rank-based estimate that can make simultaneous inference on all model parameters, including the location of the change point, in a computationally efficient manner. We also develop a score-like test for the existence of a change point, based on a weighted CUSUM process. This test only requires fitting the model under the null hypothesis in absence of a change point, thus it is computationally more efficient than likelihood-ratio type tests. The asymptotic properties of the test are derived under both the null and the local alternative models. Simulation studies and two real data examples show that the proposed methods are robust against outliers and heavy-tailed errors in both parameter estimation and hypothesis testing.

1. Introduction

Segmented linear regression is commonly used for dealing with data in which the relationship between response and explanatory variables is approximately piecewise linear. Such data can be encountered in many applications in medical research, biology, ecology, insurance and finance studies. For example, in hydrological studies, the transportation of particles in gravel bed streams is often described as occurring in phases, with a relatively stable transport rate at low discharge, and a drastic increase after the discharge passes a certain threshold (Ryan et al., 2002). Another example arises from a study of the maximal running speed (MRS) data of land mammals (Garland, 1983), which shows that the logarithm of MRS increases stably with the logarithm of the body mass, and gradually decreases after reaching a certain point. The common feature between these examples is that the response and the covariate of interest show a piecewise linear relationship that has varying slopes over different domains of the covariate. Besides estimating the regression coefficients, identifying the threshold at which a change of relationship occurs is also a primary interest in statistical analyses.

In this article, we focus on an important special case of segmented linear regression: the so-called bent line regression. This type of regression model comprises of two line segments with different slopes intersecting at a change point, and is used for modeling data with a continuous segmented relation. The two examples mentioned above demonstrate such a relation. As the location of the change point is unknown, the likelihood function of this model is non-differentiable with respect to the location of the change point, complicating parameter estimation and statistical inference. Many works have been done to estimate parameters for bent line regression models with normally distributed responses, for example, Quandt (1958, 1960), Sprent (1961), Hinkley (1969), Feder (1975), Gallant and Fuller (1973), Chappell (1989), and many others. Most of these methods are based on the grid-search approach (Lerman, 1980), which estimates the regression coefficients for a series of fixed change points on a grid, and then exhaustively searches for the point that maximizes the likelihood function. While generating reasonable estimates, this approach is computationally expensive and the statistical inference of its estimators is difficult to derive. Recently, Muggeo (2003) proposed a clever estimation method for this model. By using a simple linearization technique, this method allows simultaneous inference for all model parameters in a computationally efficient manner.

Although the aforementioned models work well when normality holds, datasets in real applications often have outliers or heavy-tails, which can substantially influence the fitting of the models and the accuracy of parameter estimation. For instance, the MRS data includes several extremely slow outliers, which are animals living in environments where high running speed does not give a selective advantage, for example, sloths. The relationship between body mass and running speed for these animals is drastically different from that for most animals living in environments where speed is important. Even though these animals contribute little information towards the understanding of how body mass affects the maximal running speed, they markedly influence the estimation results. In such situations, a robust estimation procedure usually is desirable. A common way to obtain robust estimates is rank-based regression. Rank-based regression makes no assumption on the distribution of the response. It is robust against outliers and heavy-tailed errors, while maintaining high efficiency. The inference for rank-based regression models, in absence of change points, has been well developed since the first work by Jureckova (1971) and Jaeckel (1972), see Abebe et al. (2001), Hettmansperger and McKean (2011), and the references therein. However, to the best of our knowledge, no analogous work has been done when a change point is involved.

In this article, we introduce a robust rank-based bent linear regression with an unknown change point. Our contribution is two-fold. First, we propose a robust estimator for the bent line regression. The main idea of our estimation procedure is to replace the residual sum of squares in the segmented procedure of Muggeo (2003) with the rank dispersion function in standard rank-based regressions (Jaeckel, 1972). As a result, it not only achieves robustness against outliers and heavy-tailed errors, but also inherits the merit of Muggeo’s segmented method, providing simultaneous estimation and inference for all model parameters, including the location of the change point. It can be implemented readily using existing packages for standard rank-based regression. As we will show, the proposed estimator is more robust than the segmented regression proposed by Muggeo (2003), while maintaining high efficiency. Second, we contribute a computationally efficient test statistic for testing the existence of a change point. Although there are many tests developed on determining the existence of a change point in linear regression (Andrews, 1993; Bai, 1996; Hansen, 1996), quantile regression (Qu, 2008; Li et al., 2011; Aue et al., 2014; Zhang et al., 2014), transformation models (Kosorok and Song, 2007), time series models (Chan, 1993; Cho and White, 2007), no analogous tests have been developed in the context of robust bent line regression. Our test is motivated from the test for structural change in regression quantiles (Qu, 2008). It is a weighted CUSUM type statistic based on sequentially evaluated subgradients for a subsample. One advantage of this test is that it only requires fitting the model under the null hypothesis in absence of a change point. Thus it is computationally more efficient than the likelihood-ratio type tests, such as the sup-quasi-likelihood-ratio type statistics proposed by Lee et al. (2011) for detecting general structural changes, which requires fitting the models under both null and alternative hypotheses. The limiting distributions of the proposed test statistic under both the null and local alternative models are derived, and the implementation procedures are provided. Both the estimating procedure and testing procedure are implemented in the R package Rbent (Zhang and Li, 2016), available from CRAN.

The rest of the article is organized as follows. Section 2 introduces the main methodology, including the rank-based estimation procedure and the test for the existence of a change point. Sections 3 and 4 evaluate the performance of the proposed estimate using simulation studies and two real data examples, respectively. Section 5 provides the conclusion with possible future enhancement. All the technical proofs are presented in the Appendix.

2. Methodology

2.1. Robust bent line regression model

Let {(Y_i, X_i, Z_i), i = 1,⋯, n} be a sample of n independent and identically distributed observations, where Y_i is the response variable, X_i is a p × 1 vector of linear covariates, Z_i is a scalar covariate whose relationship with Y_i changes at a change-point location. To capture the linear relationship between the response Y_i and the covariates X_i, and the segmented relationship between the response Y_i and the explanatory variable Z_i, we consider the piecewise linear model

$$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+\beta Z_i+\gamma {(Z_i-\tau )}_{+}+e_i,i=1,\dots ,n,$$ (1)

where θ = (α^⊤, β, γ) ^⊤ are unknown coefficients, τ is the change point, (Z_i −τ)₊ = max(Z_i − τ, 0) = (Z_i − τ)I (Z_i > τ), and e_i are independent and identical random errors with an unknown distribution F (·). The vector α is the linear regression coefficients for X_i, the scalar β is the slope relating Y_i to Z_i for the segment before the change point, and γ is the difference in slope between the segments before and after the change point. It is commonly assumed γ ≠ 0 for identifiability of τ in model (1). In Section 2.2, we develop a formal test for this assumption.

As discussed in the Introduction, many existing methods for model (1) assume Ee_i = 0 and Var(e_i) < ∞, see Quandt (1958), Chappell (1989), Muggeo (2003), and therein references. Similar to the ordinal least squares, these methods can be very sensitive to outliers. When the error distribution has extremely heavy tails, such as the Cauchy distribution, the assumption of E(e_i) = 0 is violated and these methods are not appropriate. This motivates us to seek a robust regression approach based on ranks.

2.1.1. Rank-based estimator for bent line regression

To achieve robustness in the bent line regression model, we consider the rank-based estimator based on Jaeckel’s dispersion function, which was introduced by Jureckova (1971) and Jaeckel (1972) in the context of classical linear models without change-points. The main idea of rank-based estimation is to replace the Euclidean norm in the objective function of the ordinary least square estimator, ${\Vert \mathit{e}\Vert }_2^2={\displaystyle \sum _{i=1}^n}{e}_i{e}_i$, by a pseudo-norm

$${\Vert \mathit{e}\Vert }_{\varphi }=\sum _{i=1}^n\varphi \left(\frac{R_i}{n+1}\right)e_i,$$ (2)

where e = (e₁, …, e_n) are residues, R_i is the rank of the ith residual e_i among all residuals, and ϕ(·) is a non-decreasing and square-integrable score function defined on the unit interval (0, 1) satisfying ∫ ϕ(u)du = 0 and ∫ ϕ(u)²du = 1. The rank-based estimator then is obtained by minimizing ||e||_ϕ, which is also called the dispersion function. Comparing with the ordinary least squares estimator, the rank-based estimator achieves robustness by downweighting the contribution of large residuals in the sum of residual square through ranks in the score function. Here we obtain the rank-based estimator for model (1) by minimizing the following dispersion function

$$D(\mathit{\theta },\tau )=\sum _{i=1}^n\varphi \left(\frac{R_i}{n+1}\right)e_i,$$ (3)

where R_i is the rank of the ith residual e_i = Y_i − α ^⊤X_i − βZ_i − γ(Z_i − τ)₊.

The score function typically is selected according to the shape of underlying distribution of the error (Hettmansperger and McKean, 2011). Some commonly-used score functions include the Wilcoxon score function, $\varphi (t)=\sqrt{12}(t-0.5)$, and the sign score function, ϕ(t) = sgn(t − 0.5). It is worth to note that the rank-based regression with the sign score function is equivalent to the least absolute deviations regression (LAD). But for symmetric and moderately heavy-tailed distributions, the Wilcoxon score function has been shown to yield robust and relatively efficient estimators. Hence, we use the Wilcoxon score function throughout this paper.

2.1.2. Iterative estimating procedure for the rank-based estimator

One complication in estimating (θ, τ) is that the objective function D(θ, τ) is not differentiable with respect to τ, since the indicator function I(Z_i > τ) is not differentiable with respect to τ. A possible solution is to follow a grid-search approach commonly-used for piecewise linear models (Quandt, 1958), which estimates θ for a series of fixed τ on a grid and then exhaustively searches for τ that maximizes the likelihood function. However, this approach is computationally intensive, and the asymptotic properties of the change point τ are difficult to derive.

To circumvent this problem, we adopt the linear reparameterization technique proposed by Muggeo (2003). The main idea is to approximate (Z_i −τ)₊ using the first-order Taylor’s expansion, such that τ can be reparameterized as a coefficient term in a continuous linear model and estimated along with other regression coefficients as in the standard regression. Comparing with the grid-search method, this method reduces the computational burden and allows the asymptotic properties of all parameters to be derived easily using standard asymptotic theory.

Specifically, we apply the first-order Taylor’s expansion around τ⁽⁰⁾, provided that τ⁽⁰⁾ is close to τ:

$${(Z_i-\tau )}_{+}\approx {(Z_i-{\tau }^{(0)})}_{+}+(-1)I(Z_i>{\tau }^{(0)})(\tau -{\tau }^{(0)}).$$

Then, model (1) can be approximated by the following model,

$$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+\beta Z_i+\gamma {(Z_i-{\tau }^{(0)})}_{+}+\eta [-I\{Z_i>{\tau }^{(0)}\}]+e_i,$$ (4)

where η = γ(τ −τ⁽⁰⁾). For a given τ⁽⁰⁾, by viewing (Z_i − τ⁽⁰⁾)₊ and −I {Z_i >τ⁽⁰⁾} as two new covariates, model (4) takes the form of the standard linear regression. The rank-based estimate of regression coefficients for model (4) can be obtained using the standard rank-based estimation as

$$({\widehat{\mathit{\theta }}}^{(1)},{\widehat{\eta }}^{(1)})=arg\underset{\mathit{\theta },\eta }{min}\sum _{i=1}^n\sqrt{12}\left(\frac{R_i^{(0)}}{n+1}-0.5\right)e_i^{(0)},$$

where θ̂⁽¹⁾ = (α̂⁽¹⁾, β̂⁽¹⁾, γ̂⁽¹⁾), and $R_i^{(0)}$ is the rank of the ith residual $e_i^{(0)}=Y_i-{\mathit{\alpha }}^{\top }{\mathit{X}}_i-\beta Z_i-\gamma {(Z_i-{\tau }^{(0)})}_{+}-\eta (-I\{Z_i>{\tau }^{(0)}\})$. The estimate for change-point τ can be updated by

$${\widehat{\tau }}^{(1)}={\widehat{\tau }}^{(0)}+\frac{{\widehat{\eta }}^{(1)}}{{\widehat{\gamma }}^{(1)}}.$$

The iterative algorithm is summarized in Algorithm 1.

Algorithm 1.

Initialize parameters: θ̂(0) = (α̂(0), β̂(0), γ̂(0)) and τ̂(0), setting η̂(0) with a small value, such as 0.01. Fix τ̂(s) at each step s, estimate parameters θ̂(s+1) = (α̂(s+1), β̂(s+1), γ̂(s+1)) and η̂(s+1) by the rank-based regression estimate for the following linear model: $$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+\beta Z_i+\gamma {(Z_i-{\tau }^{(s)})}_{+}+\eta (-I\{Z_i>{\tau }^{(s)}\})+e_i.$$ (5) That is, $$({\widehat{\mathit{\theta }}}^{(s+1)},{\widehat{\eta }}^{(s+1)})=arg\underset{\mathit{\theta },\eta }{min}\sum _{i=1}^n\sqrt{12}\left(\frac{R_i^{(s)}}{n+1}-0.5\right)e_i^{(s)},$$ where $R_i^{(s)}$ is the rank of the ith residual $e_i^{(s)}=Y_i-{\mathit{\alpha }}^{\top }{\mathit{X}}_i-\beta Z_i-\gamma {(Z_i-{\tau }^{(s)})}_{+}-\eta (-I\{Z_i>{\tau }^{(s)}\})$ among all residuals $e_1^{(s)},\dots ,e_n^{(s)}$. Update the change-point estimate τ̂(s+1) by $${\widehat{\tau }}^{(s+1)}={\widehat{\tau }}^{(s)}+\frac{{\widehat{\eta }}^{(s+1)}}{{\widehat{\gamma }}^{(s+1)}}.$$ (6) Repeat steps (ii)–(iii) until convergence criterion holds, e.g. ||θ̂(s+1) − θ̂(s)||∞ < 10−5. Here, ${\Vert \mathit{v}\Vert }_{\infty }=\underset{j}{max}\mid v_j\mid$ for any v ∈ ℝq.

Remark 1

By viewing Y_i as the response variable and X_i, Z_i, (Z_i − τ^(s))₊, (−1)I(Z_i > τ^(s)) as the explanatory variables, fitting the non-linear and non-differentiable model (1) is equivalent to iteratively fitting the standard rank-based linear model (5). This fitting procedure can be easily implemented using the standard rank-based regression and computed using existing software tools, such as R package Rfit.

Based on an argument similar to that in Muggeo (2003), when the algorithm converges, the estimated coefficients, denoted as (θ̂, η̂), are consistent and asymptotically normally distributed. By the standard theory of the rank-based linear regression (Hettmansperger and McKean, 2011), (θ̂, η̂) have an asymptotically normal distribution. Using (6), the standard error estimate of the change point estimator τ̂ can be obtained from its Wald statistics. Specifically, by the linear approximation for the ratio of two random variables, the variance of τ̂ is given by

$$\text{Var}(\widehat{\tau })=\frac{\text{Var}(\widehat{\eta })+{(\widehat{\eta }/\widehat{\gamma })}^2\text{Var}(\widehat{\gamma })-2(\widehat{\eta }/\widehat{\gamma })\text{Cov}(\widehat{\eta },\widehat{\gamma })}{{\widehat{\gamma }}^2}.$$ (7)

When the algorithm converges, η̂ is expected to be approximately zero. Then from (7), the standard error of τ̂ is simply SE(τ̂) = SE(η̂)/| γ̂|. The 100(1 − α)% Wald-based confidence interval is given by

$$[\widehat{\tau }-z_{\alpha /2}\text{SE}(\widehat{\tau }),\widehat{\tau }+z_{\alpha /2}\text{SE}(\widehat{\tau })],$$

where z_α/2 is the (1 − α/2)th percentile of the standard normal distribution.

2.2. Test the existence of a change-point

Note that the convergence of the iterative algorithm depends on the existence of a threshold effect, i.e. γ ≠ 0. If γ = 0, the change point τ is not identifiable and its estimation is ill-conditioned. Therefore, it is important to test the existence of a threshold effect in the regression model (1).

Here, we consider the null and alternative hypotheses

$$H_0:\gamma =0\text{for}\text{any}\tau \in \mathrm{\Gamma }\text{vs.}{H}_1:\gamma \ne 0\text{for}\text{some}\tau \in \mathrm{\Gamma },$$

where Γ is the range set of all τ’s. To construct our test statistic, we take a cumulative subgradient approach that is in spirit similar to the test for structural change in quantile regression in Qu (2008). The key idea of this approach is to construct the test statistic using sequentially evaluated subgradients of the objective function under H₀ for a subsample, in a fashion similar to the standard CUSUM test (Ploberger and Kramer, 1992; Bai, 1996). One advantage of this approach is that it is a score-like test statistic that can be obtained by only fitting the null model, thus it is computationally more efficient than the sup-quasi-likelihood-ratio statistics in Lee et al. (2011), which requires fitting both the null and alternative models.

Specifically, we define

$$R_n(\tau ,\widehat{\mathit{\xi }})=\frac{1}{\sqrt{n}}\sum _{i=1}^n\sqrt{12}\left(\frac{R(Y_i-{\widehat{\mathit{\xi }}}^{\top }{\mathit{W}}_i)}{n+1}-0.5\right)(Z_i-\tau )I(Z_i\le \tau ),$$

where ξ̂ ≡ (α̂, β̂) is the estimator of the coefficients ξ = (α, β) under the null hypothesis H₀,

$$\widehat{\mathit{\xi }}=arg\underset{\mathit{\xi }}{min}\sum _{i=1}^n\sqrt{12}\left(\frac{R(Y_i-{\mathit{\xi }}^{\top }{\mathit{W}}_i)}{n+1}-0.5\right)(Y_i-{\mathit{\xi }}^{\top }{\mathit{W}}_i),$$ (8)

where ${\mathit{W}}_i={({\mathit{X}}_i^{\top },Z_i)}^{\top }$ are covariates and R(Y_i − ξ^⊤W_i) is the rank of the ith residual Y_i − ξ^⊤W_i among all the residuals (Y₁ − ξ^⊤W₁,⋯, Y_n −ξ^⊤W_n). R_n(τ, ξ̂) is a variant of the negative subgradient of the rank-based objective function (3) with respect to γ under H₀, for the subsample with Z_i up to the threshold τ. Intuitively, when there is no bent line, ξ̂ would be a good estimator for its population value, then the estimated residuals ê_i = Y_i − ξ̂^T W_i would be close to 0. Meanwhile, when there exists a change point, ξ̂ would be significantly different from the true value. Consequently, ê_i would depart from 0 in a systematic fashion related to Z_i, resulting in a large absolute value of R_n(τ, ξ̂). Since the change point is unknown, we need to search through all the possible locations. Therefore, we propose the test statistic

$$T_n=\underset{\tau \in \mathrm{\Gamma }}{sup}\left|R_n(\tau ,\widehat{\mathit{\xi }})\right|.$$

This statistic can be viewed as a weighted CUSUM statistic based on the ranks of estimated residuals under the null hypothesis. It is intuitively plausible to reject H₀ when T_n is too large. This intuition will be formally verified by Theorem 2.1. It implies that R_n(τ, ξ̂) converges to a Gaussian process with mean zero, and the size of such a process can be used to test for the existence of a change point.

To derive the large-sample inference for T_n, we consider the local alternative model,

$$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+\beta Z_i+n^{-1/2}\gamma {(Z_i-\tau )}_{+}+e_i,i=1,\dots ,n,$$ (9)

where τ is the change-point location and γ ≠ 0. For ease of presentation, we define some notations. Denote F (·) and f(·) as the cumulative distribution function and density function of the random error e, respectively, and the scale parameter c_ϕ = {∫ϕ′(F (u))f(u)dF (u)}⁻¹, which is presented in Hettmansperger and McKean (2011). Define $S_{wn}=n^{-1}{\sum }_{i=1}^n{\mathit{W}}_i{\mathit{W}}_i^T$ and $S_w=\mathrm{E}[{\mathit{W}}_i{\mathit{W}}_i^T]$,

$$\begin{array}{ll}\hfill S_{1n}(\tau )& =n^{-1}\sum _{i=1}^n\sqrt{12}f(e_i){\mathit{W}}_i(Z_i-\tau )I(Z_i\le \tau ),\hfill \\ \hfill S_1(\tau )& =\mathrm{E}\left[\sqrt{12}f(e_i){\mathit{W}}_i(Z_i-\tau )I(Z_i\le \tau )\right],\hfill \\ \hfill S_{2n}(\tau )& =n^{-1}\sum _{i=1}^n\sqrt{12}\gamma f(e_i){\mathit{W}}_i{(Z_i-\tau )}_{+},\hfill \\ \hfill S_2(\tau )& =\mathrm{E}\left[\sqrt{12}\gamma f(e_i){\mathit{W}}_i{(Z_i-\tau )}_{+}\right],\hfill \end{array}$$

and $q(\tau )=c_{\varphi }S{(\tau )}^{\top }{S}_w^{-1}{S}_2(\tau )$.

The following theorem is essential to the large-sample inference for using T_n.

Theorem 2.1

Under regular conditions in the Appendix A, for the local alternative model (9), R_n(τ, ξ̂) has the asymptotic representation

$$R_n(\tau ,\widehat{\mathit{\xi }})=\frac{1}{\sqrt{n}}\sum _{i=1}^n\sqrt{12}[F(e_i)-0.5][(Z_i-\tau )I(Z_i\le \tau )-c_{\varphi }{S}_1{(\tau )}^{\top }{S}_w^{-1}{\mathit{W}}_i]+q(\tau )+o_P(1).$$ (10)

Furthermore, T_n converges weakly to the process $\underset{\tau }{sup}\mid G(\tau )+q(\tau )\mid$, where G(τ) is the Gaussian process with mean zero and covariance function

$$W({\tau }_1,{\tau }_2)=E\left[\{(Z_1-{\tau }_1)I(Z_1\le {\tau }_1)-c_{\varphi }{S}_1{({\tau }_1)}^{\top }{S}_w^{-1}{\mathit{W}}_1\}\times \{(Z_1-{\tau }_2)I(Z_1\le {\tau }_2)-c_{\varphi }{S}_1{({\tau }_2)}^{\top }{S}_w^{-1}{\mathit{W}}_1\}\right].$$

Remark 2

Under the null hypothesis H₀, q(τ) equals 0 for all τ, whereas q(τ) is a nonzero function of τ under the local alternative model. Thus, the proposed test statistic can distinguish the alternative hypothesis from the null hypothesis. This supports the intuitive interpretation of the proposed test statistics for the existence of the change point.

The following theorem implies that the power of the test statistic T_n approaches 1 under the local alternative model whose order of γ is arbitrarily close to n^−1/2.

Theorem 2.2

Under regular conditions in the Appendix A, for the local alternative model,

$$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+\beta Z_i+n^{-1/2}{a}_n\gamma {(Z_i-\tau )}_{+}+e_i,i=1,\cdots ,n,$$

for any increasing sequence a_n → ∞, we have $\underset{n\to \infty }{lim}P(\mid T_n\mid \ge t)=1$ for any t > 0.

However, the limiting null distribution of T_n is nonstandard, because the covariance of test statistic T_n involves the estimation for the cumulative distribution function F (·) and the density function f(·) of errors. To obtain critical values, we use a wild bootstrap method similar to that in He and Zhu (2003) for quantile regression, based on the asymptotic representation of R_n(τ, ξ̂) in (10). The algorithm is summarized in Algorithm 2.

Remark 3

Note that the statistic $R_n^{\ast }(\tau ,\widehat{\mathit{\xi }})$ (defined in Algorithm 2) depends on the bandwidth h through the kernel estimator Ŝ_1n(τ). To choose the optimal bandwidth, one can use Silverman’s rule of thumb (Silverman, 1986), h = 1.06σ̂n^−1/5, where σ̂ is the standard deviation of the estimated residual ê_i (i = 1, …, n) under the null hypothesis. We also perform a sensitivity analysis to evaluate how the choice of h affects the performance of the proposed test procedure (Section 3.2).

In the Appendix, we prove the following result, which implies the validity of the bootstrap resampling scheme.

Theorem 2.3

Under both the null and the local alternative hypotheses, $R_n^{\ast }(\tau ,\widehat{\mathit{\xi }})$ converges to the Gaussian process G(t) as n → ∞.

Algorithm 2.

Generate iid {u1,⋯, un} where ui is generated from N (0, 1). Calculate the test statistic $T_n^{\ast }={sup}_{\tau \in \mathrm{\Gamma }}\left|R_n^{\ast }(\tau ,\widehat{\mathit{\xi }})\right|$, where $$R_n^{\ast }(\tau ,\widehat{\mathit{\xi }})=\frac{1}{\sqrt{n}}\sum _{i=1}^n{u}_i\sqrt{12}\left[{\widehat{F}}_n({\widehat{e}}_i)-0.5\right]\times \left[(Z_i-\tau )I(Z_i\le \tau )-{\widehat{c}}_{\varphi }{\widehat{S}}_{1n}(\tau )S_{wn}^{-1}{\mathit{W}}_i\right],$$ and $${\widehat{S}}_{1n}(\tau )=\frac{1}{n}\sum _{i=1}^n\sqrt{12}\widehat{f}({\widehat{e}}_i){\mathit{W}}_i(Z_i-\tau )I(Z_i\le \tau ),$$ F̂n(·) is the empirical distribution function of the estimated residuals êi = Yi − ξ̂⊤Wi under the null hypothesis, $\widehat{f}({\widehat{e}}_i)=n^{-1}{\displaystyle \sum _{j=1}^n}{K}_h({\widehat{e}}_i-{\widehat{e}}_j)$ is a kernel density estimate for the density function f(êi), Kh(·) = K(·/h)/h, K(·) is a kernel function, and h > 0 is a bandwidth. Here, ĉϕ is the consistent estimator for the scale parameter cϕ, which can be readily obtained from the R package Rfit. Repeat Steps 1–2 with NB times to obtain $T_n^{\ast (1)},\cdots ,T_n^{\ast (\text{NB})}$. Calculate the p-value by ${\widehat{p}}_n={\text{NB}}^{-1}{\displaystyle \sum _{j=1}^{\text{NB}}}I\{T_n^{\ast (j)}\ge T_n\}$.

3. Simulation studies

3.1. Estimation

To evaluate the finite sample performance of the proposed estimation procedure (Section 2.1), we conduct several simulation studies using data generated from the following model:

$$Y_i={\beta }_0+\beta Z_i+\gamma {(Z_i-0.5)}_{+}+e_i,i=1,\dots ,n,$$

with Z_i ~ Uniform(−2, 2), τ = 0.5, and (β₀, β, γ) = (3, 2.5, −4). Three different error distributions are considered: (1) a standard normal distribution; (2) a t-distribution with three degrees of freedom, t₃; and (3) a contaminated standard normal distribution, with 10% observations from a standard Cauchy distribution. For each setting, we generate a sample of n = 200 independent observations (Z_i, Y_i) with 1, 000 repetitions.

To evaluate the performance of our estimator, we assess the accuracy of estimation and the appropriateness of Wald-based confidence intervals, and compare its performance with Muggeo’s method, which was implemented in R package segmented. The results are summarized as below (Table 1).

Table 1.

Performance comparison between the proposed estimator and Muggeo’s estimator, based on 1,000 simulated samples of 200 observations, for the three error distributions in the simulation studies.

		Muggeo				Proposed
Case		β0	β1	β2	τ	β0	β1	β2	τ
1	Bias	0.013	0.012	−0.024	−0.006	0.026	0.023	−0.011	−0.017
	SD	0.136	0.128	0.311	0.086	0.152	0.135	0.316	0.090
	ESE	0.131	0.126	0.303	0.074	0.150	0.131	0.308	0.077
	MSE	0.019	0.016	0.097	0.007	0.024	0.019	0.100	0.008
	CP	0.948	0.951	0.944	0.916	0.958	0.942	0.934	0.916
	AL	0.514	0.495	1.186	0.292	0.586	0.514	1.208	0.301
2	Bias	0.021	0.024	−0.161	0.012	0.031	0.031	−0.052	−0.011
	SD	0.221	0.217	0.552	0.143	0.170	0.153	0.372	0.101
	ESE	0.218	0.209	0.514	0.121	0.176	0.161	0.378	0.093
	MSE	0.049	0.048	0.330	0.021	0.030	0.024	0.141	0.010
	CP	0.935	0.935	0.946	0.901	0.967	0.962	0.950	0.931
	AL	0.853	0.819	2.015	0.476	0.689	0.632	1.481	0.366
3	Bias	38.694	20.100	90.527	−0.041	0.020	0.017	−0.011	−0.011
	SD	2383.566	1216.455	3691.305	0.439	0.159	0.140	0.324	0.097
	ESE	5.615	3.564	7.396	0.216	0.154	0.137	0.323	0.080
	MSE	5.678 × 107	1.479 × 107	1.362 × 107	0.195	0.026	0.020	0.105	0.009
	CP	0.928	0.931	0.938	0.820	0.944	0.934	0.940	0.903
	AL	22.009	13.970	28.993	0.848	0.604	0.538	1.265	0.314

Muggeo: the Muggeo’s segmented estimator; Proposed: the proposed estimator; Bias: the empirical bias; SD: the empirical standard error; ESE: the average estimated standard error; MSE: the average of estimated mean square error. CP: 95% coverage probability; AL: the average length of 95% confidence intervals.

1. When the error term follows a standard normal distribution, both estimators work well and have comparable performance: both estimators are unbiased, the estimated standard errors (ESE) are close to the standard deviations (SD), and the empirical coverage probabilities (CP) approach the nominal level. The mean square errors (MSE) and the average lengths (AL) of Muggeo’s estimators are slightly smaller than those of the proposed estimators. This is not surprising, since rank-based estimators for traditional linear regressions with a normal error can achieve 95% relative efficiency of the ordinary least squares (Hettmansperger and McKean, 2011).

2. When the error term follows a t₃ distribution, both methods work reasonably well, but our estimators have smaller SDs and MSEs than the Muggeo’s estimators. In addition, the confidence intervals (CIs) of our estimators are shorter than those of Muggeo’s estimators, and the empirical coverage probabilities of our CIs are closer to the nominal level than those of Muggeo’s CIs for most estimators.

3. When the error term follows a contaminated standard normal distribution with 10% contamination from a standard Cauchy distribution, Muggeo’s method generates biased estimators with drastically inflated SDs and MSEs. However, our method still provides unbiased estimates, reasonable SDs and MSEs. While Muggeo’s CIs are unreasonably wide with low empirical coverage probabilities, the empirical coverage probabilities of our CIs are still close to the nominal level, and the lengths of CIs are as reasonable as cases 1 and 2.

In short, comparing with Muggeo’s estimators, our estimators achieve robustness against outliers and heavy-tailed errors.

3.2. Type I error and power analysis

We evaluate the type I error and power of the testing procedure in Section 2.2. As Muggeo (2003) did not provide a test for the existence of a change point, we derive a weighted-CUSUM test statistic for Muggeo’s model (see Appendix B). We then compare its performance with our test statistic for the ranked-based bent line regression. We simulate the data from the same simulation settings as the ones in the previous section, with threshold effects at γ = −2, −1, 0, 1, 2. In the testing procedure, we use the Epanechnikov kernel K(u) = 3/4(1 − u²)I(|u| ≤ 1), and set the number of bootstrap NB = 1, 000, the bandwidth h = 1.06σ̂n^−1/5, and the nominal significance level at 5%.

As shown in Table 2, when the error term follows a standard normal distribution, both tests have type I errors close to the nominal level and have reasonable power. However, when the error term is distributed as a t₃ distribution or is contaminated with a Cauchy distribution, the test based on Muggeo’s method is anti-conservative, with high power but also drastically inflated type I errors. This is mainly because Muggeo’s method is based on the ordinary least squares, thus it is sensitive to outliers. In contrast, our method maintains the nominal level of Type I errors for all error distributions, while having reasonable power.

Table 2.

Comparison of the testing procedure based on our estimator and the testing procedure based on Muggeo’s estimator for the three error distributions in the simulation studies. Type I error and power are calculated at the significance level of 5% from 1,000 simulated samples of 200 observations.

Case	γ	0	−2	−1	1	2
	Method
1	Muggeo	0.048	1.000	0.944	0.941	1.000
	Proposed	0.048	1.000	0.924	0.913	1.000
2	Muggeo	0.298	0.999	0.872	0.861	1.000
	Proposed	0.037	0.996	0.722	0.738	0.997
3	Muggeo	0.497	0.997	0.878	0.884	0.996
	Proposed	0.027	0.836	0.626	0.602	0.831

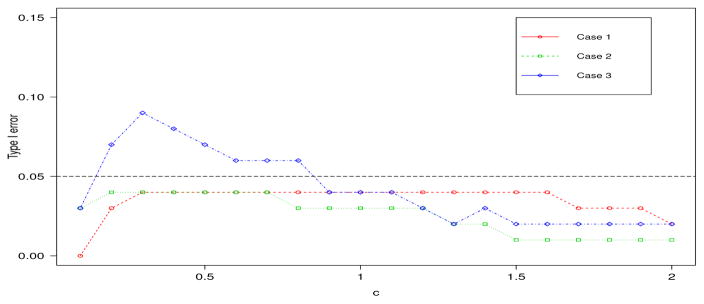
We also assess the sensitivity of the proposed method to the choice of bandwidth. Here we set the bandwidth as h = cσ̂n^−1/5, and calculate the type I errors at a series of c ∈ [0.1, 2] for each error distribution. As shown in Figure 1, the proposed test is not sensitive to the choice of h, giving reasonable type I errors across a wide range of c.

Figure 1.

Type I errors of the proposed testing procedure at different bandwidths h = cσ̂n ^−1/5 for the three error distributions in the simulation studies, with c ∈ [0.1, 2]. Each type I error is calculated based on 100 samples of 200 observations at the significant level of 5%.

4. Applications

4.1. Bedload transport data

In this section, we analyze a bedload transport dataset collected during snow-melt runoff in 1998 and 1999 at Hayden Creek near Salida, Colorado (Ryan and Porth, 2007). Bedload transport measures the transportation of particles in a flowing fluid along the bed. In gravel bed streams, bedload transport is generally described as occurring in phases, involving a transition from primarily low rates of sand transport (Phase I) to higher rates of sand and coarse gravel transport (Phase II) (Ryan and Porth, 2007). It has been reported that the relationship between transport and water discharge is substantially different in the two phases. The transition of the relationship has been used to define the shift in the phase of transport (Ryan et al., 2002).

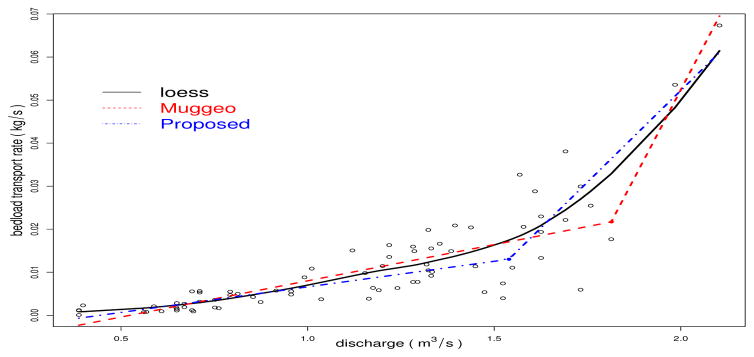
In this dataset, the discharge rate (m³/s) and the rate of bedload transport (kg/s) were collected for 76 observations. The dataset has been previously analyzed by Ryan and Porth (2007), using a piecewise linear regression model. However, as they pointed out, the dataset has very few observations at higher flows, making it difficult to fit the piecewise linear regression model. The loess curve indeed shows a segmented pattern with a visual estimate of a change point at around Z_i = 1.5m³/s. The two points with the highest transport (Y_i = 0.0536, 0.0673) are indicated as outliers (p-value= 2.2 × 10⁻¹⁶ ) by Grubbs test (Grubbs, 1950).

Here we analyze the dataset using the bent line regression,

$$Y_i=\alpha +\beta Z_i+\gamma {(Z_i-\tau )}_{+}+e_i,i=1,\dots ,n,$$

where Z_i is the discharge, Y_i is the bedload transport rate, τ is the location of the change-point, and e_i is the error with unknown distribution. Here a change point indicates the discharge at which a phase transition of transport occurs.

We first test the existence of a change point using the procedure in Section 2.2. Our test indicates that the pattern of segmentation is statistically significant (p-value = 0.028). Therefore, it is valid to estimate the parameters from the bent line regression model. For comparison, we fit the data using Muggeo’s method (Muggeo, 2003) and our method. The fitted curves are displayed in Figure 2 and the estimated parameters are summarized in Table 3. For both methods, the fitted line below the change point has a flatter slope with less variability, while the line above the change point has a significantly steeper slope and more variability. This reflects the physical characteristics of phases I and II, respectively, and is in accordance with the analysis in Ryan and Porth (2007). The estimated change point is 1.813 by Muggeo’s method and 1.539 by our method. Visual inspection of the fitted lines indicates that Muggeo’s change point is heavily influenced by the two outliers, whereas our estimate is more robust and is closer to the visual estimate from the loess curve.

Figure 2.

Fitted curves for Hayden Creek data, where “● ” indicates the location of estimated change-point.

Table 3.

The estimated parameters and total prediction errors (PE) for Hayden Creek data. Their standard errors are listed in parentheses.

	α	β	γ	τ	PE
Muggeo	−0.0088 (0.0018)	0.0168 (0.0016)	0.1473 (0.0636)	1.8126 (0.1022)	0.0045
Proposed	−0.0053 (0.0017)	0.0119 (0.0016)	0.0733 (0.0077)	1.5394 (0.0275)	0.0038

To evaluate the performance of model fitting, we use a K-fold cross-validation. Specifically, we divide the data into K equal-sized subgroups, denoted as D_k for k = 1, · · · , K. The kth prediction error is given by

$${\text{PE}}_k=\sum _{i\in D_k}{\left[Y_i-{\widehat{Y}}_i^{(-k)}\right]}^2,$$

where ${\widehat{Y}}_i^{(-k)}={\widehat{\alpha }}^{(-k)}+{\widehat{\beta }}^{(-k)}{Z}_i+{\widehat{\gamma }}^{(-k)}{(Z_i-{\widehat{\tau }}^{(-k)})}_{+}$, and parameters α̂ ^(−k), β̂ ^(−k), γ̂ ^(−k) τ̂ ^(−k) are estimated by using the data from all the subgroups other than D_k. The total prediction error is $\text{PE}={\sum }_{k=1}^K{\text{PE}}_k$. Here, we set K = 4. The total prediction error of our method (0.0038) is 15.6% less than that of Muggeo’s method (0.0045).

4.2. Maximal running speed data

In this section, we analyze the dependency of the maximal running speed (MRS) on body size for land mammals, using a dataset of 107 land mammals collected by Garland (1983). It is known that the fastest mammals are neither the largest nor the smallest, so the dependency is non-monotonic. To model this dependency, Huxley and Teissier (1936) introduced an allometric equation,

$$\mathit{MRS}=exp(a)\times {\mathit{mass}}^b,$$

where constants a and b may vary after the mass exceeds some change point. This suggests a linear relationship between log(MRS) and log(mass) with a possible change point (Chappell, 1989; Li et al., 2011).

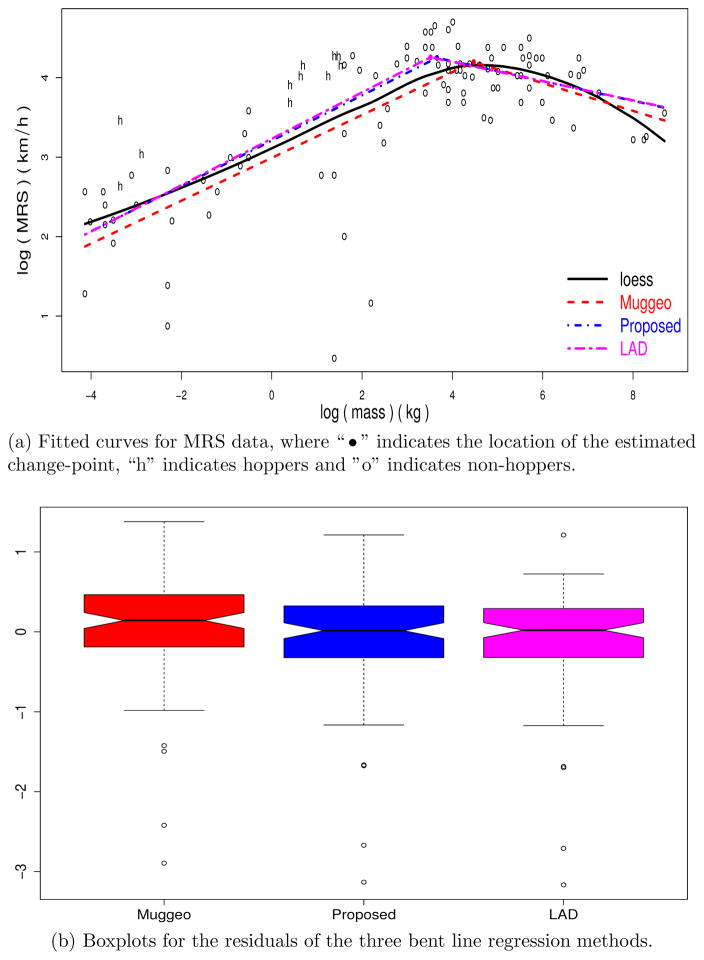
Figure 3a plots this dataset on the log scale. The animals are labeled according to whether they ambulate by hopping or not, which is believed to affect the running speed. The plot indeed shows that there is a slope change in the relation between of log(MRS) and log(mass). In addition, it shows that there are several extremely slow animals in the dataset. These animals live in environments where speed is not important for survival and contribute little to the understanding of how MRS depends on body size. The Grubbs test implies that the three slowest animals (Y = 0.204, 0.470 and 0.875) are outliers. This dataset has been analyzed by Li et al. (2011) using a bent line quantile regression model. To handle these outliers, they focused on the median and higher quantiles.

Figure 3.

MRS data analysis.

Here we analyze this data set using the bent line regression model,

$$Y_i={\alpha }_0+{\alpha }_1{X}_i+\beta Z_i+\gamma {(Z_i-\tau )}_{+}+e_i,i=1,\dots ,n,$$ (11)

where Y_i is log(MRS), Z_i is log(mass), X_i = I (the ith mammal is a hopper), τ is the change-point location, and e_i is the error with an unknown distribution. Our test for the existence of a change point shows that the segmented pattern is highly significant (p-value= 0), which indicates that the estimates and inference from our model are valid. For comparison, we fit the data using our method, Muggeo’s method, and bent line quantile regression (Li et al., 2011).

As shown in Table 4, all three methods indicate that hopping has a positive effect (α₁ > 0) on MRS. They all report that log(MRS) increases (β > 0) with the increase of log(mass) at first, but then it drops (β + γ < 0) at a certain point. However, the estimated change point is somewhat different, at exp(3.658) = 38.78 kg, exp(4.472) = 87.53 kg, and exp(3.515) = 33.6kg for our method, Muggeo’s method and the bent line quantile regression model with 50% quantile (a.k.a., least absolute deviations regression, LAD), respectively. Our estimated coefficients based on Wilcoxon score function are similar to those of bent line median regression. This is unsurprising, as the rank-based regression with the sign score function ϕ(t) = sgn(t − 0.5) is equivalent to LAD. In addition, though all the three methods have similar slopes (β) before the change point, Muggeo’s method has a much lower intercept (α₀) than our method and bent LAD, resulting a lower fitted line. This is likely because Muggeo’s method is sensitive to the three outliers with low MRS. A close examination of the residuals confirms this conclusion: the median of residuals from Muggeo’s method has a larger departure from zero than those from our method and LAD (Figure 3b). This indicates that our method and LAD are much more robust. We performed a five-fold cross validation as in Section 4.1 for all the three methods. The prediction error of our method (36.959) is smaller than those of Muggeo’s method (37.549) and the LAD method (37.243).

Table 4.

The estimated parameters and total prediction errors (PE) for MRS data. Their standard errors are listed in parentheses.

	α0	α1	β	γ	τ	PE
Muggeo	2.991 (0.078)	0.841 (0.189)	0.270 (0.024)	−0.444 (0.092)	4.472 (0.445)	37.549
Proposed	3.208 (0.060)	0.640 (0.140)	0.285 (0.022)	−0.409 (0.051)	3.658 (0.338)	36.959
LAD	3.232 (0.099)	0.606 (0.458)	0.292 (0.031)	−0.413 (0.058)	3.515 (0.130)	37.243

5. Discussion

In this paper, we developed a rank-based estimation procedure for segmented linear regression model in presence of a change-point. By combining a linear reparameterization technique for segmented regression models with rank-based estimation, our estimator is both robust against outliers and heavy-tailed errors and is computationally efficient. We also proposed a formal testing procedure for the existence of a change point. Our results showed that this test is robust while maintaining high power.

Our work currently is only applicable for detecting one change point. It can be extended to handle multiple change points. Here we briefly outline the extension for two scenarios. The first scenario concerns the model with multiple change points on one variable,

$$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+\beta Z_i+\sum _{k=1}^K{\gamma }_k{(Z_i-{\tau }_k)}_{+}+e_i,i=1,\dots ,n,$$

where (τ₁, · · · , τ_K ) is the change point, α is the linear regression coefficient for X_i, β is the slope relating Y_i to Z_i for the segment before the change point, and γ_k is the diffierence in slope between the segments before and after the kth change point τ_k. If the number of change points K is known priori, the estimating procedure in Section 2.1 can be readily extended to this case as follows. By a first-order Taylor expansion, the approximation model at each iteration step s is given by

$$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+\beta Z_i+\sum _{k=1}^K{\gamma }_k{(Z_i-{\tau }_k^{(s)})}_{+}+\sum _{k=1}^K{\eta }_k(-I\{Z_i>{\tau }_k^{(s)}\})+e_i.$$

The change points can be successively approximated by ${\widehat{\tau }}_k^{(s+1)}={\widehat{\tau }}_k^{(s)}+{\widehat{\eta }}_k^{(s+1)}/{\widehat{\gamma }}_k^{(s+1)}$, in a fashion similar to Algorithm 1. When K is unknown, the estimation and the test of the change points would be more complicated. One possibility is to determine the number of change points by extending the idea of permutation test procedure proposed by Kim et al. (2009) for segmented line regression with normally distributed response to rank-based regression. Other methods include the binary segmentation procedure (Bai, 1997; Qu, 2008), the wild binary segmentation procedure (Fryzlewicz, 2014), or information-based criterion with penalties (e.g., Lavielle, 2005; Ciuperca, 2014). Once the number of change points is determined, we can apply the estimation procedure above to obtain the regression coefficients and the locations of change points.

The second scenario concerns the model with change points occurred on multiple covariates. That is,

$$Y_i={\mathit{\alpha }}^{\top }{\mathit{X}}_i+{\mathit{\beta }}^{\top }{\mathbf{Z}}_i+{\mathit{\gamma }}^{\top }{({\mathbf{Z}}_i-\mathit{\tau })}_{+}+e_i,$$

where Z_i is the vector of covariates that have change points, and β and τ are the corresponding vectors of change-points and regression parameters, respectively. We can easily extend the proposed estimating procedure to this case. By applying a vector version of the first order Taylor expansion at τ ⁽⁰⁾, we can obtain

$${\mathit{\gamma }}^{\top }{({\mathbf{Z}}_i-\mathit{\tau })}_{+}={\mathit{\gamma }}^{\top }{({\mathbf{Z}}_i-{\mathit{\tau }}^{(0)})}_{+}+(-1)I({\mathbf{Z}}_i>{\mathit{\tau }}^{(0)}){\mathit{\gamma }}^{\top }(\mathit{\tau }-{\mathit{\tau }}^{(0)}),$$

where Z_i > t ⁽⁰⁾ is defined componentwise. The estimation can be proceeded in a way similar to Algorithm 1.

Highlights (for review).

• Robust bent line regression is considered.

• A rank-based estimate via linear reparameterization technique.

• A score-like test for the existence of a change point, based on a weighted CUSUM process.

Appendix A

The Appendix contains the technical details of proofs.

Regular Conditions.

• (A1)The density f is absolutely continuous with a bounded first-order derivative and f > 0.
• (A2)The design vector satisfies $\underset{1\le i\le n}{max}\Vert W_i\Vert =o_P(n^{1/2})$ and $\underset{n\to \infty }{lim}\frac{1}{n}{\sum }_{i=1}^n{W}_i{W}_i^T=S_w$ is positive definite matrix. Here, ||·|| is the Euclidean norm.
• (A3)The change-point τ lies in a bounded closed interval.
• (A4)The symmetric kernel function K(·) with compact support I satisfies ∫_I K(u)du = 1 and has a bounded first derivative.
• (A5)The bandwidth h satisfies h → 0 and nh → ∞ as n → ∞.

  We first provide the following convergence results.

Lemma 5.1

Under the regular conditions, as n → ∞, we have

1. $S_{wn}\stackrel{P}{\to }{S}_w$,

2. $\underset{\tau }{sup}\mid S_{1n}(\tau )-S_1(\tau )\mid \stackrel{P}{\to }0$,

3. $\underset{\tau }{sup}\mid {\widehat{S}}_{1n}(\tau )-S_1(\tau )\mid \stackrel{P}{\to }0$,

4. $\underset{\tau }{sup}\mid S_{2n}(\tau )-S_2(\tau )\mid \stackrel{P}{\to }0$.

Proof of Lemma 5.1

For (i), it is easily obtained by using the law of large number.

For (ii), by the law of large number, $S_{1n}(\tau )\stackrel{P}{\to }\mathrm{E}{S}_{1n}(\tau )=S_1(\tau )$ for any given τ. Then the uniformly convergence follows with the similar arguments used in Lemma 1 of Hansen (1996).

For (iii), it is sufficient to show that $\underset{\tau }{sup}\mid {\widehat{S}}_{1n}(\tau )-S_{1n}(\tau )\mid =o_P(1)$. We can write

$$\begin{array}{l}{\widehat{S}}_{1n}(\tau )-S_1(\tau )=\frac{1}{n}\sum _{i=1}^n\sqrt{12}\left[\widehat{f}({\widehat{e}}_i)-f({\widehat{e}}_i)\right]{\mathit{W}}_i(Z_i-\tau )I(Z_i\le \tau )+\frac{1}{n}\sum _{i=1}^n\sqrt{12}[f({\widehat{e}}_i)-f(e_i)]{\mathit{W}}_i(Z_i-\tau )I(Z_i\le \tau )+S_{1n}(\tau )-S_1(\tau )\\ \equiv I_1+I_2+I_3.\end{array}$$

Clearly, $\underset{\tau }{sup}\mid I_1\mid =o_P(1)$ by the uniform convergence of the kernel density estimator.

Note that

$$\mid I_2\mid \le \frac{1}{n}\sum _{i=1}^n\sqrt{12}\mid {\mathit{W}}_i(Z_i-\tau )I(Z_i\le \tau )\mid \underset{i}{max}\left|f(Y_i-{\widehat{\mathit{\xi }}}^T{\mathit{W}}_i)-f(Y_i-{\mathit{\xi }}^T{\mathit{W}}_i)\right|.$$

By the Conditions (A4) and (A5), and ||ξ̂ − ξ|| = O_P(n^−1/2) in the proof of Theorem 2.1, and the mean-value theorem, we get

$$\underset{i}{max}\left|f(Y_i-{\widehat{\mathit{\xi }}}^T{\mathit{W}}_i)-f(Y_i-{\mathit{\xi }}^T{\mathit{W}}_i)\right|\le \underset{i}{max}\Vert {\mathit{W}}_i\Vert ·\mid f^{\prime }({\zeta }^T{\mathit{W}}_i)\mid ·\Vert \widehat{\mathit{\xi }}-\mathit{\xi }\Vert =o_P(1),$$

where ζ lies in the segment between ξ̂ and ξ. Thus, $\underset{\tau }{sup}\mid I_2\mid =o_P(1)$.

Furthermore, $\underset{\tau }{sup}\mid I_3\mid =o_P(1)$ follows from (ii), and hence (iii) holds.

The proof of (iv) is similar to that of (ii) and is omitted here.

Proof of Theorem 2.1

Note that

$$\widehat{\mathit{\xi }}\equiv (\widehat{\mathit{\alpha }},\widehat{\beta })=arg\underset{\mathit{\alpha },\beta }{min}\sum _{i=1}^n\sqrt{12}\left(\frac{R(Y_i-{\mathit{\xi }}^T{\mathit{W}}_i)}{n+1}-0.5\right)\times (Y_i-{\mathit{\xi }}^T{\mathit{W}}_i),$$

which is equivalent to solve the estimating equation,

$$\begin{array}{l}{S}_n(\mathit{\xi })=-\frac{d}{d\mathit{\xi }}\sum _{i=1}^n\sqrt{12}\left(\frac{R(Y_i-{\mathit{\xi }}^T{\mathit{W}}_i)}{n+1}-0.5\right)\times (Y_i-{\mathit{\xi }}^T{\mathit{W}}_i)\\ =\sum _{i=1}^n\sqrt{12}\left(\frac{R(Y_i-{\mathit{\xi }}^T{\mathit{W}}_i)}{n+1}-0.5\right){\mathit{W}}_i.\end{array}$$

Under the local alternative model (9), that is,

$$Y_i={\mathit{\alpha }}^T{\mathit{X}}_i+\beta Z_i+n^{-1/2}\gamma {(Z_i-\tau )}_{+}+e_i,i=1,\dots ,n,$$

we have

$$\begin{array}{l}{S}_n(\mathit{\xi })=\sum _{i=1}^n\sqrt{12}\left[\frac{R\{e_i+n^{-1/2}\gamma {(Z_i-\tau )}_{+}\}}{n+1}-0.5\right]{\mathit{W}}_i\\ =\sum _{i=1}^n\sqrt{12}\left[\frac{n}{n+1}{F}_n\left(e_i+n^{-1/2}\gamma {(Z_i-\tau )}_{+}\right)-0.5\right]{\mathit{W}}_i\\ =\sum _{i=1}^n\sqrt{12}\left[F\left(e_i+n^{-1/2}\gamma {(Z_i-\tau )}_{+}\right)-0.5\right]{\mathit{W}}_i+o_P(1)\\ =\sum _{i=1}^n\sqrt{12}\left[F\left(e_i\right)-0.5+f\left(e_i\right)n^{-1/2}\gamma {(Z_i-\tau )}_{+}\right]{\mathit{W}}_i,\end{array}$$

where the last equality is followed by Taylor expansion.

By the Theorem A.3.8 in Hettmansperger and McKean (2011), it yields that

$$n^{-1/2}{S}_n(\widehat{\mathit{\xi }})=n^{-1/2}{S}_n(\mathit{\xi })-\frac{1}{c_{\varphi }}\left(\frac{1}{n}\sum _{i=1}^n{\mathit{W}}_i{\mathit{W}}_i^T\right)\sqrt{n}(\widehat{\mathit{\xi }}-\mathit{\xi })+o_P(1).$$

Note that n^−1/2 S_n(ξ̂) = 0, and by Lemma 5.1, it follows that

$$\sqrt{n}\left(\widehat{\mathit{\xi }}-\mathit{\xi }\right)=c_{\varphi }{S}_w^{-1}{n}^{-1/2}\sum _{i=1}^n\sqrt{12}[F(e_i)-0.5]W_i+c_{\varphi }{S}_w^{-1}{n}^{-1/2}\sum _{i=1}^n\sqrt{12}\gamma n^{-1/2}f(e_i){(Z_i-\tau )}_{+}{W}_i+o_P(1).$$

Now, under the local alternative model (9), we can write R_n(τ, ξ̂) as

$$\begin{array}{l}{R}_n(\tau ,\widehat{\mathit{\xi }})=\frac{1}{\sqrt{n}}\sum _{i=1}^n\sqrt{12}\left[\frac{R\left(e_i-{(\widehat{\mathit{\xi }}-\mathit{\xi })}^T{\mathit{W}}_i+n^{-1/2}\gamma {(Z_i-\tau )}_{+}\right)}{n+1}-0.5\right](Z_i-\tau )I(Z_i\le \tau )\\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n\sqrt{12}\left[\frac{n}{n+1}{F}_n\left\{e_i-{(\widehat{\mathit{\xi }}-\mathit{\xi })}^T{\mathit{W}}_i+n^{-1/2}\gamma {(Z_i-\tau )}_{+}\right\}-0.5\right](Z_i-\tau )I(Z_i\le \tau )\\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n\sqrt{12}\left[F(e_i)-0.5-f(e_i){(\widehat{\mathit{\xi }}-\mathit{\xi })}^T{\mathit{W}}_i+n^{-1/2}f(e_i)\gamma {(Z_i-\tau )}_{+}\right](Z_i-\tau )I(Z_i\le \tau ),\end{array}$$

where the last equality is used Taylor expansion.

By plugging in the representation for $\sqrt{n}(\widehat{\mathit{\xi }}-\mathit{\xi })$ and some algebraic manipulation, we have

$$R_n(\tau ,\widehat{\mathit{\xi }})=n^{-1/2}\sum _{i=1}^n\sqrt{12}\left[F(e_i)-0.5\right]\left[(Z_i-\tau )I(Z_i\le \tau )-c_{\varphi }{S}_1(\tau )S_w^{-1}{W}_i\right]+q(t)+o_P(1).$$

The remainder conclusion for weak convergence of R_n(t, ξ̂) is easily obtained by following the proofs in Stute (1997).

Proof of Theorem 2.2

The proof follows the same line as that for Theorem 2.1, then it is omitted for saving space.

Proof of Theorem 2.3

We divide the proof into three steps.

First, we show that the covariance function of $R_n^{\ast }$ converges to that of R. Define

$$R_n^{\ast \ast }(\tau )=n^{-1/2}\sum _{i=1}^n{u}_i\sqrt{12}\left[F_n(e_i)-0.5\right]\left[(Z_i-\tau )I(Z_i\le \tau )-c_{\varphi }{S}_1(\tau )S_w^{-1}{W}_i\right].$$

By the fact that the uniformly convergence of F̂_n (·)−F_n(·) and ĉ_ϕ−cϕ, along with the uniform convergence of Ŝ_1n(τ) − S₁(τ) in Lemma 5.1, we can easily show $R_n^{\ast }(\tau )$and $R_n^{\ast \ast }(\tau )$ are asymptotically equivalent in the sense that

$$\underset{\tau }{sup}\Vert R_n^{\ast }(\tau )-R_n^{\ast \ast }(\tau )\Vert =o_P(1).$$

Note that u_i’s are independent of (Y_i, X_i, Z_i), and Eu_i = 0, Var(u_i) = 1. Then, for any τ₁, τ₂, the covariance function of $R_n^{\ast \ast }$ is

$$\begin{array}{l}\text{Cov}(R_n^{\ast \ast }({\tau }_1),R_n^{\ast \ast }({\tau }_2))\\ =\frac{1}{n}\sum _{i=1}^n\mathrm{E}(u_i^{2}12{[F(e_i)-0.5]}^2\{(Z_i-{\tau }_1)I(Z\le {\tau }_1)-c_{\varphi }{S}_1{({\tau }_1)}^T{S}_w^{-1}W\}\\ \times \{(Z_i-{\tau }_2)I(Z_i\le {\tau }_2)-c_{\varphi }{S}_1{({\tau }_2)}^T{S}_w^{-1}W\})\\ =\mathrm{E}\left[\{(Z-{\tau }_1)I(Z\le {\tau }_1)-c_{\varphi }{S}_1{({\tau }_1)}^T{S}_w^{-1}W\}·\{(Z-{\tau }_2)I(Z\le {\tau }_2)-c_{\varphi }{S}_1{({\tau }_2)}^T{S}_w^{-1}W\}\right].\end{array}$$

which is the same as the covariance of R.

Second, it is easily to show that any finite-dimensional projection of $R_n^{\ast }(\tau )$ converges to that of R(τ), by the central limit theorem.

Third, $R_n^{\ast }(\tau )$ is uniformly tight. Note that the class of all indicator functions I(Z ≤ t) is a Vapnik-Chervonenskis (VC) class of functions. Then, the class of functions

$${\mathcal{F}}_n=\{(Z_i-\tau )I(Z_i\le \tau )-c_{\varphi }{S}_{1n}(\tau )S_w^{-1}{W}_i:\tau \in R^1\}$$

is a VC class of functions. Thus, by the equicontinuity lemma 15 of (Pollard, 1984), one can show that $R_n^{\ast }(\tau )$ is uniformly tight. Then, by the Cramer-Wold device, the proof of Theorem 2.3 is completed.

Appendix B

This Appendix provides the algorithm for testing the existence of a change-point via the wild bootstrap method based on Muggeo’s method.

Similarly, the test statistic based on the Muggeo’s segmented regression is given by

$${\stackrel{\sim }{T}}_n=\underset{\tau \in T}{sup}\left|{\stackrel{\sim }{R}}_n(\tau ,\stackrel{\sim }{\mathit{\xi }})\right|$$

where

$${\stackrel{\sim }{R}}_n(\tau ,\stackrel{\sim }{\mathit{\xi }})=\frac{1}{\sqrt{n}}\sum _{i=1}^n\left(Y_i-{\stackrel{\sim }{\mathit{\xi }}}^T{\mathit{W}}_i\right)(Z_i-\tau )I(Z_i\le \tau ),$$

where ξ̃ is obtained by Muggeo’s method under the null hypothesis.

The algorithm for the wild bootstrap method based on Muggeo’s method is summarized as follows.

Algorithm 3.

Step 1 Generate iid {u1, … , un} from the standard normal distribution N(0, 1). Step 2 Calculate the test statistic $${\stackrel{\sim }{R}}_n^{\ast }(\tau )=\frac{1}{\sqrt{n}}\sum _{i=1}^n{u}_i\left[(Z_i-\tau )I(Z_i\le \tau )-{\stackrel{\sim }{S}}_{1n}(\tau )S_{wn}^{-1}{W}_i\right],$$ where $${\stackrel{\sim }{S}}_{1n}(\tau )=\frac{1}{n}\sum _{i=1}^n{W}_i(Z_i-\tau )I(Z_i\le \tau ).$$ Step 3 Repeat Steps 1–2 with NB times to obtain ${\stackrel{\sim }{T}}_n^{\ast (1)},\cdots ,{\stackrel{\sim }{T}}_n^{\ast (NB)}$. Calculate the p-value as ${\stackrel{\sim }{p}}_n=\frac{1}{NB}{\displaystyle \sum _{j=1}^{NB}}I\{{\stackrel{\sim }{T}}_n^{\ast (j)}\ge T_n\}$