Atomistic Modeling of Ion Conduction through the Voltage-Sensing Domain of the Shaker K⁺ Ion Channel

Abstract

Voltage-sensing domains (VSDs) sense changes in the membrane electrostatic potential and, through conformational changes, regulate a specific function. The VSDs of wild-type voltage-dependent K⁺, Na⁺, and Ca²⁺ channels do not conduct ions, but they can become ion-permeable through pathological mutations in the VSD. Relatively little is known about the underlying mechanisms of conduction through VSDs. The most detailed studies have been performed on Shaker K⁺ channel variants in which ion conduction through the VSD is manifested in electrophysiology experiments as a voltage-dependent inward current, the so-called omega current, which appears when the VSDs are in their resting state conformation. Only monovalent cations appear to permeate the Shaker VSD via a pathway that is believed to be, at least in part, the same as that followed by the S4 basic side chains during voltage-dependent activation. We performed μs-timescale atomistic molecular dynamics simulations of a cation-conducting variant of the Shaker VSD under applied electric fields in an experimentally validated resting-state conformation, embedded in a lipid bilayer surrounded by solutions containing guanidinium chloride or potassium chloride. Our simulations provide insights into the Shaker VSD permeation pathway, the protein-ion interactions that control permeation kinetics, and the mechanism of voltage-dependent activation of voltage-gated ion channels.

TOC image

INTRODUCTION

Voltage-dependent ion channels open and close in response to changes in the membrane potential, and are known to play a key role in the generation and propagation of electrical impulses in excitable cells. Voltage-dependent K⁺, Na⁺, and Ca²⁺ channels (Kv, Nav, and Cav, respectively) consist of four subunits, each of which contains six transmembrane segments (S1 through S6). Segments S5–S6 from all four subunits contribute to the formation of a pore domain, which includes the ion conduction pathway and the activation gate. Segments S1 through S4 in each subunit make up a voltage-sensing domain (VSD)^{1, 2}. Voltage sensitivity in VSDs is conferred by a series of highly conserved basic sidechains in the S4 segment. These sidechains are stabilized in a transmembrane configuration by the formation of fully solvated salt-bridges with a set of highly conserved acidic side chains in S1–S3³.

The VSDs of Kv, Nav, and Cav channels do not conduct ions under normal physiological conditions, but they can become permeable through mutations, particularly of the S4 basic side chains^{4, 5}. VSD conduction in Nav1.4 and Cav1.1 channel mutants is the cause of some hypokalemic and normokalemic periodic paralyses^5–10, whereas VSD conduction through mutated Nav1.5 leads to cardiac arrhythmias^11–13. Mutations of the S4 basic side chains in other voltage-dependent ion channels have been associated with a number of genetic diseases; thus, it is possible that ion conduction by VSDs may play a central role in their pathophysiology^{7, 14}.

Cation conduction through the pore domain of voltage-dependent channels is reasonably well understood at the molecular level¹⁵. In contrast, relatively little is known about the underlying mechanisms of conduction through VSDs. In K⁺ channel VSD variants, selective cation conduction occurs only at hyperpolarizing potentials (negative on the intracellular side). The available experimental evidence from Shaker K⁺ channel variants indicates a strong selectivity towards guanidinium ions (Gdm⁺) relative to alkali metal cations, suggesting that ions permeating through the VSD may follow, at least in part, the same pathway as the S4 basic side chains during voltage-dependent activation^{4, 16}. This has motivated the use of atomistic molecular dynamics simulations (MD) of cation conduction in Kv VSD variants under a hyperpolarizing potential as a way to validate models of the Kv VSD in a resting state by comparing with experimental data on omega-currents^17–19.

Delemotte et al.¹⁷ developed a down-state VSD model from the crystal structure of Kv 1.2 using distance restraints and reported two K⁺ permeation events in a 40-ns atomistic simulation under an applied voltage of the VSD in a lipid bilayer upon neutralization of the R294 charge (equivalent to R362 in Shaker). The structure of the VSD conductive variant was identified as a “swollen-stable” conformation exhibiting a hydrated pathway connecting the intracellular and extracellular sides. Khalili-Araghi et al.¹⁸ performed 100-ns timescale atomistic MD simulations under an applied voltage of the Kv1.2 VSD R294S/E226D variant (equivalent to Shaker R326S/E283D) using a model of the Kv1.2 channel in a closed state^{20, 21} observing tens of conduction events of both K⁺ and Cl⁻ ions with a roughly 2:1 selectivity for the cation. A detailed structural analysis of the ion permeation pathway was found to be consistent with the experimental evidence from Shaker K⁺ VSD variants^{4, 16}, and a region at the top of the extracellular vestibule lined with acidic side chains was identified as putative selectivity filter for cation conduction under a hyperpolarizing potential. Jensen et al.¹⁹ performed 10-μs timescale atomistic MD simulations of the Kv1.2-Kv2.1 paddle-chimera VSD²² in a down-state conformation. They observed K⁺ currents in the R296S (equivalent to R365S in Shaker) and R287N variants and identified the K⁺ permeation pathway. These studies represent a significant advance towards the elucidation of a molecular mechanism of ion conduction through VSDs, but are limited by the simulation timescales and/or the lack of a resting-state VSD model for Shaker that could be directly compared to the available experimental evidence^{4, 16}.

To gain additional insights into the underlying molecular mechanisms of ion conduction through VSDs, the omega current, we performed atomistic MD simulations on the μs timescale of the Shaker VSD variant R362S/E283D/S357C/M356D (the so-called big omega-current or BOM mutant¹⁶) in a resting-state embedded in a phospholipid bilayer immersed in a guanidinium chloride or potassium chloride solution under an applied electric field. Our simulations, conducted on the same timescale as the elementary permeation events that give rise to the omega current, reveal the Shaker VSD permeation pathway and the protein-ion interactions that give rise to differences in the permeation kinetics of K⁺ and Gdm⁺ ions.. The simulations of Gdm⁺ ion permeation, not considered in any of the previous simulation studies, also give new insights into the mechanism of voltage-dependent activation.

METHODS

Molecular dynamics simulation system setup and equilibration

To model the Shaker VSD in a resting state, we used one of the state-dependent structural models (specifically, the C3 conformation) of the native Shaker VSD reported by Henrion et al.²³. These atomistic models were generated by comparative modeling with the Kv1.2 paddle chimera crystallographic structure²², constrained by inter-residue distance data from electrophysiology recordings of Cd²⁺-bridged double cysteine Shaker variants²³. The initial simulation system was composed of one native Shaker VSD (residues 225–379) in a resting conformation (denoted C3 by Henrion et al.²³) and 180 1-palmytoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC) lipid molecules (90 per leaflet), and fully hydrated in 150 mM KCl, for a total of 51,294 atoms. The CHARMM-GUI²⁴ and the VMD software package²⁵ were used to assemble the system.

The initial simulation system equilibration, performed with the wild-type VSD, consisted of 5000 steps of energy minimization with all protein atoms subjected to harmonic positional restraints, followed by a 100 ps MD simulation at constant volume and temperature (300 K). The system was then run for several ns at constant temperature (300 K) and pressure (1 atm) with the protein backbone atoms under harmonic positional restraints. The restraints were released by decreasing the force constant gradually over 10 ns. The wild-type Shaker VSD simulation was equilibrated at constant temperature and pressure for 343 ns.

The wild-type system simulation was performed with the NAMD 2.9 software package²⁶. The CHARMM27 and CHARMM36 force fields^27–29 were used for the protein and lipids, respectively, and the TIP3P model was used for water³⁰. The smooth particle mesh Ewald method^{31, 32} was used to calculate electrostatic interactions. Short-range, real-space interactions were cut off at 11 Å via a switching function. A reversible, multiple time-step algorithm³³ was employed to integrate the equations of motion with a time step of 4 fs for electrostatic forces, 2 fs for short-range, non-bonded forces, and 1 fs for bonded forces. All bond lengths involving hydrogen atoms were held fixed using the SHAKE³⁴ and SETTLE³⁵ algorithms. A Langevin dynamics scheme was used for temperature control, and a Nosé-Hoover-Langevin piston was used for pressure control^{36, 37}.

The big omega-current (BOM) VSD system was generated by performing mutations R362S, E283D, S357C, and M356D on the pre-equilibrated conformation of the wild-type Shaker VSD system. The BOM system was solvated in either 500 mM guanidinium chloride (GdmCl) or 500 mM KCl for a total number of atoms of 55,698 or 55,140, respectively. The systems were re-equilibrated using a similar procedure as described above for the wild-type VSD system.

Microsecond timescale molecular dynamics simulations

Atomistic MD simulations on the μs timescale were performed on Anton, a special-purpose computer for molecular dynamics simulations of biomolecules³⁸, under a range of hyperpolarized (intracellular side negative) applied potentials (Tables 1 and 2). The CHARMM27 and CHARMM36 force fields^27–29 were used for the protein and lipids, respectively, and the TIP3P model was used for water³⁰. A reversible, multiple time-step algorithm³⁹ was employed to integrate the equations of motion with a time step of 6 fs for the long-range non-bonded forces, and 2 fs for short-range non-bonded and bonded forces. The k-Gaussian split Ewald method⁴⁰ was used for long-range electrostatic interactions. All bond lengths involving hydrogen atoms were constrained using SHAKE³⁴. The simulations were performed at constant temperature (300 K) and pressure (1 atm), using Nose-Hoover chains⁴¹ and the Martyna-Tobias-Klein barostat³⁶. The RESPA algorithm and the temperature and pressure controls were implemented using the multigrator scheme⁴².

Table 1.

Trajectory lengths and permeation events for the 500 mM GdmCl system

Applied voltage (mVa)	Number of Gdm+ permeation events	Trajectory length (μs)
−250	3	9.35
−500	11	3.53b
−750	6	2.9c

^aApplied voltages were modeled as constant electric fields along the transmembrane direction with a magnitude equal to the indicated voltage value divided by the value of the thickness of the dielectric barrier along the VSD axis (23 Å).

^bTotal trajectory length was 4.47 μs; VSD distorts around a bound Gdm⁺ ions after 3.53 μs.

^cTotal trajectory length was 3.11 μs; VSD swells with water and ions, resulting in non-selective permeation after 2.9 μs.

Table 2.

Trajectory lengths and permeation events for the 500 mM KCl system

Applied voltage (mVa)	Number of K+ permeation events	Trajectory length (μs)
−250	0	4.71
−500	1	5.61
−750	2	3.76b

^aApplied voltages were modeled as constant electric fields along the transmembrane direction with a magnitude equal to the indicated voltage value divided by the value of the thickness of the dielectric barrier along the VSD axis (23 Å).

^bTotal trajectory length was 4.33 μs; VSD swells with water and ions, resulting in non-selective permeation after 3.76 μs.

To model the applied membrane potential used in electrophysiology recordings, a transmembrane potential was imposed as a constant electric field, with a magnitude determined by the potential profile around the center of the VSD calculated using linearized Poisson-Boltzmann theory⁴³. We used a range of hyperpolarizing (negative on the intracellular side) applied electric fields with magnitudes equal to 250 mV, 500 mV, or 750 mV over 23 Å. The specific value for the thickness of the dielectric barrier (23 Å) was taken from a linearized Poisson-Boltzmann calculation of the electrostatic potential along a transmembrane axis passing through the center of the VSD, as previously described⁴⁴. Over the full length of the simulation cell, the electric field magnitudes we used correspond to 956 mV, 1913 mV, and 2870 mV, respectively. Molecular graphics and simulation analyses were performed using VMD 1.9.1²⁵.

RESULTS

Identification of ion permeation events

We performed simulations of the Shaker BOM VSD in a resting state conformation embedded in a lipid bilayer in either 500 mM KCl or 500 mM GdmCl aqueous solution, and under a constant electric field along the transmembrane direction with three different magnitudes (Tables 1 and 2). The lowest magnitude corresponds to the membrane potential used in the experimental recording of the omega current. The higher magnitudes were used to increase the number of permeation events within the timescale of the simulation. The VSD conformation was based on the so-called C3 model of Henrion et al., which is consistent with metal-bridge electrophysiological data for the Shaker resting state²³.

The VSD architecture exhibits two crevices exposed to either the extracellular or intracellular spaces, which are readily hydrated in the membrane environment^{3, 44}. We define ion permeation through the VSD as translocation events from one VSD crevice to the other. Consistent with experimental observations^{4, 16}, we only observed cation permeation from the extracellular side to the intracellular side under hyperpolarizing potentials. A total of 20 Gdm⁺ and 3 K⁺ permeation events were observed over trajectories on the μs timescale, as detailed in Tables 1 and 2, and depicted in Figures 1 and 2. These permeation events were observed at various magnitudes of the applied electric field. The details of the permeation mechanism for either ion (see below) did not depend on the applied electric field magnitude. Therefore, we assume that the larger electric field magnitudes in the simulations only lowered the overall kinetic barriers for permeation without affecting the actual permeation mechanism.

Figure 1.

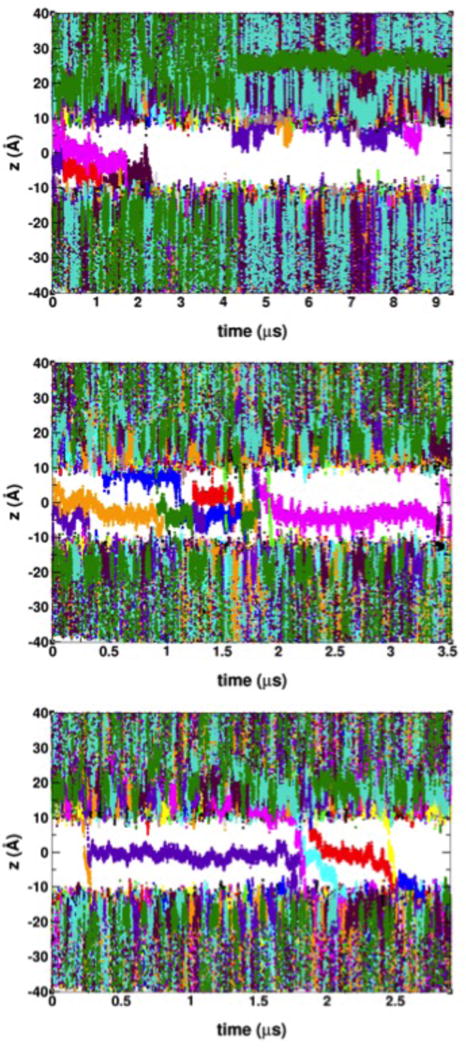
Time-dependence of the position of Gdm⁺ ions along the transmembrane direction with respect to the bilayer center at applied voltages of −250 mV (top panel), −500 mV (middle panel), and −750 mV (bottom panel). Permeation events are shown by traces crossing the gap between membrane extracellular side (z > 0) and the intracellular side (z < 0). Ions are identified with an arbitrary 16-color scheme.

Figure 2.

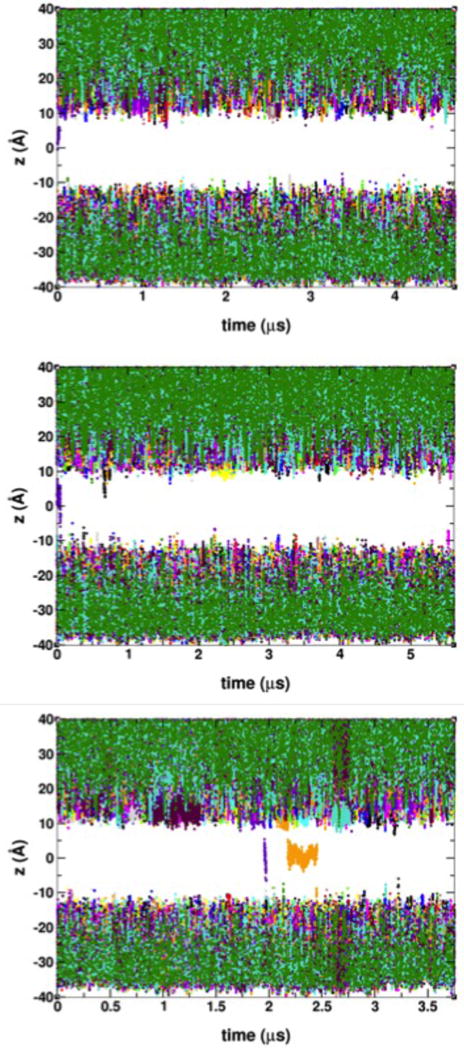
Time-dependence of the position of K⁺ ions along the transmembrane direction with respect to the bilayer center at applied voltages of −250 mV (top panel), −500 mV (middle panel), and −750 mV (bottom panel). Permeation events are shown by traces crossing the gap between membrane extracellular side (z > 0) and the intracellular side (z < 0). Ions are identified with an arbitrary 16-color scheme.

The permeation pathway and binding sites in the BOM VSD

The Shaker BOM VSD is hydrated throughout, and exhibits a local maximum in the water number density profile at around ~2.5 Å from the bilayer center (Figure 3). This hydration pattern, where the VSD develops two constricted regions and a water bleb in the middle, has been described in the crystallographic structure of a voltage-gated proton channel, whose permeation pathway is located within the VSD⁴⁵. In contrast, the corresponding profile in the wild-type Shaker VSD reveals a single constriction at the center of the bilayer where the water density drops to an absolute minimum (Figure 3).

Figure 3.

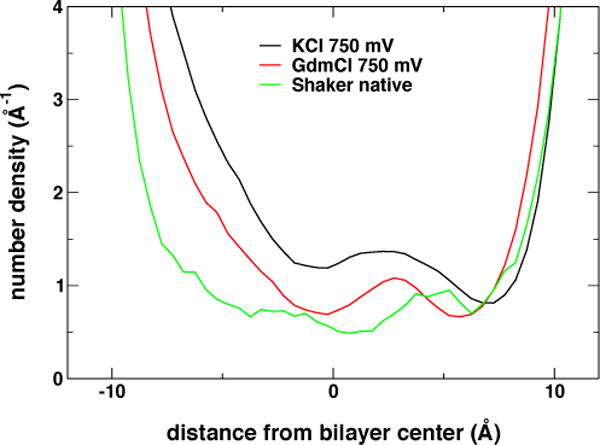
Transmembrane distribution of water molecules in the VSD computed over a ~2-μs trajectory range when cations were present in the VSD (BOM mutants), or over the last 100 ns of the native (wild-type) VSD simulation trajectory.

Partitioning of K⁺ and Gdm⁺ ions in the lipid bilayer is dramatically different (Figure 4): Gdm⁺ ions accumulate at the polar/apolar interface (i.e., in the region adjacent to the lipid carbonyls) of the membrane while K⁺ ions do not. This result is consistent with partition free energy calculations reported in the literature for Gdm⁺ and Arg sidechain analogs^46–48. Gdm⁺ ions at the polar/apolar interface are admitted to the VSD permeation pathway by a lateral opening to the extracellular crevice between the S3 and S4 helices (Figures 5A and 5B). Once a Gdm⁺ enters the VSD permeation pathway, it may become solvated by waters without further interaction with the protein or, alternatively, bind to a site in the extracellular crevice formed by the side chains of residues E247 (in S1), D283 (in S2), and Y323 (in S3) (Figures 5A and 5B). In contrast, K⁺ ions only enter the VSD through the extracellular solvent where they immediately bind to the same binding site as Gdm⁺ (Figure 5C and 5D).

Figure 4.

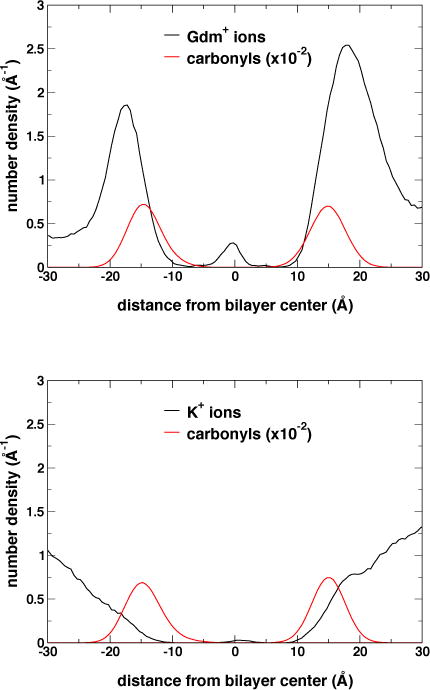
Transmembrane distribution of cations and lipid carbonyl moieties computed over a ~2-μs trajectory range when cations are present in the VSD for the GdmCl (top panel), and KCl (bottom panel) simulation trajectories at −750 mV.

Figure 5.

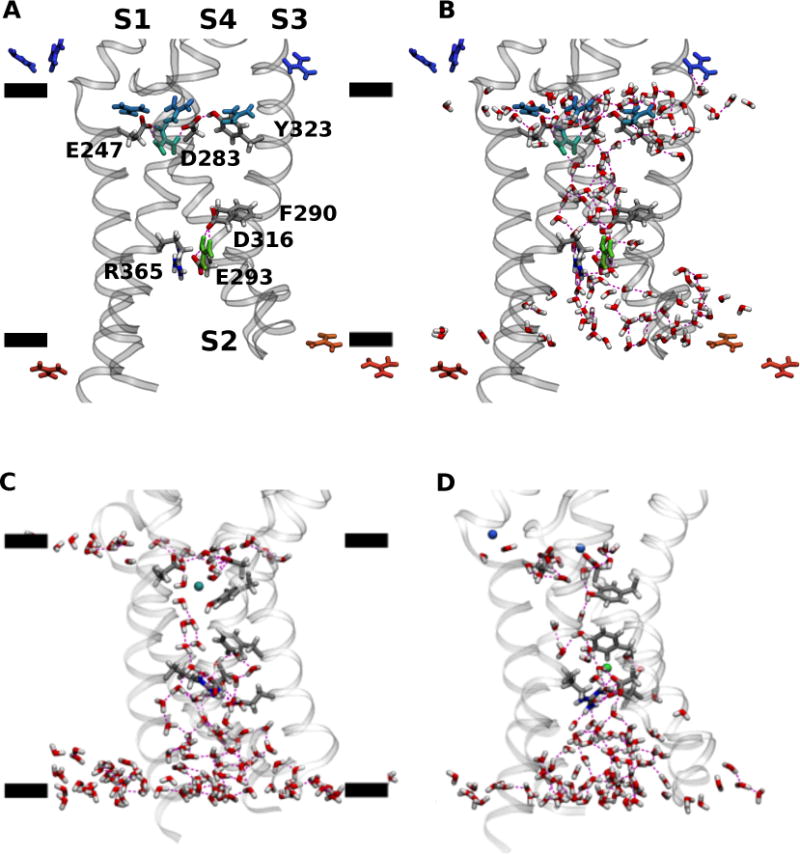
Configuration snapshots of VSD from the GdmCl (A and B), and KCl (C and D) simulation trajectories at −750 mV. Panels A and B show the same configuration snapshot. Panels C and D show different configuration snapshots. The side chains involved in interactions with the permeating ions are shown as licorice and labeled in the panel A. Cations within 20 Å from the lipid bilayer center measured along the transmembrane direction are shown as licorice and colored using a BGR color scale denoting position along the transmembrane direction with respect to the bilayer center (green, origin; blue, 20 Å; red, −20 Å). Waters in the first two solvation shells around the VSD and within 15 Å from the lipid bilayer center are shown in licorice. The black bars in panels A and C indicate the mean position of lipid carbonyl moieties along the transmembrane direction. H bond interactions are drawn as broken lines.

A comparison to the Henrion et al. wild-type VSD C3 structure solvated in a lipid bilayer (Figure 6), suggests that this binding site is formed as a consequence of the mutations in the BOM variant. The removal of the R362 sidechain (through the R362S mutation) and the E283D mutation appear to provide enough space for the Y323 sidechain to flip inwards where, in conjunction with D283 and E247, forms a large hydrated entryway that favors the binding of cations. The role played by the three residues differs in the two systems. In KCl, the Y323 hydroxyl and D283 carboxyl groups participate in the solvation of the K⁺ ion (Figure 5C). In GdmCl, there is a persistent hydrogen-bond interaction between Y323 and D283 that contributes to the lateral opening of the extracellular crevice into the lipid bilayer interface, and the Gdm⁺ can form salt-bridge interactions with D283 and E247 (Figures 5A and 5B). In both cases, the ion eventually becomes entirely solvated by waters in the extracellular crevice.

Figure 6.

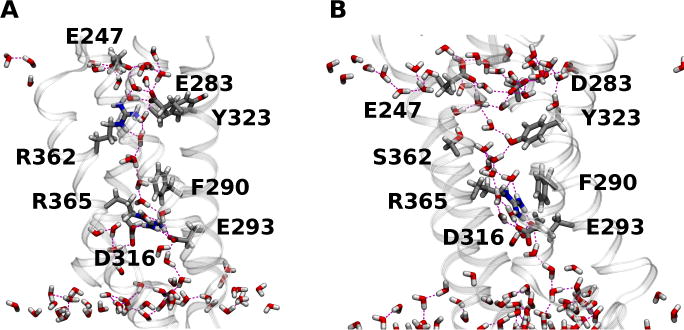
(A) Configuration snapshot of the native Shaker VSD; and (B) the BOM VSD in the KCl simulation. The side chains involved in interactions with the permeating ions in the BOM mutant VSD systems, the BOM S362 side chain, and the wild-type R362 and E283 side chains are shown as licorice. Waters in the first two solvation shells around the VSD and within 15 Å from the lipid bilayer center are shown in licorice. H bond interactions are drawn as broken lines.

Translocation occurs when the ion is released into another binding site in the intracellular crevice, comprised of the side chains of F290, E293 (in S2) and D316 (S3) (Figure 5). In addition, the cation may interact with R365 (in S4) when it is bound to the intracellular binding site. The intracellular binding site has been previously identified by Tao et al.⁴⁹ as the so-called gating charge transfer center (GTC), a putative binding site for the transfer of the S4 positive charges through the membrane electric field during voltage-dependent activation. Permeation is completed once the ion is released from this binding site and into the intracellular cavity (Figures 7 and 8).

Figure 7.

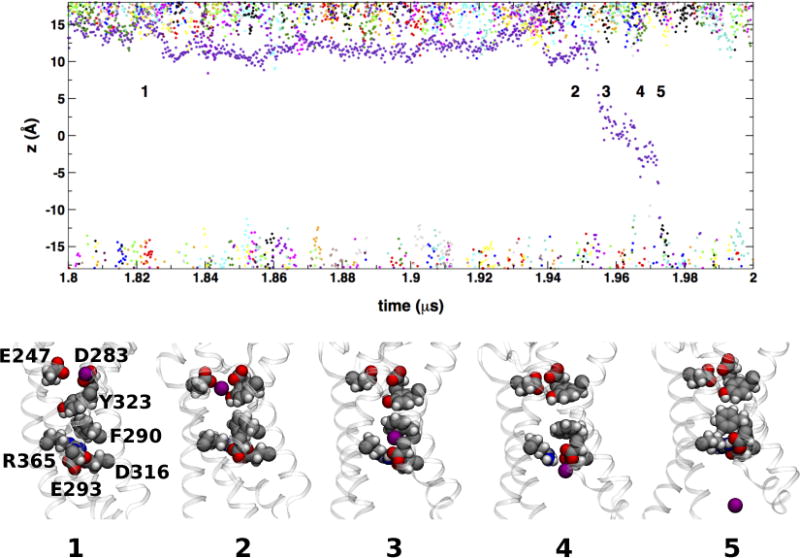
A K⁺ ion permeation event. The top panel shows a detail of the time-dependence of cation transmembrane positions in the KCl simulation at −750 mV (see Figure 2). The labeled configurations snapshots show a single K⁺ ion (purple filled-sphere) from entry into the VSD from the extracellular side of the membrane (snapshot 1) to release into the intracellular side (snapshot 5). Side chains forming the extracellular (E247, D283, and Y323) and intracellular (F290, E293, D316, and R365) binding sites are shown as filled-spheres.

Figure 8.

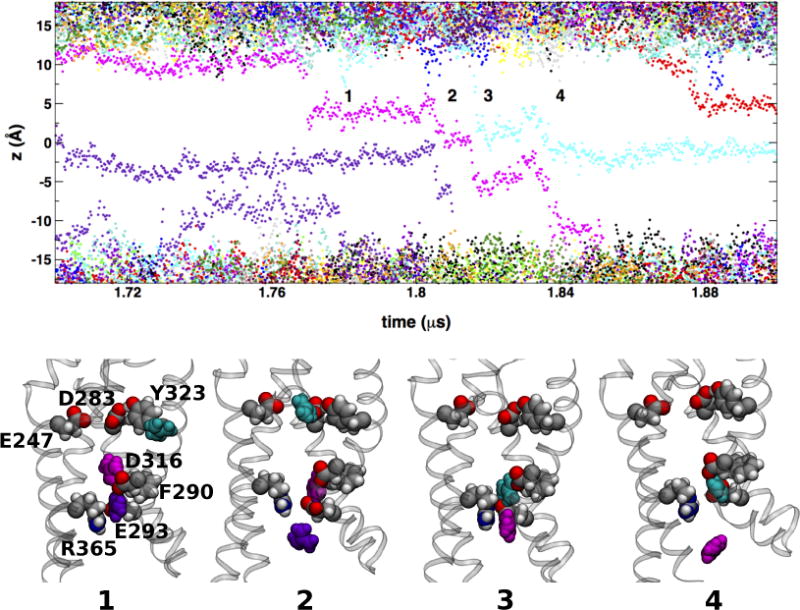
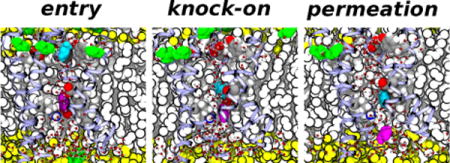
A pair of Gdm⁺ permeation events. The top panel shows a detail of the time-dependence of cation transmembrane positions in the GdmCl simulation at −750 mV (see Figure 1). The labeled configurations snapshots show three Gdm⁺ ion (cyan, magenta, and purple filled-sphere) from the entry of the cyan into the VSD from the extracellular polar/apolar membrane interface (snapshot 1) to release the release of the magenta ion into the intracellular side (snapshot 4) through two knock-on translocation events. Side chains forming the extracellular (E247, D283, and Y323) and intracellular (F290, E293, D316, and R365) binding sites are shown as filled-spheres.

Permeation mechanisms in the BOM VSD

In addition to the preferential partitioning of Gdm⁺ at the lipid bilayer interface (Figure 4), the differences in the number of permeation events between K⁺ and Gdm⁺ can be explained by the manner in which each ion interacts with the VSD (Figures 7 and 8). In the case of K⁺, binding to the intracellular site is favored by the localized nature of the ion charge distribution; the ion is fully coordinated through electrostatic interactions with D316 and E293, and cation-π interactions with F290 (see Figures 5D and 7). In addition, R365 appears to provide steric hindrance, essentially blocking K⁺ from being ejected into the intracellular space. The overall configuration of the bound-K⁺ intracellular binding site is reminiscent of that of the GTC configuration around K302 in the up-state crystal structures of the Kv1.2 paddle chimera channel⁴⁹, thus suggesting a stabilization of K⁺ vs. Gdm⁺ at the GTC. In contrast, in the presence of Gdm⁺ ions, F290 is facing the lipid bilayer hydrocarbon core away from the VSD permeation pathway, and the Gdm⁺ ion forms favorable stacking interactions with R365 (Figure 8).

The K⁺ permeation events occur independently from each other (Figures 2 and 7). In contrast, in all of the twenty events involving Gdm⁺, permeation occur through a two-ion “knock-on” mechanism, where the entrance of a second Gdm⁺ into the VSD drives translocation of the first Gdm⁺ into the intracellular space (Figures 1 and 8). The knock-on event occurs near the region of the intracellular binding site, when a bound Gdm⁺ is pushed out into the intracellular crevice as a second Gdm⁺, solvated in the extracellular crevice, enters the intracellular binding site.

DISCUSSION

Our observation of cation displacement over ~3–5 μs is qualitatively consistent with electrophysiological measurements on eukaryotic channels.^{4, 16} Moreover, we consistently observe a total number of Gdm⁺ permeation events greater than the number of K⁺ permeation at all voltages, which is consistent with the larger conductance measured for Gdm⁺ vs. K⁺ reported by Tombola et al.¹⁶ However, the sporadic occurrence of these events indicates that much longer MD trajectories would be required to accurately calculate ion conductance through the VSD. Nevertheless, the events observed provide important insights on the mechanism of ion permeation through the VSD.

We observe several different pathways available to monovalent cations entering the VSD. Tombola et al.¹⁶ presented a model in which the cations typically enter between the interface of the VSD and the pore domain. The physiological omega pore exists as part of a tetrameric assembly, where the alpha-current runs through the pore domain and the omega current through the four VSDs. Thus, a limitation of our BOM model is that it is a monomer of only the VSD (S1–S4), and hence the effects of the pore region (S5–S6) on ion permeation through the VSD are not represented.

A fragment of the Shaker channel containing the VSD but lacking the pore domain (named Shaker-iVSD) was recently found to conduct leak currents in multiple conformations, including the resting state, without the need of mutations in the S4 helix or elsewhere in the protein.⁵⁰ The observed currents were carried by protons and cations as large as N-methyl-D-glucamine. Our work focused primarily on the BOM VSD, as we did not observe a fully connected permeation pathway in the native VSD. The number of permeation events observed in our study indicates that much longer simulation times would be necessary to detect ion permeation in the native VSD. It should be noted however that the structural and functional information used to generate our model and interpret our data is based on VSDs from full-length channels. Therefore, even if our simulations are carried out without the pore domain, our results might not be representative of what happens in the truncated Shaker-iVSD.

In addition to describing the mechanistic role of the GTC residues in the cation binding event, we were able to observe every amino acid interaction with the permeating cation on an atomistic scale. Tombola et al.¹⁶ characterized interactions between permeating cations and the omega-pore, and determined which residues change the omega current and what type of interaction the side chain has with the permeating cation (i.e., steric hindrance, electrostatic, null, or indirect). The residues shown to have the largest impact on the omega current are S240 in S1, E283, C286, F290 in S2, T329 in S3, and Q354, S367, L348, and A359 in S4. The BOM variant is a quadruple mutant of R362S, S357C, E283D and M356D. Consistent with inferences from the experiments, we find that residue D283 plays a role in the outer binding site, while F290 plays a role in the inner binding site of the BOM variant.

Our simulations are the first to report both K⁺ and Gdm⁺ permeation through an atomistic model of the Shaker BOM VSD. By analyzing the differences between the two types of events, we are able to shed light on why the Gdm⁺ permeation rate is larger than the K⁺ permeation rate. The experimentally inferred picture of Gdm⁺ permeation suggests that the cation pathway overlaps with the S4 arginine pathway, which is a particularly appealing argument considering the molecular similarities between Gdm⁺ and the guanidine moiety on the arginine side chain. Additionally, recent reports on the evolutionary design principles of voltage-dependent ion channels VSDs highlight the importance of the highly conserved nature of the acidic and basic residues in the VSD^{51, 52}. These studies support the notion that the VSD structure has evolved over time to create an electrostatically favorable environment through which it is able to conduct cationic gating charges across the hydrophobic bilayer. Thus, not surprisingly, we find that permeation of the Gdm⁺ ion is a more favorable event (i.e., occurs more frequently) than K⁺ permeation, since the Gdm⁺ is able to exploit the same binding sites that have evolved over time into stable locations of the gating charges.

Because maintaining an ionic gradient across the cell membrane is important in excitable cells, the typical voltage-dependent ion channel has a VSD designed to be nonconducting and selective for gating charge residues over the monovalent cations readily available in the cellular environment (i.e. K⁺ and Na⁺). However, when the quadruple BOM mutant is created, both K⁺ and Gdm⁺ cations are able to permeate the pore in the VSD. Based on the atomistic details we observed during our simulations, we propose that the reason K⁺ permeates slower than Gdm⁺ is due to its high charge density and smaller size, which allows it to participate in strong Coulombic interactions both in the extracellular and intracellular binding sites, and cation-π interactions with F290. In contrast, the delocalized charge and size of the Gdm⁺ ion precludes it from participating in the same strong, electrostatically driven interactions, and enables it to form favorable stacking interactions with R365. Thus, the bound Gdm⁺ ion is not held as strongly within the VSD, which explains why Gdm⁺ permeate at lower voltages. Additionally, the sterically bulky hydrophobic F290 side chain is pushed out by the binding of Gdm⁺ to face the bilayer rather than towards the inside of the VSD, where it is normally located in the absence of a nearby Gdm⁺ ion. This finding is consistent with the fact that the F290A mutation produces a large increase in omega current in the Shaker channel¹⁶.

Removing the F290 side chain from the permeations pathway allows two Gdm⁺ ions to bind into the modified gating charge transfer center, facilitating the knock-on mechanism of permeation. Due to the limited simulation time and the relatively low number of permeation events detected for K⁺, we cannot exclude a contribution of the knock-on mechanism to the permeation of K⁺. However, based on our observations, the knock-on mechanism does not appear to be involved in K⁺ conduction.

According to Tombola et al.,⁴ K⁺ currents through the VSD are enhanced by small concentrations of Gdm⁺. Our GdmCl simulations may offer insight into this phenomenon. Based on the observed two-ion knock-on Gdm⁺ permeation mechanism, our hypothesis is that the Gdm⁺ ion may get lodged into the intracellular binding site and then ‘hold the door open’ for other positive ions to pass. The mechanism may involve the bound Gdm⁺ relieving the steric hindrance by pushing the cap of the GTC (F290) outward. This modifies the GTC in such a way that the potassium ions may be able to enter the site at lower voltages or at lower concentrations.

Our observations recapitulate Kv VSD activation features reported by Tao et al.⁴⁹ and suggest that the architecture of the VSD has evolved to allow the permeation of large Gdm⁺ ions through the center of the VSD more easily than the physiologically available monovalent cations. The similarity in molecular size and charge of a Gdm⁺ with the side chain guanidine of arginine residues supports the experimentally proposed^{4, 16} notion that the path followed by the Gdm⁺ can overlap with the motions of the S4 arginines.

SUMMARY

To gain insight into the molecular mechanisms of ion conduction through VSDs, we performed atomistic molecular dynamics simulations on the μs timescale of the so-called BOM variant of the Shaker VSD, which was previously shown to carry particularly large omega-currents. The VSD was in an experimentally validated resting-state conformation, surrounded by a lipid bilayer and by solutions containing guanidinium chloride or potassium chloride, and under applied electric fields. Our simulations reveal the Shaker VSD permeation pathway and the protein-ion interactions that control permeation kinetics. The simulations of guanidinium ion permeation also provide new insights into the mechanism of voltage-dependent activation of voltage-gated ion channels.