Experimental Determination of Partitioning in the Fe-Ni System for Applications to Modeling Meteoritic Metals

Abstract

Experimental trace element partitioning values are often used to model the chemical evolution of metallic phases in meteorites, but limited experimental data were previously available to constrain the partitioning behavior in the basic Fe-Ni system. In this study, we conducted experiments that produced equilibrium solid metal and liquid metal phases in the Fe-Ni system and measured the partition coefficients of 25 elements. The results are in good agreement with values modeled from IVB iron meteorites and with the limited previous experimental data. Additional experiments with low levels of S and P were also conducted, to help constrain the partitioning behaviors of elements as a function of these light elements. The new experimental results were used to derive a set of parameterization values for element solid metal-liquid metal partitioning behavior in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C ternary systems at 0.1 MPa. The new parameterizations require that the partitioning behaviors in the light-element-free Fe-Ni system are those determined experimentally by this study, in contrast to previous parameterizations that allowed this value to be determined as a best-fit parameter. These new parameterizations, with self-consistent values for partitioning in the end-member Fe-Ni system, provide a valuable resource for future studies that model the chemical evolution of metallic phases in meteorites.

1. Introduction

During differentiation, cooling, and crystallization of planetary bodies, the composition of metallic liquids can dramatically affect the partitioning behavior of elements. In particular, the “light element” content of a metallic liquid – those elements that are present in the liquid at wt% levels with atomic numbers lower than Fe – can have a significant influence. Understanding how light elements such as S, P, and C affect partitioning behavior is crucial for investigating the early evolution of planetesimals in the Solar System and interpreting textures and the chemical compositions of phases measured in a large variety of meteorites. For example, using iron meteorites, the crystallization of metallic cores of asteroid-sized bodies have been modeled over a range of S contents to establish the bulk compositions of these cores and the processes involved during their crystallization (e.g. Chabot and Haack, 2006; Goldstein et al., 2009). Trace elements in ureilites have been used to determine the roles of S-rich or C-rich metallic melts early in the evolution of their parent body (e.g. Warren et al., 2006; Rankenburg et al., 2008; Hayden et al., 2011). The trace element composition of metal in pallasites has been used to develop and constrain different hypotheses proposed for the origins of these meteorites (Wasson and Choi, 2003; Yang et al., 2010; Boesenberg et al., 2012).

Given these applications, previous experimental studies have focused on determining the influence of light elements in metallic systems, such as S, P, and C, on solid metal-liquid metal trace element partitioning behavior (e.g. Willis and Goldstein, 1982; Jones and Drake, 1983; Malvin et al., 1986; Chabot et al., 2003). Based on the experimental results, Jones and Malvin (1990) produced a parameterization expression for solid metal-liquid metal partitioning in the Fe-Ni-S and Fe-Ni-P systems, to aid in interpreting the observed behaviors and in applying the results to meteoritic systems. Chabot and Jones (2003) presented updated parameterization expressions, based heavily on Jones and Malvin (1990), with slight variations to the specific equations. Changes to specific parameterizations for certain elements arose as new experimental data were acquired in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems, improving the overall agreement between the parameterizations and experimental data and expanding the parameterizations to include additional elements (Chabot et al., 2006; 2007; 2009; Corrigan et al., 2009).

However, the parameterized expressions of both Jones and Malvin (1990) and Chabot and Jones (2003) and subsequent applications of these expressions treated the solid metal-liquid metal partitioning behavior of elements in the Fe-Ni system as a free parameter, as determined by the best fit to the experimental dataset as a whole for each element. Allowing the Fe-Ni partitioning value to be a free parameter was necessary for many elements, given data for only a handful of elements for solid metal-liquid metal partition coefficients measured in the Fe-Ni system were available. Parameterizations were derived independently for the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems, and there was no requirement that the parameterizations in these different light-element-bearing systems would have the same end-member partitioning value in the Fe-Ni system. This resulted in parameterizations that were not self-consistent with each other and thus complicated applications to meteoritic systems, in particular to systems with multiple light-elements.

Given this motivation, this experimental study determined the solid metal-liquid metal partition coefficient for elements in the Fe-Ni system and developed parameterization expressions for partitioning in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems, which are self-consistent in the endmember Fe-Ni system. Details of the experimental methods and analysis, the derivation of the parameterization parameters for each element, and some general summarizing thoughts on applying these results to future studies of the formation and evolution of meteorite parent bodies are provided in this paper.

2. Experimental and Analytical Methods

All experiments were conducted at the Johns Hopkins University Applied Physics Laboratory using evacuated silica tubes in 0.1 MPa Deltech vertical tube furnaces, similar to the techniques used in previous studies in this lab involving solid metal-liquid metal experiments (Chabot et al., 2007; 2009). Commercially purchased powders of high purity Fe and Ni were used for the starting mixtures, and a mixture of trace elements was created from powders of V, Cr₂O₃, Mn, Co, Cu, Zn, Ga₂O₃, Ge, As, Mo, Ru, Rh, Pd, Ag₂O, Sn, Sb, H₂WO₄, Re, Os, Ir, Pt, Au, PbO, and Bi. This trace element mixture along with the Fe and Ni powders were ground in acetone to produce a starting composition that resulted in each trace element being doped at roughly ~100-300 ppm. Previous work has demonstrated that doping at this level does not affect the solid metal-liquid metal partitioning behavior in the Fe-Ni-S system (Chabot et al., 2003). Approximately 200 mg of this starting mixture was placed directly in a high-purity silica glass tube. Each silica tube was subsequently evacuated and sealed while under vacuum. The sealed tube was hung in the vertical tube furnace at a temperature of 1500°C for 7–12 hours. At a temperature of 1250°C, Malvin et al. (1986) conducted a time series study, demonstrating that similar solid metal-liquid metal trace element partitioning behavior was achieved for experiments that were conducted for as little as 5 hours. Since our experiments involved a higher temperature of 1500°C, our durations of 7–12 hrs are sufficient to reach equilibrium partitioning behavior. At the end of the experiment’s duration, the silica tube was removed from the furnace and immersed in water to quench the experiment. The silica tube was then broken open to access the sample, which resembled a metallic bead of material. Though the starting powders were placed directly in the silica glass tubes, the final run products showed no significant interaction with the silica tubes and were easily removed from the tubes following the completion of the experiment. Each sample was set in epoxy and sliced using a diamond saw to reveal multiple cross sections of the sample. Cross sections were set in epoxy and polished with alumina powder.

Experiments were analyzed for major elements (Fe and Ni) using a JEOL 8900L electron microprobe at the Carnegie Institution of Washington. For each experimental run product, a back-scattered electron (BSE) image was obtained, to determine if the experiment had produced two coexisting phases of solid metal and liquid metal and, if so, to identify the boundaries between these phases. At 1500°C, the Fe-Ni phase diagram (Bild and Drake, 1978) shows a field with two stable phases, one solid and one liquid, but the compositional difference between the equilibrium solid and liquid is only ~2 wt% Ni. This small compositional difference between the phases meant that reliably discerning the presence of two phases with an optical microscope, as was commonly done for previous solid metal-liquid metal experimental studies, was not possible. However, BSE images revealed coexisting solid metal and liquid metal phases. In total, three experiments with equilibrium Fe-Ni solid metal and liquid metal phases were produced, and BSE images of these three samples are shown in Fig. 1.

Figure 1.

Back scattered electron images of Fe-Ni experiments at 1500°C. The compositional difference between the coexisting solid and liquid phases is small, and the liquid metal and solid metal phases are best distinguished by their distinctive textures. The liquid metal has a fine-grained dendritic quench texture, typical of quenched metallic liquids, and the solid metal phase is compositional homogenous. Large-scale brightness variations in the BSE images are due to crystal properties of the runs rather than compositional differences. A. Run #JG3: solid = 9.7 wt% Ni, liquid = 10.9 wt% Ni. B. Run #JG4: solid = 10.3 wt% Ni, liquid = 11.9 wt% Ni. C. Run #JG5: solid = 11.3 wt% Ni, liquid = 12.7 wt% Ni.

The Fe and Ni concentrations of the solid metal and liquid metal phases were measured by the electron microprobe using a 15 kV and 30 nA beam and counting times of 30 s. Analyses were obtained with a raster beam of 10 μm by 10 μm, with >10 analyses acquired for each of the two phases. The solid metal had a homogeneous Fe and Ni composition, with brightness variations in the solid metal phase, as shown in the BSE images of Fig. 1, due to the crystal properties within the solid metal rather than compositional differences, as verified by electron microprobe analyses and the laser ablation ICP-MS analyses described in the next paragraph. The liquid metal quenched to a dendritic texture, with slight compositional variations of up to ~2 wt% Ni between individual analyses; large-scale brightness variations seen in the BSE images of Fig. 1 were also inspected by electron microprobe and laser ablation ICP-MS analyses and were not associated with compositional differences but reflect variations in the quench crystal properties. Additionally, electron microprobe and laser ablation ICP-MS measurements were made at different regions of the sample, such as the two liquid-metal regions visible in Fig. 1B, and the results indicated that the compositions of the liquid and solid phases were uniform throughout each run product. For each of the solid and liquid phases, the multiple measurements were averaged to determine the composition, and errors were calculated as twice the standard deviation of the mean, with the results listed in Table 1. The measured Fe and Ni compositions are generally consistent with those expected from the Fe-Ni phase diagram (Bild and Drake, 1978), with the liquid metal phase having on average 1.4 wt% more Ni than the equilibrium solid metal. However, the Ni contents of the solid phase and of the liquid phase are both slightly higher by ~2 wt% Ni than expected for a run at 1500°C, suggesting that the experiments might have experienced a temperature closer to 1495°C based on the Fe-Ni phase diagram (Bild and Drake, 1978).

Table 1.

Experimental partitioning results from the Fe-Ni system. All errors are ±2σ.

Run #	JG3	JG4	JG5
Temperature (˚C)	1500	1500	1500
Duration (hours)	7.5	7.5	12
Liquid Metal
Fe (wt%)	88.8 ± 0.5	87.4 ± 0.4	86.7 ± 0.5
Ni (wt%)	10.9 ± 0.3	11.9 ± 0.3	12.7 ± 0.4
V (ppm)	110 ± 30	120 ± 80	90 ± 40
Cr (ppm)	74 ± 13	80 ± 20	74 ± 12
Mn (ppm)	19 ± 2	22 ± 11	28 ± 12
Co (ppm)	220 ± 20	286 ± 9	235 ± 13
Cu (ppm)	170 ± 30	158 ± 9	140 ± 20
Zn (ppm)	130 ± 20	144 ±12	120 ± 30
Ga (ppm)	61 ± 8	81 ± 13	65 ± 2
Ge (ppm)	130 ± 30	140 ± 20	135 ± 14
As (ppm)	300 ± 70	270 ± 80	190 ± 60
Mo (ppm)	140 ± 20	200 ± 20	133 ± 10
Ru (ppm)	59 ± 2	82 ± 1	74 ± 5
Rh (ppm)	65 ± 2	104 ± 8	65 ± 3
Pd (ppm)	115 ± 1	126 ± 21	80 ± 14
Ag (ppm)	20 ± 11	11 ± 3	–
Sn (ppm)	710 ± 290	340 ± 110	390 ± 150
Sb (ppm)	570 ± 160	400 ± 120	370 ± 160
W (ppm)	45 ± 2	73 ± 6	53.1 ± 1.2
Re (ppm)	34 ± 3	59 ± 5	57 ± 11
Os (ppm)	31 ± 7	52 ± 2	46 ± 9
Ir (ppm)	39 ± 11	69 ± 3	62 ± 8
Pt (ppm)	62 ± 10	89 ± 9	70 ± 2
Au (ppm)	151 ± 20	215 ± 60	200 ± 50
Pb (ppm)	510 ± 430	70 ± 20	323 ± 34
Bi (ppm)	420 ± 370	59 ± 13	290 ± 110
Solid Metal
Fe (wt%)	90.2 ± 0.3	89.7 ± 0.2	88.32 ± 0.13
Ni (wt%)	9.7 ± 0.2	10.25 ± 0.13	11.32 ± 0.12
V (ppm)	65 ± 4	73 ± 3	46 ± 2
Cr (ppm)	63 ± 4	63 ± 8	57 ± 4
Mn (ppm)	13 ± 2	15 ± 1	15.8 ± 1.2
Co (ppm)	228 ± 12	273 ± 8	218 ± 6
Cu (ppm)	111 ± 6	122 ± 6	140 ± 20
Zn (ppm)	80 ± 30	97 ± 6	70 ± 20
Ga (ppm)	48 ± 6	61 ± 2	49.1 ± 1.4
Ge (ppm)	85 ± 3	89 ± 3	84 ± 4
As (ppm)	70 ± 8	69 ± 9	42.7 ± 0.9
Mo (ppm)	93 ± 14	145 ± 7	89 ± 3
Ru (ppm)	73 ± 7	96 ± 6	86 ± 4
Rh (ppm)	64 ± 7	102 ± 3	62 ± 3
Pd (ppm)	62 ± 10	71 ± 5	42.2 ± 1.3
Ag (ppm)	3.6 ± 0.1	1.6 ± 0.3	–
Sn (ppm)	80 ± 20	50 ± 2	49 ± 2
Sb (ppm)	64 ± 4	59 ± 7	45 ± 2
W (ppm)	49 ± 5	68 ± 2	50 ± 3
Re (ppm)	66 ± 4	90 ± 3	90 ± 3
Os (ppm)	68 ± 2	89 ± 5	75 ± 3
Ir (ppm)	71 ± 4	103 ± 4	90 ± 4
Pt (ppm)	68 ± 6	87 ± 2	65 ± 3
Au (ppm)	57 ± 4	82 ± 9	70 ± 5
Pb (ppm)	15 ± 7	1.8 ± 0.6	7.3 ± 0.2
Bi (ppm)	6 ± 2	0.7 ± 0.2	3.1 ± 0.5
D(solid metal/liquid metal)				Weighted Average
Ni	0.89 ± 0.03	0.86 ± 0.02	0.89 ± 0.03	0.874 ± 0.015
V	0.6 ± 0.2	0.6 ± 0.4	0.5 ± 0.3	0.57 ± 0.15
Cr	0.9 ± 0.2	0.8 ± 0.2	0.77 ± 0.13	0.81 ± 0.10
Mn	0.68 ± 0.13	0.7 ± 0.3	0.6 ± 0.2	0.66 ± 0.10
Co	1.02 ± 0.11	0.95 ± 0.04	0.93 ± 0.06	0.95 ± 0.03
Cu	0.65 ± 0.13	0.77 ± 0.06	1.0 ± 0.2	0.77 ± 0.05
Zn	0.6 ± 0.3	0.67 ± 0.07	0.6 ± 0.2	0.66 ± 0.06
Ga	0.8 ± 0.2	0.75 ± 0.12	0.76 ± 0.03	0.76 ± 0.03
Ge	0.64 ± 0.12	0.64 ± 0.11	0.62 ± 0.07	0.63 ± 0.05
As	0.23 ± 0.06	0.26 ± 0.09	0.22 ± 0.07	0.23 ± 0.04
Mo	0.67 ± 0.13	0.72 ± 0.09	0.66 ± 0.05	0.67 ± 0.04
Ru	1.24 ± 0.13	1.16 ± 0.08	1.17 ± 0.09	1.18 ± 0.05
Rh	0.98 ± 0.12	0.98 ± 0.08	0.96 ± 0.06	0.97 ± 0.04
Pd	0.54 ± 0.08	0.56 ± 0.10	0.53 ± 0.09	0.54 ± 0.05
Ag	0.17 ± 0.10	0.14 ± 0.05	–	0.15 ± 0.04
Sn	0.11 ± 0.05	0.15 ± 0.05	0.12 ± 0.05	0.13 ± 0.03
Sb	0.11 ± 0.03	0.15 ± 0.05	0.12 ± 0.05	0.12 ± 0.02
W	1.08 ± 0.12	0.94 ± 0.08	0.93 ± 0.06	0.95 ± 0.04
Re	1.9 ± 0.2	1.53 ± 0.14	1.6 ± 0.3	1.65 ± 0.11
Os	2.2 ± 0.5	1.70 ± 0.12	1.6 ± 0.3	1.71 ± 0.11
Ir	1.8 ± 0.5	1.49 ± 0.08	1.4 ± 0.2	1.49 ± 0.07
Pt	1.1 ± 0.2	0.98 ± 0.10	0.94 ± 0.04	0.95 ± 0.04
Au	0.38 ± 0.06	0.38 ± 0.11	0.35 ± 0.10	0.37 ± 0.05
Pb	0.03 ± 0.03	0.027 ± 0.011	0.023 ± 0.009	0.025 ± 0.007
Bi	0.015 ± 0.013	0.012 ± 0.005	0.011 ± 0.004	0.012 ± 0.003

Trace element concentrations were measured by laser ablation inductively coupled mass spectrometry (ICP-MS) microanalysis at the University of Maryland, using a similar approach applied to the analyses of previous metallic experiments (Chabot et al., 2007; 2009). Analyses were conducted using a single-collector ICP-MS (Element 2, Thermo Finnigan) coupled to a laser ablation system with an output wavelength at 213 nm (UP213, New Wave Research). The laser was operated at ~3 J/cm². Ablation sampling was done in line scan mode using a 40 μm diameter spot and 7 Hz flash rate. During ablation, the sample was moved at a rate of 10 μm/s. The length of each line varied depending on the characteristics of each experimental sample, but the length was generally between 300 to 600 μm. At least four line scans were conducted in each phase. During analysis, data were collected for the following masses: ⁵¹V, ⁵³Cr, ⁵⁵Mn, ⁵⁷Fe, ⁵⁹Co, ⁶²Ni, ⁶³Cu, ⁶⁵Cu, ⁶⁶Zn, ⁶⁷Zn, ⁶⁹Ga, ⁷¹Ga, ⁷³Ge, ⁷⁵As, ⁹⁵Mo, ⁹⁷Mo, ⁹⁹Ru, ¹⁰¹Ru, ¹⁰³Rh, ¹⁰⁵Pd, ¹⁰⁷Ag, ¹⁰⁸Pd, ¹⁰⁹Ag, ¹¹⁷Sn, ¹¹⁸Sn, ¹²¹Sb, ¹²³Sb, ¹⁸²W, ¹⁸³W, ¹⁸⁵Re, ¹⁸⁸Os, ¹⁸⁹Os, ¹⁹¹Ir, ¹⁹³Ir, ¹⁹⁴Pt, ¹⁹⁵Pt, ¹⁹⁷Au, ²⁰⁶Pb, ²⁰⁸Pb, and ²⁰⁹Bi. Analyses of two standard reference materials were conducted both before and after the analyses of the experimental run products: NIST 610 glass (Jochum and Stoll, 2008) and North Chile (Filomena) iron meteorite (electronic annex of Walker et al., 2008) using similar analytical conditions and settings. These standard reference materials provided the basis for determining calibration curves to constrain instrument drift and provide element concentrations. Element concentrations for V, Cr, Mn, Zn, As, Ag, Sn, Sb, Pb, and Bi were standardized using the NIST 610 standard. Element concentrations for Co, Cu, Ga, Ge, Mo, Ru, Rh, Pd, W, Re, Os, Ir, Pt, and Au were standardized using the North Chile (Filomena) standard. Data were processed using the LAMTRACE (Achterbergh et al., 2001) software program, which determines element concentrations using ratios of count rates for samples and standards, known concentrations in the standards, and the known concentration of an internal standard in the experimental run products, in this case Ni as determined by electron microprobe. For elements measured by two isotopes, the results were compared to confirm consistency in the measurements, and in general, the measurement from the isotope with the lower detection limit was used. The trace element composition of each phase was determined by averaging the multiple measurements obtained in each phase, and errors were calculated as twice the standard deviation of the multiple measurements.

Table 1 lists the trace element concentrations measured for the solid and liquid metal in the three Fe-Ni experiments shown in Fig. 1. Table 1 also reports the solid metal-liquid metal partition coefficient (D), defined as the elemental ratio of the weight concentrations in the solid metal to that in the liquid metal. The three independent experiments produced consistent partition coefficients. Given this consistency, a weighted average of the partition coefficients from the three experiments was determined, with each D value weighted using the associated error given in Table 1 to calculate a weighted average D value. The resulting weighted average D value was used in the parameterizations in the next section.

Though the main motivation and focus of this study was to determine the solid metal-liquid metal partitioning behavior in the light-element-free Fe-Ni system, the results from six additional experiments are reported in Table S1 supplementary material. These experiments were conducted using the same experimental and analytical approaches described above, but the runs also contained low levels of either S or P, added as commercially purchased FeS or P powders to the starting mixtures. The resulting run products had coexisting solid metal and either a S-bearing or P-bearing metallic liquid, with the P-bearing run products resembling those described in Corrigan et al. (2009) and the S-bearing run products resembling those detailed in Chabot et al. (2009). Given these compositional differences, phase recognition could be readily achieved by optical microscopy in these runs. The analysis of these runs by electron microprobe and laser ablation ICP-MS was the same as described for the Fe-Ni system experiments. These experiments, with low concentrations of either S or P, helped the parameterizations, discussed in the next section, to constrain the trace element partitioning behavior as the light-element content of the system decreased and approached the light-element-free Fe-Ni partitioning value.

3. Results

3.1. Partitioning Results and Comparisons

In total, partitioning results were obtained for 25 elements. A comparison between our newly determined solid metal-liquid metal partition coefficients and those from previous studies in the Fe-Ni system (Bild and Drake, 1978; Jones and Drake, 1983; Jones and Malvin, 1990) is shown in Fig. 2. There is generally good agreement between our results and previous measurements, with the exceptions of the D(Au) and D(Cr) values reported by Bild and Drake (1978). In contrast to our experiments conducted in evacuated and sealed silica tubes, the experiments of Bild and Drake (1978) were conducted in open alumina crucibles that allowed the experimental sample material to exchange with a mix of CO₂ and H₂ gasses used to control the oxygen fugacity conditions during the run; such experiments could be more susceptible to loss of material during the experiment, which could affect solid metal-liquid metal equilibrium behavior being achieved. The experimental results originally presented in Jones and Drake (1983), with refined analyses for some of the runs tabulated in Jones and Malvin (1990), are largely consistent with our new results within error, as shown in Fig. 2.

Figure 2.

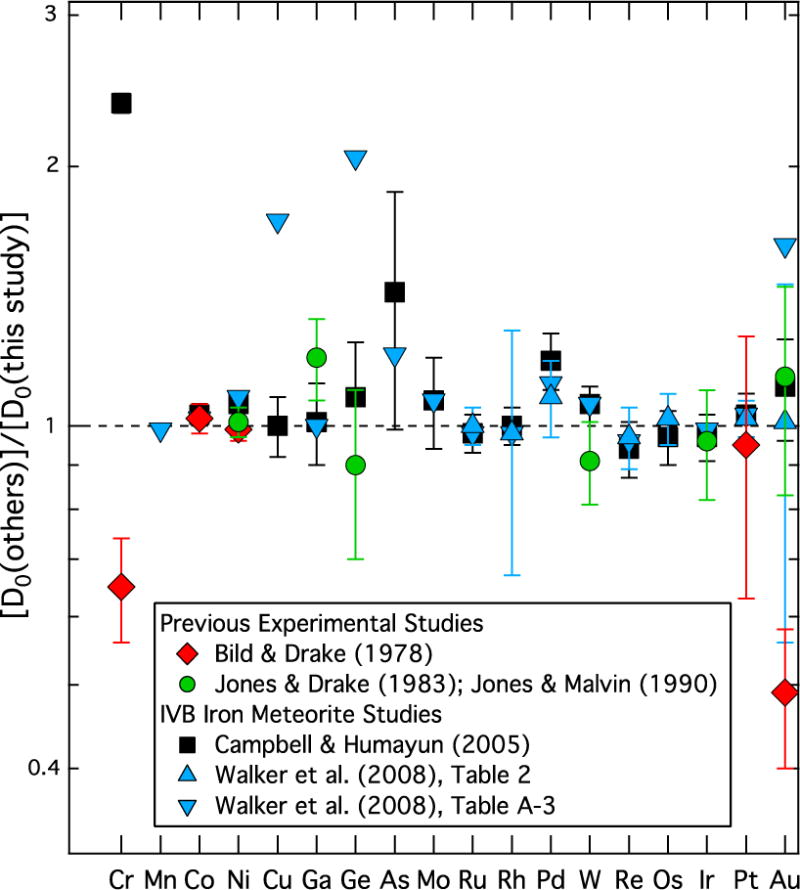
The solid metal-liquid metal partition coefficient in the Fe-Ni system (D₀) determined in this study is shown as a ratio with D₀ values determined in previous experimental studies (red symbols, Bild and Drake (1978); green symbols, Jones and Drake (1983) and Jones and Malvin (1990)) and with D₀ values modeled from chemical trends in the IVB iron meteorite group (black symbols, Campbell and Humayun (2005); blue symbols, Walker et al. (2008)). Exact agreement would fall along the dotted line at a value of unity. Errors (2σ) are derived from using those reported in the previous studies and in Table 1 and assuming independent uncertainties between the datasets in the ratio. Jones and Drake (1983) did not provide errors for D(Ga) and D(W), so 10% errors were applied, consistent with the lowest errors reported for their other experimental runs. Walker et al. (2008) values from their Table A-3 did not provides errors, so these points are plotted without error bars.

Figure 2 also compares our solid metal-liquid metal D values in the Fe-Ni system to those determined by modeling the elemental trends in the IVB iron meteorite group (Campbell and Humayun, 2005; Walker et al., 2008). Chemical trends within the IVB iron meteorite group are thought to have formed by fractional crystallization of an Fe-Ni core of an asteroid-sized parent body largely devoid of S (Willis and Goldstein, 1982; Jones and Drake, 1983; Rasmussen et al., 1984; Chabot, 2004), in contrast to the core compositions involved in the crystallization of other iron meteorite groups, such as the IIIAB, IIAB, or IVA groups (e.g. Wasson, 1999; Wasson and Richardson 2001; Chabot et al., 2004; Wasson et al., 2007; Goldstein et al., 2009; McCoy et al., 2011). As seen on Fig. 2, our experimental determinations of D in the Fe-Ni system are highly consistent with nearly all of those determined by Campbell and Humayun (2005) by modeling the IVB irons. The D(As) value reported by Campbell and Humayun (2005) has a larger error than the other elements, and their D(As) value overlaps with the value determined by our study when this error is considered. The one element for which there is considerable disagreement between our experimental D value and that modeled from the IVB irons by Campbell and Humayun (2005) is Cr, as also noted by Campbell and Humayun (2005) during a comparison to existing experimental data at the time. Subsequently, Chabot et al. (2009) specifically investigated the partitioning behavior of Cr and concluded that the Cr trends observed in iron meteorites were not due to simple fractional crystallization, but rather the presence of chromite and other phases in the iron meteorites likely were substantially effecting the behavior of Cr during iron meteorite crystallization. Thus, if the Cr concentrations measured in IVB irons are not predominantly set by fractional crystallization, one would not expect there to be agreement with the solid metal-liquid metal partitioning value.

Walker et al. (2008) also modeled the crystallization of the IVB iron meteorite groups and derived solid metal-liquid metal partitioning values for elements relative to D(Ir) or D(Os), results of which are shown on Fig. 2. Walker et al. (2008) analyzed IVB irons by two approaches: whole rock analyses and in-situ laser ablation analyses. Results from the whole rock analyses were largely focused on highly siderophile elements. By modeling the crystallization trends determined by the whole rock analyses of the IVB group, Walker et al. (2008) reported solid metal-liquid metal partitioning values for these elements relative to D(Ir) in their Table 2. As seen on Fig. 2, all of these seven values agree within error with our experimental results. Table A-3 of Walker et al. (2008) reported solid metal-liquid metal partitioning values for elements relative to D(Os), based on modeling IVB iron meteorite trends as determined by their in situ laser-ablation data. As seen on Fig. 2, the majority of these data also agree with our experimental results, with the exceptions of Cu, Ge, and Au. The in situ laser ablation ICP-MS data reported by Walker et al. (2008) for Ge are below the 3 sigma detection limit of their measurements, as labeled in their Table 3, providing a possible explanation for the discrepancy noted for this element. In contrast, the measurements reported by Walker et al. (2008) for Cu and Au are well above detection limits, requiring an alternate explanation. Table A-3 of Walker et al. (2008) lists the R-squared goodness-of-fit values for the IVB modeling of D(Au) and D(Cu) relative to D(Os) to be 0.541 and 0.162 respectively, indicating that the behavior of these elements are not well-fit by a linear function relative to D(Os) using the in situ laser ablation measurements.

Table 2.

Parameterization coefficients for partitioning in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems.

Element	Do	βSulfur	βPhosphorus	βCarbon
P	0.1*	−2.40 ± 0.10	−0.43 ±0.20	−
V	0.57 ± 0.15	3.00 ± 0.67	–	–
Cr	0.81 ± 0.1	1.66 ± 0.24	−0.7 ± 1.4	1.36 ± 0.19
Co	0.95 ± 0.03	−1.260 ± 0.088	−0.70 ± 0.47	−0.588 ± 0.060
Ni	0.874 ± 0.015	−0.517 ± 0.021	−0.016 ± 0.039	−1.282 ± 0.049
Cu	0.77 ± 0.05	1.39 ± 0.17	−1.29 ± 0.61	−1.92 ± 0.29
Zn	0.66 ± 0.06	0.99 ± 0.57	–	–
Ga	0.76 ± 0.03	−2.81 ± 0.19	−4.16 ± 0.74	−3.70 ± 0.43
Ge	0.63 ± 0.05	−3.23 ± 0.18	−4.23 ± 0.46	−2.57 ± 0.21
As	0.23 ± 0.04	−2.00 ± 0.13	−3.42 ± 0.39	−2.00 ± 0.28
Mo	0.67 ± 0.04	−1.33 ± 0.17	2.08 ± 0.50	–
Ru	1.18 ± 0.05	−3.89 ± 0.37	−0.94 ± 0.65	−1.60 ± 0.36
Rh	0.97 ± 0.04	−2.66 ± 0.24	−0.74 ± 0.50	−
Pd	0.54 ± 0.05	−0.707 ± 0.074	−0.87 ± 0.45	−3.38 ± 0.26
Ag	0.15 ± 0.04	2.88 ± 0.51	0.45 ± 0.95	–
Sn	0.13 ± 0.03	−0.84 ± 0.24	−2.20 ± 0.55	−4.65 ± 0.50
Sb	0.12 ± 0.02	−0.61 ± 0.37	−3.23 ± 0.63	−4.97 ± 0.59
W	0.95 ± 0.04	−3.88 ± 0.21	−0.67 ± 0.65	3.36 ± 0.47
Re	1.65 ± 0.11	−5.08 ± 0.21	−3.79 ± 0.68	0.27 ± 0.36
Os	1.71 ± 0.11	−5.34 ± 0.20	−5.6 ± 1.1	−2.80 ± 0.63
Ir	1.49 ± 0.07	−5.04 ± 0.25	−5.63 ± 0.68	−4.23 ± 0.65
Pt	0.95 ± 0.04	−4.20 ± 0.25	−5.68 ± 0.70	−4.81 ± 0.76
Au	0.37 ± 0.05	−1.72 ± 0.15	−3.19 ± 0.31	−4.29 ± 0.28
Pb	0.025 ± 0.007	3.0 ± 2.4	1.9 ± 1.1	–
Bi	0.012 ± 0.003	7.5 ± 4.0	1.80 ± 0.90	–

All errors are ± 2σ. See Equation (1) for the form of the regression and Equation (2) for the calculation of Fe Domains for light element i.

^*D₀ value estimated by extrapolation of the experimental data shown in Fig. 3.

Overall, our experimental results show good agreement with the limited previous experimental partitioning data, as well as with solid metal-liquid metal partition coefficients determined in the Fe-Ni system by modeling the IVB iron meteorite group. Along with demonstrating the consistency of our new experimental results, the agreement with results determined by modeling the IVB group further support the notion that the IVB parent body core was largely composed of Fe-Ni with low concentrations of light elements, such as S, (Willis and Goldstein, 1982; Jones and Drake, 1983; Rasmussen et al., 1984; Chabot, 2004; Campbell and Humayun, 2005; Walker et al., 2008) that would affect the partitioning behaviors of elements and the resulting crystallization trends.

3.2. Parameterization Expressions

We applied our Fe-Ni partitioning results to derive updated parameterizations of element partitioning behaviors in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems. The parameterization expressions used in our approach are those presented in Chabot and Jones (2003), which were derived from the earlier Jones and Malvin (1990) approach and share the same conceptual framework of envisioning the metallic liquid as being composed of “domains.” The term “domains” is used to conceptually represent the different compositional influences present in the metallic liquid and is not meant to imply a rigorous chemical definition. The calculation of the domains in the parameterization depends on the exact speciation of the light element in the metallic liquid, but in general, the metallic liquid is conceptualized as being composed of light-element-free Fe domains and light-element-bearing domains. Both studies interpreted the composition of the metallic liquid as the dominant influence on the solid metal-liquid metal partitioning behavior of trace elements, while the composition of the solid and the temperature were considered to be negligible. In the Chabot and Jones (2003) expression, for a trace element E in a system with light element i, D(E) is calculated by the equation:

$$\ln \left(D\left(E\right)\right)=\ln \left(D_0\right)+{\beta }_i\ln \left(\text{Fe}\text{Domains}\right)$$ (1)

where the quantity D₀ is the solid metal-liquid metal partition coefficient in the light-element-free Fe-Ni system, β_i is a constant specific to the element E being fit and the light element i, and Fe Domains is defined as the fraction of free Fe atoms available in the liquid metal. Fe Domains is parameterized using speciation based on the relevant Fe binary system phase diagrams (Massalski et al., 1990), with FeS for the Fe-Ni-S system, Fe₃P in the Fe-Ni-P system, and Fe₃C in the Fe-Ni-C system as follows:

$$Fe\mathit{\text{Domains}}=\{\begin{array}{c}\frac{1-2X_S}{1-X_S}\text{for FeS }\\ \frac{1-4X_P}{1-3X_P}{\text{for Fe}}_3\mathrm{P}\\ \frac{1-4X_C}{1-3X_C}{\text{for Fe}}_3\mathrm{C}\end{array}$$ (2)

where X_i corresponds to the molar fraction of light element i in the liquid. For example, in the Fe-Ni-S system, as the liquid metal composition approaches ~36 wt% S, the Fe Domains fraction goes to zero because there is one S atom for every Fe atom, resulting in the FeS endmember composition. The value of β_i is determined by best-fit regressions to experimental data based on the linear equation given in Eq. 1. Figure 3 demonstrates the application of this approach, plotting ln(D(E)) vs ln(Fe Domains). The slope of the best-fit lines on Fig. 3 provide the value of β, and the lines also represent the final parameterized expressions.

Figure 3.

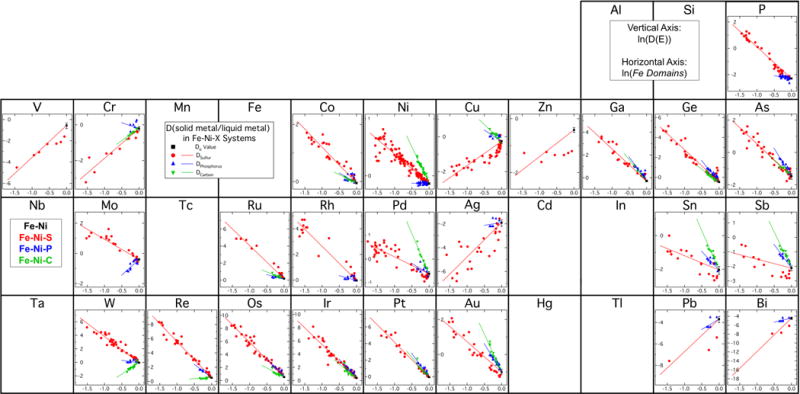
Periodic table showing parameterization results for partition coefficients in Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems. In the figure, ln(D(E)) is plotted on the vertical axis, with different scales for different elements, and ln(Fe Domains) is plotted on the horizontal axis, with the same scale for all elements. The black square shows the D₀ value determined by this experimental study in the Fe-Ni system. The red, blue, and green symbols are experimental data points for solid metal/liquid metal partitioning in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems respectively. The new parameterization expressions for the S, P, and C-bearing systems were constrained to use the D₀ value determined in this study and are shown as solid lines. The parameterized lines end roughly at the eutectic points of their respective systems.

Previous applications of these expressions and others treated D₀ as a free variable in the fits, which allowed different values for D₀ depending on the parameterization approach used, the experimental data included, and the light element system examined. Our new experimental determinations of D₀ fixed this value to produce a consistent set of parameterization expressions.

Numerous experimental datasets were used to constrain the partition coefficients in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems. In particular, data from the Fe-Ni-S system were taken from Chabot and Drake (1997); Chabot et al. (2003; 2007; 2009); Fleet and Stone (1991); Fleet et al. (1999); Jones et al. (1993); Jones and Drake (1983 Jones and Drake (1986); Jones and Malvin (1990); Liu and Fleet (2001); Lodders and Palme (1991); Malvin et al. (1986); and Willis and Goldstein (1982). Data from the Fe-Ni-P system were taken from Narayan and Goldstein (1982); Willis and Goldstein (1982); Malvin et al. (1986); Jones and Malvin (1990); and Corrigan et al. (2009). Data from the Fe-Ni-C system were from Willis and Goldstein (1982) and compiled in the main text and appendix of Chabot et al. (2006). The experimental results listed in Table S1 were also used to determine the best-fit parameterization values. To isolate the effects of each light element in the parameterized expressions, experimental studies that involved multiple light-elements were not included, such as experiments in the Fe-Ni-S-P or Fe-Ni-S-C systems. The influence of Ni content on the partitioning behavior is not included in the parameterizations expressions in equations 1 and 2, which was shown by Chabot et al. (2007) to be an appropriate assumption for systems with Ni contents <~20 wt%. Thus, in the parameterizations in this study, only experimental data with <20 wt% Ni were included to determine the best fit results.

Using the weighted average values tabulated in Table 1, the value of D₀ was fixed for each element, and β_i was determined by linear regressions of all data available for each element in each light element system. The resulting parameterization fits are shown on Fig. 3, and Table 2 provides the best-fit coefficients for all elements. Overall, the parameterizations reproduce the large changes in D due to the presence of S, P, or C in the metallic liquid while also sharing a self-consistent partitioning value in the light-element-free Fe-Ni system.

Figure 3 is formatted as a periodic table, to enable an examination for any systematic trends in the partitioning behaviors. The data and fits in Fig. 3 are plotted against the quantity of Fe Domains, defined in equation 2. The best-fit lines in each system only extend to roughly the eutectic composition in each system, approximated as 5 wt% C, 11 wt% P, and 32 wt% S for the plots in Fig. 3, as solid metal and liquid metal do not coexist in equilibrium at higher light-element compositions in these systems at 0.1 MPa.

Indeed, some neighboring row pairs on the periodic table, such as Ga and Ge, Ru and Rh, or Sn and Sb, display similar partitioning trends to each other in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems. The vertical pair of Mo and W, in the same column of the periodic table, share the similarity that both elements display dramatically different partitioning behaviors in the Fe-Ni-S and Fe-Ni-P systems. Moving from left to right across a row in the periodic table, there appears to be a general trend with elements on the left having lower partition coefficients in the P- and C-bearing systems than in the S-bearing system which gradually changes to elements on the right having larger partition coefficients in the P- and C-bearing systems than in the S-bearing system. The origin of this trend is unclear, but may be related to atomic radius.

From Fig. 3 it is clear that the identity of the light element in the system, whether S, P, or C, can have a large influence on the solid metal-liquid metal partition coefficient and that S, P, and C can have substantially different effects. In formulating the parameterization expressions, Chabot and Jones (2003) hypothesized that in this formulation, for elements that have increasing solid metal-liquid metal partition coefficients as the light-element content of the liquid increases, a single β value could capture the partitioning behavior regardless of whether the specific light element was S, P, or C. The thinking behind this hypothesis was that the partitioning behavior of these elements were being controlled simply by “avoiding” the light element that was present and thus the availability of Fe Domains in the liquid would be the dominant control. Given the limited data available at the time for partitioning in the Fe-Ni-P and Fe-Ni-C systems, this hypothesis showed potential (e.g., Ir in Fig. 3). However, subsequent experimental studies (Chabot et al., 2006; Corrigan et al., 2009) demonstrated that different β values for different light element systems are required, even when the element displayed light element avoidance in all three systems (e.g., Au in Fig. 3). Additionally, the extensive datasets now available and plotted in Fig. 3 clearly disprove this hypothesis and show the need for different β values for different light element systems. Variation in β values scales differently for each light element system. A natural question arises then of how to accurately handle partitioning in a system that contains multiple light elements, as such systems have relevance to natural parent body systems. Jones and Malvin (1990) recommended using a weighted average approach, which seems to be the current best option, given the different partitioning behaviors observed depending on the light elements present. Equation 15 in Jones and Malvin (1990) presents on possible way of deriving a combined β value for a system with multiple light elements.

In Fig. 3, focusing on specific elements reveals that while the parameterizations do a pretty good job overall fitting the experimental data, there are some cases where the data are not fit as well. For elements that exhibit S-loving, chalcophile, behavior rather than S avoidance, it has been suggested that parameterization as a function of the availability of FeS Domains, rather than Fe Domains, might better capture the functional form of these experimental data (Chabot and Drake, 1997; Chabot et al., 2009). In Fig. 3, the elements Cu and Zn provide examples of elements parameterized as having chalcophile behavior in the Fe-Ni-S system but have poor fits to many data points as parameterized as a function of Fe Domains. Additionally, the parameterizations for the chalcophile elements of Pb and Bi, for which the experimental data are limited, predict extremely low partition coefficients near the eutectic composition in the Fe-Ni-S system. It is not clear if such low D values would be achieved in nature for this system, in particular for Bi, or if this is an artifact that results from applying this parameterization approach to these chalcophile elements.

Perhaps the most unexpected discrepancy in Fig. 3 is that the majority of experimental results for Pd, Sn, Sb, and Au under low S contents (<15 wt%) in the Fe-Ni-S system have D values that fall systematically below the parameterized line. Since the parameterizations purposefully fixed the light-element-free D₀ value to be that determined by our new experiments, this discrepancy reveals that the best-fit parameterization does not match these measurements at lower S contents while fitting data at higher S contents. Notably these are not chalcophile elements, so we would expect them to be adequately fit as a function of the Fe Domains in the liquid. The low S content data points in Fig. 3 also include new experiments (Table S1) that follow the same trends, so there does not seem to be a systematic difference in the experimental or analytical approach that can explain this discrepancy. This discrepancy also cannot be attributed to the specific D₀ value used for these four elements being too high, as the D₀ values used for Pd, Sn, Sb, and Au show very good agreement and consistency with D₀ values inferred from experiments conducted in the Fe-Ni-P and Fe-Ni-C systems for all four elements (Fig. 3). This is another unexpected observation, given that the solid metal in the S-bearing system is nearly pure Fe-Ni while solid metal in the other two systems contain ~0.2 wt% or more P or C. Thus, one might predict the best agreement between the experimentally measured partition coefficients in the Fe-Ni system and the Fe-Ni-S system, but the opposite is observed for Pd, Sn, Sb, and Au, which show good agreement between the Fe-Ni, Fe-Ni-C, and Fe-Ni-P systems.

The crystal structure of the Fe-Ni metal can have an effect on the solid metal-liquid metal partition coefficients. However, the data plotted in Fig. 3 show partitioning behavior for a solid Fe-Ni alloy phase with a face-centered cubic (fcc) γ crystal structure, and this is expected to be true for all of the experiments shown, regardless of whether the data are from the Fe-Ni, Fe-Ni-P, Fe-Ni-C, or Fe-Ni-S systems. More specifically, our Fe-Ni experiments are consistent with the compositions shown on the Fe-Ni binary phase diagram (Bild and Drake, 1978), showing that the solid metal is a fcc γ crystal structure. The binary Fe-P system has a body-center cubic (bcc) α Fe alloy solid in equilibrium with a P-rich liquid (Massalski et al., 1990), but the addition of Ni to the system stabilizes the fcc γ crystal structure (Villars et al., 1995). The Fe-C system can have liquid in equilibrium with solid fcc γ Fe alloy until temperatures above 1493°C, when δ-Fe, with a bcc structure, is the stable solid phase (Raynor and Rivlin, 1988), but again, the presence of Ni stabilizes the formation of the fcc γ solid crystal structure rather than the δ-Fe structure at these higher temperatures (Villars et al., 1995). Similarly, the Fe-S binary system has fcc γ-Fe in equilibrium with a S-bearing liquid until a temperature of 1365°C, above which the bcc δ-Fe solid structure is stable (Massalski et al., 1990), but the presence of Ni results in fcc γFe alloy being the solid crystal structure (Hsieh et al., 1982). In these Fe-Ni ternary systems, the exact amount of Ni required to ensure the fcc γ phase is the crystal structure of the solid depends on the specific system and the temperature, but the ~10 wt% Ni concentrations in our experiments in Table S1 and commonly used in other experimental studies is more than sufficient according to the referenced phase diagrams.

Furthermore, Corrigan et al. (2009) conducted experiments with coexisting bcc α and fcc γ solids in the Fe-Ni-P system and found that for the 22 elements studied, most elements partitioned roughly equally between the two solids, with variations in element concentrations that were generally less than a factor of two. In particular, the bcc/fcc partition coefficient determined by Corrigan et al. (2009) for Pd was 0.84±0.05, for Sn was 1.39±0.6, for Sb was 1.09±0.05, and for Au was 0.85±0.05. Thus, the similar discrepancy observed for all four of these elements between the lower S content partitioning values and the fitted parameterizations in Fig. 3 is not consistent with being due to the difference expected from the solid metal being bcc rather than fcc structure, given that these four elements do not have similar preferences for the solid metal structure.

Overall, the parameterizations shown in Fig. 3 and documented in Table 2 capture an extensive range of solid metal-liquid metal partitioning behaviors for a large number of elements. However, like any parameterizations, there are limits to their accuracies, and future studies should consider these limitations when applying the parameterizations to model the formation and evolution of meteoritic metals. In particular, the common practice of plotting elemental trends from iron meteorite crystallization models against Au (e.g. Wasson, 1999; Wasson and Richardson, 2001; Wasson and Choi, 2003; Chabot, 2004; Wasson et al., 2007) should be thoughtfully evaluated by future studies, given that our results suggest D(Au) is more poorly understood at low S contents than other elements. It may be that a better choice than Au for an element by which to evaluate iron meteorite crystallization models is As, as suggested by Wasson et al. (1999).

4. Summary

Using experimentally determined values for partitioning in the light-element free Fe-Ni system, new parameterizations were derived for the solid metal-liquid metal partitioning behavior of 25 elements in the Fe-Ni-S, Fe-Ni-P, and Fe-Ni-C systems. The new parameterizations force all of the expressions to be consistent with the Fe-Ni experimental values and thus all of the new parameterizations predict consistent partitioning behaviors in the light-element free endmember system that they share. Along with being self-consistent, the parameterizations use data previously scattered among multiple studies, and thus they provide one compiled source for the current best parameterizations for these 25 elements in these systems.

One of the most direct applications of the parameterizations will be toward understanding the crystallization of iron meteorites. The crystallization of iron meteorites involves solid metal forming from a metallic liquid, and S, P, and C-bearing phases are commonly observed in iron meteorites (e.g. Goldstein et al., 2009). The parameterized expressions in this work will be used in crystallization models that seek to investigate the processes and compositions experienced during the crystallization of asteroidal cores, such as the role of liquid immiscibility (Ulff-Møller, 1998), the importance of mixing in the core (Wasson, 1999; Wasson and Richardson, 2001; Wasson et al., 2007), and the variety of bulk core compositions (Chabot, 2004). Though iron meteorites provide a natural application for the results of this study, investigations of the origin and formation of metal in other meteorite types can also be advanced though application of these new parameterizations, such as interpreting the role of S- and C-bearing metallic melts in the genesis of ureilites (Warren et al., 2006; Rankenburg et al., 2008; Hayden et al., 2011), or evaluating the genetic relationships among metallic compositions in pallasites and comparing their formation to iron meteorites (Wasson and Choi, 2003; Yang et al., 2010). The parameterized expressions presented here are the current best ones for modeling solid metal-liquid metal partitioning behavior and provide a resource for future studies that investigate the formation and evolution of meteoritic metal.