Evaluating Force Field Performance in Thermodynamic Calculations of Cyclodextrin Host–Guest Binding: Water Models, Partial Charges, and Host Force Field Parameters

Abstract

Computational prediction of noncovalent binding free energies with methods based on molecular mechanical force fields has become increasingly routine in drug discovery projects, where they promise to speed the discovery of small molecule ligands to bind targeted proteins with high affinity. Because the reliability of free energy methods still has significant room for improvement, new force fields, or modifications of existing ones, are regularly introduced with the aim of improving the accuracy of molecular simulations. However, comparatively little work has been done to systematically assess how well force fields perform, particularly in relation to the calculation of binding affinities. Hardware advances have made these calculations feasible, but comprehensive force field assessments for protein–ligand sized systems still remain costly. Here, we turn to cyclodextrin host–guest systems, which feature many hallmarks of protein–ligand binding interactions but are generally much more tractable due to their small size. We present absolute binding free energy and enthalpy calculations, using the attach-pull-release (APR) approach, on a set of 43 cyclodextrin-guest pairs for which experimental ITC data are available. The test set comprises both α- and β-cyclodextrin hosts binding a series of small organic guests, each with one of three functional groups: ammonium, alcohol, or carboxylate. Four water models are considered (TIP3P, TIP4Pew, SPC/E, and OPC), along with two partial charge assignment procedures (RESP and AM1-BCC) and two cyclodextrin host force fields. The results suggest a complex set of considerations when choosing a force field for biomolecular simulations. For example, some force field combinations clearly outperform others at the binding enthalpy calculations but not for the binding free energy. Additionally, a force field combination which we expected to be the worst performer gave the most accurate binding free energies – but the least accurate binding enthalpies. The results have implications for the development of improved force fields, and we propose this test set, and potential future elaborations of it, as a powerful validation suite to evaluate new force fields and help guide future force field development.

Introduction

Accurate binding affinity prediction using molecular mechanics force fields has long been a goal of the computer-aided drug design (CADD) community. Molecular mechanics offers lower computational cost than quantum mechanical approaches, which makes it tractable on systems relevant to drug design (i.e., full proteins), while still maintaining an explicit atom description of the system, which is likely necessary to produce accurate results. However, choosing which force field to use can be a daunting task, as new options are constantly being introduced. There are traditional variants with long development trees, notably OPLS,^1,2 AMBER,³ CHARMM,^4,5 and GROMOS⁶ as well as newer or more exotic force fields, such as Kirkwood-Buff FF,⁷ CHARMM Drude,^8,9 induced dipole,^10,11 AMOEBA,¹² GEM*,¹³ Jorgensen’s atoms-in-molecules approach,¹⁴ QMDFF,¹⁵ ReaxFF,¹⁶ X-Pol,¹⁷ and many others. These options pertain primarily to the treatment of the protein and ligand, but there are also several frequently used water models such as TIP3P,¹⁸ TIP4Pew,¹⁹ and SPC/E,²⁰ and new ones are being added, such as OPC,²¹ TIP3P-FB,²² TIP4P-FB,²² TIP4P-D,²³ and iAMOEBA.²⁴ However, tests of the ability of these force fields to replicate experimental data are, arguably, sparse.

Perhaps the experimental data type most widely used to evaluate force fields today is the free energy of hydration of small molecules,^2,25,26 with some use also of nucleic acid structure^27,28 and protein structure.^5,23,29,30 Indeed, although the accurate calculation of binding affinities is a core goal of CADD methods, few studies have used noncovalent binding thermodynamic data to test force fields in the context of explicit solvent methods. (Two recent studies using cyclodextrin-guest binding free energies as tests in the context of implicit solvent models deserve mention, however.^31,32) In order to test the accuracy of force fields for the calculation of binding thermodynamics, it would perhaps appear ideal to use protein–ligand data, since these are most directly relevant to the challenge of drug design. However, the accuracy of such calculations depends not only on the choice of force field but also on setup choices, like the protonation states of binding site residues; and the possibility of slow protein motions means that it is difficult to be confident that the calculations are well converged. As a consequence, the level of agreement with experiment may not reliably reflect the accuracy of the force field. In recent years, host–guest systems have emerged as valuable models for testing the accuracy of simulation methods in the context of noncovalent binding.³³⁻³⁵ Host–guest systems feature many characteristics of protein–ligand binding (desolvation, H-bonds, rotational restriction), while being small enough for precise thermodynamic calculations to be tractable. In addition, unlike proteins, one can often have high confidence in the assignment of protonation states at a given pH. These characteristics make it easier to attribute the level of accuracy to the choice of force field. It is worth noting that, although blinded community challenges like SAMPL³³⁻³⁵ now often include host–guest systems, interpreting the results can be complicated by the relatively small number of cases and the lack of systematic testing of force field variations.

Here, in order to inform our ongoing effort to incorporate binding calculations into force field development,³⁶ we report binding free energy and enthalpy results for 43 host–guest pairs, computed using several different water models, partial charge assignment methods, and host force field parameters. The experimental study from which we draw these systems³⁷ makes for an ideal test case: 1) it contains several compounds of various sizes for each of three guest classes, including ammoniums, cyclic alcohols, and carboxylates; 2) these functional groups are attached to both linear and cyclic aliphatic scaffolds, as well as phenyl groups; and 3) these guests are tested with two closely related host molecules of different sizes, α-cyclodextrin (αCD) and β-cyclodextrin (βCD). In addition, the experimental data includes high quality ITC measurements of both binding free energy and binding enthalpy, along with NMR data which reports chemical shifts of both the host and guest.

Our results provide insight for researchers wondering how changes in water model, partial charge assignment method, and other force parameters influence binding results. More specifically, they show that none of the force field combinations we tested proved to be superior to the others for computing both binding free energy and binding enthalpy. They reveal more than one mechanism through which entropy–enthalpy compensation can operate in binding reactions involving CDs. Finally, the test set can serve as a critical component of an overall force field optimization strategy, providing important feedback on how force field changes affect the accuracy of binding calculations.³⁸

Methods

Host–Guest Systems

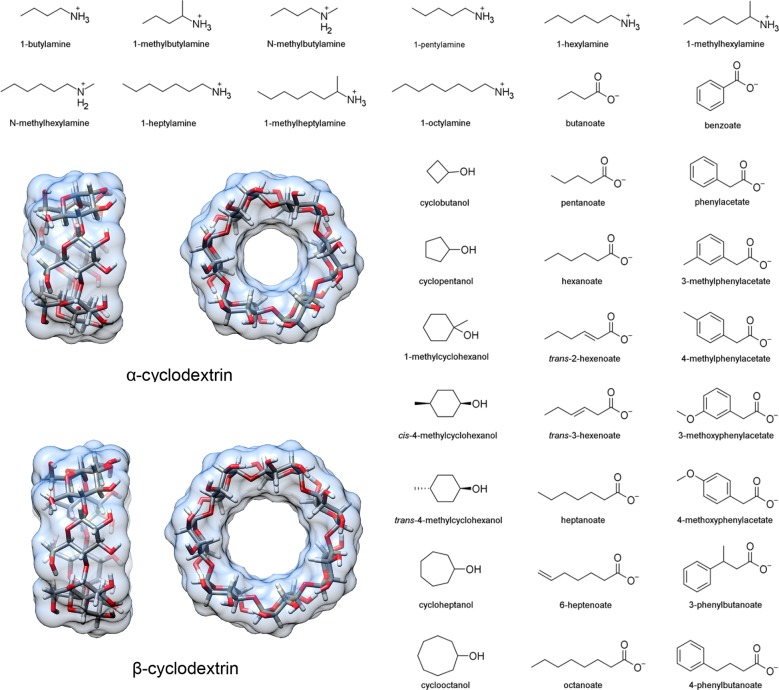
We studied the binding thermodynamics for 43 host–guest pairs from the Rekharsky et al. study.³⁷ These pairs consisted of either αCD or βCD as the host and an ammonium, carboxylate, or cyclic alcohol guest. Structures are provided in Figure 1 and are listed in Table 1, along with a brief ID used in other data tables. Note that only one stereoisomer was considered for the 1-methylammonium guests as it was unclear from the experimental details whether a mixture was used and, if so, what ratio was used. The differences in binding between enantiomers of these guests is not expected to exceed the estimated uncertainty in our calculations.³⁹

Figure 1.

Structures of the hosts (α- and β-cyclodextrin) and guests in this study. The 43 specific host–guest binding pairs and their assigned abbreviations are given in Table 1. Guest names match the convention in Tables 1 and 2 of Rekharsky et al.³⁷

Table 1. Forty-Three Host–Guest Binding Pairs Studied in This Work^c.

HG ID	host	guest[charge]	HG ID	host	guest[charge]
a-bam	αCD	1-butylamine[+1]	b-chp	βCD	cycloheptanol[0]
a-nmb	αCD	n-methylbutylamine[+1]	b-coc	βCD	cyclooctanol[0]
a-mba	αCD	1-methylbutylamine[+1]a	a-but	αCD	butanoate[-1]
a-pam	αCD	1-pentylamine[+1]	a-pnt	αCD	pentanoate[-1]
a-ham	αCD	1-hexylamine[+1]	a-hex	αCD	hexanoate[-1]
a-nmh	αCD	n-methylhexylamine[+1]	a-hx2	αCD	trans-2-hexenoate[-1]
a-mha	αCD	1-methylhexylamine[+1]a	a-hx3	αCD	trans-3-hexenoate[-1]
a-hpa	αCD	1-heptylamine[+1]	a-hep	αCD	heptanoate[-1]
a-mhp	αCD	1-methylheptylamine[+1]b	a-hp6	αCD	6-heptenoate[-1]
a-oam	αCD	1-octylamine[+1]	a-oct	αCD	octanoate[-1]
b-ham	βCD	1-hexylamine[+1]	b-pnt	βCD	pentanoate[-1]
b-mha	βCD	1-methylhexylamine[+1]a	b-hex	βCD	hexanoate[-1]
b-oam	βCD	1-octylamine[+1]	b-hep	βCD	heptanoate[-1]
a-cbu	αCD	cyclobutanol[0]	b-ben	βCD	benzoate[-1]
a-cpe	αCD	cyclopentanol[0]	b-pha	βCD	phenylacetate[-1]
a-chp	αCD	cycloheptanol[0]	b-mp3	βCD	3-methylphenylacetate[-1]
a-coc	αCD	cyclooctanol[0]	b-mp4	βCD	4-methylphenylacetate[-1]
b-cbu	βCD	cyclobutanol[0]	b-mo3	βCD	3-methoxyphenylacetate[-1]
b-cpe	βCD	cyclopentanol[0]	b-mo4	βCD	4-methoxyphenylacetate[-1]
b-mch	βCD	1-methylcyclohexanol[0]	b-pb3	βCD	3-phenylbutanoate[-1]
b-m4c	βCD	cis-4-methylcyclohexanol[0]	b-pb4	βCD	4-phenylbutanoate[-1]
b-m4t	βCD	trans-4-methylcyclohexanol[0]

^aOnly the R enantiomer was considered.

^bOnly the S enantiomer was considered.

^cThe formal charges used in the calculations are listed in brackets. See also Figure 1. Guest names match conventions in Tables 1 and 2 of Rekharsky et al.³⁷

Thermodynamic Calculations

We used the attach-pull-release (APR) method⁴⁰ to compute the absolute binding free energies. Briefly, this entails a series of umbrella sampling simulations, in which restraints controlling the host–guest complex are incrementally activated, then used to pull the host and guest apart, and finally released in such a way as to leave the guest at standard concentration. The attachment phase consisted of 15 independent windows with nonuniform spacing in the force constant that concentrated windows on the lower force constant domain. This spacing improves the precision of thermodynamic integration calculations. The pulling phase consisted of 45 independent windows, in which a distance restraint controlling the host–guest distance pulled the guest 18 Å away from the host in uniform increments of 0.4 Å. A set of dihedral restraints was added to the CD host during the attachment phase (on atoms O5_n-C1_n-O1_n-C4_n+1 and C1_n-O1_n-C4_n+1-C5_n+1) in order to limit the conformational flexibility of the host, thereby improving convergence during the pulling phase. These restraints were accounted for in the overall free energy calculation by including a release phase calculation in which the conformational restraints were gradually turned off over 15 independent windows, with the same force constant spacing as the attachment phase, in the absence of any guest. Finally, in order to compare with experimental values in which standard state of the guest is defined as 1 M, we analytically compute the work to move the unbound guest from the restricted volume enforced by the APR restraints to 1 M (i.e., 1 molecule/1660 ų). See Henriksen et al. for a complete description of this calculation.⁴⁰

For simple guest molecules, with one polar functional group, there are generally two possible binding modes in the CD cavity: one with the polar group oriented out of the CD opening with primary alcohols and one with the polar group oriented out of the wider opening with secondary alcohols (Figure 2). However, experimental data report binding free energy and enthalpy values based on a Boltzmann-weighted ensemble of these two orientations. In order to compare with experiment, we separately compute and appropriately combine the binding free energy and enthalpy for each orientation, as previously described.⁴⁰

Figure 2.

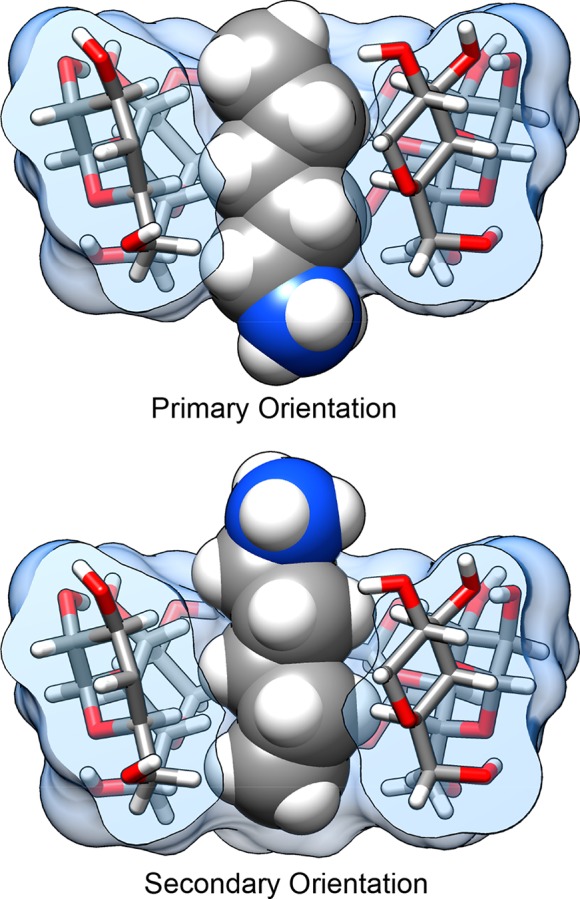
Example of the pentylammonium guest bound to the αCD host in both the primary (top) and secondary (bottom) orientations. The name of the orientation refers to the positioning of the guest polar group at the CD opening with either the primary alcohol groups or secondary alcohol groups of the cyclodextrin. One of the glucose monomers in the cyclodextrin has been removed for visualization purposes.

For some force field combinations and/or guest orientations, the binding affinity is so small or the barrier to entry/exit from the cavity is so low, that the guest could frequently leave the binding cavity during the early stages of the attachment step. This introduces a large statistical noise into the procedure, while the guest wanders around the simulation box in the bulk solvent. To prevent this behavior, a hard ″wall restraint″ is introduced during the attachment phase, which acts as a reflective sphere around the CD host and prevents the guest from completely entering bulk solvent. The wall restraints were defined as one-sided harmonic restraints between the C6 and O3 atoms of the CD host and a single atom of the guest. The distances beyond which the harmonic potential was nonzero were 12.3 and 13.5 Å for αCD and βCD, respectively. The force constant for these restraints was 50 kcal/mol-Ų.

The binding free energy was computed via a thermodynamic integration approach, using Python scripts developed by our lab, in which the restraint force constants were scaled by the λ parameter in the attachment and release phases, and the distance restraint target value was the λ parameter in the pulling phase. For comparison, we also computed the free energy with the MBAR method.⁴¹ The binding enthalpy was computed by subtracting the average potential energy of the last window of the release phase, in which the guest has been pulled far away from the host, from the mean energy of the first window of the attachment phase, in which restraint force constants are off. The uncertainties for average properties calculated in each window (e.g., restraint coordinate values and potential energies) were estimated with the blocking method⁴² and propagated into the final reported values using bootstrapping for the thermodynamic integration calculations or addition in quadrature for the binding enthalpy calculations. The binding entropy can subsequently be deduced by subtraction of the binding enthalpy from the binding free energies, and we report these values in the Supporting Information tables. A similar approach to determining cyclodextrin-guest binding thermodynamics has been reported previously.⁴³

A complete description of the APR method, thermodynamic analysis, and uncertainty estimation is provided in our earlier paper.⁴⁰ The approach in this paper matches the βCD-Hex_HMR simulations referenced in that work.

Force Field Parameters

The simulation system for each host–guest pair consisted of the following: 2000 and 2210 water molecules for αCD and βCD hosts, respectively; appropriate Na⁺ or Cl^– ions to neutralize the total system; additional 50 mM NaCl or NaH₂PO₄/Na₂HPO₄ buffer to match experimental conditions;³⁷ and a single CD host and guest molecule. As part of this investigation, we examined the influence of water model, ion parameters, partial charge assignment methods, and the CD force field. Four water models were studied: TIP3P,¹⁸ TIP4Pew,¹⁹ SPC/E,²⁰ and OPC.²¹ Ion parameters for Na⁺ and Cl^– were taken from Joung and Cheatham’s work,⁴⁴ in which the parameters were tuned for each water model, except for simulations with the OPC water model, for which we tried both Joung and Cheatham’s TIP4Pew ion parameters as well as parameters tuned specifically for matching hydration energies in OPC (distributed with AMBER; see Sections 3.5 and 3.6 in the AMBER 16 manual). Results with the NaH₂PO₄/Na₂HPO₄ buffer are reported only for the OPC water model, as these ions were observed to aggregate unrealistically into ordered structures when used with other water models. The parameters for these phosphate ions were based on those suggested by Steinbrecher et al.⁴⁵ The CD host molecules were parametrized with either the Q4MD-CD force field,⁴⁶ which uses RESP derived charges and draws many Lennard-Jones and valence parameters from GLYCAM04,⁴⁷⁻⁴⁹ or a crude ″minimal-effort″ version we created as a control. In the latter approach, a single glucose molecule, with methoxy caps on the O1 and O4 alcohols, was parametrized with AM1-BCC^50,51 partial charges and GAFF v1.7⁵² Lennard-Jones and valence parameters, using AMBER’s antechamber and parmchk2 utilites. Guest molecules used either RESP partial charges computed with the R.E.D. Server⁵³ or AM1-BCC charges computed with antechamber. Guest Lennard-Jones and valence parameters were obtained from GAFF v1.7. A complete list of the force field combinations tested is provided in Table 2.

Table 2. Summary of Simulation Sets in This Work.

simulation set ID	host FF	guest FF	solvent	guest set
Q4RG-TIP3P	Q4MD-CD	RESP/GAFF	TIP3P, Na+, Cl–	full 43
Q4RG-TIP3P-sm1	Q4MD-CD	RESP/GAFF	TIP3P, Na+, Cl–	small 15
Q4RG-TIP3P-sm2	Q4MD-CD	RESP/GAFF	TIP3P, Na+, Cl–	small 15
Q4RG-TIP3P-sm3	Q4MD-CD	RESP/GAFF	TIP3P, Na+, Cl–	small 15
Q4RG-TIP3P-shw	Q4MD-CD	RESP/GAFF	TIP3P, Na+, Cl–	small 15
Q4RG-TIP4Pew	Q4MD-CD	RESP/GAFF	TIP4Pew, Na+, Cl–	full 43
Q4RG-SPC	Q4MD-CD	RESP/GAFF	SPC, Na+, Cl–	full 43
Q4RG-OPC	Q4MD-CD	RESP/GAFF	OPC, Na+, Cl–	full 43
Q4RG-OPC-jc	Q4MD-CD	RESP/GAFF	OPC, Na+, Cl– (jc)	full 43
Q4RG-OPC-phos	Q4MD-CD	RESP/GAFF	OPC, Na+, H2PO4–, HPO42–	full 43
Q4RG-OPC-jcphos	Q4MD-CD	RESP/GAFF	OPC, Na+, H2PO4–, HPO42–, (jc)	full 43
Q4BG-TIP3P	Q4MD-CD	AM1-BCC/GAFF	TIP3P, Na+, Cl–	full 43
BGRG-TIP3P	AM1-BCC/GAFF	RESP/GAFF	TIP3P, Na+, Cl–	full 43
BGBG-TIP3P	AM1-BCC/GAFF	AM1-BCC/GAFF	TIP3P, Na+, Cl–	full 43

Simulation Settings

All simulations were performed with either the AMBER 14 or 16³ molecular dynamics software. For each simulation window, the entire system was rebuilt using AMBER’s tleap utility, thus ensuring that the initial solvent configuration in each window was independent of that in the other windows. The periodic box was orthorhombic, with dimensions of approximately 35 × 35 × 51 Å and 37 × 37 × 51 Å for αCD and βCD simulations, respectively. The host–guest system was oriented in the simulation box, via noninteracting anchor particles, which allowed the APR process to occur along the long (z) axis of the box; see Henriksen et al. for details.⁴⁰ The parameter/topology file was then hydrogen mass repartitioned (HMR) with AMBER’s parmed utility, a process which increases solute hydrogen atom masses to 3.024 Da by transferring mass from adjacent heavy atoms, thereby allowing larger simulation time steps without integration errors or significant changes to the thermodynamics.^40,54,55 All equilibration and production simulations were carried out with the GPU-capable pmemd.cuda MD engine. Equilibration consisted of 50,000 steps of energy minimization, followed by 100 ps of NVT warming from 0–298.15 K and 2000 ps of NPT equilibration at 298.15 K. Production simulations were run for a minimum of 5.0 ns out to a maximum of 50 ns, with the exact length determined by a threshold in the restraint coordinate uncertainty. All simulations used a time step of 4 fs, enabled by HMR, with a Langevin thermostat⁵⁶ and a Monte Carlo barostat.⁵⁷ The nonbonded cutoff was set to 9.0 Å, and the default AMBER PME parameters (identical for AMBER 14 and 16) were employed.

Results

We first present a comparative analysis of the various force field combinations tested in this work, focusing on how the choice of parameters affects agreement with experiment, solvent structure, and host conformation. Then we discuss how these factors combine to influence the binding modes of various guests. Finally, in order to provide context for decisions about where to focus force field development efforts, we examine various components of the binding free energy and study how variation in the tested force field parameters propagate into calculated thermodynamic quantities.

Throughout the text, we refer to the specific force field combinations using a “simulation set ID” which indicates the host, guest, and solvent force field, in that order. For example, “Q4RG-OPC” indicates that the Q4MD-CD force field was used for the cyclodextrin host, a RESP/GAFF force field was used for the guest, and the OPC water model and appropriate ion parameters were used for the solvent. Alternatively, “BGBG-TIP3P” indicates that the AM1-BCC/GAFF force field was used for both the host and guest along with the TIP3P water model and appropriate ions. Table 2 provides a complete summary of the force field combinations tested.

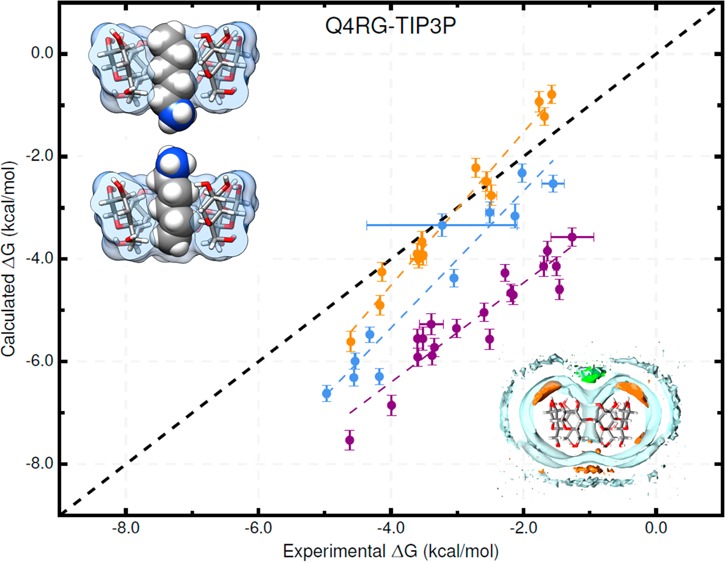
Overall Agreement with Experiment

Overall, the force field combinations we tested (Table 2) produced moderate agreement with the experimental reference data from ITC studies;³⁷ see Table 3, Tables S1 and S2, Figure 3, and Figure 4. We consider two aspects of agreement with experiment: 1) accuracy, which is reported by metrics such as slope/intercept, RMSE, MSE, and MUE, and 2) ranking ability, as reported by the coefficient of determination (R²) and Kendall’s rank correlation coefficient (τ). The binding free energy and enthalpy calculations had an RMSE range of 0.9–1.8 kcal/mol and 0.9–4.0 kcal/mol, respectively. No single force field combination emerged as superior to the others at computing both binding free energy and enthalpy. The Q4RG-TIP3P force field, which we expect would be the initial, “default” choice for an AMBER user, shows poor correlation (R² = 0.47) and significant deviation (RMSE = 1.8 kcal/mol) from experimental binding free energies, making it one of the worst force fields tested. For binding enthalpies, the Q4RG-TIP3P force field showed improved correlation (R² = 0.68) but even greater deviation from experiment (RMSE = 2.0 kcal/mol). Surprisingly, the best force field for calculating the binding free energy was the BGBG-TIP3P combination, which produced the highest correlation (R² = 0.60) and lowest deviation (RMSE = 0.9 kcal/mol) to experimental values of all force fields tested. The BGBG-TIP3P combination was expected to perform poorly because we crudely parametrized the CD host molecule and made no effort to tune its experimentally known conformational properties, as was done for the Q4MD-CD force field.⁴⁶ On the other hand, the BGBG-TIP3P combination was among the worst at calculating the binding enthalpy, showing low correlation (R²=0.39) and high deviation (RMSE = 2.6 kcal/mol) relative to experiment. The best force field for binding enthalpies, Q4RG-TIP4Pew (R² = 0.77, RMSE = 0.9 kcal/mol), produced mediocre binding free energy results, similar to those observed for Q4RG-TIP3P.

Table 3. Error Statistics between the Computed and Experimental Binding Free Energy and Binding Enthalpy for Each Force Field Combination^a.

metrics	Q4RG-TIP3P	Q4RG-TIP4Pew	Q4RG-SPC	Q4RG-OPC	Q4RG-OPC-jc	Q4RG-OPC-phos	Q4RG-OPC-jcphos	Q4BG-TIP3P	BGRG-TIP3P	BGBG-TIP3P
Binding Free Energy
slope	1.02 (0.18)	1.03 (0.16)	0.98 (0.18)	0.90 (0.12)	0.93 (0.14)	0.97 (0.15)	0.86 (0.14)	1.12 (0.17)	0.71 (0.12)	0.74 (0.10)
intercept	–1.31 (0.61)	–1.25 (0.53)	–1.24 (0.63)	–0.82 (0.43)	–0.74 (0.49)	–0.35 (0.52)	–0.67 (0.49)	–0.96 (0.57)	–0.40 (0.40)	−0.29 (0.33)
R2	0.47 (0.09)	0.54 (0.09)	0.44 (0.09)	0.57 (0.08)	0.56 (0.08)	0.53 (0.08)	0.46 (0.10)	0.52 (0.08)	0.52 (0.11)	0.60 (0.09)
Kendall’s τ	0.48 (0.07)	0.52 (0.07)	0.46 (0.08)	0.55 (0.06)	0.55 (0.07)	0.53 (0.07)	0.46 (0.08)	0.51 (0.07)	0.53 (0.08)	0.57 (0.06)
RMSE	1.80 (0.13)	1.69 (0.12)	1.67 (0.13)	0.97 (0.09)	1.03 (0.09)	1.00 (0.08)	1.03 (0.09)	1.73 (0.13)	0.92 (0.08)	0.85 (0.08)
MSE	–1.38 (0.18)	–1.36 (0.15)	–1.19 (0.18)	–0.52 (0.13)	–0.53 (0.14)	–0.26 (0.15)	−0.25 (0.15)	–1.30 (0.18)	0.48 (0.12)	0.50 (0.11)
MUE	1.53 (0.15)	1.45 (0.13)	1.43 (0.13)	0.80 (0.09)	0.87 (0.09)	0.85 (0.08)	0.87 (0.09)	1.51 (0.13)	0.79 (0.07)	0.73 (0.07)
Binding Enthalpy
slope	0.95 (0.11)	0.95 (0.08)	0.96 (0.12)	0.93 (0.08)	0.93 (0.08)	0.68 (0.07)	0.64 (0.06)	0.94 (0.11)	0.70 (0.16)	0.80 (0.18)
intercept	–1.80 (0.34)	0.10 (0.26)	–0.35 (0.36)	2.48 (0.25)	2.22 (0.25)	2.99 (0.21)	2.95 (0.19)	–1.78 (0.34)	1.26 (0.53)	1.36 (0.61)
R2	0.68 (0.08)	0.77 (0.06)	0.68 (0.07)	0.71 (0.08)	0.75 (0.07)	0.71 (0.07)	0.70 (0.08)	0.64 (0.08)	0.30 (0.11)	0.39 (0.12)
Kendall’s τ	0.62 (0.06)	0.69 (0.06)	0.62 (0.06)	0.64 (0.07)	0.65 (0.06)	0.61 (0.06)	0.58 (0.08)	0.62 (0.07)	0.44 (0.09)	0.49 (0.08)
RMSE	2.03 (0.17)	0.92 (0.09)	1.17 (0.12)	2.83 (0.16)	2.55 (0.14)	3.89 (0.14)	3.97 (0.14)	2.04 (0.18)	2.78 (0.31)	2.55 (0.24)
MSE	–1.69 (0.17)	0.21 (0.14)	–0.25 (0.18)	2.64 (0.16)	2.38 (0.15)	3.77 (0.14)	3.85 (0.15)	–1.65 (0.19)	1.99 (0.30)	1.84 (0.27)
MUE	1.73 (0.16)	0.77 (0.08)	0.95 (0.11)	2.64 (0.16)	2.38 (0.14)	3.77 (0.14)	3.85 (0.15)	1.72 (0.17)	2.26 (0.26)	2.13 (0.22)

^aAll metrics metrics were computed via sampling with replacement using 100,000 bootstrap cycles. The mean value of the bootstrap distribution is listed along with the standard error of the mean, in parentheses. Linear regressions were of the “y = mx + b” form and did not force the fit through the origin. R² is the coefficient of determination. RMSE is the root-mean-square error. MSE is the mean signed error. MUE is the mean unsigned error.

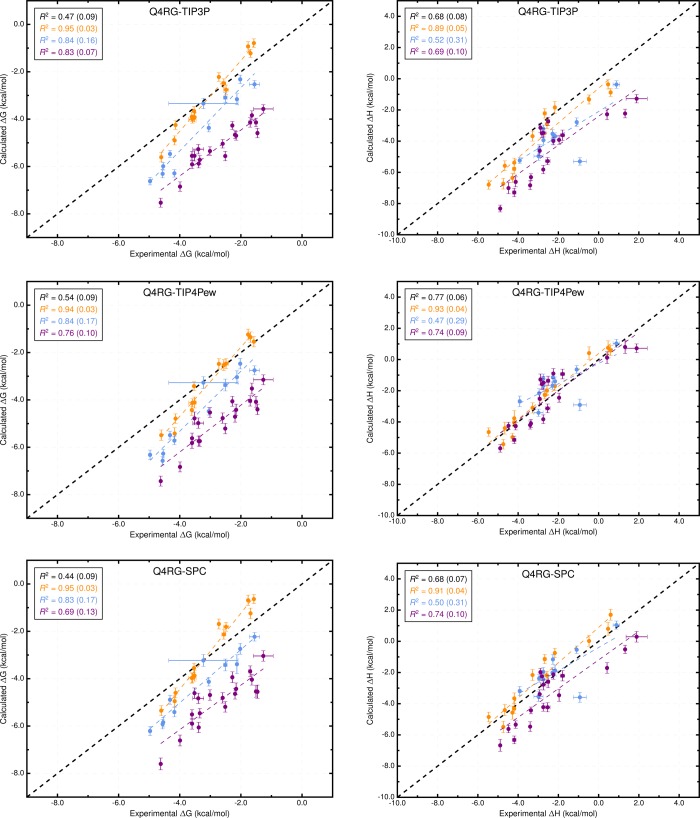
Figure 3.

Comparison of calculated binding free energies and binding enthalpies with experiment: (top row) Q4RG-TIP3P, (middle row) Q4RG-TIP4Pew, and (bottom row) Q4RG-SPC. The orange, blue, and purple colors distinguish the functional group of the guest as an ammonium, alcohol, or carboxylate, respectively. The overall R² is indicated in black followed by values for each guest functional group colored as mentioned previously.

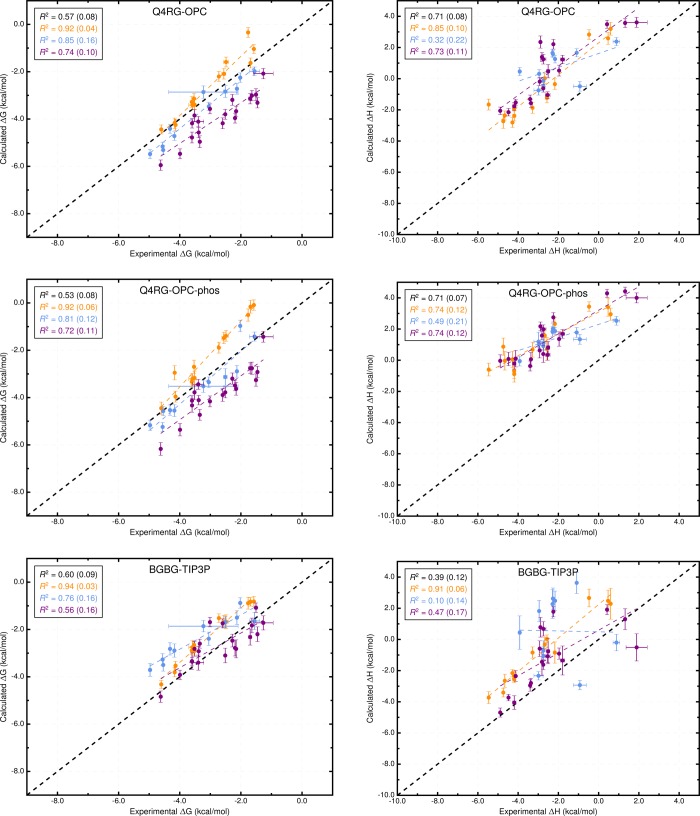
Figure 4.

Comparison of calculated binding free energies and binding enthalpies with experiment: (top row) Q4RG-OPC, (middle row) Q4RG-OPC-phos, and (bottom row) BGBG-TIP3P. The orange, blue, and purple colors distinguish the functional group of the guest as an ammonium, alcohol, or carboxylate, respectively. The overall R² is indicated in black followed by values for each guest functional group colored as mentioned previously.

Interestingly, when each class of guest molecule is considered separately, the computed binding free energies correlate better with experiment, relative to the correlation of the entire data set. For example, in the Q4RG-TIP3P data set, the R² values for ammoniums, cyclic alcohols, and carboxylates are 0.95, 0.84, and 0.83, respectively (Figure 3, top and Table S3), which greatly improves on the 0.47 overall value. However, since each group is shifted relative to one another, the accuracy successively diminishes for each group (RMSE = 0.6, 1.3, and 2.5 kcal/mol, respectively). The same trend is not generally observed for the binding enthalpy, where only the ammonium guests have significantly higher correlation (R² = 0.89) than the full data set. Similar behavior is observed for other force field combinations. Note that the statistical metrics reported here were generated using resampling with replacement, to provide uncertainty values that account for experimental uncertainty, numerical uncertainty, and differences in data set size. The uncertainties for the R² values are provided in Figure 3 and Figure 4 and Table S3.

The full data set can be subgrouped in a variety of different ways. Error metrics for the following subgroupings are provided in Table S3: ammonium guests, alcohol guests, carboxylate guests, αCD hosts, βCD hosts, n-alkyl guests, aliphatic carboxylate guests, and aromatic carboxylate guests. Some interesting observations can be made from this data. For example, comparison of the latter two groups, aliphatic and aromatic carboxylate guests, shows that although their binding free energy RMSE is similar, the correlation with experiment is much higher for the aliphatic carboxylates than the aromatic across all force field combinations. This same trend is even more pronounced for the binding enthalpy, although the RMSE differences are a bit larger. Another example involves comparing binding to the αCD host versus the βCD host. For most of the force field combinations which use the Q4MD-CD force field on the host, the RMSE values are similar between the two groups and the correlation is marginally better for the βCD group. In contrast, for the BGBG-TIP3P force field combination, the correlation is significantly higher for αCD group than the βCD group for the binding free energy and enthalpy.

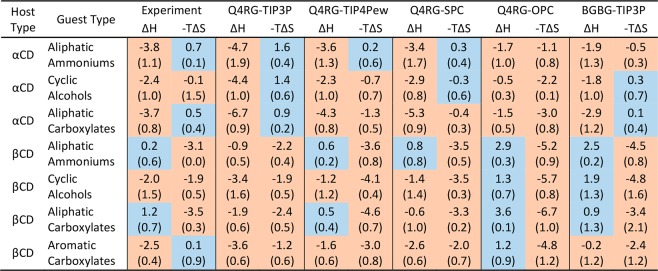
The entropic and enthalpic components of the binding free energy provide an additional perspective for comparison with experiment. Although we did not compute the entropic component directly, we obtain it from subtraction of the binding enthalpy from the binding free energy, as done in ITC experiments. From the experimental data, it was observed that some degree of entropy–enthalpy compensation occurs when comparing binding between the smaller αCD and larger βCD.³⁷ For the present guests, the binding enthalpy to αCD is generally more favorable than binding to βCD, likely reflecting stronger dispersion interactions generated by a snug fit. In contrast, the entropic contribution to the binding free energy is more favorable moving from αCD to βCD, presumably due to greater conformational freedom of the guest and the ejection of additional ordered water from the larger host. These trends are also observed in our computational values, although the magnitude of the thermodynamic components varies widely across different force field combinations (Table 4). The trend is even observed for the BGBG-TIP3P force field which, as discussed below, explores significantly different conformations than the Q4RG force field.

Table 4. Mean Enthalpic and Entropic Components of Binding Free Energy, for Each Class of Host–Guest Pair, and Their Standard Deviation, in Parentheses, Across All Guests in Each Class (kcal/mol)^a.

^aThe orange color indicates a negative, favorable value; the blue color indicates a positive, unfavorable value.

Comparison of Water Models, Ion Parameters, and Buffer Components

Changing the water model is one of the obvious force field comparisons to make in AMBER, since most AMBER solute force fields are not parametrized against a specific water model. In combination with the Q4MD-CD host force field (Q4) and the RESP/GAFF guest force field (RG), we evaluated four water models: TIP3P,¹⁸ TIP4Pew,¹⁹ SPC/E,²⁰ and OPC²¹ (Table 2). For binding free energy, the error metrics with respect to experiment are uniformly mediocre for the traditional water models (Q4RG-TIP3P, Q4RG-TIP4Pew, and Q4RG-SPC in Table 3 and Figure 3). Thus, the correlation was low (R² = 0.44–0.54), and the deviation from experiment was significant (RMSE = 1.7–1.8 kcal/mol). In general, these water models overestimate the binding affinity, particularly for carboxylate guests, leading to an MSE of −1.2 kcal/mol or worse. Relative to the four more traditional water models, the Q4RG-OPC combination showed improvement in every error metric category except slope, including higher correlation (R² = 0.57) and much lower deviation from experiment (RMSE = 1.0 kcal/mol).

More variation is observed for the binding enthalpy calculations (Table 3, Figure 3). As noted previously, Q4RG-TIP4Pew performed the best relative to experiment (R² = 0.77, RMSE = 0.9 kcal/mol), and Q4RG-SPC results were only slightly worse (R² = 0.68, RMSE = 1.2 kcal/mol). The Q4RG-TIP3P force field significantly overestimates the binding enthalpy (MSE = −1.7 kcal/mol), while the Q4RG-OPC force field underestimates by even more (MSE = 2.8 kcal/mol). The relative MSE trend observed here between Q4RG-TIP3P and QR4G-TIP4Pew is opposite to that found for the CB7 host where the binding enthalpy was overestimated significantly more by TIP4Pew than TIP3P.⁵⁸ The increase in correlation with experiment for individual guest classes over the entire data set is not as noticeable for the binding enthalpy, although for ammonium guests the R² value equals or exceeds 0.85 for all four force field combinations.

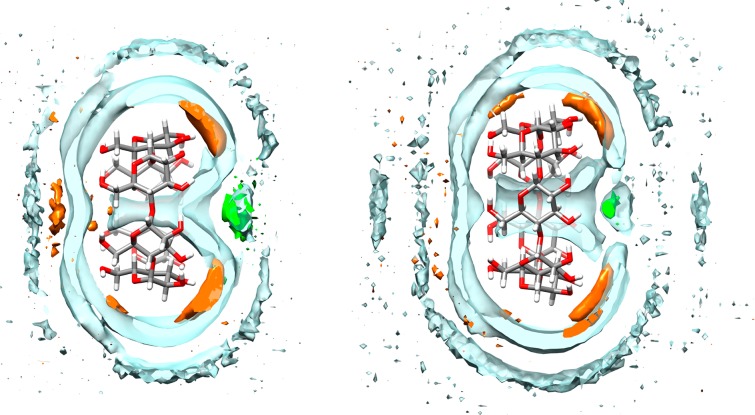
We next considered whether the structured water in the CD cavity differs significantly between water models. To evaluate this, we computed the water and sodium ion radial distribution functions (RDF) referenced to the center of mass of the unbound CD (Figure S11). For the simulation sets which used the Q4MD-CD force field, the RDFs are quite similar, suggesting that the water structure in the CD cavity does not change across the four water models we tested. Indeed, regions of solvent density around the empty CD host share the same features, differing only in the relative magnitude, and reveal a core of structured water within the CD cavity and ion binding regions near the hydroxyl group on the exterior of the CD host (e.g., Q4RG-TIP3P, Figure 5). The Q4RG-TIP4Pew and Q4RG-SPC force field combinations show a large peak in the sodium RDFs at 7–8 Å, which is not observed to the same degree for the other two solvent models. This appears to correspond with sodium binding between the O2 and O3 hydroxyls at the secondary face of the CD. Comparison of the density grids across all four solvent models suggests that the high-density water and sodium regions occupy the same locations but vary in magnitude.

Figure 5.

Density contour plots for water (clear blue), sodium ions (orange), and chloride ions (green) around αCD (left) and βCD (right). The water and ion contour levels are 1.05 and 2.00 times bulk density, respectively. For clarity, only a 2.5 Å thick surface slice is shown for each solvent component.

Although the ITC studies which generated the comparison data for this study used 50 mM sodium phosphate buffer, we chose to use equivalent ionic strength sodium chloride for most force field combinations, due to the lack of published parameters for mono- and divalent phosphate. However, we wanted to test whether phosphate buffer influenced the binding calculations, even though it is not expected to interact significantly with CD hosts. The OPC model was the only water model tested for which we did not observe unphysical aggregation of phosphate buffer ions during simulation. Therefore, we performed several more simulation sets which evaluated how changes to sodium chloride parameters or inclusion of phosphate affect the results. The Q4RG-OPC simulation set used Na⁺ and Cl^– parameters which were tuned to reproduce hydration free energies in OPC water. However, as these were not available until some time after publication of the OPC water model, several research groups have used the Joung-Cheatham parameters tuned for TIP4Pew.^59,60 The OPC-tuned parameters (R_min/2 = 1.432,2.298 Å, ε = 0.0215, 0.6366 kcal/mol for Na⁺ and Cl^–, respectively) differ substantially (Figure S18) from the Joung-Cheatham parameters (R_min/2 = 1.226,2.760 Å, ε = 0.1684, 0.0117 kcal/mol for Na⁺ and Cl^–, respectively), so we first evaluated these parameters. The Q4RG-OPC-jc simulation set is identical to the Q4RG-OPC set, with the exception of these ion parameters, and the results show very little difference in terms of absolute calculated value (Tables S8 and S9) or agreement with experiment (Table 3). We then evaluated whether inclusion of phosphate buffer at 50 mM, to exactly match experimental conditions, rather than NaCl would affect the results. We tested the phosphate buffer with both the OPC-tuned (Q4RG-OPC-phos) and Joung-Cheatham (Q4RG-OPC-jcphos) parameters for sodium. Relative to the OPC simulation sets with just NaCl buffer, the free energy calculations with phosphate buffer yield comparable error statistics with experiment (Table 3 and Figure 4). In contrast, the binding enthalpy results show a further positive shift of between 1.1 and 1.4 kcal/mol in MSE relative to the OPC/NaCl buffer, likely due to a phosphate ion binding near the CD cavity. The slope of the linear regression between calculated and experiment also changes from approximately 0.9 to 0.65 when switching from NaCl buffer to phosphate.

Impact of the Host Force Field

Most of the force field combinations studied use Q4MD-CD⁴⁶ for the CD host molecules. This force field was designed to agree with experimentally determined conformational properties of CDs, mostly from NMR data. We were interested in how this particular choice of force field might impact binding calculations. To provide a “control”, we created a CD force field using a minimal effort approach which essentially involved parametrizing the glucose monomer with AM1-BCC charges and the GAFF force field (Methods). The Lennard-Jones parameters for the two approaches are identical, and the charges are very similar (Figure S13), with maximum deviations of 0.26 or 0.13 on the C1 and O1 atoms, respectively. The primary difference between the two force fields is the dihedral parameters. The Q4MD-CD force field primarily draws its parameters from the GLYCAM04 force field,⁴⁷⁻⁴⁹ which is optimized for carbohydrates, except that the 1–4 electrostatic and 1–4 nonbonded interaction are set to 1.2 and 2.0, respectively, rather than unity, to be consistent with other major AMBER force fields.

Simulations of unbound αCD and βCD show that the conformational distribution is significantly different between these two force fields. The population histograms for the “flip” pseudotorsion, which reports the orientation of a glucose monomer relative to its neighbor, show that CD hosts in the BGBG-TIP3P simulation set have several highly populated flip orientations that are not observed in the Q4RG-TIP3P simulations (Figure S14A, B). These alternate conformations collapse the cavity of the CD molecule and prevent water from locating there (Figure S11, top). The guest binding mode appears to be less structured for BGBG-TIP3P as well. This is particularly noticeable for some of the smaller guests, such as cyclopentanol, binding to βCD (Figure S15). An overlay of distance histograms for each bound guest relative to the CD center of mass shows much more dispersed and bimodal distributions for BGBG-TIP3P than for Q4RG-TIP3P (Figure S16A,B). For some of the host–guest pairs with dispersed distance histograms, particularly the cycloalcohols, the binding was so weak or unstable that the “wall restraints” may have influenced calculated results (see Methods). In spite of what appears to be a crude force field representation, which allows excessive conformational flexibility to the host, the BGBG-TIP3P binding free energies give the highest correlation (R₂ = 0.60) and lowest RMSE (0.9 kcal/mol) to experiment of all the simulation sets tested (Table 3). On the other hand, the binding enthalpy results are poor: the correlation is poor (R² = 0.39) and the RMSE (2.6 kcal/mol) is only exceeded by the simulation sets using the OPC water model, which shifts the enthalpy in the positive direction (Table 3). Further comparison of these two host force fields is given in the “Binding Modes” section.

Comparison of the RESP and AM1-BCC Charge Models

Two common methods for partial charge assignment in AMBER are the RESP^53,61 and AM1-BCC^50,51 approaches. The latter approximates the former for a fraction of the computational cost and is implemented in and widely used via AMBER’s antechamber program. We assigned guest partial charges with both methods and noticed substantial differences for certain atom types (Figure S12), particularly the ammonium nitrogen (atom type nh) and certain aliphatic carbon atoms (c3) between aromatic groups and carboxylates. (However, compensatory changes in neighboring atom partial charges may mitigate these differences in terms of the electrostatic field generated by the entire guest molecule.) To evaluate the degree to which these differences affect the binding results, we performed a new set of simulations, Q4BG-TIP3P, keeping all parameters identical to Q4RG-TIP3P except the guest charges, which were generated with AM1-BCC instead of RESP. In terms of agreement with experiment, the error metrics for Q4BG-TIP3P are indistinguishable from Q4RG-TIP3P for both binding free energy and enthalpy (Table 3). Additionally, for both free energy and enthalpy, the correlation between the two simulation sets is high (R² > 0.92), and the slope and intercept for linear regression between the data sets are approximately 0.99 and 0.01, respectively. We conclude that guest partial charge assignment with the RESP and AM1-BCC method yields equivalent results for the host–guest pairs study in this work.

We furthermore performed binding calculations using the AM1-BCC/GAFF force field for the CD hosts and the RESP/GAFF force field for the guests, referred to as the BGRG-TIP3P simulation set. As anticipated, using mixed approaches to generate partial atomic charges – RESP for the guests and AM1-BCC for the hosts – also had little impact on the error with experiment (Table 3, compare BGRG-TIP3P and BGBG-TIP3P) or the thermodynamic decomposition (compare Figure S8 with Figure S9 and Table S13 with Table S14).

Binding Modes

The reported binding values in Table S1 are obtained from two separate calculations corresponding to the polar group of the guest lying at either the primary or secondary face of the asymmetric cavity. Inspection of the binding free energy values for each individual binding orientation is informative (Tables S4–S14). One interesting result is that, for all force field combinations using the Q4MD-CD host force field, the ammonium guests prefer, by about 0.5–2.0 kcal/mol, orienting their polar group toward the primary face, which is not expected,^37,62 particularly as one might anticipate that the cationic ammonium group could be better hydrated at the larger secondary face. With the exception of 1-methylcyclohexanol binding to βCD (b-mch), in which the nonpolar methyl group likely competes with hydroxyl group for control of the orientation, all of the carboxylate and alcohol guests prefer to orient their polar group toward the secondary face of CD. In contrast, the BGBG-TIP3P and BGRG-TIP3P force field combinations display equivalent affinity between orientations or slightly favor the secondary orientation for all guest classes.

Solvent Structure

The solvent density distribution near the binding cavity of free αCD and βCD indicates a possible explanation for the observed orientational preferences observed when using the Q4MD-CD force field for the hosts (Figure 5). The secondary face of the CD features a high density chloride binding region at the center of the opening, surrounded by several high density sodium binding zones near the secondary alcohols. In contrast, the primary side of the CD only has a moderate affinity sodium binding zone near the center of the cavity opening. Thus, it appears that the CD structure itself naturally encodes some degree of preference for placing positively charged groups at the primary face and negatively charged groups at the secondary face, at least for the Q4MD-CD force field. In contrast, the “BG″ host force field produces such a flexible, collapsed unbound host structure that well-defined localization of solvent density is not observed (data not shown).

Entropic Considerations

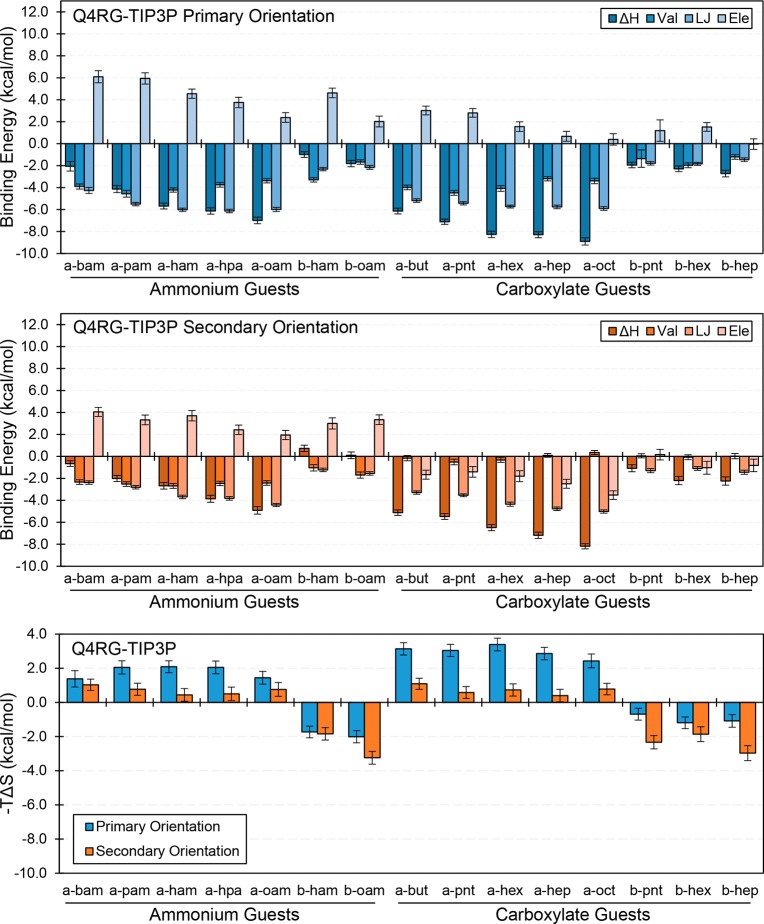
The entropic component of binding is strongly linked to the binding orientation. The entropic contribution from the secondary orientation is more favorable than that for the primary orientation for all guests in the Q4RG-TIP3P data set, except 1-methylcyclohexanol, cycloheptanol, and cyclooctanol (Table S4 and Figure 7, bottom). The unusual binding mode for these guests, as discussed below, likely accounts for deviation in the trend. One possible explanation for the relative entropic favorability of the secondary orientation lies in the interaction of the CD hydroxyls with the polar headgroup of the guest. When the guest is in the primary orientation, the polar headgroup lies nearer to all the primary face hydroxyls than when it is in the secondary orientation. This may allow it to act as a clamp, perhaps via hydrogen bonding and/or electrostatic interactions, limiting the motion of the CD. We investigated this possibility by computing the root mean squared fluctuation (RMSF) value for all CD oxygen atoms, both in the bound and unbound state. By summing the RMSF difference between the bound and unbound states we estimated a crude measure of CD flexibility for a selection n-alkyl guests binding to αCD (Figure S3, top). The difference in CD fluctuations before and after binding is clearly much larger when the guest binds in the primary orientation rather the secondary, which matches the entropic results (Figure 7, bottom). However, the increase in the RMSF difference of the secondary orientation as the alkyl chain gets longer is not reflected in the entropy results which suggests an additional mechanism is at play, possibly related to structured water.

Figure 7.

Binding enthalpy decompositions for the primary orientation (top/blue) and secondary orientation (center/orange) and entropic contribution to the free energy for both orientations (bottom) for selected guests from the Q4RG-TIP3P simulation set. The number of guest carbon atoms increases from left to right for each guest class (see Table 1 for identification). Val = valence energy, LJ = Lennard-Jones energy, Ele = electrostatic energy.

Enthalpic Considerations

The binding enthalpy for both orientations of the guest can be further broken down into component force field terms, namely the valence energy terms (bonds, angles, torsions, and 1–4 interactions), and the nonbonded Lennard-Jones (LJ) and electrostatic terms (Table S4). Focusing on a selected set of n-alkyl ammonium and carboxylate guests, we observe that the uniformly favorable binding enthalpy in the primary orientation is driven by the valence and LJ terms and opposed by the electrostatic term (Figure 7, top). Binding in the secondary orientation is more complex. The profile for ammonium guests is similar to what is observed for the primary orientation, although the magnitude of each term is generally smaller (Figure 7, center). For the carboxylate guests, however, the valence terms are negligible, whereas the electrostatic term joins the LJ term as a favorable contributor. The branched and unsaturated ammonium and carboxylate guests not shown in Figure 7 follow a similar pattern.

The cyclic alcohol guests are generally characterized by favorable valence and VDW terms along with an unfavorable electrostatic contribution (Table S4). Two exceptions to this trend are found for cycloheptanol and cyclooctanol binding to αCD. For these cases, in which the guests’ size prevents a complete fit into the host cavity, the valence energy term is unfavorable in the primary orientation, and the electrostatic energy is favorable for both orientations. The aromatic carboxylate guests bind with a variety of enthalpic profiles – although all have favorable LJ contributions – which likely reflects the various placement of substituents on the aromatic ring.

In contrast to what is observed for the Q4MD-CD force fields, the decomposed enthalpy for the “BG″ force fields reveals a completely different thermodynamic profile (Table S14 and Figure S9). First, the profile for binding in either the primary and secondary orientation is very similar (Figure S9, top and middle). Additionally, the valence term is almost always unfavorable and is driven specifically by the dihedral component which can be as large as +10–12 kcal/mol (Table S15). Finally, the LJ and electrostatic terms are large and negative for most host–guest pairs.

Structural Interpretation of the Thermodynamic Components of Binding

Here, we investigate structural explanations for the observed thermodynamic values, primarily focusing on the Q4RG-TIP3P data set.

We focus first on the valence energy term, which we consider to comprise the bond, angle, torsion, and 1–4 electrostatic and 1–4 LJ energy terms. (The 1–4 term is included because it only occurs intramolecularly, between atoms which are tethered to each other by three bonds.) The 1–4 electrostatic term is responsible for the observation that carboxylates bind with favorable valence energy in the primary orientation but not the secondary orientation (Table S15). It appears to play a key role in the magnitude of the bonded term for the other guests as well. Inspection of the CD dihedral angles suggested that the O6 and O2 hydroxyl torsions likely contribute the most to this energy term. Thus, the population histograms for these torsions in the bound state reveal unique profiles, which are dependent both on the guest functional group (ammonium vs carboxylate) and binding orientation (primary vs secondary). Figure S2 demonstrates that, relative to the unbound state (dashed lines), the four guest binding scenarios considered presently (ammonium/primary, ammonium/secondary, carboxylate/primary, carboxylate/secondary) generate unique torsion populations in the O6 and O2 hydroxyl groups of the host CD.

The LJ term, favorable in all cases, can be rationalized by considering the greater ability of the guests to pack into the CD cavity relative to water, much as previously seen for guests binding the cucurbituril CB7.⁵⁸ As expected, this term moderately scales with the size of the guest, reflecting the greater number of atoms packed into the cavity. Additionally, the magnitude of the LJ term is largest for the guest in the primary orientation, where interactions with the narrower end of the CD cavity are expected to be stronger than for the wider, secondary end.

The electrostatic energy term generally consists of large compensatory contributions: the solute–solute and solvent–solvent electrostatic energies each contribute about 20–40 kcal/mol toward favorable binding enthalpy, which is opposed by an unfavorable solute–solvent term in the range of 50–80 kcal/mol (Table S16). An exception to this is ammonium’s binding in the secondary orientation, in which the magnitude of these energies is in the range of 5–20 kcal/mol. In general, the compensatory nature of the solute–solute and solvent–solvent energies with the solute–solvent energy can be understood as the host and guest sacrificing favorable interactions with the solvent in order to form favorable interactions with each other. The magnitude of these energies and the apparent aberration of the ammoniums in the secondary orientation seem to be correlated with the degree of desolvation that the polar headgroup of the guest encounters upon binding. Indeed, an overlay of 400 trajectory snapshots showing the positions of the ammonium nitrogen or carboxylate oxygen relative to the CD host reveals a noticeable difference in the placement of the guest polar group (Figure 6). In both orientations, the ammonium guests prefer placement of their polar group further into the solvent relative to the placement of carboxylate guests. This roughly correlates with the magnitude of the electrostatic terms (Table S16).

Figure 6.

Overlay of 400 simulation snapshots, spaced 2.5 ns apart, showing the position of a carboxylate oxygen atom (red spheres) and an ammonium nitrogen atom (blue spheres) relative to the αCD host when bound in the primary orientation (left side) and secondary orientation (right side). Snapshots were taken from trajectories of the a-ham and a-hep host–guest pairs in the Q4RG-TIP3P simulation set.

Inspection of the decomposed enthalpy and entropy components for guest binding (Tables S4, S6–S8) provides some insight into how the water model force field parameters contribute to binding. For simplicity, we focus on the n-alkyl ammonium and carboxylate guests (Figure 7 and Figures S4–S6). The electrostatic component of the binding enthalpy differs the most between the water models. For example, compared to Q4RG-TIP3P (Figure 7), the electrostatic term for Q4RG-OPC increases in unfavorability by 2–6 kcal/mol (Figure S6), making binding of carboxylates in the secondary orientation unfavorable. The entropic term compensates for this by becoming uniformly favorable. It is likely that the magnitude of the water partial charges is the primary cause for this effect. For TIP3P, SPC/E, TIP4Pew, and OPC, the hydrogen charge values are 0.417, 0.424, 0.524, and 0.679, respectively. The favorability of both the mean electrostatic term and mean entropic contribution seem to correlate well with these values, with R² greater than 0.85 for the n-alkyl ammonium and carboxylate test set (Figure S10).

The link between the LJ contribution and the Lennard-Jones terms of the water model is less obvious. The TIP3P water model has the smallest σ and ε values (3.151 Å and 0.152 kcal/mol, respectively) and tends to yield more favorable average LJ contributions than the other water models by approximately 0.7 kcal/mol for both the primary and secondary orientations (Tables S4, S6–S8). The TIP4Pew, SPC/E, and OPC water models all have σ values in the 3.16 Å range; however, whereas TIP4Pew and SPC/E have an ε value between 0.155 and 0.162 kcal/mol, OPC deviates significantly with a value of 0.213 kcal/mol. This deviation does not appear to increase the LJ favorability for OPC, as its contribution is actually less favorable on average than TIP4Pew and SCP/E by about 0.1–0.3 kcal/mol. The net effect of changing the water LJ model’s parameters presumably reflects a balance between a greater loss of favorable solute–solvent interactions on binding, along with a greater gain of favorable solvent–solvent interactions as water is displaced from the surfaces of the solutes into the bulk.

Quality Assurance Testing

We performed several tests to evaluate whether our simulation setup and analysis is robust and precise. First, we evaluated whether our uncertainty estimates were reasonable. We created three smaller replicate simulation sets (Q4RG-TIP3P-sm1, Q4RG-TIP3P-sm2, Q4RG-TIP3P-sm3) with exactly identical simulation parameters as Q4RG-TIP3P, except that they used different random placements of solvent molecules during system building and different random number seeds during production simulations, and comprised just a subset of 15 host–guest pairs out of the full set of 43. Comparison of the replicate binding free energies and binding enthalpies showed excellent agreement (RMSD < 0.39 kcal/mol, R² > 0.95) with the original simulation set (Figure S17).

We then tested whether our “wall restraints” – restraints which only impose a force on a bound guest molecule when it strays too far into the bulk solvent during the attachment phase of the APR procedure – significantly affected the binding calculations. The distance at which the wall restraint potential becomes nonzero was chosen to be far enough away from the binding site that we anticipated no impact on the calculations. However, to test this, we shortened the distance at which the restraints took effect by 1 Å and tested the same 15 host–guest pairs that were studied in the replicates described above, thus forming the Q4RG-TIP3P-shw simulation set. The results again showed excellent agreement (RMSD < 0.42 kcal/mol, R² > 0.93, Figure S17), suggesting that the restraints were not impacting the calculations.

Finally, although all reported binding free energy calculations in this work used the thermodynamic integration method, we also computed free energies using the MBAR method.⁴¹ The two methods were essentially indistinguishable, with the average absolute deviation of 0.14 kcal/mol and a maximum of 0.37 kcal/mol for the Q4RG-TIP3P simulation set.

Discussion

The results described here represent, to the best of our knowledge, the most comprehensive host–guest validation panel examined to date with explicit solvent free energy methods. We evaluated several water models, host and guest force fields, ion parameters, and charge assignment methods in order to improve our understanding of the accuracy of currently available force field parameters. This effort relied on the significant performance advantage afforded by GPU processors, along with a highly automated implementation of our APR method, in order to deploy the thousands of simulations which produced this work. We expect investigations of similar scope to become more commonplace as efforts to improve force fields using automated optimization schemes become tractable for larger systems.^36,63 The following discussion highlights results from this work which could inform such future endeavors.

Force Field Selection and Development

It appears that none of the force field combinations we tested is clearly superior to the others, and the thermodynamic values they yield are remarkably wide-ranging. For example, the binding enthalpy of octanoate to αCD (“a-oct”) has a range greater than 8 kcal/mol depending on the force field combination choice. Surprisingly, the arguably crude AM1-BCC/GAFF host force field with AM1-BCC/GAFF guest parameters (i.e., the BGBG-TIP3P simulation set) outperforms all other force field combinations we tested at calculating binding free energies; but it performs poorly for binding enthalpies. However, conformational analysis of the BGBG-TIP3P simulation set casts doubt on the accuracy with which it captures the conformational preferences of the CDs and thus suggests that some of the thermodynamic results it yields may be right for the wrong reasons. In contrast, the Q4RG-TIP4Pew combination does remarkably well at calculating binding enthalpies but only does moderately well for free energies.

The fact that the correlation with experiment tends to be higher if one restricts attention to a subset of guests with the same functional group, as opposed to considering all guests together (Figure 3), suggests that force field errors could combine in unpredictable ways for more complicated molecules with multiple functional groups. Depending on the exact binding site composition of the host and guest, or protein and ligand, such errors could combine to seriously overestimate or underestimate the experimental binding thermodynamics and lead to difficulties in correctly ranking ligands by affinity. Alternatively, the errors could combine in such a way as to cancel out and yield good agreement with experiment. Unsurprisingly, this points to the critical importance of diverse training and testing sets. It will likely become increasingly important to collaborate with experimentalists in generating these data sets, rather than relying on existing data which were not developed specifically to test and guide force field development.

Entropy–enthalpy compensation appears to play a role in mitigating how changes in parameters propagate to changes in the binding free energy. We observed two such mechanisms. First, although drastic changes in enthalpy were observed when moving from the TIP3P to the OPC water model, these were accompanied by much more modest changes in free energy. In this case, it seems that entropy–enthalpy compensation likely operated through changes in the water structure driven by large changes in the magnitude of the water charges. Second, we found that, when moving from the Q4MD-CD host force field to AM1-BCC/GAFF (i.e., Q4RG-TIP3P to BGBG-TIP3P), the primary difference was found in the dihedral parameters of the CD hosts, and thus entropy–enthalpy likely operated through combined structural changes in the host and subsequently changes to the structured water within the host cavity.

Binding free energy studies which investigate charged ligands are comparatively rare, possibly due to inherent difficulty or perhaps technical challenges associated with commonly used alchemical approaches.⁶⁴ The marked difference in mean signed error for the binding free energy of each guest class, which have different net charges, suggests that there might be problems with the partial charge assignments. One possibility is that the RESP charge approach, in which partial charges are chosen to reproduce gas phase QM electrostatic potentials, does not fully take into account the electronic polarization of water which provides electronic screening of solute charges. Leontyev and Stuchebrukhov have suggested that ionic solutes, in particular, should have their gas phase partial charges scaled by 0.7 in order to account for water polarization.^65,66 Such proposals will be of interest to future studies.

Comparison with Other Host–Guest Calculations

The results of this study are broadly consistent with other host–guest calculations we have performed previously.^{36,40,58,60,67} The binding free energy is generally overestimated, albeit much more modestly for CD than for CB7 hosts. The OPC water model significantly shifts the binding enthalpy in the positive direction, which we have observed for other host–guest systems.^60,67 Additionally, as we observed with CB7,⁶⁰ valence (bonded) terms can contribute significantly to binding.

On the other hand, significant differences also emerge. For example, the OPC water model looks very promising for the CB7 system, where binding free energies and enthalpies with the TIP3P water model had been significantly overestimated, so that OPC’s positive shift in these values brought them closer to experiment (Gao et al.⁶⁰ and unpublished data). In contrast, the present results, which focus on CDs, show that, while the OPC model does yield a positive shift in the binding free energy relative to TIP3P, bringing those numbers closer to experiment, the large positive shift in binding enthalpy greatly increases its deviation from experiment. Furthermore, for octa-acid hosts,⁶⁷ the positive shift in enthalpy when moving from TIP3P to OPC is accompanied by a small negative shift in the binding free energy, moving those values further from experiment. Evidently, the influence of the water model on the agreement of the binding free energy and the enthalpy with experiment are system-dependent.

Guest Orientation

We were surprised and perplexed that the Q4MD calculations predicted that ammonium guests prefer to bind CDs in the primary orientation. Although there is not much evidence for the conventional viewpoint that n-alkyl polar groups will orient out of the secondary cavity of CDs, this does seem to be generally accepted.^37,62,68 The NMR data published by Rekharsky et al.³⁷ does not show any indication that ammoniums might be binding in the primary orientation, although it does not strongly point to binding in the secondary orientation either.

We considered whether the shift in the linear regressions between calculated and experimental binding free energy values for ammoniums and carboxylates (see Figure 3) might reflect an incorrect binding orientation of the ammoniums. However, if one ignores the primary orientation data and only uses the results from the secondary orientation, the deviation between the guest classes grows even larger, because the secondary orientation is of lower affinity than the primary orientation, and ammoniums already tended to be assigned lower affinities than carboxylates.

Directions

The present study demonstrates that host–guest systems can be used to systematically characterize and compare the accuracy of force fields in the calculation of binding thermodynamics. The present data set, and future expansions of it, highlights and should ultimately help resolve a number of questions, such as how can one selectively shift the binding affinity of host–guest pairs, depending on their polar functional groups, and what strategies can be employed in force field optimization to account for the phenomenon of entropy–enthalpy compensation, which complicates the selection of parameters that will accurately replicate both binding free energies and enthalpies. With increasing computer power, it should be possible to incorporate such data into an overall force field optimization strategy, which uses heterogeneous data sets that also include, for example, quantum mechanical calculations, pure liquid properties, and crystallographic data. Our lab will continue to investigate these questions as part of the larger community effort to improve force fields and thus advance the accuracy of binding calculations.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b00359.

• Figures S1–S18 (PDF)

• Tables S1–S16 (XLSX)

This work used computational resources from both the Triton Shared Computing Cluster at UCSD and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation grant no. ACI-1053575. M.K.G. acknowledges funding from the National Institute of General Medical Sciences (GM61300).

The contents of this paper are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.

The authors declare the following competing financial interest(s): M.K.G. has an equity interest in and is a cofounder and scientific advisor of VeraChem LLC.