Conditional local distance correlation for manifold-valued data

Abstract

Manifold-valued data arises frequently in medical imaging, surface modeling, computational biology, and computer vision, among many others. The aim of this paper is to introduce a conditional local distance correlation measure for characterizing a nonlinear association between manifold-valued data, denoted by X, and a set of variables (e.g., diagnosis), denoted by Y, conditional on the other set of variables (e.g., gender and age), denoted by Z. Our nonlinear association measure is solely based on the distance of the space that X, Y, and Z are resided, avoiding both specifying any parametric distribution and link function and projecting data to local tangent planes. It can be easily extended to the case when both X and Y are manifold-valued data. We develop a computationally fast estimation procedure to calculate such nonlinear association measure. Moreover, we use a bootstrap method to determine its asymptotic distribution and p-value in order to test a key hypothesis of conditional independence. Simulation studies and a real data analysis are used to evaluate the finite sample properties of our methods.

1 Introduction

Manifold-valued data frequently arises in many domains, such as medical imaging, computational biology, and computer vision, among many others [2, 23, 28, 11, 19]. Examples of manifold-valued data in medical imaging analysis include the Grassmann manifold, planar shapes, matrix Lie groups, deformation field, symmetric positive definite (SPD) matrices, and the shape representation of cortical and subcortical structures. Most manifold-valued objects are inherently non-linear and high-dimensional (or even infinite-dimensional), so analysis of these complex objects presents many mathematical and computational challenges.

Motivated by shape analysis, the aim of this paper is to measure a linear/nonlinear association between manifold-valued data (e.g., shape representation) and a random vector/variable (e.g., diagnosis), while controlling for the other random vector (e.g., age). Specifically, consider n independent observations {(X_i, Y_i, Z_i)}_1≤i≤n, where X_i, Y_i, and Z_i are elements in metric spaces $\mathcal{X}$, $\mathcal{Y}$, and $\mathcal{Z}$, respectively. In traditional statistics, these metric spaces are Euclidean spaces of arbitrary dimension. Correlation and regression analyses are the fundamental statistic techniques for quantifying the degree of association between X and Y, with/without the effect of a set of controlling random variables Z removed. For instance, Pearson correlation and its multivariate extension, so-called canonical correlation analysis (CCA), are powerful tools for measuring the degree of linear association between X and Y. Moreover, partial correlation measures the degree of linear association between two random variables, while controlling for a random vector. Alternatively, one may fit a regression with Y_i as response and both X_i and Z_i as covariates such that $Y_i={\beta }_0+X_i^T{\beta }_x+Z_i^T{\beta }_z+{\epsilon }_i$, where β₀, β_x, and β_z are regression coefficients and ε_i are measurement errors.

Generalizations of correlation and regression analyses to manifold-valued data are recently gaining popularity. Most existing methods for manifold-valued data are primarily on their mean and variation [5, 6, 10, 12]. Some nonparametric methods were subsequently developed for the density estimation of manifold data [3, 19, 21]. Recently, in [14], a Riemannian CCA model was proposed to measure an intrinsically linear association between manifold-valued data and a random vector (or two manifold-valued objects). Furthermore, various intrinsic regression models have been developed for manifold-valued data [13, 3, 4, 16, 24, 29, 7, 2, 19, 10, 9]. Most of these regression methods often require specifying a link function, projecting manifold-valued data to local tangent planes for computing residuals, and transporting all residuals to a common space [7].

However, when X_i or/and Y_i are manifold-valued data, little has been done on the analysis of X and Y, while controlling for Z due to at least two major challenges. First, it is computationally challenging to optimize the objective function for the regression analysis of X and Y, when the dimension of X is relatively high. Such objective function is generally not convex and has a large number of parameters. Particularly, standard gradient-based optimization methods used in the literature strongly depend on the starting value of unknown parameters. Second, most intrinsic regression models for manifold-valued data require the specification of link functions (e.g., geodesic link), but it is conceptually challenging to choose a correct appropriate link function for any regression model that provides goodness of fit to a given data set. Due to these challenges, it is difficult to make further statistical inference (e.g., hypothesis test).

We propose a conditional local distance correlation to measure the nonlinear association between X and Y, while controlling for Z. Since such distance correlation measure solely requires the specification of the distances on the metric spaces $\mathcal{X}$, $\mathcal{Y}$, and $\mathcal{Z}$, it is applicable when both X and Y are manifold-valued data in different spaces. It also enjoys four major advantages. First, it avoids the optimization of a complex objective function, since empirical distance correlation measure is the function of pairwise distance between sample points. Second, it avoids the projection of manifold-valued data to local tangent planes. Third, it has a high statistical power of detecting complex and unknown nonlinear relationships between X and Y. Fourth, it is easy to make statistical inference on the nonlinear association between X and Y, while controlling for Z.

2 Methods

2.1 Conditional local distance correlation

We review a novel distance correlation for characterizing statistical dependence between two random variables or two random vectors of arbitrary dimensions [25]. In [15], distance correlation was further extended to stochastic processes in metric spaces when such metric spaces are of strong negative type. Distance correlation as an extension of Pearson correlation has several important properties. The first and most important one is that it is zero if and only if two random vectors are independent. The second one is its computational simplicity, since empirical distance correlation is the function of pairwise distance between sample points.

We introduce a conditional local distance correlation to measure the nonlinear association between X and Y, while controlling for Z, when $\mathcal{X}$, $\mathcal{Y}$, and $\mathcal{Z}$ are metric spaces. Let d_X(·,|·), d_Y (·, ·), and d_Z(·, ·) be, respectively, the metrics of $\mathcal{X}$, $\mathcal{Y}$, and $\mathcal{Z}$. Let M( $\mathcal{X}$ |Z) (or·M( $\mathcal{Y}$ |Z denote the set of finite conditional probability measures on $\mathcal{X}$ (or $\mathcal{Y}$) given Z. We say that μ ∈ M( $\mathcal{X}$| Z) has a finite first moment if ${\displaystyle {\int }_{\mathcal{X}}{d}_X}(o,x)d|\mu |(x|z)<\infty$. we for some o ∈ $\mathcal{X}$ Similarly, we can define ν ∈ ( $\mathcal{Y}$| Z). Define a_μ (x| z):= ∫d_X(x, x′)dμ(x′|z) and D_X(μ|z):= ∫d_X(x, x′)dμ(x′|z)dμ(x|z) as finite functions when μ ∈ M|( $\mathcal{X}$ |Z) has a finite first moment. Also, we can define a_v (y |z) D_Y (ν|z) for ν ∈ M( $\mathcal{Y}$ |Z) and Y.

Definition 1

The local distance covariance $ℒ\mathcal{D}\mathcal{V}(X,Y|Z)$ between random processes X and Y with finite moments given Z is defined as the square root of

$$\begin{array}{l}ℒ\mathcal{D}{\mathcal{V}}^2(X,Y|Z)=E[\{d_X(X,X\prime )-a_{\mu }(X|Z)-a_{\mu }(X\prime |Z)+D_X(\mu |Z)\}\\ \times \{d_Y(Y,Y\prime )-a_v(Y|Z)-a_v(Y\prime |Z)+D_Y(v|Z)\}|Z],\end{array}$$

where X′ and Y′ are the independent copies of X and Y, respectively.

By setting X = Y, we obtain the local distance variance as $ℒ\mathcal{D}\mathcal{V}(X|Z)=ℒ\mathcal{D}\mathcal{V}(X,X|Z).$

Definition 2

The local distance correlation between random processes X and Y with finite moments given Z is defined as the square root of

$$ℒ\mathcal{D}{\mathcal{C}}^2(X,Y|Z)=\frac{ℒ\mathcal{D}{\mathcal{V}}^2(X,Y|Z)}{\sqrt{ℒ\mathcal{D}{\mathcal{V}}^2(X|Z)ℒ\mathcal{D}{\mathcal{V}}^2(Y|Z)}}$$

if $ℒ\mathcal{D}{\mathcal{V}}^2(X|Z)ℒ\mathcal{D}{\mathcal{V}}^2(Y|Z)>0$, or 0 otherwise.

Under the condition that the metric spaces are of strong negative type, it can be shown that $ℒ\mathcal{D}{\mathcal{C}}^2(X,Y|Z=z)=0$ if and only if X and Y given Z = z are conditionally independent. This property distinguishes the local distance correlation from the existing methods in the literature [14, 13, 3, 4, 16, 24, 29, 7, 2, 19, 7]. As shown below, it is easy to estimate $ℒ\mathcal{D}{\mathcal{C}}^2(X,Y|Z)$ and use its estimate to make statistical inference.

2.2 Estimation procedure

The next interesting question is to estimate the local distance covariance and correlation. The local distance dependence statistics are defined as follows. Let (X_i, Y_i, Z_i) for i = 1,…,n be a random sample of n independent and identically distributed random vectors from the joint distribution of random vectors (X, Y, Z). We compute two distance matrices (a_kl) = d_X(X_k, X_l) and (b_kl) = d_Y (Y_k, Y_l). For notational simplicity, it is assumed that $\mathcal{Z}=R^r$ holds. We consider a kernel function K(·) on R^r and the bandwidth h satisfying two regularity conditions as follows:

• (C1) ${\displaystyle {\int }_{{ℝ}^r}zK(z)\mathrm{d}z=0}$, ${\displaystyle {\int }_{{ℝ}^r}K(z)\mathrm{d}z=1}$, ${\displaystyle {\int }_{{ℝ}^r}|K(z)|\mathrm{d}z<\infty }$, ${\displaystyle {\int }_{{ℝ}^r}{K}^2(z)\mathrm{d}z>0}$, and ${\displaystyle {\int }_{{ℝ}^r}{\Vert z\Vert }_2^{2}K(z)\mathrm{d}z<\infty .}$
• (C2)h^r → 0, nh^r → ∞, as n → ∞

Let ω_h,k(Z) = K_h(Z − Z_k), ω_h,kl(Z) = K_h(Z − Z_k)K_h(Z − Z_l), ω_h,ijkl(Z) = K_h(Z − Z_i)K_h(Z − Z_j)K_h(Z − Z_k)K_h(Z − Z_l), and ${\omega }_h(Z)={\displaystyle {\sum }_{k=1}^n{\omega }_{h,k}(Z)}$, where K_h(Z) = K((Z − Z_k)/h)/h^r. We then introduce A_kl(Z; h) as follows:

$$A_{kl}(Z;h)=a_{kl}-{\overline{a}}_k.(Z;h)-\overline{a}{.}_l(Z;h)+\overline{a}\mathrm{..}(Z;h),$$

where a_kl = d_X(X_k, X_l), ${\overline{a}}_k.(Z;h)={\{{\omega }_h(Z)\}}^{-1}{\displaystyle {\sum }_{l=1}^n{d}_X(X_{k,}{X}_l){\omega }_{h,l}(Z)}$, $\overline{a}{.}_l(Z;h)={\{{\omega }_h(Z)\}}^{-1}{\displaystyle {\sum }_{k=1}^n{d}_X}(X_k,X_l){\omega }_{h,k}(Z)$, and

$$\overline{a}\mathrm{..}(Z;h)={\{{\omega }_h(Z)\}}^{-2}{\displaystyle \sum _{k,l=1}^n{d}_X}(X_k,X_l){\omega }_{h,kl}(Z).$$

Similarly, we can define b_kl = d_Y (Y_k, Y_l) and B_kl(Z; h). Then, the empirical local distance covariance can be defined as

$$ℒ\mathcal{D}{\mathcal{V}}_n^2(X,Y|Z;h)={\{{\omega }_h(Z)\}}^{-2}{\displaystyle \sum _{k,l=1}^n{A}_{kl}(Z;h)B_{kl}(Z;h){\omega }_{h,kl}(Z).}$$

We define the empirical local distance correlation as

$$ℒ\mathcal{D}{\mathcal{C}}_n^2(X,Y|Z;h)=\frac{ℒ\mathcal{D}{\mathcal{V}}_n(X,Y|Z;h)}{\sqrt{ℒ\mathcal{D}{\mathcal{V}}_n(X|Z;h)ℒ\mathcal{D}{\mathcal{V}}_n(Y|Z;h)}},$$

where $ℒ\mathcal{D}{\mathcal{V}}_n^2(X|Z;h)=ℒ\mathcal{D}{\mathcal{V}}_n^2(X,X|Z;h)$

2.3 Inference procedure

The next question is to make statistical inference based on LDV or LDC. Our inference procedure consists of carrying out hypothesis test and constructing confidence interval.

To test the dependence of X and Y at a fixed location Z = z, we formulate it as follows:

$$H_0:ℒ\mathcal{D}\mathcal{V}(X,Y|Z=z)=0v.s.H_1:ℒ\mathcal{D}\mathcal{V}(X,Y|Z=z)>0.$$ (1)

We calculate the p–value of $ℒ\mathcal{D}{\mathcal{V}}_n(X,Y|Z;h)$ by using a local bootstrap procedure [18, 25, 26] as follows:

1. Generate $X_j^{\ast }$ from {X₁,…,X_n} with the probability

   $$P(X^{\ast }=X_j|Z=Z_i)=\frac{{\omega }_{h,j}(Z_i)}{{\displaystyle {\sum }_{j=1}^n{\omega }_{h,j}}(Z_i)}$$

   for j = 1,…,n. Then, we compute $ℒ\mathcal{D}{\mathcal{V}}_n^{\ast }$ by using the local bootstrap sample $\{(X_i^{\ast },Y_{i,}{Z}_i):i=1,\dots ,n\}$.
2. Select a resampling number S, say 1,000. Repeat Step (i) S times and obtain $ℒ\mathcal{D}{\mathcal{V}}_{ns}^{\ast }$ for s = 1,…,S. And then the p-value of the test is given by

   $$p\approx \frac{{\displaystyle {\sum }_{s=1}^{S}I(|ℒ\mathcal{D}{\mathcal{V}}_n|>|ℒ\mathcal{D}{\mathcal{V}}_{ns}^{\ast }|)+1}}{S+1}$$

Given a confidence level α, we construct simultaneous confidence bands for $ℒ\mathcal{D}\mathcal{C}(X,Y|Z)$ as follows:

$$P(ℒ\mathcal{D}{\mathcal{C}}_n^{L,\alpha }(X,Y|Z;h)<ℒ\mathcal{D}\mathcal{C}(X,Y|Z)<ℒ\mathcal{D}{\mathcal{C}}_n^{U,\alpha }(X,Y|Z;h))=1-\alpha ,$$

where $ℒ\mathcal{D}{\mathcal{C}}_n^{L,\alpha }(X,Y|Z;h)$ and $ℒ\mathcal{D}{\mathcal{C}}_n^{U,\alpha }(X,Y|Z;h)$ are the lower and upper limits of simultaneous confidence band, respectively. We use a bootstrap method to approximate the bounds:

1. Resample $(X_i^{\ast },Y_i^{\ast }{Z}_i^{\ast }),i=1,\dots ,n$ from {(X_k, Y_k, Z_k): k = 1,…,n} with the probability

   $$P((X^{\ast },Y^{\ast },Z^{\ast })=(X_j,Y_j,Z_j)|Z=Z_i)=\frac{{\omega }_{h,j}(Z_i)}{{\displaystyle {\sum }_{j=1}^n{\omega }_{h,j}}(Z_i)}$$

   for j = 1,…,n, then compute $ℒ\mathcal{D}{\mathcal{C}}_n^{\ast }$ by the bootstrap sample $\{(X_i^{\ast },Y_i^{\ast }{Z}_i^{\ast }):i=1,\dots ,n\}$.

2. Repeat Step (I) with resampling number S times and obtain $ℒ\mathcal{D}{\mathcal{C}}_{ns}^{\ast },s=1,\dots ,S$ And then the simultaneous confidence band is given by the quantiles at α and 1 − α of $ℒ\mathcal{D}{\mathcal{C}}_{ns}^{\ast },s=1,\dots ,S$.

Like many other smoothing-based method, the performance of the proposed method depends upon the bandwidth h. It is widely acknowledged that the optimal h for nonparametric estimation is generally not optimal for testing. Selecting h to achieve optimal statistical power for (1) is an open problem. In practice, h can not be too large, since the conditional local distance covariance tends to the unconditional one. That is, an inappropriately large bandwidth h will yield a much larger false positive rate when X and Y are dependent. For simplicity, we consider the bandwidth h to eliminate the effect of Z on X and Y in the maximum extent. That is, the bandwidth h is chosen to minimize the mean of local distance covariance at every location Z = z. The intuition for the choice of h comes from partial correlation, whose aim is to eliminate the effect of Z on X and Y by the regression of Z on X and Y.

3 Numerical Studies

3.1 Simulations

We use two simulation studies to examine the finite sample performance of LDC. We consider the directional data on the unit sphere R^p, which denoted by $S^{p-1}=\{\mathrm{x}\in R^p:{\Vert \mathrm{x}\Vert }_2=1\}$ for, both X and Y. Under the canonical Riemannian metric on S^p−1 induced by the canonical inner product on R^p, the geodesic distance between any two points X and X′ is equal to d_X(X, X′) = arccos(X^T X′). The sample size is set to be n = 300 and 400 in order to examine the finite sample performance of local distance estimate. We calculate the rejection rate at the significance level α = 0.05 and S = 200. Moreover, 200 replications are used for each simulation setting.

Simulation 1

We set p = 3 and consider the spherical coordinate of S², denoted as (r, θ, ϕ), where r ∈ [0, ∞), θ ∈ [0, 2π], and ϕ ∈ [0, π], respectively, represent the radial distance, inclination (or elevation), and azimuth. The simulation datasets {(X_i, Y_i, Z_i) ∈ S²×S²×R: i = 1,…,n} were generated as follows:

• (I.1) $X_i=(1,{\theta }_i^x,{\varphi }_i^x)$, $Y_i=(1,{\theta }_i^y,{\varphi }_i^y)$, and $Z_i\sim U(\frac{\pi }{5},\frac{4\pi }{5})$;
• (I.2) $X_i=(1,{\theta }_i^x,Z_i+{\epsilon }_i^x)$, $Y_i=(1,{\theta }_i^y,Z_i+{\epsilon }_i^y)$, and $Z_i\sim U(\frac{\pi }{5},\frac{4\pi }{5})$;
• (I.3) $X_i=(1,{\theta }_i,Z_i+{\epsilon }_i^x)$, $Y_i=(1,{\theta }_i+{\epsilon }_i,Z_i+{\epsilon }_i^y)$, and $Z_i\sim U(\frac{\pi }{5},\frac{4\pi }{5})$;
• (I.4)Half of samples (Z ∼ U(−π+0.5, 0)) are generated from (I.2) and the other half (Z ∼ U(0, π−0.5)) are from (I.3);

where ${\theta }_i^x$, ${\varphi }_i^x$, ${\theta }_i^y$, and ${\varphi }_i^y$ were independently simulated from the Uniform distribution U(−π, π) and the ε_i, ${\epsilon }_i^x$, and ${\epsilon }_i^y$ were independently simulated from the normal distribution N(0, 0.2). Therefore, X and Y are independent in (I.1), whereas they are dependent in (I.2) and (I.3). In contrast, X and Y are conditionally independent given Z in (I.1) and (I.2), whereas they are conditionally dependent in (I.3). For (I.4), the first half of samples are conditionally independent and the second half of samples are conditionally dependent given Z.

Figure 1 presents the estimated LDCs between X and Y given Z and their p-values. The Type I error rates based on the local bootstrap procedure are well maintained under the prefixed significance level, while the power of rejecting the null hypothesis is good. As the sample size n increases, simultaneous confidence bands become narrower and the value of local distance correlation is close to zero under the true conditional independence. We use the function e.cp3o in R package ecp to detect the change point of local distance correlation in (I.4). The estimated change point is very close to the true value of change point.

Fig. 1.

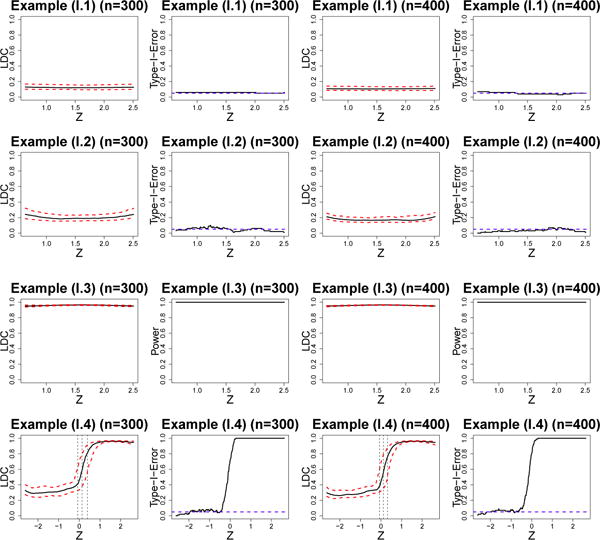
Figures of local distance correlation (95% confidence bands) and Type-I-Error/Power for n = 300 and n = 400 in simulation 1.

Simulation 2

We consider the von Mises-Fisher distribution, of which the data can be spherical or hyper-spherical. A p-dimensional unit random vector $x({\Vert x\Vert }_2=1)$ is set to be p-variate von Mises-Fisher distribution M_p(μ, κ). We set p = 10 and simulated μ from the multivariate normal distribution N(0, I₁₀). The simulated datasets were generated as follows:

• (II.1)X_i ∼ M₁₀(μ_x, 15), Y_i ∼ M₁₀(μ_y, 15), and Z_i ∼ N(0, 0.5);
• (II.2) $X_i=X_i^1+{\xi }_i$ and $Y_i=Y_i^1+{\xi }_i$, where $X_i^1\sim M_{10}({\mu }_x,15)$, $Y_i^1\sim M_{10}({\mu }_y,15)$, and ξ_i = (u₁ Z_i…,u₁₀ Z_i), in which Z_i ~ U(−1, 1) and $u_1,\dots u_{10}\in \left\{-\frac{7}{24},\frac{7}{24}\right\}$ with equal probability. Then, we project X_i and Y_i to the unit spherical surface;
• (II.3)X_i ∼ M₁₀(μ_x, 15), Y_i = RX_i, and Z_i ∼ N(0,0.5) where R is a rotation matrix along the direction μ_x of μ_y
• (II.4)Half of samples (Z ~ U(−5, 0) were generated from (II.1) and the other half (Z ~ U(0, 5) were from (II.3).

Similar to Simulation 1, X and Y are independent in (II.1), whereas they are dependent in (II.2) and (II.3). However, X and Y are conditionally independent given Z in (II.1) and (II.2), while they are conditionally dependent given Z in (II.3). The first half of samples are conditionally independent and the second half of samples are conditionally dependent given Z in (II.4). Inspecting Figure 2 reveals that the proposed methods work well.

Fig. 2.

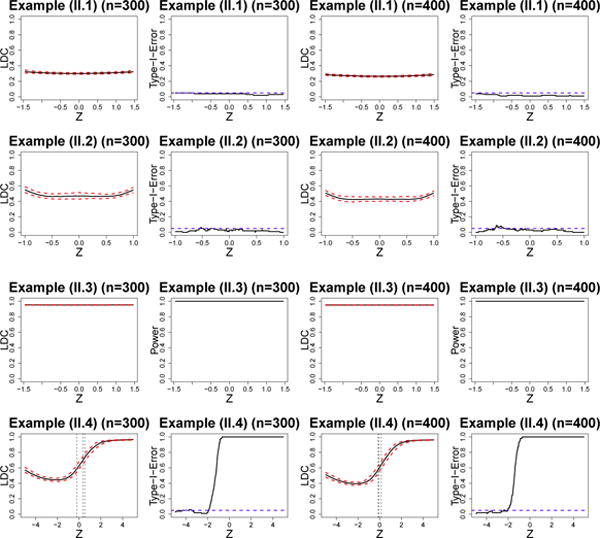
Figures of local distance correlation (95% confidence bands) and Type-I-Error/Power for n = 300 and n = 400 in simulation 2.

3.2 Real Data Analysis

Alzheimer disease (AD) is a disorder of cognitive and behavioral impairment that markedly interferes with social and occupational functioning. It is an irreversible and progressive brain disease that slowly destroys memory and thinking skills, and eventually even the ability to carry out the simplest tasks. AD affects almost 50% of those over the age of 85 and is the sixth leading cause of death in the United States. The corpus callosum (CC), the largest white matter structure in the brain, has been a structure of high interest in many neuroimaging studies of neuro-developmental pathology. It contains homotopic and heterotopic interhemispheric connections and is essential for communication between the two cerebral hemispheres. Individual differences in CC and their possible implications regarding interhemispheric connectivity have been investigated in last several decades [27, 20].

We consider the CC contour data of the ADNI1 study. We processed the CC shape data for each subject in the ADNI1 study as follows. We used FreeSurfer package [8] to process each T1-weighted MRI, whereas the midsagittal CC area was calculated in the CCseg package.

We are interested in characterizing the change of the CC contour shape and its association with several key covariates of interest, such as age and diagnosis. We focused on n = 409 subjects with 223 healthy controls (HCs) and 186 AD patients at baseline of the ADNI1 study. Each subject has a CC planar contour Y_i with 50 landmarks and nine covariates, including gender, age, handedness, marital status (Widowed, Divorced, and Never married), education length, retirement, and diagnosis. The demographic information is shown in Table 1. We treat the CC planar contour Y_i as a manifold-valued response in the Kendall planar shape space and all covariates in the Euclidean space.

Table 1.

Demographic information for all participants.

Disease status	Number of subjects	Age (years)	Females/males
Healthy control	223	62–90 (76.25)	107/116
AD	186	55–92 (75.42)	88/98

The first scientific question of interest is to characterize the relationship between CC shape data and each of the nine covariates. Table 2 presents the distance correlation statistics for correlating CC data with each of the nine covariates. It reveals that the shape of CC planar contour are highly dependent on gender, education length, age and AD diagnosis at the significant level α = 0.05. It may indicate that gender, age and AD diagnosis are the most significant influence factors of CC planar contour, which agree with [1, 17, 22].

Table 2.

The distance correlation (Dcor) statistics for correlating CC contour data and nine covariates. The significance level is 0.05.

covariates	Dcor	P–value
Gender	0.186	0.001
Handedness	0.094	0.420
Marital Status	0.108	0.383
Education length	0.166	0.010
Retirement	0.108	0.165
Age	0.245	0.001
Diagnosis	0.190	0.001

The second scientific question of interest is to characterize the relationship between CC shape data and AD diagnosis given age. Figure 3 presents the conditional local distance correlation of CC planar contour and AD diagnosis given age as a function of age. As age increases, the value of the conditional local distance correlation increases. It implies that diagnosis and CC are dependent with each other as age changes. Figure 4 presents the mean age-dependent CC trajectories for healthy controls and AD within each gender group. It can be observed that there is a major difference of the shape between the AD disease and healthy both in male and female groups. The splenium seems to be less thinner and the isthmus is rounded in subjects with AD disease than in healthy controls.

Fig. 3.

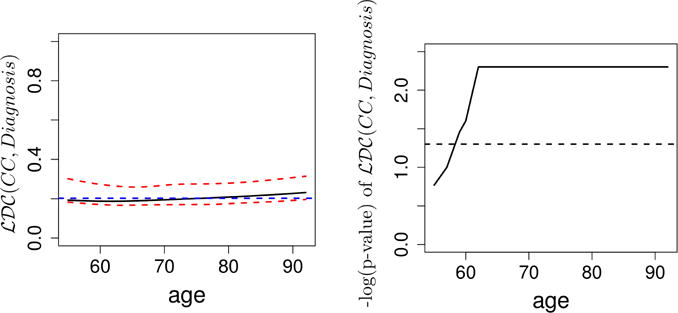
Figures of estimated local distance correlation and the corresponding negative log₁₀(p-values) between CC planar contour and Diagnosis given Age.

Fig. 4.

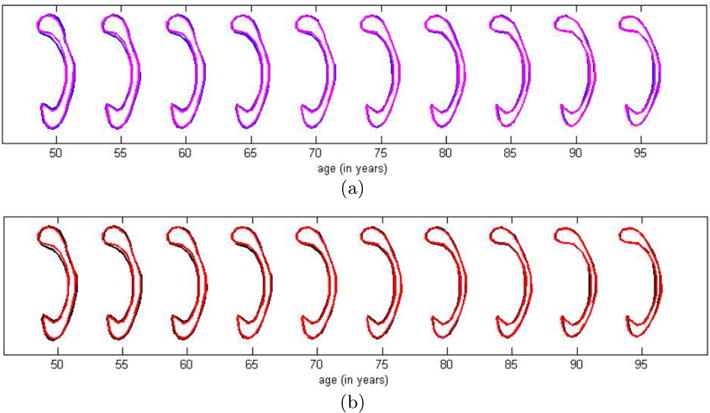
ADNI data: Mean trajectories within each gender group: (a) female group (blue - normal; magenta - AD); (b) male group (black - normal; red - AD)

4 Conclusion

We proposed a local distance correlation for modeling data with manifold valued responses and applied this method to a variety of applications, such as the responses restricted to the sphere, shape spaces. The proposed method can detect complex nonlinear relationship and keeps the computational simplicity. In future, we will further investigate the theoretical properties of the new method and other applications in imaging analysis.