Dielectric screening effect of electronic polarization and intramolecular hydrogen bonding

Abstract

Recent site‐resolved hydrogen exchange measurements have uncovered significant discrepancies between simulations and experimental data during protein folding, including the excessive intramolecular hydrogen bonds in simulations. This finding indicates a possibility that intramolecular charge–charge interactions have not included sufficient dielectric screening effect of the electronic polarization. Scaling down peptide atomic charges according to the optical dielectric constant is tested in this study. As a result, the number of intramolecular hydrogen bonds is lower than using unscaled atomic charges while reaching the same levels of helical contents or β‐hairpin backbone hydrogen bonds, because van der Waals interactions contribute substantially to peptide folding in water. Reducing intramolecular charge–charge interactions and hydrogen bonding increases conformational search efficiency. In particular, it reduces the equilibrium helical content in simulations using AMBER force field and the energy barrier in folding simulations using CHARMM force field.

Introduction

As a landmark advance in scientific computing, folding of small proteins has become accessible in molecular dynamics simulations at the atomic level in millisecond timescale.1, 2, 3, 4 Recent site‐resolved hydrogen exchange and other biophysical measurements5 uncovered several significant discrepancies between the simulations6 and experimental data in regions of the energy surface outside of the native basin, including the excessive intramolecular hydrogen bonds in simulations. These findings suggest possible adjustments of the charge–charge interactions between intramolecular hydrogen bonding groups.

In widely applied all‐atom simulations, each atom is represented by a point charge with covalent bond constraints and a 6–12 Lennard‐Jones potential, widely called van der Waals interactions.7 Hydrogen bonding is represented by the Coulomb interactions between atomic charges of the polar groups. The structural polarization is represented by the charge redistribution of the atomic motion. The electronic polarization is currently not calculated in widely used force field methods for the purpose of saving computing time. Over the years, various polarizable models have been applied,8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 representing the next level of molecular simulations. Given the size of the protein‐solvent system and the time scale of folding, the current computing speed has not reached the level for protein folding simulations with polarization calculations.

The continuum solvent model or semi‐microscopic model19, 20, 21 calculations usually include the average electronic polarization effect in the dielectric constants. In simulations with explicit solvent, the widely used water models, such as the SPC, TIP3P, and TIP4P models,22, 23, 24, 25 are mean field models with fixed atomic charges parameterized to reproduce equilibrium properties of liquid water. Based on the liquid water dipole moment of ∼3.0 D,26, 27, 28, 29 it is believed that the dipole moments of the widely used water models in the range of 2.1 to 2.4 D include the average dielectric screening effect of the electronic polarization.30, 31, 32 In widely used force field parameters of biomolecules, the total charge of a charged amino acid is equal to that of an electron or a proton, indicating that its atomic charges have not included the dielectric screening effect of the electronic polarization. Without the electronic polarization calculation, these atomic charges need to be scaled down according to the optical dielectric constant of ∼2.30, 31, 32 The excessive intramolecular hydrogen bonds found in folding simulations5 suggest that the atomic charges of neutral amino acids have not included sufficient dielectric screening effects of the electronic polarization and need to be scaled down according to a proper dielectric constant. Most non‐polar organic liquids, such as the liquid alkanes or benzene, have their dielectric constants in the range of 1.4–2.5,33, 34 which are largely from the electronic polarization contribution and are close to the optical dielectric constant of water from electronic polarization contribution at electrical field frequency greater than 10 THz.35, 36 A dielectric constant value of 1.5–2 has been suggested for macromolecules and proteins.37, 38 As a first approximation, the dielectric constant of 2 is assumed in this qualitative study to scale down peptide atomic charges, and the optimal scaling factor could be found in more quantitative studies in the future. Water parameters are not changed. A previous study39 has shown that peptide folding occurs in simulations without change–charge interactions and hydrogen bonding, suggesting a possibility of scaling down charge–charge interactions.

Materials and Methods

The AMBER force field40 and software package41 are applied to molecular dynamics (MD) simulations of peptide folding with explicit solvent and periodic boundary conditions. The CHARMM force field42 and the NAMD program43 are applied to verify the qualitative results. As a first approximation, the peptide atomic charges of both force fields are scaled by a factor of $1/\sqrt{2}$ to include the dielectric screening effect of the electronic polarization in intramolecular charge–charge interactions. The parameters of the Lennard‐Jones potential and covalent bond constraints are used without changes. The TIP3P water parameters, including atomic charges, are used without any changes.

Multiple constant volume simulations are carried out on an α‐helix forming peptide and a β‐hairpin forming peptide, starting from different unfolded structures generated from high temperature simulations at 900K. For comparison, the same numbers of simulations are carried out from the same starting structures using the standard force field atomic charges. The effect of scaling peptide atomic charges on peptide solution density is tested in NPT ensemble simulations. The cutoff distance is 8 Å, the time step 0.002 picoseconds (ps), and the bond length connecting to hydrogen atoms constrained using the SHAKE algorithm.44

Results

α‐helix folding

The α‐helix is a widely available basic secondary structure with a well‐defined geometry. Its folding has been studied extensively using computational methods.45, 46, 47, 48, 49 Early peptide folding simulations45, 50 were carried out successfully on synthetic peptide sequences. Among these peptides, a well characterized alanine‐based α‐helical peptide51 Ac(AAQAA)₃Y‐NH₂ is studied here. The peptide is solvated with 1529 water molecules in constant volume simulations with periodic boundary conditions. A group of 16 simulations is carried out at 273K for 60 ns starting from 16 unfolded structures with scaled (by $1/\sqrt{2}$) peptide atomic charges of the AMBER force field. For comparison, another group of 16 simulations are carried out from the same starting structures using standard AMBER atomic charges.

In all simulations, helical segments are observed, including partial helices and two‐segment helices. These structures are interconverting during simulations. With scaled peptide atomic charges, the whole peptide folded into a single helix in 11 of the 16 simulations. A helical structure observed at 39 ns in the simulation #3 is shown in Figure 1, where the majority of backbone hydrogen bonds is in the (i, i + 4) α‐helix pattern and a small number of hydrogen bonds in the (i, i + 3) 3₁₀ helix pattern. The hydrogen‐oxygen distances are slightly larger because the strength of charge–charge interactions is reduced. With the standard AMBER atomic charges, the whole peptide folded into a single helix in 12 of the 16 simulations, and different types of structures are more stable, interconverting less frequently. A helical structure observed at 50 ns in the simulation #2 is shown in Figure 1, with more (i, i + 4) backbone hydrogen bonds. The structures are displayed using the molecular graphics software of Schrodinger LLC. The hydrogen bonds in the figure are based on the default hydrogen bond criteria of the software, which include the maximum oxygen‐hydrogen distance of 2.5Å, the minimum donor angle of 120°, and the minimum acceptor angle of 90°. The geometrical hydrogen bond criteria are used in this study because the energy‐based definitions are force field parameter dependent.

Figure 1.

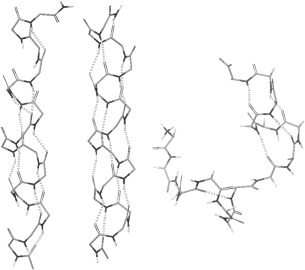
From left, a helical structure observed during simulations with scaled AMBER peptide atomic charges, a structure with the standard AMBER atomic charges, and a structure with scaled CHARMM peptide atomic charges. The C‐terminus is in the upper portion of each structure. Hydrogen bonds are shown as dotted lines. For a clear view of the backbone structure, non‐polar hydrogen atoms, side chains, and water molecules are not shown

As a measure of the progress of helix folding, the number of helical residues is calculated based on backbone dihedral angles. In literatures,46, 47, 48, 49, 52 several dihedral angle criteria of the helical conformation have been used, such as ϕ = −57° ± 30° and ψ = −47° ± 30°, ϕ = −65° ± 35°, and ψ = −42.5° ± 37.5°, ϕ = −65° ± 35°, and ψ = −37° ± 30°, and so forth. In this study, when the ϕ, ψ angles of two or more consecutive amino acid residues are within 30° from the standard α‐helical angles (ϕ = −57° and ψ = −47°), these residues are assumed to be in the helical conformation, which include the majority of α‐helix and 3₁₀ helix residues. The average percentage of helical residues over the 16 simulations at every 0.2 ns is shown in Figure 2 (left), as the helical contents. With scaled peptide atomic charges (solid line), it reaches an equilibrium value of 59.7% in 50 ns. With standard AMBER atomic charges (dash‐dotted line), the helical content is higher at 80.6%.

Figure 2.

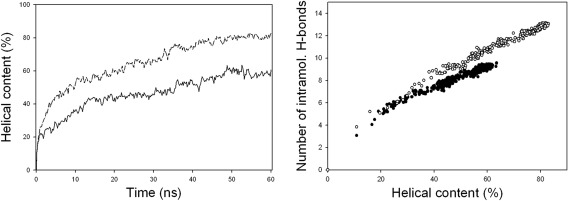
The left figure shows the average helical content over the 16 simulations with scaled AMBER peptide atomic charges (solid line) and with the standard AMBER atomic charges (dash‐dotted line). The right figure shows the average number of peptide intramolecular hydrogen bonds over the 16 simulations with scaled AMBER peptide atomic charges (filled circle) and with the standard AMBER atomic charges (open circle)

To address the issue of excessive intramolecular hydrogen bonds, the total number of peptide intramolecular hydrogen bonds is calculated with the same geometrical criteria as those used in Figure 1 and its average value over the 16 simulations at different helical contents is shown in Figure 2 (right). With the same helical content, the total number of the peptide intramolecular hydrogen bonds is lower with the scaled peptide atomic charges. The standard force field simulations have more peptide intramolecular hydrogen bonds at the same helical content during folding, as found in the experimental benchmarking study.5 In NPT ensemble simulations with scaled peptide atomic charges, the same qualitative features of helix folding are observed and the solution density is in the range of 1.00–1.01, showing that with a sufficient number of water molecules, the volume is mainly determined by water parameters.

Using scaled CHARMM peptide atomic charges and the NAMD program, helix folding of this peptide is tested in two simulations starting from unfolded structures. The peptide is solvated with 1570 water molecules in constant volume simulations with periodic boundary conditions. Helical turns and helical segments are observed within 30 ns in both simulations. A structure observed at 13.9 ns in the second simulation is shown in Figure 1. For comparison, simulations with standard CHARMM atomic charges are carried out from the same starting structures. With standard atomic charges, structures with one helical turn are observed, but the turn has not developed into longer helical segments during the simulations up to 100 ns. Peptide atomic charge scaling reduces energy barriers and the folding time in simulations using CHARMM force field, and reduces the equilibrium helical content in simulations using AMBER force field, making the difference smaller between the results from the two force fields.

β‐hairpin folding

Computational studies of another important secondary structure, the β‐sheet, are not as widely available as those of the α‐helix. With limited computing resources, a small peptide is the first choice for a folding simulation. Blanco et al.53 have successfully designed a small β‐hairpin peptide YQNPDGSQA, and Wu et al.54 have carried out a folding simulation of this peptide using standard AMBER parameters and an enhanced conformational search method.55

Using scaled (by $1/\sqrt{2}$) AMBER peptide atomic charges, a group of 20 simulations of this peptide is carried out at 300K for 80 ns starting from 20 unfolded structures. For comparison, another group of 20 simulations are carried out from the same starting structures using the standard AMBER atomic charges. The peptide is solvated with 1273 water molecules in constant volume simulations with periodic boundary conditions. During simulations structures are recorded, and hydrogen bonds are calculated using the same geometrical criteria as in the helix folding section. With scaled peptide atomic charges, structures with 3 or 4 β‐hairpin backbone hydrogen bonds are observed in 11 of the 20 simulations. A structure observed at 61.62 ns in simulation #3 is shown in Figure 3. Its hydrogen bonding pattern is consistent with the model structure based on NOE data.53 With the standard AMBER atomic charges, structures with 1 or 2 β‐hairpin backbone hydrogen bonds are observed, such as the structure at 64.47 ns of the simulation #20 shown in Figure 3, but no structures with 3 or 4 β‐hairpin backbone hydrogen bonds consistent with the NOE based model structure are observed within 80 ns in any of the 20 simulations. A much longer simulation time is needed for β‐hairpin folding with standard AMBER atomic charges without enhanced conformational search techniques. β‐hairpin folding using the scaled peptide atomic charges shows higher conformational search efficiency.

Figure 3.

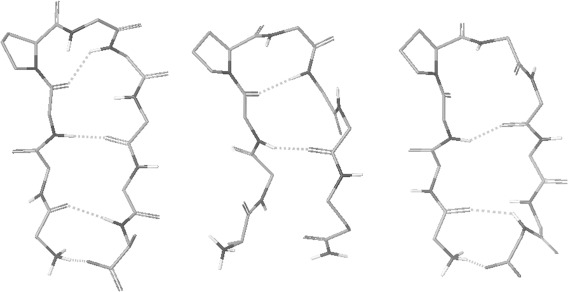
From left, a β‐hairpin structure observed during simulations with scaled AMBER peptide atomic charges, a structure with the standard AMBER atomic charges, and a structure with scaled CHARMM peptide atomic charges. The N‐terminus is on the left side of each molecule. Other descriptions about the atom display are the same as in Figure 1

Unlike for helical structures, the backbone dihedral angle‐based criteria are not widely available for β‐hairpin structures, except for the two residues at the β‐turn. The number of the β‐hairpin backbone hydrogen bonds consistent with the model structure based on NOE data53 is used as a measure of the β‐hairpin folding and its average values over the 20 simulations at every 0.2 ns are shown in Figure 4 (left). Their 80 ns average is 0.45 with the scaled peptide atomic charges (solid line) and 0.42 with standard AMBER atomic charges (dotted line). The average number of intramolecular hydrogen bonds over the 20 simulations vs. that of the backbone hydrogen bonds during the simulations is shown in Figure 4 (right). The filled circles show the average numbers of intramolecular hydrogen bonds using the scaled peptide atomic charges and the open circles show those using standard AMBER atomic charges, which is higher than the filled circles by 1.2 hydrogen bonds on average. With the same number of β‐hairpin backbone hydrogen bonds, reduced charge–charge interactions result in smaller total number of peptide intramolecular hydrogen bonds, because van der Waals interactions in the peptide‐solvent system contribute substantially to folding.39, 56, 57 Reduced hydrogen bonding in intermediate structures increases the conformational search efficiency.

Figure 4.

The left figure shows the average numbers of β‐hairpin backbone hydrogen bonds over the 20 simulations with scaled AMBER peptide atomic charges (solid line) and with the standard AMBER atomic charges (dotted line). The right figure shows the average peptide intramolecular hydrogen bonds over the 20 simulations with scaled AMBER peptide atomic charges (filled circle) and with the standard AMBER atomic charges (open circle)

Using scaled CHARMM peptide atomic charges and the NAMD program, β‐hairpin folding of this peptide is tested in two simulations at 300K. The peptide is solvated with 1002 water molecules in constant volume simulations with periodic boundary conditions. Staring from unfolded structures, structures with 3 β‐hairpin backbone hydrogen bonds are observed in both simulations. Figure 3 shows such a structure observed at 7.685 ns of the second simulation. From the same starting structures, two simulations are carried out with standard CHARMM atomic charges. Structures with one β‐hairpin backbone hydrogen bond appear multiple times, but structures with more than one β‐hairpin backbone hydrogen bond are not observed during the two simulations up to 120 ns. Using scaled CHARMM peptide atomic charges, energy barriers in β‐hairpin folding simulations are reduced, making the conformational search more efficient.

Discussion

The recent experimental benchmarking study5 found excessive intramolecular hydrogen bonds in protein folding simulations, indicating a possible overestimate of intramolecular charge–charge interactions. Based on the approximate dielectric screening effect of the electronic polarization, peptide atomic charges are scaled down in this study. As a result, the number of intramolecular hydrogen bonds is lower than using unscaled atomic charges while reaching the same levels of helical contents or β‐hairpin backbone hydrogen bonds, because van der Waals interactions in the peptide‐solvent system contribute substantially to peptide folding.39, 56, 57 Reducing intramolecular charge–charge interactions lowers the stability of hydrogen bonded intermediate structures and energy barriers in the folding landscape, making the conformational search more efficient. The faster folding favors higher cooperativity in folding kinetics. These results are in better agreement with experimental observations in folding energetics and kinetics.5 The peptide atomic charge scaling factor may be further optimized in more quantitative studies in the future, including possible adjustments of Lennard‐Jones parameters of peptide atoms. More accurate dielectric screening at each atomic position in every protein‐solvent structure during folding simulations can be calculated using polarizable models or quantum mechanical models when sufficient computing resources become available.