Family structure and childhood anthropometry in Saint Paul, Minnesota in 1918

Abstract

Concern with childhood nutrition prompted numerous surveys of children’s growth in the United States after 1870. The Children’s Bureau’s 1918 “Weighing and Measuring Test” measured two million children to produce the first official American growth norms. Individual data for 14,000 children survives from the Saint Paul, Minnesota survey whose stature closely approximated national norms. As well as anthropometry the survey recorded exact ages, street address and full name.

These variables allow linkage to the 1920 census to obtain demographic and socioeconomic information. We matched 72% of children to census families creating a sample of nearly 10,000 children. Children in the entire survey (linked set) averaged 0.74 (0.72) standard deviations below modern WHO height-for-age standards, and 0.48 (0.46) standard deviations below modern weight-for-age norms.

Sibship size strongly influenced height-for-age, and had weaker influence on weight-for-age. Each additional child six or underreduced height-for-age scores by 0.07 standard deviations (95% CI: −0.03, 0.11). Teenage siblings had little effect on height-forage. Social class effects were substantial. Children of laborers averaged half a standard deviation shorter than children of professionals. Family structure and socio-economic status had compounding impacts on children’s stature.

1. Introduction

The existence of strong connections between children’s nutrition, childhood growth, and later-life socio-economic and health outcomes have been well-known to both academics and the general public since the late nineteenth century (Tanner, 1981). Indeed, measuring the purely correlational relationship between anthropometric development and intelligence was important in the development of statistics by scholars such as Karl Pearson (Lee Rodgers & Nicewander, 1988; Pearson, 1906). Modern medical and social science scholars have moved beyond correlational analyses to show that growth has “plasticity” (Mascie-Taylor & Bogin, 1995) being both a little rigid and a little flexible. More specifically, growth potential is largely determined by genetic inheritance (rigidity), but the extent of its achievement depends on environmental conditions, broadly conceived, over the growth period (flexibility) (Silventoinen, 2003). Moreover, people are capable of surviving poor conditions in one period of their life and catching up on some of their missed potential growth and development later in their childhood or adolescence (Bogin, 1999). Thus, poor nutrition in childhood is manifested in both stature growth below genetic potential, and compromised neurocognitive development (Heckman, 2007). The association—commonly observed across time and space—between being short and having somewhat poorer educational and economic outcomes arises from the same underlying cause: a shortfall in net nutrition during the first two decades of life. Because compromised growth has important consequences for children’s lives it is important to understand its causes.

In this paper we address a modern version of that question with old data, asking how family structure and household economic resources affected the stature of young children. We use a survey of height and weight for children aged 0–6 in Saint Paul, Minnesota carried out in 1918 as part of a national survey of young children’s anthropometry (Lathrop, 1921; Peixotto, 1918; Rude, 1919). The very existence of this large dataset from 1918 shows the long-standing interest in measuring children’s growth. The survey explicitly marked children with sub-standard growth for potential follow-up and intervention, showing that the consequences of compromised growth have been known for a long time.

We measure the correlates of childhood growth in Saint Paul by linking the 1918 anthropometric survey to the more detailed demographic and socio-economic information collected in the 1920 census. From the 1920 census we are able to derive measures of household structure and resources including: home-ownership, father’s occupation as a measure of social class, and the number of co-resident siblings and their ages. The data on family structure permits a test of the quality-quantity trade-off using stature-for-age as a measure of child quality. As Hatton shows in an article in this issue, stature, and more broadly health, may be a more responsive domain to child quality-quantity trade-offs than outcomes such as education (Hatton, 2016). In modern settings birth order and family size have been found to have large effects on physical fitness and stature in egalitarian and low-fertility Sweden (Barclay & Myrskylä, 2014) (Myrskylä, Silventoinen, Jelenkovic, Tynelius, & Rasmussen, 2013). By contrast the early twentieth century United States was characterized by relatively large families and relatively low incomes. These are similar conditions to the two British cohorts—from the 1890s, and 1920s through early 1930s—studied by Hatton and co-authors who found large effects of sibship size on stature (Bailey, Hatton, & Inwood, 2016; Hatton & Martin, 2010). Oberg’s study of Swedish conscripts also found that additional siblings were associated with reduced stature, particularly for men born between the 1880s and early 1910s (Öberg, 2015). As in Britain and the United States, this was an era of differential fertility decline where better educated parents reduced fertility earlier (J. D. Hacker, 2003).

The findings from modern scholars using historical data illustrate how the domain of research on childhood growth and development has changed since the collection of the original data. In the early twentieth century United States—and other high income countries in Europe and Australasia—much of the research on childhood growth and development focused on establishing population norms and variability for single variables, and statistical associations between different bodily dimensions at an individual level (Baldwin, 1921). The connection of compromised growth to the social and economic circumstances of children’s families was frequently acknowledged but largely unexamined. For example, authors were concerned to describe their samples as being distinctly of private school children (Gray & Ayres, 1931; Gray & Fraley, 1926; Wallis, 1931), “native white” children (Clark, Sydenstricker, & Collins, 1922), or “colored” children (Mustard & Waring, 1926). Occasionally authors with measurements on nearly all the pupils in a city’s school system would feel confident enough to describe their sample as “representative” (Faber, 1925). Explicitly measuring the multivariate relationship between social class, family resources, and children’s growth was beyond the capacity of those researchers.

Concerns about the relationship between poverty and children’s nutrition re-emerged in North America and Europe during the Great Depression (Kiser & Stix, 1933). In countries including Britain and New Zealand school-based nutrition programs were instituted during the Depression in response to these concerns (Atkins, 2005; New Zealand Milk Board, 1978). These policies managed to address both concerns about farmers’ incomes—by buying large quantities of agricultural output—and children’s nutrition. In the United States widespread government subsidies and provision of food and drink for children began on a small scale late in the Depression, and then increased significantly in the decades after World War II through the school lunch program (Levine, 2010).

Subsequently, increasing understanding of the links between nutrition, physical growth and development have had a significant impact on policy towards children since World War II. Particularly in lower-income societies, a significant focus of public policy from the 1950s through the 1980s was reducing the incidence of childhood malnutrition (Onis, Frongillo, & Blössner, 2000). More recently, policy makers and health practitioners in lower and middle income countries have been challenged by increasingly prevalent childhood obesity, at the same time as large numbers—but lower proportions—of children remain undernourished (Popkin, 2002). In the United States and other high-income countries nutritional interventions such as subsidized meals at schools have succeeded at reducing the prevalence of children not receiving enough calories. The dominant childhood nutrition policy challenge in high-income countries is now overweight and obesity (Ogden, Carroll, Kit, & Flegal, 2012). Yet while more children are now at risk of overweight, a substantial number of American children still live in households experiencing “food insecurity” (Cook & Frank, 2008). The modern pattern and challenge of childhood diet in the United States is low quality nutrition, with children eating a diet often sufficient in calories from processed food, but lacking important micronutrients important for physical and cognitive development. This is in stark contrast to the calorie deficit sustained over many years that poorer children endured in the early twentieth century. Thus, the association of early-life malnutrition with socioeconomic status, and the effect of malnutrition on later outcomes remain an important research question and policy challenge.

2. Childhood growth as a measure of well being

Stature is a summary measure of the effect of nutrition, environmental conditions, disease, and physical workload on the body during childhood- and early adulthood-growth (Bogin, 1999; Eveleth & Tanner, 1990). Sustained nutritional deficits while a person is growing result in individual stature falling short of maximum potential height. Children and adolescents put calories to the immediate task of replenishing energy and fighting disease, before they can grow taller. If a growing person is persistently sick or expending more calories than they take in, growth will slow. When these nutritional deficits are widespread across the population, average stature will fall (Jelenkovic, et al., 2011; Silventoinen, 2003).

There are three main causes of nutritional deficits, which while analytically separate are not mutually exclusive: (1) limitation in the availability of calories, (2) persistent bouts of infectious disease while energy intake is constant, (3) elevated energy expenditure while energy intake and disease exposure are constant. The incorporation of energy expenditure and loss, alongside food intake, motivates the concept of ‘net nutrition’ (Steckel, 1986). Changes in the average stature of the population are subject to several influences. Thus changes in average stature do not identify the causes of change. Rather, changes in average stature show when different cohorts, who are presumed to have the same genetic potential for achieving a particular height, have grown at different rates. Once these periods of changing stature are identified, the contemporaneous influences on net nutrition must be investigated to identify the potential causes of changing stature. Since the 1970s stature has been widely and increasingly used to measure the biological standard of living in an historical and comparative context (Floud, Wachter, & Gregory, 1990; Komlos, 1998; Steckel, 2013).

Much of the literature on stature as a measure of population well being in the past has focused on adults who have achieved their terminal height. Scholars have largely used samples drawn from military and prison sources, where institutional requirements to classify and identify individuals led to the collection of heights from large numbers of individuals, mostly men (Steckel, 2008, 2009). In the United States, nineteenth century slave trade manifests have provided another source for studying stature in historical populations. Notably, the slave manifests include women and children as well as adult men. From these sources Steckel and colleagues have shown that slave children had a distinctive growth pattern. Slave children deprived of nutrients at a very young age when they could not make a contribution as workers, but caught up somewhat later in childhood when fed more because they were working (Steckel, 1986).

In less extreme circumstances than slavery the stature of children can also reveal important trends in how society treats children in different circumstances. Shortfalls in mean stature-for-age for particular groups can highlight the more or less favoured position of girls or boys. Before the early twentieth century decline in child labour, children’s earnings were an important component of family income. One might expect to see boys do better within the family, that is be taller for their age than girls in the same family, because boys were fed more to reflect their earning potential. Yet physical labour may retard childhood growth potential, so that children exposed to the labour market may end up shorter. Children in smaller and larger families may also have a differing growth pattern. First-born and higher-order children may be expected to be taller for their age than their younger siblings because more of their growth period occurs when there is less competition within the household for resources. In short, there are multiple influences including gender, family and household composition, and labour market opportunities and needs on young children’s ability to reach their growth potential. The net effect of these influences across different families is reflected in average stature, conditional on family circumstances and gender. As in the anthropometric literature more broadly, research on children’s stature identifies a societal rather than individual effect.

A complication of using childhood stature as a measure of well being is that children are growing. The shortest six-year old will almost certainly be taller than the tallest two-year old. Girls and boys also have different growth norms, though male and female infants begin life with very similar distributions of height and weight. In order to compare children’s stature across different ages and sexes we normalize stature. The standard approach in the recent anthropometric literature is to compare the historical stature of children to modern growth norms (E. B. Schneider, 2016).

Research on children’s stature during the late nineteenth and early twentieth century is most abundant for Britain. Examining school children, Bernard Harris found that early twentieth century British girls tended to be slightly taller for their age than boys, but after puberty boys overtook girls in comparisons to modern growth standards (Harris, 1995). In a slightly different context Schneider found that girls entered orphanages in late nineteenth century Boston and London at lower percentiles of modern height standards than boys, suggesting girls were worse off (E. Schneider, 2016 (forthcoming)). In the inter-war era Hatton and Martin found that boys and girls in the Boyd-Orr survey of working class families in Britain reached the same height-for-age compared to modern standards. Hatton and Martin found more significant effects of family size and structure on childhood stature. Birth order and family size both had a negative effect on children’s stature: children born later in larger families were shorter than their peers born earlier to the same parents (Hatton & Martin, 2010). Thus, despite rapid growth in the use of stature to study well being in the past there is only a relatively small literature on children’s stature before World War II.

The relatively small size of the literature on young children’s growth in the nineteenth and early twentieth centuries does not reflect a lack of data collected at the time. Indeed, as Baldwin showed in an extensive bibliography, data on stature for millions of children had been published by the early 1920s (Baldwin, 1921), reflecting a contemporary interest in growth from physiologists, psychologists and the broader social policy and public health community (Tanner, 1981). Yet compared to the records available for adults and teenagers in military and prison records, relatively little individual level data has survived with measurements of children’s stature.

The uniqueness of this paper highlights how much original data was destroyed. In 1918 the United States government set out to measure the height and weight of five million children for Children’s Year (Peixotto, 1918). Two million cards were received by the Children’s Bureau in Washington. National growth norms for children up to age six were published, based on the selection of the best 172,000 measurements (Woodbury, 1921). The data that we use from Saint Paul, Minnesota, appears to be the only surviving microdata from the nationwide data collection.¹

3. Historical background

The Children’s Year campaign in the United States came out of both a growing interest in child welfare (Ruis, 2013), and a specific wartime concern that children’s nutrition would be compromised by the allocation of food to soldiers, workers, and other countries. Wartime concerns for children’s nutrition were not unique to the United States, motivating, for example, the collection of data on children’s nutrition in Germany during the “Hungerblockade” (Cox, 2015). Shortly after the United States entered the war the Women’s Committee of the National Council of Defense and the Federal Children’s Bureau looked at how other countries had addressed questions of children’s nutrition during the war, and the American bureaucrats “expected to profit by the experiences of other warring countries.”² American officials were impressed that England and France both took measures to improve the standard of living from maternity through childhood and the infant mortality rate decreased during World War I. In England infant mortality fell to the lowest it had ever been during war times (Rude, 1919). Motivated by these examples of government support for children’s welfare work President Wilson set aside $150,000 to fund the project with a goal to save the lives of 100,000 children a year through a three step program (Titzel, 1919).

On April 6th, 1918, the first portion of the campaign, the Weight and Measuring Test, began when the Women’s Committee of Council of National Defense sent out seven million cards across the country for all children under six years of age to be weighed and measured by their parents (Lathrop, 1921). Researchers at the Children’s Bureau recognized the presence of inaccuracies and 100,000 physical examinations were made by doctors and nurses to estimate the reliability of the cards received. The contemporary analyses of the data from the Weighing and Measuring Test focused on variations in stature across geographical differences, urban versus rural homes, and the nationality of parents or grandparents (Woodbury, 1921).

The Children’s Year campaign extended beyond the Weighing and Measuring Test of preschool children (Rude, 1919). Other activities in the campaign included the “Back-to-School” welfare committee for each school in the country. The purpose of the campaign was to encourage children to stay in school until at least age 16, although minimum legal leaving ages in most states remained lower. Many had left school early with the incentive of the wartime wages to make up for their fathers who had gone to war. Keeping children in school for two additional years beyond the common compulsory schooling age of 14 was promoted as an investment in future generations. The “Recreation Drive” attempted to increase physical activity among children. Organized activities in schools promoted increased physical adeptness and skill, a better-trained eye, and more developed reflexive skills.

The publicity for the Children’s Year Campaign brought a lot of attention to hygiene issues that needed to be addressed for the widespread welfare of the nation’s children. New services for communities were funded, more regulations for milk were implemented, and Children’s Bureau proposed mandatory birth registrations throughout the country (Rude, 1919). A public education campaign focused on infant mortality, trying to raise awareness of the United States’ relatively high infant mortality rate (Peixotto, 1918).

The collection of the data in Saint Paul, Minnesota was part of the broader Children’s Year campaign. In Saint Paul the effort was organized by the Women’s Branch of the Ramsey County division of the Minnesota Commission of Public Safety. The Commission of Public Safety took a broad role in organizing the state’s war effort undertaking, among other things, a complete agricultural census of production, a survey of immigrant assimilation, and monitoring the behaviour and speech of people and organizations thought to be subversive (Chrislock, 1991). Little documentation survives about the Ramsey County women’s decision to take part in the Children’s Bureau campaign. Minutes for their fortnightly meetings during 1917 and 1918 make no mention of the Weighing and Measuring Test, and how it was organized. However, the survey cards describing individuals record where children were measured, and who measured them giving us some insight into the data collection process. Nearly all of the children in the Saint Paul data appeared to have been measured by registered nurses or doctors. One in six of the children were measured at the offices of the Child Welfare Association or at a child welfare “station” at one of the city’s big department stores. In short, what we can glean about the process of the survey suggests that it was largely carried out by public health and medical professionals giving us greater confidence in the quality of the data.

Although the Saint Paul data was not included in the national growth norms published in the early 1920s, the microdata provides an opportunity to examine how social class and family structure influenced childhood growth in early twentieth century America. To what extent was Saint Paul a typical urban environment for American children in 1918? In 1920, the closest U.S. decennial census to the Weighing and Measuring Test, Saint Paul had a population of 235,000. With its contiguous neighbour Minneapolis, the Twin Cities had a population of more than 600,000. Like other Midwestern and East Coast cities the population was largely white and either immigrants themselves or the descendants of immigrants. In Saint Paul 77% of the population was native-born white, and 57% of those had at least one foreign-born parent (Ruggles, Genadek, Goeken, Grover, & Sobek, 2015). Thus, two thirds of the city was foreign-born or of foreign descent. The African American population was small, and at the time of the 1918 survey few African Americans had settled in Saint Paul. Just sixty-one African American children are present in the data; too few for us to draw any separate conclusions about this population. The Great Migration of African Americans to Midwestern and Northeastern cities was underway at precisely the time the Weighing and Measuring Test was taking place, making it less likely that African American children would be included in the data (Taylor, 1988). More broadly Saint Paul, and the Twin Cities in general, had a smaller African American population than other comparable cities. While 3,400 African Americans were resident in Saint Paul in 1920 there were few young children in the population (just 262 aged six or under).

Saint Paul was an industrial city: Nine per cent of the population, and a quarter of working men were engaged in manufacturing. Compared to Minneapolis where large-scale flour milling dominated manufacturing employment and output, Saint Paul’s manufacturing was on a smaller scale (Hartsough, 1925; Wills, 2005). Clothing, printing, and shoe making were among the single largest industries in the city, all industries structured around relatively small workshops and factories (Bureau of the Census, 1922). The largest employers in Saint Paul were railroads: nearly one in five working men were employed on the railroads in some capacity, reflecting the junction of three major railroads in Saint Paul. Clerical work for the state government and work in distribution industries associated with the railroads were a final important aspect of Saint Paul’s occupational structure (Ruggles, et al., 2015).

The health and nutritional environment of the city was somewhat better than the American average. Infant mortality rates from 1915–18 averaged 78/1000 live births, compared to a rate of 95 for white children in other American cities (Bureau of the Census, 1916–1920). As in other American cities retail food prices increased in the Twin Cities during World War I. Yet the run-up in nominal prices was no more pronounced in Saint Paul than elsewhere in the country. Reflecting its situation as a moderately sized city close to areas of significant agricultural production Saint Paul’s retail prices for key foods were typically lower than in other American cities. Across a range of different products, meat and dairy prices in Saint Paul in December 1917 were 15% lower than national urban averages (Bureau of Labor Statistics, 1922).

Thus, Saint Paul children who were weighed and measured in 1918 were demographically similar to their peers in other large cities: they were often the children or grandchildren of European immigrants, and their parents, mostly their fathers in this era, worked in occupations and industries that were representative of the urban United States in 1920. But Saint Paul children had experienced somewhat better health and nutritional conditions than children in larger and denser cities such as New York, Boston, or Chicago.

4. The Saint Paul Children’s Year dataset

The original record cards for 14,252 Saint Paul children in the Weighing and Measuring Test are preserved at the Minnesota Historical Society. The cards are one half of a standard US Letter piece of paper and record the name, address, age or date of birth, height and weight, and serious illness of children (Figure 1). Demographic information about parents was written onto some of the cards by some of the social workers and nurses who took the survey, but was not systematically collected. Reflecting the organization of the data collection, the cards are archived geographically by wards of the city. Within each ward the cards were ordered alphabetically, such that siblings were clearly identifiable: living at the same address and sharing a surname. Sibling relationships were confirmed during the process of linking to the census, as family relationships were directly enumerated in the census. The volume of cards for data entry required us to photograph each record, and undertake data entry offsite. Six undergraduate interns working under the supervision of the authors photographed the records and entered the data. When the interns had completed data entry on their assigned cards, they undertook blind verification of cards entered by another student to assess error rates and correct errors.

Figure 1.

Example of Weighing and Measuring Test survey instrument

The demographic information on the cards is limited, and analysis of the social and economic correlates of children’s stature and weight would not be possible with the original dataset. The proximity of the 1920 U.S. census, taken on January 1st, to the 1918 Weighing and Measuring Test allowed us to collect additional social and economic information about the children by linking the children to the census. Initial links were undertaken by a second cohort of trained undergraduate interns, searching on Ancestry.com who then entered data on the household the children were living in. With just 18 months passing between the anthropometric data collection and the census, a high proportion of children were still observed to be living at the same address. The initial hand-linked data were supplemented by machine-linking to an electronic dataset of the complete 1920 census. Overall, we matched 70% (9,963) of the children to a census record. For children with full anthropometric data, and thus usable in the analyses, the match rate was 72%. Accounting for known under-enumeration (J. David Hacker, 2013), and infant mortality over 18 months we linked 78% of surviving and enumerated children to a census record.

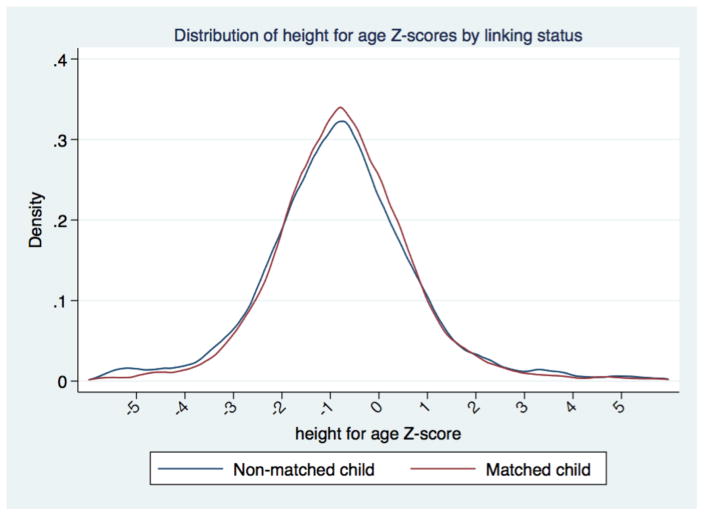
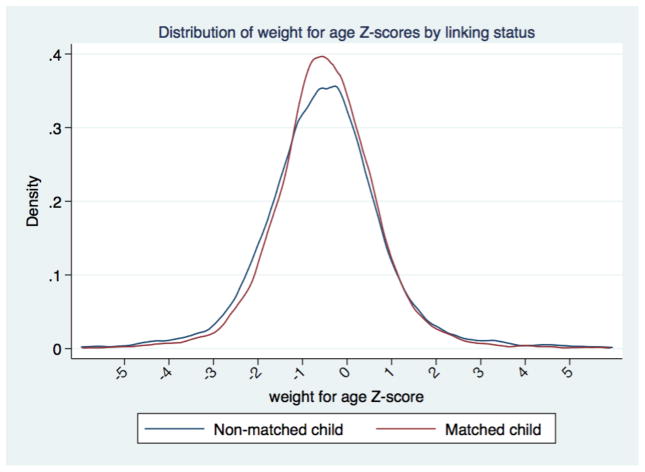
The matched subjects did not differ substantively from their un-matched peers. Height-for-age Z scores for unmatched children averaged slightly lower (−0.77) than for matched children (−0.72) (Figure 2). Weight-for-age Z scores differed by the same amount (Figure 3). While both of these differences reached conventional levels of statistical significance, the magnitude of the difference was small. Thus, we are confident that our inferences about the social structure of childhood growth are not affected by substantial biases from the linking process. Characteristics of the matched households in which the children were found are presented in Table 1. We observe a high proportion of our sample still living in Minnesota 18 months later, reflecting that non-migrants are easier to link than migrants. The household heads were largely employed in industrial and service occupations, with one in five being professionals or managers. Labor markets were still tight in 1920, and only 6% of household heads did not record an occupation. We compare our sample to the entire population of children under age 7 in Saint Paul in 1920, and find that our matched sample is very similar to the general population of children, particularly on socio-economic dimensions.

Figure 2.

Distribution of height-for-age Z scores by link status

Figure 3.

Distribution of weight-for-age Z scores by link status

Table 1.

Characteristics of the matched sample and Saint Paul children in 1920

Characteristic	Proportion of sample	Saint Paul children < 7
Resident in MN in 1920	0.97	N/A
Head of household’s nativity
Born in MN	0.39	0.37
Born in USA	0.21	0.18
Born abroad	0.40	0.45
Head of household’s occupation
Professional, manager, owner	0.21	0.18
Clerical, sales, service	0.17	0.20
Trades, craftsmen, operatives	0.45	0.48
Laborers	0.11	0.11
No occupation/out of labor force	0.06	0.04
Owned house	0.49	0.49
Ward of city
1	0.13	0.12
2	0.08	0.11
3	0.01	0.01
4	0.01	0.01
5	0.11	0.11
6	0.11	0.11
7	0.08	0.08
8	0.13	0.13
9	0.08	0.07
10	0.10	0.08
11	0.05	0.11
12	0.12	0.07

The most significant deviations are an over-representation of one ward of the city (Twelve), and corresponding under-representation of another (Eleven). Ward Twelve lay to the east of Saint Paul’s Como Lake, while Ward Eleven was geographically much larger incorporating the Macalester/Groveland and Highland Park neighbourhoods. Compared to Ward Eleven, the Twelfth Ward was slightly better off with higher occupational-income scores for household heads, but similarly low (0.29 to 0.34) home ownership rates. Across the entire city there was a nearly equal split between owners and renters. Low-density single-family dwellings dominated the housing stock in both wards. Despite this discrepancy we conclude the households in which we found children from the anthropometric survey are fairly typical of Saint Paul families. The greatest threat to the generalizability of our results is not the matching process, but the slightly better urban health and nutritional environment in Saint Paul, compared to other American cities at the same time.

5. Patterns of physical growth

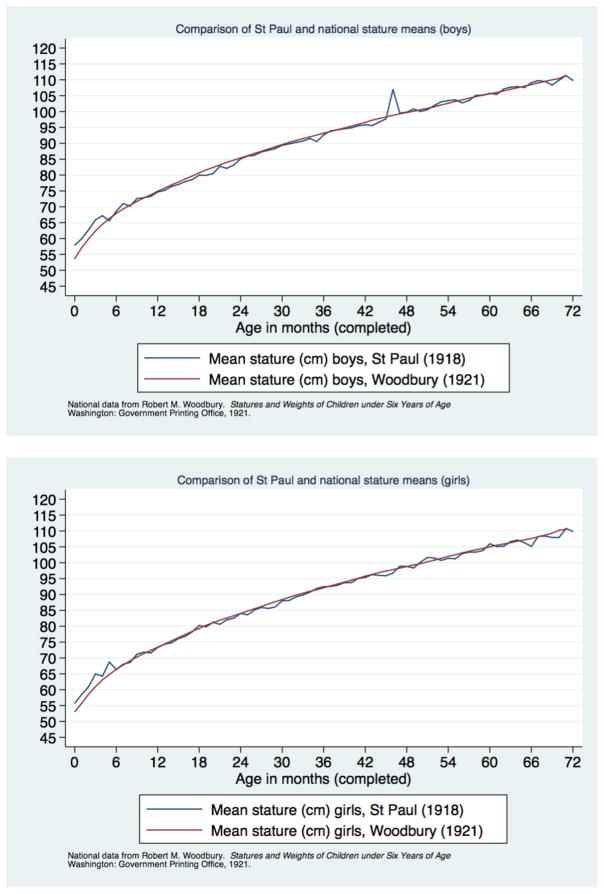
Our goal in the analysis is to assess the extent of social and ethnic differentials in stature, and their variation with family structure. Children’s growth in Saint Paul closely paralleled the norms found in the national data from the Weighing and Measuring Test (Figure 4). We calculated mean height within 10-week rolling averages, and compared to the national norms from Woodbury (Woodbury, 1921). A small spike in the average stature for boys in Saint Paul around four years of age is the only idiosyncratic variation from the national norms. A more systematic deviation in average height and weight appears for infants, both male and female. The Saint Paul children were taller and heavier than the corresponding national norms until about the age of six months, which appears to be a consequence of selection into the sample.

Figure 4.

Comparison of Saint Paul and national stature means

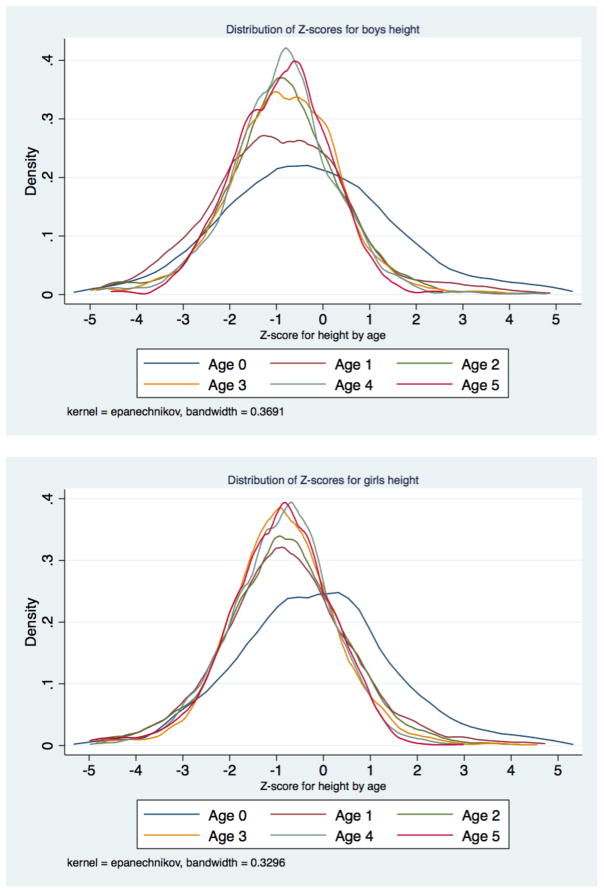
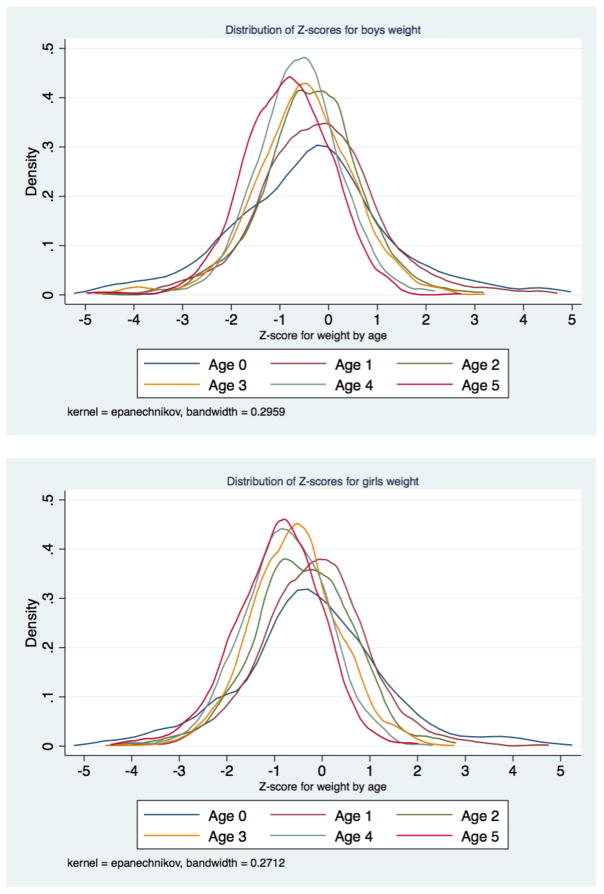
The distribution of height-for-age Z scores for infants was clearly different than for children one year of age and over (Figure 5). Weight-for-age Z scores for infants were also more skewed toward modern norms than for older children (Figure 6). However, weight-for-age Z scores were less skewed towards modern norms than height-for-age Z scores. There are two potential explanations for this pattern in our data: selection into the sample and growth faltering. It is likely that both factors are present to some degree. While the organizers of the Weighing and Measuring Test aimed to select a large sample of children, they failed to achieve a complete census of children’s anthropometry. The 1918 survey includes 14,252 children, and the population of this cohort in 1918 was likely to have been 28,000 accounting for under-enumeration and mortality (J. David Hacker, 2013).

Figure 5.

Distribution of height-for-age Z scores in Saint Paul

Figure 6.

Distribution of weight-for-age Z scores in Saint Paul

Infants are more likely to have been selected for the sample in a different way, given that measurement often took place at health centers and other locations outside the house. We suspect that less robust infants were less likely to be taken out of the house, and be weighed and measured off-site. Moreover, the height of infants is difficult to measure because infants must be measured in a prone position to be measured accurately. Infants in our sample who were measured by nurses or in an institutional setting such as the Baby Welfare “station” were 0.16 standard deviations (t=2.19) shorter than babies measured in other settings, suggesting that measurement quality may be an issue for the infants in the sample. By contrast among children aged 1–5 there were smaller differences (0.06 standard deviations shorter, t=2.10) between nurse- or institutionally measured children and children measured in other settings. Thus, we are left with some concerns about the quality of measurement in infants in our sample, and in the remainder of the analysis we conduct sub-group analyses that exclude infants to test the sensitivity of our results to the inclusion of this group. As an additional check on the robustness of the results we include a dummy for infants in our regressions.

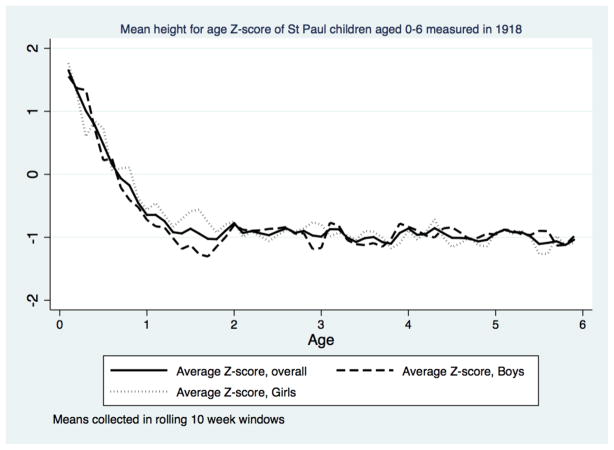
However, the pattern of falling height-for-age and weight-for-age Z-scores that we observe is consistent with growth faltering similar to that seen in developing countries today. Across multiple world regions the weight- and height-for-age Z-scores of children in low- and middle-income countries begin close to 0, and decline in the first two years of life. Declines in height-for-age Z-scores are larger and occur earlier in life, compared to weight-for-age norms (Shrimpton, et al., 2001; Victora, de Onis, Hallal, Blössner, & Shrimpton, 2010). Comparing the profile of growth faltering in Saint Paul with modern developing countries leads to several conclusions. First, children in Saint Paul showed the same pattern of greater faltering in height than weight. After infancy the average height-for-age score in Saint Paul was essentially constant for both boys and girls (Figure 7). The similarity of the height-for-age profile for girls and boys suggests that gender discrimination in nutritional resources for these children was limited; a result confirmed in our regression analyses in the following sections.

Figure 7.

Growth faltering in height-for-age scores

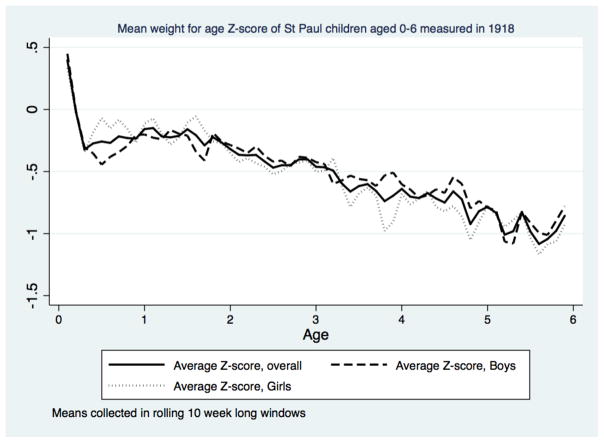
Second, faltering took place over a longer period for weight. Even after infancy in Saint Paul, the trajectory of the weight-for-age Z scores is negative (Figure 8). Compared to modern standards children were getting lighter at every age. As their average height-for-age scores were essentially constant after infancy, the implication is that weight-for-height in Saint Paul children declined as they grew older. Recalling that the Z-scores reference children to modern height and weight standards, what we observe is a pattern of accumulating shortfalls from modern standards. Even in Saint Paul, which was well-off and healthy by the standards of urban America, the average child was significantly lighter and shorter than modern standards. Yet comparing children in Saint Paul in 1918 to developing countries shows them to be taller at the same age than children in South-East Asia and Africa today. This reinforces from a sample of children the conclusions reached by scholars studying adult stature that Americans in the early twentieth century were well-fed and tall in global comparison.

Figure 8.

Growth faltering in weight-for-age scores

6. Family structure, resources, and growth

Our analysis focuses on estimating the effect of three aspects of children’s home environment on physical growth. First, we are interested in any differential effects of gender on height and weight, which may reveal whether children of different sexes in the same family were treated differently. As overall means of height-for-age and weight-for-age show little difference in the growth profile of girls and boys it seems unlikely that we will uncover important effects within the family that were not visible in the overall population.

Second, we ask how children’s position within their own family structure affected growth. Following other authors we measure family structure in two ways: birth order and family size. We observe the families in the census, where only co-resident living children were enumerated with the survey subjects. Thus, for the youngest children in large families we may not observe the earlier birth orders if those teenage or young-adult siblings have already left the house. To capture this ambiguity in our sources we describe the variable as “sibling order” rather than a true birth order.

Sibling order varies across individuals within a family, while family size is the same for all individuals within a family. Moreover, sibling order and family size are highly correlated because higher sibling orders only exist in larger families. As families were larger in the past, this issue is more acute in historical data than modern surveys. Across all the individuals in our sample the correlation between family size and sibling order was 0.82. The effect of sibling order is thus a comparison of children within the same family, while the effect of family size is a comparison between families in the sample. In order to properly identify these effects we use family fixed effects regressions to account for the similarity of family size (and other family characteristics) between children in the same family. These regressions identify the effect of children’s different birth order within the same family. Because birth order and family size are so highly correlated, we follow Booth and Kee (2009) in using a sibling order index that normalizes children’s sibling order for family size by comparing a given child to the average child within that family. This measure is less highly correlated with family size, and allows better identification of the effects of sibling order independent of changing family size.

Third, we ask how children’s growth is affected by the social class of their family. Our principal measure of social class is the occupation of the head of household. In nearly all cases this is the father of the child concerned. We conclude by putting these elements together in regressions of height- or weight-for-age scores on measures of family structure and size, the age and gender of the child, and measures of family resources and social position including the head’s occupation, home ownership and the presence of teenage siblings characterized by their labor market status. These measures allow us to see whether larger families were able to provide for younger children through the labor of older siblings.

Throughout our results we compare our findings to the most similar study in the existing literature; Hatton and Martin’s study of the Boyd-Orr cohort in 1930s Britain (Hatton & Martin, 2010). Hatton and Martin found both significant cohort and birth-order effects. For children aged 7–12 Hatton and Martin found that average stature increased nearly 3cm a decade, but that these effects were offset by younger children being shorter. Each additional child reduced stature by 0.6, implying a difference in average stature at the same age of 3cm between the first and sixth children in a family.

In comparing our results to theirs, several differences in the samples must be kept in mind. Our sample is closer to a study of the general population whereas the Boyd-Orr cohort was deliberately selected as a sample of poorer households. Our birth cohort is 8–20 years earlier than theirs, with infants in our sample born in 1917/18 compared to 1937–9 in the Boyd-Orr sample, and older children in Boyd-Orr born in the mid-1920s. Moreover, the Boyd-Orr sample measured the height and weight of a wider age-range, whereas our study is of children from 0–6. Hatton and Martin focus their results on children aged 2 and over, and thus we restrict some of our estimates to this age group. Because of this desire for comparability and our concern with the selection and measurement of infants in our sample we present results for 0–6 year olds, 1–6 year olds and 2–6 year olds.

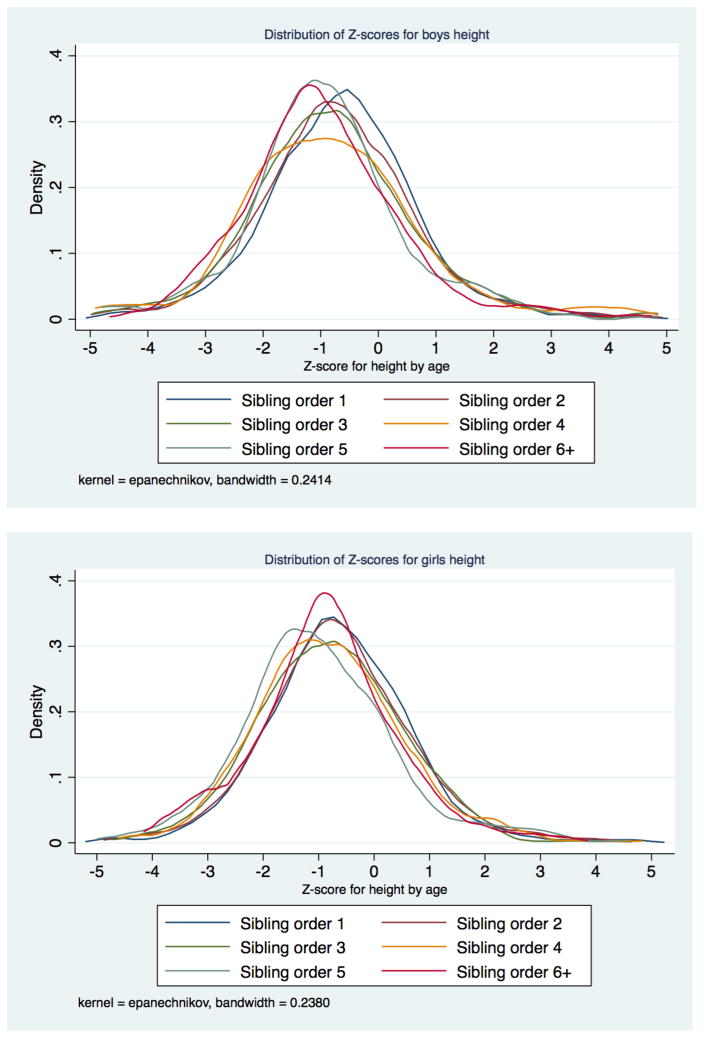
Similar to Hatton and Martin we find that both birth order (Table 2) and family size (Table 3) were negatively associated with measures of childhood growth. The average height-for-age of first and second-born children was 2/3 of a standard deviation below modern norms, whereas children with a birth order of 5 or higher were nearly a whole standard deviation below modern height norms. Similarly, children with an earlier birth order weighed more for their age than later-born children, though the gradient was not as steep as for height. Average stature-for-age changed more than average weight-for-age with higher birth orders. With children of birth order 5 or higher approximately 0.3 standard deviations shorter than first-born children a naïve first approximation of the effect of birth order is that each additional birth order decreased stature by 0.06 standard deviations up to a birth order of 5 or 6. In larger families with higher birth orders there was no large continuing decline in stature. This pattern in the means by birth order suggests how family size and birth order need to be considered together. Despite this difference in the observed averages there was some overlap in the distribution of height-for-age scores by birth order (Figure 9). For example, one in ten children of birth order 5 or greater had a height-for-age score above the average for first-born children, while 45% of third-order children were taller for their age than the average first-born.

Table 2.

Birth order and childhood growth

Sibling order	N	Mean Age	Mean Height for Age Z-Score	Mean Weight for Age Z-Score
One	3280	2.883	−0.641	−0.474
Two	2224	2.773	−0.691	−0.454
Three	1354	2.801	−0.756	−0.505
Four	824	2.735	−0.782	−0.536
Five	465	2.895	−0.964	−0.585
Six +	765	2.834	−0.925	−0.595
Total	8912	2.826	−0.725	−0.496

Table 3.

Family size and childhood growth

Number of children < 18	N	Mean age	Mean Height for Age Z-Score	Mean Weight for Age Z-Score
One	1384	2.422	−0.593	−0.467
Two	2498	2.642	−0.583	−0.381
Three	1947	2.971	−0.729	−0.495
Four	1274	3.103	−0.799	−0.557
Five	791	3.042	−0.919	−0.622
Six	432	3.136	−1.022	−0.649
Seven	271	3.009	−1.087	−0.727
Eight	140	2.894	−0.843	−0.456
Nine	81	2.939	−1.224	−0.750
Ten +	94	2.927	−0.714	−0.558
Total	8912	2.826	−0.725	−0.496

Figure 9.

Distribution of height-for-age scores by order in family

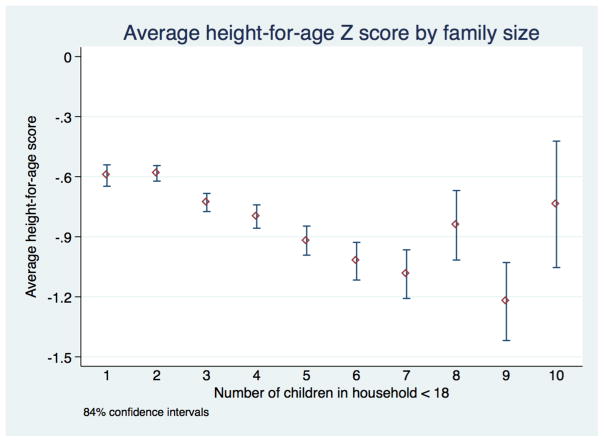
A similar pattern of declining height-for-age with family size is observed, though the pattern is not as monotonic as observed for birth order (Table 3). The observed means in height- and weight-forage scores by family size appear to cluster, as can be seen in Figure 10. We are primarily interested in measuring the significance of differences between family size groups, rather than establishing confidence intervals for each group individually. Thus we use 84% confidence intervals, for which non-overlapping confidence intervals with other groups can be interpreted as differences in group means at a conventional 5% level.

Figure 10.

Average height-for-age scores by family size

Children in families of 1–2 children have nearly identical height-for-age scores, and the weight for age scores of children in families of 1–3 children are also similar. A cluster of similar height-for-age means is also seen in families of three and four children, with a slight drop-off to families of five children. Children in households with six or seven children are clearly shorter for their age than those in families with only 1–4 children. We see relatively few children in larger families, and our estimates of their average height-for-age scores are less precise. The magnitude of the differences is significant: the average child in a family of 6 or 7 children is half a standard deviation shorter. At age 3 this is equivalent to a boy being 1.9 cm shorter.

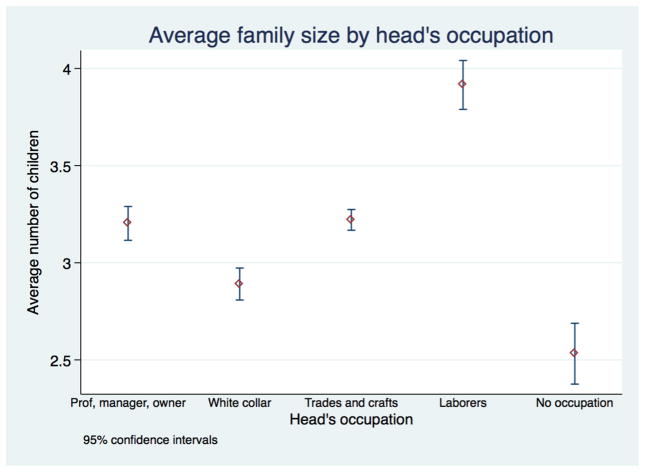
We turn next to examining how household’s social class, which we measure by the occupation of the head of household, affect children’s growth outcomes. Mean family size differed across occupational groups as can be seen in Figure 11 which displays average family size among different occupational groups, calculated at the level of the child. The average child of a professional or trades worker lived in a family of 3.2 children, while white collar workers—among whom are found clerical, salespeople and service sector workers—averaged just under 3 children. Laborers’ children lived in significantly larger families that averaged 3.9 children. It must be noted that these are not completed family sizes, but observed family sizes in the census. Younger families may proceed to have more children, while the children of older parents may be observed without their older siblings who have left home. The number of children in the household in our survey is a measure of both potential resources for the child, and potential competition for those resources. Moreover, the figures show that while we observe some very high birth orders and family sizes, the average child lived in a household of 3 children, and 90% lived in households of 6 or fewer children.

Figure 11.

Family size differed significantly across social class

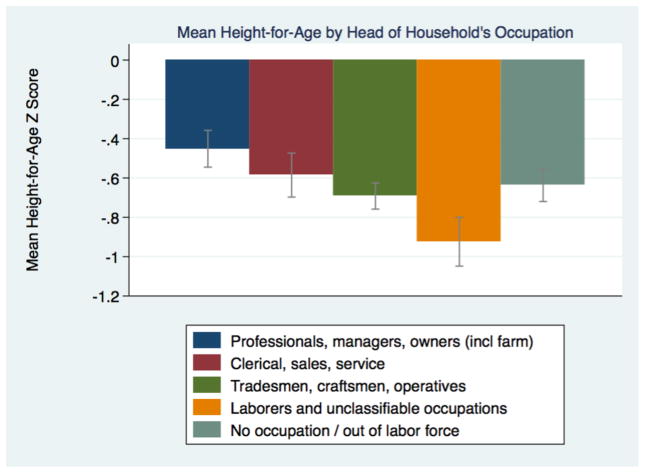
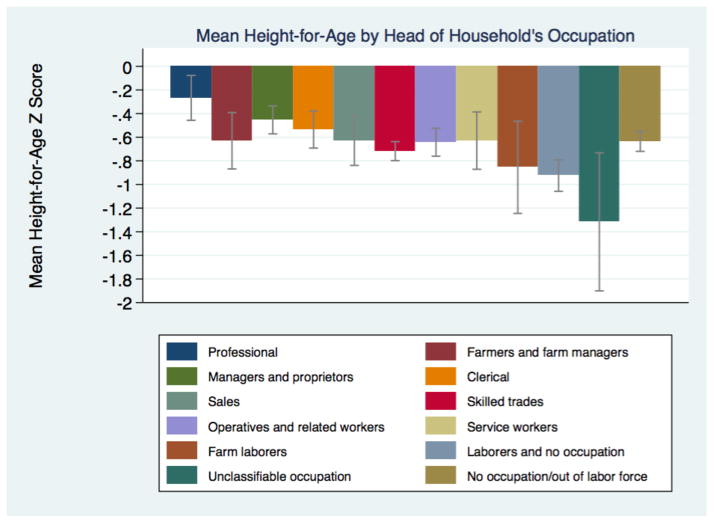
We classify occupations into the United States 1950 occupational coding scheme used by IPUMS, and then group these occupations into five broader categories that indicate social classes. We group professionals, managers and farm owners into one class; white and pink collar workers in clerical, sales and service occupations into another; skilled and semi-skilled tradesmen and operatives in another; and laborers in a final class. We leave in a group of their own household heads that did not report an occupation (6% of the children had a household head in this category). Differences in height-for-age means were significant across both occupational and social class groupings. The children of professionals and managers in particular were clearly taller than the children of both farm and industrial laborers (Figures 11 and 12). Grouping similar occupations together we see that the children of laborers stood half a standard deviation shorter than the children of professionals, owners and managers. The children of white-collar workers and industrial workers were between these extremes, and in the expected direction: white-collar workers’ children were taller.

Figure 12.

Social class and mean stature for children in Saint Paul

6.1 Modeling childhood growth

Although there are sizeable observed differences in children’s stature across birth order, family size, and social class it is clear that these factors are inter-related. We begin to disentangle the effects of family size, sibling order and social class on children’s growth by running a series of regressions that parallel Hatton and Martin’s analyses of the Boyd-Orr sample (Hatton & Martin, 2010). Our full model specification is slightly different, because the 1920 census collected less information on household resources and income than the Boyd-Orr survey.

Our measures of family structure are constructed from the 1920 census listing, and allow us to construct the following indicators of family structure: sibling order, whether a child was first-born, sex, and whether a child was a twin. From the 1918 survey we include a measure of the child’s exact age when measured. The enumeration of families in the United States census asked that individuals be returned where they were normally resident. Thus older siblings temporarily away from home on census night should be recorded in the census. Our measure of sibling order will differ from the true early-life environment when there is a large age gap between the measured children (aged 0–6 in 1918) and a significantly older sibling who left home before the 1920 census. We identify multiple-births as individuals in the same household who share a common exact age and parent. Just 0.7% of the surveyed children matched to the census were part of a multiple birth. We conduct parallel analyses of the influence of family structure on both height and weight for age.

We then add additional measures of family composition that distinguish between different types of co-resident children in the household. We identify separately the effect of siblings who were also measured in the survey, and are thus close in age to the individual child. By definition these children are also young, below school-age and at a rapid point in their growth curve. They may thus be more competitive for resources and attention with similar children in the family. We measure the number of children aged 0–12 who were not measured in the 1918 survey in another variable. Like the subjects of the 1918 survey these children are too young to work, and thus are potentially competitive for resources with the measured children. We measure the number of teenagers in the household separately, and distinguish in two different variables between teenagers who are working and those who do not indicate an occupation. Teenagers, being at least 7 years older than the measured children, may not compete for parental attention and resources in the same way as children of the same age. Yet teenagers are also going through a growth spurt of their own, and thus place demands on household resources. However, teenagers in this era were also potentially in the labor force. In our sample 38% of teenage siblings reported an occupation, compared to 3% of the mothers of surveyed children. Teenage employment has potentially offsetting effects on the welfare of young children. By bringing additional income into the household it eases the force of resource dilution. However, as Carolyn Moehling has shown for the same time period, teenage employment also gave teenagers bargaining power over family expenditure decisions (Moehling, 2005). The net effect of these influences is ambiguous in our data where we lack information on family expenditures.

In our full models we also include variables that describe the household’s social class and background to address the question of potential family resources. The three variables we can construct for all households are the occupation of the head of household, a dummy variable for owning or renting the house, and the migration status of the household head. We differentiate between migrants from abroad and out-of-state, and compare them to heads born in Minnesota. Following common practice in this literature, we exclude from all estimates children whose height or weight placed them 6 or more standard deviations from modern growth standards (Vidmar, Cole, & Pan, 2013).

6.2 Results

Like Hatton and Martin (2010) we observe a negative gradient in mean height-for-age across birth order. But unlike them, we find that this association is maintained in a family fixed-effects regression with no additional controls, suggesting that birth order has an effect that is distinct from the characteristics of families with higher birth order children (Table 4). Adding additional controls increases the size of this effect in specifications that exclude infants due to our concerns about selection and measurement error. In specifications that include infants each additional birth order reduces stature by 0.035 standard deviations, similar to the naïve estimate suggested by the gradient in mean height across birth order (Table A1). In a model estimated on children 2–6, and thus closer to the Boyd-Orr estimates the effect of a higher birth order is a 0.06 decline in stature. Recalling that 90% of children were in households of 6 or fewer children, the impact of birth order is such that a sixth born child will average 0.2 to 0.3 standard deviations shorter at a given age than her first-born sibling. At age 5 this makes the sixth-born child 1cm shorter than their first-born sibling all else being equal.

Table 4.

Birth order and childhood stature: Family fixed-effects regression with no additional controls

Sample restriction	Birth order co-efficient	z
All children (no restriction on n. measured kids)	−0.042	−5.17
Excluding infants	−0.068	−8.33
Children 2 and over	−0.078	−9.08
Children in households with > 1 measured child	−0.033	−2.69
Excluding infants	−0.078	−6.33
Children 2 and over	−0.093	−7.20

Table A1.

Family fixed effects regressions for height and weight for age

	Height for age		Weight for age
	All children > 1 child in family		All children > 1 child in family
Sibling order	−0.039	−0.034	−0.028	−0.035
	−3.703	−2.351	−3.314	−3.134
First born	0.050	0.292	0.011	0.162
	1.300	4.900	0.345	3.435
Female	0.041	0.111	−0.004	0.013
	1.426	2.575	−0.153	0.374
Multiple birth	−0.527	−0.505	−0.299	−0.29
	−2.870	−2.716	−1.965	−1.965
Age (years)	−0.075	−0.096	−0.154	−0.171
	−7.885	−6.402	−19.825	−14.319
Infant	0.685	0.914	−0.294	−0.007
	11.967	9.991	−6.426	−0.093
Constant	−0.505	−0.600	0.067	0.068
	−9.652	−7.802	1.599	1.133
N	8908	3848	9297	4025
R2
Within	0.075	0.052	0.064	0.080
Between	0.037	0.009	0.037	0.042
Overall	0.043	0.013	0.040	0.054

Note: Cells contain co-efficient estimates and t-statistics

Although we estimate the same model as Hatton and Martin, our estimates may differ from theirs for several reasons. First, the support of our distribution differs: we only observe children between the ages of 0 and 6. If disadvantage for later-born children continues to accumulate this would be consistent with a larger effect of birth order observed in the Boyd-Orr sample. Second, our sample is closer to a general population sample and the estimates reflect that we have higher-order children from better off households. The fifth child of a lawyer is likely to suffer less than the fifth child of a janitor, attenuating the population-wide impact of birth order.

We also observe that without additional controls the effect of birth order on weight-for-age and BMI-for-age is positive, reflecting that higher-order children tend to have higher birth weights. When we control for the same additional factors as in Table 5 (gender, multiple birth status, and age in years) we find that birth order has a negative effect on weight for age. Our estimate is very stable across 1–6 and 2–6 year olds, whether measured alone or with other children in the family also measured. We estimate that each additional birth order reduces weight-for-age norms by 0.028 – 0.036 standard deviations, with estimates statistically significant at the 0.1% level (Table A1). As these estimates are close to those estimated for height-for-age reductions with increases in birth order, the impact of birth order on BMI is small in magnitude, and cannot be distinguished from 0. Thus, like Hatton and Martin we find that the effect of family structure on children’s growth is found in stature, and not in BMI.

Table 5.

Birth order and childhood stature: Family fixed effects regression controlling for first born, sex, multiple birth, age in years

Sample restriction	Birth order co-efficient	z
All children (no restriction on n. measured kids)	−0.039	−3.68
Infants included, with dummy variable	−0.039	−3.65
Excluding infants	−0.048	−4.61
Children 2 and over	−0.060	−.4.61
Children in households with > 1 measured child	−0.035	−2.35
Infants included, with dummy variable	−0.036	−2.49
Excluding infants	−0.036	−2.38
Children 2 and over	−0.045	−5.30

We integrate our analyses of birth order, family size and social class in a series of regressions for children’s height-for-age. Following Booth and Kee we also re-formulate our measure of sibling order in a sibling order index (Booth & Kee, 2009). The sibling order index is the ratio of the child’s own birth order (or sibling order in our data) to the average sibling order in the family. By construction it averages 1.0 within a family, and across families. A useful property of the index is that the same unit shift in birth order in a small family will change the index more than in a large family. In a family of 5 the average birth order is 3, and the second child’s index is 0.66 (2/3) while the last child’s is 1.66 (5/3). By contrast in a family of 10 the average birth order is 5.5, and the second child’s index is 0.36 (2/5.5) while the fifth child’s index value is 0.9 (5/5.5). Thus in a larger family there is a smaller change in the index for the same shift in sibling order.

Our sibling order index averages 1.16 across the sample, reflecting the fact that we have a sample of young children whose birth order is likely to be higher. The purpose of the birth order index is to purge birth order of some of its correlation with family size. In our sample the correlation of sibling order with family size is 0.82, whereas the birth order index has a correlation of only 0.28 with family size. Again this reflects the fact that our sample is, by design, of young children and there is less variation in sibling order than in a sample of children of all ages. In families that only include young children the sibling orders will all be low (95% of our sample were in households with 1 or 2 measured children). By contrast in families with older—unmeasured in the 1918 survey—children the sibling orders for younger children measured in the survey will all be high. Thus mechanically our measured sample includes a wide range of sibling orders, but the variation is constrained.

Our first full estimate of the impact of sibling order and family size retains a linear specification for sibling order. As discussed above we control for family composition, migration and occupational status of the head, and home ownership. Including these controls reduces the impact of sibling order in a model including all children to a reduction of 0.026 standard deviations (Table A2). However the effect is noticeably stronger for children aged 2–6, consistent with the growth faltering observed in unconditional means for height-for-age. Young children, both 0–6 also measured in the survey and unmeasured siblings, had a negative impact on an individual child’s stature, by approximately −0.04 standard deviations. For families with closely spaced children it would be possible to have 5–6 pre-teen children, and the impact on each child’s stature would be significant, with a combined impact of approximately −0.25 standard deviations. This is consistent with the resource dilution hypothesis. Older children, whether working or not, had small positive impacts on young children’s stature, suggesting that on balance teenagers benefited their younger siblings. We also observed a cohort effect, with children born early in the 1910s shorter for their age than their peers born during World War I. This is a somewhat surprising result, given the concerns motivating the survey but consistent with evidence of plentiful access to food in the Midwest and improving nutrition in this era. Occupational effects remained strong with the children of blue collar workers significantly shorter. Again this is consistent with the resource dilution hypothesis.

Table A2.

Family fixed effects regressions for height for age with linear measure of sibling order

	Height for age
	All children	Children 2–6 years
Sibling order (integer)	−0.026	−0.074
	−1.436	−3.655
First born	0.034	0.064
	0.843	1.483
Numbers of classes of children in household
Other surveyed children	−0.049	−0.072
	−2.077	−3.176
Unmeasured children 0–12	−0.039	−0.030
	−2.485	−1.933
Working teenagers	0.007	0.064
	0.176	1.644
Non-working teenagers	0.034	0.082
	1.016	2.402
Female	0.04	−0.035
	1.385	−1.152
Multiple birth	−0.53	−0.444
	−2.885	−2.400
Age (years)	−0.074	−0.047
	−7.414	−3.407
Infant	0.684
	12.003
Nativity of household head
Head born in Minnesota (reference)
Head born elsewhere in U.S.	0.032	0.080
	0.756	1.825
Head born abroad	−0.045	−0.099
	−1.221	−2.631
Occupation of household head
Professionals, managers, owners (including farm): Reference
Clerical, sales and service	−0.172	−0.207
	−3.351	−3.877
Tradesmen and operatives	−0.207	−0.241
	−4.964	−5.633
Laborers and unclassifiable occupations	−0.414	−0.425
	−7.029	−7.074
No occupation/out of labor force	−0.341	−0.388
	−4.781	−5.297
Renting household	−0.087	−0.093
	−2.726	−2.795
Constant	−0.228	−0.163
	−3.282	−1.914
N	8908	5678
R2
Within	0.072	0.042
Between	0.048	0.041
Overall	0.055	0.045

Note: Cells contain co-efficient estimates and t-statistics

Turning to the models with the sibling order index instead of the linear specification, we find generally similar results for the variable describing family composition, migration, and socio-economic status (Table A3). The effect of sibling order remains significant in these models, with a co-efficient of −0.07 to −0.15 depending on specification and exclusion restrictions. In results not reported for children aged 1–6 the coefficient on the sibling order index was −0.11, intermediate between the estimates for 0–6 and 2–6 year olds. The interpretation of the sibling order index may be made more concrete by example. For a child in a family of 3, moving from being first born to third born changes the birth order index by 1 unit (0.5 to 1.5) with the co-efficient implying that stature will fall 0.11 to 0.15 standard deviations. Compare with the estimate from Table 5 that implied that a change in birth order of 2 units would decrease stature by 0.07 to 0.12 standard deviations. For the third child in a family of five, a move to being the fifth child increases the birth order index by 0.66, implying a fall in stature of 0.07 to 0.10 standard deviations. Again, this is very similar to the magnitudes suggested in Table 5. The robustness of the estimates to adding additional controls for socio-economic status and family size, and changing the functional form of the birth order variable are reassuring.

Table A3.

Family fixed effects regressions for height for age including sibling order index

	Height for age
	All children	Children 2–6 years
Sibling order index	−0.073	−0.155
	−1.486	−3.000
First born	0.016	0.046
	0.341	0.932
Numbers of classes of children in household
Other surveyed children	−0.067	−0.111
	−2.760	−4.582
Unmeasured children 0–12	−0.057	−0.076
	−4.444	−5.604
Working teenagers	−0.004	0.023
	−0.102	0.672
Non-working teenagers	0.016	0.027
	0.581	0.994
Female	0.040	−0.035
	1.392	−1.149
Multiple birth	−0.535	−0.467
	−2.916	−2.527
Age (years)	−0.073	−0.043
	−7.421	−3.131
Infant	0.686
	12.037
Nativity of household head
Head born in Minnesota (reference)
Head born elsewhere in U.S.	0.033	0.083
	0.786	1.902
Head born abroad	−0.044	−0.097
	−1.196	−2.594
Occupation of household head
Professionals, managers, owners (including farm): Reference
Clerical, sales and service	−0.172	−0.208
	−3.357	−3.898
Tradesmen and operatives	−0.207	−0.241
	−4.973	−5.648
Laborers and unclassifiable occupations	−0.414	−0.427
	−7.038	−7.104
No occupation/out of labor force	−0.338	−0.383
	−4.732	−5.219
Renting household	−0.088	−0.093
	−2.752	−2.800
Constant	−0.167	−0.074
	−1.714	−0.675
N	8908	5678
R2
Within	0.072	0.042
Between	0.048	0.040
Overall	0.055	0.044

We decomposed family size into plausibly different influences. Teenagers, whether working or not, have little effect on the stature of their younger siblings measured in this survey. However, there are strong effects of additional young children in the household that are in addition to any effects of birth order. Having another sibling measured in the survey decreased stature for the measured child by 0.07 standard deviations, while other pre-teen children reduced stature by 0.06 to 0.08 standard deviations. It is important to note that these effects are in addition to any that come through the sibling order index, and together suggest that higher order children in large families were likely to have been significantly shorter than their peers from smaller families. Family size is likely to affect stature in two ways: resource-dilution and crowding (Hatton, 2016). The 1920 census is unfortunately silent on both these questions containing no measures of dwelling size, income or unemployment. Thus our estimate of the effects of family size is a net one, combining the effect of crowding and the resource dilution that occurs as a given family income is shared among more children. While we cannot measure this directly without measures of income or unemployment, the small impact of teenage siblings on young children’s stature suggests that resource dilution may be attenuated by spacing and distance in age from competing siblings (Barclay & Myrskylä, 2014).

The children of domestic migrants were notably taller than the children of their Minnesota born peers, likely reflecting a positive selection effect among migrants. The children of foreign-born men were shorter by about the same extent, 0.10 of a standard deviation. Finally the regressions confirm the significant effects of social class that were observed in the unconditional means. Compared to the children of professionals, the children of white-collar workers and tradesmen were about 0.2 standard deviations shorter. Laborers’ children were another 0.2 standard deviations shorter again. The size of these coefficients on occupations are marginally less than the observed difference in means, showing that some of the class differences are the result of differences in family size and structure. When we interact with the birth order index and indicators of migration, we find no large differential effects of birth order in any subgroup. A final measure of family resources is whether a household owned or rented their dwelling. In the samples of 1–6 and 2–6 year olds we observe a significant negative effect of living in a rented dwelling on height-for-age, of 0.07 to 0.08 standard deviations. Taken together, our estimates imply that family structure and social class influences on stature for age were compounding rather than offsetting. Higher order children from lower social classes in large families were significantly shorter than their similarly aged peers in smaller and better off families.

We find similarly significant effects of family composition and sibling order on weight-for-age, with coefficients of similar magnitude and orientation to those in the corresponding regressions of stature for age (Table A4). Because of the similar magnitudes in height and weight-for-age, the impact on BMI of many variables is modest and statistically insignificant.

Table A4.

Family fixed effects regressions for weight for age including sibling order index

	Weight for age
	All children	Children 2–6 years
Sibling order index	−0.035	−0.076
	−0.869	−1.84
First born	−0.004	0.024
	−0.106	0.624
Female	−0.004	−0.066
	−0.159	−2.715
Numbers of classes of children in household
Other surveyed children	−0.019	−0.053
	−0.977	−2.669
Unmeasured children 0–12	−0.052	−0.049
	−4.963	−4.497
Working teenagers	0.013	0.024
	0.453	0.861
Non-working teenagers	0.001	0.001
	0.029	0.028
Multiple birth	−0.328	−0.416
	−2.145	−2.699
Age (years)	−0.151	−0.166
	−18.997	−15.749
Infant	−0.295
	−6.459
Nativity of household head
Head born in Minnesota (reference)
Head born elsewhere in U.S.	−0.004	0.055
	−0.107	1.542
Head born abroad	−0.004	−0.063
	−0.149	−2.058
Occupation of household head
Professionals, managers, owners (including farm): Reference
Clerical, sales and service	−0.103	−0.156
	−2.456	−3.629
Tradesmen and operatives	−0.138	−0.198
	−4.04	−5.724
Laborers and unclassifiable occupations	−0.209	−0.234
	−4.352	−4.791
No occupation/out of labor force	−0.242	−0.178
	−4.141	−3.001
Renting household	−0.037	−0.023
	−1.431	−0.864
Constant	0.251	0.441
	3.182	5.04
N	9297	5872
R2
Within	0.062	0.049
Between	0.043	0.064
Overall	0.047	0.066

7. Conclusion

In a general population sample of early twentieth century urban American children that closely matches the population of children in the city it was take we observe significant differences in stature for age by social class and family structure. We began the paper by identifying a pattern of “growth faltering”—that height-for-age and [to a lesser extent] weight-for-age scores of children in 1918 declined as children aged. Put simply, toddlers in 1918 Saint Paul were closer to their modern peers than pre-school children. This finding is consistent with the quality-quantity trade-off that as parents have more children, they are able to invest slightly less in each individual child. Height is an important indicator of these trade-offs because unlike schooling it is not regulated—there are no requirements to have your child attain a certain height—and reflects the accretion of literally thousands of parental decisions about how much to feed children across their growth period.

The pattern of slightly taller toddlers compared to pre-schoolers is consistent with what we know about both the childhood growth pattern, and birth intervals in early twentieth century families. The velocity of growth is rapid in the first two years of life, and then slows gradually before increasing again in the teenage years (Bogin, 1999). Birth spacing in the early twentieth century before the widespread availability of reliable contraception was shorter than in the modern United States. A contemporary study of families in Gary, Indiana found that 56% of all second or higher-order births occurred less than 24 months after the preceding birth (Hughes, 1923). In the modern United States the median interval between births is over three years (Copen, Thoma, & Kirmeyer, 2015). Thus many young children in early twentieth century families were competing for resources and parental attention with newly arrived infant siblings, whose needs appear to have taken priority.

We can make an estimate of the effect of changing family size and birth order on the growth of children’s stature by simulating how average stature would have changed if children in 1918 had come from families of modern size. Recall that we found our children to average 0.72 standard deviations below modern height-for-age scores. By definition, this overall mean is the linear combination of sibling-order specific mean stature-for-age weighted by the distribution of sibling order. Re-weighting these means by the modern distribution of birth-order for urban American children does not substantially change the estimates. The effect is to increase mean height-for-age Z-scores by 0.04 standard deviations (Table 6). A similar calculation reweighting the distribution of sibship size by modern means increases mean height-for-age Z-scores by 0.08 standard deviations. Taken together these imply at least a modest positive effect of declining fertility on childhood nutrition of 0.12 standard deviations. Another way to estimate of the effect of declining fertility on stature is to apply mean sibship size for young children to the regression models in Table A2. In 1920 children aged 0–6 had an average of 2.5 own siblings in their household, compared to an average of 1.25 for similarly-aged children in the United States since 2000; a decline of 1.25 siblings (Ruggles et al, 2015). Assuming none of these siblings are teenagers the coefficients in Table A2 suggest declining sibship size would increase stature by 0.05 to 0.10 standard deviations, or half a centimetre at age 5. These are conservative calculations, and abstract from the benefits that would accrue to children from less crowding and improved per-capita income in smaller households.

Table 6.

Sibling order and childhood stature: Effect of imposing modern birth order distribution on Saint Paul data

Sibling order	Saint Paul, 1918	2010–2014 urban U.S.	Mean Height Z-score	Mean Z score weighted by
				1918	2010–2014
1	0.370	0.523	−0.640	−0.237	−0.334
2	0.250	0.312	−0.694	−0.173	−0.216
3	0.151	0.112	−0.755	−0.114	−0.085
4	0.092	0.036	−0.776	−0.072	−0.028
5	0.053	0.011	−0.962	−0.051	−0.011
6	0.035	0.004	−0.918	−0.032	−0.004
7	0.023	0.002	−1.006	−0.023	−0.002
8	0.013	0.001	−0.999	−0.013	−0.001
9	0.007	0.000	−0.950	−0.007	0.000
10	0.003	0.000	−0.582	−0.002	0.000
11	0.001	0.000	−0.387	0.000	0.000
12	0.001	0.000	−0.312	0.000	0.000
13	0.001	0.000	−0.457	0.000	0.000
14	0.000	0.000	−2.179	−0.001	0.000
Height-for-age Z-score mean				−0.724	−0.680

Improved stature was not the only consequence of declining fertility, as stature itself impacts life chances. Our estimates of the effect of family size and birth order are stable across different specifications of the model, and different measures of birth order. Our estimates imply that the first and second born children of professionals and managers would average 0.75 to 1 standard deviations taller than the later-born children of laborers. Assuming these differentials persist into adulthood the gap in stature between the early-born to professionals and later-born to laborers would be on the order of 6–8cm. The social consequences of reduced stature are not as visible at this age, and we plan to extend our linked sample to the 1930 and 1940 censuses to investigate this question further. In 1930, many of the children will be on the margins of school attendance, able to decide or not whether to continue their high school education. In 1940, boys in the sample will be in early adulthood, and we can obtain measures of salary and wages from the census.

We can use estimates from various related literatures to suggest the rough magnitude of the future effects of large social class differences in stature. The international literature from developing countries suggests that a 1 standard deviation decrease in stature is associated with a reduction in completed schooling of around six months. These can be paired with estimates of the returns to an additional year of education, which were around 10% in this era. Put together with our estimates these figures imply that earnings for shorter children from poorer (laborers) families might have been 2.5–5% lower owing to the effects of reduced stature, depending on family size. These are important effects, suggesting how the life chances of children in different families differed depending on the resources a family was able to provide, and the competition with other family members for resources.

Our estimates of these magnitudes relies on international estimates of how stature affects schooling, because there are few modern studies of the social correlates of children’s stature in the United States. This alone suggests important changes in how children’s growth is understood and measured between the early twentieth century and today. At the beginning of the twentieth century social class and familial differences in stature were large, and the subject of significant social investigation. In the late twentieth and early twenty-first century there are no publications that examine the social correlates of children’s stature. The object of concern in children’s nutrition is now weight and BMI, a significant contrast to early twentieth century Saint Paul where BMI did not differ significantly among children of different social classes. Social variations in nutrition remain important, but the dimensions have changed in many important respects.

Figure 13.

Household heads’ occupation and mean stature for age Z scores in Saint Paul, 1918.