Practical implementation of Channelized Hotelling Observers: Effect of ROI size

Abstract

Fundamental to the development and application of channelized Hotelling observer (CHO) models is the selection of the region of interest (ROI) to evaluate. For assessment of medical imaging systems, reducing the ROI size can be advantageous. Smaller ROIs enable a greater concentration of interrogable objects in a single phantom image, thereby providing more information from a set of images and reducing the overall image acquisition burden. Additionally, smaller ROIs may promote better assessment of clinical patient images as different patient anatomies present different ROI constraints. To this end, we investigated the minimum ROI size that does not compromise the performance of the CHO model. In this study, we evaluated both simulated images and phantom CT images to identify the minimum ROI size that resulted in an accurate figure of merit (FOM) of the CHO’s performance. More specifically, the minimum ROI size was evaluated as a function of the following: number of channels, spatial frequency and number of rotations of the Gabor filters, size and contrast of the object, and magnitude of the image noise. Results demonstrate that a minimum ROI size exists below which the CHO’s performance is grossly inaccurate. The minimum ROI size is shown to increase with number of channels and be dictated by truncation of lower frequency filters. We developed a model to estimate the minimum ROI size as a parameterized function of the number of orientations and spatial frequencies of the Gabor filters, providing a guide for investigators to appropriately select parameters for model observer studies.

1. INTRODUCTION

Observer models are a popular and powerful way to predict the diagnostic performance of human readers in a number of medical imaging modalities. Compared to human observers, these models are more time-efficient and provide an objective measure of image quality [1, 2]. For this reason their use has been increasingly investigated to guide optimization tasks. Channelized Hotelling observers (CHO) are among the most investigated models owing to their demonstrated good correlation with human performance results [3-5]. CHO models require the acquisition of large datasets to appropriately estimate image statistics, which is particularly burdensome for CT applications [6]. Additionally, CHO models are developed for and applied to specific imaging tasks (i.e. detection of objects of different sizes and contrast) and numerous samples are required for each specific task. Thus, acquiring images of phantoms with high concentrations of objects can provide data for a wide range of clinical tasks with fewer image acquisitions (Figure 1 (a)). However, this strategy constrains the ROI size surrounding an investigated object, and therefore, it is necessary to understand the effect of ROI size on the performance of the CHO model as well as to investigate appropriate mitigation strategies.

Figure 1.

(a) CT image quality insert phantom with high concentration of interrogable objects, designed for observer model studies to maximize image quality assessment for a set of acquired CT images. The phantom diameter is ~10 cm. (b) The phantom used for the experimental study. The largest ROI size that can be used for each object is approximately 1.5 cm in diameter, resulting in an ROI size of 20 or fewer pixels for reconstructed FOV larger than 35 cm.

2. METHODS

2.1 Design and assumptions of CHO model

In this study, we used Gabor filters to channelize images for the CHO model. Gabor filters have been shown to provide an effective representation of the human visual system [7]. The general form of the Gabor function can be expressed as

$$G(f)=\text{exp}[-4(\mathit{ln}2)\left({(x-x_0)}^2+\frac{{(y-y_0)}^2}{{{\omega }_s}^2}\right]\cos [2\pi f_c((x-x_0)\mathit{cos}\theta +(y-y_0)\mathit{sin}\theta )+\beta ]$$ (eq. 1)

where ω_s is the channel width, f_c the central frequency (both in cycles per pixels), θ the orientation angle and β a phase offset.

In this study, unless otherwise specified, the following Gabor filter parameters were used to channelize the images:

• a)5 frequency passbands, with center frequencies $f_c=\frac{3}{256},\frac{3}{128},\frac{3}{64},\frac{3}{32},\frac{3}{16}$ and widths ω_s= 112.96,56.48,28.24,14.12,7.06;
• b)4 orientations: $\theta =0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{4}$;
• c)1 phase β = 0.

Thus a total of 20 channels were used in our reference CHO implementation. The channel selection was similar to other seminal works in the literature and this model was validated with human observer data [4, 8].

The figure of merit (FOM) chosen to assess the performance of the CHO was the detectability index, d’, computed as the difference between the means of the signal present (tS0) and absent (tN0) test statistic distributions, respectively, divided by the quadratic mean of the standard deviations of the two distributions: $d^{\prime }=\frac{\overline{t_{S0}}-\overline{t_{N0}}}{\sqrt{\frac{1}{2}({{\sigma }_{t_{S0}}}^2+{{\sigma }_{t_{N0}}}^2)}}$.

2.2 Experimental setup

Four 2.5 cm diameter cylinders, which contained eight concentric 5-cm long cylindrical objects of different dimensions (3, 6 and 9 mm diameter) and contrast relative to background (10, 15 and 45 HU) were inserted into an anthropomorphic abdominal phantom representing a small adult (24 cm lateral dimension) (Figure 1 (b)). The phantom was scanned 60 times at the clinical dose level in our practice) on a 192-slice CT scanner (Somatom Force, Siemens Healthcare). Images were reconstructed with different fields-of-view (FOV) ranging from 15 to 55 cm and the largest possible square-shaped region of interest (ROI) inscribed within each insert was used (~1.5 cm linear dimension). For each configuration, 180 signal-present and signal-absent images (3 images/scan) were used to determine the d’ for the object.

2.3 Simulation setup

In order to have greater flexibility and control of the parameter space in the investigation, we set up simple simulations to probe the potential factors that influence the minimum ROI size resulting in an accurate figure of merit (FOM) of the CHO’s performance. Two-dimensional images (1 mm pixels, 10 cm FOV unless otherwise specified) were created by adding a circular object (default: 10 mm diameter) to Gaussian noise and 10,000 samples were generated for each configuration investigated. Each image was progressively cropped to reduce the ROI size and then channelized with the selected Gabor filters (cropped to match the image ROI). Subsequently, d’ for the CHO model was computed from the set of channelized images. Several different configurations were evaluated: (1) object size: 5-20 pixel diameter; (2) magnitude and correlation of image noise; (3) number of channels: interleaving up to 5 additional spatial frequencies and an additional 4 orientations, as well as removing intermediate frequencies or orientations from the base channels; and (4) selection of spatial frequencies: base frequencies were scaled by [0.5, 1.5, 2, 2.5, 3, 4] and implemented with 8 orientations and 1 phase (40 total channels).

2.4 Parametric model of ROI failure and mitigation strategies

Once the existence of a minimum ROI size was identified below which the CHO’s performance is grossly inaccurate, the parameters that were shown to influence the failure point were combined in a parametric model.

Finally, we investigated possible mitigation strategies that that could yield uncompromised FOMs under certain experimental circumstances:

- ROI interpolation: starting with initial images cropped below the ROI failure point (20 pixels in linear dimension with our default Gabor configuration), we interpolated them to increase their linear dimension, channelize with appropriately scaled Gabor frequencies to reflect the fact that such interpolated data would still appear on the observer’s monitor as having the same physical size, and computed the SNR for the CHO model as for previous studies

- ROI padding: we investigated the effect of artificially increasing the ROI size by padding it with different patterns, from uniform values to random background signal of different magnitude. All padded ROIs had a linear dimension of 100 pixels.

3. RESULTS

3.1 Experiments

In Figure 2, we plot the d’ for the 8 objects (one curve for each) as a function of the number of pixels (linear dimension) in the ROI for a given FOV. Regardless of the object’s native d’, there is a failure point in CHO performance when the ROI is smaller than approximately 20×20 pixels, corresponding in our case to an image reconstructed FOV larger than 35 cm - considering the 1.5×1.5 cm² physical size constraint of the ROI.

Figure 2.

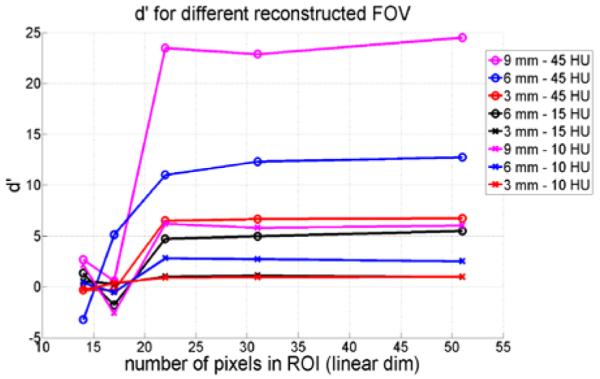
d’ vs number of pixels in ROI for different objects – experimental CT data

3.2 Simulations

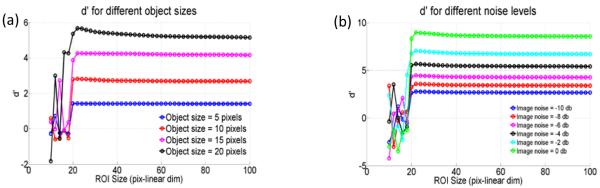
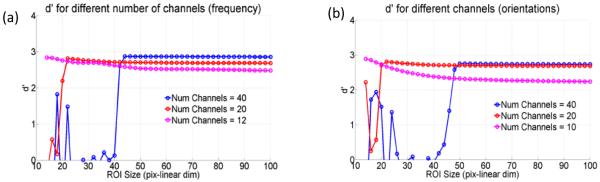
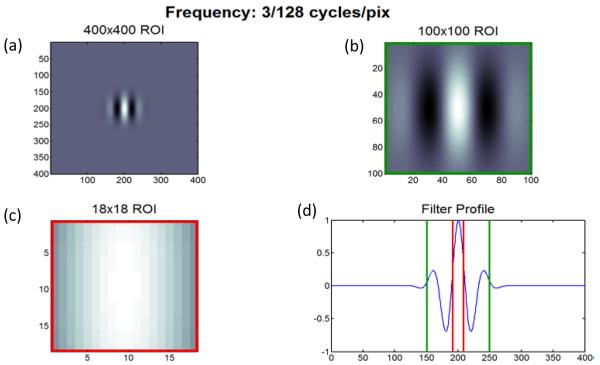
Of the parameters we investigated, size of the object, as well as magnitude and correlation of the simulated noise showed no significant influence on the minimum ROI size, as shown in Figure 3. In Figure 4, we plot the d’ as a function of ROI size for different number of frequency channels (Fig. 4(a)) and orientations (Fig. 4(b)). The data show that both parameters significantly shift the minimum ROI size required to achieve acceptable CHO performance. In Figure 5(a-d), we show how a given Gabor filter is truncated as the ROI size is reduced. Lower frequency Gabor filters suffer more truncation for a given ROI size, which in turns leads to failure of the CHO’s performance. This interpretation is supported by the plot in Figure 6, where we plot the d’ as a function of ROI size for sets of progressively higher spatial frequencies. The number of rotations was chosen to be 8 for all sets, for a total number of 40 Gabor filters. Data in Figure 6 indicate that the failure in the CHO’s performance observed at a given ROI size can be avoided if the lowest Gabor frequencies are removed. However, note that removing the lowest spatial frequencies may invalidate the CHO depending on the imaging task and the objectives of the model. The selection of the most appropriate set of channel filters for the CHO model is beyond the scope of this investigation.

Figure 3.

Plots of d' vs ROI size (a) for different object sizes and (b) for different noise levels. No significant influence of these parameters on the minimum ROI size is seen.

Figure 4.

Plots of d’ vs ROI size (a) for different number of spatial frequencies and (b) for different number of orientations.

Figure 5.

(a-c) Image of the lowest frequency Gabor filter (0° orientation) for different ROI sizes (a) 400×400 (b) 100×100, and (c) 18×18 pixels². (d) Plot of profile through the center of the filter showing the points of truncation for (b)(green line) and (c)(red line).

Figure 6.

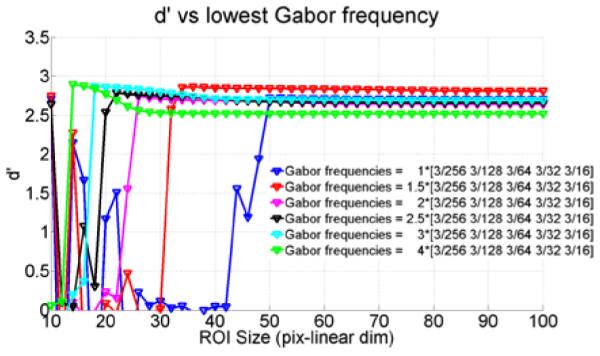
Plot of SNR d’ vs ROI size for different sets of spatial frequencies.

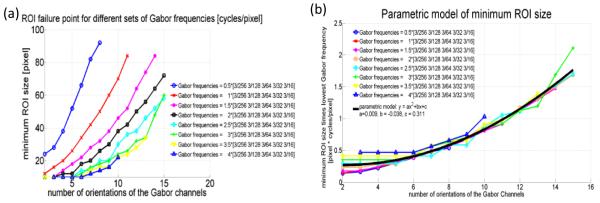
3.3 Parametric model of minimum ROI size

In figure 7(a) we show the minimum ROI necessary to avoid the failure of the CHO model for a given sets of Gabor filter frequencies and as a function of number of orientations of the Gabor filters. In Figure 7(b), we scale each curve by the lowest spatial frequency in the channel set and derive a parametric model that fits the average of all sets. The minimum ROI size required to avoid failure of the CHO model induced by truncating the lowest spatial frequency Gabor filters can therefore be expressed as:

$$\text{min}\mathit{ROI}(f_{c1},N_{\mathit{rot}})=\frac{0.009{N_{\mathit{rot}}}^2-0.038N_{\mathit{rot}}+0.311}{f_{c1}}$$

where f_c1 is the lowest spatial frequency and N_rot the number of orientations of the Gabor channels used in the CHO model, respectively. Note, this parametric model was derived for sets of Gabor filters with harmonic spatial frequencies, i.e. the 2^nd lowest spatial frequency is 2 times higher than the lowest spatial frequency. If the 2^nd lowest spatial frequency is less than 2 times higher than the lowest spatial frequency, this parametric model may need to be modified to accurately predict the minimum ROI size. The proposed parametric model is derived from empirical observations that the cropping of the Gabor filters as well as the number of orientations used in the Gabor filter set have a profound impact on the CHO performance for small ROIs. The fundamental mechanism behind the sudden failure of the CHO model when the chosen ROI size is below a certain threshold is not yet fully understood. However, the proposed parametric model provides an easy guide for investigators to appropriately select parameters for model observer studies.

Figure 7.

(a) Plot of minimum ROI size vs number of orientations. (b) Plot of normalized minimum ROI size vs number of orientations, and curve fit of data for the parametric model.

3.4 Mitigation strategies

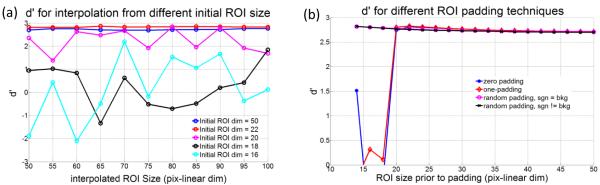
In Figure 8(a), we show that interpolating from an initial ROI that would cause a failure of the CHO model – with the default set of Gabor channels we used, that failure point resulted in 20 pixels in linear dimension for the ROI – is not an effective method to restore the CHO performance. Regardless of the final interpolated ROI size, if the initial ROI size is below the failure point and the Gabor channels are scaled during interpolation to model an observer that is not allowed to zoom in to the image, the amount of cropping of the Gabor channels is not reduced by the interpolation process and therefore the performance of the CHO performance does not improve.

Figure 8.

Investigation of different mitigation strategies. (a) Effect of interpolation of ROIs of different linear dimension prior to channelization. (b) Effect of different padding to the cropped ROI.

Conversely, Figure 8(b) shows that padding the initial ROI seems to be an effective strategy, provided the padding does not consist of a single value (i.e. zero or one padding). Padding an ROI that was too small to yield a sensible metric of the CHO model with background values, so that the final ROI size is above the failure point of the chosen set of Gabor channels as expressed by the parametric model in Equation 2, restores the performance of the CHO model, as the amount of cropping of the Gabor channels is now reduced.

4. CONCLUSIONS

Results from this investigation demonstrate that there exists a limit in the amount an ROI can be reduced and still effectively interrogated by a CHO. Moreover, the size of the ROI becomes a critical parameter near this limit; there exists a minimum ROI size below which a CHO will fail to yield an accurate FOM for a given task. This minimum ROI size is shown to be a fundamental aspect of CHO model for images that are channelized with Gabor filters. For ROI sizes above the minimum size threshold, CHO results are largely unaffected. Lastly, for CHO models in which the input images are channelized with a set of Gabor spatial frequencies such that the lowest frequency is at least half of the 2^nd lowest frequency, the minimum ROI size can be predicted with a parametric model.

These results could be useful in designing phantom-based image quality assessment where it is advantageous to include as many clinically representative objects as possible to simultaneously investigate numerous clinical imaging tasks (and thereby reduce the overall image acquisition burden). Additionally, as CHO models are applied to clinical patient images, different patient anatomies will constrain the selection of the ROI, and therefore it is necessary to understand the impact of this parameter on the derived CHO FOMs.